专题复习七:动态问题(一)
动点问题(等腰三角形问题)

中考数学专题复习研动点问题探究——等腰三角形分类讨论问题图形中的点、线的运动,构成了数学中的一个新问题——动态问题。
它通常分为三种类型:动点问题、动线问题、动形问题。
题型特点:此类问题常集代数、几何知识于一体,数形结合,有很强的综合性。
是河南中招的必考题,且每年都为压轴题,以函数与三角形和四边形结合的题目为主。
如08年为一次函数与三角形相结合,09年为二次函数与等腰三角形相结合,10年为二次函数与平行四边形相结合。
学情分析:1、这类问题无论教师做了多大的努力,对学生来说都比较困难,所以一部分学生放弃作答。
2、一部分学生对动点问题从根本上不理解,勉强照猫画虎,写了不少但不得分。
3、学生对动点问题有一定认识,对分类能进行简单尝试, 但不完整。
教学方法:1、教师在教学时引导学生把动态问题变为静态问题来解,抓住变化中的“不变量” 。
并从特殊位置点着手确定自变量取值范围, 对基本图形进行充分的分析,画出符合条件的各种草图分散难点、降低难度,将复杂问题简单化。
2、专题化,少而精。
如动点问题有等腰三角形、直角三角形、三角形相似、 四边形存在性等问题,这些都需分类讨论,分小专题复习效果更好。
本节课重点来探究动态几何中的第一类型:动点问题——等腰三角形分类讨论问题(一)自主解决(设计意图:为重点研讨作下铺垫)1、在平面直角坐标系中,已知点P (-2,-1).点T (t ,0)是x 轴上的一个动点。
当t 取何值时,△TOP 是等腰三角形?情况一:OP=OT 情况二:PO=PT T3(-4,0)情况三:TO=TP设计意图:引导学生总结以已知线段为边作等腰三角形时,通常要分三种情况讨论:以已知线段为底或为腰。
且以已知线段为腰时,以该腰不同顶点为顶角顶点有两种情况。
2、如图:已知平行四边形ABCD 中,AB=7,BC=4,∠A=30°)0,5();0,5(21T T -)0,45(4-T(1)点P 从点A 沿AB 边向点B 运动,速度为1cm/s.若设运动时间为t(s),连接PC,当t 为何值时,△PBC 为等腰三角形?若△PBC 为等腰三角形则PB=BC∴t=3(二)师生互动,探究新知如图:已知平行四边形ABCD 中,AB=7,BC=4,∠A=30°(2)若点P 从点A 沿 射线AB 运动,速度仍是1cm/s.当t 为何值时,△PBC 为等腰三角形?(小组合作交流讨论,根据分类的标准易得到下面四种情况)三、∴t=3或11或7+34或 334时 △PBC 为等腰三角形 设计意图:总结探究动点关键“化动为静,分类讨论,画出符合条件的各种草图”,注意一定要分开画.(三) 动脑创新,再探新知:(两个动点问题 ) 如图,在梯形ABCD 中,354245AD BC AD DC AB B ====︒∥,,,,∠.动点M 从B 点出发沿线段BC 以每秒2个单位长度的速度向终点C 运动;动点N 同时从C 点出发沿线段CD 以每秒1个单位长度的速度向终点D 运动.设运动的时间为t 秒.(1)求BC 的长.(2)当MN AB ∥时,求t 的值.(3)试探究:t 为何值时,MNC △为等腰三角形.(小组合作交流讨论)分析:(1)如图① ,求出BC=10A D CB M N(2)由 MNC GDC △∽△求出5017t = 解决动点问题的好助手:数形结合定相似,比例线段构方程(3)当M 、N 运动到t秒时,若⊿MNC 为等腰三角形,须分三种情况讨论:①当NC MC =时,即102t t =-∴103t = ②当MN N C =时,过N 作NE MC ⊥于E 由等腰三角形三线合一性质得()11102522EC MC t t ==-=- 在Rt CEN △中,5cos EC t c NC t-== 又在Rt DHC △中,3cos 5CH c CD ==∴535t t -=解得258t = ③当MN MC =时,过M 作MF CN ⊥于F 点.1122FC NC t == 132cos 1025t FC C MC t ===-解得6017t = 综上所述,当103t =、258t =或6017t =时,MNC △为等腰三角形 总结:直角三角形能用相似解决的问题都能用三角函数法,且用三角函数法针对性更强,更省时间。
2022年中考数学专题复习:动态几何问题

2022年中考数学专题复习:动态几何问题1.在△ABC中,AB = AC,△ABC = 30°,△BDE是等边三角形,连接CD、AE.(1)如图1,当A、B、D三点在同一直线上时,AE、BC交于点P,且AE△AC.若PC = 4,求PE的长;(2)如图2,当B、E、C三点在同一直线上时,F是CD中点,连接AF、EF,求证:AE = 2AF;(3)如图3,在(2)的条件下,AB=8,E在直线BC上运动,将△AEF沿EF翻折得到△MEF,连接DM,G是AB上一点,且BG=14AB,O是直线BC上的另一个动点,连接OG,将△BOG沿OG翻折得到△HOG,连接HM,当HM最小时,直接写出此时点D到直线EM的距离.2.如图1和图2,在△ABC中,AB=AC=5,sinC=35.点K在AC边上,点M,N分别在AB,BC上,且AM=CN=2.点P从点M出发沿折线MB﹣BN匀速移动,到达点N时停止;而点Q在AC边上随P移动,且始终保持∠APQ=∠B.(1)当点P在BC上时,求点P与点A的最短距离;(2)若点P在MB上,且PQ将△ABC的面积分成上下4:5两部分时,求MP的长;(3)设点P移动的路程为x,当0≤x≤3及3≤x≤9时,分别求点P到直线AC的距离(用含x的式子表示);(4)在点P处设计并安装一扫描器,按定角∠APQ扫描△APQ区域(含边界),扫描器随点P从M到B再到N共用时36秒.若AK=94,请直接写出点K被扫描到的总时长.3.如图,在等腰梯形ABCD中,AB△CD,AB=8cm,CD=2cm,AD=6cm.点P从A 点出发,以2cm/s的速度沿AB向B点运动(运动到B点即停止);点Q从C点出发,以1cm/s的速度沿CD−DA向A点运动(当点P停止运动时,点Q也即停止),设P、Q同时出发并运动了t秒.(1)求梯形ABCD的高和△A的度数;(2)当PQ将梯形ABCD分成两个直角梯形时,求t的值;(3)试问是否存在这样的t的值,使四边形PBCQ的面积是梯形ABCD面积的一半,若存在,请求出t的值;若不存在,请说明理由.4.如图1,点O 是正方形ABCD 两对角线的交点,分别延长OD 到点G ,OC 到点E ,使OG =2OD ,OE =2OC ,然后以OG 、OE 为邻边作正方形OEFG ,连结AG 、DE .(1)猜想AG 与DE 的数量关系,请直接写出结论;(2)正方形ABCD 固定,将正方形OEFG 绕点O 逆时针旋转,旋转角为α(0°<α<180°),得到图2,请判断:(1)中的结论是否仍然成立?若成立,请证明;若不成立,请说明理由; (3)在正方形OEFG 旋转过程中,请直接写出: △当α=30°时,△OAG 的度数;△当△AEG 的面积最小时,旋转角α的度数.5.如图1,在ABC 中,90,ACB CD ∠=︒平分ACB ∠,且AD BD ⊥于点D .(1)判断ABD △的形状;(2)如图2,在(1)的结论下,若3,75BQ DQ BQD ==∠=︒,求AQ 的长; (3)如图3,在(1)的结论下,若将DB 绕着点D 顺时针旋转()090αα︒<<︒得到DP ,连接BP ,作DE BP ⊥交AP 于点F .试探究AF 与DE 的数量关系,并说明理由.6.如图,在Rt ABCAB=,4∠=︒,5AC=.动点P从点A出发,沿AB △中,90C⊥交AC或BC于点Q,以每秒4个单位长度的速度向终点B运动.过点P作PQ AB分别过点P、Q作AC、AB的平行线交于点M.设PQM与ABC重叠部分的面积为t t>秒.S,点P运动的时间为()0(1)当点Q在AC上时,CQ的长为______(用含t的代数式表示).(2)当点M落在BC上时,求t的值.(3)当PQM与ABC的重合部分为三角形时,求S与t之间的函数关系式.(4)点N为PM中点,直接写出点N到ABC的两个顶点的距离相等时t的值.7.如图,△ABC是等边三角形,AB=4cm,动点P从A出发,以2cm/s的速度沿AB 向点B匀速运动,过点P作PQ△AB,交折线AC﹣CB于点Q,以PQ为边作等边三角形PQD,使A,D在PQ异侧,设点P的运动时间是x(s)(0<x<2).(1)AP的长为cm(用含x的代数式表示);(2)当Q与C重合时,则x=s;(3)△PQD的周长为y(cm),求y关于x的函数解析式,并写出自变量的取值范围.8.如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P 在线段BC上以3cm/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.设P点的运动时间为t.(1)CP=cm.(用含t的式子表示);(2)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;(3)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?9.如图,在Rt△ABC中,△B=90°,BC=5 ,△C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向A点匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF△BC于点F,连接DE、EF.(1)AC的长是________,AB的长是________.(2)在D、E的运动过程中,线段EF与AD的关系是否发生变化?若不变化,那么线段EF与AD是何关系,并给予证明;若变化,请说明理由.(3)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.(4)当t为何值,△BEF的面积是2 ?10.在Rt△ABC中,△BAC=90°,AB=AC,动点D在直线BC上(不与点B,C重合),连接AD,把AD绕点A逆时针旋转90°得到AE,连接DE,F,G分别是DE,CD的中点,连接FG.【特例感知】(1)如图1,当点D是BC的中点时,FG与BD的数量关系是,FG 与直线BC的位置关系是;【猜想论证】(2)当点D在线段BC上且不是BC的中点时,(1)中的结论是否仍然成立?△请在图2中补全图形;△若成立,请给出证明;若不成立,请说明理由.【拓展应用】(3)若AB=AC,其他条件不变,连接BF、CF.当△ACF是等边三角形时,请直接写出△BDF的面积.11.如图,等腰三角形△ABC的腰长AB=AC=5cm,BC=8cm,动点P从B出发沿BC 向C运动,速度为2cm/s.动点Q从C出发沿CA向A运动,速度为1cm/s,当一个点到达终点时两个点同时停止运动.点P'是点P关于直线AC的对称点,连接PP′和P′Q,P′P和AC相交于点E.设运动时间为t秒.(1)若当t的值是多少时,P'P恰好经过点A?(2)设△P′PQ的面积为y,求y与t之间的函数关系式(0<t≤4);(3)是否存在某一时刻t,使PQ平分△P′PC?若存在,求出相应的t值,若不存在,请说明理由;(4)是否存在某一时刻t,使点Q在PC的垂直平分线上?若存在,求出相应的t值,若不存在,请说明理由.12.如图,△ABC为等腰三角形,AB=AC,将CA绕点C顺时针旋转至CD,连接AD,E为直线CD上一点,连接AE;(1)如图1,若△BAC=60°,△ACD=90°,E为CD中点,AB=△BCE的面积;(2)如图2,若△ACD=90°,点E在线段CD上且△DAE+△ABC=90°,AE的延长线与BC的延长线交于点F,连接DF,求证:BC=;(3)如图3,AB=1,△BAC=90°,△ACD=105°,若BE恰好平分△AEC,点P为线段AE上的动点,点E′与点E关于直线DP对称,AE′与CD交于点Q,连接CE′,当'+-''的值最小时,直接写出CQ的值.AE CE13.已知,如图△,在平行四边形ABCD中,AB=3cm,BC=5cm,AC△AB,△ACD 沿AC的方向匀速平移得到△PNM,速度为1cm/s:同时,点Q从点C出发,沿CB方向匀速移动,速度为1cm/s,当△PNM停止平移时,点Q也停止移动,如图△,设移动时间为t(s)(0<t<4),连接PQ,MQ,MC,解答下列问题:(1)CQ=,BQ=,AP=,CP=.(2)当t为何值时,PQ∥MN;(3)设△OMC的面积为y(cm2),求y与t之间的函数关系式;(4)是否存在某一时刻t,使S△QMC:S四边形ABQP=1:4.若存在,求出t的值;若不存在,请说明理由.14.如图,等腰ABC的底边BC=8,高AD=2,M是AB中点,连接MD.动点E从点B出发,以每秒1个单位的速度沿BC向点C运动,到点C停止,另一动点F从点B出发,以相同的速度沿BC运动,到点D停止.已知点E比点F早出发1秒,当点F出发后,以EF为边作正方形EFGH,使点G、H和点A在BC的同侧,设点E运动的时间为t秒.(1)当t≥1时,用含t的代数式表示EF的长;(2)设正方形EFGH面积为S 1,正方形EFGH与ABC重叠面积为S2,当S1:S2=2时,求t的值;(3)在点F开始运动时,点P从点D出发,以每秒DM ﹣MB﹣BM﹣MD运动,到达点D停止,在点E的整个运动过程中,求点P在正方形EFGH内(含边界)的时长.15.如图1,正方形ABCD中,点P、Q是对角线BD上的两个动点,点P从点B出发沿着BD以1cm/s的速度向点D运动;点Q同时从点D出发沿着DB以2cm的速度向点B运动.设运动的时间为x s,△AQP的面积为y cm2,y与x的函数图象如图2所示,根据图象回答下列问题:(1)a=.(2)当x为何值时,APQ的面积为6cm2;(3)当x为何值时,以PQ为直径的圆与APQ的边有且只有三个公共点.16.如图1,有一张矩形纸条ABCD ,边AB 、BC 的长分别是方程27100x x -+=的两个根()AB BC >,E 为CD 上一点,1CE =. (1)连接AE ,BE ,试说明90AEB =︒∠.(2)如图2,M 为边AB 上一个动点,将四边形BCEM 沿ME 折叠,使点B ,C 分别落在点B ′,C '上,边MB '与边CD 交于点N . △如图3,当点M 与点A 重合时,求N 到ME 的距离.△在点M 从点A 运动到点B 的过程中,求点N 相应运动的路径长(路程).17.如图,已知在Rt ABC 中,90ACB ∠=︒,8AC =,16BC =,D 是AC 上的一点,3CD =,点P 从B 点出发沿射线BC 方向以每秒2个单位的速度向右运动.设点P 的运动时间为t ,连接AP .(1)当3t =秒时,求AP 的长度;(2)当ABP △为等腰三角形时,求t 的值;(3)过点D 作DE AP ⊥于点E ,连接PD ,在点P 的运动过程中,当PD 平分APC ∠时,直接写出t 的值.18.如图,已知在Rt△ABC 中,△ACB =90°,AB =10,AC =6,点D 是斜边AB 上的动点,联结CD ,作DE △CD 交射线CB 于点E ,设AD =x . (1)当点D 是边AB 的中点时,求线段DE 的长; (2)当△BED 是等腰三角形时,求x 的值; (3)如果DEy DB=,求y 关于x 的函数解析式,并写出它的定义域.19.已知:如图,在长方形ABCD 中,4cm,6cm AB BC ==,点E 为AB 中点.点P 在线段BC 上以每秒2cm 的速度由点B 向点C 运动,同时,点Q 在线段CD 上由点C 向点D 运动.设点P 的运动时间为t 秒,解答下列问题:(1)线段,BP PC 的长可用含t 的式子分别表示为 cm , cm ;(2)若某一时刻BPE 与CQP 全等,求此时t 的值和点Q 的运动速度.20.在平面直角坐标系中,点A(0,4),点B(4,0),连接AB,点P(0,t)是y 轴上的一动点,以BP为一直角边构造等腰直角△BPC(B,P,C的顺序为顺时针),且△BPC=90°,过点A作AD△x轴并与直线BC交于点D,连接PD.(1)如图1,当t=2时,求点C的坐标;(2)如图2,当t>0时,求证:△ADC=△PDB;(3)如图3,当t<0时,求DP﹣DA的值(用含有t的式子表示).。
中考数学经典总复习专题动线、动形问题完美全文

学 (2)点P 、 Q在运动的过程中,△PCQ面积S有最 大值吗?若有,请求出最大值;若没有,请说明理 由。
动点与函数相结合
抛 与物y轴线交y于= 点 x122C+,m抛x+n物与线x轴的交对于称A轴、交Bx两轴点于,
合 点D,已知A(﹣1,0),C(0,2). 作 (1)求抛物线的表达式;
学 存在,请说明理由;
y
解析:
C
AO
DB
x
动点与函数相结合
抛 与物y轴线交y于= 点 x122C+,m抛x+n物与线x轴的交对于称A轴、交Bx两轴点于,
合 点D,已知A(﹣1,0),C(0,2).
作 互
( 3)点E 是 线 段 BC上的一个动点,过点E 作x轴的垂线与抛物线相交于点F,当点E 运动到什么位置时,四边形CDBF的面积
8
1 2
3
x2+ 2
;
x+2;
∴抛物线的对称轴是x= ∴OD= .3
32.
∵C(0,2 2),
∴OC=2.
5
在Rt△OCD中,由勾股定理,得CD= .2
∵△CDP是以CD为腰的等腰三角形,
∴CP1=CP2=CP3=CD. 作CH⊥x轴于H,
∴HP1=HD=2,
∴∴DP1P(1=4.,32 4),P2(
中考数学---动线、动形问题
• 数学因运动而充满活力,数学因变化而精彩纷呈。动态题是中考 中必考的内容。
• 本节课重点来探究动态几何中的动线、动形问题。
• 一、关于动线、动形问题的解题方法:
• 1.“以静制动”,把动态问题转化成静态问题;
• 2.图形的运动主要有翻折、平移、旋转,在运动过程中,分清哪 些量不变,哪些量发生了变化,以不变的量作为解题基础,以变 化中的规律和特点作为解题的关键。
2022年中考数学专题复习:动态几何问题

2022年中考数学专题复习:动态几何问题1.如图,在Rt ABC △中,8AB =,90ACB ∠=︒,60A ∠=︒,点P 从点A 出发以每秒2个单位的速度沿AB 向终点B 运动,当点P 不与点A ,B 重合时,作120BPD ∠=︒,边PD 交折线AC CB -于点D ,点A 关于直线PD 的对称点为E ,连结ED ,EP 得到PDE △.设点P 的运动时间为t (秒).(1)直接写出线段PD 的长(用含t 的代数式表示);(2)当点E 落在边BC 上时,求t 的值;(3)设PDE △与ABC 重合部分图形的面积为S ,求S 与t 的函数关系式;(4)设M 为AB 的中点,N 为ED 的中点,连结MN .当MN 与ABC 的边垂直时,直接写出t 的值.2.如图,在Rt ABC 中,90ACB ∠=︒,60A ∠=︒,2cm =AC ,CD 是边AB 上的中线.P ,Q 两点同时从点A 出发,点P 在AC 上以1cm/s 的速度向终点C 运动;点Q 在AB 上以2cm/s 的速度向终点B 运动,以AP ,AQ 为邻边作APEQ .设点P 的运动时间为x (s ),APEQ 与ACD △重叠部分图形的面积为y (cm 2).(1)点P 到AB 的距离为_______cm .(用含x 的代数式表示)(2)当点E 落在中线CD 上时,求x 的值.(3)当02x <<时,求y 关于x 的函数解析式,并写出自变量x 的取值范围.(4)连接PQ ,当直线PQ 经过中线CD 上的三等分点时,直接写出x 的值.3.如图1,点P 、Q 分别是等边△ABC 边AB 、BC 上的动点(端点除外),点P 从顶点A 、点Q 从顶点B 同时出发,且它们的运动速度相同,连接AQ 、CP 交于点M .(1)求证:ABQ CAP ≌△△:(2)当点P 、Q 分别在AB 、BC 边上运动时,△QMC 的大小变化吗?若变化,请说明理由:若不变,求出它的度数.(3)如图2,若点P 、Q 在运动到终点后继续在射线AB 、BC 上运动,直线AQ 、CP 相交于点M ,则△QMC 的大小变化吗?若变化,请说明理由:若不变,则求出它的度数.4.如图1,ABC 与AEF 都是等边三角形,边长分别为4,FC AD 为ABC 高,连接CE ,N 为CE 的中点.(1)求证:ACF ABE ≌;(2)将AEF 绕点A 旋转,当点E 在AD 上时,如图2,EF 与AC 交于点G ,连接NG ,求线段NG 的长;(3)连接BN ,在AEF 绕点A 旋转过程中,求BN 的最大值.5.有一边长为6cm 的正方形ABCD 和等腰直角PQR ,PQ =PR ,QR =8cm .点B ,C ,Q ,R 在同一条直线l 上.当C ,Q 两点重合时,等腰直角PQR 以1cm/秒的速度沿直线l 按箭头所示方向开始匀速运动,t 秒后正方形ABCD 与等腰直角PQR 重合部分的面积为S cm 2.解答下列问题.(1)当t =3秒时,求S 的值;当t =6秒时,求S 的值;(2)当6秒≤t ≤8秒时,求s 与t 的函数关系式.(3)若重合部分的面积为152cm 时,求t 的值.6.以BC 为斜边在它的同侧作Rt DBC 和Rt ABC ,其中90A D ∠=∠=︒,AB AC =,AC 、BD 交于点P .(1)如图1,BP 平分ABC ∠,求证:BC AB AP =+;(2)如图2,过点A 作AE BP ⊥,分别交BP 、BC 于点E 、点F ,连接AD ,过A 作AG AD ⊥,交BD 于点G ,连接CG ,CG 交AF 于点H ,求证:GH CH =; (3)如图3,点M 为边AB 的中点,点Q 是边BC 上一动点,连接MQ ,将线段MQ 绕点M 逆时针旋转90︒得到线段MK ,连接PK 、CK ,当15DBC ∠=︒,4AP =时,求PK CK +的最小值.7.如图,长方形ABCD 中(长方形的对边平行且相等,每个角都是90°),AB =6cm ,AD =2cm ,动点P ,Q 分别从点A ,C 同时出发,点P 以2cm/s 的速度向终点B 移动,点Q 以1cm/s 的速度向点D 移动,当有一点到达终点时,另一点也停止运动,设运动的时间为t (s ),问:(1)当t =1s 时,四边形BCQP 面积是多少?(2)当t 为何值时,点P 和点Q 距离是3cm ?(3)当t = s 时,以点P ,Q ,D 为顶点的三角形是等腰三角形.(直接写出答案)8.如图,AE 与BD 相交于点C ,AC EC =,BC DC =,6cm AB =,点P 从点A 出发,沿A B A →→方向以3cm s 的速度运动,点Q 从点D 出发,沿D E →方向以1cm s 的速度运动,P 、Q 两点同时出发,当点P 到达点A 时,P 、Q 两点同时停止运动.设点P 的运动时间为()s t .(1)求证://AB DE .(2)写出线段BP 的长(用含t 的式子表示).(3)连接PQ ,当线段PQ 经过点C 时,求t 的值.9.如图,在Rt ABC 中,△C =90°,△A =30°,AB =4,动点P 从点A 出发,沿AB 以每秒2个单位长度的速度向终点B 运动,过点P 作PD △AC 于点D (点P 不与点A 、B 重合),作△DPQ =60°,边PQ 交射线DC 于点Q ,设点P 的运动时间为t 秒. (1)用含t 的代数式表示线段PD = ;PQ = ;CD = .(2)当点Q与点C重合时,求t的值;(3)当线段PQ的垂直平分线经过ABC一边中点时,直接写出t的值.10.在△ABC中,AB=AC=10cm.(1)如图1,AM是△ABC的中线,MD△AB于D点,ME△AC于E点,MD=3cm,则ME=cm.(2)如图2,在(1)的条件下,连接DE交AM于点F,试猜想:△FD FE(填“>”、“=”或“<”);△AM DE(填位置关系).(3)如图3,BC=8cm,点D为AB的中点.点P在线段BC上由B向C运动,同时点Q在线段CA上以每秒2cm的速度由C向A运动,设点P的运动时间为t秒.问:运动时间t为多少时,△BDP与△PQC全等?11.将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD)的斜边恰好重合.已知AB=P是AC上的一个动点.(1)当点P运动到∠ABC的平分线上时,连接DP、BP,求CP、DP的长;(2)当点P运动到什么位置时,以D,P,B,Q为顶点的平行四边形的项点Q恰好在边BC上?求出此时平行四边形的面积;(3)当点P 在运动过程中出现PD =BC 时,求此时∠PDA 的度数(直按写出答案).12.如图,在四边形ABCD 中,//AD BC ,90B ∠=︒,8cm AB =,12cm AD =,18cm BC =,点P 从点A 出发,以1cm/s 的速度向点D 运动;点Q 从点C 同时出发,以2cm/s 的速度向点B 运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设点P ,Q 运动的时间为ts .(1)CD 边的长度为________cm ,t 的取值范围为________.(2)从运动开始,当t =________时,PQ CD =.(3)在整个运动过程中是否存在t 值,使得四边形PQCD 是菱形.若存在,请求出t 值;若不存在,请说明理由.13.如图所示,四边形ABCD 为矩形,AB =6cm ,AD =4cm ,若点Q 从A 点出发沿AD 以1cm/s 的速度向D 运动,P 从B 点出发沿BA 以2cm/s 的速度向A 运动,如果P 、Q 分别同时出发,当一个点到达终点时,另一点也同时停止.设运动的时间为t (s ).(1)当t为何值时,△P AQ为等腰三角形?(2)当t为何值时,△APD的面积为6cm2?(3)五边形PBCDQ的面积能否达到20cm2?若能,请求出t的值;若不能,请说明理由.(4)当t为何值时,P、Q两点之间的距离为?14.(1)如图1,在平行四边形ABCD中,对角线AC、BD相交于O点,过点O的直线l与边AB、CD分别交于点E、F,绕点O旋转直线l,猜想直线l旋转到什么位置时,四边形AECF是菱形.证明你的猜想.(2)若将(1)中四边形ABCD改成矩形ABCD,使AB=4cm,BC=3cm,△如图2,绕点O旋转直线l与边AB、CD分别交于点E、F,将矩形ABCD沿EF折叠,使点A与点C重合,点D的对应点为D′,连接DD′,求△DFD′的面积.△如图3,绕点O继续旋转直线l,直线l与边BC或BC的延长线交于点E,连接AE,将矩形ABCD沿AE折叠,点B的对应点为B′,当△CEB′为直角三角形时,求BE 的长度.请直接写出结果,不必写解答过程.15.如图1,在△ABC中,点P为BC边中点,直线a绕顶点A旋转.若B、P在直线a的异侧,BM△直线a于点M,CN△直线a于点N,连接PM、PN;(1)延长MP交CN于点E(如图2).△求证:△BPM△△CPE;△求证:PM=PN;(2)若直线a烧点A旋转到图3的位置时,点B、P在直线a的同侧,其它条件不变.此时PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由;(3)若直线a 绕点A 旋转到与BC 边平行的位置时,其它条件不变.请直接判断四边形MBCN 的形状及此时PM =PN 还成立吗?(不必说明理由)16.边长为4的正方形ABCD 绕顶点A ,按顺时针方向旋转至正方形111AB C D ,记旋转角为α.(1)如图1,当60α=︒时,求弧1CC 的长度和线段AC 扫过的扇形面积;(2)如图2,当45α=︒时,记BC 与11D C 的交点为E ,求线段1D E 的长度; (3)如图3,在旋转过程中,若F 为线段1CB 的中点,求线段DF 长度的取值范围.17.如图,在四边形ABCD 中,△B =60°,AB =DC =4,AD =BC =8,延长BC 到E ,使CE =4,连接DE ,动点P 从点B 出发,以每秒2个单位的速度沿BC ﹣CD ﹣DA 向终点A 运动,设点P 运动的时间为t 秒(t >0).(1)当t =3时,BP = ;(2)当t = 时,点P 运动到△B 的角平分线上;(3)当0<t <6时,请用含t 的代数式表示△ABP 的面积S ;(4)当0<t <6时,直接写出点P 到四边形ABED 相邻两边距离相等时t 的值.18.已知边长为2的正方形ABCD中,P是对角线AC上的一个动点,过点P作PE△PB,PE交射线DC于点E,过点E作EF垂直AC所在的直线,垂足为点F.(1)如图,当E点在线段DC上时,求证:PB=PE;(2)在点P的运动过程中,△PEC能否为等腰三角形?如果能,直接写出此时AP的长,如果不能,说明理由;(3)在点P的运动过程中,AP、PF、FC的长度是否满足某种数量关系?若满足,试写出解答过程;若不满足,试说明理由.19.已知:正方形ABCD,点P是对角线AC所在直线上的动点,点E在DC边所在的直线上,且随着点P的运动而运动,PE=PD总成立.(1)如图1,当点P在对角线AC上时,请你猜想PE与PB有怎样的数量关系,并加以证明;(2)如图2,当点P运动到CA的延长线上时,(1)中猜想的结论是否成立?如果成立,请给出证明;如果不成立,请说明理由;(3)如图2,当点P运动到CA的反向延长线上时,请你利用图3画出满足条件的图形,并判断此时PE与PB有怎样的关系?(直接写出结论不必证明)20.已知正方形ABCD,△EAF=45°,将△EAF绕顶点A旋转,角的两边始终与直线CD交于点E,与直线BC交于点F,连接EF.(1)如图△,当BF=DE时,求证:△ABF△△ADE;(2)若△EAF旋转到如图△的位置时,求证:△AFB=△AFE;(3)若BC=4,当边AE经过线段BC的中点时,在AF的右侧作以AF为腰的等腰直角三角形AFP,直接写出点P到直线AB的距离.。
中考数学专题复习 三角形动态问题 ——动点,动线,动图(25张PPT)

∵△BPD≌△CPQ,
∴CQ=BD=6.
∴点P的运动时间
t
BP 3
4.5 3
1.5(秒)
此时
VQ
CQ t
பைடு நூலகம்
6 1.5
4(厘米/秒)
∴△BPD≌△CQP(SAS),
(2)因为VQ>VP,只能是点Q追上点P,即点Q比点P多 走AB+AC的路程 设经过x秒后P与Q第一次相遇,依题意得4x=3x+2×12, 解得x=24(秒) 此时P运动了24×3=72(厘米) 又∵△ABC的周长为33厘米,72=33×2+6, ∴点P、Q在BC边上相遇,即经过了24秒,点P与点Q第 一次在BC边上相遇.
解:(1)∵长方形ABCD, ∴∠A=∠B=90°, ∵点E为AD的中点,AD=6cm, ∴AE=3cm, 又∵P和Q的速度相等可得出AP=BQ=1cm,BP=3, ∴AE=BP, 在△AEP和△BQP中,
∴△AEP≌△BPQ( SAS), ∴∠AEP=∠BPQ, 又∵∠AEP+∠APE=90°, 故可得出∠BPQ+∠APE=90°, 即∠EPQ=90°, 即EP⊥PQ.
5.如图,已知长方形ABCD中,AD=6cm,AB=4cm,点E为AD的中点.若 点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BC 上由点B向点C运动. (1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△AEP与 △BPQ是否全等?请说明理由,并判断此时线段PE和线段PQ的位置关系; (2)若点Q的运动速度与点P的运动速度相等,运动时间为t秒,设 △PEQ的面积为Scm2 ,请用t的代数式表示S;
(1)①∵t=1(秒), ∴BP=CQ=3(厘米) ∵AB=12,D为AB中点, ∴BD=6(厘米) 又∵PC=BC-BP=9-3=6 (厘米) ∴PC=BD ∵AB=AC, ∴∠B=∠C, 在△BPD与△CQP中,
初中数学_中考专题复习 动态探究型问题教学设计学情分析教材分析课后反思
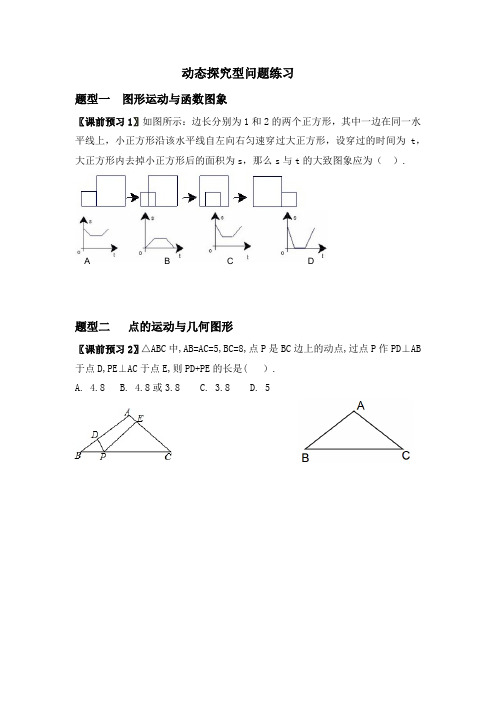
动态探究型问题练习题型一图形运动与函数图象〖课前预习1〗如图所示:边长分别为1和2的两个正方形,其中一边在同一水平线上,小正方形沿该水平线自左向右匀速穿过大正方形,设穿过的时间为t,.大正方形内去掉小正方形后的面积为s,那么s与t的大致图象应为()题型二点的运动与几何图形〖课前预习2〗△ABC中,AB=AC=5,BC=8,点P是BC边上的动点,过点P作PD⊥AB 于点D,PE⊥AC于点E,则PD+PE的长是( ).A. 4.8B. 4.8或3.8C. 3.8D. 5题型 三 动态问题中存在探究〖课前预习3〗如图,在平面直角坐标系中,点C(−3,0),点A,B 分别在x 轴,y 轴的正半轴上,且满足0132=-+-OA OB .(1) 求点A ,点B 的坐标.(2)若点P 从C 点出发,以每秒1个单位的速度沿射线CB 运动,连结AP.设△ABP 的面积为S ,点P 的运动时间为t 秒,求S 与t 的函数关系式,并写出自变量的取值范围.(3)在(2)的条件下,是否存在点P ,使以点A ,B ,P 为顶点的三角形与△AOB 相似?若存在,请直接写出点P 的坐标;若不存在,请说明理由.〖举一反三1〗如图,点P是▱ABCD边上一动点,沿A→D→C→B的路径移动,设P点经过的路径长为x,△BAP的面积是y,则下列能大致反映y与x的函数关系的图象是( ).〖举一反三2〗如图,Rt△ABC中,∠ACB=90∘,∠ABC=60∘,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为().A 2 B2.5或3.5C3.5或4.5 D2或3.5或4.5中考链接达标检测1.(2017.济宁)如图,A,B是半径为1的⊙O上两点,且OA⊥OB,点P从点A出发,在⊙O上以每秒一个单位长度的速度匀速运动,回到点A运动结束,设运动时间为x(单位:s),弦BP的长为y,那么下列图象中可能表示y与x函数关系的是( ).)0(62>+-=a c ax ax y 2721+-=x y2.(2016•济宁)如图,已知抛物线m :的顶点A 在x 轴上,并过点B (0,1),直线n : 与x 轴交于点D ,与抛物线m 的对称轴L 交于点F ,过B 点的直线BE 与直线n 相交于点E (﹣7,7).(1)求抛物线m 的解析式.(2)P 是对称轴L 上的一个动点,若以B ,E ,P 为顶点的三角形的周长最小,求点P 的坐标.(3)抛物线m 上是否存在一动点Q ,使以线段FQ 为直径的圆恰好经过点D ?若存在,求点Q 的坐标;若不存在,请说明理由.《动态探究型问题》学情分析动态探究型问题这类题目多出现在压轴题题目中,题目难度较大,试题信息量大,对同学们获取信息和处理信息的能力要求较高,是近年来中考数学的热点题型,学生遇到这类题目时都会感到恐惧。
数轴动态专题复习课件人教版七年级数学上册
课前引入
两点间距离表示方法:
(2)数轴上点A表示-5,点B表示4,动点P从点A开始,以每秒3个单 位长度的速度向右运动,经过t秒,线段BP的长度为______________ (用含t的式子表示);
课前引入
带返回的动点表示方法:
(3)数轴上点A表示-5,点B表示4,动点P从点A开始,以每秒3 个单位长度的速度向点B运动,到达点B后,立即以原速返回,设运动 时间为t秒,点P表示的数是____________;
设计意图:引导学生对用绝对值表达两点间距离的必要性的进一步思考。
平行练习2
数轴上点A表示-5,点B表示4,点C表示2,动点P从点A 开始,以每秒3个单位长度的速度向右运动,到达点C后,立 即以原速返回,动点Q从点B开始,以每秒1个单位长度的速 度向左运动,设运动时间为t,求线段PQ的长度(用含t的式
平行练习1
数轴上点A表示-5,点B表示4,动点P从点A开始,以每 秒3个单位长度的速度向右运动,动点Q从点B开始,以每秒1 个单位长度的速度向右运动,设运动时间为t,求当线段PQ的
长度等于5时,点P、Q表示的数?
设计意图:培养学生会利用绝对值表示两点间距离,进而解决问题的 能力。
典型例题
例2.数轴上点A表示-5,点B表示4,动点P从点A开始,以 每秒3个单位长度的速度向右运动,到达点B后,立即以原速 返回,动点Q从点B开始,以每秒1个单位长度的速度向左运 动,设运动时间为t,求线段PQ的长度(用含t的式子表示)?
长度?
设计意图:锻炼学生思维迁移,提取有用信息,分析解决问题的能力。
课后作业
2.数轴上点A表示-5,点B表示4,动点P从点A开始,以每 秒3个单位长度的速度向右运动,到达点B后,立即以原速返 回,动点M、Q从点B开始,分别以每秒2个单位长度和1个单 位长度的速度向左运动,设运动时间为t,当t为何值时,P到 Q的距离是P到M的距离的2倍?
中考数学专题复习32套测试题(23)动态性问题
专题:动态问题(总分100 时间:90分钟) ——命题人:(李鹊二中)崔建利动态性问题分类 1: 点动.. 2:线动.. 3:图动..4:变换.. 一:单选题(每题4分,共32分)1、如图,把一个长方形纸片沿EF 折叠后,点D 、C 分别落在D '、C '的位置,若∠EFB=620,则∠AED ’等于( )A 、580B 、600C 、620D 、5602.如图,矩形ABCD 的边AB =5厘米,BC =4厘米,动点P 从A 点出发,在折线AD —DC -CB 上以1厘米/秒的速度向B 点匀速运动,那么表示△ABP 的面积S (厘米2)与运动时间t (秒)之间的函数关系的图象是( )A B C D3在直角坐标系中A (-3,-2)圆A 的半径为1,P 为X 轴上一动点,PQ 切圆A 于Q 则PQ 值最小时P 点坐标为( )A (-4,0)B (-2,0)C (-4,0)或(-2,0)4将y=2x+2向右平移3个单位,相当于y=2x+2向下平移()个单位 A 4 B 2 C 3 D 65点A 是为直径为MN 半圆上的一个三等分点,B 点是弧AN 的中点,点P 是直径MN 上一个动点,半圆o 的半径为1,则PA+PB 的最小值为:( ) A :1 B :3/2 C :√2 D :3-16.如图,两枚同样大的硬币,其中一个固定,另一个沿其周围滚动,滚动时,两枚硬币总是保持有一点相接触(相外切),当滚动的硬币沿固定的硬币周围滚动2圈,回到原来的位置时,滚动的那个硬币自转的周数为( ) A 、1 B 、2 C 、3 D 、47.如图,直线AB 经过⊙O 的圆心,与⊙O 相交于A 、B 两点,点C 在⊙O 上,且∠AOC=300,点E 是直线AB 上的一个动点(与点O 不重合),直线EC 交⊙O 于D ,则使DE=DO 的点共有( ) A 、1个 B 、2个 C 、3 个 D 、4个8、如图,直角梯形ABCD 中,AD ∥BC ,∠B=900,AD +BC >DC ,若腰DC 上有点P ,使AP ⊥BP ,则这样的点( )(A )不存在(B )只有一个 (C )只有两个 (D )有无数个EBC 'FCD62D 'A4题图。
2014年数学中考二轮专题复习讲义:动态型问题
2014年数学中考二轮专题复习讲义:动态型问题【考纲要求】动态几何问题就是研究在几何图形的运动中伴随着一定的图形位置、数量关系的 “变”与 “不变”性.就其运动对象而言,有 “点动” “线动”和“面动”;就其运动形式而言,有“移动”“滚动”“旋转”和“翻折”等.【命题趋势】动态几何问题常集几何、代数知识于一体,数形结合,有较强的综合性,题目灵活多变,动中有静,动静结合,能够在运动变化过程中发展学生思维和空间想象能力,是中考热点,常在中考中以压轴题的形式出现.题型分类 、深度剖析:考点一、点动型问题例1、(2013·黄冈)如图,在平面直角坐标系中,四边形ABCO 是梯形,其中A(6,0),B(3,3),C(1,3),动点P 从点O 以每秒2个单位的速度向点A 运动,动点Q 也同时从点B 沿B →C →O 的线路以每秒1个单位的速度向点O 运动,当点P 到达A 点时,点Q 也随之停止,设点P 、Q 运动的时间为t(秒).(1)求经过A 、B 、C 三点的抛物线的解析式;(2)当点Q 在CO 边上运动时,求△OPQ 的面积S 与时间t 的函数关系式;(3)以O 、P 、Q 为顶点的三角形能构成直角三角形吗?若能,请求出t 的值,若不能,请说明理由;(4)经过A 、B 、C 三点的抛物线的对称轴、直线OB 和PQ 能够交于一点吗?若能,请求出此时t 的值(或范围),若不能,请说明理由.解:(1)设所求抛物线的解析式为y =ax 2+bx +c ,把A (6,0),B (3,3),C (1,3)三点坐标代入得⎩⎨⎧36a +6b +c =0,9a +3b +c =3,a +b +c =3,解得a =-315,b =4 315,c =4 35. 即所求抛物线的解析式为y =-315x 2+4 315x +4 35.2)依题意,可知OC =CB =2,∠COA =60°,∴当动点Q 运动到OC 边时,OQ =4-t ,∴△OPQ 的高为:OQ ·sin60°=(4-t )×32. 又OP =2t ,∴S =12×2t ×(4-t )×32=-32(t 2-4t )(2≤t ≤3). 3)依题意,可知:0≤t ≤3.当0≤t ≤2时,Q 在BC 边上运动,此时OP =2t ,OQ =3+(3-t )2,PQ =3+[2t -(3-t )]2=3+(3t -3)2.∵∠POQ <∠POC =60°,∴若△OPQ 为直角三角形,只能是∠OPQ =90°或∠OQP =90°.若∠OPQ =90°,则OP 2+PQ 2=OQ 2,即4t 2+3+(3t -3)2=3+(3-t )2,解得:t =1或t =0(舍);若∠OQP =90°,则OQ 2+PQ 2=OP 2,即6+(3-t )2+(3t -3)2=4t 2,解得t =2;当2<t ≤3时,Q 在OC 边上运动,此时OP =2t >4,∠POQ =∠COP =60°,OQ <OC =2,∴△OPQ 不可能为直角三角形.综上所述,当t =1或t =2时,△OPQ 为直角三角形.4)由(1)可知:抛物线y =-315x 2+4 315x +4 35=-315(x -2)2+1615 3,其对称轴为x =2.又OB 的解析式为y =33x ,∴抛物线对称轴与OB 的交点为M ⎝⎛⎭⎪⎫2,2 33.又P (2t ,0),设过P 、M 的直线解析式为y =kx +b ,∴⎩⎪⎨⎪⎧2 33=2k +b ,k 2t +b =0,解得⎩⎪⎨⎪⎧k =33(1-t ),b =-2 3t 3(1-t ),即直线PM :y =33(1-t )x - 2 3t 3(1-t ), 即3(1-t )y =x -2t .又0≤t ≤2时,Q (3-t ,3),代入上式,得:3(1-t )×3=3-t -2t ,恒成立,即0≤t ≤2时,P 、M 、Q 总在一条直线上,即M 在直线PQ 上;2<t ≤3时,OQ =4-t ,∠QOP =60°,∴Q (4-t 2,3(4-t )2),代入上式,得:3(4-t )2×3(1-t )=4-t 2-2t ,解得:t =2或t =43,均不合题意,应舍去. ∴综合所述,可知:过A 、B 、C 三点的抛物线的对称轴、直线OB 和PQ 能够交于一点,此时0≤t ≤2.归纳:探索几何图形上一个或几个动点在运动变化过程中伴随着的等量关系、变量关系、图形的特殊状态、图形间的特殊关系等题目.以点的运动带动图形的变化,常与方程、函数知识联系在一起.考点二、线动型问题例 2:(2013 年甘肃兰州)如图,量角器的直径与直角三角板ABC 的斜边AB 重合,其中量角器 0 刻度线的端点N 与点A 重合,射线CP 从CA 处出发沿顺时针方向以每秒3°的速度旋转,CP 与量角器的半圆弧交于点E,第 24 秒,点E 在量角器上对应的读数是________.解:连接OE,∵∠ACB=90°,∴A,B,C 在以点O 为圆心,AB 为直径的圆上.∴点E,A,B,C 共圆.∵∠ACE=3×24=72°,∴∠AOE=2∠ACE=144°.∴点E 在量角器上对应的读数是 144°.答案:144°归纳:本题考查的是圆周角定理.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.考点三、面动型问题:例3、(2013 ·潍坊)如图,将一个边长为 2 的正方形ABCD 和一个长为 2、宽为 1 的长方形CEFD 拼在一起,构成一个大的长方形ABEF.现将小长方形CEFD 绕点C 按顺时针旋转至CE′F′D′,旋转角为α.(1)当点D′恰好落在EF 边上时,求旋转角α的值;(2)如图,G 为BC 中点,且 0°<α<90°,求证:GD′=E′D;(3)小长方形CEFD 绕点C 按顺时针旋转一周的过程中,△DCD′与△CBD′能否全等?若能,直接写出旋转角α的值;若不能,请说明理由.(1)解:∵长方形CEFD 绕点C 顺时针旋转至CE′F′D′,∴CD′=CD=2.在Rt△CED′中,CD′=2,CE=1,∴∠CD′E=30°. ∵CD∥EF,∴∠α=30°.(2)证明:∵G 为BC 中点,∴CG=1.∴CG=CE.∵长方形CEFD 绕点C 顺时针旋转至CE′F′D′,∴∠D′CE′=∠DCE=90°.CE=CE′=CG.∴∠GCD′=∠DCE′=90°+α.∴△GCD′≌△E′CD(SAS).∴GD′=E′D(3)解:能.理由如下:∵四边形ABCD为正方形,∴CB=CD.∵CD=CD′,∴△BCD′与△DCD′为腰相等的两等腰三角形.当∠BCD′=∠DCD′时,△BCD′≌△DCD′.②当△BCD′与△DCD′为锐角三角形时,α=360°-90°2=315°.即当旋转角a的值为135°或315°时,△DCD′与△CBD′全等.归纳:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了正方形、矩形的性质以及三角形全等的判定与性质.跟踪练习:1、如下图,在矩形ABCD 中,AB=6,BC=8,点E 是BC 中点,点F 是边CD 上的任意一点,当△AEF 的周长最小时,则 DF 的长为()A.1 B.2 C.3 D.42、(2012·宜宾)如图,在△ABC中,已知AB=AC=5,BC=6,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动.且DE始终经过点A,EF与AC交于M点.(1)求证:△ABE∽△ECM;(2)探究:在△DEF运动的过程中,重叠部分能否构成等腰三角形?若能,求出BE的长;若不能,请说明理由;(3)当线段AM最短时,求重叠部分的面积.。
中考物理复习 专题(07) 动态电路分析
专题(七)动态电路分析【动态电路解题的一般步骤】一、判断电路的串、并联关系(电路类型)。
串联分压:U1U2=R1R2;并联分流:I1I2=R2R1,各支路互不影响,干路的电流受支路影响。
二、弄清各电表的类型及测量的物理量:电流表串联在电路中(相当于导线),电压表并联在电路中(相当于此处断路)。
三、动态分析:电阻R的变化引起电流、电压的变化。
1.不论是串联还是并联,如果有一个电阻变大,则总电阻变大;反之亦然。
2.由公式I=UR得,当电压不变时,电阻越大,电流就越小;由公式U=IR得,通过电阻的电流越大,它两端的电压也越大。
四、同类物理量变化量大小的比较及不同类物理量变化量间的关系及计算。
处理此类问题时:先定性地判定电流、电压如何变化,再进行同类物理量变化量大小的比较。
“不同类物理量的变化量”,主要指的是电压、电流及电功率的变化量。
当电路状态发生变化时,定值电阻:R=ΔUΔI具有普遍意义,但ΔP=ΔU×ΔI是错误的,应运用ΔP=U22R -U12R或ΔP=I22R-I12R计算[或可化简为ΔP=ΔU(I1+I2)、ΔP=ΔI(U1+U2)]。
五、动态电路变化的同时要注意保护电路,各物理量变化范围(极值)的计算。
此类问题指的是两个极值点下的I、U、R、P的计算:①电流最大时需要考虑:电流表量程、电压表量程、灯的额定电流、滑动变阻器允许通过的最大电流。
②电流最小,即电阻最大时,此时若电压表测滑动变阻器两端的电压,注意电压表示数不能超量程。
六、当电路发生变化时,利用电路特点和欧姆定律、电功和电功率的计算公式即可确定各物理量之间的比值。
串联:电流I1=I2=I,其他物理量都与电阻成正比。
并联:电压U1=U2=U,其他物理量都和电阻成反比。
针对训练类型一滑动变阻器引起的变化问题1.如图ZT7-1所示电路中,电源电压保持不变,闭合开关S,当滑动变阻器的滑片P从a端向b端滑动时,电流表A 示数,电压表V1示数,电压表V2示数,电压表V1示数与电流表A示数的比值,电压表V2示数与电流表A示数的比值,电压表V1示数的变化量与电流表A示数的变化量之比,电压表V2示数的变化量与电流表A示数的变化量之比,电路消耗的总功率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题复习七:动态问题(一)
主备:夏彪课型:复习审核:初三备课组
班级姓名学号
【方法指导】
在解这类题时,要充分发挥空间想象的能力,在运动中寻求一般与特殊位置关系;在“动”中求“静”,化“动”为“静”,抓住它运动中某一瞬间,理解图形在不同位置情况。
通过探索、归纳、猜想,正确分析变量与其它量之间的内在联系,建立变量与其它量之间的数量关系。
再充分利用直观图形,并建立方程、函数模型或不等式模型,结合分类讨论等数学思想进行解答。
【课前演练】
1.(2014•广西)如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为x,两个三角形重叠面积为y,则y关于x的函数图象是()
A B C.D.
2、如图1,弧AD是以等边三角形ABC一边AB为半径的四分之一圆周, P为弧AD上任意一点,
【例题精讲】
例1 [2014·无锡] 如图,已知点A(2,0),B(0,4),∠AOB的平分线交AB
于点C.一动点P从O点出发,以每秒2个单位长度的速度沿y轴向点B做
匀速运动,过点P且平行于AB的直线交x轴于点Q,作P,Q关于直线OC
的对称点M,N,设点P运动的时间为t(0<t<2)秒.
(1)求点C的坐标,并直接写出点M,N的坐标(用含t的代数式表示);
(2)设△MNC与△OAB重叠部分的面积为S,①试求S关于t的函数表达式;
②在图(b)的直角坐标系中,画出S关于t的函数图像,并回答:S是否有最大值?若有,写出S 的最大值;若没有,请说明理由.
例2 (2013·广东)有一副直角三角板,在三角板ABC中,∠BAC=AB=AC=6,
在三角板DEF中,∠FDE=90°,DF=4,DE=43,将这副直角三角板按如图①所示位置摆放,
点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA 方向平行移动,当点F运动到点A时停止运动.
(1)如图②,当三角板DEF运动到点D与点A重合时,设EF与BC交于点M,则∠EMC=______度;
(2)如图③,在三角板DEF运动过程中,当EF经过点C时,求FC的长;
(3)在三角板DEF运动过程中,设BF=x
角板重叠部分的面积为y,求y与x的函数表
达式,并求出对应的x的取值范围.
【当堂检测】
1.(2014•菏泽)如图,Rt △ABC 中,AC =BC =2,正方形CDEF 的顶点D 、F 分别在AC 、BC 边上, C 、D 两点不重合,设CD 的长度为x ,△ABC 与正方形CDEF 重叠部分的面积为y ,则下列图象中 能表示y 与x 之间的函数关系的是( )
3. (2014·云南昆明)如图,在平面直角坐标系中,抛物线)0(32
≠-+=a bx ax y 与x 轴交于 点A (2-,0)、B (4,0)两点,与y 轴交于点C. (1)求抛物线的解析式;
(2)点P 从A 点出发,在线段AB 上以每秒3个单位长度的速度向B 点运动,同时点Q 从B 点 出发,在线段BC 上以每秒1个单位长度向C 点运动.其中一个点到达终点时,另一个点也停止 运动.当△PBQ 存在时,求运动多少秒使△PBQ 的面积最大,最多面积是多少?
(3)当△PBQ 的面积最大时,在BC 下方的抛物线上存在点K ,使2:5S PBQ CBK =△△:S , 求K 点坐标.
.
B .
.
D .
评价: 日期:。
