小学一年级奥数9、填图与拆数(三)
奥数 一年级 教案 第八讲:填图与拆数——教师版

填图与拆数
1.请你把1、2、3这三个数填在下图中的方格中,使每行、每列和每条对角线上的三个数
字之和都相等.
2.在幻方中填入适当的数使得幻方中满足每行,每列,每条对角线上三个数的和相等。
(下
划线的是后填入的数字)
3.下列是两个幻方,你能根据左边的幻方,推测出右面的幻方怎么填吗?
答案:
方法:右图中每个数都是左图中相同位置数加上9
4. 如下面左图所示有八张卡片.卡片上分别写有1、2、3、4、5、6、7、8八个数.现在请你
重新按右图进行排列,使每边三张卡片上的数的和等于 (1)13; (2)
15
参看仁华课本第九讲例3
5. 如果要求幻方中填入适当的数使得幻方中满足每行,每列,每条对角线上三个数的和相
等。
请问幻方中A 处应该是几?
答案:如图中箭头所示,设箭头所在方格为B,因为两个箭头所在的对角线和横行三个数之和相等,并且他们都共有方格B。
所以7+17=A+18,所以A=6
6.在幻方中填入适当的数使得幻方中满足每行,每列,每条对角线上三个数的和相等。
解答:运用例5的结论,在箭头的方向上,9+6=10+5,所以左上角的方格填5。
填完如下图。
5+6+7=18。
继续填完所有方格。
【思维拓展】数学一年级思维拓展之填图与拆数(二)(附答案)

小学一年级奥数-填图与拆数(二)1.见图。
把2、3、4、5、6、7、8、9、10、11填入右图空白圆圈内,使每个大圆上四个小圆圈内的数的和都是29。
你能填吗?2.见图。
把2、3、4、6、7、10、11分别填入大圆上的小圆圈内,使每个圆上四个小圆圈中的数字和都是24。
你能填吗?3.见图。
把2、3、4、5、6填入右图的五个方格里,使横行、竖行的三个数之和等于:①11、②12、③13。
4.见图。
把5、6、7、8、9、10六个数分别填入右图中的六个圆圈里,使三角形每条边上的三个数之和都等于21。
5.见图。
把1、2、3、4、5、6、7、8、9、10这十个数分别填入圆圈里,使每个正方形的四个数相加之和都等于24。
6.见图。
把1、2、3、4、5、6、7填入右图圆圈中,使横行、竖行、斜行三个圆圈中的数相加之和都等于12。
7.见图。
把11、12、13、14、15、16、17七个数填入右图的圆圈中,使横行、竖行的圆圈中的每三个数之和都是42。
8.见图。
把1、2、3、4、5、6、7、8、9、10、11这十一个数,分别填入图中空格内,使相邻的两个或三个空格内的和等于①14、②15。
9.把1、2、3、4、5、6、7、8、9各数分别填入“七一”图形中的九个空格内,使每一横行、竖行的四个、三个或两个空格中的数相加之和都等于13。
(见下图)10.见下图。
把1、2、3、4、5、6、7各数填入“十一”图形中的七个空格里,使每一横行、竖行的三个或两个空格中的数相加之和都是10。
参考答案1.解:见图。
找关键数先填。
三个大圆相交处的小圆圈中的数是关键数。
仔细观察。
图中一个大圆上已有9和7两个数,所以这个大圆上A,B两个小圆圈(如图示)所填的两数之和应为29-(9+7)=13。
把13分拆成两数之和(注意要选用题中已给的数)只有11+2和8+5两种分拆方式可供选用;经试验可知8和5这组数不合用,只能选用11和2这组数。
最后可确定将11填入三个大圆相交处的A圈中。
小学二年级奥数(上册) 第九讲 填图与拆数(附习题及解答)
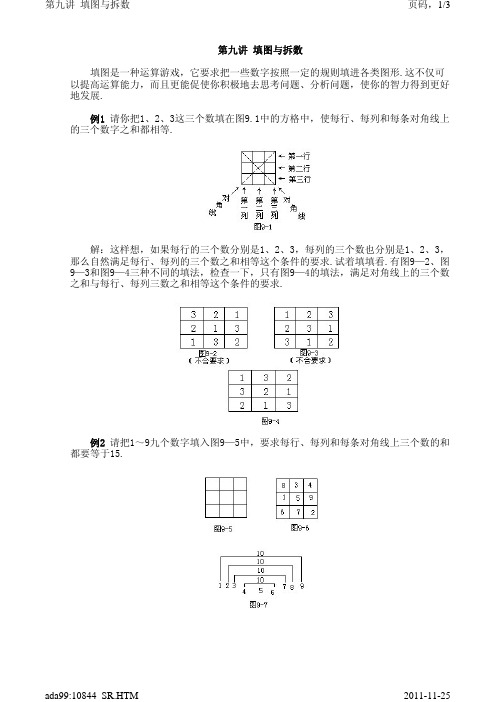
第九讲 填图与拆数填图是一种运算游戏,它要求把一些数字按照一定的规则填进各类图形.这不仅可以提高运算能力,而且更能促使你积极地去思考问题、分析问题,使你的智力得到更好地发展.例1 请你把1、2、3这三个数填在图9.1中的方格中,使每行、每列和每条对角线上的三个数字之和都相等.解:这样想,如果每行的三个数分别是1、2、3,每列的三个数也分别是1、2、3,那么自然满足每行、每列的三个数之和相等这个条件的要求.试着填填看.有图9—2、图9—3和图9—4三种不同的填法,检查一下,只有图9—4的填法,满足对角线上的三个数之和与每行、每列三数之和相等这个条件的要求.例2 请把1~9九个数字填入图9—5中,要求每行、每列和每条对角线上三个数的和都要等于15.解:从1~9这九个数字中,5是处于中间的一个数,而4与6,3与7,2与8,1与9之和都正好是10.所以5应当填在中心的空格中,而其他八个数字应当填到周边的方格中.上面图9—6就是一个符合要求的解答,把5填在中心空格后,尝试几次是不难得出这种答案的.例3 如下面图9—9所示有八张卡片.卡片上分别写有1、2、3、4、5、6、7、8八个数.现在请你重新按图 9—10进行排列,使每边三张卡片上的数的和等于:①13,②15.解:①要使每边三张卡片上的数相加之和等于13时,就要将13分拆成三个数之和.以上的分拆是分两步进行的.可以看出,因为8+5=13,所以8和5不能填在同一边(若把8和5填在同一边,再加上第三个数时必然会大于13,这不符合题目要求),也就是说,要把8和5分别填在相对的两个角上的方格里.如图9—11所示.②要使每边三张卡片上的数相加之和等于15时,就要将15分拆成三个数之和:以上的分拆也是分两步进行的.可以看出,因为8+7=15,所以8和7不能填在同一边,也就是说,要把8和7分别填在相对的两个角的方格里,如图9—12所示.例4 图9—13是由八个小圆圈组成的,每个小圆圈都有直线与相邻的小圆圈相接连.请你把1、2、3、4、5、6、7、8八个数字分别填在八个小圆圈内,但相邻的两个数不能填入有直线相连的两个小圆圈(例如,你在最上头的一个小圆圈中填了5,那么4和6就不能填在第二层三个小圆圈中了).解:答案如图9—14所示.中间的两个圈只能填1和8,是这样分析出来的:在1、2、3、4、5、6、7、8这八个数字中,只有“1”和“8”这两个数,各有一个相邻的数,也就是有六个不相邻的数.中间的两个小圆圈,每个都有六条线连着六个小圆圈,每个小圆圈中恰好能填一个与它不相邻的数.其余的数每个都有两个相邻的数,如4有两个相邻的数2和3,所以在1至8这八个数中4只有五个不相邻的数,这样4就不能填到中间的小圆圈中了.习题九1.在图9—15,9—16中,只能用图中已有的三个数填满其余的空格,并要求每个数字必须使用3次,而且每行、每列及每条对角线上的三个数之和都必须相等.2.把10、12、14这三个数填在图9—17的方格中,使每行、每列和每条对角线上的三个数之和都相等.3.在图9—18中,三个圆圈两两相交形成七块小区域,分别填上1~7七个自然数,在一些小区域中,自然数3、5、7三个数已填好,请你把其余的数填到空着的小区域中,要求每个圆圈中四个数的和都是15.4.与第3题的图相似,只是已经把1、4、6三个数填好,请你继续把图9—19填满.5.图9—20中有三个大圆,在大圆的交点上有六个小圆圈.请你把1、2、3、4、5、6六个数分别填在六个小圆圈里,要求每个大圆上的四个小圆圈中的数之和都是14.6.图9—21是由四个三角形组成的,每个三角形上都有三个小圆圈.请你把1、2、3、4、5、6、7、8、9这九个数填在九个小圆圈中,让每个三角形上的三个数之和都是15.7.图9—22是由四个扁而长的圆圈组成的,在交点处有8个小圆圈.请你把1、2、3、4、5、6、7、8这八个数分别填在8个小圆圈中.要求每个扁长圆圈上的四个数字的和都等于18.习题九解答1.解:因为空格中只能用4、6、8填,不难看出左上角的空格只能填6,见图9—23.同样道理,右下角也只能填6,见图9—24.下一步就能容易地填满其他空格了(见图9—25).在图9—16中,显然右下角应填7,见图9—26.而右上角应填5,见图9—27.这样其他空格随之就可以填满了,见图9—28.2.解:模仿例1的填法.首先将10、12、14三个数的中间数12填在中心方格中,并使一条对角线上的三个数都是12,见图9—29,第二步再按要求填满其他空格就容易了,见图9—30.3.解:这样想,图9—18中还空着四个小区域需要填入四个数:1、2、4、6.还可看出中心的一个小区域属于三个圆圈,这里应填哪个数呢?下面用拆数方法来分析确定.先见图9—18中的圆圈Ⅰ,圆中已有两个数5和7,所以空着的两个小区域应填的两个数之和为15-5-7=3.再将3分拆成3=1+2,但是在1和2中应把哪一个填到中心的小区域里,现在还不能肯定下来.再看圆圈Ⅱ,圆中已有两个数5和3,15-5-3=7,而7=1+6,即可把7分拆成7=1+6.最后看圆圈Ⅲ,15-3-7=5,而5=1+4.至此可以看出,应该把“1”填在中心的小区域了(见图9—31).4.解:模仿第3题解法拆数:要填2、3、5、7.15-4-6=5,5=2+315-1-6=8,8=3+515-1-4=10,10=3+7所以,应把3填在中心的小区域,见图9—32.5.解:如图9—33所示,因为要求大圆上的四个小圆圈中的四个数之和等于14,所以就要把14分拆成四个数相加之和,而且按题目要求这四个数要在1、2、3、4、5、6中选取;14=6+5+2+1,14=6+4+3+1,14=5+4+3+2.6.解:先将15分拆成三个数之和,并且要求各数在1、2、3、4、5、6、7、8、9这九个数中选取.用二步分拆法:15=9+6=9+5+115=8+7=8+4+315=7+8=7+6+2以上三式把九个数都用上了.这样(9,5,1)、(8,4,3)和(7,6,2)就可以分别填入角上的3个三角形中.再注意到中间的三角形的三个小圆圈分属于角上的3个三角形,所以从三组中各取一个数重新组成一组填入中间三角形,如取(9,4,2),填出下面的结果,见图9—34.注意此题填法不惟一,你还能想出别种填法吗?7.解:因为题目要求扁长圆圈上的四个数之和等于18,所以就要将18分拆成四个不相等的整数之和,而且各数要从1~8这八个数中选取.如:18=8+7+2+118=8+5+2+318=7+6+4+118=6+5+4+3即得到四组数:(8,7,2,1)、(8,5,2,3)、(7,6,4,1)、(6,5,4,3),把它们填入扁长圆圈时,注意适当调整,就可以得出题目的答案如图9—35所示.。
一年级下册数学奥数题课件 九宫格 全国通用 (共18张PPT)

什么是九宫格?
手机的解锁界面是九宫格。 魔方的每一面也是九宫格。
PART 1
九宫格
将1—9这九个数字排成三列,不论纵列、横列、斜列,每 列三个数相加都是15,如何排列?
12 3 4 5 6 7 8 9
①② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨
2
94
15
7 5 3 15
九宫之意,法以灵鬼, 二四为肩,六八为足, 左七右三,戴九履一, 五居中央。
① ②③④ ⑤ ⑥ ⑦ ⑧ ⑨
19 35 51 96 112 128 173 189 205
① ②③④ ⑤ ⑥ ⑦ ⑧ ⑨
二四为肩,六八为足, 左三右七,戴九履一,
35
205 96
336
五居中央。
51 112 173 336
按口诀填上序 号对应的数字。
128 19 189 336
336 336 336 336 336
①② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨
9 16 11 36 14 12 10 36
九宫之意,法以灵鬼, 二四为肩,六八为足, 左七右三,戴九履一, 五居中央。
13 8 15 36
36 36 36 36 36
PART 2
实战演练2
将16、17、18、19、20、21、22、23、 24这6个数,使其每一行,每一列,每 条对角线相加为60。
60 60 60
16、17、18、19、20、21、22、23、24
12 34 5 67 8
9 九宫之意,法以灵鬼, 二四为肩,六八为足, 左七右三,戴九履一, 五居中央。
60 60 60 60 60
PART 3
实战演练3
我们把这9个数字按从小到大的顺序 写下来,依次是: 19 35 51 96 112 128 173 189 205
一年级下册奥数填图与拆数【三篇】

一年级下册奥数填图与拆数【三篇】天高鸟飞,海阔鱼跃,学习这舞台,秀出你独特的精彩用好分秒时间,积累点滴知识,解决疑难问题,学会举一反三。
以下是小编为大家整理的《一年级下册奥数填图与拆数【三篇】》供您查阅。
【第一篇】例1 如右图,把3、4、6、7四个数填在四个空格里,使横行、竖行三个数相加都得_。
怎样填?解:先看竖行,最上格中已有个5。
要使5+()=_,括号里的数就要填9。
把9拆成两个数:9=3+6,(因为3和6是题中给出的数)分别填在竖行的两个空格里。
但进一步想,应该把哪一个填在中间空格里呢?这就需要看横行。
横行两头的空格应填剩下的两个数4和7,因为4和7相加和为_,而_+3=_,可见中间空格应填3。
【第二篇】例 2 如图所示。
在圆圈里填上不同的数,使每条直线上三个数相加之和都等于_。
解:见下图(1)、(2)、(3)。
把_分拆成三个不同的数相加之和,得七种分拆方式:_=9+2+1 _=8+3+1_=7+4+1 _=7+3+2_=6+5+1 _=6+4+2_=5+4+3从各式中选择有一个相同加数的两个式子。
_=1+5+6和_=1+4+7两式,将相同的加数1填在中间圆圈里,不同的加数分别填在横行和竖行的其他圆圈里。
答案有很多种不同的填法,这里只填了三种,同学们还可以自己选择另外的填法。
【第三篇】例3 如右图所示。
把1、2、3、4、5五个数填入五个圆圈里,要求分别满足以下条件:(1)使横行、竖行圆圈里的数加起来都等于8;(2)使横行、竖行圆圈里的数加起来都等于9;(3)使横行、竖行圆圈里的数加起来都等于_。
解:见下图(1)、(2)、(3)(1)将8分拆成三个数之和(注意,这三个数要从1、2、3、4、5中选取) 8=1+2+5 8=1+3+4因为中间圆圈里的数是要公用的,所以应把“1”填在中间圆圈里其他四个数填在边上;(2)解法思路与(1)相同,分拆方式如下:9=1+3+5 9=2+3+4(3)解法思路与(1)相同_=1+4+5 _=2+3+5。
一年级奥数巧填数阵图

第十二讲巧填数阵图数学乐园晶晶和莹莹来到了雪精灵国,天空中到处飘着洁白剔透的雪花,就像下面图中的样子.一个雪精灵告诉她们:“你们只要能够把1~7这七个数填在雪花的七个花瓣上,使每三个位于同一直线上的花瓣上的数之和都相等,你们就能见到雪精灵国的女王了.”你能帮她们填一填吗?.小朋友们,你喜欢这样的填数字游戏吗?要想准确的填出图中的每一个数,可不是一件容易的事,这就要我们小朋友们认真去观察图,观察数字的排列规律,这样才能找到填图的方法.下面我们就一起来学习吧!基础篇使用数字0,1,2,3,4,5,6,7,8,9做加法.在每一道题中,同一个数字不能重复出现.拓展练习(1)填数,使横行、竖行的三个数相加都得11. (2)填数,使每条线上的三个数之和都得15.在每个方格中填入适当的数,使每一横行、竖行的和以及两斜行的三个数之和都是18.要使表格中每行、每列和两条对角线上的三个数的和都为18,下面每个方框里应填什么数?拓展练习在下列两图的空格中填上数,使横行和竖行或每条对角线上的三个数相加都等于15.把1,2,3,4,5,6六个数,分别填入○内,使每条线上3个数的和相等.提高篇把3,4,5,6,7这五个数分别填入下面的空格里,使横行、竖行的三个数相加都得15.拓展练习把2,3,4,5,6这五个数分别填入圆圈中,使每条线上三个数相加的和都等于1 2.把1,2,3,4,5,7分别填入○里,使每一个大椭圆上的四个数之和等于13.把1,2,3,4,5,6,7这七个数分别填入○里,使每条直线上的三个数相加的和都为12.拓展练习把1~9这九个数字填入下列圆圈内,使每条横线、竖线、斜线连接起来的三个圆圈内的数之和都等于15.把2,3,4,5,6,7,8这七个数分别填入圆圈中,使两个正方形中四个数之和相等19.拓展:如果使两个正方形中四个数之和相等21,又应该怎样填?我会做一做把1,2,3,4,5,6,7这7个数分别填入右图中,使得每条直线上的3个数的和相等.练习十二1. 在下面的○里填上适当的数,使每条线上的三个数之和都是12.2.把3~8这6个数,填在下图中使得每行、每列和两条对角线上的三个数的和都为18.3. 把1,2,3,4,5这五个数分别填入下面的○里,使横行、竖行的三个数相加都得10.4. 把3,4,5,7,9,11,13这七个数分别填入○里,使每条直线上的三个数相加的和都为20.5. 将1,2,3,4,5,6这6个数分别填入下图中,使两个大圆上4个数的和都等于14.6.把数字1,2,3,5,6,7,9填在下面的○里,使每边上的和为15.小朋友,你在少年宫里走过“勇敢者的道路”吗?道路崎岖,充满艰难险阻.但是,它能培养小朋友的勇敢精神和不怕困难的毅力.这里有两幅图,也叫“勇敢者的道路”.图中的道路狭窄、曲折,不易通过,需要小朋友细心和有耐心.现在请小朋友用一枝铅笔,按照图中箭头的方向画出通行路线,而且线条不能碰到两边的“围墙”.小朋友,这可真不容易哦!。
一年级9宫格数学题

一年级9宫格数学题可以用500-800字回答如下:题目:这是一个9宫格数学游戏。
每个数字在每一行、每一列和每个宫内只能出现一次。
根据给定的数字,完成这个九宫格,使数字1-9每个数字都出现在九宫格中且每个数字只出现一次。
解答:观察九宫格可以发现,每个数字在每一行、每一列和每个宫内都只出现一次,所以解题的关键是合理地安排数字的位置,使得每行、每列和每个宫内包含1-9的数字,并且不重复。
首先,我们可以通过观察可以发现,九宫格的上半部分(从第1列到第5行)应该填充1-5这五个数字。
在下半部分(从第6列到第9行),应该填充另外四个数字,根据题目要求不能重复,因此可以考虑使用除1-5之外的其他数字。
具体来说,我们可以按照以下步骤安排数字的位置:1. 将数字6放在第6列,数字7放在第7行,形成新的行、列和宫的组合。
2. 将数字8放在第1列,形成新的行和宫的组合,同时满足该列包含数字6和8。
3. 将数字9放在第5行,形成新的列和宫的组合,同时满足该行包含数字3和9。
此时,我们可以看到每行、每列和每个宫内都包含了1-9的数字,并且没有重复。
至此,九宫格已经填满。
推理过程:从上面的推理过程可以看出,我们需要按照题目要求进行合理安排数字的位置,并考虑到行、列和宫内组合的限制条件。
具体来说,我们需要考虑到每个数字的位置是否会影响到其他数字的位置安排,是否符合题目要求每行、每列和每个宫内只出现一个数字。
解题技巧:对于一年级学生来说,在解决这类问题时可以从最简单的题目入手,逐步提高难度。
可以通过观察、尝试、调整等方法来安排数字的位置,并注意观察每行、每列和每个宫内数字的变化情况。
同时,可以多练习一些类似的题目,积累解题经验和方法。
总结:通过上面的解答过程可以看出,解决九宫格数学题的关键是合理安排数字的位置,并考虑到行、列和宫内组合的限制条件。
对于一年级学生来说,可以从最简单的题目入手,逐步提高难度,积累解题经验和方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7.见图。
把11、12、13、14、15、16、17七个数填入右图的圆圈中,使横行、竖行的圆圈中的每三个数之和都是42。
8.见图。
把1、2、3、4、5、6、7、8、9、10、11这十一个数,分别填入图中空格内,使相邻的两个或三个空格内的和等于①14、②15。
9.把1、2、3、4、5、6、7、8、9各数分别填入“七一”图形中的九个空格内,使每一横行、竖行的四个、三个或两个空格中的数相加之和都等于13。
(见下图)
10.见下图。
把1、2、3、4、5、6、7各数填入“十一”图形中的七个空格里,使每一横行、竖行的三个或两个空格中的数相加之和都是10。
习题解答
1.解:见图。
找关键数先填。
三个大圆相交处的小圆圈中的数是关键数。
仔细观察。
图中一个大圆上已有9和7两个数,所以
这个大圆上A,B两个小圆圈(如图示)所填的两数之和应为29-(9+7)=13。
把13分拆成两数之和(注意要选用题中已给的数)
只有11+2和8+5两种分拆方式可供选用;经试验可知8和5这组数不合用,只能选用11和2这组数。
最后可确定将11填入三个大圆相交处的A圈中。
接着可较容易地填上其他数了。
2.解:见图。
由中间的大圆圈上的三个已知数1,5,8,可求出这个大圆上的最后一个数:24-(1+5+8)=10,这样还剩下2、3、4、6、7、11六个数未被选用。
应把它们分别填入六个小圆圈。
仔细观察可知:
另外的两个大圆相交处的小圆圈(B圈)中的数是关键数。
而且有一个大圆上已经给出了数9,所以该大圆上其余三个小圆圈所填数之和应为24-9=15。
因而将15分拆成三个数之和(注意必须选用题中所给的数)
15=7+6+2
经尝试B圈中只能填6。
然后再确定左边大圆上三个小圆圈应填的数是11、4和3。
3.解:见下图,解题思路与例3相同,略写如下:
2+3+4+5+6=20。
①11+11-20=2即中间格填2。
②12+12-20=4即中间格填4。
③13+13-20=6即中间格填6。
4.解:见图解题思路与例4相同,略写如下:
21+21+21=63
5+6+7+8+9+10=45
63-45=18(三个角上的三个数之和)
分拆18=5+6+7即三个角上的三个圆圈里应填5、6、7。
5.解:见图,
找关键数先填,不难看出,标有字母A和B的两圆圈中的数是关键数,因为它们是正方形公用的数,解法:
1+2+3+4+5+6+7+8+9+10=55
24+24+24=72
72-55=17
17=10+7=9+8(这就是两组关键数10和7,以及9和8)。
6.解:见图,找关键数先填。
不难看出,中间圆圈里的数是关键数。
求关键数:
1+2+3+4+5+6+7
=28
12+12+12=36
36-28=8(相当两个中间圆圈里的数之和)
8÷2=4(就是一个中间圆圈里的数)
12-4=8
行三个数之和他是12。
7.解:先求关键数:横行和竖行公用的两个圆圈的数是关键数。
11+12+13+14+15+16+17=98
42+42+42=126
126-98=28(28是横行和竖行公用的两个圆圈里的数的和)将28分拆:
(见下面三个图)。
8.解:先求关键数。
六字的“点”和“横”公用的方格中的数是关键数。
方法1:
14×5=70
1+2+3+4+5+6+7+8+9+10+11=66
公用的方格中的数是70-66=4再适当选择其他的数填入其他空格。
方法2:见下图
15×5=75 75-66=9
公用的方格中填9,再适当选择其他各数填入方格。
9.解:见下图,求关键数即共用方格中的数
1+2+3+4+5+6+7+8+9=45
13×4=52 52-45=7
10.解:见下图,先确定“十”字中间方格中的数
1+2+3+4+5+6+7=28
10×3=30
30-28=2(中间方格中的数)。
经典例题:
本讲主要介绍在填图与拆数中找关键数的思考方法。
1 如右图所示。
把三个1、三个2、三个3分别填在九个格内,使横行、竖行、斜行三个数加起来的和都等于6。
解:找关键数先填。
因为中间格的数和横行、竖行、斜行都有关,所以它是关键数,确定了它,其他各格就容易填了。
(1)尝试法:若中间填“1”,再填其他格,如右图。
结果有一条斜线上的数都是1,其和为3,不合题目要求。
若中间格填“3”,再填其他格,如右图结果有一条斜行上的数都是3,其和为9,不合题目要求。
若中间格填“2”,再填其他格,经检查,符合题目要求,如图。
(2)分析法:显然在每一横行、竖行和斜行只能填一个“1”或一个“3”。
因为若填两个1后,即使再填一个最大的3,这一行的这三个数之和才是5,小于6,不符合题目要求;同样,若填两个3后,即使再填一个最小的数1,这一行的三个数之和就是7,大于6,也不符合题目要求。
如果在一行里填入两个“2”,即使在此行里再填一个2,这一行的三个数之和也可等于6,符合题要求。
由此得出,中间方格必须填“2”。
中间方格填好之后其他各格中的数也就容易填出了。
2 如图。
把1、2、3、4、5填入右图的圆圈中,使每条斜线上的三个数相加之和都是8。
解:中间圆圈里的数是个关键数,应该首先确定它。
如何确定它呢?这样想:假如我们已经按题目要求把1、2、3、4、5填入了五个圆圈中,这样每条斜线上的三个数相加都得8。
那么当我们把两条斜线上的数都加起来,它们的和应为8+8=16,
但是五个圆圈中所填数之和应为
1+2+3+4+5=15,
两个和数之差是1,即:16-15=1。
这个差是如何产生的呢?这是因为把两条斜线上的和数相加时,中间圆圈中的数被加了两次,即多加了一次。
把一个数多加了一次和就多了1,可见此数是1。
然后,再求每条斜线两端的数。
可求出两数之和应为8-1=7把7分拆成两个数,有两种分拆方式:
把2和5填入一条斜线两端的圆圈中。
把3和4填入另一条斜线两端的圆圈中。
3 如图所示。
把1、2、3、4、5、6、7七个数填在右图中的七个圆圈里,每个数只能用一次,使每条线上的三个数相加之和都等于12。
解:见图。
中间圆圈里的数是关键数,应该如何确定它呢?
与例2的想法类似。
假设已经按题目要求把数全部填入了圆圈,那么每条线上的三个圆圈中的数相加应该都得12。
我们如果进一步把三条直线上的数都加起来,得数应为:12+12+12=36。
不难看出,这样就把中间圆圈里那个数加了三次。
因而它比七个圆圈中的数相加之和:1+2+3+4+5+6+7=28
多了 36-28=8
也就是8应是中间圆圈里的数的2倍所以中间圆圈里的数应是8的一半,
即 8÷2=4
下面再确定每条线上另外的两个圆圈里的数,方法如下:12-4=8
4 如图所示。
把1、2、3、4、5、6六个数分别填入右图的圆
圈里,使三角形每条边上三个数之和都等于9。
解:见图。
三个角上圆圈里的数是关键数,因为它们中的每个都是两条边上共有的数。
先确定关键数。
这样想:六个数之和是1+2+3+4+5+6=21每条边上三个数之和是9,9+9+9=27这样算每个角上圆圈里的数都被加了两次,因此角上三个圆圈中的数之和是
27-21=6
把6分拆成三个数之和:6=1+2+3;
把1、2、3分别填入三个角上的圆圈里,其余的圆圈里的数就容易填了。
