振动波动部分例题及作业
振动波动作业习题及解答

Ch.10.振动、Ch.11波动作业习题及解答AωOXt =0图2A图1ωt =0OX=010-1. 一小球与轻弹簧组成的谐振动系统,振动规律为0.05cos(8π3),x =t +π(t 的单位为秒, x 的单位为米)。
求: (1) 振动的角频率、周期、振幅、初相、速度和加速度的最大值; (2) t =1s 、t =2s 、t =10s 时刻的相位; (3) 分别画出位移、速度和加速度与时间的关系曲线。
解(1): 将小球的运动方程0.05cos(8π3),x =t +π与谐振动的表达式0cos()x A t ωϕ=+比较知,系统的角频率、周期、振幅和初相分别为:108π(s );=2(4)s ;0.05(m );3;T A πωπωπϕ-====系统振动速度、加速度的表式分别为02220sin(4sin(8π3)(m s);cos( 3.2cos(8π3)(m s )v =dx /dt =-A t t +πa =dv /dt =-A t t +πωωϕπωωϕπ+)=-0.+)=-速度和加速度的最大值为:12220.4π 1.26(m s );=3.2π31.6(m s )m m v A a A ωω--==≈=≈ 解(2): 由相位表达式0()8/3t t t ϕωϕππ=+=+知, t =1s 、t =2s 、t =10s 时刻振子的相位分别为:2549241333333(1s )8π(2s )16(10s )80t +t t +ππππππϕϕπϕπ=====+====;; 解(3): x (t ), v (t ), a (t )曲线如下图所示。
10-2.(选作题)某个与轻弹簧相连的小球,沿X 轴作振幅为A 的简谐振动,周期为T 。
其振动表达式用余旋函数表示。
若t =0时小球的运动状态分别为:(1) 0x A =-; (2) 过平衡位置向X正向运动; (3) 过x =0.5A 向X 负向运动; (4) 过x =X 正向运动。
振动和波动习题课(改)

x)
yBP
Acos[ t
2
(30 x)]
l
两波同频率,同振幅,同方向振动,所以相干静止的点满足:
(t 2 x) [t 2 (30 x)]
l
l
(2k 1)
k 0,1,2,...
化简后 30 2x kl
30 2x kl O x
X
因为: l u 4m
x 15 k 2
1
3
x 3 102 sin(4t 1 ) (SI)
2
6
画出两振动的旋转矢量图,并求合振动的振动
方程.
x1
5
102
cos(4t
1 3
)
x2
3
102
sin(4t
1 6
)
3
102
cos(4t
1 6
1 2
)
3 102 cos(4t 2 ) 3
x x1 x2
1
2 102 cos(4t 1 )
7.一简谐振动曲线如图所示,试由图确
定在t=2s时刻质点的位移为
,速
度为
。
t=2s, x=0
Vm
A
2 A
T
3
102
8.已知两个简谐振动 曲线如图所示,
X1的位相比X2的位相
A) 落后 1
2
C) 落后
B) 超前 1 √
2
D) 超前
9.一简谐振动的振动曲线如图,求此振动的 周期。
解: =/3+ /2=5/6 t=5= 5/6 = /6
2
之间)
(1)2 1 2k k 0,1,2,
A A1 A2 振动加强; 此时有= 1= 2
A1
大学物理振动波动例题习题

振动波动一、例题(一)振动1.证明单摆是简谐振动,给出振动周期及圆频率。
2. 一质点沿x 轴作简谐运动,振幅为12cm ,周期为2s 。
当t = 0时, 位移为6cm ,且向x 轴正方向运动。
求: (1) 振动表达式;(2) t = 0.5s 时,质点的位置、速度和加速度;(3)如果在某时刻质点位于x =-0.6cm ,且向x 轴负方向运动,求从该位置回到平衡位置所需要的时间。
3. 已知两同方向,同频率的简谐振动的方程分别为:x 1= 0.05cos (10 t + 0.75π) 20.06cos(100.25)(SI)x t π=+求:(1)合振动的初相及振幅.(2)若有另一同方向、同频率的简谐振动x 3 = 0.07cos (10 t +ϕ 3 ), 则当ϕ 3为多少时 x 1 + x 3 的振幅最大?又ϕ 3为多少时 x 2 + x 3的振幅最小?(二)波动1. 平面简谐波沿x 轴正方向传播,振幅为2 cm ,频率为 50 Hz ,波速为 200 m/s 。
在t = 0时,x = 0处的质点正在平衡位置向y 轴正方向运动,求:(1)波动方程(2)x = 4 m 处媒质质点振动的表达式及该点在t = 2 s 时的振动速度。
2. 一平面简谐波以速度m/s 8.0=u 沿x 轴负方向传播。
已知原点的振动曲线如图所示。
求:(1)原点的振动表达式;(2)波动表达式;(3)同一时刻相距m 1的两点之间的位相差。
3. 两相干波源S 1和S 2的振动方程分别是1cos y A t ω=和2cos(/2)y A t ωπ=+。
S 1距P 点3个波长,S 2距P 点21/4个波长。
求:两波在P 点引起的合振动振幅。
4.沿X 轴传播的平面简谐波方程为:310cos[200(t )]200x y π-=- ,隔开两种媒质的反射界面A 与坐标原点O 相距2.25m ,反射波振幅无变化,反射处为固定端,求反射波的方程。
波动与振动-答案和解析

1. 一简谐振动的表达式为)3cos(ϕ+=t A x ,已知0=t 时的初位移为, 初速度为s -1,则振幅A = ,初相位 =解:已知初始条件,则振幅为:(m )05.0)309.0(04.0)(222020=-+=-+=ωv x A 初相: 1.1439.36)04.0309.0(tg )(tg 1001或-=⨯-=-=--x v ωϕ因为x 0 > 0, 所以 9.36-=ϕ2. 两个弹簧振子的的周期都是, 设开始时第一个振子从平衡位置向负方向运动,经过后,第二个振子才从正方向的端点开始运动,则这两振动的相位差为 。
解:从旋转矢量图可见,t = s 时,1A 与2A反相,即相位差为。
3. 一物块悬挂在弹簧下方作简谐振动,当这物块的位移等于振幅的一半时,其动能是总能量的 (设平衡位置处势能为零)。
当这物块在平衡位置时,弹簧的长度比原长长l ∆,这一振动系统的周期为 解:谐振动总能量221kA E E E p k =+=,当A x 21=时4)2(212122EA k kx E p ===,所以动能E E E E p k 43=-=。
物块在平衡位置时, 弹簧伸长l ∆,则l k mg ∆=,lmgk ∆=,振动周期gl km T ∆==ππ224. 上面放有物体的平台,以每秒5周的频率沿竖直方向作简谐振动,若平台振幅超过 ,物体将会脱离平台(设2s m 8.9-⋅=g )。
解:在平台最高点时,若加速度大于g ,则物体会脱离平台,由最大加速度g A v A a m ===22)2(πω 得最大振幅为1A 1A 2Ax=t .0=t 5.0=t(m)100.11093.9548.94232222--⨯≈⨯=⨯==ππv g A 5. 一水平弹簧简谐振子的振动曲线如图所示,振子处在位移零、速度为A ω-、加速度为零和弹性力为零的状态,对应于曲线上的 点。
振子处在位移的绝对值为A 、速度为零、加速度为-2A 和弹性力-kA 的状态,对应于曲线的 点。
振动波动例题

解:
t =0
x =0 y =0
y0= 0.03 cos(2 ×2.5 t π ) π 2
v0
π j= 2
π 2 x π y = 0.03 cos 2 ×2.5 t 2 π 0.24 π 50 x π 0.03 cos 5 t π =
2 6 0.03 cos 5 (t 10 x ) π π = 2 6
例1. 有一个和轻弹簧相联的小球,沿x 轴作振幅为A的简谐振动,其表达式用余弦 函数表示。若t =0 时,球的运动状态为: (1)x0=-A; (2)过平衡位置向x 正方向运动; (3)过x=A/2处向 x 负方向运动; A (4)过 处向 x 正方向运动; 2 试用矢量图示法确定相应的初相的值,并写 出振动表式。
由波形图得:t =1/3 s时
y/cm
10
x0
v< 0 y0 =-0.05
o
-5
20
x/cm
1 0.05 0.1cos( j ) 3
1 2 j 3 3
j
3
波动方程为:
πx + π y =10cos π t 20 3
O点(x =0)的振动方程为:
cm (1)
π π 解: A =0.24m ω = 2 = 2 = π =1.57s-1 T 2 4 x 0 = A =0.24m φ =0 t =0 v0 = 0
振动方程为: x = 0.24 cosπ t 2 (1) t =0.5s cos (π × 0.5 ) x = 0.24 2 = 0.24 cos 0.25π
= 0.24 ×
2 =0.17m 2
(2)
大学物理习题详解—振动与波动部分
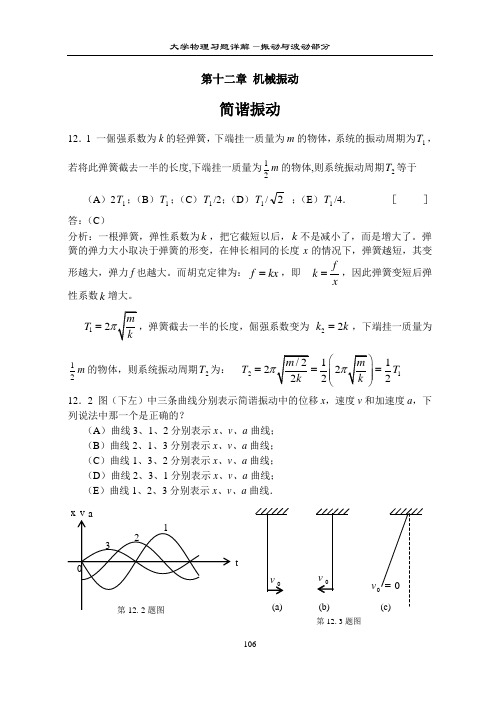
第十二章 机械振动简谐振动12.1 一倔强系数为k 的轻弹簧,下端挂一质量为m 的物体,系统的振动周期为1T ,若将此弹簧截去一半的长度,下端挂一质量为12m 的物体,则系统振动周期2T 等于 (A )21T ;(B )1T ;(C )1T /2;(D )1T /2 ;(E )1T /4. [ ] 答:(C )分析:一根弹簧,弹性系数为k ,把它截短以后,k 不是减小了,而是增大了。
弹簧的弹力大小取决于弹簧的形变,在伸长相同的长度x 的情况下,弹簧越短,其变形越大,弹力f 也越大。
而胡克定律为:f kx =,即 fk x=,因此弹簧变短后弹性系数k 增大。
12T = 22k k =,下端挂一质量为12m 的物体,则系统振动周期2T 为: 2T 1112222T ⎛=== ⎝ 12.2 图(下左)中三条曲线分别表示简谐振动中的位移x ,速度v 和加速度a ,下列说法中那一个是正确的?(A )曲线3、1、2分别表示x 、v 、a 曲线; (B )曲线2、1、3分别表示x 、v 、a 曲线; (C )曲线1、3、2分别表示x 、v 、a 曲线; (D )曲线2、3、1分别表示x 、v 、a 曲线; (E )曲线1、2、3分别表示x 、v 、a 曲线.第12. 3题图v (a)(b)t答:(E )分析:位移x 与加速度a 的曲线时刻都是反相的,从图上看曲线1、3反相,曲线2是速度v 曲线;另外,速度比位移的位相超前2π,加速度比速度的位相超前2π,从图上看曲线3比2超前了2π,3是加速度曲线;曲线2比1超前了2π,1是位移曲线12.3 在t =0时,周期为T 、振幅为A 的单摆分别处于图(上右)(a)、(b)、(c)三种状态,若选单摆的平衡位置为x 轴的原点,x 轴正向指向右方,则单摆作小角度摆动的振动表达式分别为(1) ; (2) ; (3) . 答:(1)X =A cos (t T π2-2π) (2)X =A cos (t T π2+2π) (3)X =A cos (t Tπ2+π). 分析:关键是写出初位相,用旋转矢量法最方便:ωx xx(a )φ= -π/2ω ω(b )φ= π/2(c )φ= π12.4 设振动周期为T ,则a 和b 处两振动的时间差t ∆=____________。
振动波动检测题解答
A, x k;
1 C , x (2k 1) ; 2
1 B, x k ; 2
D, x (2k 1) 4.
振动和波动检测题部分解答
解:
y y1 y2 A cos
2x 0
2x
cos 2t
cos
时
2x
(2k 1)
2
x (2k 1)
由(1)、(2)两式可得
m2 g k x
振动和波动检测题部分解答
m1x T 2 m2 g
应该选 B
振动和波动检测题部分解答
2 一简谐振动曲线如图所示,则振动周期为[ B ]
x(cm)
A,2.62s; C,2.20s;
B,2.40s; D,2.00s.
4 2
t (s )
1
o
振动和波动检测题部分解答
解:
2 振动方程为 x 4 10 cos( ) T
2
当t=0时,
x0 0.02
2 v0 A sin 0 T
3
2 x 4 cos( ) T 3
振动和波动检测题部分解答
t 1时,x 0
2 0 0.04 cos( ) T 3
y
B
O
x
L
振动和波动检测题部分解答
解:
t x 设 y反 A cos[ 2 ( ) ' ] T t L y入B A cos[ 2 ( ) ] T
y 反B
t L A cos[ 2 ( ) ] T
2L
反OB '
振动波动作业解
x A/2
2
5 3 2 6
ቤተ መጻሕፍቲ ባይዱ
2 T t 6 5 12s 5
2
2 t t T
物理系:史彭
史彭振动波动作业解
4.一质点作简谐振动,已知振动频率为 f,则振动动能的 变化频率是: [ B ]
1 1 2 E K m m[A sin( t )] 2 2 2
3 1 2 2 sin t cos t ] 10 2 [sin sin t cos cos t ] 10 2 3 3 2 2 2 cos(t ) 10 2 3 x / 2 2 y cos(t ) 10 2 u 3 2 2x 2 y cos(t ) 10 u 3
x’ x
1 x y Acos[ (t ) ] u
物理系:史彭
史彭振动波动作业解
2.一平面简谐波沿 OX 轴传播,波函数为 y A cos[2 (t x / ) ] , 则在X1=L处,介质质点振动的初相位是 ;与X1处质点振动 状态相同的其它质点的位置是 ;与X1处质点振动速度大小 相同,但方向相反的其它各质点的位置是 。 各点初相位 2x / y X1=L
3 sin (t ) 4
2
1 2 1 E kA m 2 A2 2 2
EK 3 E 4
物理系:史彭
史彭振动波动作业解
二、填空题 1.一质点作简谐振动,其振动曲线如图所示。根据此图, 它的周期 ;用余弦函数描述时初相位 。
2
x
7 t t 12
物理系:史彭
史彭振动波动作业解
2.一质点作简谐振动,周期为 T 。质点由平衡位置向 X 轴正方向运动时,由平衡位置到二分之一最大位移这段路 所需要的时间为 [ B ]
振动和波动计算题及答案
(2)x/8处振动方程为
1
yAcos[t(2/8)]Acos(t/4)1分
2
x3/8的振动方程为
3/81
yAcos[t2]Acos(t/4)1分
2
1
(3)dy/dtAsin(t2x/)
2
t=0,x/8处质点振动速度
1
dy/dtAsin[(2/8)]2A/21分
2
t=0,x3/8处质点振动速度
1
dy/dtAsin[(23/8)]2A/21分
解:由题意x1=4×10cos(2t)(SI)
4
y
-2
x2=3×10
cos(2t)(SI)
2
u
按合成振动公式代入已知量,可得合振幅及初相为
Ot=t′x
2324cos(/2/4)10
22
A4m
-2
=6.48×10
m2分
4sin(/4)3sin(/2)
arctg=1.12 rad2分
4cos(/4)3cos(/2)
(2)t= 3 s时的波形曲线方程
2x
y210cos(/10),(SI)2分
波形曲线见图2分
y(m)
y(m)
-2
2×10
u
O510152025
x(m)
O
-2
-2×10
1
234
t(s)
(b)
(a)
11.已知一平面简谐波的表达式为y0.25cos(125t0.37x)(SI)
(1)分别求x1= 10m,x2= 25 m两点处质点的振动方程;
(1)物体的振动方程;
(2)物体在平衡位置上方5 cm时弹簧对物体的拉力;
(3)物体从第一次越过平衡位置时刻起到它运动到上方5 cm处所需要的最短时间.
大学物理学振动与波动习题答案
大学物理学(上)第四,第五章习题答案第4章振动P174.4.1 一物体沿x轴做简谐振动,振幅A = 0.12m,周期T = 2s.当t = 0时,物体的位移x = 0.06m,且向x轴正向运动.求:(1)此简谐振动的表达式;(2)t = T/4时物体的位置、速度和加速度;(3)物体从x = -0.06m,向x轴负方向运动第一次回到平衡位置所需的时间.[解答](1)设物体的简谐振动方程为x = A cos(ωt + φ),其中A = 0.12m,角频率ω = 2π/T= π.当t = 0时,x = 0.06m,所以cosφ = 0.5,因此φ= ±π/3.物体的速度为v = d x/d t = -ωA sin(ωt + φ).当t = 0时,v = -ωA sinφ,由于v > 0,所以sinφ < 0,因此φ = -π/3.简谐振动的表达式为x= 0.12cos(πt –π/3).(2)当t = T/4时物体的位置为x= 0.12cos(π/2–π/3)= 0.12cosπ/6 = 0.104(m).速度为v = -πA sin(π/2–π/3)= -0.12πsinπ/6 = -0.188(m·s-1).加速度为a = d v/d t = -ω2A cos(ωt + φ)= -π2A cos(πt - π/3)= -0.12π2cosπ/6 = -1.03(m·s-2).(3)方法一:求时间差.当x = -0.06m 时,可得cos(πt1 - π/3) = -0.5,因此πt1 - π/3 = ±2π/3.由于物体向x轴负方向运动,即v< 0,所以sin(πt1 - π/3) > 0,因此πt1 - π/3 = 2π/3,得t1 = 1s.当物体从x= -0.06m处第一次回到平衡位置时,x = 0,v > 0,因此cos(πt2 - π/3) = 0,可得πt2 - π/3 = -π/2或3π/2等.由于t2 > 0,所以πt2 - π/3 = 3π/2,可得t2 = 11/6 = 1.83(s).所需要的时间为Δt = t2 - t1 = 0.83(s).方法二:反向运动.物体从x = -0.06m,向x轴负方向运动第一次回到平衡位置所需的时间就是它从x= 0.06m,即从起点向x 轴正方向运动第一次回到平衡位置所需的时间.在平衡位置时,x = 0,v < 0,因此cos(πt - π/3) = 0,可得πt - π/3 = π/2,解得t = 5/6 = 0.83(s).[注意]根据振动方程x = A cos(ωt + φ),当t = 0时,可得φ = ±arccos(x0/A),(-π < φ≦π),初位相的取值由速度决定.由于v = d x/d t = -ωA sin(ωt + φ),当t = 0时,v = -ωA sinφ,当v > 0时,sinφ < 0,因此φ = -arccos(x0/A);当v < 0时,sinφ > 0,因此φ = arccos(x0/A).可见:当速度大于零时,初位相取负值;当速度小于零时,初位相取正值.如果速度等于零,当初位置x0 = A时,φ = 0;当初位置x0 = -A时,φ= π.4.2 已知一简谐振子的振动曲线如图所示,试由图求:(1)a,b,c,d,e各点的位相,及到达这些状态的时刻t各是多少?已知周期为T;(2)振动表达式;(3)画出旋转矢量图.[解答]方法一:由位相求时间.(1)设曲线方程为x = A cosΦ,其中A表示振幅,Φ = ωt + φ表示相位.由于x a = A,所以cosΦa = 1,因此Φa = 0.由于x b = A/2,所以cosΦb = 0.5,因此Φb = ±π/3;由于位相Φ随时间t增加,b点位相就应该大于a点的位相,因此Φb = π/3.由于x c = 0,所以cosΦc = 0,又由于c点位相大于b位相,因此Φc = π/2.同理可得其他两点位相为Φd = 2π/3,Φe = π.c点和a点的相位之差为π/2,时间之差为T/4,而b点和a点的相位之差为π/3,时间之差应该为T/6.因为b点的位移值与O时刻的位移值相同,所以到达a点的时刻为t a = T/6.到达b点的时刻为t b = 2t a = T/3.到达c点的时刻为t c = t a + T/4 = 5T/12.到达d点的时刻为t d = t c + T/12 = T/2.到达e点的时刻为t e = t a + T/2 = 2T/3.(2)设振动表达式为x = A cos(ωt + φ),当t = 0时,x = A/2时,所以cosφ = 0.5,因此φ =±π/3;由于零时刻的位相小于a点的位相,所以φ = -π/3,因此振动表达式为cos(2)3tx ATπ=π-.另外,在O时刻的曲线上作一切线,由于速度是位置对时间的变化率,所以切线代表速度的方向;由于其斜率大于零,所以速度大于零,因此初位相取负值,从而可得运动方程.(3)如图旋转矢量图所示.方法二:由时间求位相.将曲线反方向延长与t轴相交于f点,由于x f= 0,根据运动方程,可得cos(2)03tTππ-=图6.2所以232f t Tπππ-=±. 显然f 点的速度大于零,所以取负值,解得 t f = -T /12.从f 点到达a 点经过的时间为T /4,所以到达a 点的时刻为t a = T /4 + t f = T /6,其位相为203a a t T Φπ=π-=. 由图可以确定其他点的时刻,同理可得各点的位相.4.3如图所示,质量为10g 的子弹以速度v = 103m·s -1水平射入木块,并陷入木块中,使弹簧压缩而作简谐振动.设弹簧的倔强系数k= 8×103N·m -1,木块的质量为4.99kg ,不计桌面摩擦,试求:(1)振动的振幅; (2)振动方程.[解答](1)子弹射入木块时,由于时间很短,木块还来不及运动,弹簧没有被压缩,它们的动量守恒,即mv = (m + M )v 0.解得子弹射入后的速度为v 0 = mv/(m + M ) = 2(m·s -1),这也是它们振动的初速度.子弹和木块压缩弹簧的过程机械能守恒,可得(m + M ) v 02/2 = kA 2/2,所以振幅为A v =-2(m). (2)振动的圆频率为ω=s -1).取木块静止的位置为原点、向右的方向为位移x 的正方向,振动方程可设为x = A cos(ωt + φ).当t = 0时,x = 0,可得φ = ±π/2;由于速度为正,所以取负的初位相,因此振动方程为x = 5×10-2cos(40t - π/2)(m).4.4 如图所示,在倔强系数为k的弹簧下,挂一质量为M 的托盘.质量为m 的物体由距盘底高h 处自由下落与盘发生完全非弹性碰撞,而使其作简谐振动,设两物体碰后瞬时为t = 0时刻,求振动方程.[解答]物体落下后、碰撞前的速度为v =物体与托盘做完全非弹簧碰撞后,根据动量守恒定律可得它们的共同速度为0m v v m M ==+这也是它们振动的初速度. 设振动方程为x = A cos(ωt + φ),其中圆频率为ω=物体没有落下之前,托盘平衡时弹簧伸长为x 1,则x 1 = Mg/k .物体与托盘碰撞之后,在新的平衡位置,弹簧伸长为x 2,则x 2 = (M + m )g/k .取新的平衡位置为原点,取向下的方向为正,则它们振动的初位移为x 0 = x 1 - x 2 = -mg/k . 因此振幅为图4.3图4.4A===初位相为arctanvxϕω-==4.5重量为P的物体用两根弹簧竖直悬挂,如图所示,各弹簧的倔强系数标明在图上.试求在图示两种情况下,系统沿竖直方向振动的固有频率.[解答](1)可以证明:当两根弹簧串联时,总倔强系数为k=k1k2/(k1+ k2),因此固有频率为2πων===.(2)因为当两根弹簧并联时,总倔强系数等于两个弹簧的倔强系数之和,因此固有频率为2πων===4.6 一匀质细圆环质量为m,半径为R,绕通过环上一点而与环平面垂直的水平光滑轴在铅垂面内作小幅度摆动,求摆动的周期.[解答]方法一:用转动定理.通过质心垂直环面有一个轴,环绕此轴的转动惯量为I c = mR2.根据平行轴定理,环绕过O点的平行轴的转动惯量为I = I c + mR2 = 2mR2.当环偏离平衡位置时,重力的力矩为M = -mgR sinθ,方向与角度θ增加的方向相反.根据转动定理得Iβ = M,即22dsin0dI mgRtθθ+=,由于环做小幅度摆动,所以sinθ≈θ,可得微分方程22ddmgRt Iθθ+=.摆动的圆频率为ω=周期为2πTω=22==方法二:用机械能守恒定律.取环的质心在最底点为重力势能零点,当环心转过角度θ时,重力势能为E p = mg(R - R cosθ),绕O点的转动动能为212kE I=ω,总机械能为21(cos)2E I mg R R=+-ωθ.环在转动时机械能守恒,即E为常量,将上式对时间求导,利用ω= dθ/d t,β=dω/d t,得0 = Iωβ + mgR(sinθ)ω,由于ω ≠ 0,当θ很小有sinθ≈θ,可得振动的微分方程22ddmgRt Iθθ+=,从而可求角频率和周期.[注意]角速度和圆频率使用同一字母(b)图4.5ω,不要将两者混淆.4.7 横截面均匀的光滑的U 型管中有适量液体如图所示,液体的总长度为L ,求液面上下微小起伏的自由振动的频率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0 2
2 A 4 或 3 3
4 A 3 2 2
O
A
x
[例2]如图的谐振动x-t 曲线,试求其振 x/m 动表达式 2 解:由图知
[例7]两列相干平面简谐波沿x轴传播。 波源S1和S2相距d=30m,S1为坐标原点, 已知x1=9m和x2=12m处的两点是相邻的 两个因干涉而静止的点。求两波的波长 和两波源的最小位相差
S1
解:设S1、S2的初相位为1 、2 因x1和x2处为相邻干涉静止点,有0x1 Nhomakorabeax2
S2
x
x x2 2 (d x1 ) 2x1 [ 2 ] [1 ] (2k 1) 2 (d 2 x1 ) 2 1 (2k 1) 2 (d 2 x2 ) 同理 2 1 (2k 3)
2 T 4s T 2
x0 A
由旋转矢量法得
0.24 0.24 x 0 x 0.24 cos t m 2 (2) t=0.5s: 1 x 0.24 cos 0.17 m 2 2 2 2 F ma m x 0.01 ( ) 0.17 2 3 4.19 10 N
v0
即
x 0, v 0
2
2
O
x
[ 例 3] 质量为 0.01kg 物体作周期为 4s 、振 幅为0.24m的简谐振动。t=0时,位移 x=0.24m。求(1)谐振动表达式;(2)t=0.5s 时 , 物体的位置和所受的力; (3) 物体从 初始位置运动至 x =-0.12m 处所需的最短 时间 解:(1)设振动表达式为 x A cos( t ) 其中 A 0.24 m
A 2 m, T 2s O 2t / s 1 2 T 设振动表达式为 x A cos( t ) v A sin( t ) t=0时: x 0 即 0 A cos 2
又
旋转矢量法
A sin 0 sin 0 2 x 2 cos(t ) m 2
0.4
y A cos(t ) A 0 . 2 m x m 0.4 m
u 2 0 . 08 2 2 2 0.4 5 又t =0时: y 0 v 0 2 y m u 2 y 0.2 cos( t ) m 5 2 0 x m 波动方程为 2 x y 0.2 cos[ (t ) ]m 5 0.08 2
0
2 (3) t min 2 3 t min 3 0.12 2 3 4 t min 0.24 x s 0.24 0 2 3 T T 或 t min 4 12 T T T 6 12 4 4 s A x A 0 3
[例4]一水平放置的弹簧振子,质量为m ,弹性系数为k,当它振动时,在什么位 置动能和势能相等?它从该位置到达平 衡位置所需的最短时间为多少?
x / cm
0.05
2 T 20
1
0.1
1振动在t=0时:
t / s 1 2 2
x0 0 v0 0
5 M 4 5 x 5 2 cos(20 t ) cm A 4
2
5 A 2 x1 5 cos(20t 2) cm x2 5 cos(20t ) cm 2 2 由旋转矢量法 A 0M 1 0M 2 5 2 cm
解: (1)
1 2 1 2 2 kx kA 2 2
2 x A 2
即
(2)
t 2 4 4
t
4
m k
O
2 A 2
x
[例5]已知两谐振动的曲线(如图),它们是 同频率的谐振动,求它们的合振动方程 解:由图知 A 5 cm T 0.1s
5 0 5
0
S1
x1
S2
相减得
4 ( x2 x1 )
2( x2 x1 ) 2 (12 9) 6 m 2 (d 2 x2 ) 2 1 (2k 3) (2k 5)
k=-2时,位相差最小
2
2 1
作业:9-1、9-7、9-9、9-11、 9-15
2振动在t=0时: x0
5 4
O
M1
x
[例6]下图为一平面余弦横波 t=0时的波 形,此波形以u=0.08米/秒的速度沿x轴 正向传播。求:a,b两点的振动方向; 0点的振动方程;波动方程 解:由波形传播过程知 a向下, b向上 y m 设 0 点振动方程为 u 0.2
a b
O
0.2
