同济大学 双语 钢结构4-Compression
同济大学房屋钢结构设计试题含答案及复习重点

试卷一22011/20~1/8较多的地区取其中的较大值。
2屋盖横向支撑以构成几何不变体系。
3刚性45、当实腹6 23 7820mm 2201A(A) 等稳定 (B) 等刚度 (C) 等强度 (D) 计算长度相等 2 A (A) 垫板数不宜少于两个 (B) 垫板数不宜少于一个 (C) 垫板数不宜多于两个 (D) 可不设垫板3 D (A) 支座竖杆中的内力 (B) 下弦杆中的最大内力 (C) 上弦杆中的最大内力 (D) 腹杆中的最大内力4、槽钢檩条的每一端一般用下列哪一项连于预先焊在屋架上弦的B(A) 一个普通螺栓 (B) 两个普通螺栓 (C) 安装焊缝 (D) 一个高强螺栓5、如轻型钢屋架上弦杆的节间距为L(D )。
(A) L (B) 0.8L (C) 0.9L (D) 侧向支撑点间距 6 C (A) 端竖杆处 (B) 下弦中间 (C) 下弦端节间 (D) 斜腹杆处 7 A(A) 可以受压 (B) 只能受拉 (C) 可以受弯 (D) 可以受压和受弯 8、某房屋屋架间距为6m 24m 24m 。
房屋C(A) 上弦横向支撑 (B) 下弦横向支撑 (C) 纵向支撑(D) 垂直支撑9、梯形屋架的端斜杆和受较大节间荷载作用的屋架上弦杆的合理C(A) 等肢角钢相连 (B) 不等肢角钢相连(C) 不等肢角钢长肢相连 (D) 等肢角钢十字相连10 C(A)屋面活荷载 (B)雪荷载(C)屋面活荷载和雪荷载两者中的较大值 (D)屋面活荷载和雪荷载20182636试卷二220123时它0.9L 4度高的连接焊透的k型坡口焊缝5至少两块填板6上玄横向支撑下玄横向支撑下玄纵向支撑竖向支撑系杆201、门式刚架轻型房屋屋面 A区取其中的较大值。
(A) 120—18 (B) 130—18 (C) 120—1 5(D) 130—1 52 B不变体系。
(A) 屋盖纵向支撑 (B) 屋盖横向支撑 (C) 刚性系杆(D) 柔性系杆3C(A) 刚性和柔性 (B) 刚性或柔性 (C) 刚性 (D) 柔性4 AB(A) 2 (B) 3 (C) 4 (D) 55 A(A) (B)不等边角钢短边相(C) (D)等边角钢相连6、屋B(A)10mm (B)20mm (C)30mm (D)40mm7 CA(A)强度 (B)刚度 (C)整体稳定 (D)局部稳定8Q≤30t度l≤6m Al~A5 A的(A) 加强上翼缘 (B) 加强下翼缘 (C) 设制动梁(D) 设制动桁架20182、为何冷弯薄壁构件在其强度和稳定性计算公式中截面特性以63、简述D6试卷三2201件起整体作填板2整体稳定3长度Lox=0.8 L Loy= 1L L为杆件的几何长度。
同济大学钢结构基本原理试验H型截面轴心受压柱实验报告

H 型截面轴心受压柱实验报告学号: 姓名: 任课老师: 实验老师:实验日期:2012年03月30日一、实验目的:1、通过试验掌握钢构件的试验方法,包括试件设计、加载装置设计、测点布置、试验结果整理等方法。
2、通过试验观察十字型截面轴心受压柱的失稳过程和失稳模式。
3、将理论极限承载力和实测承载力进行对比,加深对轴心受压构件稳定系数计算公式的理解。
二、实验原理:1、基本微分方程根据开口薄壁杆件理论,具有初始缺陷的轴心压杆的弹性微分方程为: 2、扭转失稳欧拉荷载H 型截面为双轴对称截面,因其剪力中心和形心重合,有 x 0= y 0 = 0,代入上式可得:''0()0IV IVx EI v v Nv -+= (a)''0()0IV IV y EI u u Nu -+= (b)''''2''''000()()0IV IV t EI GI r N R ωθθθθθθ---+-=(c)说明H 型双轴对称截面轴心压杆在弹性阶段工作时,三个微分方程是相互独立的,可分别单独研究。
在弹塑性阶段,当研究(a )式时,只要截面上的产于应力对称与 Y 轴,同时又有00u =和00θ=,则该式将始终和其他两式无关,可单独研究。
这样,压杆将只发生Y 方向的位移,整体失稳呈弯曲变形状态,称为弯曲失稳。
这样,式(b )也是弯曲失稳,只是弯曲失稳的方向不同而已。
对于式(c ),如果残余应力对称与 X 轴和 Y 轴分布,同时假定,00u =和00θ=则压杆将只发生绕 Z 轴的转动,失稳时杆件呈扭转变形状态,称为扭转失稳。
对于理想压杆,则有上面三式可分别求得十字型截面压杆的欧拉荷载为: 绕X 轴弯曲失稳:220xEx xEI N lπ=,绕Y 轴弯曲失稳:220yEy yEI N l π=绕Z 轴扭转失稳:222001()E t EI N GI l r ωθθπ=+ H 字型截面压杆的计算长度和长细比为:绕 X 轴弯曲失稳计算长度:00x x l l μ=,长细比0/x x x l i λ= 绕Y 轴弯曲失稳计算长度:00y y l l μ=,长细比0/y y y l i λ=绕Z 轴扭转失稳计算长度:00l l θθμ=,端部不能扭转也不能翘曲时0.5θμ=,长细比θλ=上述长细比均可化为相对长细比:λ=3、稳定性系数计算公式H 字型截面压杆的弯曲失稳极限承载力:根据欧拉公式22Ew w EA N πλ=得222y Ew w w f Eπσλλ==佩利公式:0(1)2y Excr f εσσ++=再由公式cryf σϕ=可算出轴心压杆的稳定性系数。
同济大学钢结构课程设计

单层单跨门式刚架设计计算一、设计资料(1)设计参数单层房屋为单跨门式刚架,刚架跨度30m ,长度90m ,柱距6m ,檐口标高8m ,屋面坡度1:10。
屋面材料采用压型钢板,墙面材料采用彩钢板,天沟为彩板天沟。
基础混凝土标号为C30,214.3/c f N mm =,钢材材质为Q345,22y 310k /,180/c f N mm f N mm ==。
(2)设计荷载屋面恒荷载为0.52/kN m ,活荷载为0.52/kN m ;雪荷载为 0.22/kN m ,基本风压为0.552/kN m ,地面粗糙度为B 类,风荷载体型系数如图1所示。
图1 计算模型机风荷载体型系数二、荷载组合1、 1.20 恒载 + 1.40 活载2、 1.00 恒载 + 1.40 风载3、1.00 恒载+ 1.40 x 0.90 活载+ 1.40 x 0.90 风载4、1.35 恒载三、内力计算1、计算模型(如图2)图2 节点及单元编号图2、荷载工况荷载工况如图3恒载活载左风右风图3 荷载工况图3、各工况内力恒载、活载、作风和右风作用下的钢架内力如图4—图7。
轴力图(KN)剪力图(KN)弯距图(kN.m)图4 恒载作用下钢架内力图轴力图(kN)剪力图(kN)弯距图(kN.m)图5 活载作用下钢架内力图轴力N图(kN)剪力图(kN)弯距图(kN.m)图6 左风作用下钢架内力图轴力图(kN)剪力图(kN)弯距图(kN.m)图7 右风作用下钢架内力图4、组合内力选取荷载组合1(1.20 恒载+ 1.40 活载)对构件内力值进行验算。
该组合下的构件内力值见表1。
表1 工况1下组合内力表5、构件尺寸和截面特性表2 构件尺寸和截面特性表中:面积和惯性矩的上下行分别指小头和大头的值四、构件截面验算1、宽厚比验算 翼缘板自由外伸宽厚比()2008/29.612.410-=<=,满足规程限值要求。
腹板高厚比80021097.52068-⨯=<=(),满足规程限值要求。
同济大学土木工程本科专业课设置表
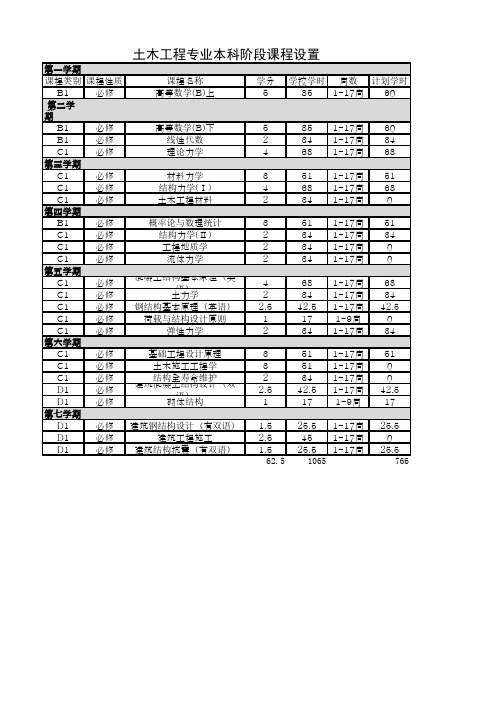
第一学期
课程类别 课程性质
课程名称
B1
必修
高等数学(B)上
第二学
期
B1
必修
高等数学(B)下
B1
必修
线性代数
C1
必修
理论力学
第三学期
C1
必修
材料力学
C1
必修
结构力学(Ⅰ)
C1
必修
土木工程材料
第四学期
B1
必修
概率论与数理统计
C1
必修
结构力学(Ⅱ)
C1
必修
工程地质学
C1
必修
流体力学
25.5 1-17周 45 1-17周 25.5 1-17周
1065
25.5 0
25.5 766
D1
必修
建筑工程施工
D1
必修 建筑结构抗震(有双语)
学分 学校学时 周数 计划学时
5
85 1-17周 60
5
85 1-17周 60
2
34 1-17周 34
4
68 1-17周 68
3
51 1-17周 51
4
68 1-17周 68
2
34 1-17周 0
51 1-17周 51
2
34 1-17周 34
2
34 1-17周 0
第五学期 C1 C1
必修 必修
混凝土结构基本原理(英 土语力)学
C1
必修 钢结构基本原理(英语)
C1
必修
荷载与结构设计原则
C1
必修
弹性力学
第六学期
C1
必修
基础工程设计原理
同济大学 木结构

Leff
Δ
Axial load P (kN)
P
Displacement Δ (mm)
Compression members
(1) Strength
N An
≤
fc
N
where N —— compression
An —— net area
fc —— compression strength
(2) Stability
and modulus of elasticity
If log applied have not been cut out the checking parts, the design
values of compressive resistance strength and bending resistance strength parallel to grain and modulus of elasticity will be increased by 15%.
Strength For some import dimension lumber, there are design values of strength in our timber code.
Strength For some import dimension lumber, there are design values of strength in our timber code.
Technical Specification for Light Wood-Frame Constructions, DG/TJ08-2059-2009
Leff
Δ
buckling and material failure)
同济大学钢结构基本原理课后习题答案完全版

第二章如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
图2-34 σε-图(a )理想弹性-塑性 (b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化)(2)弹性阶段:tan E σεαε==⋅非弹性阶段:'()tan '()tan yyy y f f f E f E σεαεα=+-=+-如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少? 2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610yf E ε===⨯卸载后残余应变:0c ε= 可恢复弹性应变:0.00114y c εεε=-=(2)B 点:卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f E εε=-= 可恢复弹性应变:0.00114y c εεε=-=(3)C 点:卸载前应变:0.0250.0350.06'c y F f E σεε-=-=+= 卸载后残余应变:0.05869c c E σεε=-= 可恢复弹性应变:0.00131y c εεε=-=试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
同济大学钢结构基本原理PPT课件

、纤维横向 受拉强度低
强度(MPa)/ 弹性模量 (MPa)/6000/
25
拉力下脆性
234-420)/ 206000/
78.5
理想弹塑性材 料,好
拉45、压800/ /70000/ 25
拉力下脆性
60-200 (1mm 厚)/
13
大跨度结构
——飞机库、候机楼、体育场馆、会展中心等公共建筑 结构体系:网架网壳(螺栓球节点、焊接球节点)
14
结构体系:钢管桁架(直接汇交焊接节点、铸钢件节点)
组焊完成的构件
15
结构体系:预张力结构
16
高耸塔桅 ——电视、无线发射、观光等
17
其他结构
幕墙支承、压力容器、折板结构、桥塔、桥面梁板、水箱、船舶、 车厢、基坑维护、地下管线、脚手架
铆接连接 普通螺栓连接 高强螺栓连接
焊接连接
轴心受力柱 受弯梁 压弯构件
钢结构基本原理
多高层框架结构 大跨度空间结构 厂房刚架排架结构
高耸结构 桥梁结构 特种结构
……
8
建筑钢结构设计
9
4、钢结构特点
1) 预制拼装——产品化、工业化、干作业 施工速度快 2) 材质均匀理想稳定——计算模型确定、精度高 安全性好 3) 材料强度高——板件薄、构件细长 轻型、稳定性问题 4) 塑性韧性好——抗震性能好、动力承载性能好 5) 耐腐蚀性能差——防腐措施 6) 耐热性能好、耐火性能差——防火措施
钢结构基本原理
1
整体概述
概况一
点击此处输入相关文本内容 点击此处输入相关文本内容
概况二
点击此处输入相关文本内容 点击此处输入相关文本内容
概况三
同济大学钢结构基本原理课后习题答案完全

第二章如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
图2-34 σε-图(a )理想弹性-塑性 (b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化)(2)弹性阶段:tan E σεαε==⋅非弹性阶段:'()tan '()tan yyy y f f f E f E σεαεα=+-=+-如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少? 2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610yf E ε===⨯卸载后残余应变:0c ε= 可恢复弹性应变:0.00114y c εεε=-=(2)B 点:卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f E εε=-= 可恢复弹性应变:0.00114y c εεε=-=(3)C 点:卸载前应变:0.0250.0350.06'c y F f E σεε-=-=+= 卸载后残余应变:0.05869c c E σεε=-= 可恢复弹性应变:0.00131y c εεε=-=试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Mechanical imperfection
residual stress
Flexural equilibrium equation
EIy '' Ny 0
EIy '' Ny Ne0
elastic
N ym eo /(sec 1) 2 NE
Elastic-plastic
Compression members
Refer to §5.1
introduction
Compression members in structures - truss members - bracing - pinned columns Structural shapes commonly used in compression members
BASIC PRINCIPLES OF STEEL STRUCTURES
Prepared by: Dr. Feng ZHOU
Room: Rui’an Building 207A ( welcome to walk-in)
Phone: 15800660849
BASIC PRINCIPLES OF STEEL STRUCTURES
Effective length
Effective length factor for different end constraint
- End constraint: bending and torsional deformation
- Constraint types: free end, pinned, fixed end - Effective length factor: Table 5-4 in page 101
N-y
Compression members
Effects of initial imperfections
Geometrical imperfection
initial out-of-straightness (crookedness), initial eccentricity
Mechanical imperfection
It - torsional constant
2 2 r02 (Ix Iy) / A x 0 y0
Relate to torsion problem
A - cross-section area
y0
Centroid o
x0
where a shear force can be applied without inducing any torsion
residual stress
Ideal stress-strain curve and buckling curve
stress-strain curve with residual stress and corresponding buckling curve
Compression members
- doubly symmetric - singly symmetric - unsymmetric
Compression members
possible failure modes
• Material yield, squash load
• Member (overall) buckling
• Plate (local) buckling
A=0:
Compression members
column theory
Pcr l n EI
Pcr
l / n 2
2 EI
•
values of n larger than 1 are not possible unless the compression member is physically restrained from deflecting at the points where the reversal of curvature would occur.
u = 1.0
u = 2.0
u = 0.5
u = 0.7
How about the critical stress? E N E / A 2 E / 2
ul i
Compression members
More on effective length
Minor axis buckling
members
Local buckling of plate element Laced and battened compression members Rigidity of compression members Design of axially loaded compression members
N u An f y
Design equation
N Nu / R An f y / R An f d
N fd An
Compression members
member (overall) buckling
Compression members
plate (local) buckling
Topic 4 Compression members
Compression members
Outlines
Introduction Resistance of cross-section Overall stability of uniform (solid-web) compression
N
•
Pcr
2 EI
l
2
2 EA Pcr 2
“Euler load”
N N N
where, E — modulus of elasticity of the material I — moment of inertia of the cross-section area with respect to the minor principle axis l — length between points of supported
EI ω IV GI t '' Nx0v '' Ny 0u '' ( Nr02 R ) '' 0
where:Ix、Iy - moment of inertia with respect to x, y axis
Iw - warping constant N
Y (v) Shear center S(x0, y0) X (u)
Compression members
Refer to §5.3, §5.5
basic concept of stability
After temporary transverse load P is removed
N
N
△
< Ncr ,δ= 0,equilibrium state is stable N = Ncr ,δ kept small, critical state > Ncr ,δ increases,equilibrium state is unstable
Compression members
Effects of initial imperfections
Geometrical imperfection
initial out-of-straightness (crookedness), initial eccentricity
Mechanical imperfection
Compression members
equilibrium equations of elastic buckling for ideal members
Z(rotation)
N
EI x v IV Nv '' Nx0 '' 0
EI yu IV Nu'' Ny0 '' 0
δ
P
N
N
stable
critical
unstable
Critical buckling load —the load that is just large enough to maintain the deflected shape when the temporary transverse load is removed.
Equilibrium equation
EIy Ny 0
''
N N y A cos x B sin x EI EI
Pcr l n EI
At x=0, y=0:
At x=l, y=0:
N B sin EI l 0
or N (1 yom / ym ) N E
N
N-y
N ult N E
Compression members
Effects of initial imperfections
Geometrical imperfection
initial out-of-straightness (crookedness), initial eccentricity
Ib=∞ Ib=∞
Major axis buckling
u=1.0
支撑
u=0.5
Compression members
Member (overall) bucking modes
(1) Flexural buckling (2) Torsion buckling
