离散时间控制系统作业答案
自动控制原理例题详解线性离散控制系统的分析与设计考习题及答案

精心整理----------2007--------------------一、(22分)求解下列问题: 1. (3分)简述采样定理。
解:当采样频率s ω大于信号最高有效频率h ω的2倍时,能够从采样信号)(*t e 中 完满地恢复原信号)(t e 。
(要点:h s ωω2>)。
2.(3分)简述什么是最少拍系统。
解:在典型输入作用下,能以有限拍结束瞬态响应过程,拍数最少,且在采样时刻上无稳态误差的随动系统。
3.(34.(x()∞5.(5解:(G 6.(5试用Z 解:二、((i X s )z 图11.(5分)试求系统的闭环脉冲传递函数()()o i X z X z ; 2.(5分)试判断系统稳定的K 值范围。
解:1.101111111()(1)(1)11(1)1(1)()1e11e 1e G G z z Z s s z Z s s z z z z z z z e z -------⎡⎤=-⎢⎥+⎣⎦⎡⎤=--⎢⎥+⎣⎦=-----=---=-11010*******1e ()()e 1e ()1()1e (1e )(e )(1e )(1e )e e o i K X z KG G z z X z KG G z K z K z K K z K K ------------==-++--=-+--=-+- 2.(5三、(8已知(z)1Φ=1.(3分)简述离散系统与连续系统的主要区别。
解:连续系统中,所有信号均为时间的连续函数;离散系统含有时间离散信号。
2.(3分)简述线性定常离散系统的脉冲传递函数的定义。
解:在系统输入端具有采样开关,初始条件为零时,系统输出信号的Z 变换与输入信号的Z 变换之比。
3.(3分)简述判断线性定常离散系统稳定性的充要条件。
解:稳定的充要条件是:所有特征值均分布在Z 平面的单位圆内。
4.(5分)设开环离散系统如图所示,试求开环脉冲传递函数)(z G 。
解:22522510252510()[[25e e (e e )eT T T T Tz z z G z Z Z s s z z z z -----=⨯==++---++ 5.(5分)已知系统差分方程、初始状态如下:0)(2)1(3)2(=++++k c k c k c ,c(0)=0,c(1)=1。
高国燊《自动控制原理》(第4版)(章节题库 线性离散(时间)控制系统分析)

第8章 线性离散(时间)控制系统分析
1.试根据定义
确定下列函数的
和闭合形式的E (
z ):解:(1
)由欧拉公式
可得(2)将
E
(s )展成部分分式,有
式中
于是
经采样拉普拉斯变换,得
故有
2.求下列各函数的z反变换:
解:(1)采用幂级数法。
则采样函数为
(2)采用反演积分法。
有三个极点,则有
相应的采样函数为
用幂级数法验证:
故有
(3)因为
所以
查z变换表,可知
则有
用反演积分法验证
有两个根,而
则有
(4)采用反演积分法
有三个极点,则有
相应的采样函数为
用幂级数法验证
故有
(5)因为
所以
查z变换表,可知则有
3.试根据定义
确定下列函数的E*(s)的闭合形式和E(z):(1)e(t)=sinωt;
(2)
解:(1)
(2)
4.试求的z变换。
解:求z变换的另一种方法是直接利用z变换表。
先将E(s)展为部分分式,然后由表求每一部分分式项的z变换,并将它们组合在一起便可得E(z)。
(1)将E(s)展成部分分式,则有
(2)求每一个部分分式项的z变换:与相应的z变换为
与
相应的z变换为所以
令T=1,有
5.求解下列差分方程,结果以c(nT)表示:
解:(1)因为。
自动控制原理第7章离散控制系统

Z变换
01
Z变换是分析离散时间信号和系统 的有力工具,它将离散时间信号 或系统转化为复平面上的函数或 传递函数。
02
Z变换的基本思想是通过将离散时 间信号或系统进行无限次加权和 ,将其转化为一个复数域上的函 数或传递函数。
离散状态方程
离散状态方程是描述离散控制系统动 态行为的数学模型,它的一般形式为 $mathbf{dot{x}}(k) = Amathbf{x}(k) + Bu(k)$,其中 $mathbf{x}(k)$表示在时刻$k$的系 统状态向量,$u(k)$表示在时刻$k$ 的输入向量,$A$和$B$是系统的系 数矩阵。
稳态误差主要来源于系统本身的结构 和参数,以及外部干扰和测量噪声。
离散控制系统的动态响应分析
动态响应定义
动态响应是指系统在输入信号作 用下,系统输出信号随时间变化 的特性。
动态响应的描述方
式
动态响应可以通过系统的传递函 数、频率特性、根轨迹图等方式 进行描述。
优化动态响应的方
法
通过调整系统参数、改变系统结 构、引入反馈控制等方法,可以 优化系统的动态响应。
离散控制系统的仿真工具与实例
仿真工具介绍
离散控制系统的仿真工具用于模拟和测试系统的性能和稳定性。常见的仿真工具包括MATLAB/Simulink、 LabVIEW等。这些工具提供了丰富的数学函数库和图形化界面,方便用户进行系统建模和仿真。
仿真实例分析
通过具体的仿真实例,可以深入了解离散控制系统的性能和特点。例如,可以设计一个温度控制系统,通过调整 系统参数和控制算法,观察系统在不同工况下的响应特性和稳定性。通过对比不同方案,可以评估各种参数和控 制策略对系统性能的影响,为实际应用提供参考和依据。
现代控制理论课后习题答案

现代控制理论课后习题答案第⼀章习题1.2求下列多项式矩阵()s D 和()s N 的两个不同的gcrd:()2223(),()1232s s s s s s s s s ??++== ? ?+-??D N 解:()()22232321s s s s s s s++ =++ ? ?D S N S ; ()3r 2,1,2E -:223381s s s s s s ??++ ?-- ? ???;()3r 2,3,3E :223051s s s s s ??++ ?- ? ???;()3r 1,3,2E s --:01051s s ?? ?- ? ;()3r 2,1,5E s -:01001s ?? ?;()3r 3,1,1E -:01000s ?? ? ? ???;()1r 2,3E :01000s ?? ? ? ???;()1r 1,2E :00100s ?? ?;所以⼀个gcrd 为001s ??;取任⼀单模矩阵预制相乘即可得另⼀个gcrd 。
1.9 求转移矩阵t A e (1)已知1141??=A ,根据拉⽒反变换求解转移矩阵tA e 。
(2) 已知412102113-?? ?= ? ?-??A ,根据C-H 有限项展开法求解转移矩阵t A e 。
解:(1)11()41s s s --??-= ?--??I A1110.50.50.250.2511(3)(1)(3)(1)13131()4141110.50.5(3)(1)(3)(1)(3)(1)3131s s s s s s s s s s s s s s s s s s s s s s s --+---+-+??-+-+ ? ?-=== ? ?---+ ?-+ ? ?-+-+-+-+?I A 3311330.5e 0.5e 0.25e 0.25e e ()e e 0.5e 0.5e t t t t t t tt t s ------??+-??=-= ??? ?-+?A L I A (2)由2412()12(1)(3)0113λλλλλλ--?? ?=--=--= ? ?--??A I -,得1,233,1λλ== 对1,23λ=,可以计算1,2()2rank λ=A I -,所以该特征值的⼏何重数为1。
控制系统仿真答案
控制系统仿真答案一.选择题二.名词解释及简答题1.系统的三个属性是什么?请解释其具体含义。
答:系统的三个属性:整体性、相关性、隶属性。
整体性:各部分(子系统)不能随意分割。
相关性:各部分(子系统) 以一定的规律或方式相联系,由此决定了其特有的性能。
隶属性:不能清楚的分出系统“内部”与“外部”,常常需要根据研究的问题来确定哪些属于系统的内部因素,哪些属于外部环境,其界限也是随不同的研究目的而变化,将这一特性称之为隶属性。
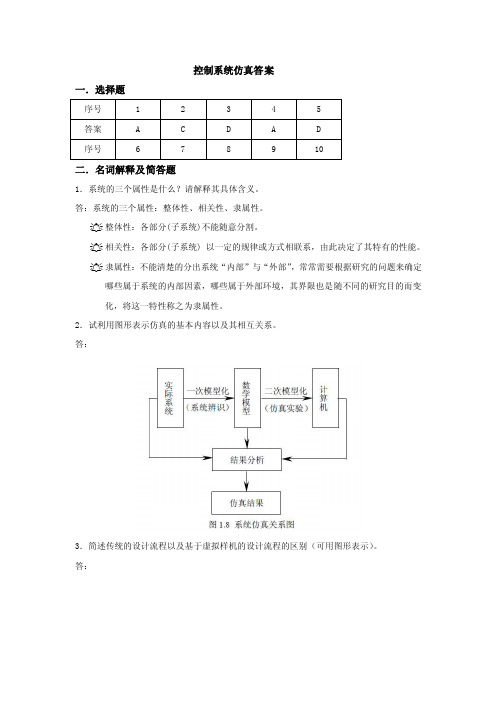
2.试利用图形表示仿真的基本内容以及其相互关系。
答:3.简述传统的设计流程以及基于虚拟样机的设计流程的区别(可用图形表示)。
答:三.判断题,正确的在括号内打“√”,错误的打“╳”,并改正错误结论重新阐述。
1.(√)为了限制所研究问题涉及的范围,一般用系统边界把被研究的系统与系统环境区分开来。
2.(╳)模型按数学模型的形式分为:物理仿真、数学仿真、数学-物理混合仿真或半实物仿真。
改1:按模型的性质分为:物理仿真、数学仿真、数学-物理混合仿真或半实物仿真。
改2:按数学模型的形式分为:连续系统仿真、离散事件系统仿真、离散—连续系统仿真。
3.(√)series函数可以将两个系统按串联方式连接,它即适合于连续时间系统,也适合于离散时间系统。
4.(√)S-函数为Simulink的“系统”函数,它是能够响应Simulink求解器命令的函数,采用非图形化的方法实现一个动态系统。
5.(╳)Matlab在执行运算符的优先级的时候,逻辑运算符“<”的优先级要高于矩阵乘法运算“*”的优先级。
改:Matlab在执行运算符的优先级的时候,逻辑运算符“<”的优先级要低于矩阵乘法运算“*”的优先级。
四、2、main(){float x,money;Scanf(“%f/n”,&x);If(x<50) then money=2.5*xElse if(x>=50 and x<100)Else if (x>=100)Then money=2.5*x*(1-0.2) ;Printf(“money=%f”,money);}五.综合题1.编程实现以下图形绘制。
高国燊《自动控制原理》(第4版)(名校考研真题 线性离散(时间)控制系统分析)

一、填空题1.离散系统输出响应的Z 变换为:()2320.3680.2642 1.6320.632z z C z z z z +=-+-则系统输出在前两个采样时刻的值为______,______。
[重庆大学()C nT ()0C =()C T =2006年研]【答案】0;0.3682.零阶保持器的传递函数是______,加入零阶保持器______会影响采样系统的稳定性。
[北京交通大学2009年研]【答案】;不1e Ts s--二、问答题1.如何判断离散系统的稳定性。
并图示说明之。
[东北大学研]答:由于Z 变换与拉普拉斯变换之间的映射关系为,其中T 为采样周期,在s平面内当系统稳定时所有特征根位于左半平面,映射到Z 平面中则是单位圆内,对应的映射关系如图8-1所示。
图8-1于是判断离散系统的稳定性时,只需判断其特征方程的根的模是否大于1,当其模大于1时,系统不稳定;模等于1时,系统临界稳定;当其模小于1时,系统稳定,为了能位于右半平面;位于左半平面;对应的映射关系如图8-2所示。
所示得到关于ω的特征方程,使用劳斯判据进行判断。
图8-22.线性定常离散系统的稳定性除了与系统结构参数有关之外,还与哪些因素有关?[南京航空航天大学2008年研]答:线性定常离散系统的稳定性除了与系统结构参数有关之外,还与采样周期T有关,当系统开环增益一定时,T越小,稳定性越好。
三、计算题1.先用Z变换法求解下面的微分方程,再求其终值e(∞)。
e(k+2)+3e(k+1)+2e(k)=0,已知e(0)=0,e(1)=1。
[浙江大学研]解:将善分方程两沩讲行Z变换可以得到:将e(0)=0,e(1)=1代入整理可以得到:2.已知z变换求离散时间函数z(k)和采样函数[清华大学研]解:由对照典型函数的z 变换表可以得到即其中T为采样周期,为单位脉冲。
3.某离散系统如图8-3所示,试求其闭环脉冲传递函数[四川大学研]图8-3解:由题意,可以得到如下方程整理得到对式(3)两边进行z变换得到:(4)由两边进行Z 变换得到:(5)联立式(4),式(5),消去中间变量可以得到4.线性定常离散系统如图8-4所示,写出闭环系统的脉冲传递函数。
《自动控制原理》试卷及答案(a6套)
自动控制原理试卷A(1)1.(9分)设单位负反馈系统开环零极点分布如图所示,试绘制其一般根轨迹图。
(其中-P 为开环极点,-Z ,试求系统的传递函数及单位脉冲响应。
3.(12分)当ω从0到+∞变化时的系统开环频率特性()()ωωj j H G 如题4图所示。
K 表示开环增益。
P 表示开环系统极点在右半平面上的数目。
v 表示系统含有的积分环节的个数。
试确定闭环系统稳定的K 值的范围。
4.(12分)已知系统结构图如下,试求系统的传递函数)(,)(s E s C,3==p v (a ),0==p v (b )2,0==p v (c )题4图题2图5.(15分)已知系统结构图如下,试绘制K 由0→+∞变化的根轨迹,并确定系统阶跃响应分别为衰减振荡、单调衰减时K 的取值范围。
6.(15分)某最小相位系统用串联校正,校正前后对数幅频特性渐近线分别如图中曲线(1)、(2)所示,试求校正前后和校正装置的传递函数)(),(),(21s G s G s G c ,并指出Gc (S )是什么类型的校正。
7.(15分)离散系统如下图所示,试求当采样周期分别为T=0.1秒和T=0.5秒输入)(1)23()(t t t r ⋅+=时的稳态误差。
8.(12分)非线性系统线性部分的开环频率特性曲线与非线性元件负倒数描述曲线如下图所示,试判断系统稳定性,并指出)(1x N和G (j ω)的交点是否为自振点。
参考答案A(1)1、 根轨迹略,2、 传递函数)9)(4(36)(++=s s s G ;单位脉冲响应)0(2.72.7)(94≥-=--t ee t c tt 。
3、 21,21,21><≠K K K 4、6425316324215313211)()(G G G G G G G G G G G G G G G G G G s R s C ++++= 642531632421653111)()(G G G G G G G G G G G G G G G G G s R s E +++-= 5、 根轨迹略。
控制系统数字仿真模拟题
控制系统数字仿真模拟题一、填空题1、数值积分法中,计算精度p=2的是 梯形法2、 混合法 是机理模型法和统计模型法的结合3、柔性制造系统属于 离散事件 系统.4、零极点增益形式可用于分析系统的 稳定性 和 快速性5、 现实性 、 简洁性 、 适应性 是建立系统模型应该依照的原则.6、系统的三大要素为: 实体 、 属性 和活动。
7、通常仿真时多采用四阶龙格 库塔法 、其原因就是这种计算公式的截断误差较小.8、 相似论 是系统仿真的主要依据.9、一个电机转速控制系统中,属于电机所具有的属性的为: 电机转速10、我们在选择数值算法的时候要 考虑精度 、 计算速度 以及稳定性等原则进行.二、单选题1.运行下列命令后A1=[1,2,3;4,5,6;7,8,9];A2=A1;A3=cat(1,A1,A2),系统输出结果为( B )A.123147456258789369B.123456789147258369C.123456789D.147258369 2.设某一系统的状态方程矩阵为a=[-3,1;1,-3];b=[1,1;1,1];c=[1,1;1,-1];d=[0]并且执行后得可控性矩阵和可观性矩阵的秩分别为cam=ctrb(a ,b)=1,rcam=rank(cam)=2,因此这一系统为( D )A.不可控且不可观的系统B.可控且可观的系统C.可控但不可观的系统D.不可控但可观的系统3.可以将模块按照顺时针进行旋转的快捷键为( A )A.ctrl+rB.ctrl+yC.alt+rD.alt+y4.在Matlab 系统中,调用Simulink环境的工具栏图标为( A )A. B. C.5.下列符号中可以引导注释行的是( D )A.&B.@C.$D.%6.若A=412303214--⎡⎤⎢⎥-⎢⎥⎢⎥-⎣⎦,则C=(A>0)&(A<3)的结果为( B )A.001001011B.001000010C.111110110D.0011100107.MATLAB系统中若要使系统选择short和shortE中最好的表示,则采用命令( C )A.shortB.shortEC.shortGD.longE8.列出工作内存中的变量名称以及细节,只需在命令窗口输入( A )A.whatB.whoC.echoonD.whose9.设一个五阶魔方阵B=magic(5),提取B阵的第1行,第2行的第1,3,5个元素的命令为( B )A.B(1,2:[1,3,5])B.B([1:2],[1,3,5])C.B([1:2],1:3:5))D.B(1:2;[1,3,5])10.下列命令中可以创建起始值为0,增量值为0.5,终止值为10的等差数列的是( A )A.a=0:0.5:10B.a=linspace(0,10,0.5)C.linspace(0,10,10)D.logspace(0,1,11)11.若a=[102;300;130;111],则any(a)=( C )A.011B.110C.111D.10012.设s=‘haha’,可以看到字符s的ascii码值的命令为( C )A.size(s)B.isstr(s)C.abs(s)D.eval(s)13.PSPICE是( B )软件.A.模型及混合信号仿真软件B.模拟电路仿真软件C.机械系统动力学自动分析软件D.大型通用有限元分析软件14.将多项式2(22)(4)(1)s s s s++++展开的命令中正确的是( D )A.conv([1,2,2],conv([4,1],[1,1]))B.conv([2,2,1],conv([4,1],[1,1]))C.conv([2,2,1],conv([1,4],[1,1]))D.conv([1,2,2],conv([1,4],[1,1]))15.w=conv([1,2,3],conv([1,2],[1,1]))的值为( C )A.3111372B.2713113C.1511136D.151422219三、判断题1.影响系统而又不受系统直接控制的全部外界因素的集合叫外部活动.( 错)2.系统仿真就是建立系统的动态模型并在模型上进行实验(或试验).(对)3.状态方程是直接描述系统输入和输出量之间的制约关系,是连续控制系统其他数学模型表达式的基础.( 错)4.global可以定义全局变量,全局变量的作用域是该MATLAB函数的整个工作区,其他的函数不能对它们进行存取和修改( 错)5.MATLAB中clf用于清除图形窗口上的旧图形(对)6.控制系统的数学模型有状态空间表达式,微分方程和积分方程( 错)7.仿真就是利用模型(物理模型或数学模型)代替实际系统进行实验和研究(对)8.离散相似法采样周期的选择应该满足香农定理(采用定理)(对)9.通常情况下,模拟仿真较数字仿真精度高( 错)10.机理模型法需要对系统的内部结构和特性完全的了解,但其精度较低( 错)11.绘制系统根轨迹的命令式是rlocus(对)12.仿真所遵循的基本原理是相似原理,即几何相似和数学相似(对)13.在MATLAB中,plot命令用于绘制三维图形( 错)14.绘制系统单位阶跃响应曲线的命令是step(对)15.系统仿真有三个基本的活动是模型建立,模型变换和模拟实验( 错)16.机理模型法就是对已知结构,参数的物理系统运用相应的物理定律或定理,经过合理的分析简化建立起来的各物理量间的关系(对)17.欧拉法的计算精度p=3( 错)18.绘制系统单位脉冲响应曲线的命令是implus(对)19.MATLAB的含义为矩阵实验室(对)20.margin(G)的含义是计算系统的相角裕度和幅值裕度(对)四、问答题:1.什么是仿真?它的主要优点是什么?它所遵循的基本原则是什么?[答案]:系统仿真是以相似原理,系统技术,信息技术及其应用领域有关的专业技术为基础,以计算机和各种专用物理效应设备为工具,利用系统模型对真实的或设想的系统进行动态研究的一门多学科的综合性技术.它是非常重要的设计自动控制系统或者评价系统性能和功能的一种技术手段.仿真的主要优点是:方便快捷,成本低廉,工作效率和计算精度都很高.它所遵循的基本原则是相似性原理.2.控制系统CAD可解决那些问题?[答案]:控制系统CAD可以解决以频域法为主要内容的经典控制理论和以时域法为主要内容的现代控制理论.此外,自适应控制,自校正控制以及最优控制等现代控制测略都可利用CAD 技术实现有效的分析与设计.3.控制系统建模的基本方法有哪些?他们的区别和特点是什么?[答案]:控制系统的建模方法大体有三种:机理模型法,统计模型法和混合模型法.机理模型法就是对已知结构,参数的物理系统运用相应的物理定律或定理,经过合理的分析简化建立起来的各物理量间的关系.该方法需要对系统的内部结构和特性完全的了解,精度高.统计模型法是采用归纳的方法,根据系统实测的数据,运用统计规律和系统辨识等理论建立的系统模型.该方法建立的数学模型受数据量不充分,数据精度不一致,数据处理方法的不完善,很难在精度上达到更高的要求.混合法是上述两种方法的结合.4.什么是离散系统?什么是离散事件系统?如何用数学的方法描述它们?[答案]:本课程所讲的”离散系统”指的是离散时间系统,即系统中状态变量的变化仅发生在一组离散时刻上的系统.它一般采用差分方程,离散状态方程和脉冲传递函数来描述.离散事件系统是系统中状态变量的改变是由离散时刻上所发生的事件所驱动的系统.这种系统的输入输出是随机发生的,一般采用概率模型来描述.5.动态系统仿真中常用的数值算法有哪几类,分别是什么?[答案]:主要有求解线性和非线性微分方程的数值积分法和计算线性时不变动态系统的离散相似法.其中,数值积分法主要有:欧拉(Euler)法,梯形法,龙格—库塔(Runge-Kutta)法和阿达姆斯(Adams)法;离散相似法主要有:置换法和相似变换法.6.为什么说模拟仿真较数字仿真精度低?其优点如何?.[答案]:由于受到电路元件精度的制约和容易受到外界的干扰,模拟仿真较数字仿真精度低,但模拟仿真具有如下优点:(1)描述连续的物理系统的动态过程比较自然和逼真;(2)仿真速度极快,失真小,结果可信度高;(3)能快速求解微分方程.模拟计算机运行时各运算器是并行工作的,模拟机的解题速度与原系统的复杂程度无关;(4)可以灵活设置仿真试验的时间标尺,既可以进行实时仿真,也可以进行非实时仿真;(5)易于和实物相连.7.采样控制系统数字仿真中连续部分离散化时的步长h如何选取?[答案]:(1)若仿真的任务仅要求计算系统输出y(t)而不要求计算系统内部状态变量,且连续部分的整体脉冲传递函数G(z)=Z[Gh(s)G0(s)]较易求出时,可选h=T(2)若连续部分整体脉冲传递函数G(z)=Z[Gh(s)G0(s)]不易求出;或仿真的任务要求计算系统输出y(t)和内部状态变量;或被控对象含有非线性环节时,可选h=T/N(N为正整数).8.采样控制系统数字仿真有哪几种方法?[答案]:采样控制系统仿真通常有差分方程递推求解法,双重循环方法,应用MATLAB控制工具箱时域响应分析函数法和Simulink仿真法.9.计算机仿真有哪些优点?[答案]:(1)对尚处于论证或设计阶段的系统进行研究,唯一的方法就是仿真.(2)经济,安全,效率高.(3)研究系统非常方便灵活.10.评价优化方法的优劣的应该考虑哪些因素?[答案]:三方面因素:(1)收敛性:收敛性的好坏表示某种优化方法适用范围的大小,具体表示算法对于相当一类目标函数均能找到最优点.(2)收敛速度:为了求出同样精度的最优点,不同的优化方法所需要的迭代次数不同,迭代次数少的优化方法收敛速度较快.(3)每步迭代所需的计算量:每步迭代所需的计算量也是决定寻优速度的另一重要因素.。
第8章 线性离散时间控制系统
一阶保持器复现原信号的准确度与零阶保持器相比有所 提高。但由于在式(8-16)中仍然忽略了高阶微分,一阶保持器 的输出信号与原连续信号之间仍有不同。
第8章 线性离散时间控制系统 由式(8-16)可知,一阶保持器的响应可以分解为阶跃响应
和斜坡输入响应之和。将式(8-16)的微分形式变换成式(8-17) 的差分形式,对应的传递函数为式(8-18)。
第8章 线性离散时间控制系统
图8-6 零阶保持器输入信号与输出信号的关系
第8章 线性离散时间控制系统 下面推导零阶保持器的表达式。利用泰勒级数展开公式,
可以得到
如果略去含 Δt、(Δt)2等项,可得
第8章 线性离散时间控制系统 这就是零阶保持器的公式。由式(8-11)可得零阶保持器输出 信号的完整表达式为
第8章 线性离散时间控制系统
第8章 线性离散时间控制系统
8.1 信号采样与采样定理 8.2 信号保持器 8.3 离散系统的数学模型 8.4 离散系统的稳定性分析 8.5 离散系统的稳态误差 8.6 离散系统的动态性能 8.7 离散系统的校正
第8章 线性离散时间控制系统
8.1 信号采样与采样定理
8.1.1 概述 离散时间系统(简称离散系统)是指系统中全部或一部分
进而输入给计算机控制器。也就是说,采样后的离散信号必 须能够保留有原连续信号的完整或近似完整的信息。因此, 周期T 的设定非常重要。
采样定理(也叫Shannon定理)从理论上给出了必须以多 快的采样周期(或多高的采样频率)对连续信号进行采样,才能 保证采样后离散信号可以不失真地保留原连续信号的信息。 换句话说,采样定理给出了对采样周期的限定条件,即采样周 期要在多短时间之内,才能保证采样后的离散信号保留有采 样之前的连续信号的尽量多的信息。
西南交《计算机控制系统》离线作业
计算机控制系统第1次作业一、单项选择题(只有一个选项正确,共17道小题)1.D/A变换器将数字编码信号转换为相应的时间连续模拟信号,通常要完成2种变换:答案:(B )(A) 采样保持、编码(B) 解码、保持(C) 编码、保持(D) 采样保持、解码2. 通常将时间断续幅值连续的信号称为:答案:(D )(A) 连续信号(B) 模拟信号(C) 数字信号(D) 采样信号3.答案:(A )(A)(B)(C)(D)4. 如果连续信号中所含频率分量的最高频率为,那么就完全可以用周期为T的均匀采样值来描述,T满足:答案:(C )(A)(B)(C)(D)5.答案:(B )(A)(B)(C)(D)6.答案:(A )(A)(B)(C)(D)7. 采样周期T是影响稳定性的重要参数,一般来说,T减小,稳定性____。
答案:(B )(A) 增大(B) 减小(C) 不变(D) 不确定8. 对于单位负反馈闭环连续系统,其相应的采用零阶保持器的离散系统的稳态误差与采样周期T的关系为____。
答案:( D )(A) 稳态误差随着T增大而增大(B) 稳态误差随着T增大而减小(C) 稳态误差与T不确定(D) 稳态误差与T无关9. 在离散系统中,已知脉冲传递函数的极点,若脉冲响应则脉冲响应为答案:(C )(A) 正负交替收敛脉冲序列(B) 单调发散脉冲序列(C) 正负交替发散脉冲序列(D) 单调衰减脉冲序列10. 下面关于一阶向后差分的离散化方法,说法错误的为答案:(D )(A)(B)(C)(D)11.答案:(C )(A)(B)(C)(D)12. 下面关于数字PID调节器说法错误的是答案:(B )(A) 增大比例系数可以加快系统的响应速度及减少稳态误差,但过大的比例系数可能加大系统超调;(B) 积分环节可以消除或减少控制系统的稳态误差,增加积分时间常数,有利于增加系统的稳定性,减少超调量,加快系统静态误差的消除;(C) 增加微分时间常数将有助于加速系统的动态响应,使系统超调量减少;(D) 微分作用有可能放大系统的噪声,减低系统的抗干扰能力;13.答案:(A )(A) F(B) F,G(C) F,G,C(D) F,C14.答案:(D )(A) S(B) S,Q(C) Q,R(D) Q15.对于计算机连续域-离散化设计方法,控制器等效传递函数中的是指()环节。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
脉冲传递函数变成状态空间表示: ①脉冲传递函数具有 m 重根时,从脉冲传递函数推导 Jordan 形式的状态空间表示! ②Obtain the state-space equation for the following pulse-transfer function, and then draw the block diagram for the state-space form.
1 When r (t ) 1(t ) t , determine the interval of the k which should make ess 0.05. 3
Solution: First we will analyze the stability of the system: G(s) G(z) 判断 G(z)的稳定性 0 < k < 23.94 r(t) = t, Kv=1. ess=1 r(t) = t2, Ka= 0, ess=inf
k 0
③Find the initial value and final value for each of the following functions:
X ( z)
10 z 1 1 , X ( z) 1 1 z (1 z 1 ) 2
Solution x(0)=1,x()=1 x(0)=0,x()= ④有关 z 传递函数比较综合的题目: 由下述差分方程描述的系统
Y ( z) 5 X ( z ) ( z 1) 2 ( z 5)
Solution:
Y ( z) 5 5 0 3 2 2 X ( z ) ( z 1) ( z 5) z 7 z +11z 5
1 0 0 0 0 0 1 , 0 , C 5 0 0 5 11 7 1
y(k ) y(k 1) 0.24 y(k 2) u(k ) u(k 1)
式中 u(k)、 y(k)为系统的输入输出信号, 假设 y(k)=0 k<0, 当输入为单位阶跃序列时, 确定 y(k)的解析解。 解:
G( z ) Y ( z) 1 z 1 z2 z z z 2 ( z 1) Y ( z ) G ( z ) U ( z ) U ( z ) 1 z 1 0.24 z 2 z 2 z 0.24 z 1 ( z 1)( z 0.4)( z 0.6) Y ( z) z ( z 1) 25 / 3 14 / 3 12 z ( z 1)( z 0.4)( z 0.6) z 1 z 0.4 z 0.6 25 14 y(k ) 1(k ) (0.4) k 12(0.6) k 3 3
X ( z) 3z 2 5 z ( z 1) 2 ( z 2)
Solution Note that the X(z) has two poles z1=1 (two order) and z2=2. Hence, from residue computation equation, we obtain
*图讲完后的作业: ①Ppt 表中倒数第一、第二行的脉冲传递函数的求解。 C(s) R(s) G1(s) G2(s) + H(s)
C(z)
C ( z)
G2 ( z )G1 R( z ) 1 G1G2 H ( z )
R(s) +
G(s) H(s)
C(s)
C(z)
-
C( z)
GR( z ) 1 GH ( z )
②use Jury stability criterion and 修正 Routh criterion to analyze the stability of the system :
A( z) 45z 3 177z 2 119z 39 0
roots([45 -177 119 -39]) ans = 3.1894 0.3720 + 0.3652i
③When time delay is larger than the sampling period, try to obtain the state-space model of zero-order-hold sampling of the continuous-time system. ④2.12(a) 外部模型讲完后的作业: ①Let us find the z-transform of the(部分分式法或留数法均可) 1 s3 X (s) 2 , X ( s) e Ts ( s 1)( s 2) s ( s 1) Solution
x( k )
d 3z 2 5 z ( z 1) 2 z k 1 2 dz ( z 1) ( z 2)
3z 2 5 z ( z 2) z k 1 2k 1 2 k 2 ( z 1) ( z 2) z 2 z 1
A( z ) 1 KG( z ) 0 z 2 (0.368K 1.368) z 0.368 0.264K 0 A(1) 0.632K 0 K 0 A(1) 2.736 6.104K 0 K 26.382 0 K 2.394 A(0) 1 5.182 K 2.394
0.3720 - 0.3652i >> abs(ans) ans = 3.1894 0.5213 0.5213 ③ G(z) R(s) T _
D(z) ZOH
G(s)
Y(s)
G( s)
1 , D( z ) k , T 0.ine steady-state error coefficients and steady-state error when the input is t and t2 respectively, where k =1.
X ( z) 10 z ( z 1)( z 0.2)
Solution X ( z) 10 12.5 12.5 12.5 z 12.5 z , X ( z) , x(kT) 12.5(1 0.2k ), k 0 z ( z 1)( z 0.2) z 1 z 0.2 z 1 z 0.2 (c) Find the x(kT) k 0 for (留数法)
a. T = 0.5, k = 6 and 10, compute the ess respectively; b. T = 0.5, determine the range of the k for satisfying ess 0.05. 解:
G( z ) (1 z 1 )Z{ G( s) 1 e T k (1 e T ) z } , Q ( z ) D ( z ) G ( z ) s z e T ( z 1)( z e T )
Determine the range of K when system is stable where 1 G( s) , T 1, D( z ) k s( s 1) Solution:
G ( z ) (1 z 1 ) Z { G( s) 0.368z 0.264 } s ( z 1)( z 0.368)
1 0 1 , 1, C 1 0 0 . 16 1
Solution: Y ( z) z2 2 U ( z ) z z 0.16 第四章作业 ①Ppt24 页,例子 4.5
G(z) T _
D(z) ZOH
R(s)
G(s)
Y(s)
z 1
1 z 1 k Q( z ) , z 1 T T
ess
1 0.5 T 0.042 1 K p K v 2k
T 0.05 k 5 2k
b.
ess
with the stability condition 0 < k < 8.15, we conclude that
1 r (t ) 1(t ) t , ess=essp+essv=0+(1/3k) 0.05. K6.67 23.94 > k 6.67 3
④ Ppt 例子 4.6 系统框图如③中所示: where
G( s ) 1 kz , D( z ) , r (t ) 1(t ) 0.5t , s 1 z 1
A(1) 0 k 2(1 e T ) 1 e T
A(0) 1
a. when T = 0.5, k should satisfy 0 < k < 8.15, so we should only need to compute ess for k = 6.
K p lim Q( z ) , K v lim
②
(a) Find the x(kT) k 0, for(long-division)
X ( z) 10 z 5 ( z 1)( z 0.2)
Solution
X ( z) 10z 1 17 z 2 18.4 z 3 ...
(b) Find the x(kT) k 0 for(部分分式法)
③ Obtain the state-space equation for the following difference equation, and then draw the block diagram for the state-space form. y(k 2) y(k 1) 0.16 y(k ) u(k 1) 2u(k ) y(0)=y(1)=u(0)=0 Solution: Y ( z) z2 2 U ( z ) z z 0.16 1 0 0 , , C 2 1 0.16 1 1 ④compute the z-pulse transfer function.
