传热学MATLAB温度分布大作业完整版
传热大作业 第4版4-23

东南大学能源与环境学院课程作业报告课程名称:传热学作业名称:传热学大作业——利用matlab程序解决热传导问题院(系):能源与环境学院专业:热能与动力工程姓名:姜学号:完成时间:2012 年11 月8日评定成绩:审阅教师:目录一.题目及要求 (3)二.各节点离散化的代数方程..............................3&13 三.源程序......................................................5&16 四.不同初值时的温度分布情况...........................7&18 五.冷量损失的计算.......................................12&24 六.计算小结 (27)传热大作业——利用matlab 程序解决复杂热传导问题姓名:姜 学号: 班级:成绩:____________________一、题目及要求计算要求:一个长方形截面的冷空气通道的尺寸如附图所示。
假设在垂直于纸面的方向上冷空气及通道墙壁的温度变化很小,可以忽略。
试用数值方法计算下列两种情况下通道壁面中的温度分布及每米长度上通过壁面的冷量损失:(1) 内、外壁面分别维持在10℃及30℃;(2) 内、外壁面与流体发生对流传热,且有110f t C =︒、2120/()h W m K =⋅,230f t C =︒、224/()h W m K =⋅。
(取管道导热系数为0.025/()W m K λ=⋅)二、各节点的离散化的代数方程1、基本思想:将导热问题的温度场,用有限个离散点上的值的集合来代替,通过求解按一定方法建立起来的关于这些值的代数方程,来获得离散点上被求物理量的值。
2、基本步骤:(1)建立控制方程以及定解条件:对于(1)问有:2.2m3m 2m1.2m h 1、t f1h 1、t f2导热微分方程22220t t x y ∂∂+=∂∂定解条件为第一类边界条件对(2)问有: 导热微分方程22220t t x y ∂∂+=∂∂定解条件为第三类边界条件(2)区域离散化:如下图所示,用一系列与坐标轴平行的网格线把求解区域划分成许多子区域,以网格线的交点作为需要确定温度值的空间位置,称为节点。
(完整word版)matlab绘制温度场

通过在室内的某些位置布置适当的节点,采集回来室内的温湿度以及空气质量等实际参数。
首先对室内空间建模,用一个无限细化的三维矩阵来模拟出室内的温度分布情况,针对采集回来的数据,采用插值法和适当次数的拟合函数的拟合,得出三维矩阵的实际值的分布,最后结合matlab软件绘制出计算出的温度场的三维图像。
一.数据的采集与处理因为影响人的舒适感的温度层只是室内的某一高度范围内的温度,而温度传感器虽然是布置在一个平面内,但是采用插值法和拟合函数法是可以大致再现出影响人的舒适感的温度层的温度变化的。
同时,在构建出的三维模型中,用第三维表示传感器层面的温度。
在传感器层面,传感器分布矩阵如下:X=【7.5 36.5 65.5】(模型内单位为cm)Y=【5.5 32.5 59.5】Z=【z1 z2 z3;z4 z5 z6;z7 z8 z9;】(传感器采集到的实时参数)采用meshgrid(xi,yi,zi,…)产生网格矩阵;首先按照人的最小温度分辨值,将室内的分布矩阵按照同样的比例细化,均分,使取值点在坐标一定程度上也是接近于连续变化的,从而才能最大程度上使处理数据得来的分布值按最小分辨值连续变化!根据人体散热量计算公式:C=hc(tb-Ta)其中hc为对流交换系数;结合Gagge教授提出的TSENS热感觉指标可以计算出不同环境下人的对环境温度变化时人体温度感知分辨率,作为插值法的一个参考量,能使绘制出的温度场更加的符合人体的温度变化模式。
例如按照10cm的均差产生网格矩阵(实际上人对温度的分辨率是远远10cm大于这个值的,但是那样产生的网格矩阵也是异常庞大的,例如以0.5cm为例,那么就可以获得116*108=12528个元素,为方便说明现已10cm为例):[xi yi]=meshgrid(7.5:10:65.5,5.5:10:59.5)xi =7.5000 17.5000 27.5000 37.5000 47.5000 57.50007.5000 17.5000 27.5000 37.5000 47.5000 57.50007.5000 17.5000 27.5000 37.5000 47.5000 57.50007.5000 17.5000 27.5000 37.5000 47.5000 57.50007.5000 17.5000 27.5000 37.5000 47.5000 57.50007.5000 17.5000 27.5000 37.5000 47.5000 57.5000yi =5.5000 5.5000 5.5000 5.5000 5.5000 5.500015.5000 15.5000 15.5000 15.5000 15.5000 15.500025.5000 25.5000 25.5000 25.5000 25.5000 25.500035.5000 35.5000 35.5000 35.5000 35.5000 35.500045.5000 45.5000 45.5000 45.5000 45.5000 45.500055.5000 55.5000 55.5000 55.5000 55.5000 55.5000产生网格矩阵之后,就可以在测得的实时数据的基础上,通过相关的温度场的专业的估算函数,以及相关的数值处理函数来估计整个分布面(有最小的分辨率)上的温度了。
报告

大作业报告【9-16】题目略 分析过程:● 第一步,建立节点温度差分方程。
有题目可以看出,本题有7类不同的节点,需要7个不同的方程。
由于y x ∆=∆在原始方程中将它们消去后有: 1、底边的中间5个点满足的方程:x q t t t t w j i j i j i j i ∆+++=-+-1,,1,1,222λλλλ2、右边对流换热的中间3个点满足的方程:∞∆+--∆+++=+t B t t t t B i j i j i j i j i i 22)42(1,1,,1,3、左边绝热部分的中间3个点满足的方程:1,1,,1,222+-+++=j i j i j i j i t t t t λλλλ4、上边恒温点满足的方程:w j i t t =.5、中间5×3的网格里的点满足的方程:1,1,,1,1,4+-+-+++=j i j i j i j i j i t t t t t6、左下角的既属于绝热层又接受加热的点:0)(2)(22,1,,,1=-+-+∆⋅++j i j i j i j i w t t t t x q λλ 7、右下角的既被加热又与流体有对流换热的点:0)(2)(2)(22,,1,,,1=-⋅∆⋅+-+-+∆⋅+-j i f j i j i j i j i w t t y h t t t t x q λλ● 第二步,采用高斯-塞德尔迭代法进行迭代:建立矩阵,左下点为原点(1,1),i 值向右增加,j 值向上增加。
按照上面7种类型的分组依次进行计算,每次计算直接用计算结果代替原值,完成一轮迭代。
程序设定200次迭代。
根据最终结果判断,100次迭代就已经结果收敛。
● 结果分析: Matlab 运算结果:表1 节点的温度分布(i为横行,j为竖列)5 400 400 400 400 400 400 4004 397.1890 396.8375 395.7156 393.5919 389.9486 383.6080 371.52583 394.2443 394.4454 392.4332 388.7034 382.5945 372.9575 357.94582 394.2443 393.4299 390.8685 386.1939 378.7685 367.6818 351.89201 395.0363 394.1616 391.4168 386.4354 378.6037 367.1090 351.1356 节点/˚C 123456 7做出三维分布图像:结果分析:由数值计算结果,可以看出:1、最顶部的点温度恒定,满足题设条件。
2013年matlab应用作业
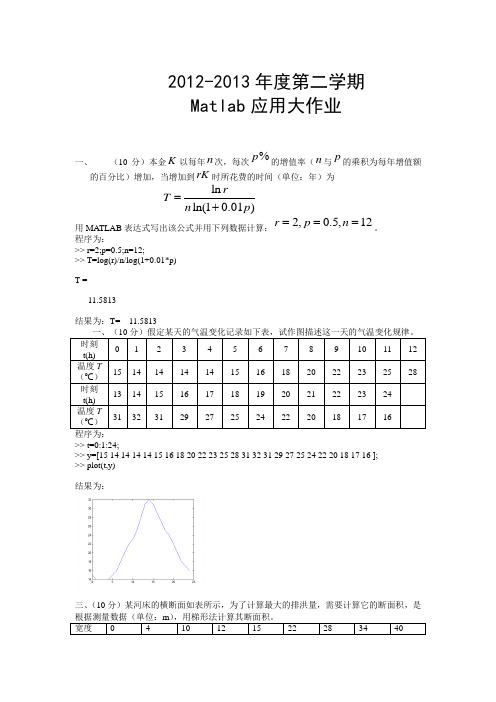
程序为:
>> x=0:2:24;
>> y=[12 9 9 10 18 24 28 27 25 20 18 15 13];
>> x1=13;y1=interp1(x,y,x1,'spline')
2)本金 以每年 次,每次 的增值率( 与 的乘积为每年增值额的百分比)增加,当增加到 时所花费的时间(单位:年)为
用MATLAB表达式写出该公式并用下列数据计算: 。
程序为:
>> r=2;p=0.5;n=12;
>> T=log(r)/n/log(1+0.01*p)
甲(百箱)
乙(百箱)
现有
原料(kg)
6
5
60
工人(名)
10
20
150
获利(万元)
10
9
程序为:
>> c=[-10 -9];
>> a=[10 20;6 5];
>> b=[150;60];
>> aeq=[];
>> beq=[];
>> vlb=[0 0];
>> vub=[8 12];
>> [x,f]=linprog(c,a,b,aeq,beq,vlb,vub)
>> p=polyfit(t,y,2)
p =
-0.0445 1.0711 4.3252
>> x=30;
>> f(x)=-0.0445*x^2+1.0711*x+4.3252
利用matlab求解圆柱内稳定温度分布

数学物理方法论文(圆柱体齐次边界条件以及matlab的可视化)学院: 信息院年级: 2011级班级: 通信一班姓名: ***一、应用背景:现在由于公寓楼采用集体供暖的措施,需要在地下铺设圆柱形长管道,而对于管道的半径选取需要进行一定的计算,才能使得热水在传送过程中不会因温度过低而达不到用户的要求。
对于以上的问题,我们可以简化到应用数学中来解决。
二、简化例题:若一供暖公司采用的运输管道为标准圆柱体,其半径为ρ。
,长为L ,设管入口有均匀分布的强度为q 。
的热流流入,出口有相同的热流流出,管道侧面保持温度为0℃。
求解管道内的稳恒温度。
三、例题解答:解: 因为上下底非齐次边界的非齐次项是常数,故可较易化成齐次边界。
这样本征值问题就变成傅里叶级数本征问题,而不是贝塞尔函数本征问题,同时系数的求解也较为简单。
令 z 01kq =νv kq u +=0则v 的定解问题为:⎪⎪⎪⎩⎪⎪⎪⎨⎧=-===∆===z k q v L z z z z 00200,00ρρννν 分离变数得到的本征值问题为:⎪⎩⎪⎨⎧===+==0',0'0"02L z z Z Z Z h Z 解得 ()......2,1,0,==n Ln h n πz Ln A Z n n πcos =,问题在柱内的有限解为:()⎪⎪⎭⎫⎝⎛∞=⋅=∑ρππρνL n n n I z L n A z 00cos , 由初始条件,得z kq IA n z L n L n 00ncos -=∑∞=⋅⎪⎪⎭⎫⎝⎛ππρ将上式右端展为傅里叶余弦级数,则有()dz L zn z k q L n LI n LA ππρcos 2000⋅-=⎰L L z n z n L L z n n L Ln L k I q 02000si n c o s 2-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛⋅+=πππππρ()()[]112-2000--⎪⎭⎫ ⎝⎛=nn L L n L k Iq ππρ ()()()⎪⎩⎪⎨⎧+===12,402000220m n L n I n k Lq m n πρπ但不等于,()()()00,2-01000000=-==⎰I kL q zdz k q LI A L ()∑∞=+⋅⎪⎭⎫ ⎝⎛++⎪⎭⎫⎝⎛++=∴0002020012cos 12121242-m z L m L m I m L m I k L q k L q ππρπρπνν+=∴kqu四、以上问题的Matlab 的可视化:建立圆柱体:t=linspace(-pi,pi,200); y=linspace(0,4,200); [T,Y]=meshgrid(t,y); X=sin(T); Z=cos(T); mesh(X,Y,Z); axis equal由于本题中需要四维的数学建模(三维立体图形,再加一维的温度坐标),对于专业知识要求较高,以现有的知识水平还无法对四维进行分析求解,因此采用三维坐标(二维管道的横截面,再加一维的平面温度分布),进行求解。
传热学数值计算大作业

数值计算大作业一、用数值方法求解尺度为100mm×100mm 的二维矩形物体的稳态导热问题。
物体的导热系数λ为1.0w/m·K。
边界条件分别为: 1、上壁恒热流q=1000w/m2; 2、下壁温度t1=100℃; 3、右侧壁温度t2=0℃; 4、左侧壁与流体对流换热,流体温度tf=0℃,表面传热系数 h 分别为1w/m2·K、10 w/m2·K、100w/m2·K 和1000 w/m2·K;要求:1、写出问题的数学描述;2、写出内部节点和边界节点的差分方程;3、给出求解方法;4、编写计算程序(自选程序语言);5、画出4个工况下的温度分布图及左、右、下三个边界的热流密度分布图;6、就一个工况下(自选)对不同网格数下的计算结果进行讨论;7、就一个工况下(自选)分别采用高斯迭代、高斯——赛德尔迭代及松弛法(亚松弛和超松弛)求解的收敛性(cpu 时间,迭代次数)进行讨论;8、对4个不同表面传热系数的计算结果进行分析和讨论。
9、自选一种商业软件(fluent 、ansys 等)对问题进行分析,并与自己编程计算结果进行比较验证(一个工况)。
(自选项)1、写出问题的数学描述 设H=0.1m微分方程 22220t tx y∂∂+=∂∂x=0,0<y<H :()f th t t xλ∂-=-∂ 定解条件 x=H ,0<y<H :t=t 2 y=0,0<x<H :t=t1t 1t 2h ;t fq=1000 w/m 2y=H ,0<x<H :tq yλ∂-=∂ 2、写出内部节点和边界节点的差分方程 内部节点:()()1,,1,,1,,122220m n m n m nm n m n m n t t t t t t x y -+-+-+-++=∆∆左边界: (),1,,1,1,,,022m n m n m n m nm n m n f m n t t t t t t x x h y t t y y y xλλλ-++---∆∆∆-+++∆=∆∆∆右边界: t m,n =t 2上边界: 1,,1,,,1,022m n m n m n m nm n m n t t t t t t y y q x x x x yλλλ-+----∆∆∆+++∆=∆∆∆ 下边界: t m,n =t 13、求解过程利用matlab 编写程序进行求解,先在matlab 中列出各物理量,然后列出内部节点和边界节点的差分方程,用高斯-赛德尔迭代法计算之后用matlab 画图。
大作业题(2014版)——中科院传热学(雁栖湖校区)

(注意:如发现作业中互相拷贝及抄袭者,此次作业成绩全将记为 一矩形平板 0 x a , 0 y b ,内有均匀恒 定热源 g 0 , 在 x 0 及 y 0 处绝热, 在x a及y b 处保持温度 T1 , 初始时刻温度为 T0 , 如右图 1 所示: 1、求 t 0 时,矩形区域内的温度分布 T x, y, t 的解 析表达式; 2、若 a 18m , b 12m , g 0 1W m3 , T1 600 K , T0 200 K ,热传导系数 热扩散系数 0.8 m 2 s 。 请根据 1 中所求温度分布用 MATLAB k 1.0W m K , 软件绘出下列结果,并加以详细物理分析: (a) 300s 内,在同一图中画出点 (0,4) 、 (0,8) 、 6,0 、 (12,0) 、 (9,6) (单位:m) 温度随时间的变化 (b) 200s 内,画出点 (18,4) 、 (18,8) 、 6,12 、 (12,12) 、 (9,6) (单位:m)处,分 别沿 x、y 方向热流密度值随时间的变化 (c) 画出 t 50s、 75s、 100s、 125s、 150s 时刻区域内的等温线 (d) 300s 内,在同一图中画出点 9,0 , 9, 6 (单位:m)在其他参数不变时 g 0 分 别等于 1W m 3 , 2W m3 , 3W m3 情况下的温度、热流密度 (e) 600s 内,在同一图中画出点(9,6)(单位:m)在其它参数不变情况时热导率 分别为 0.5W m K 、 1.0W m K 和 1.5W m K 时的温度、热流密度 (f) 600s 内,在同一图中画出点(9,6) (单位:m)在其它参数不变情况时热扩散 系数分别为 0.4 m 2 s 、 0.8 m 2 s 和 1.2 m 2 s 时的温度、热流密度 3、运用有限差分法计算 2 中(b)、(d)和(e),并与解析解结果进行比较,且需将数 值解与解析解的相对误差减小到万分之一以下; 4、附上源! )
传热学数值计算大作业

传热学数值计算大作业传热学数值计算大作业一选题《传热学》第四版P179页例题 4-3二相关数据及计算方法1.厚2δ=0.06m的无限大平板受对称冷却,故按一半厚度作为模型进行计算2. δ=0.03m,初始温度t0=100℃,流体温度t∞=0℃;λ=40W/(m.K),h=1000W/(m2.K),Bi=h*△x/λ=0.25;3.设定Fo=0.25和Fo=1两种情况通过C语言编程(源程序文件见附件)进行数值分析计算;当Fo=0.25时,Fo<1/(2*(1+Bi)),理论上出现正确的计算结果;当Fo=1时,Fo>1/(2*(1+Bi)),Fo>0.5,理论上温度分布出现振荡,与实际情况不符。
三网格划分将无限大平面的一半划分为6个控制体,共7个节点。
△x=0.03/N=0.03/6=0.005,即空间步长为0.005m四节点离散方程绝热边界节点即i=1时,tij+1=2Fo△ti+1j+(1-2Fo△)tij 内部节点即0tij+1=tij(1-2Fo△Bo△-2Fo△)+2Fo△ti-1j+2Fo△Bo△tf五温度分布线图(origin)六结果分析1 空间步长,时间步长对温度分布的影响空间步长和时间步长决定了Bo和Fo,两者越小计算结果越精确,但同时计算所需的时间就越长。
2 Fo数的大小对计算结果的影响编程时对Fo=1及0.25的情况分别进行了计算,发现当Fo=1时,各点温度随时间发生振荡,某点的温度高反而会使下一时刻的温度变低,违反了热力学第二定律,因此在计算中对Fo的选取有限制。
为了保证各项前的系数均为正值,对于内节点,Fo>0.5;对于对流边界节点,Fo<1/(2*(1+Bi))。
3 备注在Fo=0.25时,为了反映较长时间后温度的分布,取T=600,并选取了其中部分时刻的温度输出进行画图。
图像显示,随着时间的增长,各点温度趋向一致。
而当Fo=1时由于结果会出现振荡,只取T=6观察即可。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
东南大学能源与环境学院课程作业报告作业名称:传热学大作业——利用matlab程序解决热传导问题院系:能源与环境学院专业:建筑环境与设备工程学号:姓名:2014年11月9日一、题目及要求1.原始题目及要求2.各节点的离散化的代数方程3.源程序4.不同初值时的收敛快慢5.上下边界的热流量(λ=1W/(m℃))6.计算结果的等温线图7.计算小结题目:已知条件如下图所示:二、各节点的离散化的代数方程各温度节点的代数方程ta=(300+b+e)/4 ; tb=(200+a+c+f)/4; tc=(200+b+d+g)/4; td=(2*c+200+h)/4 te=(100+a+f+i)/4; tf=(b+e+g+j)/4; tg=(c+f+h+k)/4 ; th=(2*g+d+l)/4ti=(100+e+m+j)/4; tj=(f+i+k+n)/4; tk=(g+j+l+o)/4; tl=(2*k+h+q)/4tm=(2*i+300+n)/24; tn=(2*j+m+p+200)/24; to=(2*k+p+n+200)/24; tp=(l+o+100)/12 三、源程序【G-S迭代程序】【方法一】函数文件为:function [y,n]=gauseidel(A,b,x0,eps)D=diag(diag(A));L=-tril(A,-1);U=-triu(A,1);G=(D-L)\U;f=(D-L)\b;y=G*x0+f;n=1;while norm(y-x0)>=epsx0=y;y=G*x0+f;n=n+1;end命令文件为:A=[4,-1,0,0,-1,0,0,0,0,0,0,0,0,0,0,0;-1,4,-1,0,0,-1,0,0,0,0,0,0,0,0,0,0;0,-1,4,-1,0,0,-1,0,0,0,0,0,0,0,0,0;0,0,-2,4,0,0,0,-1,0,0,0,0,0,0,0,0;-1,0,0,0,4,-1,0,0,-1,0,0,0,0,0,0,0;0,-1,0,0,-1,4,-1,0,0,-1,0,0,0,0,0,0;0,0,-1,0,0,-1,4,-1,0,0,-1,0,0,0,0,0;0,0,0,-1,0,0,-2,4,0,0,0,-1,0,0,0,0;0,0,0,0,-1,0,-1,0,4,0,0,0,-1,0,0,0;0,0,0,0,0,-1,0,0,-1,4,-1,0,0,-1,0,0;0,0,0,0,0,0,-1,0,0,-1,4,-1,0,0,-1,0;0,0,0,0,0,0,0,-1,0,0,-2,4,0,0,0,-1;0,0,0,0,0,0,0,0,-2,0,0,0,24,-1,0,0;0,0,0,0,0,0,0,0,0,-2,0,0,-1,24,-1,0;0,0,0,0,0,0,0,0,0,0,-2,0,0,-1,24,-1;0,0,0,0,0,0,0,0,0,0,0,-1,0,0,-1,12];b=[300,200,200,200,100,0,0,0,100,0,0,0,300,200,200,100]';[x,n]=gauseidel(A,b,[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]',1.0e-6) xx=1:1:4;yy=xx;[X,Y]=meshgrid(xx,yy);Z=reshape(x,4,4);Z=Z'contour(X,Y,Z,30)Z =139.6088 150.3312 153.0517 153.5639108.1040 108.6641 108.3119 108.1523 84.1429 67.9096 63.3793 62.4214 20.1557 15.4521 14.8744 14.7746 【方法2】>> t=zeros(5,5);t(1,1)=100;t(1,2)=100;t(1,3)=100;t(1,4)=100;t(1,5)=100;t(2,1)=200;t(3,1)=200;t(4,1)=200;t(5,1)=200;for i=1:10t(2,2)=(300+t(3,2)+t(2,3))/4 ;t(3,2)=(200+t(2,2)+t(4,2)+t(3,3))/4;t(4,2)=(200+t(3,2)+t(5,2)+t(4,3))/4;t(5,2)=(2*t(4,2)+200+t(5,3))/4;t(2,3)=(100+t(2,2)+t(3,3)+t(2,4))/4;t(3,3)=(t(3,2)+t(2,3)+t(4,3)+t(3,4))/4; t(4,3)=(t(4,2)+t(3,3)+t(5,3)+t(4,4))/4; t(5,3)=(2*t(4,3)+t(5,2)+t(5,4))/4;t(2,4)=(100+t(2,3)+t(2,5)+t(3,4))/4;t(3,4)=(t(3,3)+t(2,4)+t(4,4)+t(3,5))/4;t(4,4)=(t(4,3)+t(4,5)+t(3,4)+t(5,4))/4;t(5,4)=(2*t(4,4)+t(5,3)+t(5,5))/4;t(2,5)=(2*t(2,4)+300+t(3,5))/24;t(3,5)=(2*t(3,4)+t(2,5)+t(4,5)+200)/24;t(4,5)=(2*t(4,4)+t(3,5)+t(5,5)+200)/24;t(5,5)=(t(5,4)+t(4,5)+100)/12;t'endcontour(t',50);ans =100.0000 200.0000 200.0000 200.0000 200.0000 100.0000 136.8905 146.9674 149.8587 150.7444 100.0000 102.3012 103.2880 103.8632 104.3496 100.0000 70.6264 61.9465 59.8018 59.6008 100.0000 19.0033 14.8903 14.5393 14.5117【Jacobi迭代程序】函数文件为:function [y,n]=jacobi(A,b,x0,eps)D=diag(diag(A));L=-tril(A,-1);U=-triu(A,1);B=D\(L+U);f=D\b;y=B*x0+f;n=1;while norm(y-x0)>=epsx0=y;y=B*x0+f;n=n+1;end命令文件为:A=[4,-1,0,0,-1,0,0,0,0,0,0,0,0,0,0,0;-1,4,-1,0,0,-1,0,0,0,0,0,0,0,0,0,0; 0,-1,4,-1,0,0,-1,0,0,0,0,0,0,0,0,0; 0,0,-2,4,0,0,0,-1,0,0,0,0,0,0,0,0;-1,0,0,0,4,-1,0,0,-1,0,0,0,0,0,0,0; 0,-1,0,0,-1,4,-1,0,0,-1,0,0,0,0,0,0; 0,0,-1,0,0,-1,4,-1,0,0,-1,0,0,0,0,0;0,0,0,-1,0,0,-2,4,0,0,0,-1,0,0,0,0;0,0,0,0,-1,0,-1,0,4,0,0,0,-1,0,0,0;0,0,0,0,0,-1,0,0,-1,4,-1,0,0,-1,0,0;0,0,0,0,0,0,-1,0,0,-1,4,-1,0,0,-1,0;0,0,0,0,0,0,0,-1,0,0,-2,4,0,0,0,-1;0,0,0,0,0,0,0,0,-2,0,0,0,24,-1,0,0;0,0,0,0,0,0,0,0,0,-2,0,0,-1,24,-1,0;0,0,0,0,0,0,0,0,0,0,-2,0,0,-1,24,-1;0,0,0,0,0,0,0,0,0,0,0,-1,0,0,-1,12];b=[300,200,200,200,100,0,0,0,100,0,0,0,300,200,200,100]'; [x,n]=jacobi(A,b,[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]',1.0e-6); xx=1:1:4;yy=xx;[X,Y]=meshgrid(xx,yy);Z=reshape(x,4,4);Z=Z'contour(X,Y,Z,30)n =97Z =139.6088 150.3312 153.0517 153.5639108.1040 108.6641 108.3119 108.152384.1429 67.9096 63.3793 62.421420.1557 15.4521 14.8744 14.7746四、不同初值时的收敛快慢1、[方法1]在Gauss 迭代和Jacobi 迭代中,本程序应用的收敛条件均为norm(y-x0)>=eps ,即使前后所求误差达到e 的-6次方时,跳出循环得出结果。
将误差改为0.01时,只需迭代25次,如下[x,n]=gauseidel(A,b,[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]',0.01)运行结果为 将误差改为0.1时,需迭代20次,可见随着迭代次数增加,误差减小,变化速度也在减小。
[方法2]通过 i=1:10判断收敛,为迭代10次,若改为1:20,则迭代20次。
2、在同样的误差要求下,误差控制在e 的-6次方内,Gauss 迭代用了49次达到要求,而Jacobi 迭代用了97次,可见,在迭代中尽量采用最新值,可以大幅度的减少迭代次数,迭代过程收敛快一些。
在Gauss 中,初值为100,迭代46次达到精确度1.0e-6,初值为50时,迭代47次,初值为0时,迭代49次,初值为200时迭代50次,可见存在一个最佳初始值,是迭代最快。
这一点在jacobi 迭代中表现的尤为明显。
五、上下边界的热流量:上边界t=200℃,∞t =10℃,所以,热流量Φ1=λ*[2*100-200x y ∆∆+x y a∆∆t -200+x y ∆∆b t -200+x y ∆∆c t -200+2*t -200d x y ∆∆] =1*(100/2+(200-139.6088)+(200-150.3312)+(200-153.0517)+(200-153.5639)/2) =230.2264W 下边界热流量Φ2=|λ*[x y ∆∆mi t -t +x y∆∆o j t -t +x y ∆∆p k t -t +2*t -t q l x y ∆∆]- h*(2*10-100x y ∆∆+x *t -t n ∆∆∞y +x *t -t o ∆∆∞y +x *t-t m ∆∆∞y +2*t -t p x y ∆∆∞)|=|1*((84.1429-20.1557)+(67.9096-15.4521)+(63.3793-14.8744)+(62.4214- 14.7746)/2)-10*(90/2+(20.1557-10)+(15.4521-10)+(14.8744-10)+(14.7746-10)/2)| = |-489.925|W =489.25W六、温度等值线Gauss:Yacobi:七、计算小结导热问题进行有限差分数值计算的基本思想是把在时间、空间上连续的温度场用有限个离散点温度的集合来代替,即有限点代替无限点,通过求解根据傅里叶定律和能量守恒两大法则建立关于控制面内这些节点温度值的代数方程,获得各个离散点上的温度值。
