圆锥曲线内接四边形的四极点调和分割定理(东南大学徐文平新定理)
调和平均定理圆锥曲线

调和平均定理圆锥曲线几何观点用一个平面去截一个二次锥面,得到的交线就称为圆锥曲线(conic sections)。
通常提及的圆锥曲线包含椭圆,双曲线和抛物线,但严苛来说,它还包括一些发育情形。
具体内容而言:1) 当平面与二次锥面的母线平行,且不过圆锥顶点,结果为抛物线。
2) 当平面与二次锥面的母线平行,且过圆锥顶点,结果发育为一条直线。
3) 当平面只与二次锥面一侧相交,且不过圆锥顶点,结果为椭圆。
4) 当平面只与二次锥面一侧平行,且不过圆锥顶点,并与圆锥的对称轴横向,结果为圆。
5) 当平面只与二次锥面一侧相交,且过圆锥顶点,结果为一点。
6) 当平面与二次锥面两侧都平行,且不过圆锥顶点,结果为双曲线(每一支为此二次锥面中的一个圆锥面与平面的交线)。
7) 当平面与二次锥面两侧都相交,且过圆锥顶点,结果为两条相交直线。
代数观点在笛卡尔平面上,二元二次方程的图像是圆锥曲线。
根据判别式的不同,也包含了椭圆、双曲线、抛物线以及各种退化情形。
焦点--准线观点(严格来讲,这种观点下只能定义圆锥曲线的几种主要情形,因而不能算是圆锥曲线的定义。
但因其使用广泛,并能引导出许多圆锥曲线中重要的几何概念和性质)。
取值一点p,一直线l以及一非负实常数e,则至p的距离与l距离之比是e的点的轨迹就是圆锥曲线。
根据e的范围不同,曲线也各不相同。
具体如下:1) e=0,轨迹为圆(椭圆的特例);2) e=1(即到p与到l距离相同),轨迹为抛物线 ;3) 0<e<1,轨迹为椭圆;4) e>1,轨迹为双曲线的一支。
(以下以氢铵几何方式描述主要的圆锥曲线通用型的概念和性质,由于大部分性质就是在焦点-准线观点下定义的,对于更通常的发育情形,有些概念可能将不适用于。
)考虑焦点--准线观点下的圆锥曲线定义。
定义中提到的定点,称为圆锥曲线的焦点;定直线称为圆锥曲线的准线;固定的常数(即圆锥曲线上一点到焦点与准线的距离比值)称为圆锥曲线的离心率;焦点到准线的距离称为焦准距;焦点到曲线上一点的线段称为焦半径。
圆锥曲线进阶版公式定理大全

圆锥曲线进阶版公式定理大全一、椭 圆1. 点P 处的切线PT 平分△PF 1F 2在点P 处的外角.(椭圆的光学性质)2. PT 平分△PF 1F 2在点P 处的外角,则焦点在直线PT 上的射影H 点的轨迹是以长轴为直径的圆,除去长轴的两个端点.(中位线)3. 以焦点弦PQ 为直径的圆必与对应准线相离.以焦点半径PF 1为直径的圆必与以长轴为直径的圆内切.(第二定义)4. 若000(,)P x y 在椭圆22221x y a b +=上,则过0P 的椭圆的切线方程是00221x x y ya b+=.(求导)5. 若000(,)P x y 在椭圆22221x y a b+=外 ,则过Po 作椭圆的两条切线切点为P 1、P 2,则切点弦P 1P 2的直线方程是00221x x y ya b+=.(结合4) 6. 椭圆22221x y a b+= (a >b >0)的左右焦点分别为F 1,F 2,点P 为椭圆上任意一点12F PF γ∠=,则椭圆的焦点角形的面积为122tan 2F PF S b γ∆=.(余弦定理+面积公式+半角公式)7. 椭圆22221x y a b+=(a >b >0)的焦半径公式:10||MF a ex =+,20||MF a ex =-(1(,0)F c - , 2(,0)F c 00(,)M x y ).(第二定义)8. 设过椭圆焦点F 作直线与椭圆相交 P 、Q 两点,A 为椭圆长轴上一个顶点,连结AP 和AQ 分别交相应于焦点F 的椭圆准线于M 、N 两点,则MF ⊥NF9.过椭圆一个焦点F的直线与椭圆交于两点P、Q, A1、A2为椭圆长轴上的顶点,A 1P和A2Q交于点M,A2P和A1Q交于点N,则MF⊥NF. MN其实就在准线上,下面证明他在准线上根据第8条,证毕10. AB 是椭圆22221x y a b+=的不平行于对称轴的弦,M ),(00y x 为AB 的中点,则22OM ABb k k a⋅=-,即0202y a x b K AB-=。
圆锥曲线的Ptolemy定理

注:若a=b,则λij =1,定 理 1 就 是 Ptolemy 定理,故定理1是 Ptolemy定理的推广.
定理2 四边 形 A1A2A3A4 是 双 曲 线ax22 -yb22 =1(a>0,b>0)一支上内接四边形,直线 AiAj 的 斜率为 Kij,则λ12 ·λ34|A1A2|·|A3A4|+λ23 · λ41|A2A3|·|A4A1|=λ13·λ24|A1A3|·|A2A4|.
|A2A3|·|A4A1|
( ) =2b2
cosθ2+θ3-2θ1-θ4
-cosθ3
+θ4
-θ1 2
-θ2
而λ13·λ24|A1A3|·|A2A4|
(1)
( ) =2b2
cosθ2+θ3-2θ1-θ4
-cosθ3
+θ4
-θ1 2
-θ2
(2)
由(1)、(2)得,λ12 ·λ34|A1A2|·|A3A4|+λ23 · λ41|A2A3|·|A4A1|=λ13·λ24|A1A3|·|A2A4|. 定理1证完.
2
+
b a
2
[( ) ]} bsinθj-bsinθi acosθj-acosθi
2
+1
1/2
槡 =
[(sinθj-sinθi)2+(cosθj-cosθi)2]b2 (bsinθj-bsinθi)2+(acosθj-acosθi)2
=|AbiAj|槡(sinθj-sinθi)2 + (cosθj-cosθi)2 ,
注:定 理 3 中 的 四 边 形 A1A2A3A4 不 一 定 是 凸 的 ,也 有 可 能 是 一 个 折 四 边 形 .
槡 =b cosθj2cosθi[1-(cosθjcosθi+sinθjsinθi)]
【参考借鉴】尺规作图五点定椭圆的方法.docx
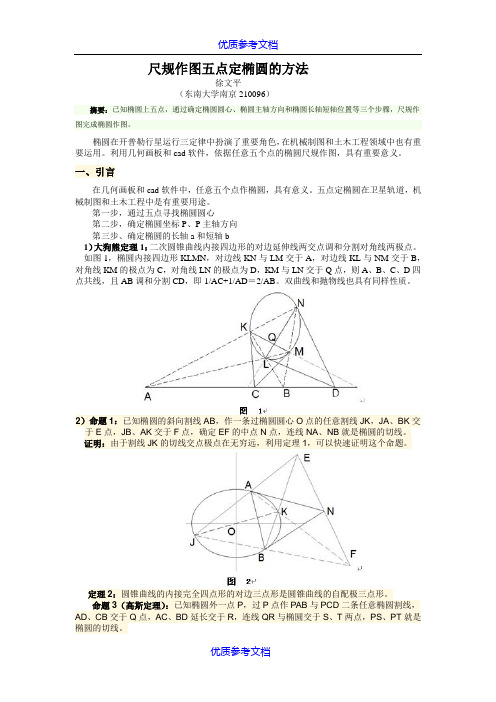
尺规作图五点定椭圆的方法徐文平(东南大学南京210096)摘要:已知椭圆上五点,通过确定椭圆圆心、椭圆主轴方向和椭圆长轴短轴位置等三个步骤,尺规作图完成椭圆作图。
椭圆在开普勒行星运行三定律中扮演了重要角色,在机械制图和土木工程领域中也有重要运用。
利用几何画板和cad软件,依据任意五个点的椭圆尺规作图,具有重要意义。
一、引言在几何画板和cad软件中,任意五个点作椭圆,具有意义。
五点定椭圆在卫星轨道,机械制图和土木工程中是有重要用途。
第一步,通过五点寻找椭圆圆心第二步,确定椭圆坐标P、P主轴方向第三步、确定椭圆的长轴a和短轴b1)大狗熊定理1:二次圆锥曲线内接四边形的对边延伸线两交点调和分割对角线两极点。
如图1,椭圆内接四边形KLMN,对边线KN与LM交于A,对边线KL与NM交于B,对角线KM的极点为C,对角线LN的极点为D,KM与LN交于Q点,则A、B、C、D四点共线,且AB调和分割CD,即1/AC+1/AD=2/AB。
双曲线和抛物线也具有同样性质。
2)命题1:已知椭圆的斜向割线AB,作一条过椭圆圆心O点的任意割线JK,JA、BK交于E点,JB、AK交于F点,确定EF的中点N点,连线NA、NB就是椭圆的切线。
证明:由于割线JK的切线交点极点在无穷远,利用定理1,可以快速证明这个命题。
定理2:圆锥曲线的内接完全四点形的对边三点形是圆锥曲线的自配极三点形。
命题3(高斯定理):已知椭圆外一点P,过P点作PAB与PCD二条任意椭圆割线,AD、CB交于Q点,AC、BD延长交于R,连线QR与椭圆交于S、T两点,PS、PT就是椭圆的切线。
图3二、通过五点寻找椭圆圆心原理:通过已知五点,作椭圆切线,获得割线的极点,将割线的极点和割线中点连接并延伸,必定通过椭圆的圆心。
图4问题1:只有五点,没有坐标轴和原点,椭圆斜的,割线PQ的切线极点如何办?切线方法:帕斯卡定理(五点+一个切点二次)做切线,或者如图5方法作切线。
椭圆焦点弦的优美性质及其简证(东大徐文平)

椭圆焦点弦的优美性质及其简证徐文平,东南大学 南京(210096)摘要:针对椭圆焦点弦,发现了一组优美的性质,运用极点与极线的知识,进行了快速简捷证明。
关键词:圆锥曲线、椭圆焦点弦、椭圆切线、极点与极线、调和分割文献[1]李康海老师发现了圆锥曲线焦点弦的一个有趣性质,读后深受启发。
笔者感觉李老师的证明方法比较繁琐,通过思考,作者找到了快速简捷证明,并又发现了椭圆焦点弦的一些优美的性质,供大家参考。
定理1:过椭圆一个焦点F 的直线与椭圆交于P 、Q 点,点A 、B 为椭圆长轴上的顶点,AP 和BQ 交于M ,BP 和AQ 交于N ,点C 为MN 的中点,则有以下一些优美的性质。
1) MF ⊥NF ;2) MN 的中点C 为焦点弦PQ 的极点,即PC 、QC 与椭圆相切; 3) FC ⊥PQ ;4) MF 平分∠PFB 角,NF 平分∠QFB 角。
图 1针对定理1中的4个性质,进行简捷证明,具体如下:性质1:假设()0,a A -,()0,a B ,()0,c F ,()m t M ,,()n t N ,。
设椭圆的方程为12222=+by a x ,直线PQ 的方程为c y k x +⋅=(0≠c ),依据极点与极线的基本知识,ΔMNF 为自配极三角形,极点M 与NF 极线对应,极点N与MF 极线对应,极点F 与MN 极线对应。
椭圆外任意一点()00y x W ,,对应的极线方程为:1220=+byy a x x o 当椭圆焦点()0,c F 为极点时,极点F 对应的MN 极线方程为:c a x /2=, 因此 ()m c a M ,/2,()n c a N ,/2。
极点M 对应的NF 极线方程为:1/222=⋅+⋅bym a x c a (1) 由于M 极点对应的NF 极线通过点()n c a N ,/2,则: 1//2222=⋅+⋅bnm a c a c a (2) 整理得:)/1(222c a b mn -=2224/⎪⎪⎭⎫ ⎝⎛-==-c c a c b mn (3)由(3)式可知,ΔMNF 满足直角三角形斜边上的高的平方等于它分斜边两部分的乘积的条件,所以ΔMNF 是直角三角形,所以MF ⊥NF 。
圆锥曲线内接四边形的一个性质(3)doc-圆锥曲线内接四边形的一个性质

圆锥曲线内接四边形的一个性质(一道高考试题的溯源与拓展)100025 北京市日坛中学(延静里校区) 邱继勇在我们利用一般化、特殊化、类比的思维方法,对北京市2004年高考数学试卷第17题的研究过程中,发现了圆锥曲线内接四边形的一个性质.下面将我们的研究过程简述如下.一、从圆说起如图1,四边形ABCD 内接于⊙O ,若直线BD AC AD BC CD AB 与、与、与中,有一对直线与直径MN 所在的直线的夹角相等,则另外两对直线与直线MN 所夹的角也相等.证明:不妨设直线与、BD AC 直径的夹角相等.设BD AC DA CD BC AB 、、、、、与直径MN 所在的直线的交点分别为F E G T H S 、、、、、.在△和GDF △HCE 中, 图1∵ ∠=GDF ∠HCE ,∠=DFG ∠CEH ,∴ △GDF ∽△HCE .∴ ∠=DGF ∠CHE . ∴ 直线BC AD 、与直线MN 所夹的角相等. 在△和TDG △SBH 中,∵ ∠=DGT ∠CHE (已证),∠CHE =∠SHB ,∴ ∠=DGT ∠BHS .又∵ ∠=GDT ∠HBS ,∴ △TDG ∽△SBH .∴ ∠=GTD ∠HSB , ∴ 直线AB DC 、与直线MN 所夹的角相等. (用同样的方法,可以证明另外两种情形,这里不赘述.)圆是圆锥曲线的特殊情况,圆经过压缩变换可以变化为椭圆,圆中的这个性质可以推广到椭圆中去吗?进一步,在双曲线、抛物线中这个性质还成立吗?事实上,经过我们的推证,结论依然正确.二、椭圆、双曲线、抛物线内接四边形的一个性质我们利用方程022=++++F Ey Dx Cy Ax ,把椭圆、双曲线、抛物线的情况一起证明.证明之前,我们先定义一下圆锥曲线的主轴:椭圆的长轴、双曲线的实轴、抛物线的对称轴所在的直线,称为圆锥曲线的主轴.如图2,四边形ABCD 内接于常态圆锥曲线c :022=++++F Ey Dx Cy Ax (C A 、不同时为零).若直线BD AC AD BC CD AB 与、与、与(斜率均存在且不为零)中,有一对直线与圆锥曲线的主轴的夹角相等,则另外两对直线与圆锥曲线的主轴所夹的角也相等.证明:不妨设圆锥曲线的主轴为x 轴,且设直线x BD AC 与、轴的夹角相等. 设点D C B A 、、、坐标分别为),(11y x A 、),(22y x B 、),(33y x C 、),(44y x D , 直线BD AC 、、、的方程分别为:AB :0111=++p y n x m ,BC :0222=++p y n x m ,CD :0333=++p y n x m ,DA :0444=++p y n x m .∵ 点C A 、在曲线c 上, 图2∴ ⎩⎨⎧=+=+)2(.................1)1(....................123232121y x y x βαβα (2)-(1),得)()(13131313y y x x x x y y k AC ++-=--=βα. 同理可得:)()(24242424y y x x x x y y k BD ++-=--=βα ∵ 直线BD AC 、与x 轴所夹的角相等,∴ BD AC k k -=,0=+BD AC k k .∴ 042423131=--+--x x y y x x y y .……………………………...(3) 042423131=+++++x x y y x x y y …………………………….…(4) 由(3)、(4)得:-+++)(34431221y x y x y x y x 0)(14233241=+++y x y x y x y x …………(5) ++++)(34431221y x y x y x y x 0)(14233241=+++y x y x y x y x …………(6) 由(5)、(6)得:034431221=+++y x y x y x y x (7)014233241=+++y x y x y x y x ………………………………(8)同理:)()(12121212y y x x x x y y k AB ++-=--=βα,)()(34343434y y x x x x y y k DC ++-=--=βα, ∴ =+BD AC k k +--1212x x y y ))(()()(341214233241241342313434x x x x y x y x y x y x y x y x y x y x x x y y --+++-+++=-- 将(8)式代入,得:=+BD AC k k ))(()(341224134231x x x x y x y x y x y x --+++………………(9) 又∵+++-=+1212(y y x x k k DC AB βα)3434y y x x ++ βα-=))(()()(34121423324124134231y y y y y x y x y x y x y x y x y x y x +++++++++ 再将(8)式代入,得:βα-=+DC AB k k ))((341224134231y y y y y x y x y x y x +++++………….(10) (9)式-(10)式:)(24134231y x y x y x y x +++[+--))((13412x x x x βα))((13412y y y y ++]=0 若+--))((13412x x x x βα))((13412y y y y ++=0,则有))(())((34123412x x x x y y y y --++=))(())((34123412x x x x y y y y ----. ∴ 03241=+y y y y .结合平行截割定理讨论,可知:AB ∥DC ∥x 轴,它与直线BD AC DC AB 、、、的斜率不为零矛盾.∴ 024134231=+++y x y x y x y x∴ 0=+DC AB k k ∴ 直线AB DC 、与x 轴所夹的角相等.同理可证:直线BC AD 、与x 轴所夹的角相等.(用同样的方法,可以证明另外两种情形.)说明:当方程)0(122≠=+αββαy x 中,βα、异号时表示双曲线;当βα、均正时表示椭圆.2.抛物线内接四边形的一个性质如图(3),四边形ABC D 内接于常态抛物线c :)0(22>=p px y .若直线BD AC AD BC CD AB 与、与、与(斜率均存在且不为零)中,有一对直线与x 轴的夹角相等,则另外两对直线与x 轴所夹的角也相等.证明:不妨设直线x BD AC 与、轴的夹角相等.设),(11y x A 、),(22y x B 、),(33y x C 、),(44y x D ,直线BD AC DC AB 、、、的斜率分别为BD AC DC AB k k k k 、、、.∵ 点C A 、在曲线c 上,∴ ⎩⎨⎧==32312122px y px y , 图(3) 求差得:1313132y y p x x y y k AC +=--=. 同理可得:2424242y y p x x y y k BD +=--=. 由0=+BD AC k k ,++422y y p 0231=+y y p , 得:04321=+++y y y y . 而 ))(()(222432143214321y y y y y y y y p y y p y y p k k DC AB +++++=+++=+=0, ∴ 0=+DC AB k k ∴ 直线AB DC 、与x 轴所夹的角相等.同理可证:直线BC AD 、与x 轴所夹的角相等.(用同样的方法,可以证明另外两种情形.)综上所述,可得圆锥曲线内接四边形的性质:四边形ABCD 内接于常态圆锥曲线c .若直线BD AC AD BC CD AB 与、与、与(斜率均存在且不为零)中,有一对直线与主对称轴(焦点所在的对称轴)的夹角相等,则另外两对直线与主对称轴所夹的角也相等.三、北京市2004年高考数学试卷第17题溯源与推广北京市2004年高考数学试卷第17题:如图(4),过抛物线)0(22>=p px y 上一定点),(00y x P )0(0>y 作两条直线,分别交抛物线于),(11y x A 、),(22y x B .(Ⅰ) 求该抛物线上纵坐标为2p 的点到焦点F 的距离. 图(4)(Ⅱ) 当PB PA 、的斜率存在且倾斜角互补时,求21y y y +的值,并证明直线AB 的斜率是非零常数. 本题的关键是“直线AB 的斜率是非零常数”的这个常数是什么?我们还是从圆说起:如图(5),在本文开头的(一)中,让点C D 、在上运动变化,当点C D 、重合于一点P 时,保持PB PA 、与直径的夹角相等,此时割线DCT 变为⊙O 的切线PT ,显然,∠=ASM ∠PTM .即直线AS 、直线PT 与直径MN所在的直线夹角相等.所以,“直线AB 的斜率是非零常数”的这个常数是“曲线上经过点),(00y x P 的切线的斜率的相反数”. 图 (5)到此,不难看出北京市2004年高考数学试卷第17题,是本文所述圆锥曲线性质的一个特例,它还可以扩充到椭圆、双曲线中去.命题:过圆锥曲线c :βααββα、,0(122≠=+y x 不同时为负数)上一定点),(00y x P )0(0>y 作两条直线,分别交曲线c 于A 、B 两点,当PB PA 、的斜率存在且倾斜角互补时,则直线AB 的斜率是常数.本文通过特殊化、一般化的思维方法,通过解析几何问题的证题通法,将一道高考试题的“来龙去脉”展现给大家,意在说明这种研究问题的方法.本文在撰写过程中,得到特级教师郭璋老师的鼎力帮助,在此表示衷心的感谢.2005-1-8豆丁网(DocIn )是全球优秀的C2C 文档销售与分享社区。
从欧拉几何定理到彭色列闭合定理(欧拉--彭色列—大狗熊线)
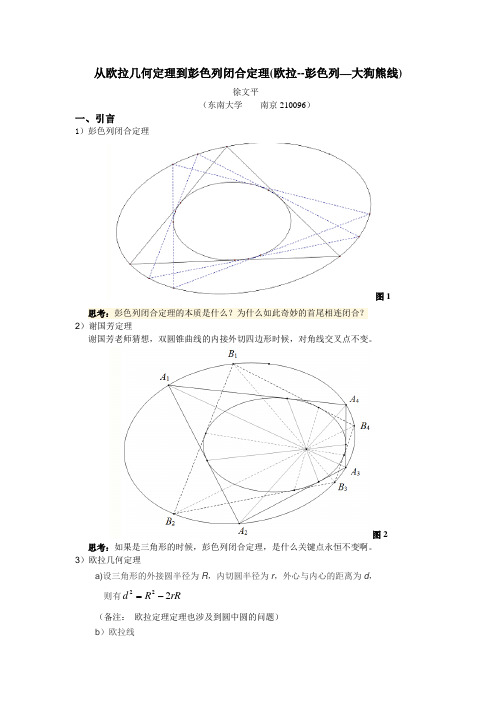
从欧拉几何定理到彭色列闭合定理(欧拉--彭色列—大狗熊线)徐文平(东南大学 南京210096)一、引言1)彭色列闭合定理图1思考:彭色列闭合定理的本质是什么?为什么如此奇妙的首尾相连闭合?2)谢国芳定理谢国芳老师猜想,双圆锥曲线的内接外切四边形时候,对角线交叉点不变。
图2思考:如果是三角形的时候,彭色列闭合定理,是什么关键点永恒不变啊。
3)欧拉几何定理 a)设三角形的外接圆半径为R ,内切圆半径为r ,外心与内心的距离为d ,则有rR R d 222-=(备注: 欧拉定理定理也涉及到圆中圆的问题)b )欧拉线(三角形ABC的垂心H,九点圆圆心V,重心G,外心O共线,称为欧拉线)图3c)欧拉九点圆三角形三边的中点,三高的垂足和三个欧拉点(连结三角形各顶点与垂心所得三线段的中点)九点共圆。
通常称这个圆为九点圆(nine-point circle),或欧拉圆、费尔巴哈圆。
九点圆具有许多有趣的性质,例如:1. 三角形的九点圆的半径是三角形的外接圆半径之半;2. 九点圆的圆心在欧拉线上,且恰为垂心与外心连线的中点;3. 三角形的九点圆与三角形的内切圆,三个旁切圆均相切(费尔巴哈定理);4. 九点圆心(V),重心(G),垂心(H),外心(O)四点共线,且HG=2OG,OG=2VG,OH=2OV。
图44)欧拉--彭色列--大狗熊线大狗熊定理:三角形内切圆的切点三角形的垂心H,九点圆圆心V,重心G与三角形内心I、外心O共线(欧拉--彭色厉--大狗熊线),三角形作彭色列闭合变换时,五心位置恒定不变。
(备注:三角形内切圆的切点三角形的外心就是三角形ABC的内心I)图 5 (彭色列闭合变换时切点三角形的重心不变)(三角形在圆中圆中,作彭色列闭合变化时候,切点三角形的垂心H,九点圆圆心V,重心G不变,非常奇妙的发现,作业:作图试试切点三角形的垂心H,九点圆圆心V,重心G,是不是雷打不动啊)谢国芳定理,双圆锥曲线的内接外切四边形时候,对角线交叉点不变。
圆锥曲线中的“四心”
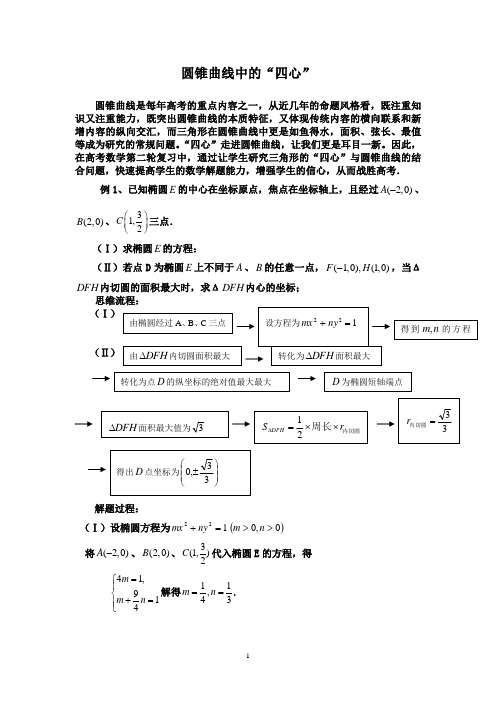
圆锥曲线中的“四心”圆锥曲线是每年高考的重点内容之一,从近几年的命题风格看,既注重知识又注重能力,既突出圆锥曲线的本质特征,又体现传统内容的横向联系和新增内容的纵向交汇,而三角形在圆锥曲线中更是如鱼得水,面积、弦长、最值等成为研究的常规问题。
“四心”走进圆锥曲线,让我们更是耳目一新。
因此,在高考数学第二轮复习中,通过让学生研究三角形的“四心”与圆锥曲线的结合问题,快速提高学生的数学解题能力,增强学生的信心,从而战胜高考.例1、已知椭圆E的中心在坐标原点,焦点在坐标轴上,且经过(2,0)A-、(2,0) B、31,2C⎛⎫⎪⎝⎭三点.(Ⅰ)求椭圆E的方程:(Ⅱ)若点D为椭圆E上不同于A、B的任意一点,(1,0),(1,0)F H-,当ΔDFH内切圆的面积最大时,求ΔDFH内心的坐标;(Ⅰ)(Ⅱ)解题过程:(Ⅰ)设椭圆方程为122=+nymx()0,0>>nm将(2,0)A-、(2,0)B、3(1,)2C代入椭圆E的方程,得41,914mm n=⎧⎪⎨+=⎪⎩解得11,43m n==.∴椭圆E 的方程22143xy+= .(Ⅱ)||2FH =,设ΔDFH 边上的高为hh S DFH =⨯⨯=∆221当点D 在椭圆的上顶点时,h,所以DFH S ∆设ΔDFH 的内切圆的半径为R ,因为ΔDFH 的周长为定值6.所以,621⨯=∆R S DFH所以R3.所以内切圆圆心的坐标为3.点石成金:的内切圆的内切圆的周长∆∆⨯∆⨯=r S 21例2、椭圆长轴端点为B A ,,O 为椭圆中心,F 为椭圆的右焦点,且1=⋅FB AF1=.(Ⅰ)求椭圆的标准方程;(Ⅱ)记椭圆的上顶点为M ,直线l 交椭圆于Q P ,两点,问:是否存在直线l ,使点F 恰为PQM ∆的垂心?若存在,求出直线l 的方程;若不存在,请说明理由。
思维流程:(Ⅱ)→消元解题过程:(Ⅰ)如图建系,设椭圆方程为22221(0)x y a b ab+=>>,则1c =又∵1=⋅FB AF 即 22()()1a c a c a c +⋅-==- ∴22a = 故椭圆方程为2212xy +=(Ⅱ)假设存在直线l 交椭圆于Q P ,两点,且F 恰为P Q M ∆的垂心,则设1122(,),(,)P x y Q x y ,∵(0,1),(1,0)M F ,故1=PQ k , 于是设直线l 为 y x m =+,由2222y x m x y =+⎧⎨+=⎩得2234220x mx m ++-=∵12210(1)(1)MP FQ x x y y ⋅==-+-又(1,2)i i y x m i =+=得1221(1)()(1)0x x x m x m -+++-= 即212122()(1)0x x x x m m m ++-+-= 由韦达定理得 222242(1)033m m m m m -⋅--+-=解得43m =-或1m =(舍) 经检验43m =-符合条件.点石成金:垂心的特点是垂心与顶点的连线垂直对边,然后转化为两向量乘积为零.例3、在椭圆C :13422=+yx中,21F F 、分别为椭圆C 的左右两个焦点,P为椭圆C 上的且在第一象限内的一点,21F PF ∆的重心为G ,内心为I . (Ⅰ)求证:21F F IG λ=;(Ⅱ)已知A 为椭圆C 上的左顶点,直线l 过右焦点2F 与椭圆C 交于N M ,两点,若AN AM ,的斜率21,k k 满足2121-=+k k ,求直线l 的方程.解题过程:(Ⅰ)设),(00y x P ,重心),(y x G ,由已知可知)0,1(1-F ,)0,1(2F则31)1(0+-+=x x ,30++=y y )3,3(00y x G ∴由00212121y y F F S F PF ==∆ 又内切圆r F F PF PF S F PF )(21212121++=∆0321y r S F PF ==∴∆内切圆 ∴内心I 的纵坐标为30yIG∴∥21F F 即21F F IG λ=.(Ⅱ)若直线l 斜率不存在,显然120k k +=不合题意; 则直线l 的斜率存在.设直线l 为)1(-=x k y ,直线l 和椭交于11(,)M x y ,22(,)N x y 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆锥曲线内接四边形的四极点调和分割定理徐文平(东南大学南京210096)摘要:在圆锥曲线内接四边形的极点与极线问题研究过程中,发现了圆锥曲线内接四边形的四极点调和分割定理,即圆锥曲线内接四边形的对边延伸线交点调和分割对角线极点。
运用极点与极线的知识,进行了新定理的简单证明,并提出了过圆锥曲线上一点作切线的尺规作图新方法。
关键词:圆锥曲线、内接四边形、二次曲线切线、极点与极线、调和分割射影几何创始人大数学家笛沙格采用投射取截法来实现二次圆锥曲线的连续变化,只要改变截景平面的位置,就可使圆的截景从圆连续变为椭圆、抛物线和双曲。
因此,对于圆成立的许多性质,都可通过取截景的方法来证明它们对其他二次圆锥曲线也成立.这就提供了一种相当简便的方法。
圆锥曲线的内接四边形有许多的奇妙性质,作者在研究圆锥曲线切线的性质过程中,发现了圆锥曲线内接四边形的四极点调和分割定理,供大家鉴析。
新定理1:圆锥曲线内接四边形的对边延伸线两交点调和分割对角线两极点。
椭圆、双曲线或者抛物线的内接四边形KLMN,对边线KN与LM交于A,对边线KL 与NM交于B,对角线KM的极点为C,对角线LN的极点为D,KM与LN交于Q点,则A、B、C、D四点共线,且AB调和分割CD,即1/AC+1/AD=2/AB。
图 1图 2图 3射影几何的极点与极线知识是研究圆锥曲线切线问题的强有力工具,下面以引理形式给出一些相关的初等几何经典定理和射影几何定理,以便用于证明新定理成立。
引理1:二次圆锥曲线 的内接完全四点形的对边三点形是圆锥曲线的自配极三点形。
引理2:圆锥曲线中的极线共点于P,则这些极线相应的极点共线于P相应的极线。
反之亦然,称为极点与相应极线对偶性。
引理3(帕斯卡定理):设六边形ABCDEF内接于椭圆,直线AB与DE交于点X,直线CD与FA交于点Z,直线EF与BC交于点Y,则X、Y、Z三点共线。
当椭圆内接六边形ABCDEF在两处各有2个顶点重合,即当B(C)点重合,E(F)点重合,椭圆内接六边形ABCDEF退化为椭圆内接四边形AB(C)DE(F),BY与EY退化为切线,帕斯卡定理仍然成立,即圆内接四边形的对边两交点与对角线极点共线。
图 5引理4(牛顿定理3):椭圆的外切四边形的对角线的交点和以切点为顶点的四边形对角线交点重合。
图 6引理5 (麦克马林定理):假设K 、L 、M 、N 四点是椭圆的外切四边形FGEH 的4个切点,椭圆的内接四边形KLMN 的对角线KM 、LN 相交于Q 点,则F 、Q 、E 、B 四点共线,A 、G 、Q 、H 四点共线。
图 7证明:在图7中,极点F 点的极线是KN ,极点E 点的极线是LM 。
又依据引理1可知,ΔAQB 为自配极三角形,极点B 与AQ 极线对应,极点Q 与AB 极线对应。
F 、E 、Q 、B 四极点相对应的KN 、LM 与AQ 、AB 四条极线交汇共点于A 点。
依据引理2可知,F 、E 、Q 、B 四点共线于A 点的极线上,引理成立。
同理,A 、G 、Q 、H 四点也共线。
引理6 (调和分割):对于线段AB 的内分点C 和外分点D ,满足DBAD CB AC =,则称点C 、D 调和分割线段AB 或A 、B 、C 、D 是调和点列。
调和点列的等价判定形式:(1)点A 、B 调和分割线段CD ; (2)ABAD AC 211=+ ; (3)BD AC BC AD CD AB ∙=∙=∙22 当D 点在无穷远处时,调和点列只剩下A 、B 、C 三点,则有2AC =AB ,即AC =BC 。
证明1(椭圆情况):如图8,椭圆内接四边形KLMN 的对角线KM 、LN 交于Q 点,KN 、LM 对边延伸线交于A 点,KL 、NM 对边延伸线交于B 点,C 点为对角线KM 的极点,D 点为对角线LN 的极点。
K 、L 、M 、N 四点为椭圆外切四边形EHFG 的四个切点。
则AB 调和分割CD ,且AQ 调和分割GH ,且BQ 调和分割EF 。
图 8在图8中,由引理1可知,极点A 与QB 极线对应,极点B 与AQ 极线对应,极点Q 与AB 极线对应,ΔAQB 为自配极三角形。
由帕斯卡定理可知,A 、B 、C 、D 四点共线,且AB 为Q 点的极线,四极点共线成立。
由牛顿定理可知,椭圆的外切四边形的对角线的交点和以切点为顶点的四边形对角线交点重合,椭圆外切四边形EHFG 的对角线EF 、GH 交于Q 点和以K 、L 、M 、N 四个切点为顶点的椭圆内接四边形KLMN 的对角线KM 、LN 交点Q 重合。
由麦克马林定理可知,椭圆外切四边形EHFG 的对角线EF 为A 点关于椭圆的极线。
同时,引理1可知,QB 也为A 点关于椭圆的极线。
因此,F 、Q 、E 、B 四点共线。
同理可知,A 、G 、Q 、H 四点共线,AH 为B 点关于椭圆的极线。
推理分析图8可知,ΔFCD 中FB 、CH 、DG 三线共点交于E 点,由赛瓦定理得: 1=⋅⋅GCFG HF DH BD CB ∵ΔFCD 被直线AH 所截,由梅涅劳斯定理得:1=⋅⋅ADCA GC FG HF DH 由上面两个式子得: ADCA BD CB = 整理得:: DBAD CB AC = 或 AB AD AC 211=+ ∴A 、B 、C 、D 四点共线,CD 调和分割AB ,新定理1证明成立。
由射影几何知识可得,以F 点为射影点,A 、G 、Q 、H 四点共线,AQ 调和分割GH ,由射影几何知识可得,以D 点为射影点,B 、E 、Q 、E 四点共线, BQ 调和分割EF 。
证明2(双曲线情况):双曲线内接四边形KLMN 的对角线KM 、LN 交于Q 点,KN 、LM 对边延伸线交于A 点,KL 、NM 对边延伸线交于B 点,C 点为对角线KM 的极点,D 点为对角线LN 的极点,双曲线上K 、L 、M 、N 四点切线延伸互相交于E 、F 、G 、H 四点。
则AB 调和分割CD ,且AQ 调和分割GH ,且BQ 调和分割EF 。
图 9如图9中,由引理1可知,极点A 与QB 极线对应,极点B 与AQ 极线对应,极点Q 与AB 极线对应,ΔAQB 为自配极三角形。
由帕斯卡定理,可知A 、B 、C 、D 四极点共线,且AB 是Q 点的极线。
极点G 点的极线是LK ,极点H 点的极线是MN 。
又依据引理1可知,ΔAQB 为自配极三角形,极点A 与BQ 极线对应,极点Q 与AB 极线对应。
A 、G 、Q 、H 四极点相对应的QB、LK与AB、MN四条极线交汇共点于B点。
依据引理2可知,A、G、Q、H四点共线,且为于B点的极线。
同理可知,B、E、Q、F四点共线,BE为A点关于椭圆的极线。
易知,LN、KM、EF、GH四线交于Q点,可见牛顿定理3在双曲线情况下也成立。
推理分析可知,ΔFCD中FB、CH、DG三线共点交于E点,且ΔFCD被直线AH所截交于G点,构成熟知的经典几何图形。
采用类似上述证明1中椭圆切线问题处理方法,易证AB调和分割CD,即1/AC+1/AD=2/AB。
由射影几何知识可得,以F点为射影点分析A、G、Q、H四点连线,AQ调和分割GH,由射影几何知识可得,以D点为射影点分析B、E、Q、F四点共线,BQ调和分割EF。
证明3(抛物线情况):抛物线内接四边形KLMN的对角线KM、LN交于Q点,KN、LM对边延伸线交于A点,KL、NM对边延伸线交于B点,C点为对角线KM的极点,D 点为对角线LN的极点,抛物线上K、L、M、N四点切线延伸互相交于E、F、G、H四点。
则AB调和分割CD,且AQ调和分割GH,且BQ调和分割EF。
图10如图10,采用上述证明2中类似双曲线切线问题处理方法,易证A、B、C、D四点共线,A、G、Q、H四点共线,Q、E、B、F四点共线。
推理分析可知,ΔFGH中FQ、CH、DG三线共点交于E点,且ΔFGH被直线AD所截交于C点,构成熟知的经典几何图形。
采用类似上述证明1中椭圆切线问题处理方法,易证AQ调和分割GH。
由射影几何知识可得,以F点为射影点,分析A、B、C、D四点连线,可知AB调和分割CD,即1/AC+1/AD=2/AB。
由射影几何知识可得,以D点为射影点分析B、E、Q、F四点共线,BQ调和分割EF。
推理1:当有心圆锥曲线内接四边形的其中一条对角线通过有心圆锥曲线圆心时,则另一条对角线的极点必定平分有心圆锥曲线内接四边形的对边延伸线两交点的连线。
推理1是新定理1的一种特殊情况,如图1、2中,对于椭圆和双曲线,当有心圆锥曲线内接四边形KLMN的对角线LN通过有心圆锥曲线圆心时,对角线LN的极点D在无穷远处,调和点列只剩下A、B、C三点,则对角线KM的极点C必定平分有心圆锥曲线内接四边形KLMN的对边延伸线两交点AB的连线,即AC=CB。
推理2:当抛物线内接四边形的其中一条对角线与抛物线对称轴平行时,则另一条对角线的极点必定平分抛物线内接四边形的对边延伸线两交点的连线。
推理2也是新定理1的一种特殊情况,如果抛物线内接四边形KLMN的对角线LN与抛物线对称轴平行的竖向直线,N点在无穷远处,抛物线内接四边形KLMN中的对边线KN 退化为过K点的竖向直线,抛物线内接四边形KLMN中的对边线M N退化为过M点的竖向直线。
对角线LN的极点D在无穷远处,调和点列只剩下A、B、C三点,对角线KM的极点C必定平分抛物线内接四边形KLMN的对边延伸线两交点AB的连线,即AC=CB。
新定理的运用(圆锥曲线切线尺规作图):圆锥曲线包括椭圆、双曲线和抛物线,圆锥曲线切线问题是几何学研究的重要课题之一,如果采用解析几何方法确定圆锥曲线切线将是比较繁琐。
因此,必须想办法寻找一种简明的纯几何的尺规作图方法确定圆锥曲线切线,以方便实际工程应用。
依据推理1、2,作者提出一种过圆锥曲线上一点作切线的尺规作图新方法。
例题1:已知椭圆Y的一斜向割线AB,作一条过椭圆圆心O点的任意割线JK,与椭圆Y相交于J、K两点。
JA、BK交于E点,作AK、JB交于F点。
确定EF的中点N点,连线NA、NB就是椭圆的切线。
(如果过椭圆心的辅助割线JK是在x轴上,则椭圆切线做法更简单,此时EF为竖向垂线。
)图 11例题2:已知双曲线的斜向割线AB,点J、K是双曲线的顶点,JA、BK交于E点,JB、AK交于F点,确定EF的中点N点,连线NA、NB就是双曲线的切线。
(如果JK为过双曲线中心的任意割线,双曲线切线做法也成立。
)图 12例题3:已知抛物线的斜向割线AB,点J是抛物线上任意一点,JA与B点竖垂线交于F点,JB与A点竖垂线交于E点,确定EF的中点N点,连线NA、NB就是抛物线的切线。
(如果点J是抛物线的顶点,则抛物线切线做法更简单,此时EF为水平线。
