(完整版)组合逻辑电路
组合逻辑电路
Y2 A2 A1 A0 m2 Y3 A2 A1A0 m3
Y6 A2 A1A0 m6 Y7 A2 A1A0 m7
3. 5. 2二进制译码器的应用
一、用译码器实现组合逻辑电路
因为n个输入变量的二进制泽码器的输出为其对应的2n个最小 项(或最小项的反)，而任一逻辑函数均可表示为最小项表达 式(即标准与或式)的形式，故利用二进制泽码器和门电路可 实现单输出或多输出组合逻辑电路的设计。使用方法为:当泽 码器的输出为低电平有效时，选用与非门;当泽码器的输出为 高电平有效时，选用或门。
(4) 分析电路的逻辑功能。由真值表可以看出:当A, B输入状 态相同时，Y=0;当A同时，Y=1。故此电路具有异或门的逻 辑功能，所以该电路是由4B输入状态不个与非门构成的异或 逻辑电路。
上一页 下一页 返回
3.2 组合逻辑电路的分析
「例3.2.2]已知组合逻辑电路如图3.2.2所示，试分析该电路 的逻辑功能。
当输入A3=1时，低位片CT74LS138(1)因A3 =1而禁止泽码， 输出 Y0 ~ Y7 均为高电平1,高位片CT74LS138(2)工作，这时 输入A3A2A1A0 ，在1000~1111之间变化时， Y8 ~ Y15 对应的输 出端输出有效的低电平0。
中，I 7的优先级别最高，I6 次之，其余依此类推，I 0 的级别最 低。
上一页 下一页 返回
3. 4 编码器
也就是说，当 I7 =0时，其余输入信号不沦是0还是1都不起作 用，电路只对 I 7 进行编码，输出 Y2Y1Y0 = 000，此码为反码，其 原码为111，其余类推。可见，这8个输入信号优先级别的高 低次序依次为 I 7、I 6、I 5、I 4、I 3、I 2、I1、I 0
3. 5. 1二进制译码器 将输入二进制代码按其原意转换成对应特定信号输出的逻辑
组合逻辑电路
E 为使能端，表示低电平有效。
列真值表 分析逻辑功能
输入
E A1 A0 1 任意
输出 F
0
E 为选通端、低电平有效。 0 0 0 D0
操作端A1A0为00、01、
0 0 1 D1
10、11时，分别选中D0、
0 1 0 D2
D1、D2、D3到输出F 。
0 1 1 D3
4选1数据选择器。
由传输门构成的4选1数据选择器
设两个四位二进制数分别为C3C2C1C0和 D3D2D1D0，输出为S3S2S1S0
S3S2S1S0 A3 A2 A1A0 B3B2B1B0 CI
M=0时 B3B2B1B0 M (D3D2D1D0 )
S3S2S1S0 C3C2C1C0 D3D2D1D0 0
M=1时 B3B2B1B0 M (D3 ?D2 D1 D0 )
0 1 1 1 1 0 F1 101110
110110
111010 1 1 1 1 1 1 F2
其他
A B CD
00
ABCD中：
F1 A多BC数为AB1D时，ACFD1=B1C；D 表F决2 电A全B路C部D：为1时，F2 = 1。
多数通过和一致通过
常用组合电路及其分析
1 加法器
由5个逻辑门组成的2 输入、2 输出逻辑
这种加法运算称为“半加〞运算，完成半加
运算的电路称为“半加器〞。
半加器逻辑符号如图
A
Σ
S
B
CO C
两个二进制数相加时，
还需要考虑低位的进位， A i
Bi
称为“全加〞运算。 C i-1
Σ
Si
CI CO C i
完成全加运算的电路称为“全加器〞
第4章 组合逻辑电路(完整版)
A B
& AB
G1
A B A B
真值表
A 0 0 1 1 B 0 1 0 1 F 1 0 0 1
&
G5
F
1
G2
A
&
G4
A B
同或门电路 A B
1
G3
B
=
F A B A B
F
A B A B A@安阳师范学院物理与电气工程学院_2013 B A B CopyRight
2个信号用1位二进制信号进行编码4个信号用2位二进制信号进行编码8个信号用3位二进制信号进行编码常见的编码器有8线3线有8个输入端3个输出端16线4线16个输入端4个输出端等等
第四章 组合逻辑电路
第四章
4.1 概述
组合逻辑电路
4.2 组合逻辑电路的分析与设计方法 4.3 常用的组合逻辑电路 4.4组合逻辑电路中的竞争冒险现象
8
P ABC
第四章 组合逻辑电路
（2）化简与变换：
Y A B C ABC A B C ABC A B C ABC
A B C ABC
（3）由表达式列出真值表。
Y A B C ABC
（4）分析逻辑功能 ： 当A、B、C三个变量 不一致时，电路输出为 “1”，所以这个电路称为 “不一致电路”。
向量函数形式：
给定逻 辑功能
设计
画出 逻辑图
6
Y=F(A)
CopyRight @安阳师范学院物理与电气工程学院_2013
4.2 组合逻辑电路的分析和设计方法
1、组合逻辑电路的分析方法
分析： 给定逻辑图 分析步骤：
第三章组合逻辑电路
（一）二进制译码器
八个译码输出的逻辑表达式：
每一个输出都对应着一种输入状态的组合， 所以也叫做状态译码器。
第三章组合逻辑电路
2． 3线-8线译码器 74HC138
1
第三章组合逻辑电路
利用74HC138的使能端E 2
，可以扩展译码器输入
的变量数。74HC138构成的4线-16线译码器。
第三章组合逻辑电路
74HC138所构成的八路数据分配器的逻辑框图
第三章组合逻辑电路
五、数据比较器
在数字系统中，经常需要对两组二进制数或二—十进制数进行 比较，用来比较两组数字的电路称为数字比较器。只比较两组数 字是否相等的数字比较器称同比较器。不但比较两组数是否相等， 而且还比较两组数的大小的数字比较器称大小比较器或称数值比 较器。下面只介绍数值比较器。
第三章组合逻辑电路
共阴极半导体7段数码管BS201
第三章组合逻辑电路
a）管脚排列图 b）内部接线图
共阳极LED数码管
第三章组合逻辑电路
a）管脚排列图 b）内部接线图
各段笔划的组合能显示出十进制数0～9及某些英文字母。 半导体数码管的优点是工作电压低（1.7～1.9Ｖ），体积小， 可靠性高，寿命长（大于一万小时），响应速度快（优于10ηs）， 颜色丰富等，目前已有高亮度产品，缺点是耗电比液晶数码管大， 工作电流一般为几毫安至几十毫安。
三位二进制编码器 a) 示意图 b) 内部原理图
第三章组合逻辑电路
三位二进制编码器真值表
三位二进制编码器有八个输入端（可与八个开关或其它逻 辑电路相连）和三个输出端，因此，它也称为8线-3线编码器。 三个编码器输出的逻辑表达式为：
第三章组合逻辑电路
第三章组合逻辑电路ppt课件
3.3 若干常用中规模组合逻辑电路 表3-3-1 3位二进制普通编码器真值表
《数字电子技术》
3.3 若干常用中规模组合逻辑电路
由于普通编码器在任何时刻 I0 ~ I7 当中仅有一个 取值为1，即只有真值表中所列的8种状态，而且它
的（ 28 8 ）种状态均为约束项。因此，由真值表
A
&
1
F2
C
B
&
C
图3.2.1 【例1】逻辑电路图
《数字电子技术》
3.2 组合逻辑电路的分析和设计方法
§3.2.2 组合逻辑电路的设计方法
所谓“设计”：即根据给出的实际逻辑问题，求出实 现这个逻辑功能的最简逻辑电路。
所谓“最简”：是指所用器件最少，器件种类最少， 而且器件之间的连线也最少。
一、设计步骤 （1）进行逻辑抽象
【例1】试用两片74LS148接成16线-4线优先编码器，
将－的优11先11权’最1低6个。146位个二低进A电0A制平1~5代输A码1入5 ，信其号中
编为‘0000
的A优0 先权最高，
接成的电路图如图3.3.4所示：
《数字电子技术》
3.3 若干常用中规模组合逻辑电路
图3.3.4 用两片74LS148接成的16线－4线优先编码器逻辑图
I7
)
S
Y0 (I1I2 I4 I6 I3 I4 I6 I5 I6 I7 ) S
（由功能表第一行体现）。
《数字电子技术》
3.3 若干常用中规模组合逻辑电路
（2）YS 为选通输出端，其表达式为：
YS I0 I1 I2 I3 I4 I5 I6 I7 S
此式表明：只有当所有的编码输入端均为高 电平（即没有编码输入），且S=1（ S 0 ）
第9章组合逻辑电路
P1 A
P2 B C
P3 BC P4 P1 P2 A(B C)
P5 A P3 ABC
Y P4 P5 A(B C) ABC
（2）用卡诺图化简输出函数表达式。
Y A(B C) ABC A(B C) ABC AB AC AB AC
0
1
0
0
1
0
0
0
1
1
1
1
0
0
0
1
0
1
1
1
1
0
1
1
1
1
1
表9.2 真值表
9.1.3组合逻辑电路的设计
（3）由真值表写出输出变量函数表达式并化简：
Y ABC ABC ABC ABC AB BC AC （4）画出逻辑电路如图9.2所示。
AB
C 00 01 11 10
A
00 0 1 0
（1）确定输入、输出变量，定义逻辑状态的含义。
设A、B、C代表三个人，作为电路的三个输入变量，当A、 B、C为1时表示同意，为0表示不同意。将Y设定为输出变 量，代表决意是否通过的结果，当Y为1表示该决意通过， 当Y为0表示决意没有通过。
（2）根据题意列出真值表，如表9.2所示。
A
B
C
Y
0
0
0
0
0
• （2）根据真值表写逻辑表达式，并化简成最简“与或” 逻辑表达式。
• （3）选择门电路和型号。 • （4）按照门电路类型和型号变换逻辑函数表达式 • （5）根据逻辑函数表达式画逻辑图。
• 例9.2 设计一个三人表决器电路，当两个或两个以上的人 表示同意时，决意才能通过。 解：根据组合逻辑电路的设计方法，可按如下步骤进行。
组合逻辑电路
4.2.1 组合逻辑电路的分析方法
b.化简： Y ((A • (ABC)) • (B • (ABC)) • (C • (ABC)))
A • ( ABC) B • ( ABC) C • ( ABC) ( A B C)(A B C) AB AC AB BC AC BC
设计一个举重裁判表决电路。举重比赛有3个裁判， 一个主裁判和两个副裁判。只有当两个或两个以上 裁判判决成功，并且其中有一个为主裁判时，表明 选手举重成功。
4.2.2 组合逻辑电路的设计方法
4.2.2 组合逻辑电路的设计方法
分组任务2 设计交通灯监视电路，并用与非门和非门实现
设计一个监视交通灯工作状态的逻辑电路，每一组交 通灯由红、黄、绿3盏灯组成。正常工作情况下，任何 时候必有一盏灯点亮，而且只允许有一盏灯点亮。而 当出现其他5种点亮状态时，电路发生故障，这时要求 发出故障信号，以提醒维修人员前去修理。
1
＆＆
AB
C
图4.2.3 练习中的逻辑电路
解：输出端的逻辑式为
00000 0 0 11 0 0 1010 0 11 0 1 10010 1 01 01
由真值表 可知，为 全加器
YY12
A B AB (A
C
B)C
110 01 11111
4.2.2 组合逻辑电路的设计方法
组合逻辑电路的设计就是根据给出的实际逻辑问 题，求出实现这一逻辑功能的最简单逻辑电路。
由于输入端为8个，输出
端为3个，故也叫做8线
－3线编码器
4.3.1 编码器
其输出输入的真值表为
输入
输出
I0 I1 I2 I3 I4 I5 I6 I7 Y2 Y1 Y0
(完整版)第五章组合逻辑电路典型例题分析
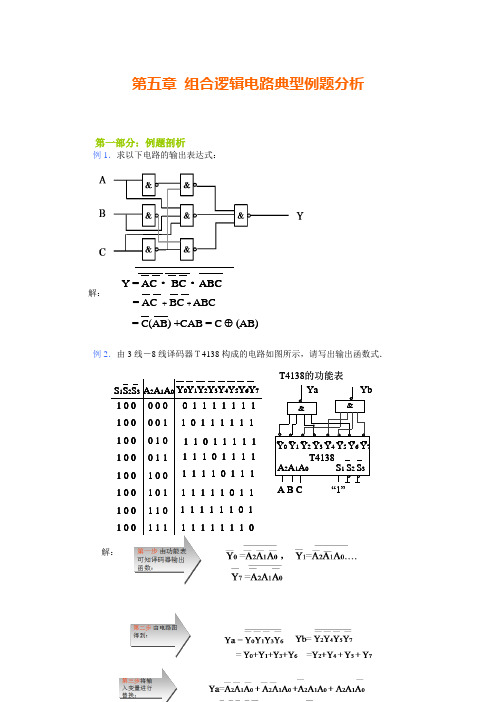
第五章 组合逻辑电路典型例题分析第一部分：例题剖析例1．求以下电路的输出表达式：解：例2．由3线－8线译码器Ｔ4138构成的电路如图所示，请写出输出函数式．解：Y = AC BC ABC= AC +BC + ABC = C(AB) +CAB = C (AB) T4138的功能表&&Y 0 Y 1 Y 2 Y 3 Y 4 Y 5 Y 6 Y 7“1”T4138A B CA 2A 1A 0YaYbS 1 S 2 S 30 0 00 0 10 1 00 1 11 0 01 0 11 1 01 1 1S 1S 2S 31 0 01 0 01 0 01 0 01 0 01 0 01 0 01 0 0A 2A 1A 0Y 0Y 1Y 2Y 3Y 4Y 5Y 6Y 70 1 1 1 1 1 1 11 0 1 1 1 1 1 11 1 0 1 1 1 1 11 1 1 0 1 1 1 11 1 1 1 0 1 1 11 1 1 1 1 0 1 11 1 1 1 1 1 0 11 1 1 1 1 1 1 0例3．分析如图电路，写出输出函数Ｚ的表达式。
CC4512为八选一数据选择器。
解：例4．某组合逻辑电路的真值表如下，试用最少数目的反相器和与非门实现电路。
（表中未出现的输入变量状态组合可作为约束项）CC4512的功能表A ⨯DIS INH 2A 1A 0Y1 ⨯0 10 00 00 00 00 00 00 00 0⨯⨯⨯⨯⨯0 0 00 0 10 1 00 1 11 0 0 1 0 11 1 01 1 1高阻态 0D 0D 1D 2D 3D 4D 5D 6D 7ZCC4512A 0A 1A 2D 0 D 1 D 2 D 3 D 4 D 5 D 6 D 7DIS INHD1DA B C D Y 0 0 0 0 10 0 0 1 00 0 1 0 10 0 1 1 00 1 0 0 0CD AB 00 01 11 1000 1 0 0 101 0 1 0 1 11 ××××10 0 1 ××AB第一步画卡诺图第三步画逻辑电路图例5．写出下面组合电路的输出表达式,分析逻辑功能。
组合逻辑电路(半加器全加器及逻辑运算)
一种常见的实现方式是使 用异或门实现和S，使用 与门实现进位C。
半加器的性能分析
逻辑级数
半加器的逻辑级数通常较低，因 为它只涉及基本的逻辑运算。
可靠性
半加器的结构简单，因此具有较 高的可靠性。
延迟时间
由于逻辑级数较低，半加器的延 迟时间相对较短。
资源消耗
半加器使用的逻辑门数量相对较 少，因此在资源消耗方面较为经 济。
组合逻辑电路(半加器 全加器及逻辑运算)
• 组合逻辑电路概述 • 半加器原理与设计 • 全加器原理与设计 • 逻辑运算原理与设计 • 组合逻辑电路的分析与设计方法 • 组合逻辑电路在数字系统中的应用
目录
Part
01
组合逻辑电路概述
定义与特点
定义
无记忆性
组合逻辑电路是一种没有记忆功能的数字 电路，其输出仅取决于当前的输入信号， 而与电路过去的状态无关。
比较器
比较两个二进制数的大小关系，根 据比较结果输出相应的信号，可以 使用与门、或门和非门实现。
全加器
在半加器的基础上增加对进位的处理 ，使用与门、或门和异或门实现两个 一位二进制数带进位的加法运算。
多路选择器
根据选择信号的不同，从多个输 入信号中选择一个输出，可以使 用与门、或门和非门实现。
Part
用于实现控制系统的逻辑 控制、数据处理等功能。
Part
02
半加器原理与设计
半加器的基本原理
半加器是一种基本的组合 逻辑电路，用于实现两个 二进制数的加法运算。
它接收两个输入信号A和 B，并产生两个输出信号： 和S以及进位C。
半加器不考虑来自低位的进 位输入，因此只能处理两个 一位二进制数的加法。
组合逻辑电路的应用领域
(完整版)组合逻辑电路习题及答案.
1.组合电路如图所示，分析该电路的逻辑功能。
解：(1)由逻辑图逐级写出逻辑表达式ABC P =CP BP AP L ++=ABC C ABC B ABC A ++= (2)化简与变换CB A ABC C B A ABC C B A ABC L +=+++=++=)((3)由表达式列出真值表(4)分析逻辑功能由真值表可知，当A 、B 、C 三个变量不一致时，电路输出为“1”，所以这个电路称为“不一致电路”。
2.由3线-8线译码74LS138（输出低电平有效）和4选1数据选择器（74LS153）组成如图所示的电路，B 1、B 2和C 1、C 2为二组二进制数，试列出真值表，并说明功能。
真值表A B CL解： 输出表达式： 212101122321F D C C D C C D C C D C C =+++021*********Y C C Y C C Y C C Y C C =⋅+⋅+⋅+⋅21021210212102121021A A A C C A A A C C A A A C C A A A C C =⋅+⋅+⋅+⋅2121212121212121B BC C B B C C B B C C B B C C =⋅+⋅+⋅+⋅功能说明：由地址码C 2C 1选择B 2B 1的最小项的反变量输出3.设计一个监视交通信号灯工作状态的逻辑电路。
正常情况下，红、黄、绿灯只有一个亮，否则视为故障状态，发出报警信号，提醒有关人员修理。
要求：（1）用门电路实现（2）用3-8线译码器实现（3）用4选1数据选择器实现。
解：(1)用门电路实现真值表B 2C 1C 0 00 11 01 1F21B B 21B B 21B 21B B①逻辑抽象输入变量：R 、A 、G ，红、黄、绿灯；灯亮为1，不亮为0。
输出变量：Z--故障信号，正常工作Z 为0，发生故障Z 为1。
列出真值表②写出函数式并化简 Z R A G RAG RA G RAG RAG =++++ 经卡诺图化简得： Z R A G RA RG AG =+++ ③画出电路图(2)用3-8线译码器实现①标准与或式 03567 Z R A G RAG RA G RAG RAG m m m m m =++++=++++ ②化成与非-与非式 0356703567Z m m m m m m m m m m =++++=⋅⋅⋅⋅ ③设R =A 2、A =A 1、G =A 0 则03567Z Y Y Y Y Y =⋅⋅⋅⋅ ④画连线图(3)用4选1数据选择器实现①标准与或式 Z R A G RAG RA G RAG RAG =++++S =1时 4选1 010*********Y D A A D A A D A A D A A =+++ ②确定输入变量和地址码的对应关系令A =A 1，G = A 0 ( )()()1Z R A G R AG R AG AG =+++⋅ 则：0D R = 12D D R == 31D =4.分别用74LS153(4选1数据选择器)和74LS152(8选1)实现函数F=AB+BC+AC 。
组合逻辑电路
的54/74HC148、40H148等。其外引脚排 列图如图3.9所示。
组合逻辑电路
图3.9 3位二组合进逻制辑优电先路编码器148外引脚排列图
•
S为使能输入端，低电平有效，即只
有当S=0时，编码器才工作。YS为使能输出 端，当S=0允许工作时，如果YS=0则表示 无输入信号，YS=1表示有输入信号，有编 码输出。YEX为扩展输出端，当S=0时，只 要有编码信号，则YEX=0，说明有编码信号 输入，输出信号是编码输出；YEX=1表示不 是编码输出。
图3.6 3位二进制编码器逻辑图
组合逻辑电路
• 2. 二-十进制编码器
•
实现用四位二进制代码对一位十进制
数码进行编码的数字电路叫做二-十进制编
码 器 ， 简 称 为 BCD 码 编 码 器 。 最 常 见 的
BCD码编码器是8421BCD码编码器，它有
10根输入线，4根输出线，常称为10/4线编
这里主要讲解用小规模集成电路（即用逻
辑门电路）来实现组合逻辑电路的功能。
组合逻辑电路
• 1. 组合逻辑电路设计步骤
• （1） 列真值表。根据电路功能的文字描述， 将其输入与输出的逻辑关系用真值表的形 式列出。
• （2） 写表达式，并化简。通过逻辑化简， 根据真值表写出最简的逻辑函数表达式。
• （3） 选择合适的门器件，把最简的表达式 转换为相应的表达式。
码器。其特点也是任一时刻只允许对一个
输入信号进行编码。
组合逻辑电路
• 3. 优先编码器
•
优先编码器在多个信息同时输入时只
对输入中优先级别最高的信号进行编码，
编码具有惟一性。优先级别是由编码者事
先规定好的。显然，优先编码器改变了上
第四章组合逻辑电路-精品文档86页
Y
0
当输入A、B、C
0
中有2个或3个为 1时，输出Y为1，
0
4 否则输出Y为0。
1
所以这个电路实
际上是一种3人
0
表决用的组合电
1
路：只要有2票
或3票同意，表
1
决就通过。
1
7
例：
A B
C
逻辑图
≥1 Y1
≥1 Y3 1
Y
1
≥1
Y2
逻辑表 达式
YY12AABBCYY3Y1Y2BABCABB
第四章 组合逻辑电路
组合逻辑要点
§4.1 概述 §4.2 组合逻辑电路的分析方法和设计方法 §4.3 常用的组合逻辑电路 §4.4 组合逻辑电路中的竞争–冒险现象
1
组合逻辑要点
用门电路构成的常见组合电路的分析 和设计 掌握优先编码器、译码器、数据选择 器与全加器等中规模集成电路块。
返回主目录 2
§4.1 概述
结构的数据选择器CC14539
54
例4.3.4 两个带控制端的四选一数据选择器组成八选一数据选择器. 解: 令
m
2
Y
3
A 2A1A0
m
3
Y 4 A 2 A 1 A 0 m 4
Y
5
A2 A 1A0
m5
Y
6
A2A1A 0
m6
Y 7 A 2A1A 0 m 7
3. 带控制输入端的
译码器又是一个完
整的数据分配器
S的状态将以反码形
34
式出现在Y输出端。
真值表
35
例4.3.2 用两片3线-8线译码器74LS138组成一个4线-16线译码
第3章组合逻辑电路
第3章组合逻辑电路3.1 组合逻辑电路的概述按照逻辑功能的不同特点，可以把数字电路分成两大类，一类叫做组合逻辑电路，另一类叫做时序逻辑电路。
什么叫组合逻辑电路呢？在t=a时刻有输入X1、X2、……Zn，那么在t=a时刻就有输出Z1、Z2、……Zm，每个输出都是输入X1、X2、……Zn的函数，Z1=f1（X1、X2、……Xn）Z1=f2（X1、X2、……Xn）Zm=fm（X1、X2、……Xn）从以上概念可以知道组合逻辑电路的特点就是即刻输入，即刻输出。
任何组合逻辑电路可由表达式、真值表、逻辑图和卡诺图等四种方法中的任一种来表示其逻辑功能。
3.2 组合逻辑电路的分析方法和设计方法3.2.1组合逻辑电路的分析方法分析组合逻辑电路的目的，就是要找出电路输入和输出之间的逻辑关系，分析步骤如下：（1）根据已知的逻辑电路，写出逻辑函数表达式（采用逐级写出逻辑函数表达式），最后写出该电路的输出与输入的逻辑表达式。
（2）首先对写出的逻辑函数表达式进行化简，一般系用公式法或卡诺图法。
（3）列出真值表进行逻辑功能的分析。
以上步骤可用框图表示，如图3-2所示。
图3-2 组合逻辑电路分析框图下面举例说明对组合逻辑电路的分析，掌握其基本思路及方法。
【例3-1】 分析图3-3所示电路的逻辑功能图3-3 [例3-1]逻辑电路解：（1）写出输出Z 的逻辑表达式： Z1=B A ， Z2=B AZ=21Z Z •=B A B A • （2）化简Z=B A B A •=A B +A B=A ⊕B （3）列出真值表进行逻辑功能说明 列出该函数真值表，如表3.1所示： 表3-1 [例3-1]真值表 A B Z 0 0 0 0 1 1 1 0 1 1 13.2.2组合逻辑电路的设计方法组合逻辑电路的设计步骤与分析步骤相反，设计任务就是根据逻辑功能的要求设计逻辑电路，其步骤如下：（1）首先对命题要求的逻辑功能进行分析，确定哪些是输入变量，哪些为输出函数，以及它们之间的相互逻辑关系，并对它们进行逻辑赋值。
组合逻辑电路
工
程
应
用
对于共阴极数码管，与其配套的显示译码集成电路的输出端Ya~Yg必须是
低电平有效的，对于共阳极数码管，与其配套的显示译码集成电路的输出端 Ya~Yg应为高电平有效的。 装接显示译码器时，若出现数码管没有任何显示的故障，应先检查数码 管的公共端有没有漏接线，消隐控制端的电平设置是否正确；其次应检查数码 管与显示译码集成电路是否配套。 数码管的显示若出现缺段的故障，应先查显示译码集成电路与数码管的 连接是否良好；其次可通过替换数码管以确定器件是否良好；若数码管没问题， 则是译码集成电路有问题，应更换之。
4LSl47集成电路引脚功能图
第三节 译码器
译码的功能是把某种代码“翻译”成一个相应的输出信 号，例如把编码器产生的二进制码复原为原来的十进制数 就是一个典型的应用。
一 、通用 译码 器
通用译码器常用的有二进制译码器、二一十进制译码器。
1 ． 二进制译码器
（ 1 ）类型 将二进制码按其原意翻译成相应的输出信号 的 电 路 ， 称 为 二 进 制 译 码 器 。 2—4 线 译 码 器 ， 即 有 2 条 输 入 线 A 0 、 A 1 ， 有 4 种 输 入 信 息 00 、 01 、 10 、 11 ， 输 出 的 4 条线 Y 0 ～ Y 3 分别代表 0 、 1 、 2 、 3 四个数字。
3位二进制编码器示意图
3 位二进制编码器的逻辑 函数表达式 ：
Y 0= I 1+ I 3+ I 5+ I 7 Y 1= I 2+ I 3+ I 6+ I 7 Y 2= I 4+ I 5+ I 6+ I 7 普 通 编 码 器 在任何 时刻只 能对 0 、 1 、 2 、 … 、 7 中的一 个输入 信 号 进 行 编 号，不 允许同 时输 入两个1。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
3. 选用小规模SSI器件 4. 化简 Z R' A'G'RA RG AG
5. 画出逻辑图
Z RAG.RA.RG.AG
用与或门实现
用与非门实现
（第4章-16）
多输出组合逻辑电路的设计
多输出组合逻辑电路是指具有两个或两个以上的输出逻 辑变量的组合逻辑电路。
例2： 设计一个故障指示电路，具体要求为： （1）两台电动机同时工作时，绿灯亮； （2）一台电动机发生故障时，黄灯亮； （3）两台电动机同时发生故障时，红灯亮。
（第4章-17）
解：1. 设定A、B分别表示两台电动机这两个逻辑变量，F绿、 F黄、F红分别表示绿灯、黄灯、红灯；且用0表示电动机正常
工作，1表示电动机发生故障；1表灯亮，0表示灯灭 2.建立真值表: 按设计要求可得下表所列的真值表
A
B
F绿
F黄
F红
0
0
1
0
0
0
1
0
1
0
1
0
0
1
0
1
1
0
0
1
F绿 A B
第四章 组合逻辑电路
§ 4.1 概述 § 4.2 组合逻辑电路的分析方法和设计方法 § 4.3 若干常用的组合逻辑电路 § 4.4 组合逻辑电路中的竞争-冒险现象
（第4章-1）
第四章 组合逻辑电路
本章要求： 1.熟练掌握组合逻辑电路的分析方法和设计方法； 2.掌握标准化的中规模集成器件的逻辑功能、使
F黄 AB AB A B
逻辑电路图
F绿 A B
F红 AB
（第4章-20）
4.3 若干常用组合逻辑电路 4.3.1 编码器 • 编码：将输入的每个高/低电平信号变成一
个对应的二进制代码。 分类： 1.普通编码器 2.优先编码器
（第4章-21）
一、普通编码器
输
入
输出
• 特点：任何时刻
I0 I1 I2 I3 I4 I5 I6 I7 Y2 Y1 Y0
只允许输入一个 1 0 0 0 0 0 0 0 0 0 0
编码信号。
• 例：3位二进制 普通编码器
2.化简
A•B• A A•B•B （A B）• A （A B）• B A• B A• B
（第4章-7）
3.写真值表
真值表
ABF 000 011 101 110
4.分析逻辑功能
输入相同输出为 “0”，输入相异输 出为“1”，称为 “异或”逻辑关系。 这种电路称“异或” 门。
=1
F A B AB AB
1
DCB DC B DC A
1
&& & && &&
Y0 DC DB DC DB
&
&
&
Y2
Y1
Y0
（第4章-11）
2.列出真值表
输入 输出
DCBA
0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111
任意时刻的输出仅 取决于该时刻的输
入
不含记忆（存储）元件
（第4章-4）
二、逻辑功能的Βιβλιοθήκη 述aa12组合逻辑
yy12
电路
an
ym
组合逻辑电路的框图
y1 f1(a1a2 an ) y2 f2(a1a2 an )
ym
f
m(a1a2
a
）
n
Y F( A)
（第4章-5）
§ 4.2 组合逻辑电路的分析方法和设计方法
Y2Y1Y0
001 001 001 001 001 001 010 010 010 010 010 100 100 100 100 100
功能分析：当D、C、B、A表示的二进制
数小于或等于5时，Y0为1，当这个二进 制数在6和10之间时Y1为1，当这个二进 制数大于或等于11时Y2为1。 故这是一个判别输入的4位二进制数数 值范围的电路。
逻辑符号
输入相同输出为“1”,输入相异输出为“0”,称 为“判一致电路”(“同或门”) ,可用于判断各输 入端的状态是否相同。
（第4章-10）
例3：试分析图示电路的逻辑功能，指出该电路的用途。
解： 1.根据逻辑图写出逻辑式
Y2 DC DBA DC DBA
D
1
C
1
B
Y1 DCB DC B DC A A
F黄 AB AB A B
F红 AB
（第4章-18）
3.根据真值表求得输出逻辑函数的表达式
F绿 A B
F黄 AB AB A B
F红 AB
4.化简上述逻辑函数表达式，并转换成适当 的形式。
由于上述逻辑函数的表达式都是最简了，所 以不用再化简。
（第4章-19）
5.根据逻辑函数表达式画出逻辑电路图如下示。
出现故障，
G
Z为1
（第4章-14）
1. 抽象 • 输入变量:
红（R）、黄（A）、绿（G） • 输出变量：
故障信号（Z） 2. 写出逻辑表达式
Z R' A'G' R' AG RA'G RAG' RAG
输入变量 输 出
R AGZ 0 001 0 010 0 100 0 111 1 000 1 011 1 101 1 111
用方法，能运用这些器件设计出任何其他逻辑 功能的组合逻辑电路； 3.了解逻辑电路中的竞争-冒险现象。
（第4章-2）
§ 4.1 概述
逻
组合逻辑电路
现时的输出仅取 决于现时的输入
辑
电
路
除与现时输入有
时序逻辑电路 关外还与原状态
有关
（第4章-3）
4.1概述
一、组合逻辑电路的特点 1. 从功能上 2. 从电路结构上
4.2.1组合逻辑电路的分析方法
电路 结构
逻辑 功能
1.由给定的逻辑图写出逻辑关系表达式。
2.用逻辑代数或卡诺图对逻辑表达式进 行化简。
3.列出输入输出状态真值表。 4.分析逻辑功能。
（第4章-6）
例1：分析下图的逻辑功能。 & A•B• A
A&
A•B
B
&F
&
A•B•B
1.写出逻 辑表达式 F A• B • A• A• B • B
（第4章-8）
例 2：分析下图的逻辑功能
A . & A .B B.
1
&
A
& Y
A•B
1
B
化简
. (1) 写出逻辑式 Y = AB AB = AB +AB
（第4章-9）
(2) 列逻辑状态表
AB
Y
00 1 01 0
10 0
11 1
Y= AB +AB
逻辑式
=A B =A B
A B
=1
Y
(3) 分析逻辑功能
（第4章-12）
4.2.2 组合逻辑电路的设计方法
根据逻辑功能要求 设计 逻辑电路 设计步骤如下： (1) 由逻辑要求，列出逻辑状态表 (2) 由逻辑状态表写出逻辑表达式 (3) 简化和变换逻辑表达式 (4) 画出逻辑图
（第4章-13）
例1：设计一个监视交通信号灯状态的逻辑电路
R
A 如果信号灯 Z