(完整版)长方体与正方体知识点
五年级下册长方体和正方体知识点

五年级下册长方体和正方体知识点一、长方体和正方体的认识。
1. 长方体的特征。
- 面:长方体有6个面,每个面都是长方形(特殊情况有两个相对的面是正方形)。
相对的面完全相同。
- 棱:长方体有12条棱,相对的棱长度相等。
可以分为三组,每组有4条棱。
- 顶点:长方体有8个顶点。
2. 正方体的特征。
- 面:正方体有6个面,每个面都是正方形,并且6个面完全相同。
- 棱:正方体有12条棱,12条棱的长度都相等。
- 顶点:正方体有8个顶点。
3. 长方体和正方体的关系。
- 正方体是特殊的长方体。
当长方体的长、宽、高相等时,这个长方体就是正方体。
二、长方体和正方体的表面积。
1. 表面积的概念。
- 长方体或正方体6个面的总面积,叫做它的表面积。
2. 长方体表面积公式。
- 长方体表面积=(长×宽 + 长×高+宽×高)×2,用字母表示为S = 2(ab+ah + bh),其中a表示长,b表示宽,h表示高。
3. 正方体表面积公式。
- 正方体表面积 = 棱长×棱长×6,用字母表示为S = 6a^2,其中a表示棱长。
三、长方体和正方体的体积。
1. 体积的概念。
- 物体所占空间的大小叫做物体的体积。
2. 体积单位。
- 常用的体积单位有立方厘米(cm^3)、立方分米(dm^3)和立方米(m^3)。
- 棱长是1厘米的正方体,体积是1立方厘米;棱长是1分米的正方体,体积是1立方分米;棱长是1米的正方体,体积是1立方米。
- 1立方米 = 1000立方分米,1立方分米=1000立方厘米。
3. 长方体体积公式。
- 长方体体积=长×宽×高,用字母表示为V = abh。
4. 正方体体积公式。
- 正方体体积 = 棱长×棱长×棱长,用字母表示为V=a^3。
5. 体积单位的换算。
- 高级单位换算成低级单位乘进率,低级单位换算成高级单位除以进率。
例如:3.5m^3=3.5×1000 = 3500dm^3,2500cm^3=2500÷1000 = 2.5dm^3。
长方体与正方体知识点总结

长方体与正方体知识点总结一、长方体和正方体的认识1、长方体定义:长方体是由六个长方形(特殊情况下有两个相对的面是正方形)围成的立体图形。
特征:长方体有 6 个面,相对的两个面完全相同。
长方体有 12 条棱,相对的棱长度相等。
长方体有 8 个顶点。
长方体的棱长总和=(长+宽+高)× 42、正方体定义:正方体是用六个完全相同的正方形围成的立体图形。
特征:正方体有 6 个面,6 个面完全相同。
正方体有 12 条棱,12 条棱长度都相等。
正方体有 8 个顶点。
正方体的棱长总和=棱长×12二、表面积1、长方体的表面积定义:长方体 6 个面的总面积叫做它的表面积。
计算公式:长方体的表面积=(长×宽+长×高+宽×高)× 22、正方体的表面积定义:正方体 6 个面的总面积叫做它的表面积。
计算公式:正方体的表面积=棱长×棱长× 6三、体积1、长方体的体积定义:物体所占空间的大小叫做物体的体积。
计算公式:长方体的体积=长×宽×高用字母表示:V = abh (其中 a 表示长,b 表示宽,h 表示高)2、正方体的体积计算公式:正方体的体积=棱长×棱长×棱长用字母表示:V = a³(其中 a 表示棱长)四、容积1、定义:箱子、油桶、仓库等所能容纳物体的体积,通常叫做它们的容积。
2、单位:计量容积,一般就用体积单位。
计量液体的体积,如水、油等,常用容积单位升和毫升,也可以写成 L 和 mL。
3、换算:1 升= 1 立方分米,1 毫升= 1 立方厘米,1 升= 1000 毫升五、体积和容积的区别1、意义不同:体积是指物体所占空间的大小;容积是指容器所能容纳物体的体积。
2、测量方法不同:体积是从物体的外部测量长、宽、高;容积是从物体的内部测量长、宽、高。
3、单位名称不完全相同:体积单位一般用立方米、立方分米、立方厘米;容积单位一般用升、毫升。
(完整版)长方体和正方体知识点汇总(最新整理)
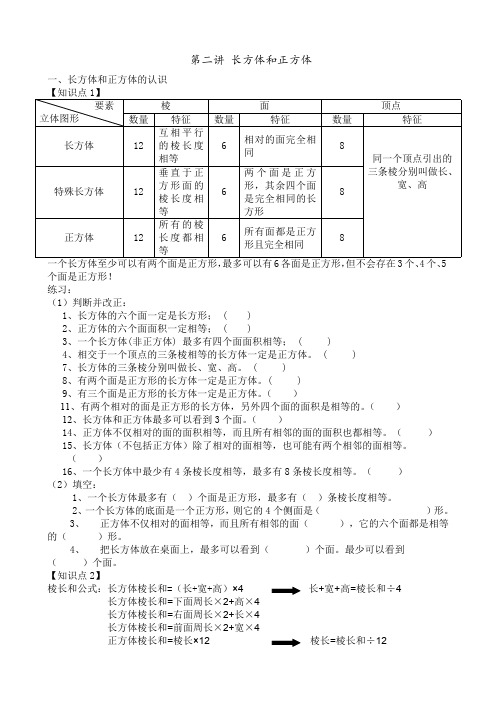
第二讲 长方体和正方体一、长方体和正方体的认识【知识点1】棱面顶点要素立体图形数量特征数量特征数量特征长方体12互相平行的棱长度相等6相对的面完全相同8特殊长方体12垂直于正方形面的棱长度相等6两个面是正方形,其余四个面是完全相同的长方形8正方体12所有的棱长度都相等6所有面都是正方形且完全相同8同一个顶点引出的三条棱分别叫做长、宽、高一个长方体至少可以有两个面是正方形,最多可以有6各面是正方形,但不会存在3个、4个、5个面是正方形!练习:(1)判断并改正:1、长方体的六个面一定是长方形; ( )2、正方体的六个面面积一定相等; ( )3、一个长方体(非正方体) 最多有四个面面积相等; ( )4、相交于一个顶点的三条棱相等的长方体一定是正方体。
( )7、长方体的三条棱分别叫做长、宽、高。
( )8、有两个面是正方形的长方体一定是正方体。
( )9、有三个面是正方形的长方体一定是正方体。
( )11、有两个相对的面是正方形的长方体,另外四个面的面积是相等的。
( )12、长方体和正方体最多可以看到3个面。
( ) 14、正方体不仅相对的面的面积相等,而且所有相邻的面的面积也都相等。
( ) 15、长方体(不包括正方体)除了相对的面相等,也可能有两个相邻的面相等。
( )16、一个长方体中最少有4条棱长度相等,最多有8条棱长度相等。
( )(2)填空:1、一个长方体最多有( )个面是正方形,最多有( )条棱长度相等。
2、一个长方体的底面是一个正方形,则它的4个侧面是( )形。
3、正方体不仅相对的面相等,而且所有相邻的面( ),它的六个面都是相等的( )形。
4、把长方体放在桌面上,最多可以看到( )个面。
最少可以看到( )个面。
【知识点2】棱长和公式:长方体棱长和=(长+宽+高)长+宽+高=棱长和÷4长方体棱长和=下面周长×2+高×4长方体棱长和=右面周长×2+长×4长方体棱长和=前面周长×2+宽×4正方体棱长和=棱长×12 棱长=棱长和÷12棱长和的变形:例如:有一个礼盒需要用彩带捆扎,捆扎效果如图,打结部分需要10厘米彩带,一共需要多长的彩带?分析:本题虽然并未直接提出求棱长和,但由于彩带的捆扎是和棱相互平行的, 因此,在解决问题时首先确定每部分彩带与那条棱平行,从而间接去求棱长和。
长方体和正方体单元知识点

长方体和正方体单元知识点1. 长方体(Rectangular Prism):长方体是由6个矩形面组成的立体图形。
它的所有对面都是相等的,并且相对的面是平行的。
长方体有8个顶点、12条边和6个面。
1.1定义:长方体的定义可以用以下几个要素来描述:-一个有6个矩形面的立体图形。
-每个面都是直角相邻的。
-所有面的边长都不相等。
-所有对面都是平行的。
1.2特征:长方体具有以下特征:-所有边长不相等。
-所有对面都是平行的。
-每个面上的相对边长相等。
-所有的角都是直角。
1.3表面积计算:长方体的表面积可以通过计算每个面的面积,并将结果相加得到。
表面积 = 2lw + 2lh + 2wh其中,l、w和h分别代表长方体的长度、宽度和高度。
1.4体积计算:长方体的体积可以通过将长度、宽度和高度相乘来计算。
体积 = lwh2. 正方体(Cube):正方体是一种特殊的长方体,其所有边长相等。
正方体有8个顶点、12条边和6个面。
正方体具有更多的对称性和特殊性质。
2.1定义:正方体的定义可以用以下几个要素来描述:-一个具有6个正方形面的立体图形。
-所有边长相等。
-所有的角都是直角。
2.2特征:正方体具有以下特征:-所有边长相等。
-所有对面都是平行的。
-每个面上的角度都是直角。
-具有更多的对称性,即旋转或反射一个正方体的结果仍然是一个正方体。
2.3表面积计算:正方体的表面积可以通过计算每个面的面积,并将结果相加得到。
表面积=6s^2其中,s代表正方体的边长。
2.4体积计算:正方体的体积可以通过将边长三次幂(即三次方)来计算。
体积=s^3其中,s代表正方体的边长。
总结:长方体和正方体都是由矩形面组成的三维立体图形。
长方体具有所有边长不相等的特征,而正方体具有所有边长相等的特征。
它们在计算表面积和体积时的公式也有所不同。
长方体的表面积为2lw + 2lh + 2wh,体积为lwh;而正方体的表面积为6s^2,体积为s^3、正方体具有更多的对称性和特殊性质。
完整版)长方体和正方体的知识点整理

完整版)长方体和正方体的知识点整理长方体和正方体的知识整理一、概念长方体是由6个长方形(特殊情况下有两个相对的面是正方形)围成的立体图形。
在长方体中,相对的面完全相同,相对的棱长度相等。
两个面相交的边叫做棱,三条棱相交的点叫做顶点。
相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高。
正方体是由6个完全相同的正方形围成的立体图形。
正方体有12条棱,它们的长度都相等,所有的面都完全相同。
长方体和正方体的面、棱和顶点的数目都一样,只是正方体的棱长都相等,正方体可以说是长、宽、高都相等的长方体,它是一种特殊的长方体。
二、长方体和正方体的棱长和表面积长方体的棱长总和=(长+宽+高)×4,长=棱长总和÷4-宽-高,宽=棱长总和÷4-长-高,高=棱长总和÷4-长-宽。
正方体的棱长总和=棱长×12,正方体的棱长=棱长总和÷12.长方体或正方体的长、宽、高同时扩大几倍,棱长总和会扩大相同的倍数。
长方体的表面积=(长×宽+长×高+宽×高)×2,无底(或无盖)长方体表面积=长×宽+(长×高+宽×高)×2,无底又无盖长方体表面积=(长×高+宽×高)×2,正方体的表面积=棱长×XXX×6.表面积的常用单位有:平方米、平方分米、平方厘米。
相邻两个面积单位之间的进率是100,1m=100dm,1dm=100cm。
三、生活实际油箱、罐头盒等都是6个面;游泳池、鱼缸、粉刷教室等都只有5个面;水管、烟囱等都只有4个面。
注意:长方体或正方体每截断一次会增加两个截面,所以这时的两个物体的表面积大于原来物体的表面积。
长方体或正方体的长、宽、高同时扩大几倍,其表面积会扩大倍数的平方倍。
比如,若长、宽、高各扩大2倍,则表面积会扩大到原来的4倍。
长方体和正方体的体积是指物体所占空间的大小。
(完整版)长方体和正方体知识点

一、知识点一:长方体和正方体的认识
6个面,每个面都是长方形(特殊的有一组对面是正方形),相对的面完全相同;有12条棱,相对的棱平行且相等;有8个顶点。
正方形有6个面,每个面都是正方形,所有的面都完全相同;有12条棱,所有的棱都相等;有8个顶点。
长方体的长、宽、高。
=(长+宽+高)×4
用字母表示:(a+b+h)×4
正方体的棱长总和= 棱长×12
用字母表示:12a
二、知识点二:长方体和正方体的表面积的计算
6个面的总面积叫做它的表面积。
=(长×宽+长×高+宽×高)×2用字母表示:S=(ab+ah+bh)×2
正方体的表面积= 棱长×棱长×6
用字母表示:S=6a2
6
7、1m2 =100dm2 1dm2 =100cm2
三、知识点三:长方体和正方体的体积的计算
= 长×宽×高
用字母表示:V=abh
正方体的体积= 棱长×棱长×棱长
用字母表示:V=a3
1m3=1000dm3 1dm3=1000cm3 1m3=100 0000cm3
长方体或正方体的体积=底面积×高
用字母表示:V=Sh
把高级单位化成低级单位,用高级单位数乘以进率;------大乘小
把低级单位聚成高级单位,用低级单位数除以进率。
-----------小除大
四、知识点三:长方体和正方体的容积的计算
L和ml)
1L=1000ml 1L= 1dm3 1ml= 1cm3
跟体积的计算方法相同,但要从里面量长、宽、高。
长方体正方体.知识点总结

长方体的再认识一、 概念1、 长方体的元素:六个面、八个顶点、十二条棱2、 长方体的三元素的特点:(主要是外观特征和数量关系)①长方体的每个面都是长方形;②长方体的十二条棱可以分为三组,每组中的四条棱的长度相等。
③长方体的六个面可以分为三组,每组中的两个面形状大小都相同。
3、 正方体是特殊的长方体。
4、 平面是平的,无边无沿,没有厚度和大小,一般用平行四边形来表示。
记作:平面ABCD 或平面α。
5、 将水平放置的平面画成一边是水平位置,另一边与水平线成45度角的平行四边形。
6、 斜二侧画法画长方体时要注意:宽画成标注尺寸的一半;看不到的线画成虚线;要标字母和尺寸,要写结论。
长方体ABCD-EFGH 、平面ABCD 、棱AB 、顶点A 。
7、 空间中两直线的位置关系有三种:相交、平行、异面① 如果两条直线在同一平面内,有唯一公共点,称这两条直线的位置关系是相交; ② 如果两条直线在同一平面内,没有唯一公共点,称这两条直线的位置关系是平行; ③ 如果两条直线既不平行也不相交,称这两条直线的位置关系是异面。
8、直线垂直于平面记作:直线P Q ⊥平面ABCD ;直线平行于平面记作:直线P Q ∥平面ABCD 。
9、 计算公式之一:(三条棱长分别是a 、b 、c 的长方体)① 棱长和 = 4()a b c ++ ; ② 体积 = abc ;③ 表面积 = 2()ab bc ac ++ ; ④ 无盖表面积 = S ab -、S bc -、S bc - 10、计算公式之二:(边长是a 正方体)① 棱长和= 12a ;②体积= 3a ;③表面积= 26a ;④无盖表面积 =25a 。
11、长方体不一定是正方体;正方体一定是长方体。
12、长方体中棱与棱的位置关系有3种,分别是平行、相交、异面。
13、长方体中棱与面的位置关系有2种,分别是:平行、垂直。
14、长方体中面与面的位置关系有2种,分别是:平行、垂直。
人教版五年级数学下册长方体和正方体知识点

学习必备精品知识点
第三章长方体和正方体
一、长方体和正方体的认识
1、长方体的特征:由6个长方形(特殊情况下有两个相对的面是正方形)围成的立体图形。
一个长方体有6个面、12条棱和8个顶点。
相对的面完全相同,相对的棱长度相等
2、长方体的长、宽、高:相交于同一顶点的三条棱的长度
3、正方体的特征:由6个完全相同的正方形围成的立体图形。
正方体有6个面、12条棱和8个顶点,6个面完全相同,12条棱长度相等
4、长方体和正方体的关系:正方体是特殊的长方体
二、长方体和正方体的表面积
1、长方体或正方体6个面的总面积,叫做它的表面积
2、长方体表面积S=(ab+ah+bh)×2
3、正方体表面积S=6a²
三、长方体和正方体的体积
1、体积:物体所占空间的大小
2、常用体积单位:cm
3、dm3、m3
3、长方体体积V=abh
4、正方体体积V=a3
5、长方体(正方体)V=Sh
6、1m3=1000dm3=1000000cm3
7、容积:容器等所能容纳物体的体积。
单位:L、mL
8、容积计算方法
①规则容器容积与体积计算方法相同,但要从里面测量数据
②不规则较小容器用量杯或量筒测量容器所能容纳液体体积
③不规则较大容器借助于液体转化成求规则容器
9、1L=1dm3=1000mL=1000cm3
10、求形状不规则物体的体积可用排水法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
长方体与正方体知识点
1、由6个长方形(特殊情况有两个相对的面是正方形)围成的立体图形叫做长方体。
两个面相交的边叫做棱。
三条
棱相交的点叫做顶点。
相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高。
长方体特点:
(1)有6个面,8个顶点,12条棱,相对的面的面积相等,相对的棱的长度相等。
(2)一个长方体最多有6个面是长方形,最少有4个面是长方形,最多有2个面是正方形。
2、由6个完全相同的正方形围成的立体图形叫做正方体(也叫做立方体)。
正方体特点:
(1)正方体有12条棱,它们的长度都相等。
(2)正方体有6个面,每个面都是正方形,每个面的面积都相等。
(3)正方体可以说是长、宽、高都相等的长方体,它是一种特殊的长方体。
3、长方体、正方体有关棱长计算公式:
长方体的棱长总和=(长+宽+高)×4=长×4+宽×4+高×4 L=(a+b+h)×4
长=棱长总和÷4-宽-高 a=L÷4-b-h
宽=棱长总和÷4-长-高 b=L÷4-a-h
高=棱长总和÷4-长-宽 h=L÷4-a-b
正方体的棱长总和=棱长×12 L=a×12
正方体的棱长=棱长总和÷12 a=L÷12
4、长方体或正方体6个面和总面积叫做它的表面积。
长方体的表面积=(长×宽+长×高+宽×高)×2 S=2(ab+ah+bh)
无底(或无盖)长方体表面积= 长×宽+(长×高+宽×高)×2 S=2(ab+ah+bh)-ab S=2(ah+bh)+ab 无底又无盖长方体表面积=(长×高+宽×高)×2 S=2(ah+bh)贴墙纸
正方体的表面积=棱长×棱长×6 S=a×a×6 用字母表示: S= 6a2
生活实际:油箱、罐头盒等都是6个面 游泳池、鱼缸等都只有5个面 水管、烟囱等都只有4个面。
注意1:用刀分开物体时,每分一次增加两个面。
(表面积相应增加)
注意2:长方体或正方体的长、宽、高同时扩大几倍,表面积会扩大倍数的平方倍。
(如长、宽、高各扩大2倍,表面积就会扩大到原来的4倍)。
5、物体所占空间的大小叫做物体的体积。
长方体的体积=长×宽×高 V=abh
长=体积÷宽÷高 a=V ÷b ÷h
宽=体积÷长÷高 b=V ÷a ÷h
高=体积÷长÷宽 h= V ÷a ÷b
正方体的体积=棱长×棱长×棱长 V=a ×a ×a = a 3读作“a 的立方”表示3个a 相乘,(即a ·a ·a ) 长方体或正方体底面的面积叫做底面积。
长方体(或正方体)的体积=底面积×高 用字母表示:V=S h (横截面积相当于底面积,长相当于高)。
注意:一个长方体和一个正方体的棱长总和相等,但体积不一定相等。
6、箱子、油桶、仓库等所能容纳物体的体积,通常叫做他们的容积。
固体一般就用体积单位,计量液体的体积,如水、油等。
常用的容积单位有升和毫升也可以写成L 和ml 。
1升=1立方分米 1毫升=1立方厘米 1升=1000毫升
(1 L = 1 dm 3 1 ml = 1 cm 3
)
长方体或正方体容器容积的计算方法,跟体积的计算方法相同。
但要从容器里面量长、宽、高。
(所以,对于同一个物体,体积大于容积。
)
注意:长方体或正方体的长、宽、高同时扩大几倍,体积就会扩大倍数的立方倍。
(如长、宽、高各扩大2倍,体积就会扩大到原来的8倍)。
*形状不规则的物体可以用排水法求体积,形状规则的物体可以用公式直接求体积。
排水法的公式:V 物体 =V 现在-V 原来
也可以 V 物体 =S ×(h 现在- h 原来)
V 物体 = S ×h 升高
8、【体积单位换算】 大单位 小单位 小单位
大单位
×进率
÷进率
进率: 1立方米=1000立方分米=1000000立方厘米 (立方相邻单位进率1000) 1立方分米=1000立方厘米=1升=1000毫升
1立方厘米=1毫升
1平方米=100平方分米=10000平方厘米
1平方千米=100公顷=1000000平方米
注意:长方体与正方体关系
把长方体或正方体截成若干个小长方体(或正方体)后,表面积增加了,体积不变。
重量单位进率,时间单位进率,长度单位进率
【单位换算】 大单位 小单位
小单位 大单位
长度单位:1千米 =1000 米 1 分米=10 厘米 1厘米=10毫米 1分米=100毫米 1米=10分米=100厘米=1000毫米 (相邻单位进率10) 面积单位:1平方千米=100公顷 1平方米=100平方分米
1平方分米=100平方厘米 1公顷=10000平方米 (平方相邻单位进率100) 质量单位:1吨=1000千克 1千克=1000克
人 民 币:1元=10角 1角=10分 1元=100分
×进率
÷进率。
