机电系统动力学仿真matlab课后答案
电机与拖动基础及MATLAB仿真习题答案(第四章)

电机与拖动基础及MATLAB仿真习题答案(第四章)4-14 ⼀台直流电动机技术数据如下:额定功率PN=40kW ,额定电压UN=220V ,额定转速nN=1500r/min ,额定效率η=87.5%,求电动机的额定电流和额定负载时的输⼊功率?解:(1)额定电流(2)输⼊功率4-15 ⼀台直流发电机技术数据如下:额定功率PN=82kW ,额定电压UN=230V ,额定转速nN=970r/min ,额定效率η=90%,求发电机的额定电流和额定负载时的输⼊功率?解:(1)额定电流(2)输⼊功率4-16 已知⼀台直流电机极对数p=2,槽数Z 和换向⽚数K 均等于22,采⽤单叠绕组。
试求:(1)绕组各节距;(2)并联⽀路数。
解:(1)第⼀节距5424222y 1=-=±=εp z ,为短距绕组。
单叠绕组的合成节距及换向器节距均为1,即1y ==k y第⼆节距415y 12=-=-=y y(2)并联⽀路数等于磁极数,为4。
4-17 已知直流电机极数2p=6,电枢绕组总导体数N=400,电枢电流Ia=10A ,⽓隙每极磁通Φ=2.1×10-2Wb ,试求:(1)采⽤单叠绕组时电枢所受电磁转矩;(2)绕组改为单波保持⽀路电流ia 不变时的电磁转矩。
解: 电枢绕组为单叠绕组时,并联⽀路对数a=p=3,电磁转矩 m N I a pN T a ?==Φ=38.1310021.0314.3240032π如果把电枢绕组改为单波绕组, 保持⽀路电流a i 的数值不变,则电磁转矩也不变,仍为 13.369m N ?,因为⽆论是叠绕组还是波绕组,所有导体产⽣的电磁转矩的⽅向是⼀致的, 保持⽀路电流a i 不变,就保持了导体电流不变,也就保持了电磁转矩不变。
也可以⽤计算的⽅法: 单叠绕组时并联⽀路数为6,⽀路电流 A I i a a 6106==改为单波绕组, 保持⽀路电流a i 的数值不变,仍为A 610,⽽并联⽀路数为2 (a=1), 电枢电流A i I a a 3102== 电磁转矩 m N T ?==38.13310021.0114.324003。
MATlab 仿真部分习题答案
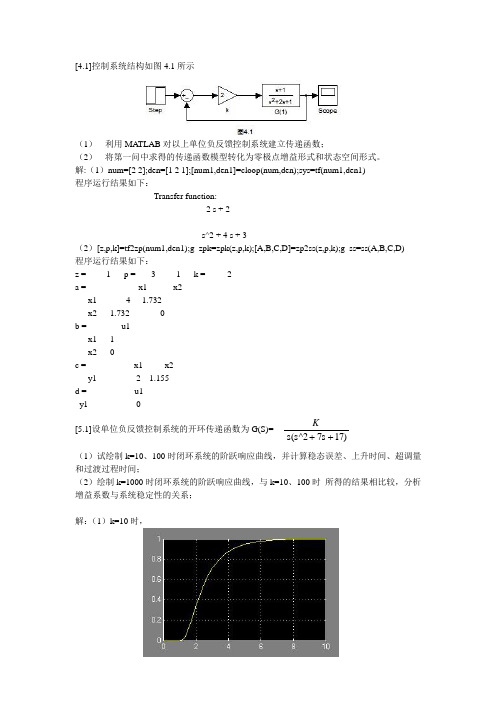
[4.1]控制系统结构如图4.1所示(1)利用MATLAB对以上单位负反馈控制系统建立传递函数;(2)将第一问中求得的传递函数模型转化为零极点增益形式和状态空间形式。
解:(1)num=[2 2];den=[1 2 1];[num1,den1]=cloop(num,den);sys=tf(num1,den1)程序运行结果如下:Transfer function:2 s + 2-------------s^2 + 4 s + 3(2)[z,p,k]=tf2zp(num1,den1);g_zpk=zpk(z,p,k);[A,B,C,D]=zp2ss(z,p,k);g_ss=ss(A,B,C,D)程序运行结果如下:z = -1 p = -3 -1 k = 2a = x1 x2x1 -4 -1.732x2 1.732 0b = u1x1 1x2 0c = x1 x2y1 2 1.155d = u1y1 0K[5.1]设单位负反馈控制系统的开环传递函数为G(S)=+s(s^2+7s17)(1)试绘制k=10、100时闭环系统的阶跃响应曲线,并计算稳态误差、上升时间、超调量和过渡过程时间;(2)绘制k=1000时闭环系统的阶跃响应曲线,与k=10、100时所得的结果相比较,分析增益系数与系统稳定性的关系;解:(1)k=10时,K=100时,K=10时,利用MA TLAB工作区输入程序:num=[10];den=[1,7,17,0];[z,p,k]=tf2zp( num,den);运行得z,p,k的值p= -3.5+2.1794*i -3.5-2.1794*i k=10G=zpk([ ],[-3.5+2.1794*i,-3.5-2.1794*i],10);c=dcgain(G);[y,t]=step(G);plot(t,y)[Y,K]=max(y);timetopeak=t(k);percentovershoot=100*(y-c)/cn=1;while y(n)<c n=n+1;end risetime=t(n) i=length(t);while(y(i)>0.98*c&y(i)<1.02*c) i=i-1;End setllingtime=t(i) 运行程序结果为:稳定值c=0.5882,响应时间setllingtime=1.0096s,上升时间risetime=1.1989s,最大峰值时间timetopeak=1.4356,超调量percentovershoot=0.555% 同理得k=100时,稳定值c=5.882,响应时间setllingtime=1.0096s, 上升时间risetime=1.1989s,最大峰值时间timetopeak=1.4356,超调量percentovershoot=0.555%(3)k=1000时,由其响应曲线可知,增益系数越大,其稳定性越差。
matlab课后习题答案(附图)

matlab课后习题答案(附图)习题2.1画出下列常见曲线的图形y (1)⽴⽅抛物线3x命令:syms x y;ezplot('x.^(1/3)')(2)⾼斯曲线y=e^(-X^2);命令:clearsyms x y;ezplot('exp(-x*x)')(3)笛卡尔曲线命令:>> clear>> syms x y;>> a=1;>> ezplot(x^3+y^3-3*a*x*y)(4)蔓叶线命令:>> clear>> syms x y;>> a=1ezplot(y^2-(x^3)/(a-x))(5)摆线:()()tsin-=,=-by1命令:>> clear>> t=0:0.1:2*pi;>> x=t-sin(t);>>y=2*(1-cos(t)); >> plot(x,y)7螺旋线命令:>> clear >> t=0:0.1:2*pi; >> x=cos(t); >> y=sin(t); >> z=t;>>plot3(x,y,z)(8)阿基⽶德螺线命令:clear>> theta=0:0.1:2*pi;>> rho1=(theta);>> subplot(1,2,1),polar(theta,rho1)(9) 对数螺线命令:cleartheta=0:0.1:2*pi;rho1=exp(theta);subplot(1,2,1),polar(theta,rho1)(12)⼼形线命令:>> clear >> theta=0:0.1:2*pi; >> rho1=1+cos(theta); >> subplot(1,2,1),polar(theta,rho1)练习2.21. 求出下列极限值(1)nnn n3→命令:>>syms n>>limit((n^3+3^n)^(1/n)) ans = 3(2))121(lim n n n n ++-+∞→命令:>>syms n>>limit((n+2)^(1/2)-2*(n+1)^(1/2)+n^(1/2),n,inf) ans = 0(3)x x x 2cot lim 0→命令:syms x ;>> limit(x*cot(2*x),x,0) ans = 1/2 (4))(coslimcm xx ∞→命令:syms x m ; limit((cos(m/x))^x,x,inf) ans = 1(5))111(lim 1--→exx x命令:syms x>> limit(1/x-1/(exp(x)-1),x,1) ans =(exp(1)-2)/(exp(1)-1) (6))(2lim x x xx -+∞>> limit((x^2+x)^(1/2)-x,x,inf)ans = 1/2练习2.41. 求下列不定积分,并⽤diff 验证:(1)+x dxcos 1>>Clear >> syms x y >> y=1/(1+cos(x)); >> f=int(y,x) f =tan(1/2*x) >> y=tan(1/2*x); >> yx=diff(y ,x); >> y1=simple(yx) y1 =1/2+1/2*tan(1/2*x)^2 (2)+exdx1clear syms x yy=1/(1+exp(x));f=int(y,x) f =-log(1+exp(x))+log(exp(x)) syms x yy=-log(1+exp(x))+log(exp(x)); yx=diff(y,x); y1=simple(yx) y1 = 1/(1+exp(x)) (3)dx x x ?sin 2syms x yy=x*sin(x)^2; >> f=int(y,x) f =x*(-1/2*cos(x)*sin(x)+1/2*x)-1/4*cos(x)^2-1/4*x^2 clearsyms x y y=x*(-1/2*cos(x)*sin(x)+1/2*x)-1/4*cos(x)^2-1/4*x^2; yx=diff(y,x); >> y1=simple(yx) y1 = x*sin(x)^2 (4)xdx ?sec3syms x y y=sec(x)^3;f=int(y,x) f =1/2/cos(x)^2*sin(x)+1/2*log(sec(x)+tan(x)) clear syms x yy=1/2/cos(x)^2*sin(x)+1/2*log(sec(x)+tan(x)); yx=diff(y,x); y1=simple(yx) y1 =1/cos(x)^32. 求下列积分的数值解 1)dx x-10clearsyms xy=int(x^(-x),x,0,1) y =int(x^(-x),x = 0 .. 1) vpa(y,10) ans =1.291285997 2)xdx e x cos3202?πclearsyms xy=int(exp(2*x)*cos(x)^3,x, clear syms xy=int((1/(2*pi)^(1/2))*exp(-x^2/2),x,0,1) y =7186705221432913/36028797018963968*erf(1/2*2^(1/2))*2^(1/2)*pi^(1/0,2*pi) y =22/65*exp(pi)^4-22/65vpa(ans,10)(3)dx xe21221-π>> clear >> syms x>> y=int(1/(2*pi)^(1/2)*exp(-x^2/2),0,1); >> vpa(y,14) ans =.341344746068552(4)>> clear >> syms x>> y=int(x*log(x^4)*asin(1/x^2),1,3); Warning: Explicit integral could not be found. > In sym.int at 58 >> vpa(y,14) ans = 2.45977212823752(5) >> clear >> syms x1判断下列级数的收敛性,若收敛,求出其收敛值。
电机与拖动基础及MATLAB仿真习题答案(第四章)

4-14 一台直流电动机技术数据如下:额定功率PN=40kW ,额定电压UN=220V ,额定转速nN=1500r/min ,额定效率η=%,求电动机的额定电流和额定负载时的输入功率 解:(1)额定电流(2)输入功率4-15 一台直流发电机技术数据如下:额定功率PN=82kW ,额定电压UN=230V ,额定转速nN=970r/min ,额定效率η=90%,求发电机的额定电流和额定负载时的输入功率 解:(1)额定电流(2)输入功率4-16 已知一台直流电机极对数p=2,槽数Z 和换向片数K 均等于22,采用单叠绕组。
试求:(1)绕组各节距;(2)并联支路数。
解:(1)第一节距5424222y 1=-=±=εp z ,为短距绕组。
单叠绕组的合成节距及换向器节距均为1,即1y ==k y第二节距415y 12=-=-=y y(2)并联支路数等于磁极数,为4。
4-17 已知直流电机极数2p=6,电枢绕组总导体数N=400,电枢电流Ia=10A ,气隙每极磁通Φ=×10-2Wb ,试求:(1)采用单叠绕组时电枢所受电磁转矩;(2)绕组改为单波保持支路电流ia 不变时的电磁转矩。
解: 电枢绕组为单叠绕组时,并联支路对数a=p=3,电磁转矩 m N I a pN T a ⋅=⨯⨯⨯⨯⨯=Φ=38.1310021.0314.3240032π 如果把电枢绕组改为单波绕组, 保持支路电流a i 的数值不变,则电磁转矩也不变,仍A U P I N N N N 79.207875.022010403=⨯⨯==ηkWI U P N N 71.4579.2072201=⨯=⨯=A U P I N N N 5.35623010823=⨯==KW P P N 11.911==η为m N ⋅,因为无论是叠绕组还是波绕组,所有导体产生的电磁转矩的方向是一致的,保持支路电流a i 不变,就保持了导体电流不变,也就保持了电磁转矩不变。
东北林业大学机电工程学院电气matlab实验内容答案

实验一 MATLAB 运算基础1.先求下列表达式的值,然后显示MA TLAB 工作空间的使用情况并保存全部变量。
(1)22sin8511z e ︒=+ clear ;z1=2*sin(85/180*pi)/(1+exp(2))(2)12ln(2z x =+,其中2120.455i +⎡⎤=⎢⎥-⎣⎦clear ;x=[2,1+2*i;-0.45,5];z2=log(x+sqrt(1+x^2))/2(3)0.30.33sin(0.3), 3.0, 2.9, 2.8,,2.8,2.9,3.02a ae e z a a --=+=--- clear ;a=(-3:0.1:3);z3=((exp(0.3*a)-exp(-0.3*a))/2).*sin(a+0.3)(4)2220141122123t t z t t t t t ⎧≤<⎪=-≤<⎨⎪--≤<⎩,其中t =0:0.5:2.5clear for t=0:0.5:2.5 if t>=0 & t<1 z4=t^2elseif t>=1 & t<2 z4=t^2-1 else z4=t^2-2*t-1 end end 2.已知12344347873657A -⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,131203327B -⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦求下列表达式的值:(1) A+6=B 和A-B+I(其中I 为单位矩阵)。
(2) A*B 和A.*B 。
(3) A^3和A^.3 。
(4) A/B 和B\A 。
(5)[A ,B]和[A([1,3],;);B^2] 。
clearA=[12,34,-4;34,7,87;3,65,7]; B=[1,3,-1;2,0,3;3,-2,7]; Z1=A+6*B I=eye(3,3) Z11=A-B+IZ21=A.*B % The second A^3 % The third A.^3A/B % The forth B\A[A,B] % The fifth [A([1,3],:);B^2] 3.设有矩阵A 和B12345678910111213141516171819202122232425A ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦, 30161769023497041311B ⎡⎤⎢⎥-⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎣⎦(1) 求它们的乘积C 。
matlab课后习题及答案详解

matlab课后习题及答案详解第1章练习题1.安装matlab时,在选择组件窗口中哪些部分必须勾选,没有勾选的部分以后如何补安装?在安装matlab时,安装内容由选择组件窗口中个复选框是否被勾选来决定,可以根据自己的需要选择安装内容,但基本平台(即matlab选项)必须安装。
第一次安装没有选择的内容在补安装时只需按照安装的过程进行,只是在选择组件时只勾选要补装的组件或工具箱即可。
2.matlab操作方式桌面存有几个窗口?如何并使某个窗口瓦解桌面沦为单一制窗口?又如何将瓦解过来的窗口再次置放至桌面上?与其他计算机语言相比较,matlab语言注重的特点就是什么?matlab系统由那些部分共同组成?在matlab操作桌面上有五个窗口,在每个窗口的右上角有两个小按钮,一个是关闭窗口的close按钮,一个是可以使窗口成为独立窗口的undock按钮,点击undock按钮就可以使该窗口脱离桌面成为独立窗口,在独立窗口的view菜单中选择dock……菜单项就可以将独立的窗口重新防止的桌面上。
matlab具备功能强大、使用方便、输出简便、库函数多样、开放性弱等特点。
matlab系统主要由开发环境、matlab数学函数库、matlab语言、图形功能和应用程序接口五个部分组成。
3.如何设置当前目录和搜寻路径,在当前目录上的文件和在搜寻路径上的文件存有什么区别?命令历史窗口除了可以观测前面键入的命令外,除了什么用途?当前目录可以在当前目录浏览器窗口左上方的输入栏中设置,搜索路径可以通过选择操作桌面的file菜单中的setpath菜单项来完成。
在没有特别说明的情况下,只有当前目录和搜索路径上的函数和文件能够被matlab运行和调用,如果在当前目录上有与搜索路径上相同文件名的文件时则优先执行当前目录上的文件,如果没有特别说明,数据文件将存储在当前目录上。
命令历史窗口除了用作查阅以前键入的命令外,还可以轻易执行命令历史窗口中选取的内容、将选取的内容拷贝到剪贴板中、将选取内容轻易拷贝到m文件中。
机电动力系统Matlab分析举例

华中科技大学电气学院博士研究生课程《机电动力系统仿真分析》试题1. 双馈感应发电机,定子接∞电网(s U 、f 保持恒定),转子由理想正弦波VVVF 电源供电。
设电机参数及控制方式同【例4.2】,试仿真分析: 输出功率1P 由1.5kw →1.8kw →1.5kw 的动态调节过程(cos ϕ、s 保持为额定值); 功率因数cos ϕ由0.9→1.0→0.9的动态调节过程(1P 、s 保持为额定值); 转差率s 由0.05→0.10→0.05的动态调节过程(1P 、cos ϕ保持为额定值); 结果讨论(建议结合一组具有不同控制精度或P 参数的仿真结果进行)。
解:(1)标么化处理:功率:B 1500VA P =电压:B 220311.127V U == 电流:B B B 2/3 3.214A I P U == 速度:B 250314.16rad /s ωπ=⨯= 阻抗:B B B /96.81Z U I ==Ω 电感:B B B /0.308H L Z ω== 转矩:B B B /10.61N m T pP ω==∙ 时间:B B 1/0.0032s t ω== 标么化后有:S 12s r s r m 1, 1.0,0.05,0.0386,0.0329,0.988, 1.01,0.948U r r L L L ωω========(2)建立仿真模型:据课本p228,变速恒频发电机状态方程为: .X AX BU =+ 式中2(,,,,)(,,,,)(0,,,,)Tds qs dr qr T Tds qs dr qr e s dr qr e X i i i i U u u u u T U u u T ω==-=-512123434550000001000000000000100000r m r m m sm s s r r ms r r m s mr s s mr s qrdr L L L L B L L L L b r L a r L a a r L a r L A r L a r L a a r L a r L a i a i -⎡⎤⎢⎥-⎢⎥⎢⎥=-Λ⎢⎥-⎢⎥⎢⎥⎣⎦-⎡⎤⎢⎥-⎢⎥⎢⎥=-⎢⎥Λ-⎢⎥⎢⎥-⎣⎦221122123122412555()()1.5s r m s r m r m s m m s r m L L L a L L L a L L a L L a L L L a pL b pb JωωωωωωωωΛ=-=-=-=-=-==Λ 设实施动态调控前电机以速度0r ω稳态运行,定子电压、频率、输出功率和功率因数分别为0s U 、10ω、10P 和0cos ϕ,则初始条件确定如下:1000000000001000000101000000102010023cos sin cos sin cos cos sin s s ds s qs s s s s s s dr ms s s s qr mr P I U i I i I U L I r I i L L I r I i L ϕϕϕωϕϕωωϕϕωωωω===++=-==-取q 轴与定子电压矢量重合, 0ds qs su u U ==控制指令值为1***11*11**21*****2*****2**/(1.5cos )sin cos (sin cos )/()(cos sin )/()()()1.5(s s ds s qs s dr s s s s s m qr s s s s m r dr r dr m qs r qr qr r qr r dr m ds m m qs dr ds I P U i I i I i U L I r I L i L I r I L u r i L i L i u r i L i L i T pL i i i ϕϕϕωϕϕωωϕϕωωωωωω====++=-=-=+-=+-=-**)qr i转子电压的动态控制控制方程: *****222*****222()()dr dr m qs r dr r qr m qs r qr qr qrmds r dr r qr r drm dsu u L i r i L i L i L i u u L i L i r i L i L i ωωωωωω=+∆+∆-∆+-∆=-∆+∆+∆+-∆式中,各状态变量的增量统一定义为:*x x x ∆=- 2(,,,,)ds qs dr qr x i i i i ω= (3)仿真模型建立及仿真结果:根据上述数学模型编写S-function ,建立a )的仿真模型如下:图1-1(a )仿真结果:图1-21(cos 、s保持为额定值)同样的方法建立系统b)、c)的仿真模型,仿真过程如下:仿真结果:图1-4 cos 由0.8→0.9→1.0→0.9→0.8的动态调节过程P、s保持为额定值)(1仿真结果:图1-6 s 由0.05→0.1→0.15→0.10→0.05的动态调节过程(1P 、cos ϕ保持为额定值,P =500)图1-7 s 由0.05→0.1→0.15→0.10→0.05的动态调节过程(1P 、cos ϕ保持为额定值,P =1000)图1-8 s由0.05→0.1→0.15→0.10→0.05的动态调节过程P、cos 保持为额定值,P=1500)(1(4)结果讨论:以转差率的动态响应为例来分析P参数对系统动态及稳态性能的影响。
(完整版)MATLAB)课后实验答案[1]
![(完整版)MATLAB)课后实验答案[1]](https://img.taocdn.com/s3/m/a428921bf524ccbff12184eb.png)
实验一 MATLAB 运算基础1.先求下列表达式的值,然后显示 MATLAB 工作空间的使用情 况并保存全部变量解:4.完成下列操作:(1) 求[100,999] 之间能被21整除的数的个数。
(1) z i 2sin 85° 1 e 2Z 2 卯(x L),其中x2 0.45 2i 5Z 3 0.3a 0.3a e e 2sin (a 0.3)3.0, 2.9,L ,2.9, 3.0 Z 4t 2t 2 t 2 1 2t 其中 t=0:0.5:2.5(2) 建立一个字符串向量,删除其中的大写字母。
解: (1)结果:m=100:999;n=fin d(mod(m,21)==0);len gth( n)ans =43(2).建立一个字符串向量例如:ch二'ABC123d4e56Fg9:则要求结果是: ch二'ABC123d4e56Fg9:k=fi nd(ch>='A'&ch<='Z'); ch(k)=[] ch =123d4e56g9 实验二MATLAB 矩阵分析与处理1.设有分块矩阵A E 3 3 °2 3 R 3 2S 2 2 ,其中E 、R 、0、S 分别为单位矩阵、随机矩阵、零矩阵和对角阵,试通过数值计算验证A 2 E R RS 0 S 22 3 4 1 1 1 3 4 5 1 1 1 4 5 6 x , 0.95 x 2 0.67 x 3 0.52(1) 求方程的解。
(2) 将方程右边向量元素 b 3改为0.53再求解,并比较 b 3的变化和解的相对变化。
(3)计算系数矩阵A 的条件数并分析结论。
解:M 文件如下: 解:M 文件如下; 5.下面是一个线性方程组:实验三选择结构程序设计1. 求分段函数的值。
x2x 6 x 0且x 3y x2 5x 6 0 x 5且x 2 及x 3x2x 1 其他用if语句实现,分别输出x=-5.0,-3.0,1.0,2.0,2.5,3.0,5.0 时的y值。
