专题50:圆与圆的位置关系2021届新课改地区高三数学一轮专题复习(解析版)
第49讲 直线与圆的位置关系(解析版)2021届新课改地区高三数学一轮专题复习

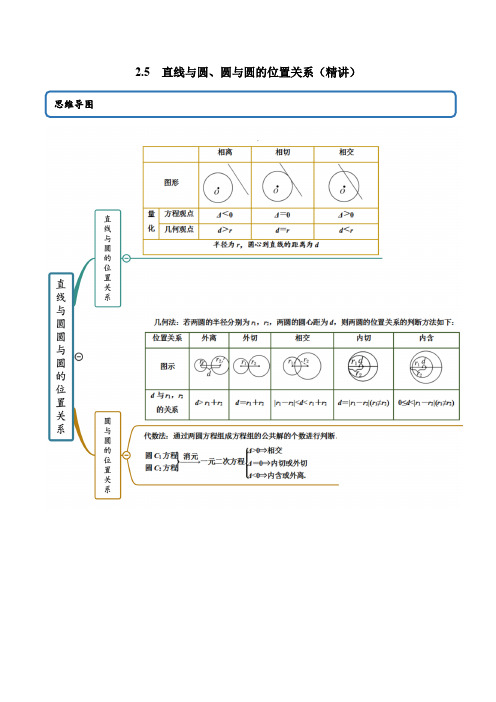
Δ<0 d>r
Δ=0 d=r
Δ>0 d<r
(2)圆的切线方程的常用结论
①过圆 x2+y2=r2 上一点 P(x0,y0)的圆的切线方程为 x0x+y0y=r2;
②过圆(x-a)2+(y-b)2=r2 上一点 P(x0,y0)的圆的切线方程为(x0-a)(x-a)+(y0-b)(y-b)=r2;
③过圆 x2+y2=r2 外一点 M(x0,y0)作圆的两条切线,则两切点所在直线方程为 x0x+y0y=r2.
12+(-1)2 选 C.
4、过点(2,3)与圆(x-1)2+y2=1 相切的直线的方程为________________.
【答案】 x=2 或 4x-3y+1=0
【解析】 ①若切线的斜率存在时,设圆的切线方程为 y=k(x-2)+3,由圆心(1,0)到切线的距离为半径 1, 得 k=4,所以切线方程为 4x-3y+1=0;②若切线的斜率不存在,则切线方程为 x=2,符合题意,所以直
【解析】(2) 由 ax-y+2-a=0 得直线 l 恒过点 M(1,2).又因为点 M(1,2)在圆 C 的内部,当 MC 与 l
垂直时,弦长最短,所以 kMC·kl=-1,所以2-1×a=-1,解得 a=2 . 1-3
(3)由题意,得圆心 C(3,1),半径 r=3 且∠ACB=90°,则圆心 C 到直线 l:ax-y+2-a=0 的距离为
3 线方程为 4x-3y+1=0 或 x=2.
5、直线 l:3x-y-6=0 与圆 x2+y2-2x-4y=0 相交于 A,B 两点,则 AB=________.
【答案】 10
【解析】 由 x2+y2-2x-4y=0,得(x-1)2+(y-2)2=5,所以该圆的圆心坐标为(1,2),半径 r= 5,又圆
2-5 直线与圆、圆与圆的位置关系(精讲)(解析版)
2.5 直线与圆、圆与圆的位置关系(精讲)考点一直线与圆的位置关系【例1】(1)(2021·遵义师范学院附属实验学校)圆22(3)(3)8x y-+-=与直线3460x y++=的位置关系是()A.相交B.相切C.相离D.无法确定(2).(2021·全国高二专题练习)直线():120l kx y k k R-++=∈与圆22:5C x y+=的公共点个数为()A.0个B.1个C.2个D.1个或2个(3)(2021·黑龙江哈尔滨市)若过点()4,3A的直线l与曲线22231x y有公共点,则直线l的斜率的取值范围为()A.⎡⎣B.(C.33⎡-⎢⎣⎦D.,33⎛-⎝⎭(4)(2021·浙江高二期末)已知曲线y=与直线10kx y k-+-=有两个不同的交点,则实数k的取值范围是()A.13,24⎡⎫⎪⎢⎣⎭B.30,4⎛⎫⎪⎝⎭C.12,23⎡⎫⎪⎢⎣⎭D.12,43⎡⎫⎪⎢⎣⎭【答案】(1)C (2)D (3)C (4)A【解析】(1)圆心为()3,3,半径r =()3,3到直线3460x y ++=的距离为333462755d r ⨯+⨯+==>所以直线与圆相离故选:C(2)将直线l 的方程变形为()210k x y ++-=,由2010x y +=⎧⎨-=⎩,可得21x y =-⎧⎨=⎩,所以,直线l 过定点()2,1P -,()22215-+=,即点P 在圆C 上,因此,直线l 与圆C 相交或相切.故选:D.(3)由题意,易知,直线l 的斜率存在,设直线l 的方程为()34y k x -=-,即340kx y k -+-= 曲线22231x y 表示圆心()2,3,半径为1的圆,圆心()2,3到直线340kx y k -+-=的距离应小于等于半径1,1≤,即2k -≤,解得k ≤≤.故选:C. (4)曲线y =22(2)1(0)x y y -+=≥,则该曲线表示圆心为(2,0),半径为1的圆的上半部分,直线10kx y k -+-=过定点(1,1)--,如图,当[)12,k k k ∈时,曲线与直线有两个不同的交点,1=,得34k =或0k =,所以234k =,1101112k --==--,所以实数k 的取值范围是13,24⎡⎫⎪⎢⎣⎭. 故选:A .【一隅三反】1.(2021·江苏南京市·高二期末)直线10x +=与圆()2211x y -+=的位置关系是( ) A .直线过圆心 B .相切C .相离D .相交【答案】B【解析】圆()2211x y -+=的圆心为()1,0 ,半径1r =圆心()1,0到直线10x +=的距离1d r ===所以直线10x -+=与圆()2211x y -+=相切故选:B 2.(2021·四川成都市)若圆22()1(0)x a y a -+=>与直线3y x =只有一个公共点,则 a 的值为( ) A .1 BC .2D.【答案】C【解析】因圆22()1(0)x a y a -+=>与直线3y x =只有一个公共点,则直线0x -=与圆22()1x a y -+=切线,圆心(,0)a 到该直线距离为半径1,1||2a =⇔=,而0a >,则有2a =,所以 a 的值为2.故选:C3.(2021·浙江高二期末)直线:1l y ax a =-+与圆224x y +=的位置关系是( )A .相交B .相切C .相离D .与a 的大小有关【答案】A【解析】直线l :1=-+y ax a ,即()11y a x =-+恒过()1,1,而221124+=<,故()1,1点在圆内, 故直线与圆必然相交.故选:A .4.(2021·全国高二专题练习)若直线0x y b +-=0y +=有公共点,则b 的取值范围是( ) A.[- B.[C .[1,1]-D.[【答案】B【解析】根据题意,y =,变形可得x 2+y 2=1(0y ≤),为圆x 2+y 2=1的下半部分,若直线x +y ﹣b =0与曲线y =有公共点,则当直线经过点A 时,直线x +y ﹣b =0与曲线y =有公共点此时b =1=1,解可得bb <0,则b =,则b的取值范围为[;故选:B .5.(2021·河北保定市·高二期末)(多选)已知圆22:(1)(1)169C x y -+-=,直线:450,l kx y k k R --+=∈.则下列选项正确的是( )A .直线l 恒过定点B .直线l 与圆C 的位置可能相交、相切和相离 C .直线l 被圆C 截得的最短弦长为12D .直线l 被圆C 截得的最短弦长对应的k 值为34-【答案】AD【解析】由直线:450,l kx y k k R --+=∈得():54,l y k x k R -=-∈, 所以直线l 过定点()4,5,故A 选项正确;此时将点()4,5代入圆22:(1)(1)169C x y -+-=得22(41)(5125)169-+<-=,所以点()4,5在圆内,故直线l 与圆C 的位置是相交,故B 选项错误;当直线l 与过点()4,5和圆心的直线垂直时,直线l 被圆C截得的弦长最短,为24=,此时直线l 的斜率为1351441k -==---,故C 选项错误,D 选项正确.故选:AD 考点二 直线与圆的弦长【例2】(1)(2021·四川成都市)直线1y x =-被圆22220x y y ++-=截得的弦长为( ) A .1B .2CD.(2).(2021·浙江高二期末)已知直线:0l kx y k -+-=被圆224x y +=截得的弦长为点(),m n 是直线l 上的任意一点,则22m n +的最小值为( )A .1B .2C .3D .4【答案】(1)B (2)A【解析】(1)圆的标准方程为()2213x y ++=,圆心为()0,1-,半径为r =所以圆心到直线的距离d ==2l ===,故选:B .(2)圆224x y +=的圆心为()0,0,半径为2r,圆心到直线的距离1d ==, 所以22m n +的最小值为21d =.故选:A 【一隅三反】1.(2021·安徽省泗县第一中学)直线40x y -+=被圆22(2)(2)2x y ++-=截得的弦长为( ) AB.C.D.【答案】B【解析】圆22(2)(2)2x y ++-=的圆心()2,2-到直线40x y -+=的距离为:0d ==.即圆心过直线40x y -+=直线被圆22(2)(2)2x y ++-=截得的弦长等于圆的直径:.故选:B . 2.(2021·浙江高二期末)已知过点()1,3P 的直线l 被圆()2224x y -+=截得的弦长为l 的方程是( ) A .43130x y +-= B .34150x y +-=C .34150x y +-=或1x =D .43130x y +-=或1x =【答案】D【解析】圆()2224x y -+=的圆心为点()2,0,半径为2r,圆心到直线l 的距离为1d ==.①若直线l 的斜率不存在,则直线l 的方程为1x =,此时圆心到直线l 的距离为1,合乎题意; ②若直线l 的斜率存在,可设直线l 的方程为()31y k x -=-,即30kx y k -+-=, 圆心到直线l的距离为1d ===,解得43k =-.此时直线l 的方程为43130x y +-=.综上所述,直线l 的方程为43130x y +-=或1x =. 故选:D.3.(2021·贵溪市实验中学高二期末)直线y kx =被圆222x y +=截得的弦长为( )A .B .2C D .与k 的取值有关【答案】A【解析】由于圆222x y +=的圆心在直线y kx =上,所以截得弦为圆222x y +=,故截得的弦长为故选:A4.(2021·天水市第一中学高二期中)已知直线0x ay a +-=和圆220x y x +-=的交点为A ,B ,且1AB =,则实数a 的值为( ) A .2 B .1C .12D .1-【答案】C【解析】由220x y x +-=得2211()24x y -+=,即圆心1(,0)2,半径12r =,因为12AB r ==,所以直线0x ay a +-=过圆心,即102a -=,解得12a =,故选:C5.(2021·全国高二课时练习)若P (2,-1)为圆(x -1)2+y 2=25的弦AB 的中点,则直线AB 的方程是( ) A .x -y -3=0 B .2x +y -3=0 C .x +y -1=0 D .2x -y -5=0【答案】A【解析】圆(x -1)2+y 2=25的圆心为M (1,0). 因为直线MP 与AB 垂直,所以k AB =-1MPk =-10(1)12---=1.又因为直线AB 过点P (2,-1),所以直线AB 方程为y +1=x -2,即x -y -3=0.故选:A6.(2021·辽宁辽阳市·高二期末)已知圆22:4850C x y x y +-+-=,直线:20l mx y m --=. (1)证明:直线l 与圆C 相交.(2)设l 与圆C 交于,M N 两点,若MN =,求直线l 的倾斜角及其方程. 【答案】(1)证明见解析;(2)答案见解析.【解析】(1)证明:直线:2()0l m x y --=过定点()2,0,因为224250-⨯-<,所以点()2,0在圆C 的内部,故直线l 与圆C 相交. (2)圆C 的标准方程为()2225()42x y -++=,则圆C 的圆心坐标为4(2,)C -,半径为5,且圆心C 到直线l 的距离d ==因为MN==d ==,得3m =±当3m=时﹐直线l 的方程为)2y x =-,倾斜角为6π当m =l 的方程为)23y x =--,倾斜角为56π 考点三 圆上的点到直线距离【例3】(1)(2021·福建三明市·高二期末)圆()2222x y -+=上动点到直线20x y ++=的距离的最小值为( ) AB .C.D .(2)(2021·四川巴中市·(文))圆22(1)(1)4xy ++-=上到直线:0l x y ++=的距离为1的点共有( ) A .1个B .2个C .3个D .4个【答案】(1)A (2)C【解析】(1)∵圆()2222x y -+=,∴圆心()2,0,半径r =∴圆心到直线的距离d ==,∴圆()2222x y -+=上的点到 直线20xy ++=的距离最小值为=,故选:A.(2)由题知,圆心(1,1)-到直线:0l x y ++=12=<,则直线l 与圆相交,由圆的半径为2知,圆上到直线的距离为1的点有3个.故选:C 【一隅三反】1.(2021·六安市裕安区新安中学)已知半径为2的圆经过点(1,0),其圆心到直线34120x y -+=的距离的最小值为( ) A .0 B .1 C .2 D .3【答案】B【解析】半径为2的圆经过点(1,0),设圆心坐标为(,)a b ,则圆的方程为22(1)(0)4a b -+-=所以该圆的圆心的轨迹是以(1,0)为圆心,2为半径的圆故圆心到直线34120x y -+=的距离的最小值为点(1,0)152215=-=故选:B2.(2021·全国高二课时练习)已知点M 是直线3420x y +-=上的动点,点N 为圆22(1)(1)1x y +++=上的动点,则||MN 的最小值为 A .45B .1C .95D .135【答案】A【解析】MN 的最小值为3424155N l d r -----=-=,选A. 3.(2021·全国高二专题练习)在圆()2224x y -+=上有且仅有两个点到直线340x y a ++=的距离为1,则a 的取值范围为__________. 【答案】()()21,111,9---【解析】由圆的方程知其圆心为()2,0,半径2r,设圆心到直线340x y a ++=的距离为d ,则65ad +=; 圆上有且仅有两个点到直线340x y a ++=的距离为1,则12rd r <<+, 即6135a+<<,解得:2111a -<<-或19a -<<, a ∴的取值范围为()()21,111,9---.故答案为:()()21,111,9---.考点四 圆与圆的位置关系【例4】(1)(2021·浙江高二期末)圆221:(1)1C x y -+=与圆222:(4)(4)17C x y -+-=的位置关系为( ) A .内切B .相切C .相交D .外离(2)(2021·北京高二期末)已知圆1O 的方程为22()()4x a y b -+-=,圆2O 的方程为22(1)1x y b +-+=,其中,a b ∈R .那么这两个圆的位置关系不可能为( ) A .外离B .外切C .内含D .内切【答案】(1)C (2)C【解析】圆()221:11C x y -+=的圆心为1(1,0)C ,半径11r =,圆()()222:4417C x y -+-=的圆心为2(4,4)C ,半径2r =所以211212151r r C C r r -=<==<+= C (2)由两圆的标准方程可得()1,O a b ,12r =,()20,1O b -,21r =;则12121O O r r =≥=-,所以两圆不可能内含.故选:C.【一隅三反】1.(2021·全国高二专题练习)圆2220x y x +-=与圆22(1)(2)9x y -++=的位置关系为( ) A .内切 B .相交 C .外切 D .相离【答案】A【解析】圆221:20C x y x +-=,即22(1)1x y -+=,表示以1(1,0)C 为圆心,半径等于1的圆.圆222:(1)(2)9C x y -++=,表示以2(1,2)C -为圆心,半径等于3的圆.∴两圆的圆心距|20|2d =--=,231=-,故两个圆相内切.故选:A.2.(2021·江西上高二中高二其他模拟(文))已知圆()221:210C x y x my m R +-++=∈关于直线210x y ++=对称,圆2C 的标准方程是()()222316x y ++-=,则圆1C 与圆2C 的位置关系是( )A .相离B .相切C .相交D .内含【答案】B【解析】22210x y x my +-++=即222124mm x y ,圆心1,2m ⎛⎫- ⎪⎝⎭,因为圆1C 关于直线210x y ++=对称,所以圆心1,2m ⎛⎫-⎪⎝⎭在直线210x y ++=上, 即12102m ⎛⎫+⨯-+= ⎪⎝⎭,解得2m =,()()22111x y -++=,圆心()1,1-,半径为1, ()()222316x y ++-=,圆心()2,3-,半径为4,5,因为圆心间距离等于两圆半径之和,所以圆1C 与圆2C 的位置关系是相切, 故选:B.3.(2021·全国高二(文))已知圆1C 的标准方程是()()224425x y -+-=,圆2C :22430x y x my +-++=关于直线10x ++=对称,则圆1C 与圆2C 的位置关系为( )A .相离B .相切C .相交D .内含【答案】C【解析】由题意可得,圆()()221:4425C x y -+-=的圆心为()4,4,半径为5因为圆222:430C x y x my +-++=关于直线10x ++=对称,所以2102m-+=(),得m =所以圆()(222:24C x y -+=的圆心为(2,,半径为2,则两圆圆心距12C C =因为1252725C C -<<<=+,所以圆1C 与圆2C 的位置关系是相交, 故选:C .4.(2021·四川凉山彝族自治州·高二期末(文))已知圆221:1C x y +=和圆()()2222:20C x y r r +-=>,若圆1C 和2C 有公共点,则r 的取值范围是( ) A .(]0,1 B .(]0,3C .[]1,3D .[)1,+∞【答案】C【解析】由题意可知,圆1C 的圆心为()10,0C ,半径为1,圆2C 的圆心为()20,2C ,半径为r ,所以,122C C =,由于两圆有公共点,则1211r C C r -≤≤+,即1210r r r ⎧-≤≤+⎨>⎩,解得13r ≤≤.故选:C.5.(2021·山东聊城市·高二期末)已知圆()()()221:80C x a y a a -+-=>与圆222:220C x y x y +--=没有公共点,则实数a 的取值范围为( ) A .()0,2 B .()4,+∞C .()()0,24,+∞D .()()()0,10,24,⋃⋃+∞【答案】C【解析】圆1C 的圆心为()11,,C a a r =,圆2C 的圆心为()21,1C ,半径2r =圆心距12|1|d C C a ===-因为两圆没有公共点,所以两圆的位置关系为外离或者内含则12d r r >+或12d r r <-1|a ->1|a -<02a <<或4a >故选:C考点五 圆与圆相交弦【例5】(1)(2021·湖南湘潭市)已知圆221:40C x y +-=与圆222:44120C x y x y +-+-=相交于,A B两点,则两圆的公共弦AB =A .B .CD .2(2)(2021·天津市南仓中学高二期末)已知圆221:4C x y +=和圆()222:2600C x y ay a ++-=>的公共弦长为2,则实数a 的值为( )A BC .2D【答案】(1)A (2)A【解析】(1)圆221:40C x y +-=与圆222:44120C x y x y +-+-=相减得AB 所在的直线方程:20x y -+=.∵圆221:40C x y +-=的圆心()10,0C ,2r ,∴圆心()0,0到直线AB :20x y -+=的距离d ==,则AB===.故选A(2)圆221:4C x y +=的圆心()10,0C ,半径12r =,圆222:260C x y ay ++-=即()2226x y a a ++=+,圆心()20,C a -,半径226r a ,圆1C 和圆2C 的公共弦方程为()2222264x y x y ay +-++-=,即1y a=, 圆心()10,0C 到1y a=的距离为1a ,因为公共弦长为2,所以222121a,解得3a=或3-,故选:A. 【一隅三反】1.(2021·辽宁高三其他模拟)圆O :229x y +=与圆1O :()()222316x y -+-=交于A 、B 两点,则AB =( )A .6B .5C .13D .13【答案】D【解析】圆O 的半径3r =,圆1O 的半径14r =,1OO = 故在1AOO中,22211111cos sin 2r OO r AOO AOO r OO +-∠===⇒∠=⋅,故1sin 2AB r AOO AB =∠=⇒=. 故选:D2.(2021·山东济南市·高二期末)(多选)已知圆221:1C x y +=和圆222:40C x y x +-=的公共点为A ,B ,则( )A .12||2C C =B .直线AB 的方程是14x =C .12AC AC ⊥D .||2AB =【答案】ABD【解析】圆1C 的圆心是()0,0,半径11r =,圆()222:24C x y -+=,圆心()2,0,22r =,122C C ∴=,故A 正确;两圆相减就是直线AB 的方程,两圆相减得1414x x =⇒=,故B 正确; 11AC =,22AC =,122C C =,2221212AC AC C C +≠,所以12AC AC ⊥不正确,故C 不正确;圆心()0,0到直线14x =的距离14d =,2AB ===,故D 正确. 故选:ABD3.(2021·全国高二课时练习)(多选)圆221:20x y x O +-=和圆222:240O x y x y ++-=的交点为A ,B ,则有( )A .公共弦AB 所在直线方程为0x y -= B .线段AB 中垂线方程为10x y +-=C .公共弦ABD .P 为圆1O 上一动点,则P 到直线AB 距离的最大值为12+【答案】ABD【解析】对于A ,由圆221:20x y x O +-=与圆222:240O x y x y ++-=的交点为A ,B ,两式作差可得440x y -=,即公共弦AB 所在直线方程为0x y -=,故A 正确;对于B ,圆221:20x y x O +-=的圆心为()1,0,1AB k =,则线段AB 中垂线斜率为1-,即线段AB 中垂线方程为:()011y x -=-⨯-,整理可得10x y +-=,故B 正确;对于C ,圆221:20x y x O +-=,圆心1O ()1,0到0x y -=的距离为d ==1r =所以AB ==,故C 不正确; 对于D ,P 为圆1O 上一动点,圆心1O ()1,0到0x y-=的距离为2d =,半径1r =,即P到直线AB 1+,故D 正确.故选:ABD考点六 切线及切线长【例6-1】(2021·浙江高二单元测试)由直线1y x =+上的点向圆()2231x y -+=作切线,则切线长的最小值为( ) A.1 BC .D .3【答案】B【解析】切线长的最小值是当直线1y x =+上的点与圆心距离最小时取得,圆心(3,0)到直线的距离为d =圆的半径为1==B .【例6-2】(1)(2021·全国)经过点M 的圆2210x y +=的切线方程是( )A .100x -= B 2100y -+= C .100x -+=D .2100x +-=(2)(2021·重庆字水中学高二期末)(多选)过点(2,0)作圆222690x y x y +--+=的切线l ,则直线l 的方程为( )A .3460x y +-=B .4380x y +-=C .20x -=D .20x +=(3)(2021·全国)过点(2,2)-作圆224x y +=的切线,若切点为A 、B ,则直线AB 的方程是( ) A .20x y ++=B .20x y -+=C .20x y +-=D .20x y --=【答案】(1)D (2)BC (3)B【解析】(1)222(6)10+=,M ∴在圆上,且2OM k =,∴过M 的切线斜率为1OMk -=∴过M 的切线方程为:2)y x =-,即2100x +-=.选:D .(2)22222690(1)(3)1x y x y x y +--+=∴-+-=圆心(1,3)到直线2x =距离等于1,所以直线l 的方程可以为2x = 当直线l 的斜率存在时,设:(2)l y k x =-441:(2)438033k l y x x y =∴=-∴=--∴+-=故选:BC(3)根据题意,设(2,2)P -,圆224x y +=的圆心为(0,0)O ,半径2r ,有||OP ==则2222||||||4PA PB OP r ==-=,则以P 为圆心,||PA 为半径为圆为22(2)(2)4x y ++-=,即224440x y x y ++-+=, 公共弦所在的直线即直线AB ,则222244440x y x y x y ⎧+=⎨++-+=⎩,变形可得20x y -+=; 即直线AB 的方程是20x y -+=;故选:B.【例6-3】(2021·四川眉山市·高二期末(文))圆221:1C x y +=与圆222:870C x y y +-+=公切线的条数为( ) A .0 B .1 C .2 D .3【答案】D【解析】221:1C x y +=的圆心坐标1(0,0)C ,半径为11r =;222:870C x y y +-+=化为标准方程为()222:49C x y +-=,所以圆心坐标2(0,4)C ,半径为23r =,则12124C C r r ==+,所以两个圆外切,所以公切线条数为3条.故选:D.【例6-4】(2021·全国高二课时练习)已知P (x ,y )是直线kx +y +3=0(k >0)上一动点,PA ,PB 是圆C :2x +2y -2y =0的两条切线,.A 、B 是切点,若四边形PACB k 的值为( )A BC .D .【答案】A【解析】圆22:20C x y y +-=的圆心(0,1),半径是1r =,由圆的性质知:2PBC PACB S S ∆=四边形,四边形PACBPBC S ∆∴的最小值1(2rd d =是切线长)d ∴=最小值所以|PC|2=,所以20,k k k ∴=>∴=故选:A .【一隅三反】1.(2021·全国高二课时练习)P 是直线x +y -2=0上的一动点,过点P 向圆22:(2)(8)4C x y ++-=引切线,则切线长的最小值为( )A .B .C .2D .2【答案】C【解析】∵圆22:(2)(8)4C x y ++-=,∴圆心(2,8)C -,半径2r .由题意可知,点P 到圆22:(2)(8)4C x y ++-=的切线长最小时,CP 垂直于直线20x y +-=.∵圆心到直线的距离d ==2=.故选:C.2.(2021·西安市铁一中学高二期末(理))由直线2y x =+上的点向圆22(4)(2)1x y -++=引切线,则切线长的最小值为A B C .D 【答案】B【解析】圆心(4,2)A -,半径1r = ,圆心到直线的距离d ==则切线长的最小值=3.(2021·安徽马鞍山市·马鞍山二中高二期末(文))若从坐标原点O 向圆22:12270C x y x +-+=作两条切线,切点分别为A ,B ,则线段AB 的长为( )A .32B .3CD .【答案】D【解析】圆C 标准方程是22(6)9x y -+=,圆心为(6,0)C ,半径为3r =,所以,A B 关于OC 对称,即关于x 轴对称,而OA CA ⊥,6,3OC CA ==,所以OA =,所以2AB ==.故选:D . 4.(2021·重庆市南坪中学校高二月考)过坐标原点O 作圆(x ﹣2)2+(y ﹣3)2=4的两条切线,切点为A ,B .直线AB 被圆截得弦AB 的长度为( )A B C .13D .13【答案】B【解析】如图所示,易得OC =故213OB BC AB OC ⋅===.故选:B5.(2021·浙江高二期末)过点()2,1作圆224x y +=的切线,切线的方程为( ) A .34100x y +-=B .3420x y --=C .2x =或3420x y --=D .2x =或34100x y +-=【答案】D 【解析】圆224x y +=的圆心为()0,0,半径2r ,过点()2,1作圆224x y +=的切线,当直线的斜率不存在时,直线方程为2x =,满足条件,当直线的斜率存在时,设斜率为k ,则直线方程为()12y k x -=-,即210kx y k --+=,则2d ==,解得34k =-,故切线方程为34100x y +-=, 综上可得切线方程为34100x y +-=或2x =故选:D6.(2021·全国高二课时练习)经过点()2,1M -作圆225x y +=的切线,则切线的方程为 A .250x y --=B 50y ++=C 5y +=D .250x y ++=【答案】A 【解析】因为点()2,1M -在圆225x y +=上,所以1k 2OM =-,因此切线斜率为2,故切线方程为()y 12x 2+=-,整理得2x y 50.--=7.(2021·安徽池州市·高二期末(理))若圆221:2440C x y x y +---=,圆222:61020C x y x y +---=,则1C ,2C 的公切线条数为( )A .1B .2 C.3 D .4【答案】B【解析】依题意,圆()()221:129C x y -+-=,圆心为()1,2,半径为3; 圆()()222:3536C x y -+-=,圆心为()3,5,半径为6;因为()123,9C C ==,故圆1C ,2C 相交,有2条公切线,故选:B.8.(2021·六安市裕安区新安中学高二开学考试(理))若圆22(1)(3)4x y -+-=与圆22(2)(1)5x y a +++=+有且仅有三条公切线,则a =( ) A .-4B .-1C .4D .11【答案】C 【解析】圆22(1)(3)4x y -+-=的圆心为()1,3,半径为2, 圆22(2)(1)5x y a +++=+的圆心为()2,1--()5a >-,两圆有且仅有三条公切线,∴两圆外切,2=4a =.故选:C. 9.(2021·四川眉山市·仁寿一中高二开学考试(文))已知点(,)P x y 是直线240x y -+=上一动点,直线,PA PB 是圆22:20C x y y ++=的两条切线,,A B 为切点,C 为圆心,则四边形PACB 面积的最小值是( )A .2BC .D .4 【答案】A【解析】圆22:20C x y y ++=即22(y 1)1x ++=,表示以C (0,-1)为圆心,以1为半径的圆. 由于四边形PACB 面积等于122PA ACPA ⨯⨯⨯=,而PA =故当PC 最小时,四边形PACB 面积最小.又PC 的最小值等于圆心C 到直线240x y -+=的距离d ,而d ==故四边形PACB 2=,故选A.考点七 实际生活运用【例7】(2021·上海高二专题练习)如图,某海面上有O 、A 、B 三个小岛(面积大小忽略不计),A 岛在O 岛的北偏东45︒方向距O岛B 岛在O 岛的正东方向距O 岛20千米处.以O 为坐标原点,O 的正东方向为x 轴的正方向,1千米为单位长度,建立平面直角坐标系.圆C 经过O 、A 、B 三点.(1)求圆C 的方程;(2)若圆C 区域内有未知暗礁,现有一船D 在O 岛的南偏西30°方向距O 岛40千米处,正沿着北偏东45︒行驶,若不改变方向,试问该船有没有触礁的危险?【答案】(1)2220600x y x y +--=(2)该船有触礁的危险【解析】(1)如图所示,(40,40)A 、(20,0)B ,设过O 、A 、B 三点的圆C 的方程为220x y Dx Ey F ++++=,得:222040404040020200F D E F D F =⎧⎪++++=⎨⎪++=⎩,解得20D =-,60E =-,0F =,故所以圆C 的方程为2220600x y x y +--=,圆心为(10,30)C,半径r =(2)该船初始位置为点D,则(20,D --,且该船航线所在直线l 的斜率为1,故该船航行方向为直线l:200x y -+-=,由于圆心C 到直线l的距离d ==<,故该船有触礁的危险.【一隅三反】1.(2021·重庆巴蜀中学高一期中)如图,某个圆拱桥的水面跨度是20米,拱顶离水面4米;当水面下降1米后,桥在水面的跨度为( )A .B .C .D .【答案】C 【解析】以圆拱桥的顶点为坐标原点,建立如图所示的平面直角坐标系,则圆拱所在圆的圆心位于y 轴负半轴上,设该圆的圆心为()0,a -,0a >,则该圆的方程为()222x y a a ++=,记水面下降前与圆的两交点为A ,B ;记水面下降1米后与圆的两交点为C ,D ; 由题意可得,()10,4A --,则()()222104a a -+-+=,解得292a =, 所以圆的方程为222292922x y ⎛⎫⎛⎫++= ⎪ ⎪⎝⎭⎝⎭, 水面位下降1米后,可知C 点纵坐标为5y =-, 所以2222929522x ⎛⎫⎛⎫+-+= ⎪ ⎪⎝⎭⎝⎭,解得2120x =,则此时的桥在水面的跨度为2CD x ===米.故选:C.2.(2021·上海高二专题练习)有一种大型商品,A 、B 两地都有出售,且价格相同,某地居民从两地之一购得商品后运回的费用是:每单位距离,A 地的运费是B 地运费的2倍﹐已知A 、B 两地相距6千米,顾客购物的唯一标准是总费用较低.建立适当的平面直角坐标系(1)求A 、B 两地的售货区域的分界线的方程﹔(2)画出分界线的方程表示的曲线的示意图,并指出在方程的曲线上、曲线内、曲线外的居民如何选择购货地.【答案】(1)()22516x y -+=;(2)答案见解析.【解析】(1)以线段AB 的中点O 为坐标原点,AB 所在直线为x 轴建立如下图所示的平面直角坐标系xOy ,则点()3,0A 、()3,0B -,设每单位距离B 的运费为a 元,设售货区域内一点为(),P x y ,若在两地的购货费用相同,则2=()22516x y -+=, 故在A 、B 两地的售货区域的分界线的方程为()22516x y -+=;(2)由(1)可知,A 、B 两地的售货区域的分界线是以点()5,0为圆心,以4为半径的圆,所以,在圆()22516x y -+=上的居民从A 、B 两地购货的总费用相同.由2>()22516x y -+>, 所以,在圆()22516x y -+=外的居民从B 地购货便宜;由2<()22516x y -+<,所以,在圆()22516x y -+=内的居民从A 地购货便宜.考点八 综合运用【例8】(2021·全国高二课时练习)已知圆C 的圆心坐标为C (3,0),且该圆经过点A (0,4).(1)求圆C 的标准方程;(2)若点B 也在圆C 上,且弦AB 长为8,求直线AB 的方程;(3)直线l 交圆C 于M ,N 两点,若直线AM ,AN 的斜率之积为2,求证:直线l 过一个定点,并求出该定点坐标.(4)直线l 交圆C 于M ,N 两点,若直线AM ,AN 的斜率之和为0,求证:直线l 的斜率是定值,并求出该定值.【答案】(1)(x ﹣3)2+y 2=25;(2)x =0或7x +24y ﹣96=0;(3)证明见解析,(﹣6,﹣12);(4)证明见解析,34-. 【解析】(1)圆以(3,0)为圆心,||5AB =为半径,所以圆的标准方程为()22325x y -+=.(2)①k 不存在时,直线l 的方程为:0x =,||8AB ==,满足题意;②k 存在时,设直线l 的方程为:4y kx =+,3d ==3,724d k ==∴=-, 所以直线l 的方程为:724960x y +-=,综上所述,直线l 的方程为0x =或724960x y +-=.(3)设直线MN :y kx t =+,()11,M x kx t +,()22,N x kx t +,1212442AM AN kx t kx t k k x x +-+-⋅=⋅= ()()()()2212122440k x x k t x x t ⇒-+-++-=①联立方程()()()22222126160325y kx t k x kt x t x y =+⎧⎪⇒++-+-=⎨-+=⎪⎩, 所以()122261kt x x k --+=+,2122161t x x k-=+代入① 得()()()()()()2222216426410k t kt k kt t k --+--++-+=, 化简得26t k =+,所以直线l 的方程为:26t y x t ⎛⎫=++ ⎪⎝⎭,所以过定点()6,12--. (4)设直线AM :y =kx +4,联立方程()()()222241680325y kx k x k x x y =+⎧⎪⇒+--=⎨-+=⎪⎩, 所以M 点的坐标为22268464,11k k k k k ⎛⎫--++ ⎪++⎝⎭, 同理N 点的坐标为22268464,11k k k k k ⎛⎫+--+ ⎪++⎝⎭. 所以34M N MN M N y y k x x -==--, 故直线l 的斜率是定值,且为34-. 【一隅三反】 1.(2021·全国高二课时练习)已知圆()()22:1225C x y -+-=和直线()():211740l m x m y m +++--=.(1)证明:不论 m 为何实数,直线l 都与圆 C 相交于两点;(2)求直线被圆 C 截得的最短弦长并求此时直线l 的方程;(3)已知点(,)P x y 在圆C 上,求22x y +的最大值.【答案】(1)证明见解析(2)250x y --=(3)30+【解析】(1)由()():211740l m x m y m +++--=得(27)40x y m x y +-++-=,由27040x y x y +-=⎧⎨+-=⎩,得31x y =⎧⎨=⎩,即直线l 经过定点(3,1), 因为22(31)(12)25-+-<,所以点(3,1)在圆()()22:1225C x y -+-=内,所以不论 m 为何实数,直线l 都与圆 C 相交于两点.(2)由()()22:1225C x y -+-=可知,圆心(1,2)C ,半径为5,设(3,1)M ,设圆心C 到直线l 的距离为d ,则||d CM≤==,当且仅当CM l ⊥时,圆心C 到直线l 的距离为d 最大,此时直线被圆 C截得的弦长最短,最短弦长为==,因为211132CM k -==--,所以直线l 的斜率为2, 所以直线l 的方程为12(3)y x -=-,即250x y --=.(3)设坐标原点为O ,则||OC =,所以max ||||55OP OC =+=,所以2222||x y OP +==的最大值为25)30=+2(2021·浙江高二单元测试)已知圆22(3)(4)16x y -+-=,直线1:0l kx y k --=,且直线1l 与圆交于不同的两点,P Q ,定点A 的坐标为(1,0).(1)求实数k 的取值范围;(2)若,P Q 两点的中点为M ,直线1l 与直线2:240l x y ++=的交点为N ,求证:||||AM AN ⋅为定值.【答案】(1)4(,)(0,)3-∞-⋃+∞(2)10【解析】(1)因为圆22(3)(4)16x y -+-=与直线1l 与交于不同的两点,4<,即2340k k +>,解得43k <-或0k > (2)由0{240kx y k x y --=++=可得245()2121k k N k k --++, 由220{(3)(4)16kx y k x y --=-+-=可得2222(1)(286)890k x k k x k k +-+++++= 设P Q ,两点横坐标分别为12x x ,,则21222861k k x x k+++=+ 得22224342()11k k k k M k k +++++,所以AM AN ⋅=10== 3.(2021·内蒙古包头市·高二期末(文))已知圆O :228x y +=,()1,2M -是圆O 内一点,()4,0P 是圆O 外一点.(1)AB 是圆O 中过点M 最长的弦,CD 是圆O 中过点M 最短的弦,求四边形ACBD 的面积;(2)过点P 作直线l 交圆于E 、F 两点,求OEF 面积的最大值,并求此时直线l 的方程.【答案】(1);(2)4,)4y x =-. 【解析】(1)过M 最长的弦为直径,最短的弦为垂直于OM 的弦,圆的半径R =OM =所以AB =CD ==所以1122ABCD S AB CD =⨯⨯=⨯=四边形(2)OE OF ==1sin 2OEF S OE OF EOF =⨯⨯⨯∠△, 当90EOF ∠=︒时,OEF 面积的最大值为4,此时,O 到l 的距离为2,4OP =所以l 的倾斜角为30或150︒,则l 的斜率为±l 的方程为)43y x =±-.。
2025高考数学一轮复习-2.3-圆与圆的位置关系【课件】

(1)2 或-5 [C1(m,-2),r1=3,C2(-1,m),r2=2,由题意知 |C1C2|=5,(m+1)2+(m+2)2=25,解得 m=2 或 m=-5.]
(2)[解] 设所求圆的方程为(x-a)2+(y-b)2=16, 由圆与直线 y=0 相切、半径为 4, 则圆心 C 的坐标为 C1(a,4)或 C2(a,-4). 已知圆(x-2)2+(y-1)2=9 的圆心 A 的坐标为(2,1),半径为 3. 由两圆相切,则|CA|=4+3=7 或|CA|=4-3=1.
当| 50-k-1|=5,即 50-k=6,即 k=14 时,两圆内切.当 | 50-k-1|<5<1+ 50-k,
即 14<k<34 时,两圆相交. 当 50-k+1<5, 即 34<k<50 时,两圆外离.
[跟进训练] 1.已知圆 C1:x2+y2-2ax-2y+a2-15=0,圆 C2:x2+y2-4ax -2y+4a2=0(a>0).试求 a 为何值时,两圆 C1,C2 的位置关系为: (1)相切;(2)相交;(3)外离;(4)内含.
为(0,2),半径长 r2=2;1=r2-r1<|O1O2|= 5<r1+r2=3,即两圆相
交.]
3.已知两圆 x2+y2=10 和(x-1)2+(y-3)2=10 相交于 A,B 两点,则直线 AB 的方程是________.
x+3y-5=0 [由两圆方程消去二次项得 10-2x+1-6y+9= 10,
(4)若两圆有公共点,则|r1-r2|≤d≤r1+r2.
() ()
[答案] (1)× (2)× (3)× (4)√
系为(
2.圆 O1:x2+y2-2x=0 和圆 O2:x2+y2-4y=0 的位置关 )
A.相离
高考数学总复习(一轮)(人教A)教学课件第八章 平面解析几何第4节 直线与圆、圆与圆的位置关系

2
圆 C1:x +y
+D1x+E1y+F1=0( + -4F1>0)与
2
2
C2:x +y +D2x+E2y+F2=0
( + -4F2>0)相交时:
(1)将两圆方程直接作差,消去x2,y2得到两圆公共弦所在直线方程;
(2)两圆圆心的连线垂直平分公共弦;
(3)x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0(λ∈R)表示过两圆
3
相交
|r1-r2|<d<r1+r2
2
内切
d=|r1-r2|
1
内含
d<|r1-r2|
0
1.圆的切线方程常用结论
(1) 过 圆 x2+y2=r2(r>0) 上 一 点 P(x0,y0) 的 圆 的 切 线 方 程 为
x0x+y0y=r2.
(2)过圆x2+y2=r2外一点M(x0,y0)作圆的两条切线,则两切点所在直
C2:x2+y2-10x-12y+45=0.
(1)求证:圆C1和圆C2相交;
2
2
(1)证明:因为 C1:(x-1) +(y-3) =11,
圆心 C1(1,3),半径 r1= ;
2
2
C2:(x-5) +(y-6) =16,
圆心 C2(5,6),半径 r2=4.
所以|C1C2|= (-) + (-) =5,
圆C:x2+y2=r2,点A(a,b),则下列说法正确的是(
2021届山东高考数学一轮创新:第8章 第4讲 直线与圆、圆与圆的位置关系

d=|2+2×1+-41-3|=355,所以弦长为 2 r2-d2=2
22-3
5
52=
2 55 5.
解析
2
PART TWO
经典题型冲关
题型一 直线与圆的位置关系的判断
1.直线 kx-y+2-k=0 与圆 x2+y2-2x-8=0 的位置关系为( )
A.相交或相切或相离
B.相交或相切
C.相交
D.相切
答案
2.小题热身
(1)直线 x-y+1=0 与圆 x2+y2=1 的位置关系为( )
A.相切
B.相交但直线不过圆心
C.直线过圆心
D.相离
解析
圆心(0,0)到直线
x-y+1=0
的距离
d=
1= 2
22,而
0<
22<1.故
选 B.
解析 答案
(2)已知直线 l:y=k(x+ 3)和圆 C:x2+(y-1)2=1,若直线 l 与圆 C
为 3.
圆心到直线 kx-y+2-k=0 的距离为|k+1+2-k2k|= 1+2 k2<2,所以直线
与圆相交.
解法三:由 kx-y+2-k=0 得 y=kx+2-k,
代入 x2+y2-2x-8=0,得
x2+(kx+2-k)2-2x-8=0,
整理得(1+k2)x2-(2k2-4k+2)x+k2-4k-4=0,
解析 由xx22+ +yy22- -44=x+04,y-12=0, 得 4x-4y+8=0, 即 x-y+2=0.
解析
(4)在平面直角坐标系 xOy 中,直线 x+2y-3=0 被圆___.
解析 圆心为(2,-1),半径 r=2.圆心到直线的距离
直线与圆、圆与圆的位置关系课件-2025届高三数学一轮复习

≤ + ,解得−
≤≤
.
−−
+
=
+
≤ ,即
考点二 直线与圆位置关系的应用
角度1 圆的切线问题(链接高考)
例2 (2023·新课标Ⅰ卷)过点 , − 与圆 + − − = 相切的两条直
(2)过圆 + = 外一点 , 作圆的两条切线,则两切点所在
直线方程为 + = .
2.圆与圆的位置关系的常用结论
(1)两圆相交时,其公共弦所在的直线方程由两圆方程相减得到.
(2)两个圆系方程
①过直线 + + = 与圆 + + + + = 交点的圆系方
(其中不含圆 ,所以注意检验 是否满足题意,以防丢解).
1.若经过点 −, − 的直线与圆 + = 相切,则该直线在轴上的截
距为(
A.
)
√
C.−
B.5
解析:选C.因为 −
+ −
D.−
= ,所以点在圆上,
所以切线方程为− − = ,令 = 得 =
+ − − = 相交.
方法三:圆的方程可化为 −
+ = ,
所以圆的圆心为 , ,半径为3.
圆心到直线 − + − = 的距离为
+−
+
=
+
≤ < ,所以直线与圆相交.故选C.
高考数学一轮总复习课件:圆与圆的位置关系

【解析】 设圆心到直线l:mx+y+3m- 3 =0的距离为d,
则弦长|AB|=2
12-d2 =2
3
,得d=3,即
|3m- 3| m2+1
=3,解得m=
- 33,则直线l:x- 3y+6=0,数形结合可得|CD|=co|sA3B0°| =4.
(3)【多选题】已知直线l与圆C:x2+y2+2x-4y+a=0相交
因为kMN=65- -31=34,所以两圆的公切线的斜率是-43. 设切线方程为y=-43x+b,则有43×143+23+-1b= 11. 解得b=133±5 311. 容易验证,当b=133+5 311时,直线与后一圆相交,舍去. 故所求公切线方程y=-43x+133-5 311, 即4x+3y+5 11-13=0.
状元笔记
在研究弦长及弦中点问题时,可设弦AB两端点的坐标分别 为A(x1,y1),B(x2,y2).
(1)若OA⊥OB(O为原点),则可转化为x1x2+y1y2=0,再结 合根与系数的关系,代入方程简化运算过程,这在解决垂直关 系问题中是常用的.
(2)若弦AB的中点为(x0,y0),圆的方程为x2+y2=r2, xx1222+ +yy1222= =rr22, ,∴k=yx22- -yx11=-xy22+ +xy11=-xy00.
2+P→C·(C→B+C→A)+C→B·C→A=|P→C|2-1=(x-1)2+(x+1)2-1=2x2
+1,所以P→A·P→B的最小值为1,故选D.
授人以渔
题型一 圆与圆的位置关系
例1 已知两圆x2+y2-2x-6y-1=0和x2+y2-10x-12y+ m=0.求:
(1)m取何值时两圆外切? (2)m取何值时两圆内切,此时公切线方程是什么? (3)求m=45时两圆的公共弦所在直线的方程和公共弦的 长.
高三数学圆与圆的位置关系试题答案及解析

高三数学圆与圆的位置关系试题答案及解析1.在平面直角坐标xoy中,设圆M的半径为1,圆心在直线上,若圆M上不存在点N,使,其中A(0,3),则圆心M横坐标的取值范围 .【答案】【解析】设,由得:化简得:,表示为以为圆心,2为半径的圆,由题意得圆B与圆无交点,即或,解得圆心M横坐标的取值范围为:【考点】动点轨迹,圆与圆位置关系2.设m,n∈R,若直线l:mx+ny-1=0与x轴相交于点A,与y轴相交于点B,且l与圆x2+y2=4相交所得弦的长为2,O为坐标原点,则△AOB面积的最小值为________.【答案】3【解析】∵l与圆相交所得弦的长为2,=,∴m2+n2=≥2|mn|,∴|mn|≤.l与x轴交点A(,0),与y轴交点B(0,),∴S=·|△AOB |||=·≥×6=3.3.已知圆和两点,,若圆上存在点,使得,则的最大值为()A.B.C.D.【答案】B【解析】由题意知,点P在以原点(0,0)为圆心,以m为半径的圆上,又因为点P在已知圆上,所以只要两圆有交点即可,所以,故选B.【考点】本小题主要考查两圆的位置关系,考查数形结合思想,考查分析问题与解决问题的能力. 4.已知圆C的方程为,若以直线上任意一点为圆心,以l为半径的圆与圆C没有公共点,则k的整数值是()A.l B.0C.1D.2【答案】【解析】由题意知,直线过定点,圆与圆相离.圆心到直线大于,所以,,解得,故的整数值为,选.【考点】圆与圆的位置关系,点到直线的距离公式.5.圆:与圆:的公共弦长等于.【答案】【解析】将的方程化为标准方程得:.将两圆方程相减得公共弦所在直线的方程为:.圆心到弦的距离为,所以弦长.【考点】两圆的位置关系及弦长.6.如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成,两相接点M、N均在直线x=5上.圆弧C1的圆心是坐标原点O,半径为r1=13;圆弧C2过点A(29,0).(1)求圆弧C2所在圆的方程;(2)曲线C上是否存在点P,满足PA=PO?若存在,指出有几个这样的点;若不存在,请说明理由;(3)已知直线l:x-my-14=0与曲线C交于E、F两点,当EF=33时,求坐标原点O到直线l 的距离.【答案】(1)x2+y2-28x-29=0.(2)P不存在(3)【解析】(1)由题意得,圆弧C1所在圆的方程为x2+y2=169.令x=5,解得M(5,12),N(5,-12),又C2过点A(29,0),设圆弧C2所在圆方程为x2+y2+Dx+Ey+F=0,则,解得所以圆弧C2所在圆的方程为x2+y2-28x-29=0.(2)假设存在这样的点P(x,y),则由PA=PO,得(x-29)2+y2=30(x2+y2),即x2+y2+2x-29=0.由解得x=-70(舍去);由解得x=0(舍去).所以这样的点P不存在.(3)因为圆弧C1、C2所在圆的半径分别为r1=13,r2=15,因为EF>2r1,EF>2r2,所以E、F两点分别在两个圆弧上.设点O到直线l的距离为d,因为直线l恒过圆弧C2所在圆的圆心(14,0),所以EF=15+,即=18,解得d2=,所以点O到直线l的距离为.7.已知圆C1:x2+y2-2y=0,圆C2:x2+(y+1)2=4的圆心分别为C1,C2,P为一个动点,且直线PC1,PC2的斜率之积为-.(1)求动点P的轨迹M的方程;(2)是否存在过点A(2,0)的直线l与轨迹M交于不同的两点C,D,使得|C1C|=|C1D|?若存在,求直线l的方程;若不存在,请说明理由.【答案】(1)+y2=1(x≠0)(2)不存在【解析】(1)两圆的圆心坐标分别为C1(0,1),和C2(0,-1),设动点P的坐标为(x,y),则直线PC1,PC2的斜率分别为(x≠0)和 (x≠0).由已知条件得=-(x≠0),即+y2=1(x≠0).所以动点P的轨迹M的方程为+y2=1(x≠0).(2)假设存在满足条件的直线l,易知点A(2,0)在椭圆M的外部,当直线l的斜率不存在时,直线l与椭圆M无交点,此时不符合题意,所以直线l斜率存在,设为k,则直线l的方程为y=k(x-2).联立方程组得(2k2+1)x2-8k2x+8k2-2=0,①依题意Δ=-8(2k2-1)>0,解得-<k<.当-<k<时,设交点分别为C(x1,y1),D(x2,y2),CD的中点为N(x,y),则x1+x2=,则x==,所以y0=k(x-2)=k=.要使|C1C|=|C1D|,必须C1N⊥l,即k·kC1N=-1,所以k·=-1,即k2-k+=0,因为Δ1=1-4×=-1<0,∴k2-k+=0无解,所以不存在直线,使得|C1C|=|C1D|,综上所述,不存在直线l,使得|C1C|=|C1D|.8.若圆x2+y2=4与圆x2+y2+2ax-6=0(a>0)的公共弦的长为2,则a=________.【答案】1【解析】x2+y2+2ax-6=0(a>0)可知圆心为(-a,0),半径为,两圆公共弦所在方程为(x2+y2+2ax-6)-(x2+y2)=-4,即x=,所以有2-2=2解得a=1或-1(舍去).9.设集合,,若存在实数,使得,则实数的取值范围是___________.【答案】【解析】首先集合实际上是圆上的点的集合,即表示两个圆,说明这两个圆相交或相切(有公共点),由于两圆半径都是1,因此两圆圆心距不大于半径这和2,即,整理成关于的不等式:,据题意此不等式有实解,因此其判别式不大于零,即,解得.【考点】两圆位置关系及不等式有解问题.10.若点和点到直线的距离依次为和,则这样的直线有()A.条B.条C.条D.条【答案】C【解析】以点为圆心,以为半径长的圆的方程为,以点为圆心,且以为半径的圆的方程为,则直线为两圆的公切线,,即圆与圆外切,因此两圆的公切线有条,即直线有三条,故选C.【考点】1.两圆的位置关系;2.两圆的公切线11.圆与圆的位置关系为( )A.内切B.相交C.外切 D相离【答案】B【解析】两圆圆心间的距离,两圆半径的差为和为,因为,故两圆相交,选B.【考点】圆与圆的位置关系.12.若直线y=kx与圆-4x+3=0的两个交点关于直线x+y+b=0对称,则()A.k=1,b=-2B.k=1,b=2C.k=-1,b=2D.k=-1,b=-2【答案】A【解析】:若直线与圆的两个交点关于直线对称,则直线与直线垂直,故斜率互为负倒数,可知,而过弦的中点,且与弦垂直的直线必过圆心,而圆心的坐标为,代入直线得,.【考点】直线与圆的位置关系,考查学生数形结合能力.13.两圆和的位置关系是()A.相交B.外切C.内切D.外离【答案】C【解析】圆的圆心为,半径;圆的方程可以变形为,其圆心为,半径.圆心距,所以圆内切于圆.【考点】平面内两圆的位置关系.14.已知圆,直线.(Ⅰ)若与相切,求的值;(Ⅱ)是否存在值,使得与相交于两点,且(其中为坐标原点),若存在,求出,若不存在,请说明理由.【答案】(Ⅰ)(Ⅱ)m=9±2【解析】(Ⅰ)由圆方程配方得(x+1)2+(y-3)2=9,圆心为C(-1,3),半径为 r = 3, 2分若l与C相切,则得=3,∴(3m-4)2=9(1+m2),∴m =. 5分(Ⅱ)假设存在m满足题意。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第50讲:圆与圆的位置关系一、课程标准1、能根据给定圆的方程,判断圆与圆的位置关系2、能用圆与圆的关系方解决一些简单的数学问题与实际问题.二、基础知识回顾圆与圆的位置关系设圆O1:(x-a1)2+(y-b1)2=r21(r1>0),圆O2:(x-a2)2+(y-b2)2=r22(r2>0).方法位置关系几何法:圆心距d与r1,r2的关系代数法:两圆方程联立组成方程组的解的情况外离d>r1+r2无解外切d=r1+r2一组实数解相交|r1-r2|<d<r1+r2两组不同的实数解内切d=|r1-r2|(r1≠r2)一组实数解内含0≤d<|r1-r2|(r1≠r2)无解三、自主热身、归纳总结1、圆C1:x2+y2+2x=0,圆C2:x2+y2+4y=0,则两圆的位置关系是()A. 内含B. 相交C. 外切D. 外离【答案】B【解析】圆C1:(x+1)2+y2=1,圆C2:x2+(y+2)2=22,∴C1C2=5,且2-1<5<2+1,∴两圆相交.故选B.2、圆x2+y2-4=0与圆x2+y2-4x+4y-12=0的公共弦长为()A. 2B. 2 2C. 3D. 23【答案】B【解析】由⎩⎨⎧x 2+y 2-4=0,x 2+y 2-4x +4y -12=0,得x -y +2=0.又圆x 2+y 2=4的圆心到直线x -y +2=0的距离为22= 2.由勾股定理得弦长的一半为4-2=2,∴所求弦长为2 2.故选B . 3、已知圆M :x 2+y 2-2ay =0(a >0)截直线x +y =0所得线段的长度是22,则圆M 与圆N :(x -1)2+(y -1)2=1的位置关系是( )A . 内含B . 相交C . 外切D . 外离 【答案】B 【解析】圆M :x 2+(y -a)2=a 2(a>0),∴⎝ ⎛⎭⎪⎫||a 22+(2)2=a 2,解得a =2,由||2-1<()0-12+()2-12<2+1得两圆相交.故选B .4、知圆C 与圆x 2+y 2+10x +10y =0相切于原点,且过点A(0,-6),则圆C 的标准方程为____.【答案】(x +3)2+(y +3)2=18【解析】 设圆C 方程为(x -a)2+(y -b)2=r 2(r>0),则由题意得⎩⎨⎧a 2+b 2=r 2,()a +52+()b +52=()r±522,a 2+()b +62=r2解之得圆C 方程为(x +3)2+(y +3)2=18.5、半径为6的圆与x 轴相切,且与圆x 2+(y -3)2=1内切,则此圆的方程为_ _ 【答案】(x±4)2+(y -6)2=36.【解析】 由题意知,圆心可设为(a ,6),半径r =6,∴()a -02+()6-32=6-1,∴a =±4,∴所求圆的方程为(x±4)2+(y -6)2=36.6、(河北省石家庄二中2019届期末)已知圆C 1:x 2+y 2-2mx +4y +m 2-5=0与圆C 2:x 2+y 2+2x -2my +m 2-3=0,若圆C 1与圆C 2相外切,则实数m =________. 【答案】2或-5【解析】圆C 1:(x -m )2+(y +2)2=9,圆C 2:(x +1)2+(y -m )2=4,则C 1(m ,-2),r 1=3,C 2(-1,m ),r 2=2.当圆C 1与圆C 2相外切时,显然有|C 1C 2|=r 1+r 2,即m +12+m +22=5,整理得m 2+3m -10=0,解得m =-5或m =2.四、例题选讲考点一、圆与圆的位置关系例1、已知两圆x 2+y 2-2x -6y -1=0和x 2+y 2-10x -12y +m =0.(1)m 取何值时两圆外切? (2)m 取何值时两圆内切?(3)求m =45时两圆的公共弦所在直线的方程和公共弦的长.【解析】 两圆的标准方程为(x -1)2+(y -3)2=11,(x -5)2+(y -6)2=61-m ,圆心分别为M (1,3),N (5,6),半径分别为11和61-m .(1)22(51)(63)-+-=11+61-m ,解得m =25+1011. (2)当两圆内切时,因定圆的半径11小于两圆圆心距5,故只有61-m -11=5,解得m =25-1011.(3)当m =45时,4-11<|MN |=5<11+4,两圆相交,其两圆的公共弦所在直线方程为(x 2+y 2-2x -6y -1)-(x 2+y 2-10x -12y +45)=0,即4x +3y -23=0.所以公共弦长为2224133232112743⎛⎫⨯+⨯--= ⎪+⎝⎭变式1、分别求当实数k 为何值时,两圆C 1:x 2+y 2+4x -6y +12=0,C 2:x 2+y 2-2x -14y +k =0相交和相切.【解析】 将两圆的一般方程化为标准方程,得C 1:(x +2)2+(y -3)2=1,C 2:(x -1)2+(y -7)2=50-k ,则圆C 1的圆心为C 1(-2,3),半径r 1=1;圆C 2的圆心为C 2(1,7),半径r 2=50-k ,k<50.从而|C 1C 2|=(-2-1)2+(3-7)2=5. 当|50-k -1|<5<50-k +1,即4<50-k<6,即14<k<34时,两圆相交.当1+50-k =5,即k =34时,两圆外切; 当|50-k -1|=5,即k =14时,两圆内切. ∴当k =14或k =34时,两圆相切.方法总结:(1)判断两圆的位置关系多用几何法,即用两圆圆心距与半径和或差的关系判断,一般不采用代数法.(2)求两圆公共弦长的方法是在其中一圆中,由弦心距d ,半弦长l2,半径r 所在线段构成直角三角形,利用勾股定理求解.若两圆相交,则两圆公共弦所在直线的方程可由两圆的方程作差得到.考点二 圆与圆的综合问题例2、已知圆C 1:(x -a)2+(y +2)2=4与圆C 2:(x +b)2+(y +2)2=1相外切,则ab 的最大值为________.【答案】 94【解析】 由圆C 1与圆C 2相外切,可得(a +b )2+(-2+2)2=2+1=3, 即(a +b)2=9,根据基本不等式可知ab≤⎝⎛⎭⎫a +b 22=94,当且仅当a =b 时等号成立.故ab的最大值为94.变式1、已知圆C 1:(x -a)2+(y +2)2=4与圆C 2:(x +b)2+(y +2)2=1相内切, 则 a 2+b 2的最小值为__________.【答案】 12【解析】 由圆C 1与圆C 2内切,得(a +b )2+(-2+2)2=1,即(a +b)2=1.又由基本不等式a 2+b 22≥⎝⎛⎭⎫a +b 22,可知a 2+b 2≥(a +b )22=12,当且仅当a=b 时等号成立,故a 2+b 2的最小值为12.变式2、已知圆C 1:(x -a)2+(y +2)2=4与圆C 2:(x +b)2+(y +2)2=1相交”,则公共弦所在的直线方程为______________________. 【答案】 (2a +2b)x +3+b 2-a 2=0【解析】 由题意将圆C 1,圆C 2的方程都化为一般方程,得圆C 1:x 2+y 2-2ax +4y +a 2=0①,圆C 2:x 2+y 2+2bx +4y +b 2+3=0②, 由②-①得(2a +2b)x +3+b 2-a 2=0,即所求公共弦所在直线方程为(2a +2b)x +3+b 2-a 2=0.变式3、已知圆C 1:x 2+y 2+4ax +4a 2-4=0和圆C 2:x 2+y 2-2by +b 2-1=0只有一条公切线,若a ,b ∈R 且ab ≠0,则1a 2+1b2的最小值为( )A. 3B. 8C. 4D. 9 【答案】D【解析】 由题设中可知两圆相内切,其中C 1(-2a ,0),r 1=2;C 2(0,b ),r 2=1,故|C 1C 2|=a 2+4b 2,由题设可知a 2+4b 2=2-1,即a 2+4b 2=1,则1a 2+1b 2=⎝⎛⎭⎫1a 2+1b 2(a 2+4b 2)=5+4b 2a 2+a 2b 2≥5+4=9.当且仅当a 2=2b 2时等号成立.故选D.变式4、 已知A ,B 是圆C 1:x 2+y 2=1上的动点,AB =3,P 是圆C 2:(x -3)2+(y -4)2=1上的动点,则|PA →+PB →|的取值范围为____. 【答案】[]7,13【解析】 设AB 的中点为E ,则其轨迹为x 2+y 2=14,|PA →+PB →|=2||PE →,由||PE →∈⎣⎡⎦⎤72,132,∴|PA →+PB →|∈[]7,13.变式5、 求圆心在直线x +y =0上,且过两圆x 2+y 2-2x +10y -24=0,x 2+y 2+2x +2y -8=0交点的圆的方程.【解析】 (方法1)(利用圆心到两交点的距离相等求圆心)将两圆的方程联立得方程组⎩⎨⎧x 2+y 2-2x +10y -24=0,x 2+y 2+2x +2y -8=0,解这个方程组求得两圆的交点坐标A(-4,0),B(0,2). 因所求圆心在直线x +y =0上,故设所求圆心坐标为(x ,-x),则它到上面的两上交点(-4,0)和(0,2)的距离相等,故有()-4-x 2+()0+x 2=x 2+()2+x 2,即4x =-12,∴x =-3,y =-x =3,从而圆心坐标是(-3,3).又r =()-4+32+32=10,故所求圆的方程为(x +3)2+(y -3)2=10.(方法2)(利用弦的垂直平分线过圆心求圆的方程)同方法1求得两交点坐标A(-4,0),B(0,2),弦AB 的垂直平分线方程为2x +y +3=0,它与直线x +y =0交点(-3,3)就是圆心,又半径r =10,故所求圆的方程为(x +3)2+(y -3)2=10.(方法3)(用待定系数法求圆的方程)同方法1求得两交点坐标为A(-4,0),B(0,2).设所求圆的方程为(x -a)2+(y -b)2=r 2,∵两点在此圆上,且圆心在x +y =0上,∴得方程组⎩⎨⎧()-4-a 2+b 2=r 2,a 2+()3-b 2=r 2,a +b =0,解之得⎩⎨⎧a =-3,b =3,r =10,故所求圆的方程为(x +3)2+(y -3)2=10.(方法4)设所求圆的方程为x 2+y 2-2x +10y -24+λ(x 2+y 2+2x +2y -8)=0(λ≠-1), 即x 2+y 2-2()1-λ1+λx +2()5+λ1+λy -8()3+λ1+λ=0.可知圆心坐标为(1-λ1+λ,-5+λ1+λ). ∵圆心在直线x +y =0上,∴1-λ1+λ-5+λ1+λ=0,解得λ=-2.将λ=-2代入所设方程并化简,求圆的方程为x 2+y 2+6x -6y +8=0.方法总结:圆与圆的综合题目涉及到参数的问题,解题思路就是通过圆与圆的位置关系,寻求参数之间的关系,然后转化为函数的思想进行解决。
