北师大版数学一次函数考点归纳及例题详解
八年级数学上册 一次函数要点讲解 北师大版
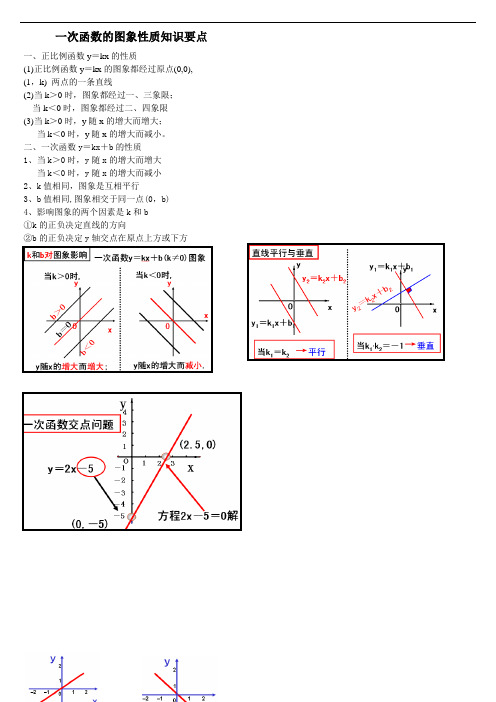
一次函数的图象性质知识要点一、正比例函数y=kx的性质(1)正比例函数y=kx的图象都经过原点(0,0), (1,k) 两点的一条直线(2)当k>0时,图象都经过一、三象限;当k<0时,图象都经过二、四象限(3)当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小。
二、一次函数y=kx+b的性质1、当k>0时,y随x的增大而增大当k<0时,y随x的增大而减小2、k值相同,图象是互相平行3、b值相同,图象相交于同一点(0,b)4、影响图象的两个因素是k和b①k的正负决定直线的方向②b的正负决定y轴交点在原点上方或下方“一次函数的应用”专题复习教学目标:1.通过本课学习使学生能够熟练地求出实际问题中一次函数的解析式;2.结合实际问题的讲练,培养学生收集、选择、处理数学信息,并作出合理的推断或大胆的猜测的能力。
教学过程:一、练习1.汽车由南京驶往相距300千米的上海,当它的平均速度是100千米/时,下面哪个图形表示汽车距上海的路程s(千米)与行驶时间t(小时)的函数关系?()42升,行驶若干小时后,途中在加油站加油若干升。
油箱Q(升)与行驶时间t(时)之间的函数关系如图所示,根据下图回答问题:(1)机动车行驶小时后加油;(2)中途加油升;说明:通过这两题的教学,使学生初步知道识图的一般步骤:(1)观察图象,捕捉有效信息;(2)对已获信息进行加工,分清变量之间的关系;(3)选择适当的数学工具,通过建模来加以解决。
二、例题解析例1.某气象研究中心观测一场沙尘暴从发生到结束全过程,开始时风暴平均每小时增加2千米/时,4小时后,沙尘暴经过开阔荒漠地,风速变为平均每小时增加4千米/时,一段时间,风暴保持不变,当沙尘暴遇到绿色植被区时,其风速平均每小时减小1千米/时,最终停止. 结合风速与时间的图像,回答下列问题:(1)在y轴()内填入相应的数值;(2)沙尘暴从发生到结束,共经过多少小时?(3)求出当x≥25时,风速y(千米/时)与时间x(小时)之间的函数关系式.(4)若风速达到或超过20千米/时,称为强沙尘暴,则强沙尘暴持续多长时间?说明:(1)从图象中可得到如下信息:沙尘暴分四个阶段:0∽4小时,风暴平均每小时增加2千米/时;4∽10小时,风速平均每小时增加4千米/时;10∽25小时,风暴速度保持不变;25小时后风暴速度平均每小时减小1千米/时,最终停止;(2)对于第(3)题引导学生观察图象得出当x≥25时,风速y(千米/时)是时间x(小时)的一次函数;(()(3)第(4)题进一步培养学生应用数学知识实际问题的能力。
北师大版初二数学上册一次函数知识点总结与基础例题

的• •一次函数一.知识回顾(一)函数1、变量:在一个变化过程中可以取不同数值的量。
常量:在一个变化过程中只能取同一数值的量。
2、函数:一般的,在一个变化过程中,如果有两个变量 x 和 y ,并且对于 x 的每一个确定的值,y 都有唯一确定的值与其对应,那么我们就把 x 称为自变量,把 y 称为因变量,y 是 x 的函数。
* 判断 Y 是否为 X 的函数,只要看 X 取值确定的时候,Y 是否有唯一确定的值与之对应3、定义域:一般的,一个函数的自变量允许取值的范围,叫做这个函数的定义域。
4、确定函数定义域的方法:(1)关系式为整式时,函数定义域为全体实数; (2)关系式含有分式时,分式的分母不等于零;(3)关系式含有二次根式时,被开放方数大于等于零; (4)关系式中含有指数为零的式子时,底数不等于零;(5)实际问题中,函数定义域还要和实际情况相符合,使之有意义。
5、函数的解读式:用含有表示自变量的字母的代数式表示因变量的式子叫做函数的解读式6、函数的图像一般来说,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面 内由这些点组成的图形,就是这个函数的图象.7、描点法画函数图形的一般步骤第一步:列表(表中给出一些自变量的值及其对应的函数值);第二步:描点(在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中数值对 应的各点);第三步:连线(按照横坐标由小到大的顺序把所描出的各点用平滑曲线连接起来)。
8、函数的表示方法列表法:一目了然,使用起来方便,但列出的对应值是有限的,不易看出自变量与函数之间的对应规律。
解读式法:简单明了,能够准确地反映整个变化过程中自变量与函数之间的相依关系,但有些实际问题 中的函数关系,不能用解读式表示。
图象法:形象直观,但只能近似地表达两个变量之间的函数关系。
(二)一次函数1、一次函数的定义一般地,形如 y = kx + b ( k ,b 是常数,且k ≠ 0 )的函数,叫做一次函数,其中x 是自变量。
北师大版数学八上一次函数的知识点及例题(精华)

【函数与变量】在一个变化过程中,我们称数值发生变化的量为变量,有些量的数值是始终不变的,我们称它为常量,如圆的面积2S r π=,S 与r 是变量,π是常量注意:在某一变化过程中,变量、常量都可能有多个。
常量可以是一个实数,也可以是一个代数式(数值始终保持不变) 【函数的概念】一般地,设在一个变化过程中有两个变量x 和y ,并且对于x 在它允许取值范围内的每一个值,y 都有唯一的值与它对应,那么就说x 是自变量,y 是x 的函数。
(实际上,函数说的就是y 是怎么样随着x 的变化而变化的,也可以管y 叫x 的变化规律)对函数概念的理解: (1)有两个变量(2)一个变量的数值随着另一个变量的变化而变化(3)自变量每确定一个值,函数有一个并且只有一个值与之对应(或多个x 的值可以对应一个y 值但不能一个x 值对应多个y 值,如y=x 2和x 2=y )(4) 我们习惯上设y 为函数,但不表示其它字母不可以作为函数,如s=vt x=6y (5)我们在写函数的时候把函数写在等号的左边,把自变量写在等号的右边例:y=2x-1 例:下列变量之间的关系不是函数关系的是( B )A 、长方形的宽一定,其长与面积B 、正方形的周长与面积C 、等腰三角形的底边与面积D 、球的体积与球的半径 【函数的表示方法】(1)列表法:通过列出自变量的值与对应函数值的表格来表示函数关系的方法叫列表法。
优点:能明显地呈现出自变量与对应的函数值缺点:只能列出部分自变量与函数的对应值,难以从表格中看出自变量与函数之间的对应规律 (2)解析法:用数学式子表示函数的方法叫解析法。
优点:简明扼要,规范准确,便于分析推导函数的性质 缺点:有些函数关系,不能用解析式表示(3)图像法:对于一个函数,把自变量与函数的每组对应值作为点的横纵坐标在直角坐标系中画出来 ,由这些点组成的图形叫这个的图像优点:形象直观,能清晰呈现函数的一些性质缺点:所画的图像是近似的,局部的,从图像上观察的结果也是近似的 【函数图像的意义】一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横坐标与纵坐标,那么坐标平面内由这些点组成的图形就是函数的图像。
北师大版数学一次函数考点归纳及例题详解

北师大版数学一次函数考点归纳及例题详解【考点归纳】考点1: 一次困数的概念.相关知识:一次函数是形如旷=心+〃〔&、.为常数,且攵工0〕的函数,特别的当.=0时函数为y = kx〔k w 0〕,叫正比例函数.【例题】】•以下函数中,y是x的正比例函数的是〔〕A. y=2x-lB. y=-C. y=2x2D. y=2x+l32 .自变量为x的函数y=mx+2-m是正比例函数,那么m二该函数的解析式为■3 .一次函数y =伏- l〕x囚+3,那么k=.4 .函数y = 〔〃?-2〕/e一〃? + 〃,当m=, n二时为正比例函数;当m=,n 时为一次函数.考点2: 一次函数图象与系数相关知识:一次函数〕,=攵工+以女工0〕的图象是一条直线,图象位置由攵、b确定, 女>0直线要经过一、三象限,攵〈.直线必经过二、四象限,.>.直线与y轴的交点在正半轴上,人<.直线与y轴的交点在负半轴上.【例题】1 .直线y=x-1的图像经过象限是〔〕A.第一、二、三象限B.第一、二、四象限C.第二、三、四象限D.第一、三、四象限2 . 一次函数y=6x+l的图象不经过〔〕A.第一象限B.第二象限C.第三象限D.第四象限3 . 一次函数片-3 x+2的图象不经过第象限.4 . 一次函数y = x+2的图象大致是〔〕5 .关于x的一次函数y=kx+k2+l的图像可能是〔〕6 .一次函数片x+力的图像经过一、二、三象限,那么b的值可以是〔〕.A.-2B.-lC.OD.27 .假设一次函数y = 〔2〃? - l〕x + 3 — 2〃?的图像经过一、二、四象限,贝ij m的取值围是.8 .一次函数的图像如下图,那么.的取值围是〔〕A.f77>0//7<2B. m>0,n>2C. /77<0z/?<2D. m<Q f n>29 .关于x的一次函数〕,=〃a+〃的图象如下图,那么1〃-/〃1-" 可化简为——10 .如果一次函数片=4x+h的图像经过第一、三、四象限,那么b的取值围是__.考点3: 一次函数的增减性相关知识:一次函数y = kx+〃〔4w0〕,当攵>0时,y随x的增大而增大,当kvO 时,y随x 的增大而减小.规律总结:从图象上看只要图象经过一、三象限,y随x的增大而增大,经过二、四象限,y随x的增大而减小.【例题】1 .写出一个具体的 > 随工的增大而减小的一次函数解析式_ ______________________2 .一次函数y=2x+3中,y的值随x值增大而.〔埴“增大〞或“减小〞〕3 .关于x的一次函数y=kx+4k-2化大0〕.假设其图象经过原点,那么k二;假设y随x的增大而减小,那么k的取值围是______ .4 .假设一次函数〕,=〔2-〃?卜一2的函数值y随x的增大而减小,那么〃7的取值围是〔〕A. /??<0B. >0C. m<2D. in > 25 .点工〔-5, a〕, 8〔4, b〕在直线y=3x+2 上,那么.b o〔埴“>〞、或“二〞号〕6 .当实数x的取值使得,口有意义时,函数尸4x+1中y的取值围是〔〕.A. y> -7B. y>9C. y>9D. y<97 .一次函数的图象经过点〔0,1〕,且满足〕,随X增大而增大,那么该一次函数的解析式可以为〔写出一个即可〕.考点4:函数图象经过点的含义相关知识:函数图象上的点是由适合函数解析式的一对x、y的值组成的,因此,假设已知一个点在函数图象上,那么以这个点的横坐标代x,纵坐标代y,方程成立.【例题】1 .直线〕,=履+〃经过点伏,3〕和〔1次〕,那么k的值为〔〕.A. y/3B. ±y/3C. "D. ±V22 .坐标平面上,假设点〔3,.在方程式3y = 2x-9的图形上,那么b值为何?A. -1B. 2C. 3D. 93 . 一次函数产2x-1的图象经过点9, 3〕,那么b.4 .在平面直角坐标系xQv中,点「〔2,.〕在正比例函数,丫 = 1工的图象上,那么点Q 〔a,3a-5〕位于第象限.5 .直线片h-】一定经过点〔〕.A. 〔1, 0〕B. 〔1, k〕C. 〔0, k〕D. 〔0, -1〕7.如下图的坐标平面上,有一条通过点〔-3, - 2〕的直线Zo假设四点〔-2 ,.〕、〔0,初、〔.0〕、.一1〕在J上,那么以下数值的判断,何者正确?〔A. a=3B.Z?> -2C.c< - 3D.d=2考点5:函数图象与方程〔组〕相关知识:两个函数图象的交点坐标就是两个解析式组成的方程组的解.1.点B, C,.的坐标如图,求直线工8与直线的交点坐标.2.如表1给出了直线/I上局部点〔% y〕的坐标值,表2给出了直线L上局部/)的坐标值.那么直线4和直线人交点坐标为X-202y31-13.直线y=x-3与y=2x+2的交点为〔-5,-8〕,那么方程组x-y-3=0C . c c的解是2x-y+ 2 = 04.如图,y =研+ 〃和、=公的图象交于点P,根据图象可得关于X、Y的二元一次方程组ax-y + b = 0 kx- y = 0的解是考点6:图象的平移【例题】1 .在平面直角坐标系中,把直线y二x向左平移一个单位长度后,其直线解析式为A. y=x+lB.y=x-1C.y 二xD. y=x-2x 表12.将直线y = 2x向右平移1个单位后所得图象对应的函数解析式为〔〕A. y = 2x-lB. y = 2x-2C. y = 2x + \D. y = 2x + 23.如图,把RtZiABC 放在直角坐标系,其中/CAB=90° , BO5,点A 、B 的坐标分别为 〔1, 0〕、〔4, 0〕,将AABC 沿x 轴向右平移,当点C 落在直线y=2x-6上时,考点7:函数图象与不等式〔组〕相关知识:函数图象上的点是由适合函数解析式的一对x 、y 的值组成的〔x 、y 〕, x 的 值是点的横坐标,纵坐标就是与这个X 的值相对应的y 的值,因此,观察x 或y 的值就是看 函数图象上点的横、纵坐标的值,比拟函数值的大小就是比拟同一个x 的对应点的纵坐标的 大小,也就是函数图象上的点的位置的上下.【例题】1 41.如下图,函数刃=忖和刈=三x + ;的图象相交于〔一1,1〕,〔2,2〕两点.当X >y 2 •J•J时,工的取值围是〔〕A. xv - 1B. —1 <x<2C. x>2D. xv - 1 或 x>22 •点工〔王,凹〕和点8〔七,为〕在同一直线¥ =履+ 8上,且攵<.,假设』,那么乃,为 的关系是:〔〕A 、> y 2B 、y l < y 2C 、y } = y 2D 、无法确定.3 .一次函数y = kx+3的图象如下图,那么不等式kx+3Vo 的解集是 O线段BC 扫过的面积为〔〕A. 4B. 8C. 16D. 8>/24 .如图,一次函数y = &+〃〔ZvO〕的图象经过点A.当〕,<3时,/的取值围是.5 .如图5,直线乙:,,=x +1与直线/, y = rnx + n相交于点P 〔.,2〕,那么关于X的不等式X + 1 > nvc + n的解集为.〔图6〕6 .如图6,直线丫 =奴+力经过工〔-],1〕和8〔-攻,0〕两点,那么不等式0v依+Z?v -x的解集为=.考点8: 一次函数解析式确实定【例题】1 .y+m与x+n成正比例〔m, n为常数〕.〔】〕试说明y是x的一次函数〔2〕当x=3时,y=5,当x=2时,y=2,求y与x之间的函数关系式.2 .Y与X成正比例,Z与X成正比例,当Z=3时,Y=1 ;当X=2/3时,Z=4,那么Y与X的函数关系式为23 .如图,直线/过A、B两点,A 〔0 , -1〕, B 〔1,0 〕,那么直线/的解析式为 .4 .一次函数y=kx+b的图像经过两点B〔2Z-1〕,求这个函数的解析式.5 .一个矩形被直线分成面积为x. y 的两局部,那么y 与x 之间的函数关系只可能是( )6 .设min {x t y}表示xy 两个数中的最小值,例如min {0,2} =0, min {12,8} =8,那么关于x 的函数y=min{2x, x+2}, y 可以表示为()D.尸x+27 .:一次函数y = ^ +〃的图象经过例(0, 2), (1, 3)两点. (I)求幺6的值;(2)假设一次函数y = h+〃的图象与x 轴的交点为4a 0),求a 的值.8 .如图,在平面直角坐标系中,A 、3均在边长为1的正方形网格格点上.⑴求线段回所在直线的函数解析式,并写出当0 « y ?2时后变量x 的取值围;⑵将线段AB 绕点B 逆时针旋转90 ,得到线段8C,请画出线段3C.假设直线BC 的函数解析考点9:与一次函数有关的几何探究问题(动点)【例题】41 .如图6,在平面直角坐标系中,直线/:),= -、x + 4分别交x 轴、y 轴于点4、8,将2x (XV 2) x + 2(x> 2)_ x + 2 (x<2)―2x (x>2)C. y=2x式为),=h+〃,那么),随x 的增大而(埴“增大〞或“减△AO8绕点.顺时针旋转90.后得到△AO&.(1)求直线A8'的解析式;(2)假设直线A3'与直线/相交于点C,求△A8C的面积.2 .在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形. 例如,图中的一次函数的图象与XV轴分别交于点4民那么△Q48为此函数的坐标三角形.3(1)求函数yn-ix+s的坐标三角形的三条边长;43(2)假设函数(?为常数)的坐标三角形周长为16, 求此三角形面积.43 .如图,直线由是一次函数y = x + l的图象,直线尸8是一次■函数y = -2x + 2的图象.(1)求工、从尸三点的坐标;(6分)(2)求四边形尸.■的面积;(6分)4 .如图,在平面直角坐标系中,一次函数丁 =攵工+5的图象经过点2A (1, 4),点B是一次函数y = %x+5的图象与正比例函数y = QX的图象的交点.(1)求点B的坐标.(2)求aAOB的面积.5.如图,在边长为2的正方形ABCD的一边BC上,一点P从B点运动到C点,设BP=X, 四边形APCD的面积为匕⑴ 写出y与x之间的函数关系式及x的取值围;⑵ 说明是否存在点P,使四边形APCD的面积为1.5?6 .如图,在平面直角坐标系中,过点B (6, 0)的直线AB与直线OATg交于点A (4. 2),功点M沿路爱0-A—C运动.(1)求直线AB的解析式.(2)求△OAC的面积.(3)当AOMC的茴积是AOAC的固积的1时, 4求出这时点M的坐标.7 .如下图,在矩形ABCD中,动点P从点B出发,沿BC, CD, DA运动至点A停止,设点P运动的路程为x, 2XABP的面积为y,如果y关于X的函数图象如下图,那么△ABC的面积是.8 ..如图1,在矩形"NP.中,动点R从点N出发,沿N-P-M方向运动至点〞处停止.设点R运动的路程为x, AMN/?的面积为y,如果),关于x的函数图象如图2所示,那么当x = 9时,点R应运动到〔〕A. N处B. P处C. 0处9.如图1,正方形O48C的边长为2,顶点4、C分别在x、y轴的正半轴上,例是8c 的中点.片o,m〕是线段0c上一动点〔C点除外〕,直线尸M交工8的延长线于点..〔1〕求点.的坐标〔用含m的代数式表示〕;〔2〕当△工尸.是等腰三角形时,求m的值;图1考点10:一次函数图象信息题〔从图像中读取信息.利用信息解题〕思路点拨::一次函数在实际中的应用是先根据条件求出一次函数的解析式,然后根据一次函数的性质解决相关问题.规律总结:先求一次函数解析式,再利用一次函数的性质,对于图象不是一条线而是由多条线段组成的,要根据函数的自变量的取值围分别求.【例题】1 .一天,亮亮感冒发烧了,早晨他烧得厉害,吃过药后感冒好多了,中午时亮亮的体温基本正常,但是下午他的体温又开始上升,直到半夜亮亮才感觉身上不那么发烫了.图中能基本反映出亮亮这一天〔.〜24时〕体温的变化情况的是〔〕BCD2 .汽车的速度随时间变化的情况如下图:⑴这辆汽车的最高时速是多少?⑵汽车在行驶了多长时间后停了下来,停了多长时间?⑶汽车在第一次匀速行驶时共用了几小时?速度是多少?在这段时间,它走了多远?3 ,有两人分别骑自行车和摩托车沿着相同的路线从甲地到乙地去,以下图反映的是这两个人行驶过程中时间和路程的关系,请根据图象答复以下问题:⑴甲地与乙地相距多少千米?两个人分别用了几小时才到达乙地?谁先到达了乙地?早到多长时间?⑵分别描述在这个过程中自行车和摩托车的行驶状态.⑶求摩托车行驶的平均速度.4 .某污水处理厂的一个净化水池设有2个进水口和】个出水口,三个水口至少翻开一个.每个进水口进水的速度由图甲给出,出水口出水的速度由图乙给出.某一天.点到6点,该水池的蓄水量与时间的函数关系如图丙所示.通过对图象的观察,小亮得出了以下三个论断:(12点到3点只进水不出水;⑵3点到4点不进水只出水,(3)4点到6点不进水也不出水.其中正确的选项是()A. (1)B. (3)C.⑴⑶D.⑴⑵⑶5 .甲、乙两组工人同时开始加工某种零件,乙组在工作中有一次停产更换设备后,乙组的工作效率是原来的2倍.两组各自加工数量y (件)与时间x (时)之间的函数图象如图所示.(1)求甲组加工零件的数量y与时间x之间的函数关系式.(2)求乙组加工岑件总量.的值.(3)甲、乙两组加工出的零件合在一起装箱,每够300件装一箱,零件装箱的时间忽略不计,求经过多长时间恰好装满第1箱?再经过多长时间恰好装满第2箱?6 .小师傅驾车到某地办事,汽车出发前油箱中有油50升,行驶假设干小时后,途中在加油站加油假设干升,油箱中剩余油量y (升)与行驶时间/(小时)之间的关系如下图.(1)请问汽车行驶多少小时后加油,中途加油多少升?(2)求加油前油箱剩余油量y与行驶时间/的函数关系式;(3)加油前后汽车都以70千米/小时的速度匀速行驶,如果加油站距目的地210千米,要到达目的地,问油箱中的油是否移用?请说明理由.7 .小明从家崎自行车出发,沿一条直路到相距2400m的邮局办事,小明出发的同时,他的爸爸以96m/min的速度从邮局沿同一条道路步行回家,小明在邮局停留2min后沿原路以原速返回,设他们出发后经过t min时,小明与家之间的距离为S】m,小明爸爸与家之间的距离为Szm,,图中折线OABD,线段EF分别是表示&、S?与t之间函数关系的图像.(1)求$2与t之间的函数关系式:(2) 小明从家出发,经过多长时间在返回途中追上爸爸?这时他们距离家还有多远?8.鞋子的“鞋码〞和鞋长〔cm〕存在一种换算关系,下表是几组“鞋码〞与鞋长换算的对应数值:[注:“鞋码〞是表示鞋子大小的一种]鞋长16192124(cm)鞋码22283238〔号〕〔1〕设鞋长为X “鞋码〞为匕试判断点〔K y〕在你学过的哪种函数的图象上?〔2〕求X、y之间的函数关系式;〔3〕如果某人穿44号“鞋码〞的鞋,那么他的鞋长是多少?9 .某医药研究所开发一种新药,如果成人按规定的剂量服用,据监测:服药后每毫升血液中含药量y与时间t之间近似满足如下图曲线:⑴分别求出,< ?和,之!时/与t之间的函数关系式; 2 2⑵据测定:每毫升血液中含药量不少于4微克时治疗疾病有效,假设某病人一天中第一次服药为7:00,那么服药后几点到几点有效210 .某公交公司的公共汽车和出租车每天从乌鲁木齐市出发往返于乌鲁木齐市和石河子市两地,出租车比公共汽车多往返一趟,如图表示出租车距乌鲁木齐市的路程y 〔单位:千米〕与所用时间x 〔单位:小时〕的函数图象.公共汽车比出租车晚1小时出发,到达石河子市后休息2小时,然后按原路原速返回,结果比出租车最后一次返回乌鲁木齐早1小时.〔1〕请在图中画出公共汽车距乌鲁木齐市的路程y 〔千米〕与所用时间X 〔小时〕的函数图象.〔2〕求两车在途中相遇的次数〔直接写出答案〕〔3〕求两车最后一次相遇时,距乌鲁木齐市的路程.11 .小颖和小亮上山游玩,小颖乘会缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颖在小亮出发后50 min 才乘上缆车,缆车的平均速度为180 m/min,设小亮出发x min后行走的路程为y m .图中的折线表示小亮在整个行走过程中y与x的函数关系.⑴小亮行走的总路程是 ___________ cm,他途中休息了min.(2)①当50&x<80时,求y与x的函数关系式;②当小颖到达缆车终点为时,小亮离缆车终点的路程是多少?1 .选择题⑴以下说法中不成立的是(A.在.v = 3x-i 中,y+1与X 成正比例;B.在中,y 与X 成正比例C.在,,= 2.+1)中,y 与x+1成正比例;D.在y=x+3中,y 与x 成正比例 (2)(X ), y1)和(Xs, y 2)是直线y=3x 上的两点,x 1>x 2l 那么y1与y2的大小关系是( )A.yi>Y2 ⑶以下说确的是( ⑸当k>0时,直线厂kx-5不经过的象限是((1)函数y=2x+m-l,当m=时,它是正比例函数.(2)假设一次函数y=bx+2的图象经过点A(-l, 1),贝ijb 二. (3)函数y=5x+l 中y 随x 的增大而;函数y=8x-3中y 随x 的增大 而・(4)y-2与x 成正比例,且x=2时,尸4,那么y 与x 的函数关系式是 _________________ ;当尸3时,x=.(5)假设关于x 的函数),= (〃 +IM"'〞是一次函数,那么, n.(6)将直线y=3x 向下平移5个单位,得到直线;将直线y=-¥5向上平移5 个单位,得到直线.(7)假设直线),=-x + a 和直线),=x + 〃的交点坐标为(6,8),那么a+b=3 .设有三个变量x 、y 、z,其中y 是x 的正比例函数,z 是y 的正比例函数,请问z 是x 的正比例函数吗?并说明理由.4 .作出函数y=2x-2的图象,并根据图象解答以下问题: ⑴当x 为何值时,y>0, y = 0, yvO?⑵指出图象与X 轴交点A,与y 轴交于点B 的坐标,并求出aAOB 的面积S.B.yi<y 2C.y!=y 2D.以上都有可能A.正比例函数是一次函数 C.正比例函数不是一次函数 (4)以下函数中,y 是x 的一次函数的是(B.一次函数是正比例函数D.不是正比例函数就不是一次函数)A.y=3x+5B.y=-3x 2C.y= — xD.y=2« A.第一象限 2 .埴空题B.第二象限C.第三象限D.第四象限5 .点燃蜡烛,根据与时间成正比例关系变短,长为21cm的蜡烛,点燃6分钟后,螃烛变短3.6 cm,设蜡烛点燃x分后变短y cm.求:⑴用x表示函数y的解析式;⑵自变量的取值围;⑶此蜡烛几分钟燃烧完?⑷画出此函数的图象.6,函数y=(2m-l)x+l-3m, m为何值时,⑴这个函数是正比例函数?⑵这个函数为一次函数?⑶函数值y随x的增大而减小?⑷这个函数图象与直线y=x+i的交点在x轴上?7.一个正比例函数和一个一次函数的图象交于点P(-2,2),且一次函数的图象与y轴相交于点Q (0, 4)(1)求这两个函数的解析式(2)在同一坐标系,’分别画出这两个函数的图象〔3〕求出A'..的面积8,y-4与x 成正比,且x=6时,y=4⑴求y 与x 的解析式⑵此直线在第一象限上有一动点P 〔x,y 〕, x 轴上有一点C 〔-2. 0〕,这条直线与x 轴交于 A,求三角形PAC 的面积与x 的函数关系式,并写出x 的取值围.一、埴空题1 .在函数y = 431中,自变量工的取值围是 __________ .2 .函数y = ;/中,当x=时,函数的值等于2.3 .一次函数前图象经过点〔-2, 3〕与〔1 ,-】〕,它的解析式是— ——, 4,出租车收费按路程计算,3km 〔包括3km 〕收费8元;超过3km 每增加1km 加收 1元,那么路程x>3km 时,车费y 〔元〕与x 化m 〕之间的函数关系式是==.5 .假设直线〕,=一工+〃和直线,v = x + b 的交点坐标为〔皿.8〕,那么〃+人=.6 .有边长为1的等边三角形卡片假设干,使用这些三角形卡片拼出边长分别是2、3、4、… 的等边三角形〔如图〕.根据图形推断每个等边三角形卡片总数S 与边长n 的关系式.二、选择题7 ,函数是研究〔 〕A.常里之间的对应关系的C.变量与常量之间对应关系的 8 .函数y 二]言 的自变量x 的取值围是〔 〕B.常量与变量之间的对应关系的 D.变量之间的对应关系的A.x>-2B.x > -2C.x4-2D.x < -29 .汽车由A地驶往相距120km的B地,它的平均速度是30km/h,那么汽车距B地路程s 〔km〕与行驶时间t〔h〕的函数关系式及自变量t的取值围是〔〕A.S=120-30t 〔0<t<4〕B.S=120-30t 〔t>0〕C.S=30t 〔0<t<40〕D.S=30t 〔t<4〕10.函数y = 3x+】,当自变量增加m时,相应的函数值增加〔〕A.3m+1B.3mC.mD.3m -11】.无论m为何实数,直线y = x+2〃?与y = -x+4的交点不可能在〔〕A.第一象限B.第二象限C.第三象限D.第四象限12.小明的父亲饭后散步,从家中走20分钟到一个离家900米的报亭看10分钟的报纸后,用15分钟返回家中,以下图形中表示小明父亲离家的距离y〔米〕与时间x 〔分钟〕之间的关系是〔〕三、解做题:14,将函数y = 2x + 3的图象平移,使它经过点〔2, -1〕,求平移后得到的直线的解析式.15.甲市到乙市的包裹邮资为每千克0.9元,每件另加手续费0.2元.求邮寄一件包裹的总邮资y 〔元〕与包裹重量x 〔千克〕之间的函数解析式,并计算一件5千克重的包寰的邮资.17.一天上午8时,小华骑自行车去县城购物,到下午2时返回家,结合图象答复:⑴小华何时第一次休息?⑵小华离家最远的距离时多少?⑶返回时平均速度是多少?⑷请你描述一下小华购物的情况.18 .如图,直线人的解析表达式为〕,=-31+ 3,且乙与x轴交于点.,直线右经过点4 B,直线k 交于点(1)求点.的坐标;(2)求直线的解析表达式;(3)求△AOC的,面积;(4)在直线.上存在异于点.的另一点尸,使得△4.尸与44).的面积相等,请直接写出点夕的坐标.♦ *3 ,19 .直线y = -:x + 6与坐标轴分别交于A、B两点,动点P、Q同时从.点出发,同时到达A点,运动停止.点Q沿线段.A运动,速度为每秒1个单位长度,点P沿路线.=B= A 运动.(1)直接写出A、B两点的坐标;(2)设点Q的运动时间为t (秒),△OPQ的面积为S,求出S与t之间的函数关系式;48(3)当5 = =时,求出点P的坐标,并直接写出以点.、P、Q为顶点的平行四边形的第四个顶点M的坐标.。
北师大版八年级数学上册 一次函数知识点总结和常考题

第1页(共40页) ()()()32100.0k ⎪⎩⎪⎨⎧<=>>b b b ()()()321000.0k ⎪⎩⎪⎨⎧<=><b b b 一次函数所有知识点总结和常考题知识点:1.变量与常量:在一个变化过程中,数值发生变化的为变量,数值不变的是常量。
2.函数:在一个变化过程中,如果有两个变量x 与y ,并且对于想x 的每一个确定的值,y 都有唯一确定的值与其对应,则x 自变量,y 是x 的函数。
3.函数解析式:用关于自变量的数学式子表示函数与自变量之间的关系的式子。
4.描述函数的方法:解析式法、列表法、图像法。
5画函数图象的一般步骤:①列表:一次函数只要列出两个点即可,其他函数一般需要列出5个以上的点,所列点是自变量与其对应的函数值②描点:在直角坐标系中,以自变量的值为横坐标,相应函数的值为纵坐标,描出表格中的个点,一般画一次函数只用两点③连线:依次用平滑曲线连接各点。
6.正比列函数:形如y=kx (k ≠0)的函数,k 是比例系数。
7.正比列函数的图像性质:⑴ y=kx (k ≠0)的图象是一条经过原点的直线;⑵增减性:①当k>0时,直线y=kx 经过第一、三象限,y 随x 的增大而增大;②当k<0时,直线y=kx 经过第二、四象限,y 随x 的增大而减小,8.一次函数:形如y=kx+b (k ≠0)的函数,则称y 是x 的一次函数。
当b=0时,称y 是x 的正比例函数。
9. 一次函数的图像性质: ⑴图象是一条直线;⑵增减性:①当k>0时, y 随x 的增大而增大;②当k<0时, y 随x 的增大而减小。
10.待定系数法求函数解析式:⑴设函数解析式为一般式;(2)把两点带入函数一般式列出方程组,求出待定系数;(3)把待定系数值再带入函数一般式,得到函数解析式11.一次函数与方程、不等式的关系:会从函数图象上找到一元一次方程的解(既与x轴的交点坐标横坐标值),一元一次不等式的解集,二元一次方程组的解(既两函数直线交点坐标值)常考题:一.选择题(共14小题)1.下列函数中,自变量x的取值范围是x≥3的是()A.y=B.y= C.y=x﹣3 D.y=2.下列各曲线中,不能表示y是x的函数的是()A .B .C .D .3.一次函数y=﹣3x﹣2的图象不经过()A.第一象限B.第二象限C.第三象限D.第四象限4.若函数,则当函数值y=8时,自变量x的值是()A .±B.4 C .±或4 D.4或﹣5.下列图形中,表示一次函数y=mx+n与正比例函数y=mnx(m,n为常数,且mn≠0)的图象的是()第1页(共40页)A .B .C .D .6.如果一个正比例函数的图象经过不同象限的两点A(2,m),B(n,3),那么一定有()A.m>0,n>0 B.m>0,n<0 C.m<0,n>0 D.m<0,n<07.已知点(﹣4,y1),(2,y2)都在直线y=﹣x+2上,则y1,y2大小关系是()A.y1>y2B.y1=y2C.y1<y2D.不能比较8.一次函数y=kx+b(k≠0)的图象如图所示,当y>0时,x的取值范围是()A.x<0 B.x>0 C.x<2 D.x>29.如图,在矩形ABCD中,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图所示,则△ABC的面积是()第1页(共40页)A.10 B.16 C.18 D.2010.如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则当x=9时,点R应运动到()A.N处B.P处 C.Q处D.M处11.关于x的一次函数y=kx+k2+1的图象可能正确的是()A .B .C .D .12.甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:①A,B两城相距300千米;②乙车比甲车晚出发1小时,却早到1小时;③乙车出发后2.5小时追上甲车;④当甲、乙两车相距50千米时,t=或.其中正确的结论有()第1页(共40页)A.1个 B.2个 C.3个 D.4个13.图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中x表示时间,y表示张强离家的距离.根据图象提供的信息,以下四个说法错误的是()A.体育场离张强家2.5千米B.张强在体育场锻炼了15分钟C.体育场离早餐店4千米D.张强从早餐店回家的平均速度是3千米/小时14.甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是()第1页(共40页)A.①②③B.仅有①②C.仅有①③D.仅有②③二.填空题(共13小题)15.函数y=中自变量x 的取值范围是.16.已知点(3,5)在直线y=ax+b(a,b为常数,且a≠0)上,则的值为.17.已知直线y=kx+b,若k+b=﹣5,kb=6,那么该直线不经过第象限.18.一次函数y=﹣2x+b中,当x=1时,y<1,当x=﹣1时,y>0.则b的取值范围是.19.小明放学后步行回家,他离家的路程s(米)与步行时间t(分钟)的函数图象如图所示,则他步行回家的平均速度是米/分钟.20.已知直线y=2x+(3﹣a)与x轴的交点在A(2,0)、B(3,0)之间(包括A、B两点),则a的取值范围是.21.“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:第1页(共40页)①“龟兔再次赛跑”的路程为1000米;②兔子和乌龟同时从起点出发;③乌龟在途中休息了10分钟;④兔子在途中750米处追上乌龟.其中正确的说法是.(把你认为正确说法的序号都填上)22.某水库的水位在5小时内持续上涨,初始的水位高度为6米,水位以每小时0.3米的速度匀速上升,则水库的水位高度y米与时间x小时(0≤x≤5)的函数关系式为.23.如图所示,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省元.第1页(共40页)24.如图,在平面直角坐标系中,点P的坐标为(0,4),直线y=x﹣3与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为.25.直线y=3x+2沿y轴向下平移5个单位,则平移后直线与y轴的交点坐标为.26.把直线y=﹣x﹣1沿x轴向右平移2个单位,所得直线的函数解析式为.27.如图,直线y=﹣x+4与y轴交于点A,与直线y=x+交于点B,且直线y=x+与x轴交于点C,则△ABC的面积为.第1页(共40页)。
北师大版八年级数学上册 一次函数知识点总结和常考题

()()()32100.0k ⎪⎩⎪⎨⎧<=>>b b b ()()()321000.0k ⎪⎩⎪⎨⎧<=><b b b 一次函数所有知识点总结和常考题知识点:1.变量与常量:在一个变化过程中,数值发生变化的为变量,数值不变的是常量。
2.函数:在一个变化过程中,如果有两个变量x 与y ,并且对于想x 的每一个确定的值,y 都有唯一确定的值与其对应,则x 自变量,y 是x 的函数。
3.函数解析式:用关于自变量的数学式子表示函数与自变量之间的关系的式子。
4.描述函数的方法:解析式法、列表法、图像法。
5画函数图象的一般步骤:①列表:一次函数只要列出两个点即可,其他函数一般需要列出5个以上的点,所列点是自变量与其对应的函数值②描点:在直角坐标系中,以自变量的值为横坐标,相应函数的值为纵坐标,描出表格中的个点,一般画一次函数只用两点③连线:依次用平滑曲线连接各点。
6.正比列函数:形如y=kx (k ≠0)的函数,k 是比例系数。
7.正比列函数的图像性质:⑴ y=kx (k ≠0)的图象是一条经过原点的直线;⑵增减性:①当k>0时,直线y=kx 经过第一、三象限,y 随x 的增大而增大;②当k<0时,直线y=kx 经过第二、四象限,y 随x 的增大而减小,8.一次函数:形如y=kx+b (k ≠0)的函数,则称y 是x 的一次函数。
当b=0时,称y 是x 的正比例函数。
9. 一次函数的图像性质: ⑴图象是一条直线;⑵增减性:①当k>0时, y 随x 的增大而增大;②当k<0时, y 随x 的增大而减小。
10.待定系数法求函数解析式:⑴设函数解析式为一般式;(2)把两点带入函数一般式列出方程组,求出待定系数;(3)把待定系数值再带入函数一般式,得到函数解析式11.一次函数与方程、不等式的关系:会从函数图象上找到一元一次方程的解(既与x轴的交点坐标横坐标值),一元一次不等式的解集,二元一次方程组的解(既两函数直线交点坐标值)常考题:一.选择题(共14小题)1.下列函数中,自变量x的取值范围是x≥3的是()A.y=B.y= C.y=x﹣3 D.y=2.下列各曲线中,不能表示y是x的函数的是()A. B. C. D.3.一次函数y=﹣3x﹣2的图象不经过()A.第一象限B.第二象限C.第三象限D.第四象限4.若函数,则当函数值y=8时,自变量x的值是()A.±B.4 C.±或4 D.4或﹣5.下列图形中,表示一次函数y=mx+n与正比例函数y=mnx(m,n为常数,且mn≠0)的图象的是()A.B.C.D.6.如果一个正比例函数的图象经过不同象限的两点A(2,m),B(n,3),那么一定有()A.m>0,n>0 B.m>0,n<0 C.m<0,n>0 D.m<0,n<07.已知点(﹣4,y1),(2,y2)都在直线y=﹣x+2上,则y1,y2大小关系是()A.y1>y2B.y1=y2C.y1<y2D.不能比较8.一次函数y=kx+b(k≠0)的图象如图所示,当y>0时,x的取值范围是()A.x<0 B.x>0 C.x<2 D.x>29.如图,在矩形ABCD中,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图所示,则△ABC的面积是()10.如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则当x=9时,点R应运动到()A.N处B.P处 C.Q处D.M处11.关于x的一次函数y=kx+k2+1的图象可能正确的是()A.B.C.D.12.甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:①A,B两城相距300千米;②乙车比甲车晚出发1小时,却早到1小时;③乙车出发后2.5小时追上甲车;④当甲、乙两车相距50千米时,t=或.其中正确的结论有()13.图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中x表示时间,y表示张强离家的距离.根据图象提供的信息,以下四个说法错误的是()A.体育场离张强家2.5千米B.张强在体育场锻炼了15分钟C.体育场离早餐店4千米D.张强从早餐店回家的平均速度是3千米/小时14.甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是()A.①②③B.仅有①②C.仅有①③D.仅有②③二.填空题(共13小题)15.函数y=中自变量x的取值范围是.16.已知点(3,5)在直线y=ax+b(a,b为常数,且a≠0)上,则的值为.17.已知直线y=kx+b,若k+b=﹣5,kb=6,那么该直线不经过第象限.18.一次函数y=﹣2x+b中,当x=1时,y<1,当x=﹣1时,y>0.则b的取值范围是.19.小明放学后步行回家,他离家的路程s(米)与步行时间t(分钟)的函数图象如图所示,则他步行回家的平均速度是米/分钟.20.已知直线y=2x+(3﹣a)与x轴的交点在A(2,0)、B(3,0)之间(包括A、B两点),则a的取值范围是.21.“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:①“龟兔再次赛跑”的路程为1000米;②兔子和乌龟同时从起点出发;③乌龟在途中休息了10分钟;④兔子在途中750米处追上乌龟.其中正确的说法是.(把你认为正确说法的序号都填上)22.某水库的水位在5小时内持续上涨,初始的水位高度为6米,水位以每小时0.3米的速度匀速上升,则水库的水位高度y米与时间x小时(0≤x≤5)的函数关系式为.23.如图所示,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省元.24.如图,在平面直角坐标系中,点P的坐标为(0,4),直线y=x﹣3与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为.25.直线y=3x+2沿y轴向下平移5个单位,则平移后直线与y轴的交点坐标为.26.把直线y=﹣x﹣1沿x轴向右平移2个单位,所得直线的函数解析式为.27.如图,直线y=﹣x+4与y轴交于点A,与直线y=x+交于点B,且直线y=x+与x轴交于点C,则△ABC的面积为.三.解答题28.如图,直线l1的解析表达式为:y=﹣3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C.(1)求点D的坐标;(2)求直线l2的解析表达式;(3)求△ADC的面积;(4)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标.29.如图:在平面直角坐标系中,有A(0,1),B(﹣1,0),C(1,0)三点坐标.(1)若点D与A,B,C三点构成平行四边形,请写出所有符合条件的点D的坐标;(2)选择(1)中符合条件的一点D,求直线BD的解析式.30.如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=﹣x+b也随之移动,设移动时间为t秒.(1)当t=3时,求l的解析式;(2)若点M,N位于l的异侧,确定t的取值范围;(3)直接写出t为何值时,点M关于l的对称点落在坐标轴上.参考答案与试题解析一.选择题(共14小题)1.D.2.C.3.A.4.D.5.A.6.D.7.A.8.C.9.A.10.C.11.C.12.B.13.C.14.A.二.填空题(共13小题)15.x≥﹣且x≠1.16.﹣.17.一.18.﹣2<b<3.19.80.20.7≤a≤9.21.①③④.22.y=6+0.3x.23.224.PM=.25.(0,﹣3).26.y=﹣x+1.27.S△ABC=S△ACD﹣S△BCD=CD•AO﹣CD•BE=×4×4﹣×4×2=4.三.解答题28.解:(1)由y=﹣3x+3,令y=0,得﹣3x+3=0,∴x=1,∴D(1,0);(2)设直线l2的解析表达式为y=kx+b,由图象知:x=4,y=0;x=3,,代入表达式y=kx+b,∴,∴,∴直线l2的解析表达式为;(3)由,解得,∴C(2,﹣3),=×3×|﹣3|=;∵AD=3,∴S△ADC(4)△ADP与△ADC底边都是AD,面积相等所以高相等,△ADC高就是点C到直线AD的距离,即C纵坐标的绝对值=|﹣3|=3,则P到AD距离=3,∴P纵坐标的绝对值=3,点P不是点C,∴点P纵坐标是3,∵y=1.5x﹣6,y=3,∴1.5x﹣6=3x=6,所以P(6,3).【点评】本题考查的是一次函数的性质,三角形面积的计算等有关知识,难度中等.29.解:(1)符合条件的点D的坐标分别是D1(2,1),D2(﹣2,1),D3(0,﹣1).(2)①选择点D1(2,1)时,设直线BD1的解析式为y=kx+b,由题意得,解得.∴直线BD1的解析式为.②选择点D2(﹣2,1)时,类似①的求法,可得直线BD2的解析式为y=﹣x﹣1.③选择点D3(0,﹣1)时,类似①的求法,可得直线BD3的解析式为y=﹣x﹣1.30.解:(1)直线y=﹣x+b交y轴于点P(0,b),由题意,得b>0,t≥0,b=1+t.当t=3时,b=4,故y=﹣x+4.(2)当直线y=﹣x+b过点M(3,2)时,2=﹣3+b,解得:b=5,5=1+t,解得t=4.当直线y=﹣x+b过点N(4,4)时,4=﹣4+b,解得:b=8,8=1+t,解得t=7.故若点M,N位于l的异侧,t的取值范围是:4<t<7.(3)如右图,过点M作MF⊥直线l,交y轴于点F,交x轴于点E,则点E、F 为点M在坐标轴上的对称点.过点M作MD⊥x轴于点D,则OD=3,MD=2.已知∠MED=∠OEF=45°,则△MDE与△OEF均为等腰直角三角形,∴DE=MD=2,OE=OF=1,∴E(1,0),F(0,﹣1).∵M(3,2),F(0,﹣1),∴线段MF中点坐标为(,).直线y=﹣x+b过点(,),则=﹣+b,解得:b=2,2=1+t,解得t=1.∵M(3,2),E(1,0),∴线段ME中点坐标为(2,1).直线y=﹣x+b过点(2,1),则1=﹣2+b,解得:b=3,3=1+t,解得t=2.故点M关于l的对称点,当t=1时,落在y轴上,当t=2时,落在x轴上.。
北师大八年级上《一次函数 》知识点总结加函数图像和求 一次函数专题

一次函数知识点总结基本概念1、变量:在一个变化过程中可以取不同数值的量。
常量:在一个变化过程中只能取同一数值的量。
例1、在匀速运动公式中,表示速度,表示时间,表示在时间内所走的路程,则变量是________,常量是_______。
例2、在圆的周长公式C=2πr中,变量是________,常量是_________.2、函数:一般的,在一个变化过程中,如果有两个变量x和y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就把x 称为自变量,把y称为因变量,y是x的函数。
*判断Y是否为X的函数,只要看X取值确定的时候,Y是否有唯一确定的值与之对应例1、下列函数(1)y=πx (2)y=2x-1 (3)y= (4)y=2-1-3x (5)y=x2-1中,是一次函数的有( )(A)4个 (B)3个 (C)2个 (D)1个3、定义域:一般的,一个函数的自变量允许取值的范围,叫做这个函数的定义域。
4、确定函数定义域的方法:(1)关系式为整式时,函数定义域为全体实数;(2)关系式含有分式时,分式的分母不等于零;(3)关系式含有二次根式时,被开放方数大于等于零;(4)关系式中含有指数为零的式子时,底数不等于零;(5)实际问题中,函数定义域还要和实际情况相符合,使之有意义。
例1、下列函数中,自变量x的取值范围是x≥2的是( )A.y= B.y= C.y= D.y=·例2、函数中自变量x的取值范围是___________.例3、已知函数,当时,y的取值范围是 ( )A. B. C. D.5、函数的图像一般来说,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.6、函数解析式:用含有表示自变量的字母的代数式表示因变量的式子叫做解析式。
7、描点法画函数图形的一般步骤第一步:列表(表中给出一些自变量的值及其对应的函数值);第二步:描点(在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中数值对应的各点);第三步:连线(按照横坐标由小到大的顺序把所描出的各点用平滑曲线连接起来)。
北师大版八年级上册数学 一次函数的图象和性质题型总结1(详细!!!)

1O OO O 一次函数图象和性质1重点:1. 一次函数关系式:y=kx+b (b ≠0) 2. K 决定走向。
趋势两直线平行则k 值相等,反之也成立两直线关于X 或Y 轴对称则K 互为相反数 两直线互相垂直则K 值互为负倒数。
3. B 决定上下平移的方向和距离B 是直线与Y 轴交点的纵坐标4. 直线Y=KX+B(K ≠0)与X 轴Y 轴交点坐标公式(0.b ) (-b/k .0)要点一 待定系数1、 若点()y ,3-在一次函数231-=x y 的图像上,则y= 。
2、 若一次函数y=(2-m )x+m 的图像经过第一、•二、•四象限,•则m•的取值范围是______.3、 函数1+=kx y 的图像过点()1,2--,则_________=k 。
4、 一次函数图像平行于直线x y 2=,且与x 轴交于点()0,3-,则这个函数的解析式是 。
5、 一次函数b x y +-=32中,y 随着x 的增大而 ,当______=b 时,函数图像经过原点。
6、 将直线121--=x y 向上平移2个单位,所得直线的解析式是 ,平移后的直线不经过第 象限。
7、 已知一次函数4+-=k kx y 的图像经过原点,则_______=k 。
8、 如果直线b kx y +=经过二、三、四象限,则_______k ,________b 。
9、 一次函数b ax y -=中,0,0><b a ,则它的图像可能是( )111b x k y +=不过第三象限。
则K___ B__ 11、 如图,线段AB 对应的函数表达式为( ) A .y=-32x+2 B .y=-23x+2C .y=-23x+2(0≤x ≤3)D .y=-23x+20(0<x<3)要点二 与坐标轴交点12、 函数23-=x y 在y 轴上的截距是 。
13、 直线32-=x y 与x 轴的交点坐标是 ,与y 轴的交点坐标是 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北师大版数学一次函数考点归纳及例题详解 【考点归纳】考点1:一次函数的概念.相关知识:一次函数是形如y kx b =+(k 、b 为常数,且0k ≠)的函数,特别的当0=b 时函数为)0(≠=k kx y ,叫正比例函数. 【例题】1.下列函数中,y 是x 的正比例函数的是( ) A .y=2x-1 B .y=3xC .y=2x 2D .y=-2x+1 2.已知自变量为x 的函数y=mx+2-m 是正比例函数,则m=________,•该函数的解析式为_________.3.已知一次函数kx k y )1(-=+3,则k = . 4.函数n m x m y n +--=+12)2(,当m= ,n= 时为正比例函数;当m= ,n时为一次函数.考点2:一次函数图象与系数相关知识:一次函数)0(≠+=k b kx y 的图象是一条直线,图象位置由k 、b 确定,0>k 直线要经过一、三象限,0<k 直线必经过二、四象限,0>b 直线与y 轴的交点在正半轴上,0<b 直线与y 轴的交点在负半轴上.【例题】1. 直线y=x -1的图像经过象限是( )A.第一、二、三象限B.第一、二、四象限C.第二、三、四象限D.第一、三、四象限 2. 一次函数y=6x+1的图象不经过( ) A .第一象限B .第二象限C .第三象限D .第四象限3. 一次函数y = -3 x + 2的图象不经过第 象限.4. 一次函数2y x =+的图象大致是( )5. 关于x 的一次函数y=kx+k 2+1的图像可能是( )6.已知一次函数y =x +b 的图像经过一、二、三象限,则b 的值可以是( ). A.-2 B.-1 C.0 D.27.若一次函数m x m y 23)12(-+-=的图像经过 一、二、四象限,则m 的取值范围是 .8. 已知一次函数y=mx +n -2的图像如图所示,则m 、n 的取值范围是( )A.m >0,n <2B. m >0,n >2C. m <0,n <2D. m <0,n >29.已知关于x 的一次函数y mx n =+的图象如图所示,则2||n m m --可化简为__ __.10. 如果一次函数y=4x +b 的图像经过第一、三、四象限,那么b 的取值范围是_ _。
考点3:一次函数的增减性相关知识:一 次函数)0(≠+=k b kx y ,当0>k 时,y 随x 的增大而增大,当0<k 时,y 随x 的增大而减小.规律总结:从图象上看只要图象经过一、三象限,y 随x 的增大而增大,经过二、四象限,y 随x 的增大而减小. 【例题】1.写出一个具体的y 随x 的增大而减小的一次函数解析式_ _2.一次函数y=-2x+3中,y 的值随x 值增大而____ ___.(填“增大”或“减小”)3.已知关于x 的一次函数y=kx+4k-2(k≠0).若其图象经过原点,则k=_____;若y 随x 的增大而减小,则k 的取值范围是________.4.若一次函数()22--=x m y 的函数值y 随x 的增大而减小,则m 的取值范围是( )A. 0<mB. 0>mC. 2<mD. 2>m5. 已知点A (-5,a ),B (4,b)在直线y=-3x+2上,则a b 。
(填“>”、“<”或“=”号)6.当实数x 的取值使得x -2有意义时,函数y =4x +1中y 的取值范围是( ).A .y ≥-7B .y ≥9C .y >9D .y ≤97.已知一次函数的图象经过点(0,1),且满足y 随x 增大而增大,则该一次函数的解析式可以为_________________(写出一个即可).考点4:函数图象经过点的含义相关知识:函数图象上的点是由适合函数解析式的一对x 、y 的值组成的,因此,若已知一个点在函数图象上,那么以这个点的横坐标代x ,纵坐标代y ,方程成立。
【例题】1.已知直线y kx b =+经过点(,3)k 和(1,)k ,则k 的值为( ).A 3B .3±C 2D .22. 坐标平面上,若点(3, b )在方程式923-=x y 的图形上,则b 值为何?A .-1B . 2C .3D . 93. 一次函数y =2x -1的图象经过点(a ,3),则a = . 12y x =的图4.在平面直角坐标系xOy 中,点P(2,a )在正比例函数象上,则点Q( 35a a -,)位于第_____象限. 5.直线y =kx -1一定经过点( ).A .(1,0)B .(1,k )C .(0,k )D .(0,-1)7. 如图所示的坐标平面上,有一条通过点(-3,-2)的直线L 。
若四点(-2 , a )、(0 , b )、(c , 0)、(d ,-1)在L 上,则下列数值的判断,何者正确? ( )A .a =3 B.b >-2C.c <-3 D .d =2考点5:函数图象与方程(组)相关知识:两个函数图象的交点坐标就是两个解析式组成的方程组的解。
1. 点A ,B ,C ,D 的坐标如图,求直线AB 与直线CD 的交点坐标.2. 如表1给出了直线l 1上部分点(x ,y )的坐标值,表2给出了直线l 2上部分(x ,y )的坐标值.那么直线l 1和直线l 2交点坐标为___ __.3.已知直线y=x-3与y=2x+2的交点为(-5,-8),则方程组30220x y x y --=⎧⎨-+=⎩的解是________。
4.如图,已知b ax y +=和kx y =的图象交于点P ,根据图象可得关于X 、Y 的二元一次方程组⎩⎨⎧=-=+-00y kx b y ax的解是 .考点6:图象的平移【例题】1. 在平面直角坐标系中,把直线y=x 向左平移一个单位长度后,其直线解析式为( ) A .y=x+1 B.y=x-1 C.y=x D. y=x-22. 将直线2y x =向右平移1个单位后所得图象对应的函数解析式为 ( ) A. 21y x =- B. 22y x =- C. 21y x =+ D. 22y x =+3. 如图,把Rt △ABC 放在直角坐标系内,其中∠CAB=90°,BC=5,点A 、B 的坐标分别为(1,0)、(4,0),将△ABC 沿x 轴向右平移,当点C 落在直线y=2x -6上时, 线段BC 扫过的面积为( ) A .4B .8C .16D .82表1 表2AB COyxxy BAO xyB AO考点7:函数图象与不等式(组)相关知识:函数图象上的点是由适合函数解析式的一对x 、y 的值组成的(x 、y ),x 的值是点的横坐标,纵坐标就是与这个x 的值相对应的y 的值,因此,观察x 或y 的值就是看函数图象上点的横、纵坐标的值,比较函数值的大小就是比较同一个x 的对应点的纵坐标的大小,也就是函数图象上的点的位置的高低。
【例题】1. 如图所示,函数x y =1和34312+=x y 的图象相交于(-1,1),(2,2)两点.当21y y >时,x 的取值范围是( ) A .x <-1 B .—1<x <2 C .x >2D . x <-1或x >22. 点A (1x ,1y )和点B (2x ,2y )在同一直线y kx b =+上,且0k <.若12x x >,则1y ,2y的关系是: ( )A 、12y y >B 、12y y <C 、12y y =D 、无法确定. 3.已知一次函数3+=kx y 的图象如图所示,则不等式03<+kx 的解集是 。
4.如图,一次函数()0y kx b k =+<的图象经过点A.当3y <时,x 的取值范围是 .5.如图5,直线1l :1+=x y 与直线2l n mx y +=相交于点P )2,(a ,则关于x 的不等式1+x ≥n mx +的解集为 。
(图6)6.如图6,直线y =kx +b 经过A (-1,1)和B (-7,0)两点,则不等式0<kx +b <-x 的解集为_ . 考点8:一次函数解析式的确定 【例题】1.已知y+m 与x+n 成正比例(m ,n 为常数)。
(1) 试说明y 是x 的一次函数(2) 当x=-3时,y=5,当x=2时,y=2,求y 与x 之间的函数关系式。
2.已知Y 与X 成正比例,Z 与X 成正比例,当Z=3时,Y=-1;当X=2/3时,Z=4,则Y 与X 的函数关系式为?3.如图,直线l 过A 、B 两点,A (0,1-),B (1,0),则直线l 的解析式为 .4. 已知一次函数y=kx+b 的图像经过两点A(1,1),B(2,-1),求这个函数的解析式.5. 一个矩形被直线分成面积为x ,y 的两部分,则y 与x 之间的函数关系只可能是 ( )6. 设min {x ,y }表示x,y 两个数中的最小值,例如min {0,2}=0,min {12,8}=8,则关于x 的函数y=min{2x ,x+2},y 可以表示为( )A. ()()2222xx y x x <⎧⎪=⎨+≥⎪⎩ B.()()2222x x y xx +<⎧⎪=⎨≥⎪⎩C. y =2xD. y =x +2图5x y BA O7.已知:一次函数y kx b =+的图象经过M (0,2),(1,3)两点. (l) 求k 、b 的值;(2) 若一次函数y kx b =+的图象与x 轴的交点为A (a ,0),求a 的值.8.如图,在平面直角坐标系中,A 、B 均在边长为1的正方形网格格点上.(1)求线段AB 所在直线的函数解析式,并写出当02y ≤≤时,自变量x 的取值范围; (2)将线段AB 绕点B 逆时针旋转90,得到线段BC ,请画出线段BC .若直线BC 的函数解析式为y kx b =+,则y 随x 的增大而 (填“增大”或“减小”).考点9:与一次函数有关的几何探究问题(动点)【例题】1.如图6,在平面直角坐标系中,直线4:43l y x =-+分别交x 轴、y 轴于点A B 、,将 AOB △绕点O 顺时针旋转90°后得到A OB ''△. (1)求直线A B ''的解析式;(2)若直线A B ''与直线l 相交于点C ,求A BC '△的面积.2.在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x ,y 轴分别交于点A ,B ,则△OAB 为此函数的坐标三角形.(1)求函数y =43-x +3的坐标三角形的三条边长; (2)若函数y =43-x +b (b 为常数)的坐标三角形周长为16, 求此三角形面积.AyOB x图6CA y x OlA 'B 'xyOA B3.如图,直线PA 是一次函数1y x =+的图象,直线PB 是一次函数22y x =-+的图象.(1)求A 、B 、P 三点的坐标;(6分) (2)求四边形PQOB 的面积;(6分)4.如图,在平面直角坐标系中,一次函数5+=kx y 的图象经过点 A (1,4),点B 是一次函数5+=kx y 的图象与正比例函数x y 32=的图象的交点。
