第6章 分配与网络模型
计算机网络教案(第6章)

6.3.3 数字数据网DDN
数字数据网(DDN,Digital Data Network)是利用数字信 道传输数据信号的数据传输网。 它的传输媒介主要是光缆,辅助于数字微波、 卫星信道 以及用户端可用的普通电缆和双绞线。 在现有的电信网(电话网或分组交换网)中,都有模拟成分 存在,需要许多模数转换及调制解调设备。而DDN则以 全数字、高速率及灵活的交叉连接复用功能为用户提供 永久性或半永久性的数字电路专线(出租)业务,为用户构 建了一个大容量的数据通信平台。数字信道与传统的模 拟信道相比,具有传输质量高、速度快、带宽利用率高 等一系列优点。
基于 ADSL 的接入网 端局或远端站 ATU-C PS 电话 分路器 用户线 PS ATU-R
区域宽带网
ATU-C ATU-C DSLAM
图3-32
至本地电话局
居民家庭
基于ADSL的接入网的组成
§6.4
异步传输方式ATM
1 ATM概述
1972年ITU-T提出了综合业务数字网(ISDN)的概 念。特别是80年代初制定的一整套关于ISDN的系列建 议,奠定了ISDN发展的基础。鉴于当时技术能力和业 务需求的限制,首先提出的只能是窄带综合业务数字网 (N-ISDN)。
2.7~3.6 km
1.4 km 0.9 km 0.3 km 4.ADSL中的“D(数字)”应理解为“使 用数字技术”。ADSL的用户线上传送 的仍然是模拟信号而不是数字信号。 ADSL在现成的用户线(铜线)的两端 各安装一个ADSL调制解调器。我国目 前采用的方案是离散多音调DMT (Discrete Multi-Tone) 调制技术。
第六章同化物的运输与分配

收缩蛋白学说
该学说的基本要点是: 第一,筛管内的P-蛋白是空心的管状物,成束贯穿于筛孔,P-蛋白的 收缩可以推动汁液流动。筛孔周围的胼胝质的产生与消失对这种蠕动进 行生理调节。 第二,空心管壁上有大量的由P-蛋白组成的微纤丝(毛),一端固定, 一端游离于筛管细胞质内,似鞭毛一样的颤动,驱动空心管内的物质脉 冲状流动。P-蛋白的收缩需要消耗代谢能量,它的作用是将化学能转变 为机械能,作为代谢动力推动液流流动。
2、维管束的功能
(1)物质长距离运输的通道
最基本最重要的功能
(2)信息物质传递的通道
信息物质主要指内源激素
(3)两通道间的物质交换 (4)对同化物的吸收与分泌 (5)对同化物的加工与储存 (6)外源化学物质及病毒等传播的通道 (7)植物体的机械支持
(二)物质运输的途径
1、研究物质运输途径的方法 (1)环割试验法
(三)转移细胞(transfer cells,TC)
在共质体与质外体的交替运输过程中,需要一种特化的薄壁细胞对物质起 转运过渡的作用,这种细胞称转移细胞 (也叫转运细胞,传递细胞)。
结构特点: 细胞壁及质膜内突生长,形成折叠片层。
功能: 1 扩大质膜的表面积,增加物质质膜内外 转运的面积; 2 质膜折叠有利于囊泡的形成,同样有利 于质膜内外物质运输。
3、韧皮部运输
韧皮部的结构与功能的一致性:
韧皮部
筛管、伴胞复合体(Sieve ElementCompanion Cell, SE-CC复合体)
成熟筛管分子的细胞质中只剩下质膜、 内质网、质体和线粒体。
筛管的细胞质中含有与阻断物质运输 有关的韧皮蛋白(P-蛋白)和胼胝质等。
筛管 伴胞 薄壁细胞
切面积×时间)=运转物浓度×运输速度
第6章(192)

第6章 神经控制系统
6.2.5 神经网络智能方法 神经网络的学习功能是一种智能行为,它与其它智能学
科有相同或相近的设计方式。将神经网络与模糊控制、人工 智能、专家系统相结合,可构成各具特色的模糊神经控制、 智能神经控制、专家神经系统等,它们形成了自己的设计方 法。一种典型的模糊神经控制系统的基本结构如图6-8所示。
第6章 神经控制系统
神经网络从根本上改变了上述设计思路,因为它不需要 被控制对象的数学模型。在控制系统中,神经网络是作为控 制器或辨识器起作用的。
控制器具有智能行为的系统,称为智能控制系统。在 智能控制系统中,有一类具有学习能力的系统,被称为学习 控制系统。学习的过程是一个训练并带有将训练结果记忆的 过程,人工神经网络控制系统就是一种学习控制系统。
第6章 神经控制系统
对于一些在控制过程中存在不确定性、存在非线性、存 在时变的被控对象,由于数学模型不明确,常规PID调节器 往往难以奏效,不能保证系统稳定性。目前能够想到的解决 办法有两个,两个办法都离不开神经网络。一个是对被控对 象使用系统辨识,PID调节器继续使用常规调节器,系统辨 识由神经网络承担;另一个是使用神经PID调节器。在系统 中引入神经网络,相应需要学习训练。
第6章 神经控制系统
由于神经控制器的设计与设计人员的素质、理解能力和 经验有关,因此设计出来的产品都可以成为设计者的成果, 这也是从事神经控制较容易出成果的原因之一。随着时间的 推移,对设计结果的评价体系终会诞生,优劣将更加清晰。
简单综合起来,神经控制器的设计方法大体有如下几种: 模型参考自适应方法、自校正方法、内模方法、常规控制方 法、神经网络智能方法和神经网络优化设计方法。
第6章计算机网络知识

大学计算机基础
各层次最主要功能归纳
应用层——与用户应用进程的接口,即相当于“做什么? ” 表示层——数据格式的转换,即相当于“对方看起来像什 么?” 会话层——会话的管理与数据传输的同步,即相当于“轮 到谁讲话和从何处讲?” 传输层——从端到端经网络透明的传送报文,即相当于“ 对方在何处?” 网络层——分组交换和路由选择,即相当于“走哪条路可 到达该处?” 数据链路层——在链路上无差错的传送帧,即相当于“每 一步该怎么走?” 物理层——将比特流送到物理媒体上传送,即相当于“对 上一层的每一步应该怎样利用物理媒体?”
大学计算机基础
网络传输介质与网络设备
4.无线传输介质 无线通信介质中的红外线、激光、微波或其他无 线电波由于不需要任何物理介质,非常适用于特殊场 合。它们的通信频率都很高,理论上都可以承担很高 的数据传输速率。 (1)无线电短波通信 (2)微波传输 (3)红外线
大学计算机基础
网络传输介质与网络设备
6.1.4 计算机网络的拓扑结构
1.总线型结构 在总线型拓扑结构中,局域网的各结点都连接 到一条单一连续的物理线路上,如图2-2所示。网上 任何一个结点的信息都可以沿着总线向两个方向传 输扩散,并且能被总线中任何一个结点所接受。
大学计算机基础
计算机网络拓扑结构的优缺点
优点: 结构简单灵活 方便设备扩充 网络速度很快 设备量较少 价格低廉 安装方便 共享资源能力强 便于广播式工作 缺点: 对线路故障敏感 只能有一个节 点来发送数据 线路上任何一处 故障会导致整个 网络的瘫痪
大学计算机基础
计算机网络系统的组成
6.1 计算机网络系统组成 6.1.1 计算机网络
计算机网络是利用网络设备和通讯线路把分布在 不同地理位置的多台计算机系统连接起来,运行网络 系统软件,实现网络资源共享的通信的系统。
计算机网络习题第6章 局域网
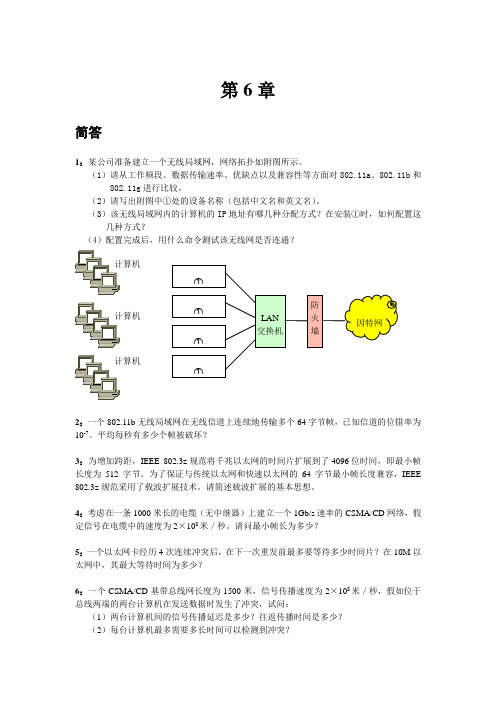
第6章简答1:某公司准备建立一个无线局域网,网络拓扑如附图所示。
(1)请从工作频段、数据传输速率、优缺点以及兼容性等方面对802.11a 、802.11b 和802.11g 进行比较。
(2)请写出附图中①处的设备名称(包括中文名和英文名)。
(3)该无线局域网内的计算机的IP 地址有哪几种分配方式?在安装①时,如何配置这几种方式?(4)配置完成后,用什么命令测试该无线网是否连通?2:一个802.11b 无线局域网在无线信道上连续地传输多个64字节帧,已知信道的位错率为10-7。
平均每秒有多少个帧被破坏?3:为增加跨距,IEEE 802.3z 规范将千兆以太网的时间片扩展到了4096位时间,即最小帧长度为512字节。
为了保证与传统以太网和快速以太网的64字节最小帧长度兼容,IEEE 802.3z 规范采用了载波扩展技术。
请简述载波扩展的基本思想。
4:考虑在一条1000米长的电缆(无中继器)上建立一个1Gb/s 速率的CSMA/CD 网络,假定信号在电缆中的速度为2×108米/秒。
请问最小帧长为多少?5:一个以太网卡经历4次连续冲突后,在下一次重发前最多要等待多少时间片?在10M 以太网中,其最大等待时间为多少?6:一个CSMA/CD 基带总线网长度为1500米,信号传播速度为2×108米/秒,假如位于总线两端的两台计算机在发送数据时发生了冲突,试问:(1)两台计算机间的信号传播延迟是多少?往返传播时间是多少?(2)每台计算机最多需要多长时间可以检测到冲突?7:为什么IEEE 802标准中要把数据链路层分为逻辑链路控制子层和介质访问控制子层?8:局域网基本技术中有哪几种拓朴结构、传输媒体和介质访问控制方法?填空9:在10BASE-T和100BASE-T以太网中,RJ-45连接器的引脚和用于发送,引脚和用于接收。
10:CSMA/CD介质访问控制方法采用了二进制指数退避算法来计算重传前的退避时间,算法如下:(1)确定基本退避时间片T= 。
计算机应用基础课件 第6章 计算机网络基础及Internet应用

目前,我国在接入Internet网络基础设施上进行了大规模的投入,已建成中
国公用分组交换数据网(ChinaPAC)和中国公用数字数据网(ChinaDDN)。
9
6.1 计算机网络基础
6.1.3 相关知识点
3.计算机网络的基本组成
通信子网:计算机网络中实现网络通信功能的设备及其软件的集合。通 信子网由网卡、线缆、集线器、中继器、网桥、路由器、交换机等设备 和相关软件组成。 资源子网:计算机网络中实现资源共享功能的设备及其软件的集合。资 源子网由联网的服务器、工作站、共享的打印机,以及其他设备和相关
目前局域网中最常见的3个协议是Microsoft的NetBEUI、Novell的
IPX/SPX和交叉平台TCP/IP。
16
6.1 计算机网络基础
6.1.3 相关知识点
6.计算机网络的体系结构和协议
TCP/IP:TCP/IP(Transmission Control Protocol/Internet Protocol)即 传输控制协议/互联网协议。 TCP/IP实际上是一组协议,包括上百个功能的协议,如:远程登录、文 件传输、电子邮件等,而TCP和IP是其中保证数据完整传输的两个基本协 议,目前是Internet最基本的协议。
第2代计算机网络
20世纪60年代中期,出现了若干台计算机互连的系统,这些计算机之间不 但可以实现彼此通信,还可以实现计算机间的资源共享。这种实现计算机之
间的通信,并以资源共享为目的的计算机通信网络称为第2代计算机网络。
7
6.1 计算机网络基础
6.1.3 相关知识点
第3代计算机网络 20世纪70年代,产生了局域网和广域网。1983年,国际标准化组织提出了 著名的开放系统互连参考模型(Dpen System Interconnect,OSI),为计 算机网络的发展提供了标准,使得计算机网络走上了标准化的轨道。体系结 构标准化的计算机网络称为第3代计算机网络。 第4代计算机网络 20世纪80年代中后期,Internet在美国出现。此后,许多其他计算机网络开 始相继接入Internet,使得Internet成为计算机网络领域中发展最快、接入用 户数最多的国际互联网。Internet的飞速发展和广泛应用,标志着计算机网 络进入了高速发展的崭新阶段——第4代计算机网络,也标志着人类社会进 入了信息化时代。
运筹学第六章图与网络分析

S
2
4
7
2 A
0 5
S
5 45 B
98
14
5
13
D
T
C
E
4
4
4
7
最短路线:S AB E D T
最短距离:Lmin=13
2.求任意两点间最短距离的矩阵算法
⑴ 构造任意两点间直接到达的最短距离矩阵D(0)= dij(0)
S A B D(0)= C D E T
SABCDET 0 25 4 2 02 7 5 20 1 5 3 4 1 0 4 75 0 15 3 41 0 7 5 7 0
e1 v1
e5
v0 e2
e3
v2
e4
e6 e7
v3
v4
(4)简单图:无环、无多重边的图称为简单图。
(5)链:点和边的交替序列,其中点可重复,但边不能 重复。
(6)路:点和边的交替序列,但点和边均不能重复。
(7)圈:始点和终点重合的链。
(8)回路:始点和终点重合的路。
(9)连通图:若一个图中,任意两点之间至少存在一条 链,称这样的图为连通图。 (10)子图,部分图:设图G1={V1,E1}, G2={V2,E2}, 如果有V1V2,E1E2,则称G1是G2的一个子图;若 V1=V2,E1E2,则称G1是G2的一个部分图。 (11)次:某点的关联边的个数称为该点的次,以d(vi)表示。
步骤:
1. 两两连接所有的奇点,使之均成为偶点;
2. 检查重复走的路线长度,是否不超过其所在 回路总长的一半,若超过,则调整连线,改 走另一半。
v1
4
v4
4
1
4
v2
v5
5
第六章 公共政策过程的理论模型

第六章公共政策过程的理论模型第一节模型及其认识论意义一、模型的含义1.简单地讲,模型就是对原型的抽象与模拟(仿真)。
它是认识主体为着一定的认识目的,依据相似性原则而构造出来的一种理念系统,以代表作为研究对象的真实系统即实际存在的事物。
2.模型有实物模型和理论模型之分。
3.公共政策分析中运用的模型一般是理论模型。
所谓理论模型或者概念模型,指的是一组概念或命题按照其相互间的本质联系被组织在一起,从而形成的一个逻辑结构严整的网络或框架。
二、模型的认识论意义第一,由于模型与原型具有相似性,因此通过解释模型而认识原型的某种本质规定性。
第二,模型是进行科学抽象的重要工具。
它能够使人们从某一特定的视角窥视到万象纷繁的现实事物的奥秘并发现其运动规律,从而使研究对象的本质特征得以凸显。
第三,模型是研究过程中资料搜集和经验观察的指南,向研究者指出了研究工作的重点和优先顺序。
三、公共政策模型必备的条件第一,必须明确把握社会发展方向。
第二,必须与宏观政策密切相关,即具备包容各项微观、具体政策的宏观特性。
第三,必须建立在注重人文特点的行为科学与注重科学程序和方法的管理科学二者相互交融的基础上。
第四,必须对宗教、意识形态等大量非理性因素持客观态度。
第五,须对时间非常敏感,并且具有历史色彩,即具有历时观察的功能。
四、为什么在进行公共政策分析时需要借助于模型呢?第一,公共政策学研究的对象是具体的,具有客观实在性,因此这门学科具有突出的实证性;同时整个研究过程又十分强调从中发现有关因素之间的因果关系或一定的相关性。
第二,决策程序是根据模型的特征,人为地编制出的政策制定与执行的步骤顺序。
通过它就可以把决策理论、方法与实践结合起来,形成一个可实施的决策流程图,即格式化、标准化、工程化的决策程序,减少决策失误,保证决策的科学性。
第二节基于西方经验的政策过程理论模型一、揭示认识论本质的政策过程理论模型政策制定者是全智全能,还是在主客观条件的限制下认识外部世界;对事物的客观规律的认识是一次完成的,还是一个渐进的从相对真理到绝对真理的过程;围绕着这样一条主线展开的,由此形成了一系列理论分析的框架或者理论模型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6.1
运输问题
这样,经过修改的问题的最优解将会代表实际运输的货物的运输 成本(从虚拟起点出发的线路没有实际运输发生)。当我们执行这个 最优解时,目的地节点处显示的运输量是这个节点需求不被满足的货 物短缺量。 2、最大化目标函数 在某些运输问题中,目标是要找到最大 化利润或者收入的解决方案。这种情况下我们只要把单位利润或者收 入作为一个系数列入目标函数中,简单地把最小改成最大,约束条件 不变,就可求得线性规划的最大值而不是最小值。 3、路线容量和或路线最小量 运输问题的线性规划模型也能 够包含一条或者更多的路线容量或者最小数量问题。例如,假设在福 斯特公司发电机问题中,约克——波士顿路线(起点3到终点1)因为 其常规的运输模式中有限空间的限制,只有1000单位的运输能力。用 x31表示约克——波士顿线路的运输量,那么这条线路的运输能力约束 为:x31 ≤ 1000,类似地,路线的最小量也可以确定下来。
j——终点下标,j=1,2,...,n;
xij——起点i到终点j之间的运输量; cij——起点i到终点j之间的单位运输成本;
si——起点i的供应量或者生产能力;
dj——终点j的需求量。 m个起点,n个终点的运输问题的线性规划的一般模型如下:
6.1
min
运输问题
c x
i 1
n
m个起点,n个终点的运输问题的线性规划的一般模型如下:
1.总的代理(供给)数不等于总的任务(需求)数。
2.目标函数最大化。 3.不可接受的分配。 代理数不等于任务数时的情形和运输问题中总供给不等于总需求时 类似。在线性规划模型中,如果代理数多于任务的数量,多余的代理将 不被指派。如果任务数多于代理数,那么线性规划模型就没有可行的解 决方案。在这种情况下,一种简单的修正方法就是加入足够多的虚拟代 理,使代理数等于任务数。
6.2 指派问题
很多决策过程都会产生指派问题。指派问题中一个很明显的特征 是一个代理只分配给一个任务,仅仅一个任务,特别是我们寻找一组 能够最优化所设立的目标的分配,例如成本最小、时间最短或者利润 最大。 为了阐述指派问题,让我们来看看福尔市场调查公司的案例,这 个公司刚刚从3个新客户那里获得市场调查项目。公司面临着给每一 个客户分配一个项目负责人的任务。最近有3个项目负责人手上没有 其他任务,可以被分配。这3个项目具有相似的优先顺序,公司希望 分配的项目负责人完成这3个项目所需总时间最短。如果每个客户只 需要一个项目负责人,那么该怎么分配?
m n
s.t.
j 1
ij ij
x
j 1
ij
si
i=1,2,...,m j=1,2,...,n
供给 需求
xij d j
i 1
m
xij ≥ 0,对所有i和j 就如先前我们提到的,如果从起点i到终点j之间的运输容量为Lij, 可以在约束里加一个xij ≤ Lij,一个包含了这种类型的约束条件的运 输问题就称为有容量限制的运输问题。类似地,如果起点i到终点j之 间必须处理的运输容量最小为Mij,那么我们在约束条件里加上最小运 输容量约束xij ≥ Mij。
6.1
运输问题
例如,x22 ≥ 2000,这个约束条件保证了最优解中保留先前承诺
的最小2000单位的订单。 4、不可接受的路线 最后一种情况,构建从每一个起点到终
点的路线并不都是可能的。为了处理这种情况,我们只需要简单地去
除网络图中相里 夫兰——圣路易斯之间的路线是不可接受的或者是不可用的,那么在
6.1
运输问题
比较线性规划模型与图6-1中的网络,会发现几个观察值。所有
线性规划模型所需的信息都能在网络图中找到,每个节点需要一个约 束条件,每一条弧需要一个变量。对应的每个起点节点出发的每条弧 上的变量值之和必须小于或者等于这个起点节点的供给,对应的去往 每个目的地节点的弧上的变量值之和必须等于这个目的地节点的需求
xij
cij=把代理i指派给任务j所花的成本
6.2 指派问题
该一般线性规划模型如下所示: m n min cij xij
i 1 j 1
s.t.
x
j 1
m i 1
n
ij
1
1
i=1,2,...,m j=1,2,...,n 对所有的i和j
代理 任务
x
ij
xij ≥ 0 ,
6.2 指派问题
西北农林科技大学
第六章 分配与网络模型
教 师:朱玉春 教授 单 位:经济管理学院
2011年
本章主要内容
6.1 6.2 6.3 6.4 6.5 6.6
运输问题 指派问题 转运问题 最短路径问题 最大流问题 生产和库存应用
6.1
运输问题
运输问题经常出现在计划货物配送和从某些供给地区到达某些需
为了解决这个指派问题,福尔的管理层必须首先考虑所有可能的 负责人——客户的分配方法,然后预测相对应的完成项目所需的时间。 3个项目负责人和3个客户可以产生9种分配方案。
6.2 指派问题
6.2 指派问题
图6-2是福尔公司指派问题的一个网络图。节点对应着项目负责 人和客户,弧代表项目负责人——客户之间的可能分配。每个起点节 点的供给和终点节点的需求都是1;把一个项目负责人指派给一个客 户的成本是这个负责人完成客户的市场调研任务所需的时间。注意指 派问题的网络图(图6-2)和运输问题的网络图(图6-1)之间的相似 性。这个指派问题其实就是运输问题的一个特殊情形,其中所有的供 给和需求量都是1,每条弧的运输量不是1就是0。 因为这个指派问题就是运输问题的一个特殊实例,那么可以设计 一个线性规划模型。定义福尔公司指派问题的决策变量为: xij 1,如果项目负责人i被分配给客户j 这里,i=1,2,3;j=1,2,3。 0,其他情况
6.1
Max
运输问题
3x11+2x12+7x13+6x14+7x21+5x22+2x23+3x24+2x31+5x32+4x33+5x34
s.t. x11+x12+x13+x14 ≤ 5000 x21+x22+x23+x24 ≤ 6000 x31+x32+x33+x34 ≤ 2500 x11+x21+x31 = 6000 x12+x22+x32 = 4000 x13+x23+x33 = 2000 x14+x24+x34 = 1500 xij ≥ 0, 克里夫兰供给 贝德福德供给 约克供给 波士顿需求 芝加哥需求 圣路易斯需求 莱克星顿需求 其中,i=1,2,3;j=1,2,3,4
图6-1中,从克里夫兰到圣路易斯之间的这条弧应当删除。线性规划
模型中的变量x13也应当被删除。解决这个有11个变量和7个约束条件 的线性规划模型得出的最优解的同时,也保证了克里夫兰——圣路易
斯之间的线路不被使用。
6.1
运输问题
6.1.2 运输问题的一般线性规划模型
为了表示这个运输问题的一般线性规划模型,我们将用到下列概念: i——起点下标,i=1,2,...,m;
电机的生产能力以及坐落在波士顿、芝加哥、圣路易斯和莱克星顿的
4个分销中心3个月的需求预测,详见教材162页。
6.1
运输问题
6.1
运输问题
6.1
运输问题
管理者想知道从每个加工厂运输到分销中心的产品运
输量应为多少。图6-1显示了12条福斯特公司可以用的配 送路线。这种图称为网络图;圆圈表示节点,连接节点的 线条表示弧。每个起点和目的地都由节点表示,每个可能 的运输路线都由弧表示。供给量写在起始节点边上,需求
量写在每个目的地节点边上。从起始节点到目的地节点之
间运输的货物数量表示了这个网络的流量。注意:直接流 量(从起点到终点)是用带箭头的线条表示的。
6.1
运输问题
对应这个福斯特公司的运输问题的目标是要确定使用哪 些路线以及每条线路上的流量是多少时,使得总的运输成本 最低。每条线路单位产品的运输费用在图6-1中的每条弧上 标明。
6.2 指派问题
比如说,在福尔公司问题中,我们有5个客户(任务)和3个项目
负责人(代理)。在加入两个虚拟的项目负责人后,我们可以建立一 个新的项目负责人与客户数量相等的指派问题。虚拟项目负责人的指 派问题的目标函数系数设为0,这样最优解的值就代表进行指派的实 际所需天数(虚拟负责人的指派是实际上不进行的)。 如果指派的备选方案是根据收入或者利润而不是时间或者成本进 行评价的,那么线性规划模型可以处理成最大化而不是最小化问题。
6.2 指派问题
根据所给信息,我们可以得到一个具有9个变量和6个约束条件 的福尔公司指派问题的线性规划模型:
min s.t. x11+x12+x13 ≤ 1 x21+x22+x23 ≤ 1 x31+x32+x33 ≤ 1 x11+x21+x31 = 1 x12+x22+x32 = 1 x13+x23+x33 = 1 xij 对特瑞的指派 对卡尔的指派 对迈克孟德的指派 客户1 客户2 客户3 10x11+15x12+9x13+9x21+18x22+5x23+6x31+14x32+3x33
≥ 0 ,其中,i=1,2,3;j=1,2,3。
6.2 指派问题
模型的计算机计算结果如下,特瑞被指派给了客户2,卡尔被指 派给了客户3,迈克孟德被指派给了客户1。总的项目完成时间为26 天。
目标函数值 = 26.000
变
量
值
0.000 1.000 0.000
