实验二动态悬挂法测定金属材料的杨氏模量
动态法测量金属的杨氏模量

L L
F S
所以: 所以:E =
F S L L
ES k = L
总结:杨氏模量是反映材料的抗拉或抗压能力。 总结:杨氏模量是反映材料的抗拉或抗压能力。 抗拉 能力
回主页
杨氏模量的测量方法:静态法 动态法(棒状)。 杨氏模量的测量方法:静态法(丝状)和动态法 动态法 静态法: 静态法
近似法和推理法 常用的处理方法:近似法 推理法 近似法 推理法。
近似法: 近似法:阻尼越小,共振频率与固有频率之间的偏移将 越小。虽然阻尼为零的情况在现实不能存在,但尽可能减小 阻尼是可以存在的。因此只要实验中找到节点位置,然后再 节点附近测量其共振频率即可近似为固有频率。 推理法: 推理法:如果在节点附近等间距分别测量不同位置的共 振频率,那么这些测得的共振频率将遵循某个规律,然后根 据该规律通过作图法获得节点处的共振频率(即固有频率)
支撑点节点附近重复测量6 注意每测1次转动测试棒1 (支撑点节点附近重复测量6次,注意每测1次转动测试棒1次)
6.改变试样,分别测量细铜棒和细钢棒的固有频率。
回主页
注意事项
1.因换能器为厚度约为0.1~0.3mm的压电 晶体,用胶粘在0.1mm左右的黄铜片上构成,故极 其脆弱,放置测试棒时一定要轻拿轻放,不能用力, 也不能敲打。 2.调节支撑点保证测试棒在竖直方向上振动。 3.信号源——换能器(放大器)——示波器均 应共“地”。
但是现实情况是,当支撑点真的 指到节点处时,金属棒却无法继续激 发测试棒振动,即使能振动亦无法接 收到振动信号(即观察不到共振现象), 即观察不到共振现象) 最终也无法得到节点处共振频率 。
回主页
面对理论要求与现实困难的冲突,该如何处理?
实验二动态悬挂法测定金属材料的杨氏模量

实验二 动态悬挂法测定金属材料的杨氏模量杨氏模量是工程材料的一个重要物理参数, 它标志着材料抵抗弹性形变的能力。
“静态拉伸法”由于受弛豫过程等的影响不能真实地反映材料内部结构的变化, 对脆性材料无法进行测量。
目前工程技术上常用“动态悬挂法”测量杨氏模量,也是国家标准指定的一种测量方法。
其基本操作是: 将一根截面均匀的试样(棒)悬挂在两只传感器(一只激振, 一只拾振)下面。
在两端自由的条件下, 使之作自由振动。
测出试样的固有基频, 并根据试样的几何尺寸、密度等参数, 测得材料的杨氏模量。
一、实验目的1.用动态悬挂法测定金属材料的杨氏模量。
2.培养学生综合应用物理仪器的能力。
3.学习确定试样节点处共振频率的方法。
二、仪器与用具动态杨氏模量实验仪(包括试样、杨氏模量测试台、信号发生器), 存贮示波器, 电子天平, 螺旋测微器, 游标卡尺三、实验原理对于一根水平放置的细棒, 以水平方向为 轴, 竖直方向为轴, 由棒的横振动方程:044222=∂∂⎪⎪⎭⎫ ⎝⎛+∂∂x yS EJ t y ρ (2.1)用分离变量法解以上方程对圆形棒得: 。
2436067.1fd m l E = (2.2)上两式中, 为杨氏模量, 为棒长, 为棒的直径, 为棒的质量, 为棒的截面积, 为棒的密度。
如果在实验中测定了试样(棒)在不同温度时的固有频率 , 即可计算出试样在不同温度时的杨氏模量 。
在国际单位制中杨氏模量的单位为( )。
本实验的基本问题是测量试样在不同温度时的共振频率。
由信号发生器输出的等幅正弦波信号, 加在传感器I (激振)上。
通过传感器I 把电信号转变成机械振动, 再由悬线把机械振动传给试样, 使试样受迫作横向振动。
试样另一端的悬线把试样的振动传给传感器II (拾振), 这时机械振动又转变成电信号。
该信号经放大后送到示波器中显示。
当信号发生器的频率不等于试样的共振频率时, 试样不发生共振, 示波器上几乎没有信号波形或波形很小。
大学物理实验报告实验35动态悬挂法测定杨氏模量

⼤学物理实验报告实验35动态悬挂法测定杨⽒模量⼤学物理实验教案实验名称:动态悬挂法测定杨⽒模量1 实验⽬的1)⽤动态悬挂法测定⾦属材料的杨⽒模量; 2)培养学⽣综合应⽤物理仪器的能⼒; 3)进⼀步熟悉⽰波器的使⽤。
2 实验仪器YM-2型动态杨⽒模量测试台1台、YM-2型信号发⽣器1台、⽰波器S16B 、天平1台、游标尺和螺旋测微计各⼀只、试样铜棒和不锈钢棒各⼀根。
3 实验原理3.1 实验原理杨⽒模量是⼯业材料的⼀个重要参数,它标志着材料抵抗弹性形变多的能⼒。
本实验将⼀根截⾯均匀的试样棒悬挂在两只传感器(⼀只振荡,⼀只拾振)下⾯,在两端⾃由的条件下,使做⾃由振动。
根据棒的振动⽅程42420y S yx EJ t ρ??+=??求解该⽅程,对圆棒得3241.6067l m E fd =(1)式中l 为棒的长度,d 为棒的直径,m 为棒的质量,f 为固有频率。
⽤悬挂法测量杨⽒模量时,共振频率和固有频率相⽐只偏低0.005%。
在本实验中测得的是共振频率,由于两者相差极⼩,故(1)式中的固有频率f 在数值上可以⽤试样的共振频率代替。
3.2 实验⽅法由(1)式,样品的尺⼨可以⽤卡尺和千分尺测量,质量的测量可以⽤天平。
固有频率f 的测量采⽤动态悬挂法进⾏。
由信号发⽣器输出的正弦波电压,加在传感器(激荡)上,通过传感器(激荡)把电信号转变成为机械振动,再由悬线把机械振动传给试样,使试样受迫做振动,试样另⼀端的悬线把试样的振动传给传感器(拾荡),这时机械振动⼜转变成电信号。
该信号经放⼤器后送到⽰波器中显⽰。
当信号发⽣器的频率不等于试样的共振频率时,试样不发⽣共振,⽰波器上⼏乎没有信号或信号波形或波形很⼩。
当信号发⽣器的频率等于试样的共振频率时,试样发⽣共振。
这时⽰波器上的波形突然增⼤,读出的频率就是试样在常温下的共振频率。
4 教学内容(1)实验装置熟悉及安装(2)实验数据测量1)分别⽤卡尺、千分尺、天平测定试样(铜棒、不锈钢棒)的长度l 、直径d 、质量m ,其中直径d 应在不同位置多次测量取其平均值。
动态法测量金属的杨氏模量

振源
接收
回主页
特殊点
基频振动
特殊点
上页 下页
特殊点
特殊点
一次谐频振动
特殊点
特殊点
特殊点
特殊点
二次谐频振动
特殊点
杨氏模量的介绍:
杨氏模量是描述固体材料抵抗形变能力的物理量,仅取 决于材料本身的物理性质。一条长度为L、截面积为S的金 属丝在力F作用下伸长ΔL。F/S叫应力,其物理意义是金属 数单位截面积所受到的力;ΔL/L叫应变,其物理意义是金属 丝单位长度所对应的伸长量。应力与应变的比叫杨氏模量。
凹槽,悬线可以挂在这些小凹槽上以防止测试棒发生左右 移动 问题二:实验中发现测试棒放置时支撑点磨损导致测试棒 不水平 改进措施:设计实验装置时可将支撑点改装成可上下调动。 问题三:电子仪器在运行过程中会产生机械振动,会对共 振频率的测量产生影响 改进措施:将信号发生器与示波器放在另一张桌子上面
0
x 4 EJ t 2
用分离变量法解方程,于是上式的通解为:
y(x,t) (B1chKx B2shKx B3 cosKx B4 sin Kx)Acos(t )
式中:
1
K 4 EJ
S
2
上式称为频率公式。频率公式对任意形状的截面、不 同边界条件的试样都成立,我们只要用特定的边界条件定 出常数K,代入特定截面的惯量矩J,就可以得到具体条件 下的计算公式了。
l 4S
2
则杨氏模量为: E 1.9978 103 l 4S 2 7.8870 102 l 3m f 2
J
J
该公式适用于各种形状的金属棒(如横截面为圆形、
方形、三角形、多边形金属棒等)对于不同的金属棒,其惯
动态悬挂法测定金属材料的杨氏模量实验报告
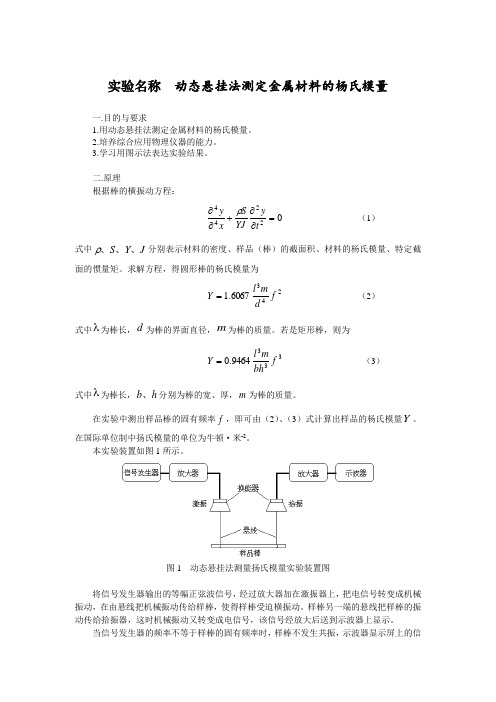
实验名称 动态悬挂法测定金属材料的杨氏模量一.目的与要求1.用动态悬挂法测定金属材料的杨氏模量。
2.培养综合应用物理仪器的能力。
3.学习用图示法表达实验结果。
二.原理根据棒的横振动方程:02244=∂∂+∂∂tyYJ S x y ρ (1) 式中J Y S 、、、ρ分别表示材料的密度、样品(棒)的截面积、材料的杨氏模量、特定截面的惯量矩。
求解方程,得圆形棒的杨氏模量为2436067.1f dm l Y = (2)式中 为棒长,d 为棒的界面直径,m 为棒的质量。
若是矩形棒,则为3339464.0f bhm l Y = (3)式中 为棒长,h b 、分别为棒的宽、厚,m 为棒的质量。
在实验中测出样品棒的固有频率f ,即可由(2)、(3)式计算出样品的杨氏模量Y 。
在国际单位制中扬氏模量的单位为牛顿·米-2。
本实验装置如图1所示。
图1 动态悬挂法测量扬氏模量实验装置图将信号发生器输出的等幅正弦波信号,经过放大器加在激振器上,把电信号转变成机械 振动,在由悬线把机械振动传给样棒,使得样棒受迫横振动。
样棒另一端的悬线把样棒的振动传给拾振器,这时机械振动又转变成电信号,该信号经放大后送到示波器上显示。
当信号发生器的频率不等于样棒的固有频率时,样棒不发生共振,示波器显示屏上的信号的幅度不大。
当信号发生器的信号频率等于样棒的固有频率时,样棒发生共振,示波器上波形幅度突然增大,读出此时的频率为共振频率。
由于样棒的固有频率与共振频率相差甚小,可作为样棒的固有频率。
三.仪器悬挂法杨氏模量测量仪,示波器,低频信号发生器,电子秤,游标卡尺,铜棒和不锈钢圆棒样品。
四.实验内容与步骤1.测定样棒的长度、直径和质量;2.在室温下不锈钢和铜的杨氏模量分别约为11102⨯牛顿·米-2和111021⨯.牛顿·米-2,先估算出共振频率,以便寻找共振点。
3.分别测出不锈钢棒和铜棒的固有频率。
4.利用(2)式分别计算出不锈钢棒和铜棒的扬氏模量。
6动态悬挂法测量金属的杨氏模量

物理实验中心实验指导书动态悬挂法测量金属的杨氏模量动态悬挂法测量金属的杨氏模量杨氏模量是工程材料的一个重要物理参数,它标志着材料抵抗弹性形变的能力。
目前工程技术上常用“动态悬挂法”测量杨氏模量。
其基本方法是:将一根截面均匀的试棒悬挂在两只传感器(一只激振,一只拾振)下面。
在两端自由的条件下,使之自由振动。
测出试件的固有基频,并根据试样的几何尺寸、密度等参数,测得材料的杨氏模量。
一、实验目的1.学习用动态法测量杨氏模量的原理和方法。
2.掌握固有频率和共振频率的概念,了解用示波器观察共振现象的基本方法。
3.了解外延测量法及其适用条件。
4.了解动态法测量杨氏模量的基本过程及其注意事项。
二、实验原理任何物体都有其固有的振动频率,这个固有振动频率取决于试样的振动模式、边界条件、弹性模量、密度以及试样的几何尺寸、形状。
只要从理论上建立了一定振动模式、边界条件和试样的固有频率及其他参量之间的关系,就可通过测量试样的固有频率、质量和几何尺寸来计算弹性模量。
1.杆振动的基本方程一细长杆做微小横(弯曲)振动时,取杆的一端为坐标原点,沿杆的长度方向为x 轴建立坐标系,利用牛顿力学和材料力学的基本理论可推出杆的振动方程:02244=∂∂⋅+∂∂tz EJ S x z ρ (1) 式中),(t x U 为杆上任一点x 在时刻t 的横向位移;E 为杨氏模量;J 为绕垂直于杆并通过横截面形心的轴的惯量矩;ρ为密度。
用分离变量法求解方程得到通解,进而得到杆的振动频率与杨氏模量的关系式,即214⎪⎪⎭⎫ ⎝⎛=S EJ k ρω。
2.杨氏模量的测量杆的振动基频满足条件π506.11=L k ,代入频率公式,同时考虑转动惯量,即可得到振动法测量杨氏模量的公式2436067.1f dmL E = (2) 式中m 为棒的质量,单位为g ,d 为棒的直径,单位为mm ,取L 的单位亦为mm ,f 为基频振动的固有频率,计算出的杨氏模量E 的单位为N/m 2。
动态法测量杨氏模量实验报告

动态法测量杨氏模量实验报告一、实验目的1、学会用动态法测量杨氏模量。
2、掌握共振频率的测量方法。
3、了解实验仪器的使用和数据处理方法。
二、实验原理杨氏模量是描述固体材料抵抗形变能力的物理量。
动态法测量杨氏模量的基本原理是基于振动系统的共振特性。
一根细长的棒,作微小横振动(弯曲振动)时,其振动方程为:$Y=\frac{4ml^3f^2}{d^4}$其中,$Y$为杨氏模量,$m$为棒的质量,$l$为棒的长度,$d$为棒的直径,$f$为棒的共振频率。
当棒在某一频率下发生共振时,振幅达到最大值。
通过测量棒的共振频率、质量、长度和直径,就可以计算出杨氏模量。
三、实验仪器1、动态杨氏模量测量仪:包括激振器、拾振器、示波器等。
2、游标卡尺:用于测量棒的长度和直径。
3、电子天平:用于测量棒的质量。
四、实验步骤1、测量棒的尺寸用游标卡尺在棒的不同位置测量其长度$l$,多次测量取平均值。
在棒的两端和中间部位测量直径$d$,同样多次测量取平均值。
2、安装实验装置将棒的一端固定在支架上,另一端通过细绳连接激振器。
拾振器安装在棒的适当位置,与示波器相连。
3、寻找共振频率开启激振器,逐渐改变其输出频率,同时观察示波器上的信号。
当示波器上显示的振幅达到最大值时,此时的频率即为共振频率$f$。
4、测量质量用电子天平测量棒的质量$m$。
5、重复测量改变拾振器的位置,重复上述步骤,测量多组数据。
五、实验数据记录与处理1、实验数据记录|测量次数|长度$l$ (mm) |直径$d$ (mm) |共振频率$f$ (Hz) |质量$m$ (g) ||::|::|::|::|::|| 1 |______ |______ |______ |______ || 2 |______ |______ |______ |______ || 3 |______ |______ |______ |______ |2、数据处理计算长度$l$、直径$d$、共振频率$f$和质量$m$的平均值。
动态法测定金属杨氏模量

量时,Q值的最小值约为50,所以共振频率和固有频率相比
0.776L 由于节点处的振动幅度几乎为零,很难激振和检测,所
可以计算出试样在此温度时的杨氏模量。系。
②长对到于 待脆求性值➢材范由料围不,于能在用延节拉长伸线点法部测分处量求出的所要振的值动。 幅度几乎为零,很难激振和检测,所
直径d(mm)
d7 .93 0 .5 00 m5 m
? f 共
本次实验的重点, 用外推法找出节点的共振频率
外推法的引入 外推法:所需数据在测量范围之外,为了求得这个数值,
其中K0 L = 0的根对应于静止状态, K1 L= 4.
005%,故实验中都是用 f共 代替 f固。
静态法:光杠杆放大原理,把及其微小
动态法测定金属杨氏模量
一、课题引入
?杨氏模量是工程材料的重要参数,它是描述材料刚性特
征的物理量,它反应材料形变(应变)与内应力之间的关系。
杨氏模量的测量方法:静态法(丝状)和动态法(棒状)。
➢ 静态法简单原理:F E L SL
缺点:①不能很真实地反映材料内部结构的变化 ②对于脆性材料不能用拉伸法测量 ③不能测量材料在不同温度下的杨氏模量
➢ 动态法优点:①能准确反映材料在微小形变时的物理性能 ②测得值精确稳定 ③对软脆性材料都能测定 ④温度范围极广(−196 ℃ ~ +2600℃)
二、实验简介
“动态法”通常采用悬挂法(或支撑法),将金属试样用 两 根悬线悬挂起来(或用两个支持点支撑起来),并激发它做弯 曲振在动一。定条件下,试样振动的固有频率取决于它的几何形 状、尺寸、质量以及它的杨氏模量,如果我们在实验中测出 一定温度下试样的固有频率、几何形状、尺寸、质量等,就 可以计算出试样在此温度时的杨氏模量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验二 动态悬挂法测定金属材料的杨氏模量
杨氏模量是工程材料的一个重要物理参数,它标志着材料抵抗弹性形变的能力。
“静态拉伸法”由于受弛豫过程等的影响不能真实地反映材料内部结构的变化,对脆性材料无法进行测量。
目前工程技术上常用“动态悬挂法”测量杨氏模量,也是国家标准指定的一种测量方法。
其基本操作是:将一根截面均匀的试样(棒)悬挂在两只传感器(一只激振,一只拾振)下面。
在两端自由的条件下,使之作自由振动。
测出试样的固有基频,并根据试样的几何尺寸、密度等参数,测得材料的杨氏模量。
一、实验目的
1、用动态悬挂法测定金属材料的杨氏模量。
2、培养学生综合应用物理仪器的能力。
3、学习确定试样节点处共振频率的方法。
二、仪器与用具
动态杨氏模量实验仪(包括试样、杨氏模量测试台、信号发生器),存贮示波器,电子天平,螺旋测微器,游标卡尺
三、实验原理
对于一根水平放置的细棒,以水平方向为x 轴,竖直方向为轴,由棒的横振动方程:
04
42
22=∂∂⎪⎪⎭⎫ ⎝⎛+∂∂x y
S EJ t y ρ (2.1)
用分离变量法解以上方程对圆形棒得:。
2
436067.1f
d m l E = (2.2)
上两式中,E 为杨氏模量,l 为棒长,d 为棒的直径,m 为棒的质量,S 为棒的截面积,ρ为棒的密度。
如果在实验中测定了试样(棒)在不同温度时的固有频率f ,即可计算出试样在不同温度时的杨氏模量E 。
在国际单位制中杨氏模量的单位为(2
-⋅m N )。
本实验的基本问题是测量试样在不同温度时的共振频率。
由信号发生器输出的等幅正弦波信号,加在传感器I (激振)上。
通过传感器I 把电信号转变成机械振动,再由悬线把机械振动传给试样,使试样受迫作横向振动。
试样另一端的悬线把试样的振动传给传感器II (拾振),这时机械振动又转变成电信号。
该信号经放大后送
到示波器中显示。
当信号发生器的频率不等于试样的共振频率时,试样不发生共振,示波器上几乎没有信号波形或波形很小。
当信号发生器的频率等于试样的共振频率时,试样发生共振。
这时示波器上的波形突然增大,这时读出的频率就是试样在该温度下的共振频率。
根据(2.2)式,即可计算出该温度下的杨氏模量。
图2.1 试样共振频率的测量
四、实验内容
1、测定试样的长度l 、直径d 和质量m ,每个物理量各测5次。
2、在室温下,不锈钢和铜的杨氏模量分别为11
102⨯(2
-⋅m N )和11102.1⨯(2
-⋅m N ),先由(2.2)式估算出共振频率f ,以便寻找共振点。
3、把试样棒用细钢丝挂在测试台上,悬挂点的位置约距离端面l 1.0和l 9.0处。
4、把信号发生器的输出与测试台的输入相连,测试台的输出与放大器的输入相接,放大器的输出与示波器的Y 输入相接。
5、把示波器触发信号选择开关置于“内置”(①②都置于左边),y 轴增益④置于最小档(左边第二档),y 轴极性置于“AC”。
6、由小到大逐渐调节信号发生器的频率,并观察示波器信号的变化,当示波器的拾振信号(交流信号)在某一频率处达到极大,则认为信号发生器的激振频率与测试棒共振,记下该频率f 因试样共振状态的建立需要有一个过程,且共振峰十分尖锐,因此在共振点附近调节信号频率时,必须十分缓慢地进行,(建议间隔Hz 1.0),直至示波器的显示屏上出现最大的信号。
7、将两悬丝以每间隔l 02.0向里靠拢,分别记下频率2f 、3f ……,直到悬挂点处于
l 224.0和l 776.0处。
8、以l 为横坐标,f 为纵坐标,作图(如图2.2),将图线延伸至l 224.0处所对应的f 即为该棒的固有频率。
9、记下室温下的共振频率f ,求出材料的杨氏模量E ,计算不确定度。
10、本实验用铜棒和钢棒各做一次。
五、实验数据
Δd=0.02mm Δl=0.01mm Δm=0.0001g
不锈钢
l/mm d/mm m/g 前端悬点f/Hz 末端悬点测量次数长度测量次数长度测量次数质量0.10L 1196.7 0.90L
1 149.8 1 6.051 1 33.543
2 0.12L 1195.9 0.88L
2 149.82 2 6.051 2 33.54
3 0.14L 1195.8 0.86L
3 149.8 3 6.02 3 33.5435 0.16L 1195.5 0.84L
4 149.8 4 6.01
5 4 33.5433 0.18L 1195.4 0.82L
5 149.8 5 6.015 5 33.5434 0.20L 1195.2 0.80L 平均值149.864 平均值 5.9764 平均值33.54328 0.22L 1195 0.78L 有效值149.8
6 有效值 5.976 有效值33.5433 平均值1195.642857
铜棒
l/mm d/mm m/g 前端悬点f/Hz 末端悬点测量次数长度测量次数长度测量次数质量0.10L 784.3 0.90L
1 149.9
2 1 5.97 1 35.1212 0.12L 784.1 0.88L
2 149.94 2 5.965 2 35.1212 0.14L 783.9 0.86L
3 149.92 3 5.96 3 35.1211 0.16L 787.
4 0.84L
4 149.92 4 5.96
5 4 35.1208 0.18L 787.2 0.82L
5 149.92 5 5.955 5 35.1209 0.20L 787.1 0.80L 平均值149.92 平均值 5.8992 平均值35.121 0.22L 787 0.78L 有效值149.92 有效值 5.899 有效值35.121 平均值785.8571429。
