《相似三角形的判定》两角定理。课件
合集下载
相似三角形的判定定理课件
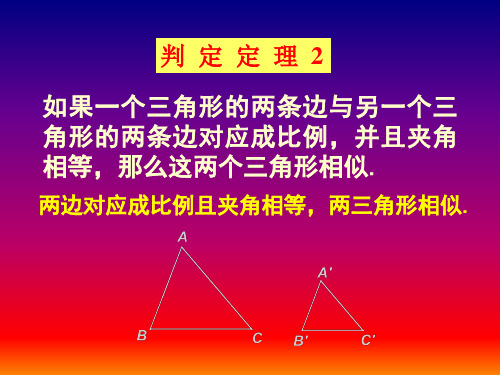
个三角形相似
•角角边定理 •边边边公理 •斜边、直角 边公理
•两 边 对 应 成 比 例 且 夹角相等,两三角 形相似.
•三边对应成比例, 两三角形相似.
例1:根据下列条件,判定△ABC和△A´B´C´
是否相似,并说明理由.
•∠A=120°,AB=7厘米,AC=14厘米,
∠A´=120°,A´B´=3厘米,A´C´=6厘米;
图
的判定方法 的判定方法
形
•定义 •边角边公理 •角边角公理
•定义 •定理 •两角对应相等,两
个三角形相似
•角角边定理 •边边边公理 •斜边、直角
•两 边 对 应 成 比 例 且 夹角相等,两三角 形相似.
边公理
全等三角形 相似三角形
图
的判定方法 的判定方法
形
•定义 •边角边公理 •角边角公理
•定义 •定理 •两角对应相等,两
挑战自我
三个边长为a的正方形ABEG、GEFH 和HFCD,矩形对角线AC的长是 ;
已知:如图,四边形ABEG 、GEFH 、 HFCD都是边长为a的正方形. 求证:△AEF∽△CEA.
证法1:∵正方形ABEG的边长为a,
证法1:∵正方形ABEG的边长为a, ∴AE= a .
证法1:∵正方形ABEG的边长为a, ∴AE= a . 在△AEF和△CEA中, AE∶EF= a∶a= . EC∶EA=2a∶ a= .
证法2:根据题意,可得 AE= a ,AF= a , AC= a . 在△AEF和△CEA中, AE∶EF= a∶a= , EC∶EA=2a∶ a= , CA∶AF = a∶ a= , ∴AE∶EF= EC∶EA= CA∶AF.
证法2:根据题意,可得 AE= a ,AF= a , AC= a . 在△AEF和△CEA中, AE∶EF= a∶a= , EC∶EA=2a∶ a= ,
•角角边定理 •边边边公理 •斜边、直角 边公理
•两 边 对 应 成 比 例 且 夹角相等,两三角 形相似.
•三边对应成比例, 两三角形相似.
例1:根据下列条件,判定△ABC和△A´B´C´
是否相似,并说明理由.
•∠A=120°,AB=7厘米,AC=14厘米,
∠A´=120°,A´B´=3厘米,A´C´=6厘米;
图
的判定方法 的判定方法
形
•定义 •边角边公理 •角边角公理
•定义 •定理 •两角对应相等,两
个三角形相似
•角角边定理 •边边边公理 •斜边、直角
•两 边 对 应 成 比 例 且 夹角相等,两三角 形相似.
边公理
全等三角形 相似三角形
图
的判定方法 的判定方法
形
•定义 •边角边公理 •角边角公理
•定义 •定理 •两角对应相等,两
挑战自我
三个边长为a的正方形ABEG、GEFH 和HFCD,矩形对角线AC的长是 ;
已知:如图,四边形ABEG 、GEFH 、 HFCD都是边长为a的正方形. 求证:△AEF∽△CEA.
证法1:∵正方形ABEG的边长为a,
证法1:∵正方形ABEG的边长为a, ∴AE= a .
证法1:∵正方形ABEG的边长为a, ∴AE= a . 在△AEF和△CEA中, AE∶EF= a∶a= . EC∶EA=2a∶ a= .
证法2:根据题意,可得 AE= a ,AF= a , AC= a . 在△AEF和△CEA中, AE∶EF= a∶a= , EC∶EA=2a∶ a= , CA∶AF = a∶ a= , ∴AE∶EF= EC∶EA= CA∶AF.
证法2:根据题意,可得 AE= a ,AF= a , AC= a . 在△AEF和△CEA中, AE∶EF= a∶a= , EC∶EA=2a∶ a= ,
相似三角形的判定PPT课件

第三章 图形的类似
3.4.1 类似三角形判定的基本定理
复习导入
定义
全等三
角形
三角、三边对应相等
的两个三角形全等
类似三 三角对应相等, 三边对应
角形
成比例的两个三角形类似
判定方法
边
角
边
角
边
角
角
角
边
边
边
边
斜边与直角边
(直角三角形)
探究新知
如图,在△ABC中,D为AB上任意一点,过点D作BC的平行线DE,交AC于点E.
∴
=
=
∠EAO=∠BAC,
∠AEO=∠B,
∠AOE=∠ACB,
当堂练习
2. 如图,已知点O在四边形ABCD的对角线AC上,OE∥CB,OF∥CD.试判
断四边形AEOF与四边形ABCD是否类似,并说明理由.
∵OF∥CD,∴△AFO∽△ADC,
∴
=
=
∠FAO=∠DAC,
DE至点F,使DE=EF. 求证:△CFE∽△ABC.
证明 ∵DE∥BC,点D为△ABC的边AB的中点,
∴AE=CE.
又∵DE=FE,∠AED=∠CEF,
∴△ADE≌△CEF.
∵DE∥BC,
∴△ADE∽△ABC.
∴△CFE∽△ABC.
知识要点
平行于三角形一边的直线与其他两边相交,截得的三角形与原
三角形类似.
求证:只要DE//BC,△ADE与△ABC始终类似.
证明:在△ADE与△ABC中,∠A=∠A.
∵DE∥BC,
分析:根据类似三角形的定
义去证明,三角对应相等,
三边对应成比例。
3.4.1 类似三角形判定的基本定理
复习导入
定义
全等三
角形
三角、三边对应相等
的两个三角形全等
类似三 三角对应相等, 三边对应
角形
成比例的两个三角形类似
判定方法
边
角
边
角
边
角
角
角
边
边
边
边
斜边与直角边
(直角三角形)
探究新知
如图,在△ABC中,D为AB上任意一点,过点D作BC的平行线DE,交AC于点E.
∴
=
=
∠EAO=∠BAC,
∠AEO=∠B,
∠AOE=∠ACB,
当堂练习
2. 如图,已知点O在四边形ABCD的对角线AC上,OE∥CB,OF∥CD.试判
断四边形AEOF与四边形ABCD是否类似,并说明理由.
∵OF∥CD,∴△AFO∽△ADC,
∴
=
=
∠FAO=∠DAC,
DE至点F,使DE=EF. 求证:△CFE∽△ABC.
证明 ∵DE∥BC,点D为△ABC的边AB的中点,
∴AE=CE.
又∵DE=FE,∠AED=∠CEF,
∴△ADE≌△CEF.
∵DE∥BC,
∴△ADE∽△ABC.
∴△CFE∽△ABC.
知识要点
平行于三角形一边的直线与其他两边相交,截得的三角形与原
三角形类似.
求证:只要DE//BC,△ADE与△ABC始终类似.
证明:在△ADE与△ABC中,∠A=∠A.
∵DE∥BC,
分析:根据类似三角形的定
义去证明,三角对应相等,
三边对应成比例。
相似三角形的判定——利用角的关系课件(湘教版)

我们通过视察三角板发现,其中有同样两个锐角 ( 30°与60°,或45°与45°) 的两个三角板大小可能 不相同,但它们看起来是类似,你能给出一个较为确定 的推论吗? ( 两个角对应相等 的两个三角形相 似)
知1-讲
根据所学知识,试着证明你的推论. 如图,在△ABC 和△A′B′C′中,已知∠A=∠A′,
由两组角分别相等判定两个三角形类似,其关键 是找准对应角.一般地,相等的角是对应角.如:公共 角、对顶角、同角(等角)的余角(补角)、同弧所 对的圆周角等都是相等的角,解题时要注意发掘题目 中的隐含条件.
知2-讲
知识点 2 用直角三角形判定定两三角形类似
例2 如图,在 Rt△ABC 中,∠C = 90°,AB = 10,AC = 8. E 是 AC 上一点,AE = 5,ED⊥AB,垂足为D. 求 AD 的长.
知1-讲
证明:∵ EF 垂直平分 AD , ∴ AF = DF . ∴∠FAD = ∠3. ∵ AD 是∠ BAC 的平分线, ∴∠1 = ∠2. 又∵∠B = ∠3-∠1 ,∠4 = ∠FAD-∠2 , ∴∠B = ∠4. 又∵∠BFA = ∠AFC , ∴△ABF ∽△CAF .
总结
知1-讲
解: ∵ ED⊥AB,
∴∠EDA=90°.
又∠C=90 °,∠A=∠A,
∴ △AED ∽△ABC.
∴ AD AE .AC AB∴ AD来自 AE AC 8 5 = 4.
AB
10
知2-讲
总结
知2-讲
由类似三角形的条件可知,如果两个直角三角形 满足一个锐角相等,那么这两个直角三角形类似.
类似三角 形的判定
第三章 图形的类似
3.4 类似三角形的判定与性质
第2课时 类似三角形的判定 ---利用角的关系
知1-讲
根据所学知识,试着证明你的推论. 如图,在△ABC 和△A′B′C′中,已知∠A=∠A′,
由两组角分别相等判定两个三角形类似,其关键 是找准对应角.一般地,相等的角是对应角.如:公共 角、对顶角、同角(等角)的余角(补角)、同弧所 对的圆周角等都是相等的角,解题时要注意发掘题目 中的隐含条件.
知2-讲
知识点 2 用直角三角形判定定两三角形类似
例2 如图,在 Rt△ABC 中,∠C = 90°,AB = 10,AC = 8. E 是 AC 上一点,AE = 5,ED⊥AB,垂足为D. 求 AD 的长.
知1-讲
证明:∵ EF 垂直平分 AD , ∴ AF = DF . ∴∠FAD = ∠3. ∵ AD 是∠ BAC 的平分线, ∴∠1 = ∠2. 又∵∠B = ∠3-∠1 ,∠4 = ∠FAD-∠2 , ∴∠B = ∠4. 又∵∠BFA = ∠AFC , ∴△ABF ∽△CAF .
总结
知1-讲
解: ∵ ED⊥AB,
∴∠EDA=90°.
又∠C=90 °,∠A=∠A,
∴ △AED ∽△ABC.
∴ AD AE .AC AB∴ AD来自 AE AC 8 5 = 4.
AB
10
知2-讲
总结
知2-讲
由类似三角形的条件可知,如果两个直角三角形 满足一个锐角相等,那么这两个直角三角形类似.
类似三角 形的判定
第三章 图形的类似
3.4 类似三角形的判定与性质
第2课时 类似三角形的判定 ---利用角的关系
相似三角形的判定 课件

2.预备定理
平行于三角形一边的直线和其他 文字
两边(或两边的延长线)相交,所构 语言
成的三角形与原三角形相似 图形 语言
在△ABC 中,D,E 分别是 AB, 符号
AC 边上的点,且 DE∥BC,则 语言
△ADE∽△ABC
3.相似三角形的判定定理
(1)判定定理 1:两角对应相等,两三角形相似. (2)判定定理 2:两边对应成比例,且夹角相等,两三 角形相似. (3)判定定理 3:三边对应成比例,两三角形相似.
4.直角三角形相似的判定
(1)两直角三角形有一个锐角相等,两直角三角形相 似.
(2)两直角三角形的两直角边对应成比例,两直角三 角形相似.
(3)两直角三角形的斜边和一条直角边对应成比例, 两直角三角形相似.
温馨提示 在证明直角三角形相似时,要特别注意直 角三角形这一隐含条件的利用.
类型 1 相似三角形的判定(互动探究)
类型 2 利用三角形相似证明比例式或等积式
[典例 2] 如图所示,EF 分别交 AB, AC 于点 F,E,交 BC 的延长线于点 D, AC⊥BC,且 AB·CD=DE·AC.
求证:AE·CE=DE·EF. 证明:因为 AB·CD=DE·AC, 所以DABE=CADC.
又因为 AC⊥BC, 所以∠ACB=∠DCE=90°. 所以△ACB∽△DCE,所以∠A=∠D. 又因为∠AEF=∠DEC, 所以△AEF∽△DEC, 所以DAEE=ECFE.所以 AE·CE=DE·EF.
相似三角形的判定
1.相似三角形的定义 (1)定义:对应角相等、对应边成比例的两个三角形 叫做相似三角形. (2)相似比(相似系数):相似三角形对应边的比值. (3)记法:两个三角形相似,用符号“∽”表示.例 如△ABC 与△A′B′C′相似,记作△ABC∽△A′B′C′.
相似三角形判定定理的证明课件

A
AB AC 边相交,截得的对应线段成比例)
A′
D
E
B
C B′
C′
过点D作AC的平行线,交BC于点F,
则 AD CF . (平行于三角形一边的直线与其他两边 AE CF .
AB CB 相交,截得的对应线段成比例)
AC CB
∵DE∥BC,DF∥AC, ∴四边形DFCE是平行四边形.
∴DE=CF.
A′
B
C B′
C′
已知:如图,△ABC和△
A′B′C′中,AABB
BC BC
=
AC AC
.
ቤተ መጻሕፍቲ ባይዱ
求证 :△ABC∽△A'B'C'
证明 :在△ABC的边AB(或它的延长线)上截取AD=A′B′,
AE=A′C′ 连接DE.
AB AC , AD AB, AB AC
A
AE AC,
AB AC . AD AE
AE DE . AC CB
AD AE DE . AB AC BC
A
A′
D
E
B
F
C B′
C′
而∠ADE=∠B,∠DAE=∠BAC,∠AED=∠C ∴△ADE∽△ABC ∵∠A=∠A′,∠ADE=∠B=∠B′,AD=A′B′ ∴△ADE≌△A′B′C′ ∴△ABC∽△A'B'C'
A
A′
D
E
B
5 类似三角形判 定定理的证明
北师版九年级上册
复习导入
判定两个三角形类似的方法有哪些?
你能对它们进行证明吗?
探究新知
如果一个三角形的两个角与另一个三角形的两 个角对应相等,那么这两个三角形类似.
相似三角形判定定理的证明-课件

VS
在微积分中的应用
在微积分中,可以利用相似三角形判定定 理证明一些几何不等式,例如面积不等式 、长度不等式等。
THANK YOU
感谢聆听
全等三角形判定定理是相似三角形判定定理的特殊情况,即当相似比为1时,两个三角 形全等。
与平行线判定定理的联系
在相似三角形中,如果两个三角形的对应边成比例且夹角相等,则这两个三角形所在的 直线平行。
在高等数学中的应用
在解析几何中的应用
在解析几何中,可以利用相似三角形判 定定理证明一些几何性质,例如直线的 斜率相等、点到直线的距离相等等。
相似比
相似三角形的对应边之间的长度 比值称为相似比。
相似三角形的性质
对应角相等
相似三角形的对应角相等,即它们的 角度大小相同。
对应边成比例
相似三角形的对应边之间成比例,即 它们的边长比值相等。
相似三角形的分类
完全相似三角形
两个三角形完全相同,即它们的对应边和对应角都相等。
相似不全等三角形
两个三角形相似但不全等,即它们的对应边和对应角有相同 的比值,但大小不同。
角角判定定理
总结词
通过两个角相等证明两个三角形相似,适用于两个角分别相等的情况。
详细描述
如果两个三角形有两个角分别相等,则这两个三角形相似。具体来说,如果一 个三角形的两个角与另一个三角形的两个角分别相等,则这两个三角形相似。
边边判定定理
总结词
通过两边成比例证明两个三角形相似,适用于两边成比例的情况。
证明几何命题
通过相似三角形的性质,可以证明一 些几何命题,例如等腰三角形、直角 三角形的性质等。
在实际问题中的应用
测量中的应用
在土地测量、建筑测量等领域,可以利用相似三角形判定定理来计算无法直接测量的距离和高度。
相似三角形的判定定理完整版课件-2024鲜版
与向量结合应用
向量是数学中的重要工具之一,而相似三角形与向量也有着紧密的联系。在解决一些与向量 相关的问题时,可以利用相似三角形的性质来简化计算或证明过程。
2024/3/28
与不等式结合应用
在一些复杂的数学问题中,可能需要将相似三角形的性质与不等式知识结合起来应用。例如, 在证明一些与线段长度或面积相关的不等式时,可以利用相似三角形的性质来构造不等式并 进行证明。
14
练习题与答案
答案
1. 是。因为$frac{DE}{D'E'} = frac{4}{2} = 2$,$frac{EF}{E'F'} = frac{5}{3}$且 $frac{DF}{D'F'} = frac{6}{4} = frac{3}{2}$,三边对应比例相等。
2. 是。因为$frac{GH}{G'H'} = frac{7.5}{6} = frac{5}{4}$,$frac{HI}{H'I'} = frac{10}{8} = frac{5}{4}$且$frac{GI}{G'I'} = frac{12.5}{10} = frac{5}{4}$,三边对应比例相等。
相似三角形定义及性质
2024/3/28
定义
对应角相等,对应边成比例的两个 三角形叫做相似三角形。
性质
相似三角形的对应角相等,对应边 成比例,且对应高、对应中线、对 应角平分线等也成比例。
4
对应角与对应边关系
对应角
两个相似三角形中,相等的角是对应 角。
对应边
两个相似三角形中,成比例的边是对应 边。在写对应边成比例时,要注意写清 对应边的顺序。
2024/3/28
相似三角形的判定3两角ppt课件
如果一个三角形的两个角与另一个三角形的两 个角对应相等,那么这两个三角形相似. (简 称:两角):
A′ 符号语言:
A
在△A´B´C´和△ABC中,
B
C B′
∵ ∠A =∠A',
C′
∠B =∠B',
∴△A´B´C´∽△ABC
练习: “雪亮工程"是以区(县)、乡(镇)、村(社区)三级综治中心为指挥平台、以综治信息化为支撑、以网格化管理为基础、以公共安全视频监控联网应用为重点的“群众性治安防控工程”。
2、有一个角等于300的两个等腰三角形是否相似? 等于1200呢?
练习: “雪亮工程"是以区(县)、乡(镇)、村(社区)三级综治中心为指挥平台、以综治信息化为支撑、以网格化管理为基础、以公共安全视频监控联网应用为重点的“群众性治安防控工程”。
3、 已知:如图,∠ABD=∠C AD=2 AC=8, 求AB 长.
例2 如图,弦AB和CD相交于⊙O内一点P,求证PA·PB=PC·PD
证明:连接AC、BD.
∵ ∠A和∠D都是 弧BC所对的圆周角,
A ∴ ∠A=∠D
同理 ∠C=∠B ∴ △PAC∽△PDB
D P O·
B
PA PC
C
PD PB
即 PA·PB=PC·PD
典例: “雪亮工程"是以区(县)、乡(镇)、村(社区)三级综治中心为指挥平台、以综治信息化为支撑、以网格化管理为基础、以公共安全视频监控联网应用为重点的“群众性治安防控工程”。
一、复习提问 “雪亮工程"是以区(县)、乡(镇)、村(社区)三级综治中心为指挥平台、以综治信息化为支撑、以网格化管理为基础、以公共安全视频监控联网应用为重点的“群众性治安防控工程”。
A′ 符号语言:
A
在△A´B´C´和△ABC中,
B
C B′
∵ ∠A =∠A',
C′
∠B =∠B',
∴△A´B´C´∽△ABC
练习: “雪亮工程"是以区(县)、乡(镇)、村(社区)三级综治中心为指挥平台、以综治信息化为支撑、以网格化管理为基础、以公共安全视频监控联网应用为重点的“群众性治安防控工程”。
2、有一个角等于300的两个等腰三角形是否相似? 等于1200呢?
练习: “雪亮工程"是以区(县)、乡(镇)、村(社区)三级综治中心为指挥平台、以综治信息化为支撑、以网格化管理为基础、以公共安全视频监控联网应用为重点的“群众性治安防控工程”。
3、 已知:如图,∠ABD=∠C AD=2 AC=8, 求AB 长.
例2 如图,弦AB和CD相交于⊙O内一点P,求证PA·PB=PC·PD
证明:连接AC、BD.
∵ ∠A和∠D都是 弧BC所对的圆周角,
A ∴ ∠A=∠D
同理 ∠C=∠B ∴ △PAC∽△PDB
D P O·
B
PA PC
C
PD PB
即 PA·PB=PC·PD
典例: “雪亮工程"是以区(县)、乡(镇)、村(社区)三级综治中心为指挥平台、以综治信息化为支撑、以网格化管理为基础、以公共安全视频监控联网应用为重点的“群众性治安防控工程”。
一、复习提问 “雪亮工程"是以区(县)、乡(镇)、村(社区)三级综治中心为指挥平台、以综治信息化为支撑、以网格化管理为基础、以公共安全视频监控联网应用为重点的“群众性治安防控工程”。
相似三角形的判定定理.ppt
探索:如果一个三角形的两条边与另一 个三角形的两条边对应成比例,并且夹角相 等,那么这两个三角形一定相似吗?
做一做:利用刻度尺和量角器画两个三
角形 △ABC 与△ABC ,使 A A,
AB AB
和 AC
AC
都等于给定的值 k
.设法比较
B 与 B的大小(或 C 与 C 的大小),
你能得出什么结论?
AB 16,AC 30.
(1)相似; (2)相似; (3)相似.
2.下面每组的两个三角形是否相似?为什么?
A 4cm
B
7cm
A
1
3
E
1
B
5cm
D 2cm 2.5cm
C
1
E
F
3.5cm
(1)相似;
F
2
3 C
(2)相似.
3.如图所示,如果有一点 E 在边AC 上, 那么点 E应该在什么位置才能使 △ADE 与 △ABC 相似呢?
与你的同伴交流,你画的三角形相似吗?
改变 k 值的大小,再试一试. △ABC 与 △ABC 还相似吗?
请大家按照上面的步骤进行,同时还要 采取不同的组取不同的 k 值法.
相似三角形的判定方法:如果一个三角形 的两条边与另一个三角形的两条边对应成比例, 并且夹角相等,那么这两个三角形相似.
想一想:两边对应成比例,其中一边的 对角对应相等,这两个三角形相似吗?
FE 36 CE 30
FE CE
AEB FEC,△AEB∽△FEC(如果一个
三角形的两条边与另一个三角形的两条边对应成比
例,并且夹角相等,那么这两个三角形相似).
例2. △ABC 和△ABC 中,AB 6cm,
相似三角形的判定全ppt课件
2024/1/27
5
相似三角形性质总结
对应边成比例
相似三角形的对应边之比等于相似比。
对应高、中线、角平分线成比例
相似三角形的对应高、中线、角平分线之 比也等于相似比。
周长比等于相似比
相似三角形的周长之比等于相似比。
2024/1/27
面积比等于相似比的平方
相似三角形的面积之比等于相似比的平方 。
6
02
相似三角形的判定全ppt课件
2024/1/27
1
目 录
2024/1/27
• 相似三角形基本概念及性质 • 判定方法一:两边成比例且夹角相等 • 判定方法二:三边成比例 • 判定方法三:直角三角形中斜边和一直角边成
比例 • 综合运用及拓展延伸 • 课堂小结与作业布置
2
01
相似三角形基本概念及性质
2024/1/27
判定方法一:两边成比例且夹角 相等
2024/1/27
7
定理内容阐述
01
02
03
定理描述
如果两个三角形有两边成 比例,并且夹角相等,则 这两个三角形相似。
2024/1/27
定理条件
两个三角形中,任意两边 长度之比等于另两边长度 之比,且这两边所夹的角 相等。
定理
8
18
05
综合运用及拓展延伸
2024/1/27
19
不同判定方法之间的联系与区别
角角角(AAA)相似
三个内角分别相等,则两个三角形相 似。此方法简单易行,但需注意AAA 相似不能推出边长成比例。
边角边(BAB)相似
两边成比例且夹角相等,则两个三角 形相似。此方法结合了边的长度和角 的大小,较为常用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
F
D
B
E
C
A
1 2
A O
C
B
A
C
C
D E
B D
D O
A D E
B
B
C
A
B
C
综合提高
如图, ⊿ABC中,CD是边AB上的高, 且AD:CD=CD:BD, 求∠C的大小.
C
A
D
B
A
D
B
C
4、如图:在Rt △ ABC中, ∠ABC=900,BD⊥AC于D 18 若 AB=6 AD=2 则AC= BD= BC= 4 √2 12√2
5、如图:在Rt △ ABC中, ∠ABC=90 , BD⊥AC于D
0
问:若E是BC中点,ED的延 长线交BA的延长线于F, 求证:AB : AC=DF : BF
三角形相似的定义;二是“平行”定理;三是“三边”定理; 四是上节课学习的“两边夹角”定理。
为了使用它,就必须创造具备定理的基本图形的条件。怎样创造呢? (把小的三角形移动到大的三角形上)。 怎样实现移动呢?
证明:在ΔABC的边AB、AC上,分别截取AD=A/B/,AE=A/C/, 连结DE。 ∵ AD=A/B/,∠A=∠A/,AE=A/C/ ∴ ΔA DE≌ΔA/B/C/(SAS) ∴ ∠ADE=∠B/, 又∵ ∠B/=∠B, ∴ ∠ADE=∠B, ∴ DE//BC, ∴ ΔADE∽ΔABC。 D A A/
(1)、已知ΔABC与ΔA/B/C/中,∠B=∠B/=750,∠C=500, ∠A/=550,这两个三角形相似吗?为什么? / A A/ A A 550
550 750 500
750 C B/ C/ B A C B/ A/ C/
B
( 2 ) 已 知 等 腰 三 角 形 ΔABC 和 ΔA/B/C/中,∠ A、∠ A/分别是顶角, 求 证 : ① 如 果 ∠ A=∠A/ , 那 么 ΔABC∽ΔA/B/C/。 ② 如 果 ∠ B=∠B/ , 那 么 ΔABC∽ΔA/B/C/。 B
应用新知:
4、判断题:
想一想
(1)所有的直角三角形都相似 .
(× )
(2)有一个锐角对应相等的两直角三角形相似.(√ )
(3)所有的等边三角形都相似.
(4)所有的等腰直角三角形都相似.
(√ )
(√ )
(5)顶角相等的两个等腰三角形相似.
(6)有一个角相等的两个等腰三角形相似.
(√ )
(× )
填一填
A
E
C
• P48 练习 1、2
C
A
D
B
例2:如图,弦AB和CD相交于圆O内一点
P,求证:PA·PB=PC·PD
证明:连接AC、BD。 ∵∠A和∠D都是弧CB所对的圆周角, ∴∠ A=∠D。 A 同理∠C=∠B (或∠APC=∠DPB) 。 ∴△PAC∽△PDB。 O· ∴
D P B
PA PC PD PB
(1)如图3,点D在AB上,当∠ ACD =∠ B 时, △ACD∽△ABC。 (或者∠ ACB=∠ ADB) (2)如图4,已知点E在AC上,若点D在AB上,则满足 条件 DE//BC ,就可以使△ADE与原△ABC相似。 (或者∠ C=∠ ADE)
A D D B 图 3 C B 图 4 D
●
(或者∠ B=∠ ADE)
C
即PA·PB=PC·PD
例2.弦AB和CD相交于⊙o内一点P,求证:PA· PB=PC· PD 证明:连接AD、BC
⌒ ∵∠A、∠C都是BD所对的圆周角
∴ ∠A=∠C 同理: ∠D=∠B(或∠APD=∠CPB) ∴△PAD∽△PCB
A
D
O
C
P B
PA PD PC PB
即PA· PB=PC· PD
E C B/ C/
∴ ΔA/B果一个三角形的两个角与另一个三角形的 两个角对应相等,那么这两个三角形相似。 可以简单说成:两角对应相等,两三角形相似。
----“两角”定理
例1、已知:ΔABC和ΔDEF中, ∠A=400,∠B=800,∠E=800,
∠F=600。求证:ΔABC∽ΔDEF A
27.2
三角形相似的判定(3)
复习
1、相似三角形有哪些判定方法? (1).定义法(不常用)
B
A
A/
C
B/
C/
(2).“平行”定理:平行于三角形一边
的直线和其他两边相交,所构成的三角形与原 三角形相似。
(3).“三边”定理:三边对应的比相等, 两个三角形相似. (4).“两边夹角”定理:两组对应边的比相 等,并且相应的夹角相等的两个三角形相似. 2、相似三角形与全等三角形有什么内在的联系呢?
BC AB AC , , A'B' A'C' B'C'
A A/
,你有什么发现?
(3)△ABC和△ A’B’C’ 相似吗? B
C
B/
C/
已知:在△ABC 和△A/B/C/ 中,
A A , B B
/
/
A
求证:ΔABC∽ △A/B/C/
A/
分析:要证两个三角形相似, 目前只有四个途径。一是 B C B/ C/
例3.已知D、E分别是△ABC的边AB,AC上的点, 若∠A=35°, ∠C=85°,∠AED=60 °求证: AD· AB= AE· AC
解: 在△ADE中,ADE=180 A AED 180 35 60 =85
A D
35° 85° 60°
ADE ACB 85
D
B
C
A E D B C
练一练
3.如图已知D、E分别是△ABC的边AB、AC 上的点,且 AD AB=AE AC 。 证明: AED=B
A D
A
D C B C
E
B
3.已知如图, ∠ABD=∠C AD=2 AC=8,求AB 解: ∵ ∠ A= ∠ A ∠ABD=∠C ∴ △ABD ∽ △ACB ∴ AB : AC=AD : AB ∴ AB2 = AD · AC ∵ AD=2 AC=8 ∴ AB =4
观察
观察两副三角尺,其中同样角度(30° 与60°,或45°与45°)的两个三角尺,它们 一定相似吗?
如果两个三角形有两组角对应相等, 它们一定相似吗?
(1)作△ABC和△ A’B’C’,使得∠A=∠A’,
∠B=∠B’,这时它们的第三个角满足∠C= ∠C’吗? (2)分别度量这两个三角形的边长,计算
C
B/
C/
例题分析
例2. 如图,△ABC中, DE∥BC,EF∥AB, 试说明△ADE∽△EFC.
B D
A
E
F
C
解: ∵ DE∥BC,EF∥AB(已知),
∴ ∠ADE=∠B=∠EFC (两直线平行,同位角相等) ∠AED=∠C. (两直线平行,同位角相等) ∴ △ADE∽△EFC. (两个角分别对应相等的 两个三角形相似.)
又 A A=35
85°
E C
B
△ADE
AD AE AC AB
△ACB
即AD AB=AE AC
例4、在四边形ABCD中,AC平分∠DAB, ∠ACD=∠ABC。求证:AC2=AB· AD
证明: AC平分DAB
BAC=CAD
又 ACD=ABC
A
D
△ACD △ABC
B
应用新知:
选一选
3.从下面这些三角形中,选出一组你喜欢的相 似的三角形证明.
5 30 45 1 105 30 4 2 30 9 2 105 45 5 2.5 6 30 4.5 4 3 30
(1)与(4)与(5)----“两角”定理 (2)与(6)--“两边夹角”定理
400
D
800
600
800 C
600
B
E
F
证明:∵ 在ΔABC中,∠A=400,∠B=800, ∴ ∠C=1800-∠A -∠B =1800-400 -800 =600 ∵ 在ΔDEF中,∠E=800,∠F=600 ∴ ∠B=∠E,∠C=∠F ∴ ΔABC∽ΔDEF(两角对应相等,两三角形相似)。
2、课堂练习
C
AC AD = AB AC AC AC=AB AD
即AC =AB AD
2
练一练
• 1、在△ABC中,∠ACB=90°,CD⊥BA 于点D。证明:AC2=AD· AB
C
B
D
A
练一练
• 2、已知梯形ABCD中,AD∥BC,∠BAD =90°,对角线BD⊥DC。 • 证明:BD2=AD· BC
F
D
B
E
C
A
1 2
A O
C
B
A
C
C
D E
B D
D O
A D E
B
B
C
A
B
C
综合提高
如图, ⊿ABC中,CD是边AB上的高, 且AD:CD=CD:BD, 求∠C的大小.
C
A
D
B
A
D
B
C
4、如图:在Rt △ ABC中, ∠ABC=900,BD⊥AC于D 18 若 AB=6 AD=2 则AC= BD= BC= 4 √2 12√2
5、如图:在Rt △ ABC中, ∠ABC=90 , BD⊥AC于D
0
问:若E是BC中点,ED的延 长线交BA的延长线于F, 求证:AB : AC=DF : BF
三角形相似的定义;二是“平行”定理;三是“三边”定理; 四是上节课学习的“两边夹角”定理。
为了使用它,就必须创造具备定理的基本图形的条件。怎样创造呢? (把小的三角形移动到大的三角形上)。 怎样实现移动呢?
证明:在ΔABC的边AB、AC上,分别截取AD=A/B/,AE=A/C/, 连结DE。 ∵ AD=A/B/,∠A=∠A/,AE=A/C/ ∴ ΔA DE≌ΔA/B/C/(SAS) ∴ ∠ADE=∠B/, 又∵ ∠B/=∠B, ∴ ∠ADE=∠B, ∴ DE//BC, ∴ ΔADE∽ΔABC。 D A A/
(1)、已知ΔABC与ΔA/B/C/中,∠B=∠B/=750,∠C=500, ∠A/=550,这两个三角形相似吗?为什么? / A A/ A A 550
550 750 500
750 C B/ C/ B A C B/ A/ C/
B
( 2 ) 已 知 等 腰 三 角 形 ΔABC 和 ΔA/B/C/中,∠ A、∠ A/分别是顶角, 求 证 : ① 如 果 ∠ A=∠A/ , 那 么 ΔABC∽ΔA/B/C/。 ② 如 果 ∠ B=∠B/ , 那 么 ΔABC∽ΔA/B/C/。 B
应用新知:
4、判断题:
想一想
(1)所有的直角三角形都相似 .
(× )
(2)有一个锐角对应相等的两直角三角形相似.(√ )
(3)所有的等边三角形都相似.
(4)所有的等腰直角三角形都相似.
(√ )
(√ )
(5)顶角相等的两个等腰三角形相似.
(6)有一个角相等的两个等腰三角形相似.
(√ )
(× )
填一填
A
E
C
• P48 练习 1、2
C
A
D
B
例2:如图,弦AB和CD相交于圆O内一点
P,求证:PA·PB=PC·PD
证明:连接AC、BD。 ∵∠A和∠D都是弧CB所对的圆周角, ∴∠ A=∠D。 A 同理∠C=∠B (或∠APC=∠DPB) 。 ∴△PAC∽△PDB。 O· ∴
D P B
PA PC PD PB
(1)如图3,点D在AB上,当∠ ACD =∠ B 时, △ACD∽△ABC。 (或者∠ ACB=∠ ADB) (2)如图4,已知点E在AC上,若点D在AB上,则满足 条件 DE//BC ,就可以使△ADE与原△ABC相似。 (或者∠ C=∠ ADE)
A D D B 图 3 C B 图 4 D
●
(或者∠ B=∠ ADE)
C
即PA·PB=PC·PD
例2.弦AB和CD相交于⊙o内一点P,求证:PA· PB=PC· PD 证明:连接AD、BC
⌒ ∵∠A、∠C都是BD所对的圆周角
∴ ∠A=∠C 同理: ∠D=∠B(或∠APD=∠CPB) ∴△PAD∽△PCB
A
D
O
C
P B
PA PD PC PB
即PA· PB=PC· PD
E C B/ C/
∴ ΔA/B果一个三角形的两个角与另一个三角形的 两个角对应相等,那么这两个三角形相似。 可以简单说成:两角对应相等,两三角形相似。
----“两角”定理
例1、已知:ΔABC和ΔDEF中, ∠A=400,∠B=800,∠E=800,
∠F=600。求证:ΔABC∽ΔDEF A
27.2
三角形相似的判定(3)
复习
1、相似三角形有哪些判定方法? (1).定义法(不常用)
B
A
A/
C
B/
C/
(2).“平行”定理:平行于三角形一边
的直线和其他两边相交,所构成的三角形与原 三角形相似。
(3).“三边”定理:三边对应的比相等, 两个三角形相似. (4).“两边夹角”定理:两组对应边的比相 等,并且相应的夹角相等的两个三角形相似. 2、相似三角形与全等三角形有什么内在的联系呢?
BC AB AC , , A'B' A'C' B'C'
A A/
,你有什么发现?
(3)△ABC和△ A’B’C’ 相似吗? B
C
B/
C/
已知:在△ABC 和△A/B/C/ 中,
A A , B B
/
/
A
求证:ΔABC∽ △A/B/C/
A/
分析:要证两个三角形相似, 目前只有四个途径。一是 B C B/ C/
例3.已知D、E分别是△ABC的边AB,AC上的点, 若∠A=35°, ∠C=85°,∠AED=60 °求证: AD· AB= AE· AC
解: 在△ADE中,ADE=180 A AED 180 35 60 =85
A D
35° 85° 60°
ADE ACB 85
D
B
C
A E D B C
练一练
3.如图已知D、E分别是△ABC的边AB、AC 上的点,且 AD AB=AE AC 。 证明: AED=B
A D
A
D C B C
E
B
3.已知如图, ∠ABD=∠C AD=2 AC=8,求AB 解: ∵ ∠ A= ∠ A ∠ABD=∠C ∴ △ABD ∽ △ACB ∴ AB : AC=AD : AB ∴ AB2 = AD · AC ∵ AD=2 AC=8 ∴ AB =4
观察
观察两副三角尺,其中同样角度(30° 与60°,或45°与45°)的两个三角尺,它们 一定相似吗?
如果两个三角形有两组角对应相等, 它们一定相似吗?
(1)作△ABC和△ A’B’C’,使得∠A=∠A’,
∠B=∠B’,这时它们的第三个角满足∠C= ∠C’吗? (2)分别度量这两个三角形的边长,计算
C
B/
C/
例题分析
例2. 如图,△ABC中, DE∥BC,EF∥AB, 试说明△ADE∽△EFC.
B D
A
E
F
C
解: ∵ DE∥BC,EF∥AB(已知),
∴ ∠ADE=∠B=∠EFC (两直线平行,同位角相等) ∠AED=∠C. (两直线平行,同位角相等) ∴ △ADE∽△EFC. (两个角分别对应相等的 两个三角形相似.)
又 A A=35
85°
E C
B
△ADE
AD AE AC AB
△ACB
即AD AB=AE AC
例4、在四边形ABCD中,AC平分∠DAB, ∠ACD=∠ABC。求证:AC2=AB· AD
证明: AC平分DAB
BAC=CAD
又 ACD=ABC
A
D
△ACD △ABC
B
应用新知:
选一选
3.从下面这些三角形中,选出一组你喜欢的相 似的三角形证明.
5 30 45 1 105 30 4 2 30 9 2 105 45 5 2.5 6 30 4.5 4 3 30
(1)与(4)与(5)----“两角”定理 (2)与(6)--“两边夹角”定理
400
D
800
600
800 C
600
B
E
F
证明:∵ 在ΔABC中,∠A=400,∠B=800, ∴ ∠C=1800-∠A -∠B =1800-400 -800 =600 ∵ 在ΔDEF中,∠E=800,∠F=600 ∴ ∠B=∠E,∠C=∠F ∴ ΔABC∽ΔDEF(两角对应相等,两三角形相似)。
2、课堂练习
C
AC AD = AB AC AC AC=AB AD
即AC =AB AD
2
练一练
• 1、在△ABC中,∠ACB=90°,CD⊥BA 于点D。证明:AC2=AD· AB
C
B
D
A
练一练
• 2、已知梯形ABCD中,AD∥BC,∠BAD =90°,对角线BD⊥DC。 • 证明:BD2=AD· BC
