第一课完全区组设计Friedman 秩和检验
秩和检验

T Tmin( n1orn2 )
3.确定P值范围并作推断
(1)当n1 ≤ 10且n2-n1≤10时,
查附表7的T界值表(P269)
(2)当n1>10或n2-n1>10时,按正态 近似公式(7.3)
相同秩次较多时,校正公式(7.4)
其中 为第j个相同秩次的个数。
二、等级资料的两样本比较(例7.4)
3. 编秩次 (1)d=0 舍去不计,用以检验的有效对子
数n相应减少。
(2)│d│同,取平均秩
4. 求秩和,并定检验统计量
T=T+ orT- (核对:T++T-=(n+1)n/2 )
5.确定P值范围并作推断
(1)当有效对子数n≤50,查附表6的
T界值表(P268)
(2)当n>50时,按正态近似公式(7.1) 相同秩次较多时,校正公式(7.2)
1. 建立检验假设,确定检验水准
H0:总体M1=M2,
即两总体分布位置相同;
H1:总体M1≠M2,
即两总体分布位置不同; α=0.05
2.计算检验统计量u 值
(1)编秩:本例为等级资料,先 按组段计算各等级的合计人数,再 确定秩次范围及平均秩次。
(2)计算秩和,确定T 并求检验统 计量u 值:
以各组段的平均秩次分别与各等级例
在实际应用中,秩和检验法有多种具体化: 配对设计的两样本比较 成组设计两样本比较的秩和检验 成组设计多样本比较的秩和检验 多个样本两两比较的秩和检验
符号检验法
检验目标:X与Y是两个连续型总体,各有分布函数
F1(x)与 F2(x) ,现从中分别抽取两个独立样本 ( X1, X 2 , , X n )与 (Y1,Y2,...,Yn ) ,要在显著性水平
4.5 完全区组设计:Friedman 秩和检验

例 某田径队对新入队的学员要进行四个部分的技术训练, 以提高学员的身体素质。为检验这四个部分的技术训练是否确实 有效,随机抽选了14 名新学员,分别接受四个部分的训练。 每个训练结束后,均进行该部分的测试,成绩以 10 分为最高。 检测结果如下表所示:
Z10.0167 Z0.09833 2.13
SE 4 4 5 4 12 3.266. 6 63
比较式 A vs B A vs C A vs D B vs C B vs D C vs D
Ri-Rj的绝对值 15-8=7 15-11.5=3.5 15-5.5=9.5 8-11.5=3.5 8-5.5=2.5 11.5-5.5=6
6(k 1)
这是大样本时基于 Friedman 秩和检验的一个方法.
如果零假设 H 0 为 i 处理和 j 处理没有区别, 那么,双边检验的统计量为 Ri R j .
对于置信水平 ,如果 Ri R j Z * 2 bk (k 1) / 6, 则拒绝零假设,这里
*
总共可比较的对数
4.5 Friedman 检验
Friedman 检验又称弗利德曼 2 检验或弗利德曼 两因素秩方差分析. 它是由 Friedman 于 1937 年提出的,后来又被 Kendall 和 Smith 发展到多元度量的协同系数相关问题上.
它是针对完全区组设计而提出的检验方法.
Friedman 检验的问题是 k 个样本的位置参数 (用1 , 2 , , k 表示)是否相等.
技术训练A
4 1 2 3 1 2 3 3 4 3 3 1 1 2 33
技术训练B
课件:秩和检验(1)

卡方检验的校正条件: • 配对四格表的χ2检验:b+c<40
• 当n>=40,且所有T>=5时,用未校正的卡方值,若 P接近检验水准,改用确切概率法; 当n>=40,但有1=<T<5时,用校正的卡方值; 当n<40或有T<1时,不能用卡方检验,改用确切概率 法。
Test Statisticsb
编秩情况列表
乙法 -甲法
Z
-.119a
Asymp. Sig. (2-tailed)
.906
a. Based on negative ranks.
b. Wilcoxon Signed Ranks Test
成组设计两样本比较的秩和检验
P154.例12.3
Analyze
Nonparametric Test
2 Independent Samples
Test Variables List:x
Grouping Variable:g
Define Group:Group1:1;Group2:2
Continue
Type Test:Mann-Whitney U
OK
结果解释
血铅 值
分组 1 2 Total
Ran ks
• P413综合分析题1
• 已知某地正常人尿氟含量的中位数为2.15mmol/L。 现在该地某厂随机抽取12名工人,测得尿氟含量 (mmol/L)如下: 2.15 2.10 2.20 2.12 2.42 2.52 2.62 2.72 3.00 3.18 3.87 5.67
单一样本与总体中位数比较
Analyze Nonparametric Test 2 Related Samples Test Pairs List:x median Test Type:Wilcoxon
7.3 Friedman秩方差分析法

例2:在不同的城市对不同人群进行血液中铅的 含量测试,一共有A,B,C三个汽车密度不同的城 市代表着三种(k=3)不同的处理.对试验者按职 业分四组(b=4)取血(4个区组).他们血液中
铅的含量列在下面表中(g /100ml)
城市(处理) І
A
80(3)
B
52(2)
C
40(1)
职业(区组)
ІІ 100(3) 76 (2) 52(1)
及其相关计算如下:
相同的秩 1.5
2.5
i
2
i3i 6
2
6
(
3 i
i
)
12
由Friedman统计量公式得
Q
12 44(41)
152
82
11.52
5.5234(41)
7.7250
Qc
1
7.7250 12
4 4 (42
1)
8.1316
铅含量比较结果可知,仅A与C有差异,其他城市居 民血铅含量间差异不显著.
6 6(4 1)
两两处理的Hollander-Wolfe计算表VS D B VS C B VS D C VS D
Ri R j
15-8=7 15-11.5=3.5 15-5.5=9.5 8-11.5=-3.5 8-5.5=2.5 11.5-5.5=6
SE
无显著差异
2.Hollander-Wolfe两处理间比较 当秩方差分析结果样本之间有差异时,Hollander
-Wolfe(1973)提出两样本(处理)间的比较公式:
Dij Ri R j / SE
式中 Ri 与 R j为第i与第j样本(处理)秩和.由
Friedman秩和检验
Ranks
Mean Rank
ci ty1
2.75
ci ty2
2.25
ci ty3
1.00
概率论
Test Statistics a
N
4
Chi-Sq uare
6.500
df
2
Asymp. Sig.
.039
Exact Sig.
.042
Point Probability
.037
a. FriedmanTest
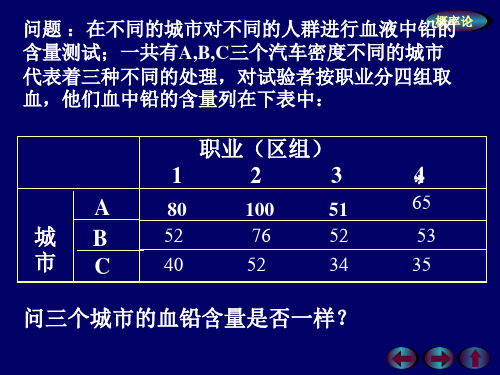
职业(区组)
1
2
3
*4
A
80
100
51
65
城B
52
34
35
问三个城市的血铅含量是否一样?
概率论
Descriptive Statistics
N MeSatnd. DeviaMtiionnimM um aximum city1 744.000200.99206 51.00100.00 city2 548.250101.84272 52.00 76.00 city3 440.25008.26136 34.00 52.00
概率论
4.检验统计量:
概率论
Qbk(1k21)i k( 1 Rib(K 21))2
12
bk(k1)
k
R2i3b(k1)
i1
对 于 固 定 的 k , 当 b 时 , 在 原 假 设 下 , Q :2 ( k 1 )
拒绝域的形式: {Q c)
问题 :在不同的城市对不同的人群进行血液中铅概的率论 含量测试;一共有A,B,C三个汽车密度不同的城市 代表着三种不同的处理,对试验者按职业分四组取 血,他们血中铅的含量列在下表中:
秩和检验

自由度为(k-1)
当各区组间出现相同秩次时,需进行校正 校正公式为
2 c
c
2
c 1
(t
3 j
t j ) bk ( k
2
1)
b为区组个数,k为处理组个数
随机化区组设计资料的多重比较
检验假设 : H0:第i组与第j组所代表的总体中位数相等 H1:第i组与第j组所代表的总体中位数不等 样本含量较大时,计算Zij值
例: 四种疾病患者痰液内嗜酸性粒细胞的检查 结果见表。问四种疾病患者痰液内嗜酸性粒细 胞的等级分布有无差别?
四种疾病患者痰液内嗜酸性粒细胞等级比较
例 数 白细胞等 级 秩次范 围 平均 秩次 秩 和 合计
支气管扩 张
肺水肿
肺癌
病毒性呼吸 道感染
支气管扩 张
肺水肿
肺癌
病毒性呼吸 道感染
(1) + ++
(2) 0 2 9
(3) 3 5 5
(4) 5 7 3
(5) 3 5 3
(6) 11 19 20
(7) 1~11 12~30 31~50
(8) 6 21 40.5
(9) 0 42 364.5
(10) 18 105 202.5
(11) 30 147 121.5
(12) 18 105
+++
6
第三节 完全随机化设计多组独立样本的 秩和检验
检验步骤
1.建立检验假设 H0:各总体的分布位置相同 H1:各总体的分布位置不同或不全相同 α=0.05 2.编秩 将各组数据混合,由小到大排序并 编秩,如遇有相等数值则取平均秩次 3.求秩和 分别将各组秩次相加。 4.计算统计量
秩 和 检 验
(2)计算检验统计量 T 1求差值d,见表12.1(4) 2编秩
编秩原则:
依差值的绝对值从小到大编秩。 编秩时遇差值等于零,舍去不计,同时样本例数减1。 遇绝对值相等差值,取平均秩次。若符号相同,既可以 顺次编秩,也可以求平均秩次,并将各 秩次冠以原差值 的正负号。
3求秩和并确定检验统计量:分别求出正 负秩之和,任取正或负秩和作为统计量。 本例T=21.5或23.5。
切数据的资料
• 计算简便
缺点
• 对于符合参数检验条件的资料其检验效能较低,
因而,对这类资料应首选参数检验
秩及秩和的概念
秩(假设按年龄大小) f m f f f m m f f m m m 15 18 25 26 29 31 32 37 41 48 51 55 1 2 3 4 5 6 7 8 9 10 11 12 秩:对数据从小到大排序,顺序号即为秩
查附表 2(t 界值表, 时)得单侧P 0.0005 , 按 0.05 水准拒绝H 0 ,接受H1 ,可认为吸烟工人的 HbCO(%)含量高于不吸烟工人的 HbCO(%)含量。
完全随机设计多个样本比较的 Kruskal-Wallis H 检验
一、多个独立样本比较的 Kruskal-Wallis H 检验
Kruskal-Wallis H 检验,用于推断计量资料 或等级资料的多个独立样本所来自的多个总体 分布是否有差别。在理论上检验假设 H 0 应为多 个总体分布相同,即多个样本来自同一总体。由 于 H 检验对多个总体分布的形状差别不敏感, 故
在实际应用中检验假设 H 0 可写作多个总体分布 位置相同。 对立的备择假设 H1 为多个总体分布位 置不全相同。
表8-10 小白鼠接种三种不同菌型伤寒杆菌的存活日数比较
4.5 完全区组设计:Friedman 秩和检验
B 3 5 10 3 4 4 10 10 5 9 4 5 5 5
C 6 9 3 10 10 6 6 3 7 7 2 4 10 8
D 8 4 8 4 6 7 5 5 6 6 6 7 9 10
1 2 3 4 5 6 7 8 9 10 11 12 13 14
试问在5%的显著性水平下四个部分技术训练的有效性有无 显著差异?
接下来的做法与 Kruskal Wallis 检验相同. 计算处理平方和(SSt )
k b 2 k 2 i 1 j 1 k i 1
SSt ( Ri R ) b (Ri R ) Ri2 b R2 bk
i 1 2 R i i 1
大样本时基于 Friedman 秩和检验的一个方法.
如果零假设 H 0 为 i 处理和 j 处理没有区别, 那么,双边检验的统计量为 Ri R j .
对于置信水平 ,如果 Ri R j Z * 2 bk (k 1) / 6, 则拒绝零假设,这里 *
总共可比较的对数
在表中加上各处理在每个区组(职业) 中的秩,得
区组(职业) 处理(城市)
I 80(3) 52(2) 40(1)
II 100(3) 76(2) 52(1)
III 51(2) 52(3) 34(1)
IV 65(3) 53(2) 35(31)
Ri 11 9 4
A B C
Q 由此算出 Q 6.5, 对于 k 3 和 b 4,W 0.815. 4 3 1
2 当 Q (k 1) 时,在水平 上拒绝 H 0; 2 当 Q (k 1) 时,不能拒绝 H 0 .
当数据有相同秩时,秩取平均值, 在某区组存在结时,此时需要对 Q 统计量进行修正: Q Qc . k b ( i3, j i , j ) 1 i 1 j 1 2 bk (k 1) 其中 i , j 为第 j 个区组的第 i 个结统计量 .
4.5 完全区组设计:Friedman 秩和检验解析
k
b
k 1 k 1 . 12
• Friedman 检验统计量 Q 为: SSt 12 k 2 2 Q Ri b bk (k 1) 4 . Var Rij (k 1)(k 1) i 1
• Friedman 建议用 k 1 k 乘 Q 得校正式 Q.
k 个样本是匹配的,可以由 k 个条件下同一组受试者构成, 也可以将受试者分为 n 组,每组均有 k 个匹配的受试者, 随机地将 n 组受试者置于 k 个条件下.
在不同受试者匹配的样本中,应尽量使不同受试者的有关 因素匹配即相似.
1. 建立假设检验
假设检验问题:
H0 : 1 2 ... k H1 : 不是所有的位置参数都相等.
3. 作出决策
对于有限的 k 和 b,有零假设下的分布表可查, Q 查的时候要作变换 W . b k 1
当查不到时,可用自由度为 k 1的 2 分布近似. 对于固定的 k,当 b 时,在零假设下有 Q ~ 2 (k 1).
4. 小结
检验步骤: ( 1 )提出假设 H 0: k 个样本间无显著差异. H1: k 个样本间有显著差异. (2)计算检验统计量 Q. (3)作出决策
2 当 Q (k 1) 时,在水平 上拒绝 H 0; 2 当 Q (k 1) 时,不能拒绝 H 0 .
当数据有相同秩时,秩取平均值, 在某区组存在结时,此时需要对 Q 统计量进行修正: Q Qc . k b ( i3, j i , j ) 1 i 1 j 1 2 bk (k 1) 其中 i , j 为第 j 个区组的第 i 个结统计量 .
Friedman 检验统计量为:
friedman秩和检验步骤
Friedman秩和检验是一种非参数检验方法,主要用于比较多组相关样本的平均值是否存在显著差异。
它适用于样本数据不满足正态分布且样本量较小的情况,不需要假设数据的具体分布情况。
Friedman秩和检验步骤如下:1. 设定假设Friedman秩和检验的原假设为各组样本之间没有显著差异,即总体具有相同的中位数。
备择假设为各组样本之间存在显著差异,总体中位数不完全相同。
2. 计算秩次对每个样本数据按大小顺序排列,并给予秩次,相同数值的样本给予相同的平均秩次,若有并列排名,则按照并列样本的个数进行平均秩次计算。
3. 计算秩和对每组样本数据计算秩和,并计算Friedman秩和检验统计量。
4. 计算检验统计量根据计算所得的秩和,使用Friedman秩和检验的公式,计算检验统计量。
5. 确定显著性水平根据问题的需要,选择显著性水平α,通常取0.05。
6. 查表比较根据样本量和自由度的不同,在Friedman秩和检验的检验表中查找对应的临界值。
7. 判断检验结果比较计算所得的检验统计量与临界值,若大于临界值,则拒绝原假设,认为各组样本之间存在显著差异;若小于临界值,则接受原假设,认为各组样本之间没有显著差异。
在进行Friedman秩和检验时,需要注意的是秩和检验对样本具有独立性要求,不适用于重复数据或者具有时间序列关系的数据。
在对样本数据进行计算时,需要注意样本量的大小和样本之间方差的差异。
Friedman秩和检验是一种适用于非参数检验的方法,适用于样本数据不满足正态分布且样本量较小的情况。
通过以上步骤的计算和比较,可以得出对多组相关样本平均值差异的结论,是一种重要的统计分析方法。
在实际的统计分析中,Friedman秩和检验是一种非常有用的工具,特别适用于需要比较多组相关样本的平均值差异的情况。
接下来将继续对Friedman秩和检验的步骤做更详细的介绍。
第一步:设定假设。
在进行Friedman秩和检验之前,首先需要明确原假设和备择假设。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
即 P W 0.8125 0.0417.
此时 0.0417 也是 p 值.
对于水平 0.05,可以拒绝零假设.
也就是说,不同汽车密度的城市居民的血铅含量的确不一样.
按照 2 2 近似,得到 p 值为 0.0388,比上面的小一点.
例 某田径队对新入队的学员要进行四个部分的技术训练, 以提高学员的身体素质。为检验这四个部分的技术训练是否确实 有效,随机抽选了14 名新学员,分别接受四个部分的训练。 每个训练结束后,均进行该部分的测试,成绩以10 分为最高。 检测结果如下表所示:
对于置信水平 ,如果
Ri Rj
Z
*
2
bk(k 1) / 6,
则拒绝零假设,这里
*
总共可比较的对数
k(k 1)
, 2
Z
*
2
为标准正态分布分位数.
显然这个检验很保守,也就是说,很不容易拒绝零假设.
设来自四个地区的四名厨师制作名菜水煮鱼,四位美食 专家评分结果如下表.
专家
由于区组的影响,Friedman 检验首先在每一个区组中计算 各个处理的秩,再把每一个处理在各区组中的秩相加.
Rij 表示在第 j 个区组中 i 处理的秩,则秩按照处理而求得的
b
(行)和为 Ri Rij ,i 1, 2, , k. j 1 注:由于区组的影响,不同区组中的秩没有可比性. 但是,如果按照不同的区组收集数据,那么同一区组中 的不同处理之间的比较时有意义的. 比如,同个年龄段中比较药品的疗效比不分年龄来比较 疗效要合理. 因此,首先应在每一个区组内分配各处理的秩,从而 得到秩数据表.
Friedman 检验的问题是 k 个样本的位置参数
(用1,2, ,k 表示)是否相等.
k 个样本是匹配的,可以由 k 个条件下同一组受试者构成, 也可以将受试者分为 n 组,每组均有 k个匹配的受试者, 随机地将 n 组受试者置于 k 个条件下.
在不同受试者匹配的样本中,应尽量使不同受试者的有关 因素匹配即相似.
其中i 为同秩观测值个数,g 为同秩组数.
当实测数值 Dij Z1-* 时,表示两处理间有差异,反之则无差异.
其中 * .
k(k 1)
或者称之为 成对处理的比较
大样本时基于 Friedman 秩和检验的一个方法.
如果零假设 H0 为 i 处理和 j 处理没有区别, 那么,双边检验的统计量为 Ri Rj .
(区组) A
地区(处理)
B
C
D
1
85 82 82 79
2
87 75 86 82
3
90 81 80 76
4
80 75 81 75
试比较四个地区的四名厨师制作名菜水煮鱼的品质是否相同.
由于不同评委在口味和美学欣赏上存在差异,因此适合用 Freidman 检验方法比较.
解:假设检验问题
H
:
0
4
个地区的京城
设 0.10, 则 * 0.10 / 4(4 1) 0.0167.
Z10.0167 Z0.09833 2.13
等级 技术训练
A
B
C
D
学员编号
1 2 3 4 5 6 7 8 9 10 11 12 13 14
10
3
6
8
2
5
9
4
4
10
3
8
6
3
10
4
3
4
10
6
5
4
6
7
7
10
6
5
6
10
3
5
10
5
7
6
8
9
7
6
5
4
2
6
3
5
4
7
4
5
10
9
6
5
8
10
试问在5%的显著性水平下四个部分技术训练的有效性有无 显著差异?
解:(1)建立假设
8.1316.
结论一:实际测量Qa
8.1316
2 0.05
3
7.82,接受备择假设,
即四个地区的水煮鱼在品质上存在显著差异.
Step 2 4 个地区所做的水煮鱼品质上有显著差异,
成对样本比较有 k k 1 6 种.
2 四种水煮鱼的秩和分别为
R1 15, R2 8, R3 11.5, R4 5.5.
Friedman 检验统计量为:
Q
12 bk(k 1)
k Ri
j1
b
k
1
2
2
12 bk(k 1)
k
R
2 j
j 1
3b(k 1).
Q 渐近服从自由度为 k 1的 2 分布. 即 Q ~ 2 (k 1).
3. 作出决策
对于有限的 k 和 b,有零假设下的分布表可查,
• Qc 的小样本零分布无表可查,但是其零分布的极限分布 与 Q 一样.
• 修正后统计量 Qc 的数学期望等于 k 1,
仍然服从 2 (k 1) 分布.
• 若实测 Q 2 (k 1),则拒绝 H0.
反之不拒绝 H0.
例 4.2 在不同的城市对不同的人群进行血液中铅含量的测试, 一共有 A, B, C 三个城市,代表着三种不同的处理 (k 3). 对试验者按职业分成四组 (b 4) 取血. 他们血铅含量如下表所示:
方案C
2 3 1 1 3 2 3 1 3 3 2 2 3 2 2.5 3 3 3
Hollandre-Wolfe 两处理间的比较
当秩方差分析结果显示处理间存在差异时, (或者想知道某两个处理的比较时)
Hollandre Wolfe(1973)提出两处理间的比较公式: Dij Ri Rj SE .
区组(职业)
I
II
III
IV
处理(城市)
A
80 100
51
65
B
52
76
52
53
C
40
52
34
35
试判断对于显著性水平 0.05,
不同汽车密度的城市居民的血铅含量是否一样.
解:建立假设检验
H0 :1 2 3 H1 : 不是所有的位置参数都相等.
在表中加上各处理在每个区组(职业) 中的秩,得
1. 建立假设检验
假设检验问题:
H0 :1 2 ... k H1 : 不是所有的位置参数都相等.
或者说,提出假设
H
:
0
k 个样本间无显著差异.
H1:
k 个样本间有显著差异.
2. 选择检验统计量
• Friedman 检验所分析的数据应是定序尺度测量. • 获得的数据排出一个 k 行 n 列的表, 列代表不同的受试者或匹配的受试小组, 行代表各种条件(处理). • Friedman 检验的实质是符号检验推广到多个处理的比较问题.
R
k
1. 2
计算总均方(MST )
kb
Var Rij MST SST bk 1
(Rij R)2 bk
i1 j 1
1 bk
k i 1
b
Ri2j R 2
j 1
bk
1 bk
bk
k
1
6
2k
1
查的时候要作变换 W
b
Q
k 1
.
当查不到时,可用自由度为 k 1的 2 分布近似. 对于固定的 k,当 b 时,在零假设下有 Q ~ 2 (k 1).
4. 小结
检验步骤:
(1)提出假设
H
:
0
k
个样本间无显著差异.
H1:
k
个样本间有显著差异.
(2)计算检验统计量 Q.
(3)作出决策
12 bk(k 1)
k
R
2 j
j 1
3n(k 1)
12(152 82 11.52 5.52 )
3 4 5 7.725,
445
Qa
1
k i 1
Q
b
(
3 i,
j
i, j )
j 1
bk(k 2 1)
1
7.725 12
4 4 (42
1)
H
:
0
四个部分技术训练的有效性无显著差异
H1: 四个部分技术训练的有效性有显著差异
(2)计算检验统计量 Q.
学员编号 技术训练A 技术训练B
1
4
1
2
1
3
3
2
4
4
3
1
5
1
2
6
2
1
7
3
4
8
3
4
9
4
1
10
3
4
11
3
2
12
1
3
13
1
4
14
2
1
合计 (Ri )
33
33
技术训练C
2 4 1 4 4 3 2 1 3 2 1 2 4 3 36
区组(职业)
I
II
III
IV
Ri
处理(城市)
A 80(3) 100(3) 51(2) 65(3) 11
B
52(2) 76(2) 52(3) 53(2)
