小波包分解中小波函数的作用
小波变换中尺度函数和小波函数的功能

小波变换中尺度函数和小波函数的功能小波变换是一种信号处理技术,广泛应用于信号分析、图像处理、数据压缩等领域。
其中的尺度函数和小波函数是关键要素,它们具有不同的功能和作用。
尺度函数是用于调整尺度的函数,它可以对信号进行放大或缩小操作。
尺度函数一般被定义为一个能量有限的函数,其尺度参数可以控制函数的宽度。
通过改变尺度参数,我们可以调整小波变换的时间或频率分辨率。
尺度函数对信号进行局部分析,可以提取出信号的重要特征,如频率信息、振幅信息等。
小波函数是用于分解信号的函数,它是由尺度函数通过平移和伸缩得到的。
小波函数是一组正交函数,其具有良好的时频局部化特性。
小波函数可以将信号分解为不同频率和时间尺度下的成分,实现信号的多尺度分析。
小波函数能够捕捉信号的瞬时特性,对瞬态信号和非平稳信号具有较好的分析效果。
尺度函数和小波函数在小波变换中起着不可替代的作用。
尺度函数通过控制尺度参数,可以实现对信号的局部分析,提取出信号的频率、振幅等特征,为信号的后续处理提供重要信息。
小波函数则通过将信号分解为不同频率和时间尺度下的成分,揭示出信号的多尺度结构,实现对信号的全局分析和重构。
在实际应用中,选择合适的尺度函数和小波函数对小波变换的结果具有重要影响。
不同的尺度函数和小波函数适用于不同类型的信号和处理任务。
因此,在进行小波变换时,我们需要根据具体情况选取合适的尺度函数和小波函数,以获得准确、可靠的分析结果。
总之,尺度函数和小波函数在小波变换中具有重要功能。
尺度函数通过调整尺度参数,实现对信号的局部分析;小波函数通过分解信号为不同频率和时间尺度下的成分,实现对信号的全局分析。
合理选择尺度函数和小波函数可以提高小波变换的性能和应用效果。
深入理解尺度函数和小波函数的功能和作用,有助于我们更好地运用小波变换进行信号处理和分析。
小波分解和小波包分解

⼩波分解和⼩波包分解这篇⽂章介绍了⼩波分解和⼩波包分解。
⼩波分解(wavelet transform )⼩波傅⾥叶变换的基本⽅程是sin 和cos ,⼩波变换的基本⽅程是⼩波函数(basic wavelet),不同的⼩波在波形上有较⼤的差异,相似的⼩波构成⼀个⼩波族(family)。
⼩波具有这样的局部特性:只有在有限的区间内取值不为0。
这个特性可以很好地⽤于表⽰带有尖锐, 不连续的信号。
⼩波变换其中 表⽰变换得到的⼩波系数,W 是正交矩阵。
是输⼊信号。
正交矩阵构造特定的⼩波函数(basic wavelet )由⼀组特定的⼩波滤波系数(wavelet filter coefficients)构成。
当选定了⼩波函数,其对应的那组⼩波滤波器系数就知道。
⽤⼩波滤波器系数构造不同维度的低通滤波器和⾼通滤波器(下⾯的例⼦中W 就是由这些系数构造出来的)。
低通滤波器可以看作为⼀个平滑滤波器(smoothing filter)。
这两个滤波器,低通和⾼通滤波器,⼜分别被称为尺度(scaling)和⼩波滤波器(wavelet filter)。
⼀旦定义好了这两个滤波器,通过递归分解算法(也称为⾦字塔算法(pyramid algorithm),树算法(tree algorithm)将得到⽔平多分辨率表⽰的信号。
树算法原始信号通过低通滤波器得到低频系数 (approximate coefficients), 通过⾼通滤波器得到⾼频系数(detail coefficients )。
把第⼀层的低频系数作为信号输⼊,⼜得到⼀组approximate coefficients 和detail coefficients 。
再把得到的approximate coefficients 作为信号输⼊,得到第⼆层的approximate coefficients 和detail coefficients 。
以此类推,直到满⾜设定的分级等级。
小波包、多小波及第二代小波

M
因此,很容易得到小波子空间的各种分解如下: jW
3121++⊕=jjjUUW
72625242++++⊕⊕⊕=jjjjjUUUUW
M
121221.
+
+
++
+⊕⊕⊕=lllljljljjUUUWL 4.14
M
文本框:
jW空间分解的子空间序列可以写作,;mljlU+
+
212,,1,0.ቤተ መጻሕፍቲ ባይዱlmLjl,,2,1L=;。子空间
序列的标准正交基为:
L,2,1=jmljlU+
+
2
{}Znntwljmljl∈.+.
+
+.:)2(2)(
22/)( 4.15
当和时,子空间序列简化为,相应的正交基简化为0=l0=mmljlU+
+
2jjWU=1{})2(2)2(22/
在感兴趣的频率点上尽可能地提高频域分辨率,在感兴趣的时间点上尽可能地提高时间分辨率,这样当用
滤波器组对信号进行分解时,短时Fourier变换的等带宽或小波变换的恒-Q带宽都不一定合适,应该按信
号特性选择相应组合的滤波器组,这就是小波包(Wave1et Packet)。
小波包的概念是由M.V.WickerhaMser,R.R.Coifman等人在小波变换的基础上,根据实际应用的需求
()()0,122=.+ktWtwll
4.1.2 小波包分解
现在令、L,2,1=lL,2,1=j,并对式(4.11)进行迭代分解,有
小波分析及小波包分析

小波分析及小波包分析在利用matlab做小波分析时,小波分解函数和系数提取函数的结果都是分解系数。
我们知道,复杂的周期信号可以分解为一组正弦函数之和,及傅里叶级数,而傅里叶变换对应于傅里叶级数的系数;同样,信号也可以表示为一组小波基函数之和,小波变换系数对应于这组小波基函数的系数。
多尺度分解是按照多分辨分析理论,分解尺度越大,分解系数的长度越小(是上一个尺度的二分之一)。
我们会发现分解得到的小波低频系数的变化规律和原始信号相似,但要注意低频系数的数值和长度与原始信号以及后面重构得到的各层信号是不一样的。
小波分解:具体实现过程可以分别设计高通滤波器和低通滤波器,得到高频系数和低频系数,并且每分解一次数据的长度减半。
小波重构,为分分解的逆过程,先进行增采样,及在每两个数之间插入一个0,与共轭滤波器卷积,最后对卷积结果求和。
在应用程中,我们经常利用各层系数对信号进行重构(注意虽然系数数少于原信号点数,但是重构后的长度是一样的),从而可以有选择的观看每一频段的时域波形。
从而确定冲击成分所在频率范围。
便于更直观的理解,小波分解,利用各层系数进行信号重构过程我们可以认为是将信号通过一系列的不同类型的滤波器,从而得到不同频率范围内的信号,及将信号分解。
小波消噪:运用小波分析进行一维信号消噪处理和压缩处理,是小波分析的两个重要的应用。
使用小波分析可以将原始信号分解为一系列的近似分量和细节分量,信号的噪声主要集中表现在信号的细节分量上。
使用一定的阈值处理细节分量后,再经过小波重构就可以得到平滑的信号。
小波常用函数[C,L]=wavedec(s,3,'db1');%用小波函数db1对信号s进行3尺度分解其中C为分解后低频和高频系数,L存储低频和高频系数的长度。
X=wrcoef(‘type’,C,L,’wname’,N)%对一维小波系数进行单支重构,其中N表示对第几层的小波进行重构X=wrcoef(‘a’,C,L,’wname’,3)%对第三层的低频信号进行重构,如果a变为d的话,表示对低频分量进行重构。
10.28小波分解总结
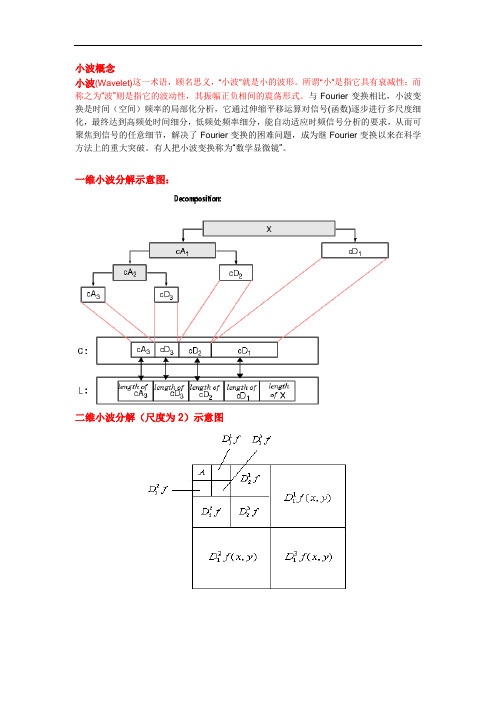
小波概念小波(Wavelet)这一术语,顾名思义,“小波”就是小的波形。
所谓“小”是指它具有衰减性;而称之为“波”则是指它的波动性,其振幅正负相间的震荡形式。
与Fourier变换相比,小波变换是时间(空间)频率的局部化分析,它通过伸缩平移运算对信号(函数)逐步进行多尺度细化,最终达到高频处时间细分,低频处频率细分,能自动适应时频信号分析的要求,从而可聚焦到信号的任意细节,解决了Fourier变换的困难问题,成为继Fourier变换以来在科学方法上的重大突破。
有人把小波变换称为“数学显微镜”。
一维小波分解示意图:二维小波分解(尺度为2)示意图二维小波分解常用函数:1)[C,S] = WAVEDEC2(X,N,'wname');该函数实现小波的N尺度(层次)分解,得到分解系数C,S为数组,存放各尺度频率的尺寸。
2)A = APPCOEF2(C,S,'wname',N);提取指定尺度N上的低频系数3)D = DETCOEF2(O,C,S,N);提取分解结构[C,S]中指定尺度N上的高频系数,O = 'h' (or 'v' or 'd', respectively), at level N.1 <= N <= size(S,1)-2[H,V,D] = DETCOEF2('all',C,S,N)4)X = WRCOEF2('type',C,S,'wname',N);'type' = 'a',('h','v' or 'd', respectively),单支重构,即重构指定尺度N上的某个频率部分5)X = WAVEREC2(C,S,'wname')多尺度图像分解后重构6)CAT(DIM,A,B) concatenates the arrays A and B along the dimension DIM.沿着行或者列来进行向量的合成,可以用于小波分解后的系数C的重新组合。
小波包变换的基本原理和使用方法

小波包变换的基本原理和使用方法引言:小波包变换(Wavelet Packet Transform)是一种信号分析技术,它在小波变换的基础上进一步拓展,能够提供更丰富的频域和时域信息。
本文将介绍小波包变换的基本原理和使用方法,帮助读者更好地理解和应用这一技术。
一、小波包变换的基本原理小波包变换是一种多分辨率分析方法,它利用小波基函数对信号进行分解和重构。
与传统的傅里叶变换相比,小波包变换能够提供更精细的频域和时域信息,适用于非平稳信号的分析。
小波包变换的基本原理如下:1. 信号分解:首先将原始信号分解为不同频率的子信号,通过迭代地将信号分解为低频和高频部分,形成小波包树结构。
2. 小波基函数:在每一层分解中,选取合适的小波基函数进行信号分解。
小波基函数具有局部性和多分辨率特性,能够更好地捕捉信号的局部特征。
3. 分解系数:分解过程中,每个子信号都会生成一组分解系数,用于表示信号在不同频率上的能量分布。
分解系数可以通过滤波和下采样得到。
二、小波包变换的使用方法小波包变换在信号处理领域有广泛的应用,包括信号去噪、特征提取、模式识别等。
下面将介绍小波包变换的常见使用方法。
1. 信号去噪:小波包变换可以提供更丰富的频域和时域信息,因此在信号去噪领域有较好的效果。
通过对信号进行小波包分解,可以将噪声和信号分离,然后对噪声进行滤波处理,最后通过重构得到去噪后的信号。
2. 特征提取:小波包变换可以提取信号的局部特征,对于信号的频率变化和时域特征有较好的描述能力。
通过对信号进行小波包分解,可以得到不同频率下的分解系数,进而提取出信号的主要特征。
3. 模式识别:小波包变换在模式识别中也有广泛的应用。
通过对信号进行小波包分解,可以得到不同频率下的分解系数,进而提取出信号的特征向量。
利用这些特征向量,可以进行模式分类和识别。
4. 压缩编码:小波包变换可以将信号进行有效的压缩编码。
通过对信号进行小波包分解,可以将信号的主要信息集中在少量的分解系数中,从而实现信号的压缩。
小波包分解PPT课件讲义

(
2
)
P0
()ˆ
l
(
2
)
ˆ
2l 1
()
G(
)ˆ l
(
2
)
P1 ( )ˆ
l
(
2
)
递推下去即可。
定理:
由正交尺度函数(x)生成的小波包{ n (x)}
满足:
(1) { n (x k)}是规范正交系。 即 n (x j), n (x k) j,k j, k, n Z (2) 2l (x j), 2l1(x k) 0 j, k, n Z
• 参数j,k,n 的意义。
小波库中的一个函数: n (2 j x k)
参数j : 尺度指标(频域参数) 参数k : 位置指标(时间参数) 参数n : 振荡次数
n (2 j x k)是中心在2-j k, 支集大小
数量级为2 j,振荡次数为n的小波函数。
对小波包的实际意义的分析:
• 当参数j固定时。
0
2、范数。
M ({xk}) {xk}
1
通常选,{xk } =(
xp)p k
k
p0
(范数愈小,能量愈集中。)
常用代价函数:
3、熵
M ({xk }) | xk |2 log | xk |2 k
(与均方意义下恢复原始信号所需的系数个数成 正比。)
常用代价函数:
4、能量对数
M ({xk }) log | xk |2
0 j
U
1 j
定理:
U
nj+1=U
2n j
U
2n1 j
证明要点:
(1) (2) (3)
U
2j n和U
2 j
n1是U
图像的小波分解原理

图像的小波分解原理
小波分解是一种将信号或图像分解成不同频率的子信号或子图像的方法。
其原理是采用小波函数作为基函数,通过不断缩放和平移这些基函数来逼近原始信号或图像。
小波函数具有时域和频域上的局部性质,可以更好地描述信号或图像的局部特征。
小波分解的过程可以简单地描述为以下几个步骤:
1. 将原始信号或图像与一个小波函数进行卷积操作,得到一个高频子信号或子图像和一个低频子信号或子图像。
2. 对低频子信号或子图像重复步骤1,进行进一步分解。
3. 重复步骤2,直到达到所期望的分解层数或者满足某个终止
条件。
在每一层分解中,低频子信号或子图像包含了原始信号或图像的大致特征,而高频子信号或子图像则包含了局部细节信息。
因此,通过多层小波分解可以逐步提取出信号或图像的不同尺度的特征,从而实现多分辨率分析。
小波分解具有许多优点,例如能够提取信号或图像的时频局部特征,适用于非平稳信号或图像的分析,具有良好的局部逼近性等。
因此,它在图像处理领域得到了广泛的应用,如图像压缩、图像增强、图像恢复等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小波包分解中小波函数的作用
In wavelet packet decomposition, the role of the wavelet function is pivotal. It serves as the building block of the analysis, enabling the signal to be decomposed into a series of components that capture its different frequency characteristics. The wavelet function, through its oscillatory nature, is able to localize the signal's features in both time and frequency domains, providing a detailed representation of the signal's structure. By adapting its shape and scale, the wavelet function can effectively capture transient and non-stationary components of the signal, making it a powerful tool for signal analysis and processing.
在小波包分解中,小波函数发挥着至关重要的作用。
它作为分析的基石,使信号能够被分解为一系列捕捉其不同频率特性的组成部分。
小波函数通过其振荡性质,能够在时间和频率域内定位信号的特征,从而提供信号结构的详细表示。
通过调整其形状和尺度,小波函数可以有效地捕捉信号的瞬态和非平稳成分,使其成为信号分析和处理的有力工具。
The selection of the wavelet function is crucial as it directly impacts the performance of the wavelet packet decomposition. Different wavelet functions exhibit different properties, such as orthogonality, symmetry, and compact support, which can be tailored to suit specific application requirements. The appropriate choice of the wavelet function can enhance the accuracy and efficiency of
the decomposition process, leading to improved signal representation and analysis outcomes.
小波函数的选择至关重要,因为它直接影响小波包分解的性能。
不同的小波函数具有不同的特性,如正交性、对称性和紧支撑性等,这些特性可以根据特定的应用需求进行调整。
选择合适的小波函数可以提高分解过程的准确性和效率,从而改善信号的表示和分析结果。
In summary, the wavelet function plays a fundamental role in wavelet packet decomposition by enabling the decomposition and representation of signals in a manner that captures their inherent features and characteristics. Its selection is a critical step in ensuring the effectiveness of the decomposition process for various signal analysis tasks.
总之,小波函数在小波包分解中发挥着基础性的作用,它使信号能够以捕捉其固有特征和特性的方式进行分解和表示。
选择适当的小波函数是确保分解过程在各种信号分析任务中有效的关键步骤。
