008-小波分析(第三讲)--小波包_二代小波_Matlab工具使用汇总
小波包、多小波及第二代小波

M
因此,很容易得到小波子空间的各种分解如下: jW
3121++⊕=jjjUUW
72625242++++⊕⊕⊕=jjjjjUUUUW
M
121221.
+
+
++
+⊕⊕⊕=lllljljljjUUUWL 4.14
M
文本框:
jW空间分解的子空间序列可以写作,;mljlU+
+
212,,1,0.ቤተ መጻሕፍቲ ባይዱlmLjl,,2,1L=;。子空间
序列的标准正交基为:
L,2,1=jmljlU+
+
2
{}Znntwljmljl∈.+.
+
+.:)2(2)(
22/)( 4.15
当和时,子空间序列简化为,相应的正交基简化为0=l0=mmljlU+
+
2jjWU=1{})2(2)2(22/
在感兴趣的频率点上尽可能地提高频域分辨率,在感兴趣的时间点上尽可能地提高时间分辨率,这样当用
滤波器组对信号进行分解时,短时Fourier变换的等带宽或小波变换的恒-Q带宽都不一定合适,应该按信
号特性选择相应组合的滤波器组,这就是小波包(Wave1et Packet)。
小波包的概念是由M.V.WickerhaMser,R.R.Coifman等人在小波变换的基础上,根据实际应用的需求
()()0,122=.+ktWtwll
4.1.2 小波包分解
现在令、L,2,1=lL,2,1=j,并对式(4.11)进行迭代分解,有
Matlab中的小波变换与小波包分析方法详解

Matlab中的小波变换与小波包分析方法详解引言近年来,小波变换在信号处理领域中得到了广泛的应用。
小波变换是一种能够捕捉信号时频特性的有效工具,可以用来分析、压缩和去噪各种类型的信号。
本文将详细介绍Matlab中的小波变换和小波包分析方法,以帮助读者更好地理解和应用这一强大的信号处理技术。
一、小波变换(Wavelet Transform)小波变换是一种将信号分解成不同尺度的基函数的技术。
与传统的傅里叶变换相比,小波变换具有更好的时频局部化特性。
Matlab中提供了丰富的小波分析工具箱,可以方便地进行小波变换的计算。
1.1 小波基函数小波基函数是小波变换的基础。
不同类型的小波基函数适用于不同类型的信号。
在Matlab中,我们可以使用多种小波基函数,如Daubechies小波、Haar小波和Morlet小波等。
1.2 小波分解小波分解是指将信号分解成多个尺度的小波系数。
通过小波分解,我们可以获取信号在不同尺度上的时频特性。
Matlab中提供了方便的小波分解函数,例如'dwt'和'wavedec'。
1.3 小波重构小波重构是指根据小波系数重新构建原始信号。
通过小波重构,我们可以恢复原始信号的时域特性。
在Matlab中,可以使用'idwt'和'waverec'函数进行小波重构。
二、小波包分析(Wavelet Packet Analysis)小波包分析是对小波变换的进一步扩展,它允许对信号进行更精细的分解和重构。
小波包分析提供了一种更灵活的信号分析方法,能够获得更详细的时频特性。
2.1 小波包分解小波包分解是指将信号分解成具有不同频带的小波包系数。
与小波分解相比,小波包分解提供了更高的分辨率和更详细的频谱信息。
在Matlab中,可以使用'wavedec'函数进行小波包分解。
2.2 小波包重构小波包重构是根据小波包系数重新构建原始信号。
小波分析课件_常用小波函数及Matlab常用指令

General characteristics: Compactly supported wavelets with least asymmetry and highest number of vanishing moments for a given support width. Associated scaling filters are near linear-phase filters. Family Symlets Short name sym Order N N = 2, 3, ... Examples sym2, sym8
bior Nr.Nd
bior 1.1 bior 1.3 bior 1.5 bior 2.2 bior 2.4 bior 2.6 bior 2.8
ld effective length of Lo_D 2 6 10 5 9 13 17
lr effective length of Hi_D 2 2 2 3 3 3 3
Family Short name Order Nr,Nd r for reconstruction d for decomposition
Biorthogonal bior Nr = 1 , Nd = 1, 3, 5 N, 3, 5, 7, 9 Nr = 4 , Nd = 4 Nr = 5 , Nd = 5 Nr = 6 , Nd = 8
图:
在命令窗口输入waveinfo('haar')
2、db系列小波
DBINFO Information on Daubechies wavelets. Daubechies Wavelets General characteristics: Compactly supported wavelets with extremal phase and highest number of vanishing moments for a given support width. Associated scaling filters are minimum-phase filters. Family Daubechies Short name db Order N N strictly positive integer Examples db1 or haar, db4, db15
Matlab小波工具箱的使用

(2011-11-10 20:12:39)转载▼分类:学科知识标签:小波分析连续小波变换尺度系数信号最近想尝试一下小波的用法,就这matlab的帮助尝试了一下它的例子,顺便翻译了一下帮助的内容,发现matlab帮助做的确实不错,浅显易懂!现把翻译的文档写出来吧,想学习的共同学习吧!小波工具箱简介小波工具箱包含了图像化的工具和命令行函数,它可以实现如下功能:l 测试、探索小波和小波包的特性l 测试信号的统计特性和信号的组分l 对一维信号执行连续小波变换l 对一维、二维信号执行离散小波分析和综合l 对一维、二维信号执行小波包分解(参见帮助Using Wavelet Packets)l 对信号或图像进行压缩、去噪另外,工具箱使用户更方便的展示数据。
用户可以做如下选择:l 显示哪个信号l 放大感兴趣的区域l 配色设计来显示小波系数细节工具箱可以方便的导入、导出信息到磁盘或matlab工作空间。
具体详见File Menu Options一维连续小波分析这一部分来测试连续小波分析的特性。
连续小波分析只需要一个小波函数cwt。
在这一部分将学到如下内容:l 加载信号l 对信号执行连续小波变换l 绘制小波系数l 绘制指定尺度的小波系数l 绘制整个尺度小波系数中的最大值l 选择显示方式l 在尺度和伪频率之间切换l 细节放大l 在普通或绝对模式下显示系数l 选择执行小波分析的尺度使用命令行执行连续小波分析这个例子是一个包含噪声的正弦波1. 加载信号load noissin可以使用whos显示信号信息2. 执行连续小波变换c = cwt(noissin,1:48,'db4');函数cwt的参数分别为分析的信号、分析的尺度和使用的小波。
返回值c包含了在各尺度下的小波系数。
对于这里,c是一个48x1000的矩阵,每一行与一个尺度相关。
3. 绘制小波系数cwt函数可以接受第四个参数,来指定函数在执行结束后是否绘制连续小波变换系数的绝对值。
MATLAB小波函数总结

MATLAB小波函数总结转自/95339593/blog/item/1827661f354d66c9a7 866996.html函数含义 *:小波通用函数Allnodes 计算树结点appcoef 提取一维小波变换低频系数appcoef2 提取二维小波分解低频系数bestlevt 计算完整最佳小波包树besttree 计算最佳(优)树* biorfilt 双正交样条小波滤波器组biorwavf 双正交样条小波滤波器* centfrq 求小波中心频率cgauwavf Complex Gaussian小波cmorwavf coiflets小波滤波器cwt 一维连续小波变换dbaux Daubechies小波滤波器计算dbwavf Daubechies小波滤波器 dbwavf(W) W='dbN' N=1,2,3,...,50ddencmp 获取默认值阈值(软或硬)熵标准depo2ind 将深度-位置结点形式转化成索引结点形式detcoef 提取一维小波变换高频系数detcoef2 提取二维小波分解高频系数disp 显示文本或矩阵drawtree 画小波包分解树(GUI)dtree 构造DTREE类dwt 单尺度一维离散小波变换dwt2 单尺度二维离散小波变换dwtmode 离散小波变换拓展模式* dyaddown 二元取样* dyadup 二元插值entrupd 更新小波包的熵值fbspwavf B样条小波gauswavf Gaussian小波get 获取对象属性值idwt 单尺度一维离散小波逆变换idwt2 单尺度二维离散小波逆变换ind2depo 将索引结点形式转化成深度—位置结点形式* intwave 积分小波数isnode 判断结点是否存在istnode 判断结点是否是终结点并返回排列值iswt 一维逆SWT(Stationary Wavelet Transform)变换iswt2 二维逆SWT变换leaves Determine terminal nodesmexihat 墨西哥帽小波meyer Meyer小波meyeraux Meyer小波辅助函数morlet Morlet小波nodease 计算上溯结点nodedesc 计算下溯结点(子结点)nodejoin 重组结点nodepar 寻找父结点nodesplt 分割(分解)结点noleaves Determine nonterminal nodes ntnode Number of terminal nodesntree Constructor for the class NTREE* orthfilt 正交小波滤波器组plot 绘制向量或矩阵的图形* qmf 镜像二次滤波器rbiowavf Reverse biorthogonal spline wavelet filtersread 读取二进制数据readtree 读取小波包分解树* scal2frq Scale to frequencysetshanwavf Shannon waveletsswt 一维SWT(Stationary Wavelet Transform)变换swt2 二维SWT变换symaux Symlet wavelet filter computation.symwavf Symlets小波滤波器thselect 信号消噪的阈值选择thodes Referencestreedpth 求树的深度treeord 求树结构的叉数upcoef 一维小波分解系数的直接重构upcoef2 二维小波分解系数的直接重构upwlev 单尺度一维小波分解的重构upwlev2 单尺度二维小波分解的重构wavedec 单尺度一维小波分解wavedec2 多尺度二维小波分解wavedemo 小波工具箱函数demo* wavefun 小波函数和尺度函数* wavefun2 二维小波函数和尺度函数wavemenu 小波工具箱函数menu图形界面调用函数* wavemngr 小波管理函数waverec 多尺度一维小波重构waverec2 多尺度二维小波重构wbmpen Penalized threshold for wavelet 1-D or 2-D de-noisingwcodemat 对矩阵进行量化编码wdcbm Thresholds for wavelet 1-D using Birge-Massart strategywdcbm2 Thresholds for wavelet 2-D using Birge-Massart strategywden 用小波进行一维信号的消噪或压缩wdencmp De-noising or compression using waveletswentropy 计算小波包的熵wextend Extend a vector or a matrix* wfilters 小波滤波器wkeep 提取向量或矩阵中的一部分* wmaxlev 计算小波分解的最大尺度wnoise 产生含噪声的测试函数数据wnoisest 估计一维小波的系数的标准偏差wp2wtree 从小波包树中提取小波树wpcoef 计算小波包系数wpcutree 剪切小波包分解树wpdec 一维小波包的分解wpdec2 二维小波包的分解wpdencmp 用小波包进行信号的消噪或压缩wpfun 小波包函数wpjoin 重组小波包wprcoef 小波包分解系数的重构wprec 一维小波包分解的重构wprec2 二维小波包分解的重构wpsplt 分割(分解)小波包wpthcoef 进行小波包分解系数的阈值处理wptree 显示小波包树结构wpviewcf Plot the colored wavelet packet coefficients.wrcoef 对一维小波系数进行单支重构wrcoef2 对二维小波系数进行单支重构wrev 向量逆序write 向缓冲区内存写进数据wtbo Constructor for the class WTBO wthcoef 一维信号的小波系数阈值处理wthcoef2 二维信号的小波系数阈值处理wthresh 进行软阈值或硬阈值处理wthrmngr 阈值设置管理wtreemgr 管理树结构。
MATLAB小波变换指令及其功能介绍(超级有用)

MATLAB小波变换指令及其功能介绍(超级有用)MATLAB小波变换指令及其功能介绍1 一维小波变换的 Matlab 实现(1) dwt函数功能:一维离散小波变换格式:[cA,cD]=dwt(X,'wname')[cA,cD]=dwt(X,Lo_D,Hi_D)别可以实现一维、二维和 N 维DFT 说明:[cA,cD]=dwt(X,'wname') 使用指定的小波基函数'wname'对信号X 进行分解,cA、cD 分别为近似分量和细节分量;[cA,cD]=dwt(X,Lo_D,Hi_D) 使用指定的滤波器组 Lo_D、Hi_D 对信号进行分解。
(2) idwt 函数功能:一维离散小波反变换格式:X=idwt(cA,cD,'wname')X=idwt(cA,cD,Lo_R,Hi_R)X=idwt(cA,cD,'wname',L)函数 fft、fft2 和 fftn 分X=idwt(cA,cD,Lo_R,Hi_R,L)说明:X=idwt(cA,cD,'wname') 由近似分量 cA 和细节分量 cD 经小波反变换重构原始信号 X 。
'wname' 为所选的小波函数X=idwt(cA,cD,Lo_R,Hi_R) 用指定的重构滤波器 Lo_R 和Hi_R 经小波反变换重构原始信号 X 。
X=idwt(cA,cD,'wname',L) 和X=idwt(cA,cD,Lo_R,Hi_R,L) 指定返回信号 X 中心附近的 L 个点。
2 二维小波变换的 Matlab 实现二维小波变换的函数别可以实现一维、二维和 N 维 DFT函数名函数功能---------------------------------------------------dwt2 二维离散小波变换wavedec2 二维信号的多层小波分解idwt2 二维离散小波反变换waverec2 二维信号的多层小波重构wrcoef2 由多层小波分解重构某一层的分解信号upcoef2 由多层小波分解重构近似分量或细节分量detcoef2 提取二维信号小波分解的细节分量appcoef2 提取二维信号小波分解的近似分量upwlev2 二维小波分解的单层重构dwtpet2 二维周期小波变换idwtper2 二维周期小波反变换----------------------------------------------------------- (1) wcodemat 函数功能:对数据矩阵进行伪彩色编码函数 fft、fft2 和 fftn 分格式:Y=wcodemat(X,NB,OPT,ABSOL)Y=wcodemat(X,NB,OPT)Y=wcodemat(X,NB)Y=wcodemat(X)说明:Y=wcodemat(X,NB,OPT,ABSOL) 返回数据矩阵 X 的编码矩阵Y ;NB 伪编码的最大值,即编码范围为 0~NB,缺省值 NB=16;OPT 指定了编码的方式(缺省值为 'mat'),即:别可以实现一维、二维和 N 维 DFTOPT='row' ,按行编码OPT='col' ,按列编码OPT='mat' ,按整个矩阵编码函数 fft、fft2 和 fftn 分ABSOL 是函数的控制参数(缺省值为 '1'),即:ABSOL=0 时,返回编码矩阵ABSOL=1 时,返回数据矩阵的绝对值 ABS(X)1. 离散傅立叶变换的 Matlab实现(2) dwt2 函数功能:二维离散小波变换格式:[cA,cH,cV,cD]=dwt2(X,'wname')[cA,cH,cV,cD]=dwt2(X,Lo_D,Hi_D)说明:[cA,cH,cV,cD]=dwt2(X,'wname')使用指定的小波基函数'wname' 对二维信号 X 进行二维离散小波变幻;cA,cH,cV,cD 分别为近似分量、水平细节分量、垂直细节分量和对角细节分量;[cA,cH,cV,cD]=dwt2(X,Lo_D,Hi_D) 使用指定的分解低通和高通滤波器 Lo_D 和 Hi_D 分解信号 X 。
小波分析中的matlab使用
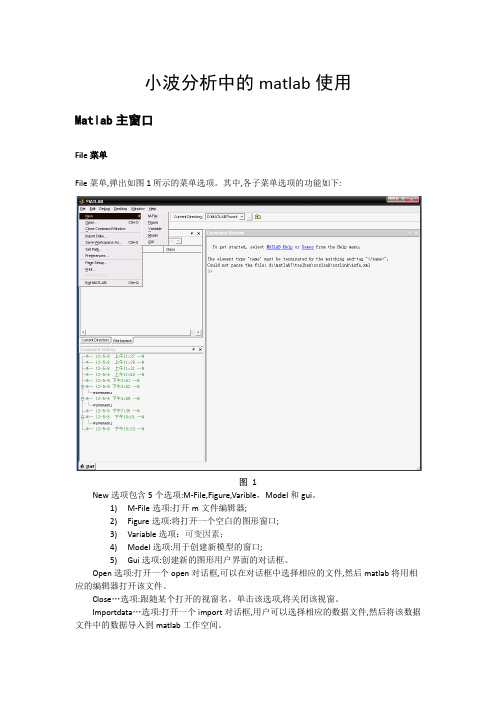
小波分析中的matlab使用Matlab主窗口File菜单File菜单,弹出如图1所示的菜单选项。
其中,各子菜单选项的功能如下:图 1New选项包含5个选项:M-File,Figure,Varible,Model和gui。
1)M-File选项:打开m文件编辑器;2)Figure选项:将打开一个空白的图形窗口;3)Variable选项:可变因素;4)Model选项:用于创建新模型的窗口;5)Gui选项:创建新的图形用户界面的对话框。
Open选项:打开一个open对话框,可以在对话框中选择相应的文件,然后matlab将用相应的编辑器打开该文件。
Close…选项:跟随某个打开的视窗名。
单击该选项,将关闭该视窗。
Importdata…选项:打开一个import对话框,用户可以选择相应的数据文件,然后将该数据文件中的数据导入到matlab工作空间。
Saveworkspaceas…选项:打开一个savetomat-File对话框,用户需要为保存的工作空间命名。
Setpath…选项:打开设置路径对话框。
通过该对话框可以更改matlab执行命令时搜索的路径。
Preferences:首选参数。
Pagesetup选项:用于设置页面布局,页面的页眉,页面所用的文字。
Print…选项:用于打印预定义好的页面内容,也可以设置一些参数。
Printselection…选项:当选中命令窗口内的一部分内容后,该选项将处于激活状态,此时单击该选项,将打印对话框中选中的内容。
Exitmatlab选项:关闭matlab。
也可以通过快捷键ctrl+O来关闭。
Edit菜单单击edit菜单,会弹出如图2所示的菜单选项。
其中,各子菜单选项的功能如下:Undo选项:取消上一次的操作。
Redo选项:重复上一次的操作。
Cut选项:剪切所选中的部分。
Copy选项:选复制被选中的部分。
Paste选项:把存放在缓冲区中的内容粘贴到光标所在的位置。
Pastespecial选项:打开导入数据向导,该向导引导用户把存放在缓冲区中的内容以特定格式存放到剪贴板变量中。
小波分析MATLAB工具箱简介

小波分析MATLAB工具箱简介MATLAB的小波分析一、小波分析用于降噪的基本过程1、分解过程:选定一种小波,对信号进行N层分解;2、作用阈值过程:对分解得到的各层系数选择一个阈值,并对细节系数进行软阈值处理;3、重建过程:降处理后的系数通过小波重建恢复原始信号;二、基本降噪模型函数一维离散小波分解命令Dwt [cA cD] = dwt(X,’wname’)使用小波’wname’对型号X 进行单层分解,求得的近似系数存放于数组cA中,细节系数存放在数组cD 中;[cA cD] = dwt(X,’wname’,’mode’,MODE) 利用MODE方式进行扩展[cA cD] = dwt(X,Lo_D,Hi_D) 利用指定滤波器进行小波分解Wanedec [C, L] = wavedec(X,N,’wname’) 使用wname的小波进行N层分解,C为层数,L为各层系数Idwt X= idwt(cA,cD,’wname’) 利用小波wname把近似系数CA和CD重建为上一层近似系数XX= idwt(cA,cD,’wname’,L) 重建至L层Waverec X= waverec(C,L,‘wname‘)重建为原始信号Wrcoef X = wrcoef(‘type’,C,L,’wname’,N) 通过分解系数重构指定的数,type为a 或者dX= wrcoef(‘type’,C,L,’wname’) 把分解系数重建至最高层Upcoef Y= upcoef(O,X,’wname’,N)用适当的滤波器作用在X上N次,求得重建系数Y,O为a表示低通滤波器,d表示高通滤波器Detcofe D= detcoef(C,L,N)从分解系数中提取第N层近似系数D= detcoef(C,L,N)提取至最后一层Appcoef A= appcoef(C,L,’wname’,N) 用小波从分解系数中提取第N层系数Wnoisest stdc = woisest(c,l,s)根据传入的小波分解系数[c,l]对s中标识的小波层数求得其标准差,作为对噪声强度的估计;Ddencmp [THR,SORH,KEEPAPP,CRIT] = ddencmp(IN1,IN2,X) 根据传入的参数IN1 和IN2所指定的方式,对输入信号X求得其降噪或压缩的各级阈值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第5层小波包分解
23号小波包重构
一个周期内约有9 个冲击,与理论 分析相符,说明 小波包分解有效
16/ 82
轴的转动周期 北京科技大学 机械工程学院
小波包---应用3
轴承外圈剥落故障
时域振动信号
最高分析频率 f = fs /2 = 20/2 = 10 KHz
每个小波包的频率带宽为
d = f /32 =312.5 Hz 频谱图中的频率范围 3500~5500 Hz 对应的小波包频宽范围 3500/312.5 ~ 5500/312.5 Hz 即为 11~18号小波包
第5层小波包分解
频域图
16号小波包重构
一个周期内约有7 个冲击,与理论 分析相符,说明 小波包分解有效
17/ 82
北京科技大学 机械工程学院
小波包---小结
小波包分解能够对每一层分解后得到的高频信号进 行再分解,提高了信号高频部分的多尺度分析能力,弥 补了小波分解的不足
小波包分解保留了信号在各个不同频率段的成分, 因此小波包分解后,信号的信息量是完整的
采用小波包分解能够提取信号中有用的频率成分, 因此可以有效地用于信号的特征提取
北京科技大学 机械工程学院
P21
P22
P23
P24
P31
P32
P34
P35
P36
P37
P38
北京科技大学 机械工程学院
12/ 82
小波包---应用1
电机振动信号,采样频率5120Hz
电机转速频率 电机转速频率的四倍频
第5层小波包分解
北京科技大学 机械工程学院
13/ 82
小波包---应用1
最高分析频率f = fs /2 = 2560 Hz 每个小波包的频率带宽为 d = f /32 = 80Hz 电机转速频率50Hz∈[0 80],即为0号小波包 电机转速频率的四倍频200Hz ∈[160 240],即2号小波包
sgn( )( ), 软阈值 ( ) 0,
, ( ) 0,
代表原始小波系数, 表示阈值处理后的小波系数,然后
再进行小波的逆变换
北京科技大学 机械工程学院 5/ 82
为什么要用小波包分析?
□
离散小波变换只是对近似信号进行再分解,而没有对 细节信号进行再分解,因此没有提高细节信号的频率 分辨率。
北京科技大学 机械工程学院
H低通滤波器 G高通滤波器
Pij是第j层小波包分解得到 的第i个小波包
7/ 82
小波包的分解
从时域来看小波包分解
每一层的小波包数目比上一层中的小波包数目增加一倍 每个小波包的数据长度比上一层小波包数据长度减半 每个小波包的时域分辨率比上一层小波包的时域分辨率减半
北京科技大学 机械工程学院 8/ 82
小波包的分解
从频域来看小波包分解
每个小波包数据是原始信号在不同频率段上的成份 小波包的频带相邻,并且带宽相等 分解的层数越多,频率段划分得越细
北京科技大学 机械工程学院 9/ 82
小波包的分解---实例
原始信号
北京科技大学 机械工程学院
10/ 82
15/ 82
小波包---应用2
轴承内圈故障
最高分析频率f = fs /2 = 20/2 = 10 KHz 每个小波包的频率带宽为 d = f /32 =312.5 Hz 频谱图中的频率范围6000~8000 Hz 对应的小波包频宽范围6000/312.5 ~ 8000/312.5 Hz。即为 18~26 号小波包
第5层小波包分解
0号小波包重构
2号小波包重构
电机转速频率
电机转速频率的四倍频
北京科技大学 机械工程学院
14/ 82
小波包---应用2
轴承内圈故障
轴承内圈出现故 障,出现冲击, 但被噪声淹没
圆锥轴承内圈轻度剥落信号
时域振动信号
频域图
由冲击引起的固 有振动频率,难 以识别轴承故障
第5层小波包分解
北京科技大学 机械工程学院
小波包分析与第二代小波
阳建宏
北京科技大学
2018/10/30
主要内容
小波包分析
第二代小波
Matlab在小波分析中的应用
北京科技大学 机械工程学院
2/ 82
离散小波的分解
□ 如果S表示原始的输入信号, DWT的概念是通过两 个互补的滤波器(高频和低频)产生A和D两个信号 A:信号的近似值 原始信号通过低频滤波器产 生,表示信号的低频分量 D:信号的细节值 原始信号通过高频滤波器产 生,表示信号的高频分量
将处理后的数据代入重构公式,一层一层向上进行重构
北京科技大学 机械工程学院
11/ 82
小波包的重构
小波包分解方法是小波分解的一般化,可为信号分析 提供更丰富和更详细的信息。例如,小波包分解的原始信 号S表示为 5 6 1 4 P P S= P + + + P 3 3 1 2
S
1 P 1
2 P 1
北京科技大学 机械工程学院
6/ 82
小波包的分解
□ □
小波包理论是在多尺度分析和Mallat算法基础上发展 起来的。 小波包分析同时分解细节信号和近似信号
S
1 P 1
2 P 1
P21
P22
P23
P24
P31
P32
P34
P35
P36
P37
P38
小波包分解算法:
近似信号
细节信号
2 i 1 i Pj (t ) HPj 1 (t ) 2i i P ( t ) GP j 1 (t ) j
小波包的重构
重构公式:
P (t ) H P
i j *
2i 1 j 1
(t ) G P (t )
* 2i j 1
H*、 G*分别为H和G的对偶算子,也为H 和 G的共轭转置矩阵
重构过程:
设原始信号经过J层小波包分解后得到 2j 个小波包
如果要重构第2 数据置零。
i
个小波包的数据号A继续 使用滤波器进行分解
北京科技大学 机械工程学院 3/ 82
离散小波的分解
小波分解树
北京科技大学 机械工程学院 4/ 82
离散小波的重构
完全重构 小波系数不经过处理,通过逆 变换重构回原始信号 S=cA1+cD1 =cA2+cD2+cD1 =cA3+cD3+cD2+cD1 单支重构 用其中某一层近似或细节系数 重构 阈值处理小波系数后重构 , 硬阈值 ( ) 0,
