0727第三章 两自由度系统振动(讲)
二自由度系统的振动PPT课件

率ω1、 ω2的简谐振动的合成。( ω1 < ω2 )
分别将ω1和ω2称为系统的第一阶固有频率和第二阶固有频 率,各阶固有频率所对应的振动分别称为系统的第一阶固 有振动和第二阶固有振动。 每个根对应一种固有振动
6.2 无阻尼多自由度系统自由振动
一些概念:
k11 m12
k21
k22
k12 m22
6.3 无阻尼二自由度系统受迫振动
坐标变换:
ui qi
(i=1,2)
代入原微分方程得到: Mqi Kqi fi
B1、B2待定
6.3 无阻尼二自由度系统受迫振动
代入微分方程组得到
k1 k2 m12
k2
k2
k2 m2
2
B1 B2
0 0
由
det
k1
k2
m1
k2
2
k2
k2
m22
0
12 22
B11 B21
B12 B22
B11
B21
B12
B22
(固有振型矩阵)
k2 (u1 u2 ) c2 (u1 u2 )
u2 f2 m2
k3u2 c3u2
6.1 建立系统微分方程组
写成矩阵形式:
m1
0
0 m2
••u••1 u2
c1 c2
c2
c2 c 2 c3
•
u1
•
u2
k1 k2
k2
k2 k2 k3
u1
u2
f1 f2
6.2.1坐标的选择与方程耦合
1 l2
J J
ml22 ml1l2
J J
ml1l2 ml12
••
第3章二自由度振动
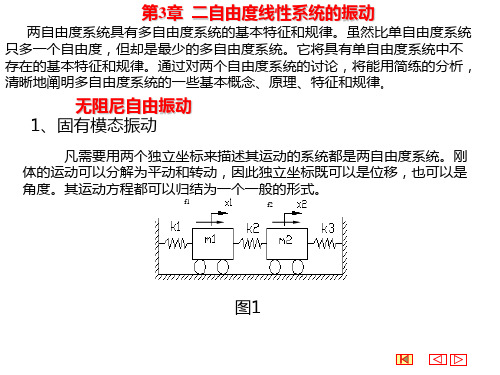
二自由度线性系统的强迫振动
我们只研究稳态振动,设微分方程组有简谐 振动的特解:
x1 x2
B1 sin t B2 sin tx1 x2源自B1 cost B2 cost
x1 x2
B1 2 sin t B2 2 sin t
将上式带入运动方程:
二自由度线性系统的强迫振动
得:
(a 2 cB1
m m e
m Jc
e
1
x
q
k
k1 2l4
k2 k1
l
3
k2l4
k
2
l
2 4
k1l3
k
1
l
2 3
x
q
0 0
动力耦合或惯性耦合
静力耦合或弹性耦合
第3章 多自由度线性系统的振动 3. 3 解耦与主坐标
坐标的耦合
动力耦合和静力耦合
广义坐标:x1,q 1
力和力矩平衡方程为
m x1 k1 ( x1l1 q 1 ) k2 ( x1 l2 q 1 ) 0
由于,这不是真实的振幅,而只是振幅的一个相对的
, 比频值率,作许振多动教时材的中两用个振幅1 相1211对 比值代;表两2 自1222由 ,度代系表统两以自n1
由度系统以n2频率作振动时的两个振幅相对比值。
二自由度自由振动
称{}1和{}2为特征向量、振型向量或模态向量。 固有频率和振型向量构成系统振动的固有模态的基本参 数,简称为模态参数。
二自由度线性系统的强迫振动
1、系统运动微分方程
m1x1 k1x1 m2x2 k2 (
x2
k2
( x2 x1 )
x1 0
)
P0
sin
t
(整理)0727第三章 两自由度系统振动(讲).

第三章两自由度系统振动§3-1 概述单自由度系统的振动理论是振动理论的基础。
在实际工程问题中,还经常会遇到一些不能简化为单自由度系统的振动问题,因此有必要进一步研究多自由度系统的振动理论。
两自由度系统是最简单的多自由度系统。
从单自由度系统到两自由度系统,振动的性质和研究的方法有质的不同。
研究两自由度系统是分析和掌握多自由度系统振动特性的基础。
所谓两自由度系统是指要用两个独立坐标才能确定系统在振动过程中任何瞬时的几何位置的振动系统。
很多生产实际中的问题都可以简化为两自由度的振动系统。
例如,车床刀架系统(a)、车床两顶尖间的工件系统(b)、磨床主轴及砂轮架系统(c)。
只要将这些系统中的主要结合面(或芯轴)视为弹簧(即只计弹性,忽略质量),将系统中的小刀架、工件、砂轮及砂轮架等视为集中质量,再忽略存在于系统中的阻尼,就可以把这些系统近似简化成图(d)所示的两自由度振动系统的动力学模型。
以图3.1(c)所示的磨床磨头系统为例分析,因为砂轮主轴安装在砂轮架内轴承上,可以近似地认为是刚性很好的,具有集中质量的砂轮主轴系统支承在弹性很好的轴承上,因此可以把它看成是支承在砂轮架内的一个弹簧——质量系统。
此外,砂轮架安装在砂轮进刀拖板上,如果把进刀拖板看成是静止不动的,而把砂轮架与进刀拖板的结合面看成是弹簧,把砂轮架看成是集中的质量,则砂轮架系统又近似地可以看成是支承在进刀拖板上的另一个弹簧——质量系统。
这样,磨头系统就可以近似地简化为图示的支承在进刀拖板上的两自由度系统。
在这一系统的动力学模型中,m1是砂轮架的质量,k1是砂轮架支承在进刀拖板上的静刚度,m2是砂轮及其主轴系统的质量,k2是砂轮主轴支承在砂轮架轴承上的静刚度。
取每个质量的静平衡位置作为坐标原点,取其铅垂位移x1及x2分别作为各质量的独立坐标。
这样x1和x2就是用以确定磨头系统运动的广义坐标。
(工程实际中两自由度振动系统) [工程实例演示]§3-2 两自由度系统的自由振动一、系统的运动微分方程(①汽车动力学模型)②以图3.2的双弹簧质量系统为例。
振动理论及工程应用3 第三章 两自由度系统的振动

例3-1 试求图示两个自由度系统振动的固有频率和主
振型。已知m1= m2=m , k1= k3=k, k2= 4k,再求该系统对以下 两组初始条件的响应:(1)t=0,x10=1cm, x20=0,
x&10 x&20 0(2) t=0,x10=1cm, x20=-1cm, x10 x20 0
表示振动位移的两个以上坐标出现在同一个运动方程式 中时,就称这些坐标之间存在静力耦联或弹性耦联。
当一个微分方程式中出现两个以上的加速度项时,称为 在坐标之间有动力耦联或质量耦联.
静力与动力耦联
m ml1
ml1 J1
x1
k1 k
k2l
2
k2l k2l 2
(4)将初始条件(1)代入式,解得
x10 A1(1) sin 1 A1(2) sin 2 1 x20 1 A1(1) sin 1 2 A1(2) sin 2 0 x10 A1(1) p1 cos1 A1(2) p2 cos 2 0 x20 A1(1)1 p1 cos1 A1(2) 2 p2 cos 2 0
设
a k11 , m11
特征方程可写为
b k12 , m11
c k 21 , m22
d k 22 m22
p 4 (a d ) p 2 ad bc 0
特征方程的两组特征根
p12,2
a
d 2
a
2
d
2
(ad
bc)
a
d 2
a d 2 bc 2
系统的稳态响应。设特解为
第三章二自由度系统

二自由度系统振动 / 不同坐标系的运动微分方程
以汽车的二自由度振动模型为例
汽车板簧以上部分被简化成为一根刚性杆,具有质量m和绕质心 的转动惯量Ic。质心位于C 点。分别在A点和B点与杆相联的弹性 元件k1、k2为汽车的前,后板簧。
若系统有 n 个自由度,则各项皆为 n 维矩阵或列向量
二自由度系统振动 / 运动微分方程
式中:
[M
]
m11 m21
m12
m22
m1
0
0
m2
[K
]
k11 k 21
[C]
c11 c21
k12
k
22
k1 k2
k2
c12
c22
2 ET x1x1
2 ET x12
m1
m12
2 ET x1x2
2 ET x2x1
m21
0
m22
2ET x2x2
2 ET x22
m2
[M
]
m11 m21
m12
m22
m1
0
0
m2
二自由度系统振动 / 能量法
(t ) (t)
如同在单自由度系统中所定义的,在多自由度系统中 也将质量、刚度、位移、加速度及力都理解为广义的。
第三章 两自由度系统的振动

设两质量块振动时按同频率和同相位作简谐振动,即:令
一组解x1 A1 sin( t )、x2 A2 sin( t ),代入方程后得: [(a 2 ) A1 bA2 ]sin( t ) 0 [cA1 (d 2 )A2 ]sin( t ) 0
(a 2 ) A1 bA2 0
cA1
(d
一阶主振型。
例
练习1 如图,推导系统的频率方程并 求主振型。设滑轮为均质圆盘, 其质量为m2,质量块质量为m1, 弹簧刚度分别为K1和K2,并假定 滑轮与绳索间无相对滑动。
解:选取广义坐标为( ),
取静x,平 衡位置作为坐标原点,
进行受力分析,建立系统的运 动微分方程:
m1x K1(x r) I0 K1(x r)r K2r 2
1) 当作用于系统的主动力都是有势力时(系统没有能
量损失时),则系统具有势能U(q1,q2,···,qn),广义力
为
Qj
U q j
( j 1, 2, , n)
代入方程得: d ( T ) T U 0 dt qj q j q j
( j 1, 2, , n)
或
d ( L ) L 0 ( j 1, 2, , n)
m1l 21 (m1gl Ka2 )1 Ka22 0 m2l 22 Ka21 (m2gl Ka2 )2 0
1 2
K2 (u2 u1)2
u1
u2
代入拉氏方程,得系统的微分方程
(m1
m2 2
)u1
m2 2
u2
(K1
K2 )u1
K2u2
0
m2 2
u1
3u2 2
u2
K 2u1
K2u2
0
m1
0727第三章 两自由度系统振动(讲)

第三章两自由度系统振动§3-1 概述单自由度系统的振动理论是振动理论的基础。
在实际工程问题中,还经常会遇到一些不能简化为单自由度系统的振动问题,因此有必要进一步研究多自由度系统的振动理论。
两自由度系统是最简单的多自由度系统。
从单自由度系统到两自由度系统,振动的性质和研究的方法有质的不同。
研究两自由度系统是分析和掌握多自由度系统振动特性的基础。
所谓两自由度系统是指要用两个独立坐标才能确定系统在振动过程中任何瞬时的几何位置的振动系统。
很多生产实际中的问题都可以简化为两自由度的振动系统。
例如,车床刀架系统(a)、车床两顶尖间的工件系统(b)、磨床主轴及砂轮架系统(c)。
只要将这些系统中的主要结合面(或芯轴)视为弹簧(即只计弹性,忽略质量),将系统中的小刀架、工件、砂轮及砂轮架等视为集中质量,再忽略存在于系统中的阻尼,就可以把这些系统近似简化成图(d)所示的两自由度振动系统的动力学模型。
以图3.1(c)所示的磨床磨头系统为例分析,因为砂轮主轴安装在砂轮架内轴承上,可以近似地认为是刚性很好的,具有集中质量的砂轮主轴系统支承在弹性很好的轴承上,因此可以把它看成是支承在砂轮架内的一个弹簧——质量系统。
此外,砂轮架安装在砂轮进刀拖板上,如果把进刀拖板看成是静止不动的,而把砂轮架与进刀拖板的结合面看成是弹簧,把砂轮架看成是集中的质量,则砂轮架系统又近似地可以看成是支承在进刀拖板上的另一个弹簧——质量系统。
这样,磨头系统就可以近似地简化为图示的支承在进刀拖板上的两自由度系统。
在这一系统的动力学模型中,m1是砂轮架的质量,k1是砂轮架支承在进刀拖板上的静刚度,m2是砂轮及其主轴系统的质量,k2是砂轮主轴支承在砂轮架轴承上的静刚度。
取每个质量的静平衡位置作为坐标原点,取其铅垂位移x1及x2分别作为各质量的独立坐标。
这样x1和x2就是用以确定磨头系统运动的广义坐标。
(工程实际中两自由度振动系统) [工程实例演示]§3-2 两自由度系统的自由振动一、系统的运动微分方程(①汽车动力学模型)②以图3.2的双弹簧质量系统为例。
机械振动基础 第三章 二自由度系统讲解
的微分方程解
的微分方程解
注:红色路线代表走不通,绿色路线代表可走通
例3.3 如图所示系统。设m1=m2=m。这是个对称系统, 对称点为k1的中点。取向右为x轴的正方向。
m1
0
0 m2
xx12
c1 c2
c2
c2 c2 c3
x1 x2
k1 k2
k2
k2 k2 k3
如果刚度矩阵是非对角矩阵,称方程存在弹性耦合
如果k2L2 k1L1=0,则刚度矩阵为对角矩阵,方程已经解耦。 这时系统垂直方向的运动与绕质心的转动独立。
3.取广义坐标为yA,yB
由
yC yB
yA yA
L1 L
L
L1
L2
yC
yA
L1 yB
yB L
yA
yA
L2 L
yA
yA yB
mij
2ET xix j
,
kij
2U xix j
,
cij
2D xix j
例如:对系统的动能函数ET
1 2 m1
x12
1 2 m2
x22
利用公式mij 2ET 得:m11 2ET =m1
xi x j
x12
m12 2ET =0 x1 x2
m21 2ET =0 x2 x1
m22 2ET =m2 x22
§3.3 不同坐标系下的运动微分方程 例3.2 汽车的二自由度振动模型如图3—3所示。
——汽车板簧以上部分被简化成为一根刚性杆,具有 质量m和绕质心的转动惯量Ic。质心位于C点。 ——分别在A点和B点与杆相连的弹性元件k1、k2为汽 车的前、后板簧。
只考虑杆的竖向运动(平动)和绕质心的转动(转动)。 系统的动能和势能为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章两自由度系统振动§3-1 概述单自由度系统的振动理论是振动理论的基础。
在实际工程问题中,还经常会遇到一些不能简化为单自由度系统的振动问题,因此有必要进一步研究多自由度系统的振动理论。
两自由度系统是最简单的多自由度系统。
从单自由度系统到两自由度系统,振动的性质和研究的方法有质的不同。
研究两自由度系统是分析和掌握多自由度系统振动特性的基础。
所谓两自由度系统是指要用两个独立坐标才能确定系统在振动过程中任何瞬时的几何位置的振动系统。
很多生产实际中的问题都可以简化为两自由度的振动系统。
例如,车床刀架系统(a)、车床两顶尖间的工件系统(b)、磨床主轴及砂轮架系统(c)。
只要将这些系统中的主要结合面(或芯轴)视为弹簧(即只计弹性,忽略质量),将系统中的小刀架、工件、砂轮及砂轮架等视为集中质量,再忽略存在于系统中的阻尼,就可以把这些系统近似简化成图(d)所示的两自由度振动系统的动力学模型。
以图3.1(c)所示的磨床磨头系统为例分析,因为砂轮主轴安装在砂轮架内轴承上,可以近似地认为是刚性很好的,具有集中质量的砂轮主轴系统支承在弹性很好的轴承上,因此可以把它看成是支承在砂轮架内的一个弹簧——质量系统。
此外,砂轮架安装在砂轮进刀拖板上,如果把进刀拖板看成是静止不动的,而把砂轮架与进刀拖板的结合面看成是弹簧,把砂轮架看成是集中的质量,则砂轮架系统又近似地可以看成是支承在进刀拖板上的另一个弹簧——质量系统。
这样,磨头系统就可以近似地简化为图示的支承在进刀拖板上的两自由度系统。
在这一系统的动力学模型中,m1是砂轮架的质量,k1是砂轮架支承在进刀拖板上的静刚度,m2是砂轮及其主轴系统的质量,k2是砂轮主轴支承在砂轮架轴承上的静刚度。
取每个质量的静平衡位置作为坐标原点,取其铅垂位移x1及x2分别作为各质量的独立坐标。
这样x1和x2就是用以确定磨头系统运动的广义坐标。
(工程实际中两自由度振动系统) [工程实例演示]§3-2 两自由度系统的自由振动一、系统的运动微分方程(①汽车动力学模型)②以图3.2的双弹簧质量系统为例。
设弹簧的刚度分别为k 1和k 2,质量为m 1、m 2。
质量的位移分别用x 1和x 2来表示,并以静平衡位置为坐标原点,以向下为正方向。
(分析)在振动过程中的任一瞬间t ,m 1和m 2的位移分别为x 1及x 2。
此时,在质量m 1上作用有弹性恢复力()12211x x k x k -及,在质量m 2上作用有弹性恢复力()122x x k -。
这些力的作用方向如图所示。
应用牛顿运动定律,可建立该系统的振动微分方程式:()()⎭⎬⎫=-+=--+00122221221111x x k x m x x k x k x m (3.1)令 2212121,,m k c m k b m k k a ==+=则(3.1)式可改写成如下形式:()()⎭⎬⎫=-+=--+00122221221111x x k x m x x k x k x m ⎭⎬⎫=+-=-+00212211cx cx xbx ax x (3.2) 这是一个二阶常系数线性齐次联立微分方程组。
(分析)在第一个方程中包含2bx -项,第二个方程中则包含1cx -项,称为“耦合项”(coupling term )。
这表明,质量m 1除受到弹簧k 1的恢复力的作用外,还受到弹簧 k 2的恢复力的作用。
m 2虽然只受一个弹簧k 2恢复力的作用,但这一恢复力也受到第一质点m 1位移的影响。
我们把这种位移之间有耦合的情况称为弹性耦合。
若加速度之间有耦合的情况,则称之为惯性耦合。
二、固有频率和主振型[创造思维:]从单自由度系统振动理论得知,系统的无阻尼自由振动是简谐振动。
我们也希望在两自由度系统无阻尼自由振动中找到简谐振动的解。
因此可先假设方程组(3.2)式有简谐振动解,然后用待定系数法来寻找有简谐振动解的条件。
设在振动时,两个质量按同样的频率和相位角作简谐振动,故可设方程组(3.2)式的特解为:()()⎭⎬⎫+=+=ϕωϕωt A x t A x n n sin sin 2211 (3.3)其中振幅A 1与A 2、频率n ω、初相位角ϕ都有待于确定。
对(3.3)式分别取一阶及二阶导数:()()()()⎪⎭⎪⎬⎫+-=+=+-=+=ϕωωϕωωϕωωϕωωt A x t A x t A x t A x n n n n n n n n sin ;cos sin ;cos 2222221111(3.4)将(3.3)、(3.4)式代入(3.2)式,并加以整理后得:()()⎪⎭⎪⎬⎫=-+-=--00221212A c cA bA A a n n ωω (3.5)上式是A 1、A 2的线性齐次代数方程组。
A 1、A 2=0显然不是我们所要的振动解,要使A 1、A 2有非空解,则(3.5)式的系数行列式必须等于零,即:22n n c cba ωω---- = 0 将上式展开得:()()024=-++-b a c c a n n ωω (3.6)解上列方程,可得如下的两个根:()bc c a c a b a c c a c a n +⎪⎭⎫ ⎝⎛-+=--⎪⎭⎫ ⎝⎛++=2222,12222 ω (3.7)由此可见,(3.6)式是决定系统频率的方程,故称为系统的频率方程(frequency equation )或特征方程(characteristic equation )。
特征方程的特征值(characteristic value )即频率n ω只与参数a ,b ,c 有关。
而这些参数又只决定于系统的质量m 1,m 2和刚度k 1,k 2,即频率n ω只决定于系统本身的物理性质,故称n ω为系统的固有频率。
两自由度系统的固有频率有两个,即12121n n n n n ωωωωω,把,且和<称为第一阶固有频率(first order natural circular frequency )。
[基频]2n ω称为第二阶固有频率(second order natural circular frequency )。
[(推广)理论证明,n 个自由度系统的频率方程是2n ω的n 次代数方程,在无阻尼的情况下,它的n 个根必定都是正实根,故主频率的个数与系统的自由度数目相等。
]将所求得的1n ω和2n ω代入(3.5)式中得: ()()()()⎪⎪⎭⎪⎪⎬⎫-=-==-=-==222221222212111121n n n n c c b a A A c c b a A A ωωβωωβ (3.8)式中:()()1211,A A ——对应于1n ω的质点m 1,m 2的振幅; ()()2221,A A ——对应于2n ω的质点m 1,m 2的振幅。
由此可见,对应于1n ω和2n ω,振幅A 1与A 2之间有两个确定的比值。
称之为振幅比(amplitude ratio )。
将(3.8)式与(3.3)式联系起来可以看出,两个m 1与m 2任一瞬间位移的比值12x x 也是确定的,并且等于振幅比12A A 。
系统的其它点的位移都可以由x 1及x 2来决定。
这样,在振动过程中,系统各点位移的相对比值都可以由振幅比确定,也就是振幅比决定了整个系统的振动形态。
因此,我们将振幅比称为系统的主振型(principal mode ),也可称为固有振型(natural mode )。
其中:1β——第一主振型,即对应于第一主频率1n ω的振幅比;2β——第二主振型,即对应于第二主频率2n ω的振幅比。
*当系统以某一阶固有频率按其相应的主振型作振动时,即称为系统的主振动(principal vibration )。
所以,第一主振动为:()()()()()()()()⎪⎭⎪⎬⎫+=+=+=11111111212111111sin sin sin ϕωβϕωϕωt A t A x t A x n n n (3.9) 第二主振动为:()()()()()()()()⎪⎭⎪⎬⎫+=+=+=22212222222222121sin sin sin ϕωβϕωϕωt A t A x t A x n n n (3.10) 为了进一步研究主振型的性质,可以将(3.7)式改写成如下形式:因为 bc c a c a n -⎪⎭⎫ ⎝⎛-+=222,122 ω bc c a c a bc c a c a a a n +⎪⎭⎫ ⎝⎛-+-=⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫ ⎝⎛--+-=-22212222ω所以因为上式的等式右边恒大于零,所以021>-n a ω,由(3.8)式知,01>βbc c a c a bc c a c a a a n +⎪⎭⎫ ⎝⎛---=⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫ ⎝⎛-++-=-22222222ω又因为因为上式的等式右边恒小于零,所以022<-n a ω,由(3.8)式知,02<β。
(说明)由此可见,01>β表示()()1211A A 和的符号相同,即第一主振动中两个质点的相位相同。
因此,若系统按第一主振型进行振动的话,两个质点就同时向同方向运动,它们同时经过平衡位置,又同时达到最大偏离位置。
而02<β,则表示第二主振动中两个质点的相位相反,永远相差180°。
当质量m 1到达最低位置时,质量m 2恰好到达最高位置。
它们一会相互分离,一会又相向运动,这样,在整个第二主振动的任一瞬间的位置都不改变。
这样的点称为“节点”(nodal point)。
振动理论证明,多自由度系统的i阶主振型一般有i-1个节点。
这就是说,高一阶的主振型就比前一阶主振型多一个节点。
阶次越高的主振动,节点数就越多,故其相应的振幅就越难增大。
相反,低阶的主振动由于节点数少,故振动就容易激起。
所以,在多自由度系统中,低频主振动比高频主振动危险。
三、系统对初始条件的响应[思维方式:]前面分析了两自由度系统的主振动,而这些主振动又都是简谐振动。
但两自由度系统在受到干扰后出现的自由振动究竟是什么形式呢?这要取决于初始条件。
从微分方程的理论来说,两阶主振动只是微分方程组的两组特解。
而它的通解则应由这两组特解相叠加组成。
从振动的实践来看,两自由度系统受到任意的初干扰时,一般来说,系统的各阶主振动都要激发。
因而出现的自由振动应是这些简谐振动的合成。
所以,在一般的初干扰下,系统的响应是:()()()()()()()()⎪⎭⎪⎬⎫+++=+++=22212111112222111111sin sin sin sin ϕωβϕωβϕωϕωt A t A x t A t A x n n n n (3.11) 式中,()()212111,ϕϕ,,A A 四个未知数要由振动的四个初始条件来决定。
