第四章(第2,3节) 两自由度系统的振动
合集下载
两自由度系统的振动
5.2
图5-5（a）表示两个摆长，质量相同的单摆，中间以弹簧相连，形成两自由度系统。
图5-5双摆拍振
取 、 表示摆的角位移，逆钟向转动为正，每个摆的受力如图5-5（b）。根据刚体绕定轴转动方程，当 、 角位移很小时，得到摆做微小振动的微分方程
,
用与前面类似的分析方法，得到系统的第一阶和第二阶固有频率为
(5-5)
保证式(5-5)具有非零解的充分必要条件是式(5-5)的系数行列式等于零，即
展开后为
(5-6)
式(5-6)唯一确定了频率 满足的条件，通常称为频率分程或特征方程。它是 的二次代数方程，它的两个特征根为
(5-7)
由于式(5-7)确定的 的两个正实根仅取决于系统本身的物理性质，与运动的初始条件无关，因此 称为系统的固有频率。较小的一个称为第一阶固有频率，较大的一个称为第二阶固有频率。
图5-9动力减振器系统中主系统的幅频特性曲线
5.6阻尼对强迫振动的影响
为了把问题简化，以上的分析都没有考虑系统的阻尼。本节以图5-10所示系统为例，讨论阻尼对两自由度系统受迫振动的影响。这个系统是在上节的动力减振器的两个质量块之间增加一个阻尼器而成。其运动微分方程为
(5-20)
仍只考虑稳态运动。若利用复指数形式，则激振力为 ，而稳态运动的形式为
解：（1）建立运动微分方程式
分别以两物体的平衡位置为坐标原点，取两物体离开其平衡位置的距离x1、x2为广义坐标，两物体沿x方向的受力图如图5-3(b)所示，它们的运动微分方程分别为
若写成(5-2)的标准形式，则
所以
解出， 。因此，系统的第一阶和第二阶固有频率为
（3）求主振型
将 、 分别代入式(5-26)，得
第
应用单自由度系统的振动理论，可以解决机械振动中的一些问题。但是，工程中有很多实际问题必须简化成两个或两个以上自由度，即多自由度的系统，才能描述其机械振动的主要特征。多自由度系统的振动特性与单自由度系统的振动特性有较大的差别，例如，有多个固有频率、主振型、主振动和多个共振频率等。本章主要介绍研究两自由度系统机械振动的基本方法。
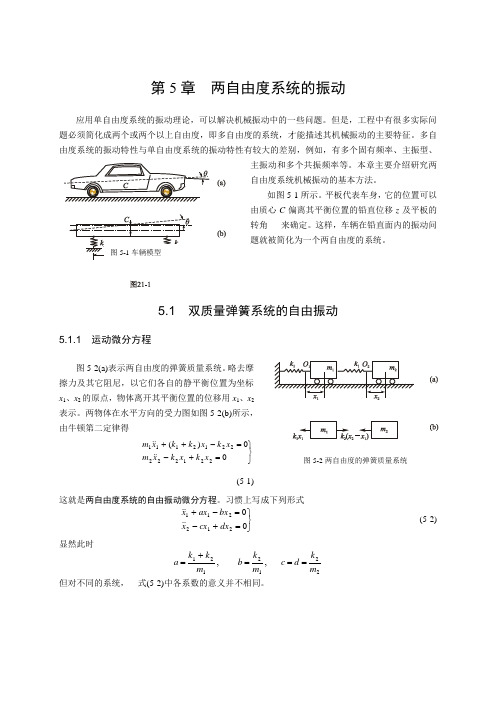
图5-5（a）表示两个摆长，质量相同的单摆，中间以弹簧相连，形成两自由度系统。
图5-5双摆拍振
取 、 表示摆的角位移，逆钟向转动为正，每个摆的受力如图5-5（b）。根据刚体绕定轴转动方程，当 、 角位移很小时，得到摆做微小振动的微分方程
,
用与前面类似的分析方法，得到系统的第一阶和第二阶固有频率为
(5-5)
保证式(5-5)具有非零解的充分必要条件是式(5-5)的系数行列式等于零，即
展开后为
(5-6)
式(5-6)唯一确定了频率 满足的条件，通常称为频率分程或特征方程。它是 的二次代数方程，它的两个特征根为
(5-7)
由于式(5-7)确定的 的两个正实根仅取决于系统本身的物理性质，与运动的初始条件无关，因此 称为系统的固有频率。较小的一个称为第一阶固有频率，较大的一个称为第二阶固有频率。
图5-9动力减振器系统中主系统的幅频特性曲线
5.6阻尼对强迫振动的影响
为了把问题简化，以上的分析都没有考虑系统的阻尼。本节以图5-10所示系统为例，讨论阻尼对两自由度系统受迫振动的影响。这个系统是在上节的动力减振器的两个质量块之间增加一个阻尼器而成。其运动微分方程为
(5-20)
仍只考虑稳态运动。若利用复指数形式，则激振力为 ，而稳态运动的形式为
解：（1）建立运动微分方程式
分别以两物体的平衡位置为坐标原点，取两物体离开其平衡位置的距离x1、x2为广义坐标，两物体沿x方向的受力图如图5-3(b)所示，它们的运动微分方程分别为
若写成(5-2)的标准形式，则
所以
解出， 。因此，系统的第一阶和第二阶固有频率为
（3）求主振型
将 、 分别代入式(5-26)，得
第
应用单自由度系统的振动理论，可以解决机械振动中的一些问题。但是，工程中有很多实际问题必须简化成两个或两个以上自由度，即多自由度的系统，才能描述其机械振动的主要特征。多自由度系统的振动特性与单自由度系统的振动特性有较大的差别，例如，有多个固有频率、主振型、主振动和多个共振频率等。本章主要介绍研究两自由度系统机械振动的基本方法。
第4章 两自由度系统的振动 [兼容模式]
![第4章 两自由度系统的振动 [兼容模式]](https://img.taocdn.com/s3/m/aeb2f70903d8ce2f00662343.png)
1998 年匈牙利的物理学家塔马 斯 · 维塞克在布达佩斯音乐学院举行 的一场音乐会上意外地发现了同步化 的现象。 演出相当成功，落幕后观众们热烈的掌声长达 3 分 钟之久，而维塞克博士便在这里发现了有趣的东西。音 乐会刚一结束，观众们雷鸣暴雨般的掌声响起，然而过 了一段时间之后，观众们的热烈的掌声显然同步化了， 变成了同一种节奏的拍手。为了答谢观众们的热情，演 奏者重新走上台来谢幕，这时的掌声又突然之间失去了 刚才的节奏，雨点般疯狂地响起。在最后长达 3 分钟的 鼓掌声中，狂热的掌声和同步的掌声依次交替出现。
2013/10/22
机械振动学-绪论
11
沿着弯弯曲曲的河道走进 茂密的森林，黄昏洒下温柔的 光辉，落在森林的枝杈上，一 闪一闪，好像一两星萤火虫的 光芒。夜渐渐深了，不知不觉， 岸边的树林被成群的萤火虫， 点成了一座星星的城堡。不过 最壮观的却是深夜的某一时刻， 好像在谁一声令下似的，所有 原来此起彼伏，各自发光的萤 火虫们，全都开始同时明暗， 变得整齐一致了！
除了萤火虫的发光之外，自然界里到 处都可以发现同步化现象。由一万多个细 胞组成的心脏搏动器总是按照同一个的节 奏产生着脉冲信号；知了每 17 年都会一起 爬到地面上来进行繁殖；秋天晚上的蟋蟀 们，也好像有谁指挥一样，齐刷刷地奏出 优美动听的大合唱。
以上现象存在着三个共同点： (1) 每个个体都在进行各 自不同的周期性运动； (2) 它们的运动节奏在某一瞬间变得 一致； (3) 它们身上都应该存在某种导致这种现象的媒介物 质。物理学家们把这种做周期性运动的个体称为“振动体”， 把通过媒介物质连接在一起的振动体称为“耦合振动体”， 又把他们同时改成同一节奏运动的现象叫做“同步化”现象。
2013/10/22
机械振动学-绪论
两自由度系统的振动
第四章 两自由度系统的振动前两章介绍了单自由度系统的振动，它是振动理论的基础，并有重要的应用价值。
但工程中许多实际问题是不能简化为单自由度系统的振动问题，它们往往需要简化成为多自由度系统。
两自由度系统是最简单的多自由度系统，无论是模型的简化、振动微分方程的建立和求解的一般方法，以及系统响应表现出来的振动特性等等。
两自由度系统和多自由度系统没有本质上的差别，而主要是量上的差别，因此研究两自由度系统是分析多自由度系统振动特性的基础。
所谓两自由度系统是指要用两个独立坐标才能确定系统在振动过程中任何瞬时的几何位置的振动系统。
4-1 无阻尼自由振动1.系统的振动微分方程作为两自由度振系的第一个例子，现在来分析图4-1（a ）所示的双弹簧系统，设弹簧的刚度分别为k 1、、 k 2，质量为m 1、m 2。
质量的位移分别用x 1、x 2表示，并以静平衡位置为坐标原点，以向下为正。
现建立系统在静平衡位置的力学条件及振动过程中的运动微分方程。
在静平衡位置，设两弹簧的伸长分别为δ1、、δ2，则由系统的受力图 4-1（b ），得系统的静平衡条件为⎭⎬⎫=-=-+0022211221δδδk g m k k g m （a ）在振动过程中，设任一瞬时t ，m 1和m 2 的位置分别为x 1和x 2，此时质量上的受力图如图4-1（c ）所示。
应用牛顿运动定律，得)()(11112222111x k x x k k g m x m +--++=δδ )(12222222x x k k g m xm ---=δ 整理后得222122222112212212111)(δδδk g m x k x k x m k k g m x k x k k xm -=-+-+=-++ } （b ）将方程（b ）的右端和方程(a)比较，就可以消去平衡项，于是得00)(1222222212111=-+=-++x k x k xm x k x k k xm } (4-1)令 ,/,/,/)(2222121m k c m k b m k k a ==+=则（4-1）式可改写成00122211=-+=-+cx cx xbx ax x } (4-2)这是联立的二阶常系数线性微分方程组。
两自由度系统的振动
固有频率与振型 根据微分方程理论，两自由度系统的自由振动微分方程的通解， 是它的两个主振动的线性组合，即
x1 (t ) = x1(1) + x1( 2) = A1(1) sin(ω1t + α1 ) + A1( 2) sin(ω2t + α 2 ) (1) ( 2) (1) ( 2) x2 (t ) = x2 + x2 = A2 sin(ω1t + α1 ) + A2 sin(ω2t + α 2 )
m1 &&1 + 2kx1 − kx 2 = 0 x 2m&&2 − kx1 + 2kx 2 = 0 x
Theory of Vibration with Applications
k3 x2
返回首页
两自由度系统的振动
例题
x m 0 &&1 பைடு நூலகம் 2k 0 2m && + − k x2
&& m1 x 1 + ( k 1 + k 2 )x 1 − k 2 x 2 = 0 && m2 x 2 − k 2 x 1 + k 2 x 2 = 0
m1 &&1 = − k 1 x 1 + k 2 ( x 2 − x 1 ) x m2 &&2 = − k 2 ( x 2 − x 1 ) x
m 0 质量矩阵 M = 0 2m
− k x1 0 x = 0 2k 2
2k K = − k − k 2k
刚度矩阵
（2）解频率方程，求ωi 将M和K代入频率方程，得
x1 (t ) = x1(1) + x1( 2) = A1(1) sin(ω1t + α1 ) + A1( 2) sin(ω2t + α 2 ) (1) ( 2) (1) ( 2) x2 (t ) = x2 + x2 = A2 sin(ω1t + α1 ) + A2 sin(ω2t + α 2 )
m1 &&1 + 2kx1 − kx 2 = 0 x 2m&&2 − kx1 + 2kx 2 = 0 x
Theory of Vibration with Applications
k3 x2
返回首页
两自由度系统的振动
例题
x m 0 &&1 பைடு நூலகம் 2k 0 2m && + − k x2
&& m1 x 1 + ( k 1 + k 2 )x 1 − k 2 x 2 = 0 && m2 x 2 − k 2 x 1 + k 2 x 2 = 0
m1 &&1 = − k 1 x 1 + k 2 ( x 2 − x 1 ) x m2 &&2 = − k 2 ( x 2 − x 1 ) x
m 0 质量矩阵 M = 0 2m
− k x1 0 x = 0 2k 2
2k K = − k − k 2k
刚度矩阵
（2）解频率方程，求ωi 将M和K代入频率方程，得
04-1zf_两自由度系统的振动
m2 x2 K2 (x2 x1) K3 x2
整理得系统运动微分方程：
m1x1 (K1 K2 )x1 K2 x2 0 m2 x2 K2 x1 (K2 K3 )x2 0
引入符号：
m1x1 m2 x2
(K1 K2
x1
K2 (
安装两个齿轮的传动轴示意图
假设： (1)相对于齿轮来说，轴的质量较小 可以忽略； (2)轴的变形较大，考虑其弹性； (3)齿轮可视为集中质量元件的刚性 圆盘。
若研究系统在纸面平面内的横向振动，
在上述假设条件下，系统可简化成图两
自由度横向振动力学模型。
两自由度横向振动力学模型
若研究系统的扭振问题，两圆盘具有 转动惯量，轴具有扭转弹性，系统可 简化为两自由度扭转振动力学模型。
x20 )2
(1x10 x20 )2 2
n2
1
arctan
n1 (2 x10 2 x10
x20 x20
)
2
arctan
n
2 (1x10 1x10
x20 x20
)
例1 图示两自由度系统。已知，ml=m2=m=0.05kg， K1=K2=K3=K=20N／m。
(1)第1个方程既含有 x1 项，也含有-bx2项； 性常微分方程组。
(2)第2个方程既含有 x2 项，也含有-cxl项。
显然，这两个方程是相互耦联的，将-bx2、-cxl称为耦合项。
与单自由度振动系统运动微分方程比较：两自由度振动系统运动
微分方程是含有耦合项的二级常微分方程组。
4.1.2 固有频率与主振型
整理得系统运动微分方程：
m1x1 (K1 K2 )x1 K2 x2 0 m2 x2 K2 x1 (K2 K3 )x2 0
引入符号：
m1x1 m2 x2
(K1 K2
x1
K2 (
安装两个齿轮的传动轴示意图
假设： (1)相对于齿轮来说，轴的质量较小 可以忽略； (2)轴的变形较大，考虑其弹性； (3)齿轮可视为集中质量元件的刚性 圆盘。
若研究系统在纸面平面内的横向振动，
在上述假设条件下，系统可简化成图两
自由度横向振动力学模型。
两自由度横向振动力学模型
若研究系统的扭振问题，两圆盘具有 转动惯量，轴具有扭转弹性，系统可 简化为两自由度扭转振动力学模型。
x20 )2
(1x10 x20 )2 2
n2
1
arctan
n1 (2 x10 2 x10
x20 x20
)
2
arctan
n
2 (1x10 1x10
x20 x20
)
例1 图示两自由度系统。已知，ml=m2=m=0.05kg， K1=K2=K3=K=20N／m。
(1)第1个方程既含有 x1 项，也含有-bx2项； 性常微分方程组。
(2)第2个方程既含有 x2 项，也含有-cxl项。
显然，这两个方程是相互耦联的，将-bx2、-cxl称为耦合项。
与单自由度振动系统运动微分方程比较：两自由度振动系统运动
微分方程是含有耦合项的二级常微分方程组。
4.1.2 固有频率与主振型
《理论力学 动力学》 第十一讲 两个自由度系统的自由振动
两个自由度系统的振动理论曾凡林哈尔滨工业大学理论力学教研组本讲主要内容1、两个自由度系统的自由振动2、两个自由度系统的受迫振动1、两个自由度系统的自由振动（1）模型的简化同一物体的振动可以简化为不同的振动模型。
C研究上下平移振动研究前后颠簸振动两个自由度系统的自由振动模型112122222122()00mxk k x k x m x k x k x ++-=üý-+=þ&&&&2212121m k d m k c m k k b ==+=，，令方程变为：11221200xbx cx x dx dx +-=-+=&&&&，根据微分方程理论，可设上列方程组的解为：)sin()sin(21q w q w +=+=t B x t A x ，其中：A 、B 是振幅；ω为角频率，θ是初始相位角。
将上式代入微分方程组，得到：)sin()sin()sin(0)sin()sin()sin(22=+++++-=+-+++-q w q w q w w q w q w q w w t dB t dA t B t cB t bA t A 整理后得到：0)(0)(22=++-=--B d dA cB A b w w ，系统振动时，方程组具有非零解, 则方程组的系数行列式必须等于零，即：22=----ww d dc b —频率行列式①固有频率1、两个自由度系统的自由振动)()(24=-++-c b d d b w w 行列式展开后得到：—系统的本征方程，又称为频率方程21,22b d w +=m 2b d +=m i ω2的两个根都是实数，而且都是正数。
ii ω2的第一个根较小，称为第一固有频率。
iii ω2的第二个根较大，称为第二固有频率。
结论：两个自由度系统具有两个固有频率，这两个固有频率只与系统的质量和刚度等参数有关，而与振动的初始条件无关。
04-1 两自由度系统的振动
2 n1, n 2
ad ad 7 3 K bc 2 2 4 4 m
2
则：
K , m
2 n1
K n1 m
5K n 2 2m
5K , 2m
2 n2
3、主振型向量与振型图
振幅比：
2 a n 1 1 b
Yanshan University
主振动：系统按某一阶固有频率和相应主振型所作的振动。
第一阶主振动：
x1(1) A1(1) sin( n1t 1 )
(1) x2
(1) (1) A2 sin( n1t 1 ) 1 A1 sin( n1t 1 )
燕山大学
Yanshan University
(a ) b 0 2 c (d )
2
将上式展开得：
ω4- (a+d)ω2+(ad-bc)=0 特征根：
称为频率方程或特 征方程
2 1, 2
ad ad (ad bc) 2 2 ad ad bc 2 2
4.1.2 固有频率与主振型
设两质量块按同频率和同相位作简谐振动，即设：
燕山大学
Yanshan University
x1 A1 sin(t ) x2 A2 sin(t )
则：
1 A1 cos( t ) x 2 A2 cos( t ) x
2 K 5K m 2m 0.5 K m
燕山大学
Yanshan University
第二阶主振型 第一阶主振型
4.1.3 无阻尼自由振动的通解 由上述分析可见：
第四章 多自由度系统
频率方程为 则频率方程为：
(1)
2 为方程的解，代入（ ），得 设 {q} = { A} sin(ωt + ϕ ) 为方程的解，代入（1），得([ K ] − ω [ M ]) { A} = {0}
[K ] − ω2 [M ] = 0
系统有n个大于零的正实根， 当 [ K ] > 0 时，系统有n个大于零的正实根， 对应固有频率
求系统的柔度矩阵[D]。 求系统的柔度矩阵 。
F1
F2
F3
EI
分析
m1
m2
m3
x
y
以三个集中质量m 离开其静平衡位置的垂直位移y 以三个集中质量m1、m2、m3离开其静平衡位置的垂直位移y1、y2、y3为 系统的广义坐标（见上图）。 系统的广义坐标（见上图）。
F1
EI
F2
F3
m1
m2
m3
x
y
由材料力学得知，当简支梁受力作用时， 由材料力学得知，当简支梁受力作用时，其挠度计算公式为 ： Pbx 2 y= (l − x2 − b2 ) , ( 0 ≤ x ≤ a ) 6 EIl 根据柔度影响系数的定义， 根据柔度影响系数的定义，我们首先在坐 处作用一单位力，则在坐标y 标y1处作用一单位力，则在坐标y1、y2、y3处 产生的挠度即分别为d 产生的挠度即分别为d11、d21、d31。
3k 则刚度矩阵为 [ K ] = − k 0
−k 4k −3k
0 −3k 7k
线弹性系统的刚度矩阵对称
第一节 运动微分方程的建立
2.柔度影响系数和位移方程 柔度影响系数和位移方程
柔度影响系数d 单位外力所引起的系统位移， 柔度影响系数 ij——单位外力所引起的系统位移，即系统第j个坐标上
(1)
2 为方程的解，代入（ ），得 设 {q} = { A} sin(ωt + ϕ ) 为方程的解，代入（1），得([ K ] − ω [ M ]) { A} = {0}
[K ] − ω2 [M ] = 0
系统有n个大于零的正实根， 当 [ K ] > 0 时，系统有n个大于零的正实根， 对应固有频率
求系统的柔度矩阵[D]。 求系统的柔度矩阵 。
F1
F2
F3
EI
分析
m1
m2
m3
x
y
以三个集中质量m 离开其静平衡位置的垂直位移y 以三个集中质量m1、m2、m3离开其静平衡位置的垂直位移y1、y2、y3为 系统的广义坐标（见上图）。 系统的广义坐标（见上图）。
F1
EI
F2
F3
m1
m2
m3
x
y
由材料力学得知，当简支梁受力作用时， 由材料力学得知，当简支梁受力作用时，其挠度计算公式为 ： Pbx 2 y= (l − x2 − b2 ) , ( 0 ≤ x ≤ a ) 6 EIl 根据柔度影响系数的定义， 根据柔度影响系数的定义，我们首先在坐 处作用一单位力，则在坐标y 标y1处作用一单位力，则在坐标y1、y2、y3处 产生的挠度即分别为d 产生的挠度即分别为d11、d21、d31。
3k 则刚度矩阵为 [ K ] = − k 0
−k 4k −3k
0 −3k 7k
线弹性系统的刚度矩阵对称
第一节 运动微分方程的建立
2.柔度影响系数和位移方程 柔度影响系数和位移方程
柔度影响系数d 单位外力所引起的系统位移， 柔度影响系数 ij——单位外力所引起的系统位移，即系统第j个坐标上
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1 cos 3
k t 2 cos m3
5k t 2m
x2
1 3
cos1t
1 3
cos2t
1 cos 3
k t 1cos m3
5k t 2m
▲若初始条件符合第一阶固有振型，则运动是按固有频
率▲若1的初简始谐条振件动符，合不第出二现阶频固率有振2的型振，动则；运动是按固有频
▲率若2的给简出谐的振任动意，初不始出条现件，1的则振运动动；将为两种固有振型的
1) 1)
C2 sin(2t 2 ) C2r2 sin(2t
2
)
x1 x2
C11 cos(1t C1r11 cos(1t
1) 1)
C22 cos(2t 2 ) C2r22 cos(2t
2
)
式中四个常数C1, C2和1, 2，由上面的四个(4方.3程-1)
0 C11 cos1 C22 cos2
0 C11 cos1 0.5C22 cos2
4.3 任意初始条件的自由振动
例题：求解初始条件的响应（例4.3-1）
求得
C1=1/3，C2=2/3，1=2= 90
代入方程(4.1-17)，得
x1
1 3
cos1t
2 3
cos2t
于是得到两个固有频率为
1
g, l
2
g l
2
k m
a2 l2
4.3 任意初始条件的自由振动
例题：求解固有频率、固有振型和初始条件的响应（例4.3-2）
系统的固有振型可以由下面方程求出
i2
ml 2
0
0 ml
2
1((2ii
) )
mgl ka2
)
(k2l2 k1l1 k1l12 k2l22
)
x
0 0
可见其耦合为静力耦合或弹性耦合。
(4.2-2)
4.2 静力耦合与动力耦合
情况2：既有弹性耦合又有动力耦合
现在以弹簧支承 处的位移x1与x2为广 义坐标来建立振动微 分方程。
因 为 x1 与 x2 同 x
12
0 0
可以看出这是静力耦合系统。其特征值问题为
2
ml
0
2
0 ml
2
12
mgl ka2
ka2
ka2 mgl ka
2
12
0 0
4.3 任意初始条件的自由振动
例题：求解固有频率、固有振型和初始条件的响应（例4.3-2）
从而得特征方程为
mgl ka2 2ml 2
ka2
det
ka2
mgl
k a2
2ml
2
(mgl ka2 2ml 2 )2 (ka2 )2 0
即
mgl ka2 2ml2 ka2
(k1 k2 (k1a2
)xO 0
k2b2 )
0
(4.2-11) (4.2-12)
m memeIO xO
k1
0
k2
k1a2
0
k2b2
xO
0 0
可见其耦合为动力耦合或惯性耦合。
4.3 任意初始条件的自由振动
(1)设在t=0时，有x10=x20=1，x10 x20 0； (2)设在t=0时，有x10=1，x20=-0.5，x10 x20 0 ； (3)设在t=0时，有x10=1，x20=0，x10 x20 0。
解：(1)将初始条件代入方程(4.1-17)及其导数方程 (4.3-1)，得
x1 cos2t cos
5k 2m
t,
x2 0.5cos2t 0.5cos
5k 2m
t
可见振动系统按第二阶固有振型作简谐振动。
(3)将初始条件代入方程(4.1-17)及其导数方程(4.3-1)，
有
1 C1 sin1 C2 sin2
0 C1 sin1 0.5C2 sin2
或 k1xOa k2xOb (4.2-8)
k1a k2b
(4.2-9)
因为x与xO之间有关系:
x xO e
图 4.2-2
(4.2-10)
4.2 静力耦合与动力耦合
情况3：动力耦合
将x与xO的关系代入方程(4.2-1)，并考虑到l1=a-e， l2=b+e ， IO=IC+me2 和 方 程 (4.2-1) 第 一 式 ， 且 利 用 对 O 点
代入方程(4.1-17)，得
x1 cos1t cos
k m
,
x2 cos1t cos
k m
可见振动系统按第一阶固有振型作简谐振动。
(2)将初始条件代入方程(4.1-17)及其导数方程(4.3-1)，
有
1 C1 sin1 C2 sin2
整理后得
m
l2
x1 l1
l1x2 l2
k1
x1
k2
x2
IC
x1 l1
x2 l2
k1l1x1
k2l2
x2
(4.2-5)
ml2x1 ml1x2 k1(l1 l2 )x1 k2 (l1 IC x1 IC x2 k1l1(l1 l2 )x1 k2l2 (l1
初始条件响应的求解式
两自由度系统的自由振动规律依赖于初始条
件x2。(0)若给x20定，初并始将条其件代x1入(0方)=x程10(,4x.21(-01)7=)x及20,其x1导(0)数(4x1.03 -1)，可以确定系统对初始条件的响应。
x1 x2
C1 sin(1t C1r1 sin(1t
4.2 静力耦合与动力耦合
耦合项概述
◆一般情况下，两自由度以上的振动系统的微分方 程组都会出现耦合项，如果以矩阵形式表示，则耦合项 体现在非对角元素上。
◆对于同一个系统，选取坐标的不同，列出的系统 运动方程的具体形式就不同。但不会影响到系统的性质， 其固有特性不变。
◆振动微分方程通过刚度项来耦合，称为静力耦合 或弹性耦合。振动微分方程通过质量项来耦合，称为动 力耦合或惯性耦合。
2
(4.3-2b)
1
tan -1
1 r2 x10 x20
r2 x10 x20
(4.3-2c)
2
tan -1
2 r1 x10 x20
r1 x10 x20
(4.3-2d)
4.3 任意初始条件的自由振动
例题：求解初始条件的响应（例4.3-1）
例4.3-1 在例4.1-1中，求系统在下面三种不同初始 条件下的自由振动规律。
叠加，频率1和2的简谐振动同时发生，不仅不再是简
谐振动，而且也不是周期振动。
4.3 任意初始条件的自由振动
例题：求解固有频率、固有振型和初始条件的响应（例4.3-2）
例4.3-2 如图4.3-1a所示的双摆，由两个摆长均为l， 质量均为m的单摆组成。上端用铰悬挂，中间距悬挂点 为a处，用刚度为k的弹簧相连，两摆在铅垂位置时弹簧 没有变形。求 (1)系统的固有频率和固有振型；(2)当t=0
时, 1=0, 2=0, 1 2 求0 系统自由振动的响应。
解：(1)取两
摆离开铅垂平衡
位置的角位移1 与2为广义坐标，
以逆时针方向为
正。
图 4.3-1
4.3 任意初始条件的自由振动
例题：求解固有频率、固有振型和初始条件的响应（例4.3-2）
任一瞬时位置，两个摆上所受的力如图4.3-1(b)所
这是一组未知量为C1, C2和1, 2的四元一次代数
方程组，解之得
4.3 任意初始条件的自由振动
初始条件响应的求解式
C1
r2
1
r1
r2 x10
x20
2
r2x10
12
x20
2
(4.3-2a)
C2
r1
1
r2
r1x10
x20
2
r1x10 x20
22
示。由转动方程式分别列出两个摆的振动微分方程为
ml21 mgl1 ka2 (2 1) ml22 mgl2 ka2 (2 1)
写成矩阵方程为
ml 2
0
0 ml
2
12
mgl ka ka2
2
ka2 mgl ka2
与有如下关系：
图 4.2-1
x1 x l1 , x2 x l2 变换后得
x l2 x1 l1x2 , l1 l2
x1 x2
l1 l2
(4.2-3) (4.2-4)
4.2 静力耦合与动力耦合
情况2：既有弹性耦合又有动力耦合
将其代入方程(4.2-1)，得
l2 )x2 l2 )x2
0 0
(4.2-6)
写成矩阵形式