【人版】2015-2016年七年级下期中数学试卷及答案解析
2015-2016第二学期期中七年级数学参考答案
2015—2016学年度第二学期期中质量评估试题七年级数学参考答案及评分标准11. 9； 12. 80°； 13.（5，0）； 14. 4； 15. 100°；16. 一 三、解答题（一）17. 解：34)2(3-----＝3+2-2-3 ……………4分 ＝0 ……………6分 18. 解：∵a ∥b∴∠2＝∠3 ……………2分 ∵∠1+∠3＝180°∴∠1+∠2＝180° ……………4分 ∴∠2＝180°-∠1 ∵∠1=118°∴∠2＝180°-118°＝62° ……………6分 19.（1）图（略） 图……………4分（2）A 1（0，6）；B 1（－1，2） ……………6分 四、解答题（二） 20. 解： )223(328)2(32---+-+-＝2232322+--+- ……………4分 ＝2 ……………7分 21. 解：∵∠1＝∠2∴AB ∥CD ……………2分 ∴∠3+∠4＝180° ……………4分 ∴∠4＝180°-∠3 ……………6分 ∵∠3＝108°∴∠4＝180°-108°＝72° ……………7分 22.(每空1分)∵AB ∥DC （已知）∴∠1=∠CFE （两直线平行，同位角相等）……………2分 ∵AE 平分∠BAD （已知）∴∠1=∠2（角平分线的定义） ……………4分 ∴∠2=∠CFE ……………5分 ∵∠CFE=∠E （已知）∴∠2=∠E …………6分 ∴AD ∥BC （内错角相等，两直线平行）． …………7分五、解答题（三） 23. 解：100)1(2=-x101±=-x …………4分 110+±=x11=x …………7分或9-=x …………9分24. 证明：∵DE ‖BC （已知）∴∠ADE ＝∠ABC (两直线平行，同位角相等) …………2分 ∵DF 、BE 分别平分∠ADE 、∠ABC ∴∠ADF ＝12∠ADE∠ABE ＝12∠ABC (角平分线的定义) …………4分∴∠ADF ＝∠ABE …………5分∴ DF ‖BE (同位角相等，两直线平行) …………7分 ∴∠FDE ＝∠DEB. (两直线平行，内错角相等) …………9分 25. 解：（1）C （0，2），D （4，2），…………2分（2）依题意，得S 四边形ABDC =AB ×OC=4×2=8； …………3分 （3）存在． …………4分。
2015-2016学年七年级下学期期中联考数学试题(含答案)
2015-2016学年七年级下数学期中测试题数 学 试 题（含答案）一、填空题(每题2分共24分)1. 在同一平面内，两条直线有 种位置关系，它们是 ；2．若直线a//b ，b//c ，则 ，其理由是 ；3.如图1直线AB ，CD ，EF 相交与点O ，图中AOE ∠的对顶角是 ，COF ∠的邻补角是 。
4．如图2，要把池中的水引到D 处，可过D 点引CD ⊥AB 于C ，然后沿CD 开渠，可使所开渠道最短，试说明设计的依据： ；5．点P （-2，3）关于X 轴对称点的坐标是 。
关于原点对称点的坐标是 。
6．把“对顶角相等”写成“如果……那么……”的形式为 。
7.如图4，170=∠，270=∠，388=∠，则4=∠_____________． 8 . 若点M （a+5,a-3）在y 轴上，则点M 的坐标为 。
9．若P （X ，Y ）的坐标满足XY ＞0，且X+Y<0,则点P 在第 象限 。
0. 如图5，AB CD ∥，BC DE ∥，则∠B 与∠D 的关系是_____________．ABCD 图2A FC EB D图1OAB DC12 图3 图43142图4c ba5 4 32 1 图6 图511.若│x2-25│+3y -=0,则x=_______,y=_______.12．如图3，四边形ABCD 中，12∠∠与满足 关系时AB//CD ，当 时AD//BC(只要写出一个你认为成立的条件)。
二、 选择题 (下列各小题的四个选项中，有且只有一个是符合题意的，把你认为符合题意的答案代号填入答题表中，每小题2分，共12分) 题 号 1 2 3 4 56 答 案1．下列各图中，∠1与∠2是对顶角的是：( )2.一个三角形的三个内角中（ ）A. 至少有一个等于90°B. 至少有一个大于90°C. 不可能有两个大于89°D. 不可能都小于60°3．如图7，一条公路修到湖边时，需拐弯绕湖而过，如果第一次拐 的角∠A 是120°，第二次拐的角 ∠B 是150°，第三次拐的角是∠Ｃ，这时的道路恰好和第一次拐弯之前的道路平行，则∠C 是（ ） Ａ、150°Ｂ、140°Ｃ、130° Ｄ、120°4．在直角坐标系中，点P （-2，3）向右平移3个单位长度后的坐标为( ) A ．（3，6） B.(1,3) C.(1,6) D.(3,3) 5. 如图6 下列条件中，不能判断直线a//b 的是（ ）A 、∠1=∠3B 、∠2=∠3C 、∠4=∠5D 、∠2+∠4=180° 6.在实数范围内，下列判断正确的是 （ ） (A) .若m=n，则n m = (B) .若22b a >, 则b a >(C) .若2a =2)(b ，则b a = (D) .若3a =3b ，则b a =7.16的平方根是（ ）（A ）2 （B ）4 （C ）－ 2或2 （D ）－ 4或48. 若a 是（-3）2的平方根，则3a 等于（ ） （A ）－3 （B ）33 （C ）33或－33 （D ）3或-3三．作图题。
2015-2016年江苏省徐州市七年级(下)期中数学试卷(解析版)
B．∠2=140° D．∠2 的大小不确定 ） D．1080° ）
3． （3 分）下列各度数不是多边形的内角和的是（ A．1800° B．540° C．1700°
4． （3 分）下列各式由左边到右边的变形，是因式分解的是（ A． （a+1） （a﹣1）=a2﹣1 B． （x﹣y） （m﹣n）=（y﹣x） （n﹣m） C．ab﹣a﹣b+1=（a﹣1） （b﹣1） D．m2﹣2m﹣3=m（m﹣2）﹣3
第 4 页（共 16 页）
．
者之间的数量关系，并说明你的理由．
第 5 页（共 16 页）
卷
参考答案与试题解析
一、选择题（每小题 3 分，共 24 分．请将答案填写在表格内） 1． （3 分） （x2）3 的计算结果为（ A．3x2 B．x6 ） C．x5 D．x8
7． （3 分）如果（an•bmb）3=a9b15，那么（ A．m=4，n=3 B．m=4，n=4
C．m=3，n=4
8． （3 分）通过计算几何图形的面积可表示一些代数恒等式，右图可表示的代数 恒等式是（ ）
A． （a﹣b）2=a2﹣2ab+b2 C． （a+b）2=a2+2ab+b2
B．2a（a+b）=2a2+2ab D． （a+b） （a﹣b）=a2﹣b2
5． （3 分）四根长度分别为 3cm、4cm、7cm、10cm 的木条，以其中三根的长为 边长钉成一个三角形框架，那么这个框架的周长可能是（ A．14cm B．17cm C．20cm ） D．21cm ）
6． （3 分） 若多项式 x2+mx+4 能用完全平方公式分解因式， 则 m 的值可以是 （ A．4 B．﹣4 C．±2 ） D．m=3，n=3 D．±4
2015-2016学年七年级第 二学期期中考试数学试题(含答案)
2015-2016学年七年级下数学期中测试题数 学 试 题（含答案）（考试时间：120分钟 满分：100分） 一、选择题：（每小题3分，共30分．）1．下列图形中，不能通过其中一个四边形平移得到的是 （ ）2．下列计算：①2n n n a a a ⋅=； ②1266a a a =+； ③33)(ab ab =；④428a a a =÷；⑤22))((b a b a b a +-=---；⑥22293)3(y xy x y x +-=-其中正确的个数为 （ ）A ．3B ．2C ．1D ．03．下列等式由左边到右边的变形中，属于因式分解的是 （ ）A ．1)1)(1(2-=-+a a aB ．22)3(96-=+-a a a C ．1)2(122++=++x x x x D ．y x y x y x 222343618∙-=- 4．若－个多边形的内角和等于它的外角和的两倍，则这个多边形的边数为 （ ） A ．6 B ．7 C ．8 D ．92·1·c·n·j·y5．若（x ＋5）（2x －n ）＝2x2＋mx －15，则 （ ） A ．m ＝－7，n ＝3 B ．m ＝7，n ＝－3 C ．m ＝－7，n ＝－3 D ．m ＝7，n ＝36.如图，如下四个条件：①∠B ＋∠BCD ＝180°，②∠1＝∠2，③∠3＝∠4，④∠B ＝∠5,其中能判定AB ∥CD 的条件的个数有 ( ) A ．1 B ．2 C ．3 D ．4第6题 第7题 第9题7．将一副直角三角板，按如图所示叠放在一起，则图中∠α为 （ ） A. 45° B. 60° C. 75° D. 90°8．在△ABC 中,∠A=2∠B=3∠C,则△ABC 是 （ ）A ．锐角三角形B ．直角三角形C ．钝角三角形D ．都有可能 9．如图，△ABC 的面积为1．第一次操作：分别延长AB,BC,CA 至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1．第二次操作：分别延长A1B1，B1C1，C1A1至点A2，B2，C2，使A2B1=A1B1，B2C1=B1C1，C2A1=C1A1，顺次连接A2，B2，C2，得到△A2B2C2，…按此规律，要使得到的三角形的面积超过2015，最少经过 次操作 . （ ）第17题图 A ．6 B ．5C ．4D ．310．∑表示数学中的求和符号，主要用于求多个数的和，∑下面的小字，1i =表示从1开始求和；上面的小字，如n 表示求和到n 为止．即1231nini xx x x x ==++++∑….则()211ni i=-∑表示（ ） A ．n2－1 B ． 12＋22＋32＋…＋n2－(1＋2＋3＋…＋ n ) C ．12＋22＋32＋…＋n2－nD ． 12＋22＋32＋…＋2i － i二、填空题：（每空2分，共16分.） 11. 计算：（－2xy ）3= ．12．甲型H7N9流感病毒的直径大约为0.000 000 08米，用科学记数法表示为 米．13．三角形两边长分别为2和8，若该三角形第三边长为奇数，则该三角形的第三边为 ．14．已知m>0，如果16)1(22+-+x m x 是一个完全平方式，那么m 的值为 ． 15．如图，将一块长方形纸条折成如图的形状，若已知∠1=110°，则∠2＝ °．16.如图，在△ABC 中，已知∠ABC=50°，∠ACB=60°，BE 是AC 边上的高，CF 是AB 边上的高，H 是BE 和CF 的交点，则∠BHC= °.17．如图，在△ABC 中E 是BC 上的一点，EC ＝2EB ，点D 是AC 的中点，AE 、BD 交于点F ，AF ＝3FE ，若△ABC 的面积为18，给出下列命题：①△ABE 的面积为6；②△ABF 的面积和四边形DFEC 的面积相等；③点F 是BD 的中点；④四边形DFEC 的面积为152．其中，正确的结论有 ．（把你认为正确的结论的序号都填上）18.如图，长方形ABCD 中，AB=4cm ，BC=3cm ，点E 是CD 的中点，动点P 从A 点出发，以 每秒1cm 的速度沿A →B →C →E 运动，最终到达点E ．若点P 运动的时间为x 秒，那么 当x=_ ___时，△APE 的面积等于52cm ． 三、解答题（本大题共10小题，共54分.） 19. 计算或化简：（本题共9分，每小题3分）（1）－22+(－21)－2－(π－5)0－|－4| （2）2244223)2()(a a a a a ÷+∙--第18题图E C D A B P第15题图 第16题图（3）)32)(32(c b a c b a -+++20．因式分解：（本题共9分，每小题3分）（1）)(6)(3a b y b a x --- （2）6442-x（3）22216)4(x x -+21．先化简，再求值（本题共4分）（2x+y ）2—（2x-y ）（2x+y ）—4xy ；其中x=2015，y=-1．22．（本题共4分）若x ＋y ＝3，且(x ＋2)（y ＋2）＝12． (1)求xy 的值； (2)求x2-xy ＋y2的值．23．（本题共4分）已知以2m a =，4n a =，32k a =，求kn m a -+23的值．24．(本题共5分)在正方形网格中，每个小正方形的边长都为1个单位长度，△ABC 的三个顶点的位置如图所示，现将△ABC 平移后得△EDF ，使点B 的对应点为点D ，点A 对应点为点E ． （1）画出△EDF ；（2）线段BD 与AE 有何关系？_________ ___；（3）连接CD 、BD ，则四边形ABDC 的面积为_______．21世纪教育网25.（本题共5分）如图，已知∠DAB+∠D=180°，AC 平分∠DAB ，且∠CAD=25°，∠B=95° 求（1）∠DCA 的度数；（2）∠DCE 的度数．26. (本题6分）先阅读下面的内容，再解决问题.例题：若m2＋2mn ＋2n2－6n ＋9＝0，求m 和n 的值． 解：∵m2＋2mn ＋2n2—6n ＋9＝0 ∴m2＋2mn ＋n2＋n2－6n ＋9＝0 ∴(m ＋n)2＋(n －3)2＝0 ∴m ＋n =0，n －3=0 即m ＝－3，n ＝3(1)若x2＋2y2－2xy ＋4y ＋4＝0，求yx 的值．(2)已知a ，b ，c 是△ABC 的三边长，且满足a2＋b2－10a －8b ＋41＝0，且c 是△ABC 中最长的边，求c 的取值范围．27．（本题共8分）（1）如图1的图形我们把它称为“8字形”，请说明A B C D∠+∠=∠+∠；图1O ABC D图4P OABCDE F图3P OA B CD E F 图5POABCDE（2）阅读下面的内容，并解决后面的问题：如图2， AP 、CP 分别平分∠BAD. ∠BCD ，若∠ABC=36°，∠ADC=16°，求∠P 的度数； 解：∵AP 、CP 分别平分∠BAD. ∠BCD ∴∠1=∠2，∠ 3=∠4由（1）的结论得： 3124P B P D ∠+∠=∠+∠⎧⎨∠+∠=∠+∠⎩①②①+②，得2∠P+∠2+∠3=∠1+∠4+∠B+∠D∴∠P =21(∠B+∠D)=26°.①如图3，直线AP 平分∠BAD 的外角∠FAD ，CP 平分∠BCD 的外角∠BCE ，若∠ABC=36°，∠ADC=16°，请猜想P ∠的度数，并说明理由.②在图4中，直线AP 平分∠BAD 的外角∠FAD ，CP 平分∠BCD 的外角∠BCE ，猜想∠P 与∠B 、∠D 的关系，直接写出结论，无需说明理由．③在图5中，AP 平分∠BAD ，CP 平分∠BCD 的外角∠BCE ，猜想∠P 与∠B 、∠D 的关系，直接写出结论，无需说明理由．4321图2OPAB CD初一年级数学学科期中考试答案 选择题：D,C,B,A,D C,C,C,C,B 填空题：11.338-y x 12. 8×810- 13. 7,9 14.5 15.55゜ 16.110゜ 17.①③④ 18.5310，三．解答题：19.计算或化简：（1）原式=-4+4-1-4 2分（2）原式=6a -6a +48a ÷2a 1分（3）原式=(a+2b)2-(3c)22分=-5 3分 =6a -6a +46a 2 分 =2244b ab a ++-9c 2 3分=46a 3分 20.因式分解：(1)原式=3x(a-b)+6y(a-b) 1分(2)原式=4（2x -16）1分(3)原式=（2x +4+4y ）(2x +4-4y) 2分=3(a-b)(x+2y) 3分 =4（x+2）(x-2) 3分 =（x+2）2(x-2)23分21.原式=22y 2分 当y=-1时，原式=2 4分 22.（1）xy=2 2分 （2）22y xy x +-=3 4分23. 4 4分24.（1）画图1分 （2）BD=AE, BD//AE 3分 （3）6 5分 25. 解：（1）∵∠DAB+∠D=180°， ∴AB ∥CD ，∴∠ACD=∠BAC ， ∵AC 平分∠DAB ， ∴∠DAC=∠BAC ， ∴∠DAC=∠DCA ， ∵∠CAD=25°， ∴∠DCA=25°；3分 （2）∵AB ∥CD ， ∴∠ECD=∠B ； ∵∠B=95，∴∠DCE=95°． 5分26.解（1）∵x2+2y2-2xy+4y+4=0 ∴x2-2xy+y2+y2+4y+4=0∴（x-y ）2+（y+2）2=0， 1分 ∴x-y=0，y+2=0，图3P OABC DEF 1 23 4解得x=-2，y=-2， 2分∴xy=（-2）-2=413分（2）∵a2+b2-10a-8b+41=0 ∴a2-10a+25+b2-8b+16=0， ∴（a-5）2+（b-4）2=0，4分 ∴a-5=0，b-4=0， 解得a=5，b=4，5分∵c 是△ABC 中最长的边， ∴5≤c ＜9． 6分27.（1）∵∠A+∠B+∠AOB=180° ∠C+∠D+∠COD=180゜∴∠A+∠B+∠AOB=∠C+∠D+∠COD ∵∠AOB=∠COD∴∠A+∠B=∠C+∠D 2分 (2) ∠P=26゜ 3分∵AP 平分BAD ∠的外角FAD ∠，CP 平分BCD ∠的外角BCE ∠, ∴12∠=∠，34∠=∠由（1）的结论得：∠PAD+∠P= ∠PCD+∠D ①∠PAB+∠P= ∠PCB+∠B ② ∵∠PAB=∠1，∠1=∠2∴∠PAB=∠2∴∠2+∠P= ∠3+∠B ③+③得∠2+∠P +∠PAD+∠P = ∠3+∠B +∠PCD+∠D 2∠P +180° = ∠B+∠D+180°∴∠P = （21∠B+∠D )=26° 6分 （3）∠p=180゜-（21∠B+∠D ) 7分 （4）∠p=90゜+（21∠B+∠D ) 8分。
2015-2016学年第二学期期中考试初一数学试卷参考答案及评分标准
2015-2016学年第二学期期中考试初一数学试卷参考答案及评分标准一、选择题（本题共有12小题，每小题3分，共36分，每小题有四个项选，其中只有一个是正确的） BABCD BCBDC DB二、填空题（每小题3分，共12分。
请把答案填在答题卷上相应的位置）13、65° 14、104° 15、27 16、400三、解答题（共52分）17、（1）‘解：原式3-------6444a a a -+=‘5---------------64a =（2）'2222223-------)4b -(44)(9a b ab a ab b a -+-+-÷=解：原式'22224-------4b 449-+-+-+=a b ab a ab‘5--- ---b 831-2+=ab 18、解：原式='2222224]22)2()(-----÷-++---y y xy y xy x y x='23------4]44(y y xy ÷-='4------y x -当x=1,y=2时原式=1-2=-1 '5------19、略20、∵已知）(//CD AB∴∠BMN+∠MND=180°（ 两直线平行，同旁内角互补 ）————2′∵MG 平分∠BMN ，NG 平分∠MND （已知）∴∠1=BMN ∠21 ∠2=MND ∠21（角平分线定义）————4′ ∴∠1+∠2=009018021=MND ∠+BMN ∠21=⨯）（ 又∵∠1+∠2+∠G=180°（ 三角形内角和为180°）————6′∴∠G=180°-（∠1+∠2）=180°-90°=90°∴MG 丄NG （ 垂直的定义 ）—————8′（3） 2.5 ， 100 ————8′22、（1） m-n —————1′（2）方法一：2)(n m -————2′方法二：mn n m 4-)(2+————3′（3）22)4-)(n m mn n m -=+（————4′（4）55==+ab b a ，解：∴2)b a -（=ab 4-)2b a +（————6′=54-72⨯=49-20=29————8′23、(1)解：过点P 作PE//AB∵AB//CD ，PE//AB （已知）∴PE//CD （平行于同一条直线的两条直线平行） ———————1′ ∴∠BPE=∠B , ∠D=∠DPE （两直线平行，内错角相等）———————2′ ∴∠B=∠BPE= ∠BPD+∠DPE=∠BPD+∠D ————3′∴∠BPD= ∠B-∠D ———————4′(2)解：不成立，∠BPD=∠B+∠D ———————5′证明：过点P 作PM//AB∵AB//CD ，PM//AB （已知）∴PM//CD （平行于同一条直线的两条直线平行） ———————6′ ∴∠2=∠B, ∠3=∠D （两直线平行，内错角相等）———————7′ ∴∠BPD= ∠2+∠3=∠B+∠D ———————8′E。
2015—2016学年度第二学期期中考试七年级数学试卷及答案
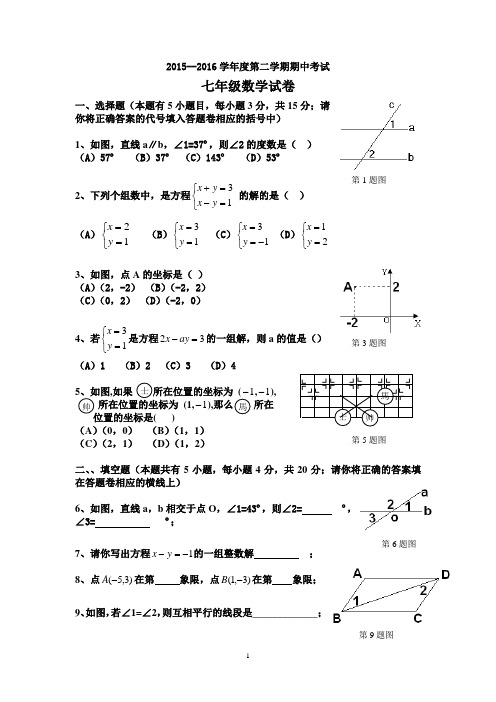
2015--2016学年度第二学期期中考试七年级数学试卷一、选择题（本题有5小题目，每小题3分，共15分；请你将正确答案的代号填入答题卷相应的括号中）1、如图，直线a ∥b ，∠1=37º，则∠2的度数是（ ）（A ）57º （B ）37º （C ）143º （D ）53º2、下列个组数中，是方程⎩⎨⎧=-=+13y x y x 的解的是（ ） （A ）⎩⎨⎧==12y x （B ）⎩⎨⎧==13y x （C ）⎩⎨⎧-==13y x （D ）⎩⎨⎧==21y x3、如图，点A 的坐标是（ ）（A ）（2，-2） （B ）（-2，2）（C ）（0，2） （D ）（-2，0）4、若⎩⎨⎧==13y x 是方程32=-ay x 的一组解，则a 的值是（）（A ）1 （B ）2 （C ）3 （D ）4,如果,1-), 所在位置的坐标为 (1,1-),所在() （A ）（0，0） （B ）（1，1）（C ）（2，1） （D ）（1，2）二、、填空题（本题共有5小题，每小题4分，共20分；请你将正确的答案填在答题卷相应的横线上）6、如图，直线a ，b 相交于点O ，∠1=43º，则∠2= º，∠3= º；7、请你写出方程1-=-y x 的一组整数解；8、点)3,5(-A 在第 象限，点)3,1(-B 在第 象限；9、如图，若∠1=∠2，则互相平行的线段是_____________；10、把点A （－4，2）向右平移3个单位长度得A1的坐标是 ；把点B （－4，2）向下平移3个单位长度得B2的坐标是 ；三、解答题（本题共5题，每小题6分，共30分）11、如图，直线a 、b 被直线c 所截若∠1=30°，∠2=150°，试说明a 与b 的位置关系。
12、解方程组 ⎩⎨⎧+==+y x y x 293213、解方程组 ⎩⎨⎧=-=+827y x y x14、如图，AD ∥BC ，AD 平分∠EAC ，∠EAD=50°，求∠B 和∠C 的度数。
2015-2016新人教版七年级数学第二学期期中考试试题(含答案)
南孙庄中学2015—2016学年度七年级第二学期期中质量检测试题（考试时间90分钟，满分100分）一、选择题（每小题3分，共20分）1、在平面直角坐标系中，点P （－5，4）位于（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限 2、下列各数中,无理数有（ ）3.1415926，227-，274π，0，，0.10 A ．1个 B ．2个 C ． 3个 D ．4个 3、实数27-的立方根为（ ）A.±3B. 3C.-3D.没有立方根4、如图是丁丁画的一张脸的示意图，如果用（0，2）表示左眼，用（2，2）表示右眼，那么嘴的位置可以表示成（ ）A ．(1，0)B ．(－1，0)C ．(－1，1)D ．(1，－1)5、如图，AD ∥BC ，∠B=30°，DB 平分∠ADE ，则∠DEC 的度数为（ ） A ．30° B ．60° C ．90° D ．120°6、如图所示，点E 在AD 的延长线上，下列条件中能判断．．．CD AB //（ ）A. 43∠=∠B. 21∠=∠C. CDE C ∠=∠D. 180=∠+∠ADC C 7、下列各式中,正确的是( )±2 B.±2=4=-2=- 8、把点A （―5，3）经过平移得到点B （3，―5），可以（ ） A.先向右平移8个单位，再向上平移8个单位 B.先向左平移8个单位，再向下平移8个单位C.先向右平移8个单位，再向下平移8个单位D.先向左平移2个单位，再向上平移2个单位9、如图，已知AB ∥CD ，直线MN 分别交AB 、CD 于点分MND ∠，若170∠=°， 则2∠的度数为（ ） A.10° B.15° C.20° D.35° 第6题图 第5题图 第4题图 B A DC 3 142E B D10、给出下列说法：（1） 两条直线被第三条直线所截，同位角相等；（2） 平面内的一条直线和两条平行线中的一条相交，则它与另一条也相交； （3） 相等的两个角是对顶角；（4） 从直线外一点到这条直线的垂线段，叫做这点到直线的距离； 其中正确的有（ ）A 0个B 1个C 2个D 3个 二、填空题（每小题3分，共21分 ）11、点A (4，－3)到x 轴的距离为 ．12、若()0232=++-n m ，则n m 2+的值是 ．13、如果点P(a ,2)在第二象限,那么点Q(-3,a )在第 象限．14．已知点P ),2(a -，Q )3,(b ，且PQ ∥x 轴，则=a _________，=b ___________ 15、把命题“内错角相等两直线平行”写成“如果……，那么……”的形式为： ________________________________________________________________． 16、在下列点中，与点A （2-，4-）的连线平行于y 轴的是 （ ） A 、（2，4-） B 、（4，)2- C 、（-2，4） D 、（-4，2） 17．3±是 的平方根3-是 的平方根；2)2(-的算术平方根是 。
人教版2015-2016年七年级下期中数学试卷含答案
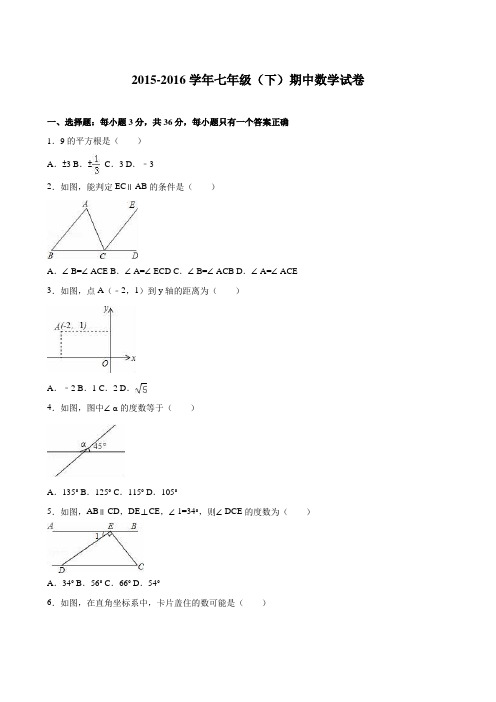
2015-2016学年七年级（下）期中数学试卷一、选择题：每小题3分，共36分，每小题只有一个答案正确1．9的平方根是（）A．±3 B．±C．3 D．﹣32．如图，能判定EC∥AB的条件是（）A．∠B=∠ACE B．∠A=∠ECD C．∠B=∠ACB D．∠A=∠ACE3．如图，点A（﹣2，1）到y轴的距离为（）A．﹣2 B．1 C．2 D．4．如图，图中∠α的度数等于（）A．135° B．125° C．115° D．105°5．如图，AB∥CD，DE⊥CE，∠1=34°，则∠DCE的度数为（）A．34° B．56° C．66° D．54°6．如图，在直角坐标系中，卡片盖住的数可能是（）A．（2，3）B．（﹣2，1）C．（﹣2，﹣2.5）D．（3，﹣2）7．若|3﹣a|+=0，则a+b的值是（）A．2 B．1 C．0 D．﹣18．估算﹣2的值（）A．在1到2之间B．在2到3之间C．在3到4之间D．在4到5之间9．已知点P位于y轴右侧，距y轴3个单位长度，位于x轴上方，距离x轴4个单位长度，则点P坐标是（）A．（﹣3，4）B．（3，4）C．（﹣4，3）D．（4，3）10．在平面直角坐标系中，将点B（﹣3，2）向右平移5个单位长度，再向下平移3个单位长度后与点A （x，y）重合，则点A的坐标是（）A．（2，5）B．（﹣8，5）C．（﹣8，﹣1）D．（2，﹣1）11．如图，已知棋子“车”的坐标为（﹣2，﹣1），棋子“马”的坐标为（1，﹣1），则棋子“炮”的坐标为（）A．（3，2）B．（﹣3，2）C．（3，﹣2）D．（﹣3，﹣2）12．如图，直线AC∥BD，AO、BO分别是∠BAC、∠ABD的平分线，那么∠BAO与∠ABO之间的大小关系一定为（）A．互余B．相等C．互补D．不等二、填空题：每小题3分，共18分13．如图，直线a∥b，∠1=125°，则∠2的度数为．14．4的算术平方根是，9的平方根是，﹣27的立方根是．15．将实数，π，0，﹣6由小到大用“＜”号连起来，可表示为．16．如图，将周长为8的△ABC沿BC方向向右平移1个单位得到△DEF，则四边形ABFD的周长为．17．如图，在长20米，宽10米的长方形草地内修建了宽2米的道路，则草地的面积为．18．观察下列各式：=2，=3，=4，…请你找出其中规律，并将第n（n≥1）个等式写出来．三、搜索相关资料解答题（共66分，要求写出解答过程）19．把下列各数的序号填在相应的横线上．①﹣0.3，②0，③，④π2，⑤|﹣2|，⑥，⑦3.1010010001…（2016春•防城区期中）如图，AB和CD相交于点O，∠C=∠1，∠D=∠2，求证：∠A=∠B．证明：∵∠C=∠1，∠D=∠2（已知）又∵∠1=∠2（）∴（等量代换）∴AC∥BD（）∴（两直线平行，内错角相等）21．我们在学习“实数”时，画了这样一个图，即“以数轴上的单位长为‘1’的线段作一个正方形，然后以原点O为圆心，正方形的对角线长为半径画弧交x轴于点A”，请根据图形回答下列问题：（1）线段OA的长度是多少？（要求写出求解过程）（2）这个图形的目的是为了说明什么？（3）这种研究和解决问题的方式，体现了的数学思想方法．（将下列符合的选项序号填在横线上）A、数形结合；B、代入；C、换元；D、归纳．22．如图，已知：AB∥DE，∠1=∠2，直线AE与DC平行吗？请说明理由．23．如图，直线AB∥CD，BC平分∠ABD，∠1=65°，求∠2的度数．24．如图，△A1B1C1是△ABC向右平移4个单位长度后得到的，且三个顶点的坐标分别为A1（1，1），B1（4，2），C1（3，4）．（1）请画出△ABC，并写出点A，B，C的坐标；（2）求出△AOA1的面积．25．位于汉江沿岸的小明家、学校、医院、游乐场的平面图如图所示．（1）建立适当的平面直角坐标系，使医院的坐标为（3，0）并写出小明家、学校、游乐场的坐标；（2）根据蜀河大坝蓄水工程需要，小明家及学校、医院、游乐场需要等距离整体迁移，已知迁移后新的小明家、学校、游乐场、医院分别用A、B、C、D表示，且这四点的坐标分别用原来各地点的横坐标都减去5、纵坐标都加上2 得到，请先在图中描出A、B、C、D的位置，画出四边形ABCD，然后说明四边形ABCD是由以小明家、学校、游乐场、医院所在地为顶点的四边形经过怎样平移得到的？26．（12分）（2016春•防城区期中）如图，已知平面内有两条直线AB、CD，且AB∥CD，P为一动点．（1）当点P移动到AB、CD之间时，如图（1），这时∠P与∠A、∠C有怎样的关系？证明你的结论．（2）当点P移动到如图（2）的位置时，∠P与∠A、∠C又有怎样的关系？请证明你的结论．参考答案一、选择题：每小题3分，共36分，每小题只有一个答案正确1．A．2．D．3．C．4．A．5．B．6．D．7．B．8．C．9．B．10．D．11．C．12．A二、填空题：每小题3分，共18分13．55°．14．：2；±3，﹣3．15．﹣6．16．10．17．144米2．18．．三、搜索相关资料解答题（共66分，要求写出解答过程）19．证明：∵∠C=∠1，∠D=∠2 （已知）又∵∠1=∠2 （对顶角相等）∴∠C=∠D（等量代换）∴AC∥BD （内错角相等，两直线平行）∴∠A=∠B（两直线平行，内错角相等）故答案为对顶角相等；∠C=∠D；内错角相等，两直线平行；∠A=∠B．21．解：（1）∵OB2=12+12=2，∴OB=，∴OA=OB=；（2）数轴上的点和实数﹣一对应关系；（3）A．22．答：AE∥DC；理由如下：∵AB∥DE（已知），∴∠1=∠3（两直线平行，内错角相等），∵∠1=∠2（已知），∴∠2=∠3（等量代换），∴AE∥DC（内错角相等，两直线平行）．23．解：∵AB∥CD，∴∠ABC=∠1=65°，∠ABD+∠BDC=180°，∵BC平分∠ABD，∴∠ABD=2∠ABC=130°，∴∠BDC=180°﹣∠ABD=50°，∴∠2=∠BDC=50°．24．解：（1）如图所示，A（﹣3，1），B（0，2），C（﹣1，4）；（2）S△AOA1=×4×1=2．25．解：（1）如图所示：小明家的坐标为：（0，0）、学校的坐标为：（2，2）、游乐场的坐标为：（5，2）；（2）∵四点的坐标分别用原来各地点的横坐标都减去5、纵坐标都加上2 得到，∴A、B、C、D的位置如图所示，则四边形ABCD是由以小明家、学校、游乐场、医院所在地为顶点的四边形经过向左平移5个单位再向上平移2个单位得到的．26．证明：（1）∠P=∠A+∠C，如图（1）延长AP交CD与点E．∵AB∥CD，∴∠A=∠AEC．又∵∠APC是△PCE的外角，∴∠APC=∠C+∠AEC．∴∠APC=∠A+∠C；（2）∠P=360°﹣（∠A+∠C）．如图（2）延长BA到E，延长DC到F，由（1）得∠P=∠PAE+∠PCF．∵∠PAE=180°﹣∠PAB，∠PCF=180°﹣∠PCD，∴∠P=360°﹣（∠PAB+∠PCD）．。
2015-2016年安徽省合肥市包河区七年级(下)期中数学试卷(解析版)
2015-2016学年安徽省合肥市包河区七年级（下）期中数学试卷一、选择题（本题共10小题，每小题3分，共30分）1．（3分）在，，，1.414，，0.1010010001（两个1之间依次增加1个0）中，无理数有（）A．2个B．3个C．4个D．5个2．（3分）下列各式中正确的是（）A．=±5B．=﹣3C．=﹣10D．=±6 3．（3分）世界上最小的开花结果植物是澳大利亚的出水浮萍，这种植物的果实像一个微笑的无花果，质量只有0.000000076克，将0.000000076克用科学记数法表示为（）A．7.6×10﹣8B．0.76×10﹣9C．7.6×108D．0.76×109 4．（3分）下列各组数中互为相反数的是（）A．﹣2与B．﹣2与C．﹣2与D．2与|﹣2| 5．（3分）如图是5×5方格子（每个小正方格的边长为1个单位长度，图中阴影部分是正方形，则此正方形的边长为（）A．3B．C．D．56．（3分）不等式组的解集是（）A．﹣1＜x≤2B．﹣1＜x＜2C．x＜﹣1，x＞2D．x＜﹣1，x≥2 7．（3分）不等式＜1的正整数解为（）A．1个B．3个C．4个D．5个8．（3分）若3x=4，9y=7，则3x﹣2y的值为（）A．B．C．﹣3D．9．（3分）若a，b均为正整数，且a＞，b＞，则a+b的最小值（）A．3B．4C．5D．610．（3分）某大型超市从生产基地购进一批水果，运输过程中质量损失10%，假设不计超市其它费用，如果超市要想至少获得20%的利润，那么这种水果的售价在进价的基础上应至少提高（）A．40%B．33.4%C．33.3%D．30%二、填空题（每小题3分，计18分）11．（3分）﹣125的立方根是．12．（3分）（8x5y2﹣4x2y5）÷（﹣2x2y）=．13．（3分）比较大小：．14．（3分）若，，则=．15．（3分）小成编写了一个程序：输入x→x2→立方根→倒数→算术平方根→，则x为．16．（3分）若x+y+z=30，3x+y﹣z=50，x，y，z都为非负实数，则M=5x+4y+2z 的取值范围是．三、解答题（共52分）17．（10分）计算：（1）（﹣2）﹣2++﹣（﹣2016）0（2）（﹣2x3）2•（﹣x2）÷[（﹣x）2]3．18．（6分）解不等式组：．19．（6分）先化简，再求值：（x+2）（x﹣2）﹣（x﹣2）2+（﹣x﹣2）（﹣x+2），其中x=4．20．（6分）解不等式：，并把解集表示在数轴上．21．（14分）应用题（1）光的速度约为3×105千米/秒，地球离太阳的距离大约为1.5×108千米，那么太阳光照射到地球的时间大约需要多少秒？（2）某地为促进淡水养殖业的发展，将淡水鱼的价格控制在每千克8元到14元之间，决定对淡水鱼提供政府补贴．设淡水鱼的市场价格为x元/千克，政府补贴为t元/千克．据调查，要使每日市场的淡水鱼供应量与日需求量正好相等，t与x应满足等式100（x+t﹣8）=270﹣3x，为使市场价格不高于10元/千克，政府补贴至少应为多少？22．（10分）观察下列等式：4×6=2414×16=22424×26=62434×36=122444×46=2024…（1）利用以上规律直接写出结果：124×126=；（2）设第一个两位数的十位数字为a，个位数字为b，请用含a、b的代数式表示并验证你发现的规律；（3）请你再找一个类似的规律（要求个位数字不与以上等式的相同，用一个算式表示即可）．2015-2016学年安徽省合肥市包河区七年级（下）期中数学试卷参考答案与试题解析一、选择题（本题共10小题，每小题3分，共30分）1．（3分）在，，，1.414，，0.1010010001（两个1之间依次增加1个0）中，无理数有（）A．2个B．3个C．4个D．5个【解答】解：，，，1.414，，0.1010010001（两个1之间依次增加1个0）中，无理数有，，一共2个．故选：A．2．（3分）下列各式中正确的是（）A．=±5B．=﹣3C．=﹣10D．=±6【解答】解：A、=5，故本选项不符合题意；B、=3，故本选项不符合题意；C、没有意义，故本选项不符合题意；D、=±6，故本选项符合题意；故选：D．3．（3分）世界上最小的开花结果植物是澳大利亚的出水浮萍，这种植物的果实像一个微笑的无花果，质量只有0.000000076克，将0.000000076克用科学记数法表示为（）A．7.6×10﹣8B．0.76×10﹣9C．7.6×108D．0.76×109【解答】解：0.000000076=7.6×10﹣8．故选：A．4．（3分）下列各组数中互为相反数的是（）A．﹣2与B．﹣2与C．﹣2与D．2与|﹣2|【解答】解：A、=2，﹣2与是互为相反数，故本选项正确；B、=﹣2，﹣2与相等，不是互为相反数，故本选项错误；C、﹣2与﹣是互为倒数，不是互为相反数，故本选项错误；D、|﹣2|=2，2与|﹣2|相等，不是互为相反数，故本选项错误．故选：A．5．（3分）如图是5×5方格子（每个小正方格的边长为1个单位长度，图中阴影部分是正方形，则此正方形的边长为（）A．3B．C．D．5【解答】解：由勾股定理可知：阴影部分的正方形的面积为：22+32=13，所以正方形的边长为：故选：C．6．（3分）不等式组的解集是（）A．﹣1＜x≤2B．﹣1＜x＜2C．x＜﹣1，x＞2D．x＜﹣1，x≥2【解答】解：，由①得，x＞﹣1，由②得，x≤2，故此不等式组的解集为：﹣1＜x≤2．故选：A．7．（3分）不等式＜1的正整数解为（）A．1个B．3个C．4个D．5个【解答】解：解不等式得，x＜4，则不等式＜1的正整数解为1，2，3，共3个．故选：B．8．（3分）若3x=4，9y=7，则3x﹣2y的值为（）A．B．C．﹣3D．【解答】解：∵3x=4，9y=7，∴3x﹣2y=3x÷32y=3x÷（32）y=4÷7=．故选：A．9．（3分）若a，b均为正整数，且a＞，b＞，则a+b的最小值（）A．3B．4C．5D．6【解答】解：∵若a，b均为正整数，且a＞，b＞，∴a≥3，b≥2，∴a+b的最小值为5，故选：C．10．（3分）某大型超市从生产基地购进一批水果，运输过程中质量损失10%，假设不计超市其它费用，如果超市要想至少获得20%的利润，那么这种水果的售价在进价的基础上应至少提高（）A．40%B．33.4%C．33.3%D．30%【解答】解：设购进这种水果a千克，进价为y元/千克，这种水果的售价在进价的基础上应提高x，则售价为（1+x）y元/千克，由题意得：×100%≥20%，解得：x≥≈33.4%，经检验，x≥是原不等式的解．∵超市要想至少获得20%的利润，∴这种水果的售价在进价的基础上应至少提高33.4%．故选：B．二、填空题（每小题3分，计18分）11．（3分）﹣125的立方根是﹣5．【解答】解：∵﹣5的立方等于﹣125，∴﹣125的立方根是﹣5．故答案为﹣5．12．（3分）（8x5y2﹣4x2y5）÷（﹣2x2y）=﹣4x3y+2y3．【解答】解：（8x5y2﹣4x2y5）÷（﹣2x2y）=（8x5y2）÷（﹣2x2y）﹣4x2y5÷（﹣2x2y）=﹣4x3y+2y3．故答案为：﹣4x3y+2y3．13．（3分）比较大小：＞．【解答】解：∵5＜＜6，∴1＜﹣4＜2，∴＞．故答案为：＞．14．（3分）若，，则=503.6．【解答】解：∵253600相对于25.36向右移动了4位，∴算术平方根的小数点要向右移动2位，∴=503.6．故答案为503.6．15．（3分）小成编写了一个程序：输入x→x2→立方根→倒数→算术平方根→，则x为±8．【解答】解：根据题意得：=，则=，x2=64，x=±8，故答案为：±8．16．（3分）若x+y+z=30，3x+y﹣z=50，x，y，z都为非负实数，则M=5x+4y+2z 的取值范围是120≤M≤130．【解答】解：由题意得，且x≥0，y≥0，z≥0由②﹣①得x﹣z=10，即x=10+z由①×3﹣②得2y+4z=40，即y=20﹣2z，又∵x≥0，y≥0，z≥0，∴0≤z≤10，∵M=5x+4y+2z=（2x+2y+2z）+（3x+y﹣z）+（y+z）=130﹣z，∴120≤M≤130．故答案为：120≤M≤130．三、解答题（共52分）17．（10分）计算：（1）（﹣2）﹣2++﹣（﹣2016）0（2）（﹣2x3）2•（﹣x2）÷[（﹣x）2]3．【解答】解：（1）原式=+3+4﹣1=6；（2）原式=4x6•（﹣x2）÷x6=﹣4x2．18．（6分）解不等式组：．【解答】解：，解不等式①得，x＜，解不等式②得，x≥﹣2，所以，不等式组的解集是﹣2≤x＜．19．（6分）先化简，再求值：（x+2）（x﹣2）﹣（x﹣2）2+（﹣x﹣2）（﹣x+2），其中x=4．【解答】解：当x=4时，原式=x2﹣4﹣（x2﹣4x+4）+x2﹣4=x2+4x﹣12=16+16﹣12=2020．（6分）解不等式：，并把解集表示在数轴上．【解答】解：去分母，得：2x﹣1+3＞3x，移项，得：2x﹣3x＞1﹣3，合并同类项，得：﹣x＞﹣2，系数化为1，得：x＜2，将解集表示在数轴上如下：21．（14分）应用题（1）光的速度约为3×105千米/秒，地球离太阳的距离大约为1.5×108千米，那么太阳光照射到地球的时间大约需要多少秒？（2）某地为促进淡水养殖业的发展，将淡水鱼的价格控制在每千克8元到14元之间，决定对淡水鱼提供政府补贴．设淡水鱼的市场价格为x元/千克，政府补贴为t元/千克．据调查，要使每日市场的淡水鱼供应量与日需求量正好相等，t与x应满足等式100（x+t﹣8）=270﹣3x，为使市场价格不高于10元/千克，政府补贴至少应为多少？【解答】解：（1）太阳光照射到地球的时间=1.5×108千米÷3×105千米/秒=500秒；答：太阳光照射到地球的时间大约需要500秒；（2）由题意知：8≤x≤10，由100（x+t﹣8）=270﹣3x，得：t=10.7﹣1.03x，当x=10时，t最小为0.4，答：政府补贴至少应为0.4元．22．（10分）观察下列等式：4×6=2414×16=22424×26=62434×36=122444×46=2024…（1）利用以上规律直接写出结果：124×126=15624；（2）设第一个两位数的十位数字为a，个位数字为b，请用含a、b的代数式表示并验证你发现的规律；（3）请你再找一个类似的规律（要求个位数字不与以上等式的相同，用一个算式表示即可）．【解答】解：（1）根据题意知124×126=12×13×100+4×6=15624，故答案为：15624；（2）两数的十位数字为a，个位数字为b、c且b、c“互补”，即b+c=10．这两数之积为（10a+b）（10a+c）=100a2+10ab+10ac+bc=100a2+10a（b+c）+bc=100a2+10a×10+bc=100a2+100a+bc=100a（a+1）+bc=100a（a+1）+b（10﹣b）．（3）52×58=3016．。
2015-2016学年安徽省合肥市瑶海区七年级下期中数学试卷含答案解析
2015-2016学年安徽省合肥市瑶海区七年级（下）期中数学试卷一、单项选择题（本题共10小题，每小题只有1个选项符合题意，每小题4分，共40分）1．下列实数中，是无理数的为（）A．0 B．﹣C．D．3.142．如图，数轴上A、B两点表示的数分别为和5.1，则A、B两点之间表示整数的点共有（）A．6个B．5个C．4个D．3个3．已知a＜b，下列式子不成立的是（）A．a+1＜b+1 B．3a＜3bC．﹣a＞﹣ b D．如果c＜0，那么＜4．下列运算中，结果是a6的式子是（）A．a2•a3 B．a12﹣a6C．（a3）3D．（﹣a）65．下列计算正确的是（）A．=±3 B．32=6 C．（﹣1）2015=﹣1 D．|﹣2|=﹣26．不等式组的解集在数轴上表示正确的是（）A．B．C．D．7．下列运算正确的是（）A．（a+b）2=a2+b2+2a B．（a﹣b）2=a2﹣b2C．（x+3）（x+2）=x2+6 D．（m+n）（﹣m+n）=﹣m2+n28．若关于x，y的二元一次方程组的解满足x+y＜505，则a的取值范围（）A．a＞2016 B．a＜2016 C．a＞505 D．a＜5059．已知（x+a）（x+b）=x2﹣13x+36，则a+b=（）A．﹣5 B．5 C．﹣13 D．﹣13或510．已知整数a1，a2，a3，a4，…满足下列条件：a1=0，a2=﹣|a1+1|，a3=﹣|a2+2|，a4=﹣|a3+3|，…依此类推，则a2016的值为（）A．﹣1007 B．﹣1008 C．﹣1009 D．﹣1010二、填空题11．不等式2x+9≥3（x+2）的正整数解是．12．一种病毒近似于球体，它的半径为0.00000000375，用科学记数法表示为．13．若x2+kx+81是完全平方式，则k的值应是．14．规定用符号[m]表示一个实数m的整数部分，例如：[]=0，[3.14]=3．按此规定[]的值为．15．已知m+n=2，mn=﹣2，则（1﹣m）（1﹣n）=．三、解答题16．计算（﹣2）﹣1﹣+（﹣3）0．17．解不等式：1﹣+x．四、（共两小题，每小题8分，共16分）18．a3•a4•a+（a2）4+（﹣2a4）2．19．解不等式组，并把解集在数轴上表示出来．．五、（共两小题，每小题10分，共20分）20．先化简，再求值：（2x+5）（2x﹣5）+2x（x+1）﹣3x（2x﹣5），其中x=2．21．定义新运算：对于任意实数a，b，都有a⊕b=a（a﹣b）+1，等式右边是通常的加法，减法及乘法运算．比如：2⊕5=2×（2﹣5）+1=2×（﹣3）+1=﹣6+1=﹣5（1）求3⊕（﹣2）的值；（2）若3⊕x的值小于16，求x的取值范围，并在数轴上表示出来．六、（本题满分12分）22．如图所示，某计算装置有一数据的入口A和一运算结果的出口B．下表是小刚输入一些数后所得的结果：A 0 1 4 9 16 25 36B ﹣2 ﹣1 0 1 2 3 4（1）若输出的数是5，则小刚输入的数是多少？（2）若小刚输入的数是225，则输出的结果是多少？（3）若小刚输入的数是n（n≥10），你能用含n的式子表示输出的结果吗？试一试．七、（本题满分12分）23．瑶海教育局计划在3月12日植树节当天安排A，B两校部分学生到郊区公园参加植树活动．已知A校区的每位学生往返车费是6元，B校每位学生的往返车费是10元，要求两所学校均要有学生参加，且A校参加活动的学生比B校参加活动的学生少4人，本次活动的往返车费总和不超过210元．求A，B两校最多各有多少学生参加？八、（本题满分14分）24．南山植物园中现有A、B两个园区，已知A园区为长方形，长为（x+y）米，宽为（x ﹣y）米；B园区为正方形，边长为（x+3y）米．（1）请用代数式表示A、B两园区的面积之和并化简；（2）现根据实际需要对A园区进行整改，长增加（11x﹣y）米，宽减少（x﹣2y）米，整改后A区的长比宽多350米，且整改后两园区的周长之和为980米．①求x、y的值；②若A园区全部种植C种花，B园区全部种植D种花，且C、D两种花投入的费用与吸引游客的收益如表：C D投入（元/平方米）12 16收益（元/平方米）18 26求整改后A、B两园区旅游的净收益之和．（净收益=收益﹣投入）2015-2016学年安徽省合肥市瑶海区七年级（下）期中数学试卷参考答案与试题解析一、单项选择题（本题共10小题，每小题只有1个选项符合题意，每小题4分，共40分）1．下列实数中，是无理数的为（）A．0 B．﹣C．D．3.14【考点】无理数．【分析】根据无理数是无限不循环小数，可得答案．【解答】解：A、0是有理数，故A错误；B、﹣是有理数，故B错误；C、是无理数，故C正确；D、3.14是有理数，故D错误；故选：C．【点评】本题考查了无理数，无理数是无限不循环小数，有理数是有限小数或无限循环小数．2．如图，数轴上A、B两点表示的数分别为和5.1，则A、B两点之间表示整数的点共有（）A．6个B．5个C．4个D．3个【考点】实数与数轴；估算无理数的大小．【分析】根据比1大比2小，5.1比5大比6小，即可得出A、B两点之间表示整数的点的个数．【解答】解：∵1＜2，5＜5.1＜6，∴A、B两点之间表示整数的点有2，3，4，5，共有4个；故选C．【点评】本题主要考查了无理数的估算和数轴，根据数轴的特点，我们把数和点对应起来，也就是把“数”和“形”结合起来，二者互相补充，相辅相成，把很多复杂的问题转化为简单的问题，在学习中要注意培养数形结合的数学思想．3．已知a＜b，下列式子不成立的是（）A．a+1＜b+1 B．3a＜3bC．﹣a＞﹣ b D．如果c＜0，那么＜【考点】不等式的性质．【分析】利用不等式的性质知：不等式两边同时乘以一个正数不等号方向不变，同乘以或除以一个负数不等号方向改变．【解答】解：A、不等式两边同时加上1，不等号方向不变，故本选项正确，不符合题意；B、不等式两边同时乘以3，不等号方向不变，故本选项正确，不符合题意；C、不等式两边同时乘以﹣，不等号方向改变，故本选项正确，不符合题意；D、不等式两边同时乘以负数c，不等号方向改变，故本选项错误，符合题意．故选D．【点评】本题考查了不等式的性质，解题的关键是牢记不等式的性质，特别是在不等式的两边同时乘以或除以一个负数时，不等号方向改变．4．下列运算中，结果是a6的式子是（）A．a2•a3 B．a12﹣a6C．（a3）3D．（﹣a）6【考点】同底数幂的乘法；合并同类项；幂的乘方与积的乘方．【分析】根据同底数幂相乘，底数不变指数相加；幂的乘方，底数不变指数相乘；有理数的乘方的意义，对各选项计算后利用排除法求解．【解答】解：A、a2•a3=a5，故本选项错误；B、不能进行计算，故本选项错误；C、（a3）3=a9，故本选项错误；D、（﹣a）6=a6，正确．故选：D．【点评】本题考查同底数幂的乘法、幂的乘方和有理数乘方的定义，熟练掌握运算性质是解题的关键．5．下列计算正确的是（）A．=±3 B．32=6 C．（﹣1）2015=﹣1 D．|﹣2|=﹣2【考点】实数的运算．【专题】常规题型；实数．【分析】原式各项利用算术平方根，乘方的意义，以及绝对值的代数意义化简得到结果，即可作出判断．【解答】解：A、原式=3，错误；B、原式=9，错误；C、原式=﹣1，正确；D、原式=2，错误，故选C．【点评】此题考查了实数的运算，熟练掌握运算法则是解本题的关键．6．不等式组的解集在数轴上表示正确的是（）A．B．C．D．【考点】解一元一次不等式组；在数轴上表示不等式的解集．【分析】先求出每个不等式的解集再求出其公共解集．【解答】解：该不等式组的解集为1＜x≤2，故选C．【点评】本题考查了不等式组解集表示．按照不等式的表示方法1＜x≤2在数轴上表示如选项C所示，解答这类题时常常因表示解集时不注意数轴上圆圈和黑点所表示意义的区别而误选D．7．下列运算正确的是（）A．（a+b）2=a2+b2+2a B．（a﹣b）2=a2﹣b2C．（x+3）（x+2）=x2+6 D．（m+n）（﹣m+n）=﹣m2+n2【考点】完全平方公式；多项式乘多项式；平方差公式．【专题】计算题．【分析】A、B选项中利用完全平方公式展开得到结果；C选项中利用多项式乘以多项式法则计算得到结果；D选项利用平方差公式化简得到结果，即可做出判断．【解答】解：A、（a+b）2=a2+b2+2ab，本选项错误；B、（a﹣b）2=a2+b2﹣2ab，本选项错误；C、（x+3）（x+2）=x2+5x+6，本选项错误；D、（m+n）（﹣m+n）=﹣m2+n2，本选项正确，故选D【点评】此题考查了完全平方公式，平方差公式，以及多项式乘以多项式法则，熟练掌握公式及法则是解本题的关键．8．若关于x，y的二元一次方程组的解满足x+y＜505，则a的取值范围（）A．a＞2016 B．a＜2016 C．a＞505 D．a＜505【考点】二元一次方程组的解；解一元一次不等式．【专题】计算题；一次方程（组）及应用．【分析】方程组两方程相加表示出x+y，代入已知不等式求出a的范围即可．【解答】解：，①+②得：4（x+y）=a+4，即x+y=，代入已知不等式得：＜505，解得：a＜2016，故选B【点评】此题考查了二元一次方程组的解，以及解一元一次不等式，熟练掌握运算法则是解本题的关键．9．已知（x+a）（x+b）=x2﹣13x+36，则a+b=（）A．﹣5 B．5 C．﹣13 D．﹣13或5【考点】多项式乘多项式．【分析】直接利用多项式乘法去括号，进而合并同类项求出答案．【解答】解：∵（x+a）（x+b）=x2﹣13x+36，∴x2+（a+b）x+ab=x2﹣13x+36，∴a+b=﹣13．故选：C．【点评】此题主要考查了多项式乘以多项式，正确掌握运算法则是解题关键．10．已知整数a1，a2，a3，a4，…满足下列条件：a1=0，a2=﹣|a1+1|，a3=﹣|a2+2|，a4=﹣|a3+3|，…依此类推，则a2016的值为（）A．﹣1007 B．﹣1008 C．﹣1009 D．﹣1010【考点】规律型：数字的变化类；列代数式．【专题】规律型；分类讨论；整式．【分析】根据题目条件求出前几个数的值，知当n为奇数时：，当n为偶数时：；把n的值代入进行计算可得．【解答】解：∵a1=0，a2=﹣|a1+1|，a3=﹣|a2+2|，a4=﹣|a3+3|，…∴a2=﹣|0+1|=﹣1，a3=﹣|a2+2|=﹣|﹣1+2|=﹣1，a4=﹣|a3+3|=﹣|﹣1+3|=﹣2，a5=﹣|a4+4|=﹣|﹣2+4|=﹣2，a6=﹣|a5+5|=﹣|﹣2+5|=﹣3，a7=﹣|a6+6|=﹣|﹣3+6|=﹣3，…，所以当n为奇数时：，当n为偶数时：；．故选：B．【点评】本题主要考查数字的变化规律，通过归纳、想象、猜想，进行规律的探索，解答时要注意分类讨论思想在解题中的应用，培养了学生的发散思维，属中档题．二、填空题11．不等式2x+9≥3（x+2）的正整数解是1，2，3．【考点】一元一次不等式的整数解．【专题】计算题．【分析】先解不等式，求出其解集，再根据解集判断其正整数解．【解答】解：2x+9≥3（x+2），去括号得，2x+9≥3x+6，移项得，2x﹣3x≥6﹣9，合并同类项得，﹣x≥﹣3，系数化为1得，x≤3，故其正整数解为1，2，3．故答案为：1，2，3．【点评】本题考查了一元一次不等式的整数解，会解不等式是解题的关键．12．一种病毒近似于球体，它的半径为0.00000000375，用科学记数法表示为 3.75×10﹣9．【考点】科学记数法—表示较小的数．【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10﹣n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．【解答】解：0.00000000375=3.75×10﹣9．故答案为：3.75×10﹣9．【点评】本题考查用科学记数法表示较小的数，一般形式为a×10﹣n，其中1≤|a|＜10，n为由原数左边起第一个不为零的数字前面的0的个数所决定．13．若x2+kx+81是完全平方式，则k的值应是±18．【考点】完全平方式．【专题】计算题；整式．【分析】利用完全平方公式的结构特征判断即可确定出k的值．【解答】解：∵x2+kx+81是完全平方式，∴k=±18．故答案为：±18．【点评】此题考查了完全平方式，熟练掌握完全平方公式是解本题的关键．14．规定用符号[m]表示一个实数m的整数部分，例如：[]=0，[3.14]=3．按此规定[]的值为4．【考点】估算无理数的大小．【专题】压轴题；新定义．【分析】求出的范围，求出+1的范围，即可求出答案．【解答】解：∵3＜＜4，∴3+1＜+1＜4+1，∴4＜+1＜5，∴[+1]=4，故答案为：4．【点评】本题考查了估计无理数的应用，关键是确定+1的范围，题目比较新颖，是一道比较好的题目．15．已知m+n=2，mn=﹣2，则（1﹣m）（1﹣n）=﹣3．【考点】多项式乘多项式．【专题】计算题．【分析】原式利用多项式乘以多项式法则计算，变形后，将m+n与mn的值代入计算即可求出值．【解答】解：∵m+n=2，mn=﹣2，∴（1﹣m）（1﹣n）=1﹣（m+n）+mn=1﹣2﹣2=﹣3．故答案为：﹣3．【点评】此题考查了多项式乘多项式，熟练掌握运算法则是解本题的关键．16．计算（﹣2）﹣1﹣+（﹣3）0．【考点】实数的运算；零指数幂；负整数指数幂．【专题】计算题；实数．【分析】原式第一项利用负整数指数幂法则计算，第二项利用算术平方根定义计算，最后一项利用零指数幂法则计算即可得到结果．【解答】解：原式=﹣﹣+1=﹣2+1=﹣1．【点评】此题考查了实数的运算，熟练掌握运算法则是解本题的关键．17．解不等式：1﹣+x．【考点】解一元一次不等式．【分析】先去分母，再去括号，移项，合并同类项，把x的系数化为1即可．【解答】解：去分母得，3﹣（x﹣1）≤2x+3+3x，去括号得，3﹣x+1≤2x+3x+3，移项得，﹣x﹣2x﹣3x≤3﹣3﹣1，合并同类项得，﹣6x≤﹣1，把x的系数化为1得，x≥．【点评】本题考查的是解一元一次不等式，熟知不等式的基本性质是解答此题的关键．四、（共两小题，每小题8分，共16分）18．a3•a4•a+（a2）4+（﹣2a4）2．【考点】幂的乘方与积的乘方；合并同类项；同底数幂的乘法．【分析】首先根据同底数幂的乘法法则：同底数幂相乘，底数不变，指数相加计算a3•a4•a，再根据幂的乘方法则：底数不变，指数相乘计算（a2）4，再根据积的乘方法则：把每一个因式分别乘方，再把所得的幂相乘计算（﹣2a4）2．最后算加减即可．【解答】解：原式=a3+4+1+a2×4+4a8，=6a8．【点评】此题主要考查了同底数幂的乘法、幂的乘方、积的乘方，关键是熟练掌握各种计算法则．19．解不等式组，并把解集在数轴上表示出来．．【考点】解一元一次不等式组；在数轴上表示不等式的解集．【分析】分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集．【解答】解：解不等式4x+6＞1﹣x，得：x＞﹣1，解不等式3（x﹣1）≤x+5，得：x≤4，所以不等式组的解集为：﹣1＜x≤4，将不等式组解集表示在数轴上如下：【点评】本题考查的是解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．五、（共两小题，每小题10分，共20分）20．先化简，再求值：（2x+5）（2x﹣5）+2x（x+1）﹣3x（2x﹣5），其中x=2．【考点】整式的混合运算—化简求值．【专题】计算题；整式．【分析】原式利用平方差公式，单项式乘以多项式法则计算，去括号合并得到最简结果，把x的值代入计算即可求出值．【解答】解：原式=4x2﹣25+2x2+2x﹣6x2+15x=17x﹣25，当x=2时，原式=34﹣25=9．【点评】此题考查了整式的混合运算﹣化简求值，熟练掌握运算法则是解本题的关键．21．定义新运算：对于任意实数a，b，都有a⊕b=a（a﹣b）+1，等式右边是通常的加法，减法及乘法运算．比如：2⊕5=2×（2﹣5）+1=2×（﹣3）+1=﹣6+1=﹣5（1）求3⊕（﹣2）的值；（2）若3⊕x的值小于16，求x的取值范围，并在数轴上表示出来．【考点】解一元一次不等式；有理数的混合运算；在数轴上表示不等式的解集．【专题】新定义．【分析】（1）根据题意得出有理数混合运算的式子，再求出其值即可；（2）先得出有理数混合运算的式子，再根据3⊕x的值小于16求出x的取值范围，并在数轴上表示出来即可．【解答】解：（1）∵a⊕b=a（a﹣b）+1，∴3⊕（﹣2）=3（3+2）+1=3×5+1=16；（2）∵a⊕b=a（a﹣b）+1，∴3⊕x=3（3+x）+1=10﹣3x．∵3⊕x的值小于16，∴10﹣3x＜16，解得x＞﹣2．在数轴上表示为：．【点评】本题考查的是解一元一次不等式，熟知不等式的基本性质是解答此题的关键．六、（本题满分12分）22．如图所示，某计算装置有一数据的入口A和一运算结果的出口B．下表是小刚输入一些数后所得的结果：A 0 1 4 9 16 25 36B ﹣2 ﹣1 0 1 2 3 4（1）若输出的数是5，则小刚输入的数是多少？（2）若小刚输入的数是225，则输出的结果是多少？（3）若小刚输入的数是n（n≥10），你能用含n的式子表示输出的结果吗？试一试．【考点】规律型：数字的变化类．【专题】图表型．【分析】（1）根据表格发现规律：A=（B+2）2；（2）根据表格发现规律：B=﹣2，根据这一规律进行计算；（2）根据表格中的规律进行表示．【解答】解：有表中数据可发现：有输入的A的值可发现输入的数字为n2，输出的B的值为n﹣2．（1）输出的数是5，则小刚输入的数是（5+2）2=49；（2）输入的数是225，则输出的结果是﹣2=15﹣2=13；（3）输入的数是n（n≥10），则输出结果为：﹣2．【点评】此题考查了数字的规律问题，能够从表格中发现规律．七、（本题满分12分）23．瑶海教育局计划在3月12日植树节当天安排A，B两校部分学生到郊区公园参加植树活动．已知A校区的每位学生往返车费是6元，B校每位学生的往返车费是10元，要求两所学校均要有学生参加，且A校参加活动的学生比B校参加活动的学生少4人，本次活动的往返车费总和不超过210元．求A，B两校最多各有多少学生参加？【考点】一元一次不等式的应用．【分析】设A校有x名学生参加，B校有（x+4）名学生参加，根据往返车费=单人费用×人数，可列出关于x的一元一次不等式，解不等式可得出x的取值范围，从而得出结论．【解答】解：设A校有x名学生参加，B校有（x+4）名学生参加，依题意得6x+10（x+4）≤210，解得：x≤10．∵x为整数，∴x最多为10，x+4=10+4=14．答：A校最多有10名学生参加，B校最多有14名学生参加．【点评】本题考查了一元一次不等式的应用，解题的关键是根据数量关系列出一元一次不等式．本题属于基础题，难度不大，解决该题型题目时，根据数量关系列出一元一次不等式（或不等式组）是关键．八、（本题满分14分）24．南山植物园中现有A、B两个园区，已知A园区为长方形，长为（x+y）米，宽为（x ﹣y）米；B园区为正方形，边长为（x+3y）米．（1）请用代数式表示A、B两园区的面积之和并化简；（2）现根据实际需要对A园区进行整改，长增加（11x﹣y）米，宽减少（x﹣2y）米，整改后A区的长比宽多350米，且整改后两园区的周长之和为980米．①求x、y的值；②若A园区全部种植C种花，B园区全部种植D种花，且C、D两种花投入的费用与吸引游客的收益如表：C D投入（元/平方米）12 16收益（元/平方米）18 26求整改后A、B两园区旅游的净收益之和．（净收益=收益﹣投入）【考点】整式的混合运算．【专题】应用题．【分析】（1）根据长方形的面积公式和正方形的面积公式分别计算A、B两园区的面积，再相加即可求解；（2）①根据等量关系：整改后A区的长比宽多350米；整改后两园区的周长之和为980米；列出方程组求出x，y的值；②代入数值得到整改后A、B两园区的面积之和，再根据净收益=收益﹣投入，列式计算即可求解．【解答】解：（1）（x+y）（x﹣y）+（x+3y）（x+3y）=x2﹣y2+x2+6xy+9y2=2x2+6xy+8y2（平方米）答：A、B两园区的面积之和为（2x2+6xy）平方米；（2）（x+y）+（11x﹣y）=x+y+11x﹣y=12x（米），（x﹣y）﹣（x﹣2y）=x﹣y﹣x+2y=y（米），依题意有：，解得．12xy=12×30×10=3600（平方米），（x+3y）（x+3y）=x2+6xy+9y2=900+1800+900=3600（平方米），（18﹣12）×3600+（26﹣16）×3600=6×3600+10×3600=57600（元）．答：整改后A、B两园区旅游的净收益之和为57600元．【点评】此题考查整式的混合运算，找出问题中的已知条件和未知量及它们之间的关系是解决问题的关键．。
(完整版)新人教版七年级数学下册期中测试卷及答案(最新整理)
A.130°
B.140°
C.150°
D.160°
角的直角三角板的两个顶点放
．（1，-2）
急刹车时汽车在地面上的滑动
是同旁内角；③∠4与_______(填序号).
则点B表示的数为
RN 七年级数学 -3- (共 6页)
16. 解方程组(8分)
⎩⎨⎧=-=+152y x y x ⎩⎨⎧=-=+6
23432y x y x 17.(8分）如右图,先填空后证明.
已知: ∠1+∠2=180° 求证：a ∥b
证明：∵ ∠1=∠3（ ），
∠1+∠2=180°（ ）
∴ ∠3+∠2=180°（ ）
∴ a ∥b （ ）
请你再写出一种证明方法.
18.（10分）在平面直角坐标系中, △ABC 三个顶点的位置如图（每个小正方形的边长均为1）.
（1）请画出△ABC 沿x 轴向平移3个单位长度,再沿y 轴向上平移2
个单位
）从码头到铁路怎样走最近，画图并说明理由；）从火车站到河流怎样走最近，画图并说明理由．
页)
23.（8分）某花农培育甲种花木2株，乙种花木3株，共需成本1700元；培育甲种花木3株，乙种花木1株，共需成本1500元。
求培育甲乙两种花木每株的成本分别为多少元？
RN 七年级数学 -6- (共 6页)。
人教版2015-2016学年七年级下册期中考试数学试题含答案
2015-2016七年级下学期期中考试数学试题一．选择题（每题3分，共30分）1.下面四个图形中，∠1与∠2是对顶角的图形是（ ）12121212A B C D2.如图，若m ∥n ，∠1 = 105°，则∠2 =（ ）A ．55°B ．60°C ．65°D ．75°3．在平面直角坐标系中，点P(－3，4)到x 轴的距离为( )A ．3B ．－3C ．4D ．－4 4.下列等式正确的是（ ）34±113 C.393-=-13 5.如图，已知直线a 、b 被直线c 所截，那么∠1的同位角是（ ）若以A 点为原点建立直角坐标系，则B 点坐标为( )A ．(－3，－4)B ．(－3，4)C ．(3，－4)D ．(3，4)7.若一个数的平方根与它的立方根完全相同，则这个数是（ ）A ．0B ．1C ．－1D ．±1, 08.张强在某旅游景点的动物园的大门口看到这个动物园的平面示意图(如图)，若以大门为坐标原点，其他四个景点大致用坐标表示肯定错误的是( )A．熊猫馆(1，4) B．猴山(6，0)C．百鸟园(5，－3) D．驼峰(3，－2)9.在同一平面内，下列说法：①过两点有且只有一条直线；②两条不相同的直线相交有且只有一个公共点；③经过直线外一点有且只有一条直线与已知直线垂直；④经过直线外一10.任何一个正整数n都可以进行这样的分解：n=s×t（s，t是正整数，且s≤t），如果p×q在n的所有这种分解中两因数之差的绝对值最小，我们就称p×q是n的最佳分解，并规定：F（n）=．例如18可分解成1×18，2×9，3×6这三种，这时就有F（18）==．给出下列关于F（n）的说法：（1）F（2）=；（2）F（12）=；（3）F（27）=3；（4）若n是一个完全平方数（正整数的平方），则F（n）=1．其中正确说法的个数是（）A．1个B．2个C．3个D．4个二．填空题（每题3分，共18分）11..如图，已知a∥b，∠1=130°，∠2=90°，则∠3=12.如图，O是直线AB上一点，∠COB=30°，则∠1=°．13.若两个连续的整数,a b满足a，则1ab的值为．14.若32-x +y x +2＝0，则4x －2y 的值是15.把命题”对顶角相等”写成“如果……那么……”的形式.___________________________________________________________________________ 16.在直角坐标系中，我们把横、纵坐标都是整数的点叫做整点．且规定，正方形的内部不包含边界上的点．观察如图所示的中心在原点、一边平行于x 轴的正方形：边长为1的正方形内部有1个整点，边长为2的正方形内部有1个整点，边长为3的正方形内部有9个整点，…，则边长为8的正方形内部的整点的个数为________．三．解答题17．将下列各数的序号填在相应的集合里.（6分）①38，②π，③3.1415926，④－0.456，⑤3.030030003……（每相邻两个3之间0的个数逐渐多1），⑥0，⑦115，⑧－39，⑨2)7(-，⑩1.0 有理数集合：{ }； 无理数集合：{ }； 正实数集合：{ }；18.计算题：（每小题4分，共8分）（1）2 （2）、19、已知：如图，AB⊥C D ，垂足为O ，EF 经过点O ，∠1=25°，求∠2，∠3的度数．（7分）b20. （8分）已知c b a 、、位置如图所示，试化简 ： ()22a b c b c b a -+-+-+21.（8分） 已知：如图，∠A=∠D ，∠B=∠C ，那么∠1与∠2互补吗？为什么？22. （8分）已知x ，y 满足xx x y 289161622---+-=，求xy 的平方根.23.（8分）先阅读理解，再回答下列问题： 因为2112=+，且221<<，所以112+的整数部分为1；因为6222=+，且362<<，所以222+的整数部分为2；因为12332=+，且4123<<，所以332+的整数部分为3；以此类推，我们会发现n n n (2+为正整数）的整数部分为＿＿＿＿＿＿，请说明理由。
南京市XX学校2015-2016年七年级下期中数学试卷含答案解析
2015-2016学年江苏省南京XX学校七年级（下）期中数学试卷一、选择题（每题2分，共20分）1．下列各计算中，正确的是（）A．a8÷a2=a4B．x3+x3=x6C．（﹣m）2•（﹣m3）=﹣m5D．（a3）3=a62．1纳米=0.000 000 001米，则2.5纳米应表示为（）米．A．2.5×10﹣8B．2.5×10﹣9C．2.5×10﹣10D．2.5×1093．下列各式从左到右的变形中，属于因式分解的是（）A．mx+nx+k=（m+n）x+k B．14x2y3=2x2•7y3C．（a+b）（a﹣b）=a2﹣b2D．4x2﹣12xy+9y2=（2x﹣3y）24．下列各式能用平方差公式计算的是（）A．（﹣a+b）（a﹣b）B．（a﹣b）（a﹣2b）C．（x+1）（x﹣1）D．（﹣m﹣n）（m+n）5．如图，给出下列条件：①∠1=∠2；②∠3=∠4；③AD∥BE，且∠D=∠B；④AD∥BE，且∠DCB=∠BAD；其中能推出AB∥DC的条件为（）A．①②B．②④C．②③D．②③④6．如图，若∠DBC=∠D，BD平分∠ABC，∠ABC=50°，则∠BCD的大小为（）A．50°B．100°C．130° D．150°7．下列条件：①∠A+∠B=∠C；②∠A：∠B：∠C=3：4：5；③∠A=∠B=∠C；④∠A=∠B=2∠C；⑤∠A=∠B=∠C，其中能确定△ABC为直角三角形的条件有（）A．2个 B．3个 C．4个 D．5个8．一个等腰三角形的两边长分别为2和5，则它的周长为（）A．7 B．9 C．12 D．9或129．现有纸片：4张边长为a的正方形，3张边长为b的正方形，8张宽为a、长为b的长方形，用这15张纸片重新拼出一个长方形，那么该长方形的长为（）A．2a+3b B．2a+b C．a+3b D．无法确定10．现有7张如图1的长为a，宽为b（a＞b）的小长方形纸片，按图2的方式不重叠地放在矩形ABCD 内，未被覆盖的部分（两个矩形）用阴影表示．设左上角与右下角的阴影部分的面积的差为S，当BC 的长度变化时，按照同样的放置方式，S始终保持不变，则a，b满足（）A．a=2b B．a=3b C．a=3.5b D．a=4b二、填空题（每空1分，共18分）11．直接写出计算结果：（1）（﹣ab）10÷（﹣ab）3=；（2）﹣（﹣3xy2）3=；（3）（﹣）﹣2=；（4）（﹣0.25）2015×42016=．12．直接写出因式分解的结果：（1）6a2﹣8ab=；（2）y3﹣y=；（3）（a+b）2﹣8a﹣8b+16=；（4）x2﹣2x﹣15=．13．某种感冒病毒的直径是0.00000012米，用科学记数法表示为米．14．若一个正多边形的每一个外角都是30°，则这个正多边形的内角和等于度．15．若4x 2+kx +9是完全平方式，则k= ．16．如图，在△ABC 中，AD ⊥BC ，AE 平分∠BAC ，∠B=50°，∠C=30°，则∠DAE= °．17．已知a m =﹣4，a n =5，则a 3m ﹣n = ．18．若2×4n ×8n =221，则n 的值为 ．19．如果等腰三角形一腰上的高与另一边的夹角为34°，那么等腰三角形的顶角为 度． 20．如图，△ABC 中∠A=30°，E 是AC 边上的点，先将△ABE 沿着BE 翻折，翻折后△ABE 的AB 边交AC 于点D ，又将△BCD 沿着BD 翻折，C 点恰好落在BE 上，此时∠CDB=82°，则原三角形的∠B= 度．21．如图所示，把一个三角形纸片ABC 的三个顶角向内折叠之后（3个顶点不重合），图中∠1+∠2+∠3+∠4+∠5+∠6= °．22．已知a=2015.2016，b=2016.2016，c=2017.2016，则代数式a 2+b 2+c 2﹣ab ﹣bc ﹣ca= ．三、计算题（共17分）23．计算（1）2（x 3）2•x 3﹣（3x 3）3+（5x ）2•x 7；（2）﹣23﹣（）﹣2+[2﹣1×（）﹣3×（﹣）0]2；（3）（a +2b ）（2a ﹣b ）﹣2a （a +2b ）；（4）（2x ﹣3y ）2（2x +3y ）2．24．化简求值：（3a+b）2﹣（3a﹣b）（3a+b）﹣5b（a﹣b），其中a=1，b=﹣．四、将下列各式分解因式（共12分）25．分解因式（1）4x2﹣36；（2）﹣4m3+8m2+32m；（3）（y2﹣1）2﹣6（y2﹣1）+9；（4）a2+ac﹣bc﹣b2．五、解答题（共33分）26．如图，已知FG⊥AB，CD⊥AB，垂足分别为G、D，∠1=∠2．求证：DE∥BC．27．如图，有足够多的边长为a的小正方形（A类）、长为a，宽为b的长方形（B类）以及边长为b 的大正方形（C类），发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式．比如图②可以解释为：（a+2b）（a+b）=a2+3ab+2b2（1）若取其中的若干个（三种图形都要取到）拼成一个长方形，使其面积为3a2+5ab+2b2，在虚框中画出图形，并根据所画图形，将多项式3a2+5ab+2b2分解因式为．（2）如图③，是用B类长方形（4个）拼成的图形，其中四边形ABCD是大正方形，边长为m，里面是一个空洞，形状为小正方形，边长为n，观察图案并判断，将正确关系式的序号填写在横线上（填写序号）①m2+n2=2（a2+b2）；②a2﹣b2=mn；③m2﹣n2=4ab．28．如图，四边形ABCD的内角∠BAD、∠CDA的角平分线交于点E，∠ABC、∠BCD的角平分线交于点F．（1）若∠F=70°，则∠ABC+∠BCD=°；∠E=°；（2）探索∠E与∠F有怎样的数量关系，并说明理由；（3）给四边形ABCD添加一个条件，使得∠E=∠F，所添加的条件为．29．在数学竞赛中有时会出现大数值的运算问题．现在学习了整式的乘法可以通过用字母代替数转化成整式问题来解决．请先阅读下面的解题过程，再解答后面的问题：例：若x=2018×2015，y=2017×2016，试比较x、y的大小．解：设a=201 7，那么x=（a+1）（a﹣2）=a2﹣a﹣2，y=a（a﹣1）=a2﹣a．∵a2﹣a﹣2＜a2﹣a，∴x＜y．问题：若x=2012×2017﹣2013×2016，y=2013×2016﹣2014×2015，试比较x、y的大小．30．先阅读后解题：若m2+2m+n2﹣6n+10=0，求m和n的值．解：等式可变形为：m2+2m+1+n2﹣6n+9=0即（m+1）2+（n﹣3）2=0因为（m+1）2≥0，（n﹣3）2≥0，所以m+1=0，n﹣3=0即m=﹣1，n=3．像这样将代数式进行恒等变形，使代数式中出现完全平方式的方法叫做“配方法”．请利用配方法，解决下列问题：（1）已知x2+y2+x﹣6y+=0，求x y的值；（2）已知△ABC的三边长a、b、c都是正整数，且满足2a2+b2﹣4a﹣6b+11=0，则△ABC的周长是；（3）a2+b2+4a﹣10b+30的最小值是．31．（1）如图1，已知△ABC，过点A画一条平分三角形面积的直线；（2）如图2，已知l1∥l2，点E，F在l1上，点G，H在l2上，试说明△EGO与△FHO面积相等；（3）如图3，点M在△ABC的边上，过点M画一条平分三角形面积的直线．32．直角△ABC中，∠C=90°，点D、E分别是△ABC边AC、BC上的点，点P是一动点．令∠PDA=∠1，∠PEB=∠2，∠DPE=∠α．（1）如图1，若点P在线段AB上，且∠α=40°，则∠1+∠2=°；（2）如图2，若点P在边AB上运动，则∠α、∠1、∠2之间有何关系？猜想并说明理由；（3）如图3，若点P运动到边AB的延长线上，则∠α、∠1、∠2之间的关系为：；（4）如图4，若点P运动到△ABC形外，则∠α、∠1、∠2之间的关系为：．2015-2016学年江苏省南京XX学校七年级（下）期中数学试卷参考答案与试题解析一、选择题（每题2分，共20分）1．下列各计算中，正确的是（）A．a8÷a2=a4B．x3+x3=x6C．（﹣m）2•（﹣m3）=﹣m5D．（a3）3=a6【考点】同底数幂的除法；合并同类项；同底数幂的乘法；幂的乘方与积的乘方．【分析】根据同底数幂的除法，底数不变指数相减；合并同类项，系数相加字母和字母的指数不变；同底数幂的乘法，底数不变指数相加；幂的乘方，底数不变指数相乘；积的乘方，把每一个因式分别乘方，再把所得的幂相乘．对各选项计算后利用排除法求解．【解答】解：A、a8÷a2=a6，故本选项错误；B、x3+x3=2x3，故本选项错误；C、（﹣m）2•（﹣m3）=﹣m5，故本选项正确；D、（a3）3=a9，故本选项错误；故选C．2．1纳米=0.000 000 001米，则2.5纳米应表示为（）米．A．2.5×10﹣8B．2.5×10﹣9C．2.5×10﹣10D．2.5×109【考点】科学记数法—表示较小的数．【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10﹣n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．【解答】解：2.5纳米=2.5×10﹣9米，故选：B．3．下列各式从左到右的变形中，属于因式分解的是（）A．mx+nx+k=（m+n）x+k B．14x2y3=2x2•7y3C．（a+b）（a﹣b）=a2﹣b2D．4x2﹣12xy+9y2=（2x﹣3y）2【考点】因式分解的意义．【分析】根据因式分解的定义判断求解．【解答】解：因为把一个多项式化为几个最简整式的积的形式，这种变形叫做把这个多项式因式分解．故A、C错误；B、左边不是多项式，也不符合定义，故错误；D、按照完全平方公式分解因式，正确．故选D．4．下列各式能用平方差公式计算的是（）A．（﹣a+b）（a﹣b）B．（a﹣b）（a﹣2b）C．（x+1）（x﹣1）D．（﹣m﹣n）（m+n）【考点】平方差公式．【分析】根据各个选项中的式子可以变形，然后看哪个式子符合平方差公式，即可解答本题．【解答】解：∵（﹣a+b）（a﹣b）=﹣（a﹣b）（a﹣b），故选项A不符合题意，（a﹣b）（a﹣2b）不能用平方差公式计算，故选项B不符合题意，（x+1）（x﹣1）=x2﹣1，故选项C符合题意，（﹣m﹣n）（m+n）=﹣（m+n）（m+n），故选项D不符合题意，故选C．5．如图，给出下列条件：①∠1=∠2；②∠3=∠4；③AD∥BE，且∠D=∠B；④AD∥BE，且∠DCB=∠BAD；其中能推出AB∥DC的条件为（）A．①②B．②④C．②③D．②③④【考点】平行线的判定与性质．【分析】根据平行线的判定条件，逐一判断，排除错误答案．【解答】解：①∵∠1=∠2，∴AD∥BC，故此选项错误；②∵∠3=∠4，∴AB∥DC，（内错角相等，两直线平行），故此选项正确；③∵AD∥BC，∴∠B+∠BAD=180°，∵∠D=∠B，∴∠D+∠BAD=180°，由同旁内角互补，两直线平行可得AB∥DC，故此选项正确；④∵AD∥BC，∴∠B+∠BAD=180°，∵∠BAD=∠BCD，∴∠B+∠BCD=180°，由同旁内角互补，两直线平行可得AB∥DC，故此选项正确；故能推出AB∥DC的条件为：②③④．故选D．6．如图，若∠DBC=∠D，BD平分∠ABC，∠ABC=50°，则∠BCD的大小为（）A．50°B．100°C．130° D．150°【考点】三角形内角和定理；角平分线的定义．【分析】根据角平分线定义求得∠DBC的度数，再根据三角形的内角和定理即可求解．【解答】解：∵BD平分∠ABC，∠ABC=50°，∴∠DBC=∠ABC=25°．又∠DBC=∠D，∴∠BCD=180°﹣25°×2=130°．故选C．7．下列条件：①∠A+∠B=∠C；②∠A：∠B：∠C=3：4：5；③∠A=∠B=∠C；④∠A=∠B=2∠C；⑤∠A=∠B=∠C，其中能确定△ABC为直角三角形的条件有（）A．2个 B．3个 C．4个 D．5个【考点】三角形内角和定理．【分析】根据直角三角形的判定对各个条件进行分析，从而得到答案．【解答】解：①、∵∠A+∠B+∠C=180°，∴∠A+∠B=∠C=×180°=90°，∴△ABC是直角三角形，故①正确；②、∵∠A：∠B：∠C=3：4：5，∴∠C=×180°=75°，故不是直角三角形；故②错误③、设∠A=x，∠B=2x，∠C=3x，则x+2x+3x=180°，解得x=30°，故3x=90°，∴△ABC是直角三角形，故③正确；④∵设∠C=x，则∠A=∠B=2x，∴2x+2x+x=180°，解得x=36°，∴2x=72°，故④错误；⑤∵∠A=∠B=∠C，∴∠A+∠B+∠C=∠C+∠C+∠C=2∠C=180°，∴∠C=90°，故⑤正确．综上所述，是直角三角形的是①③⑤共3个．故选B．8．一个等腰三角形的两边长分别为2和5，则它的周长为（）A．7 B．9 C．12 D．9或12【考点】等腰三角形的性质；三角形三边关系．【分析】题目给出等腰三角形有两条边长为2和5，而没有明确腰、底分别是多少，所以要进行讨论，还要应用三角形的三边关系验证能否组成三角形．【解答】解：当腰为5时，周长=5+5+2=12；当腰长为2时，根据三角形三边关系可知此情况不成立；根据三角形三边关系可知：等腰三角形的腰长只能为5，这个三角形的周长是12．故选C．9．现有纸片：4张边长为a的正方形，3张边长为b的正方形，8张宽为a、长为b的长方形，用这15张纸片重新拼出一个长方形，那么该长方形的长为（）A．2a+3b B．2a+b C．a+3b D．无法确定【考点】多项式乘多项式．【分析】根据题意可知拼成的长方形的面积是4a2+3b2+8ab，再对此多项式因式分解，即可得出长方形的长和宽．【解答】解：根据题意可得：拼成的长方形的面积=4a2+3b2+8ab，又∵4a2+3b2+8ab=（2a+b）（2a+3b），b＜3b，∴长=2a+3b．故选A．10．现有7张如图1的长为a，宽为b（a＞b）的小长方形纸片，按图2的方式不重叠地放在矩形ABCD 内，未被覆盖的部分（两个矩形）用阴影表示．设左上角与右下角的阴影部分的面积的差为S，当BC 的长度变化时，按照同样的放置方式，S始终保持不变，则a，b满足（）A．a=2b B．a=3b C．a=3.5b D．a=4b【考点】整式的混合运算．【分析】表示出左上角与右下角部分的面积，求出之差，根据差与BC无关即可求出a与b的关系式．【解答】解：法1：左上角阴影部分的长为AE，宽为AF=3b，右下角阴影部分的长为PC，宽为a，∵AD=BC，即AE+ED=AE+a，BC=BP+PC=4b+PC，∴AE+a=4b+PC，即AE﹣PC=4b﹣a，∴阴影部分面积之差S=AE•AF﹣PC•CG=3bAE﹣aPC=3b（PC+4b﹣a）﹣aPC=（3b﹣a）PC+12b2﹣3ab，则3b﹣a=0，即a=3b．法2：既然BC是变化的，当点P与点C重合开始，然后BC向右伸展，设向右伸展长度为x，左上阴影增加的是3bx，右下阴影增加的是ax，因为S不变，∴增加的面积相等，∴3bx=ax，∴a=3b．故选：B．二、填空题（每空1分，共18分）11．直接写出计算结果：（1）（﹣ab）10÷（﹣ab）3=﹣a7b7；（2）﹣（﹣3xy2）3=27x3y6；（3）（﹣）﹣2=4；（4）（﹣0.25）2015×42016=﹣4．【考点】同底数幂的除法；幂的乘方与积的乘方；负整数指数幂．【分析】（1）根据同底数幂的除法法则以及积的乘方法则计算即可；（2）根据积的乘方法则计算即可；（3）根据负整数指数幂的意义计算即可；（4）根据同底数幂的乘法法则与积的乘方法则计算即可．【解答】解：（1）（﹣ab）10÷（﹣ab）3=（﹣ab）7=﹣a7b7；（2）﹣（﹣3xy2）3=27x3y6；（3）（﹣）﹣2=（﹣2）2=4；（4）（﹣0.25）2015×42016=（﹣0.25）2015×42015×4=（﹣0.25×4）2015×4=（﹣1）2015×4=﹣1×4=﹣4．故答案为﹣a7b7；27x3y6；4；﹣4．12．直接写出因式分解的结果：（1）6a2﹣8ab=2a（3a﹣4b）；（2）y3﹣y=y（y+1）（y﹣1）；（3）（a+b）2﹣8a﹣8b+16=（a+b﹣4）2；（4）x2﹣2x﹣15=（x﹣5）（x+3）．【考点】提公因式法与公式法的综合运用．【分析】（1）原式提取公因式即可；（2）原式提取公因式，再利用平方差公式分解即可；（3）原式变形后，利用完全平方公式分解即可；（4）原式利用十字相乘法分解即可．【解答】解：（1）原式=2a（3a﹣4b）；（2）原式=y（y2﹣1）=y（y+1）（y﹣1）；（3）原式=（a+b）2﹣8（a+b）+16=（a+b﹣4）2；（4）原式=（x﹣5）（x+3），故答案为：（1）2a（3a﹣4b）；（2）y（y+1）（y﹣1）；（3）（a+b﹣4）2；（4）（x﹣5）（x+3）13．某种感冒病毒的直径是0.00000012米，用科学记数法表示为 1.2×10﹣7米．【考点】科学记数法—表示较小的数．【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值大于10时，n是正数；当原数的绝对值小于1时，n是负数．【解答】解：0.000 000 12米=1.2×10﹣7米．故答案为：1.2×10﹣7．14．若一个正多边形的每一个外角都是30°，则这个正多边形的内角和等于1800度．【考点】多边形内角与外角．【分析】根据任何多边形的外角和都是360°，利用360除以外角的度数就可以求出外角和中外角的个数，即多边形的边数．n边形的内角和是（n﹣2）•180°，把多边形的边数代入公式，就得到多边形的内角和．【解答】解：多边形的边数：360°÷30°=12，正多边形的内角和：（12﹣2）•180°=1800°．15．若4x2+kx+9是完全平方式，则k=±12．【考点】完全平方式．【分析】利用完全平方公式的结构特征判断即可得到结果．【解答】解：∵4x2+kx+9是完全平方式，∴k=±12，解得：k=±12．故答案为：±1216．如图，在△ABC中，AD⊥BC，AE平分∠BAC，∠B=50°，∠C=30°，则∠DAE=10°．【考点】三角形内角和定理．【分析】由三角形内角和定理可求得∠BAC的度数，在Rt△ADC中，可求得∠DAC的度数，AE是角平分线，有∠EAC=∠BAC，故∠EAD=∠EAC﹣∠EAC．【解答】解：∵在△ABC中，AE是∠BAC的平分线，且∠B=50°，∠C=30°，∴∠BAE=∠EAC===50°．在△ACD中，∠ADC=90°，∠C=30°，∴∠DAC=90°﹣30°=60°，∠EAD=∠DAC﹣∠EAC=60°﹣50°=10°．故答案是：10°．17．已知a m=﹣4，a n=5，则a3m﹣n=﹣．【考点】同底数幂的除法；幂的乘方与积的乘方．【分析】直接利用同底数幂的乘除法运算法则将原式变形进而求出答案．【解答】解：∵a m=﹣4，a n=5，∴a3m﹣n=（a m）3÷a n=（﹣4）3÷5=﹣．故答案为：﹣．18．若2×4n×8n=221，则n的值为4．【考点】同底数幂的乘法．【分析】直接利用同底数幂的乘法运算法则将原式变形求出答案．【解答】解：∵2×4n×8n=221，∴2×22n×23n=221，∴1+2n+3n=21，解得：n=4．故答案为：4．19．如果等腰三角形一腰上的高与另一边的夹角为34°，那么等腰三角形的顶角为56或68或124度．【考点】等腰三角形的性质．【分析】作出图形，分高与腰长的夹角和腰长与底边的夹角根据直角三角形两锐角互余和等腰三角形两底角相等解答．【解答】解：如图1，∵腰上的高与另一边的夹角为34°，∴∠ABD=34°，∴∠A=90°﹣∠ABD=90°﹣34°=56°，若∠CBD=34°，则∠C=90°﹣34°=56°，∴顶角∠A=180°﹣2×56°=68°；如图2，∠ABD=34°，顶角∠BAC=34°+90°=124°．综上所述，等腰三角形的顶角为56或68或124．故答案为：56或68或124．20．如图，△ABC中∠A=30°，E是AC边上的点，先将△ABE沿着BE翻折，翻折后△ABE的AB边交AC于点D，又将△BCD沿着BD翻折，C点恰好落在BE上，此时∠CDB=82°，则原三角形的∠B=78度．【考点】翻折变换（折叠问题）．【分析】在图①的△ABC中，根据三角形内角和定理，可求得∠B+∠C=150°；结合折叠的性质和图②③可知：∠B=3∠CBD，即可在△CBD中，得到另一个关于∠B、∠C度数的等量关系式，联立两式即可求得∠B的度数．【解答】解：在△ABC中，∠A=30°，则∠B+∠C=150°…①；根据折叠的性质知：∠B=3∠CBD，∠BCD=∠C；在△CBD中，则有：∠CBD+∠BCD=180°﹣82°，即：∠B+∠C=98°…②；①﹣②，得：∠B=52°，解得∠B=78°．21．如图所示，把一个三角形纸片ABC的三个顶角向内折叠之后（3个顶点不重合），图中∠1+∠2+∠3+∠4+∠5+∠6=360°．【考点】多边形内角与外角；三角形内角和定理；三角形的外角性质．【分析】由折叠可知∠1+∠2+∠3+∠4+∠5+∠6等于六边形的内角和减去（∠B'FG+∠B'GF）以及（∠C'HI+∠C'IH）和（∠A'DE+∠A'ED），再利用三角形的内角和定理即可求解．【解答】解：由题意知，∠1+∠2+∠3+∠4+∠5+∠6=720°﹣（∠B'FG+∠B'GF）﹣（∠C'HI+∠C'IH）﹣（∠A'DE+∠A'ED）=720°﹣﹣==180°+（∠B'+∠C'+∠A'）又∵∵∠B=∠B'，∠C=∠C'，∠A=∠A'，∠A+∠B+∠C=180°，∴∠1+∠2+∠3+∠4+∠5+∠6=360°．故答案为：360．22．已知a=2015.2016，b=2016.2016，c=2017.2016，则代数式a2+b2+c2﹣ab﹣bc﹣ca=5．【考点】因式分解的应用．【分析】将a2+b2+c2﹣ab﹣bc﹣ca变形为（2a2+2b2+2c2﹣2ab﹣2bc﹣2ca），即得[（a﹣b）2+（a ﹣c）2+（b﹣c）2]，代入求值即可．【解答】解：a2+b2+c2﹣ab﹣bc﹣ca=（2a2+2b2+2c2﹣2ab﹣2bc﹣2ca）= [（a2﹣2ab+b2）+（a2﹣2ac+c2）+（b2﹣2bc+c2）]= [（a﹣b）2+（a﹣c）2+（b﹣c）2]∵a=2015.2016，b=2016.2016，c=2017.2016，∴原式=×[12+42+12]=×10=5．故答案为：5．三、计算题（共17分）23．计算（1）2（x3）2•x3﹣（3x3）3+（5x）2•x7；（2）﹣23﹣（）﹣2+[2﹣1×（）﹣3×（﹣）0]2；（3）（a+2b）（2a﹣b）﹣2a（a+2b）；（4）（2x﹣3y）2（2x+3y）2．【考点】整式的混合运算；负整数指数幂．【分析】（1）根据积的乘方以及同底数幂的乘法即可求出答案．（2）根据实数运算法则即可求出答案（3）根据多项式乘以多项式法则以及单项式乘以多项式法则即可求出答案．（4）根据平方差公式以及完全平方公式即可求出答案．【解答】解：（1）原式=2x6•x3﹣27x9+25x2•x7=2x9﹣27x9+25x9=0（2）原式=﹣8﹣4+（×23×1）2=﹣12+16=4（3）原式=2a2﹣ab+4ab﹣2b2﹣2a2﹣4ab=﹣ab﹣2b2（4）原式=[（2x+3y）（2x﹣3y）]2=（4x2﹣9y2）2=16x4﹣72x2y2+81y424．化简求值：（3a+b）2﹣（3a﹣b）（3a+b）﹣5b（a﹣b），其中a=1，b=﹣．【考点】整式的混合运算—化简求值．【分析】先算乘法，再合并同类项，最后代入求出即可．【解答】解：（3a+b）2﹣（3a﹣b）（3a+b）﹣5b（a﹣b）=9a2+6ab+b2﹣9a2+b2﹣5ab+5b2=ab+7b2，当a=1=，b=﹣时，原式=×（﹣）+7×（﹣）2=．四、将下列各式分解因式（共12分）25．分解因式（1）4x2﹣36；（2）﹣4m3+8m2+32m；（3）（y2﹣1）2﹣6（y2﹣1）+9；（4）a2+ac﹣bc﹣b2．【考点】因式分解﹣分组分解法；提公因式法与公式法的综合运用．【分析】（1）先提取公因式4，再利用平方差公式分解；（2）先提取公因式﹣4m，再利用十字相乘法分解可得；（3）先将y2﹣1看做整体利用完全平方公式分解，再利用平方差公式分解可得；（4）将a2、﹣b2，ac与﹣bc结合前者利用平方差分解、后者提取公因式c，再整体提取公因式a﹣b 即可得．【解答】解：（1）原式=4（x2﹣9）=4（x+3）（x﹣3）；（2）原式=﹣4m（m2﹣2m﹣8）=﹣4m（m+2）（m﹣4）；（3）原式=（y2﹣1﹣3）2=[（y+2）（y﹣2）]2=（y+2）2（y﹣2）2；（4）原式=（a+b）（a﹣b）+c（a﹣b）=（a﹣b）（a+b+c）．五、解答题（共33分）26．如图，已知FG⊥AB，CD⊥AB，垂足分别为G、D，∠1=∠2．求证：DE∥BC．【考点】平行线的判定；垂线．【分析】根据CD⊥AB，FG⊥AB，可判定CD∥FG，利用平行线的性质可知∠2=∠BCD，已知∠1=∠2，等量代换得∠1=∠BCD，故可证DE∥BC．【解答】证明：∵CD⊥AB，FG⊥AB，∴CD∥FG，∴∠2=∠BCD，又∠1=∠2，∴∠1=∠BCD，∴DE∥BC．27．如图，有足够多的边长为a的小正方形（A类）、长为a，宽为b的长方形（B类）以及边长为b 的大正方形（C类），发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式．比如图②可以解释为：（a+2b）（a+b）=a2+3ab+2b2（1）若取其中的若干个（三种图形都要取到）拼成一个长方形，使其面积为3a2+5ab+2b2，在虚框中画出图形，并根据所画图形，将多项式3a2+5ab+2b2分解因式为（3a+2b）（a+b）．（2）如图③，是用B类长方形（4个）拼成的图形，其中四边形ABCD是大正方形，边长为m，里面是一个空洞，形状为小正方形，边长为n，观察图案并判断，将正确关系式的序号填写在横线上①③（填写序号）①m2+n2=2（a2+b2）；②a2﹣b2=mn；③m2﹣n2=4ab．【考点】因式分解的应用；多项式乘多项式．【分析】（1）画出图形，结合图象和面积公式得出即可；（2）根据题意得出a+b=m，m2﹣n2=4ab，根据平方差公式和完全平方公式判断即可．【解答】解：（1）画图如下：3a2+5ab+2b2=（3a+2b）（a+b）；（2）正确关系式的序号填写在横线上：①③．28．如图，四边形ABCD的内角∠BAD、∠CDA的角平分线交于点E，∠ABC、∠BCD的角平分线交于点F．（1）若∠F=70°，则∠ABC+∠BCD=220°；∠E=110°；（2）探索∠E与∠F有怎样的数量关系，并说明理由；（3）给四边形ABCD添加一个条件，使得∠E=∠F，所添加的条件为AB∥CD．【考点】多边形内角与外角．【分析】（1）先根据三角形内角和定理求出∠FBC+∠BCF=180°﹣∠F=110°，再由角平分线定义得出∠ABC=2∠FBC，∠BCD=2∠BCF，那么∠ABC+∠BCD=2∠FBC+2∠BCF=2（∠FBC+∠BCF）=220°；由四边形ABCD的内角和为360°，得出∠BAD+∠CDA=360°﹣（∠ABC+∠BCD）=140°．由角平分线定义得出∠DAE=∠BAD，∠ADE=∠CDA，那么∠DAE+∠ADE=∠BAD+∠CDA=（∠BAD+∠CDA）=70°，然后根据三角形内角和定理求出∠E=180°﹣（∠DAE+∠ADE）=110°；（2）由四边形ABCD的内角和为360°得到∠BAD+∠CDA+∠ABC+∠BCD=360°，由角平分线定义得出∠DAE+∠ADE+∠FBC+∠BCF=180°，又根据三角形内角和定理有∠DAE+∠ADE+∠E=180°，∠FBC+∠BCF+∠F=180°，那么∠DAE+∠ADE+∠E+∠FBC+∠BCF+∠F=360°，于是∠E+∠F=360°﹣（∠DAE+∠ADE+∠FBC+∠BCF）=180°；（3）由（2）可知∠E+∠F=180°，如果∠E=∠F，那么可以求出∠E=∠F=90°，根据三角形内角和定理求出∠DAE+∠ADE=90°，再利用角平分线定义得到∠BAD+∠CDA=180°，于是AB∥CD．【解答】解：（1）∵∠F=70，∴∠FBC+∠BCF=180°﹣∠F=110°．∵∠ABC、∠BCD的角平分线交于点F，∴∠ABC=2∠FBC，∠BCD=2∠BCF，∴∠ABC+∠BCD=2∠FBC+2∠BCF=2（∠FBC+∠BCF）=220°；∵四边形ABCD的内角和为360°，∴∠BAD+∠CDA=360°﹣（∠ABC+∠BCD）=140°．∵四边形ABCD的内角∠BAD、∠CDA的角平分线交于点E，∴∠DAE=∠BAD，∠ADE=∠CDA，∴∠DAE+∠ADE=∠BAD+∠CDA=（∠BAD+∠CDA）=70°，∴∠E=180°﹣（∠DAE+∠ADE）=110°；（2）∠E+∠F=180°．理由如下：∵∠BAD+∠CDA+∠ABC+∠BCD=360°，∵四边形ABCD的内角∠BAD、∠CDA的角平分线交于点E，∠ABC、∠BCD的角平分线交于点F，∴∠DAE+∠ADE+∠FBC+∠BCF=180°，∵∠DAE+∠ADE+∠E=180°，∠FBC+∠BCF+∠F=180°，∴∠DAE+∠ADE+∠E+∠FBC+∠BCF+∠F=360°，∴∠E+∠F=360°﹣（∠DAE+∠ADE+∠FBC+∠BCF）=180°；（3）AB∥CD．故答案为220°；110°；AB∥CD．29．在数学竞赛中有时会出现大数值的运算问题．现在学习了整式的乘法可以通过用字母代替数转化成整式问题来解决．请先阅读下面的解题过程，再解答后面的问题：例：若x=2018×2015，y=2017×2016，试比较x、y的大小．解：设a=201 7，那么x=（a+1）（a﹣2）=a2﹣a﹣2，y=a（a﹣1）=a2﹣a．∵a2﹣a﹣2＜a2﹣a，∴x＜y．问题：若x=2012×2017﹣2013×2016，y=2013×2016﹣2014×2015，试比较x、y的大小．【考点】整式的混合运算；有理数大小比较．【分析】设a=2014，将x与y变形计算，比较即可．【解答】解：设a=2014，那么x=（a﹣2）×（a+3）﹣（a﹣1）（a+2）=a2+a﹣6﹣a2﹣a+2=﹣4，y=（a﹣1）（a+2）﹣a（a+1）=a2+a﹣2﹣a2﹣a=﹣2，∵﹣4＜﹣2，∴x＜y．30．先阅读后解题：若m2+2m+n2﹣6n+10=0，求m和n的值．解：等式可变形为：m2+2m+1+n2﹣6n+9=0即（m+1）2+（n﹣3）2=0因为（m+1）2≥0，（n﹣3）2≥0，所以m+1=0，n﹣3=0即m=﹣1，n=3．像这样将代数式进行恒等变形，使代数式中出现完全平方式的方法叫做“配方法”．请利用配方法，解决下列问题：（1）已知x2+y2+x﹣6y+=0，求x y的值；（2）已知△ABC的三边长a、b、c都是正整数，且满足2a2+b2﹣4a﹣6b+11=0，则△ABC的周长是7；（3）a2+b2+4a﹣10b+30的最小值是1．【考点】因式分解的应用；非负数的性质：偶次方；三角形三边关系．【分析】（1）根据配方法，可得x，y的值，根据乘方的意义，可得答案；（2）根据配方法，可得a，b的值，在根据三角形三边的关系，可得c的值，根据三角形的周长，可得答案；（3）根据配方法，可得非负数的和，根据非负数的性质，可得答案．【解答】解：（1）等式可变形为：x2+x++y2﹣6y+9=0，即（x+）2+（y﹣3）2=0∵（x+）2≥0，（y﹣3）2≥0，∴x+=0，y﹣3=0，即x=﹣，y=3．x y =（﹣）3=﹣；（2）等式可变形为（a ）2﹣4a +（）2+b 2﹣6b +9=0，即（a ﹣）2+（b ﹣3）2=0，∵（a ﹣）2≥0，（b ﹣3）2≥0，∴a ﹣=0，b ﹣3=0，即a=1，b=3，由三角形三边的关系，得2＜c ＜4，又∵a 、b 、c 都是正整数，∴c=3，△ABC 的周长是3+3+1=7；（3）原式=a 2﹣4a +4+b 2﹣10b +25+1=（a ﹣2）2+（b ﹣5）2+1∵（a ﹣2）2≥0，（b ﹣5）2≥0，∴a 2+b 2+4a ﹣10b +30的最小值是1，故答案为：7，1．31．（1）如图1，已知△ABC ，过点A 画一条平分三角形面积的直线；（2）如图2，已知l 1∥l 2，点E ，F 在l 1上，点G ，H 在l 2上，试说明△EGO 与△FHO 面积相等； （3）如图3，点M 在△ABC 的边上，过点M 画一条平分三角形面积的直线．【考点】三角形的面积．【分析】（1）根据三角形的面积公式，只需过点A 和BC 的中点画直线即可；（2）结合平行线间的距离相等和三角形的面积公式即可证明；（3）结合（1）和（2）的结论进行求作．【解答】（1）解：取BC的中点D，过A、D画直线，则直线AD为所求；（2）证明：∵l1∥l2，∴点E，F到l2之间的距离都相等，设为h．∴S△EGH=GH•h，S△FGH=GH•h，∴S△EGH=S△FGH，∴S△EGH ﹣S△GOH=S△FGH﹣S△GOH，∴△EGO的面积等于△FHO的面积；（3）解：取BC的中点D，连接MD，过点A作AN∥MD交BC于点N，过M、N画直线，则直线MN 为所求．32．直角△ABC中，∠C=90°，点D、E分别是△ABC边AC、BC上的点，点P是一动点．令∠PDA=∠1，∠PEB=∠2，∠DPE=∠α．（1）如图1，若点P在线段AB上，且∠α=40°，则∠1+∠2=130°；（2）如图2，若点P在边AB上运动，则∠α、∠1、∠2之间有何关系？猜想并说明理由；（3）如图3，若点P运动到边AB的延长线上，则∠α、∠1、∠2之间的关系为：∠1﹣∠2﹣∠α=90°；（4）如图4，若点P运动到△ABC形外，则∠α、∠1、∠2之间的关系为：∠1+∠2﹣∠α=270°．【考点】三角形综合题．【分析】（1）如图1中，连接PC．由∠1=∠3+∠DPC，∠2=∠4+∠CPE，推出∠1+∠2=（∠DPC+∠CPE）+（∠3+∠4）=∠α+90°=130°；（2）结论：∠1+∠2=90°+∠α．连接PC．由∠1=∠3+∠DPC，∠2=∠4+∠CPE，推出∠1+∠2=（∠DPC+∠CPE）+（∠3+∠4）=90°+∠α；（3）如图3中，结论：∠1﹣∠2﹣∠α=90°．由∠1=∠3+∠C，∠3=∠α+∠2，推出∠1=∠α+∠2+90°，即∠1﹣∠2﹣∠α=90°；（4）如图4中，结论：∠1+∠2﹣∠α=270°．由∠1=∠α+∠3，∠3=∠C+∠PEC，∠PEC=180°﹣∠2，推出∠1=∠α+∠C+180°﹣∠2，推出∠1=∠α+90°+180°﹣∠2，即∠1+∠2﹣∠α=270°；【解答】解：（1）如图1中，连接PC．∵∠1=∠3+∠DPC，∠2=∠4+∠CPE，∴∠1+∠2=（∠DPC+∠CPE）+（∠3+∠4）=∠α+90°=130°，故答案为130；（2）如图2中，结论：∠1+∠2=90°+∠α．理由如下：连接PC．∵∠1=∠3+∠DPC，∠2=∠4+∠CPE，∴∠1+∠2=（∠DPC+∠CPE）+（∠3+∠4）=90°+∠α；（3）如图3中，结论：∠1﹣∠2﹣∠α=90°．理由：∵∠1=∠3+∠C，∠3=∠α+∠2，∴∠1=∠α+∠2+90°，∴∠1﹣∠2﹣∠α=90°．故答案为∠1﹣∠2﹣∠α=90°；（4）如图4中，结论：∠1+∠2﹣∠α=270°．理由：∵∠1=∠α+∠3，∠3=∠C+∠PEC，∠PEC=180°﹣∠2，∴∠1=∠α+∠C+180°﹣∠2，∴∠1=∠α+90°+180°﹣∠2，∴∠1+∠2﹣∠α=270°．故答案为∠1+∠2﹣∠α=270°；2017年5月11日。
2015-2016学年七年级下学期期中联考数学试题
第 1 页 共 6 页2015-2016学年度第二学期七年级期中联考试卷数 学时间：100分钟 满分： 120分题号 一 二 19 20 21 22 23 总分 得分一、选择题：(每小题3分，共30分) 1、327-的绝对值是……………………………………………………………【 】A.3-B.3C.13 D.31- 2、下列运算正确的是 …………………………………………………………… 【 】A ．325a b ab +=B ．325a a a ⋅= C.824a a a ÷= D ．()32626aa -=-3、已知:45781,27,9a b c ===,则,,a b c 的大小关系是…………………………【 】Ａ．a b c >> Ｂ．a c b >> Ｃ．a b c << Ｄ．b c a >> 4、16的平方根是………………………………………………………………【 】A ．4±B ．2±C ．2-D ．25、已知空气的单位体积质量为31.2410-⨯克/厘米3，31.2410-⨯用小数表示为………………………………………………………………………………… 【 】A ．0.000124B ．0.0124C ．0.00124-D ．0.001246、若23x=，45y=，则yx 22-的值为………………………………………… 【 】A ．35 B ．2- C ．355D ．65 7、加上下列单项式后，仍不能使241x +成为完全平方式的是……………… 【 】第 2 页 共 6 页A ．44x B ．4x C ．x 4- D ．2x8、长方形的面积为a ab a 2642+-，若它的一边长为2a ，则它的周长为… 【 】A ．b a 34-B ．b a 68-C ．134+-b aD ．268+-b a 9、要使代数式312m -的值在1-和2之间，则m 可以取的整数有……………… 【 】A ．1个B ．2个C ．3个D ．4个10、如图所示，数轴上表示3、13的对应点分别为C 、B ，点C 是A B 的中点， 则点A 表示的数是………… ……………………………………………………【 】A ．13-B ．313-C ．613-D ．133- 二、填空题：（每小题4分，共32分） 11、若2 1.414≈，则200≈ (保留4个有效数字)12、若x+y=3,x-y=1,则x 2+y 2= xy= .13、已知被除式是3232x x +-，商式是x ，余式是2-，则除式是 14、当x 时，代数式324x-的值不小于1 15、若()211x x x y ---=+,则x y -的值是16、若某数的两个平方根分别是23a +和15a -，则这个数是 17、若()()235x x x Ax B +-=++，则A B -=18、已知不等式组211x m n x m +>+⎧⎨-<-⎩的解集为12x -<<，则()2012m n +=19.x 2-px+16是完全平方式，则p= .三、解答题：（共58分）20、（6分）计算： ()()21223216---+---3 B C A 13第 3 页 共 6 页21、（8分）计算： ()[]()223221346ay a y a y a -÷+-⋅22、（10分）解不等式组()315412123x x x x +>+⎧⎪⎨--≤⎪⎩ ，并把解集在数轴上表示出来．23、（10分）先化简，再求值：()()()()212152323-----+x x x x x ，其中31-=x①②第 4 页 共 6 页24、（10分）若()()245314x x +-<++的最小整数解是方程153x mx -=的解，求代数式2211m m -+的的平方根的值。
河南省周口市太康县七年级数学下学期期中试题(含解析) 新人教版-新人教版初中七年级全册数学试题
某某省某某市太康县2015-2016学年七年级数学下学期期中试题一、选择题下列各小题均有四个答案其中只有一个是正确的，将正确答案的代号字母填入题后括号内1．运用等式性质进行的变形，不正确的是（）A．如果a=b，那么a﹣c=b﹣cB．如果a=b，那么a+c=b+cC．如果a=b，那么D．如果a=b，那么ac=bc2．若代数式4x﹣5与的值相等，则x的值是（）A．1B．C．D．23．若单项式2x2y a+b与﹣x a﹣b y4是同类项，则a，b的值分别为（）A．a=3，b=1B．a=﹣3，b=1C．a=3，b=﹣1D．a=﹣3，b=﹣14．不等式组的解集在数轴上可表示为（）A．B．C．D．5．一件夹克衫先按成本提高50%标价，再以8折（标价的80%）出售，结果获利28元，若设这件夹克衫的成本是x元，根据题意，可得到的方程是（）A．（1+50%）x×80%=x﹣28B．（1+50%）x×80%=x+28C．（1+50%x）×80%=x﹣28D．（1+50%x）×80%=x+286．为了开展阳光体育活动，某班计划购买毽子和跳绳两种体育用品，共花费35元，毽子单价3元，跳绳单价5元，购买方案有（）A．1种B．2种C．3种D．4种7．已知，且x﹣y＜0，则m的取值X围为（）A．m B．m C．m D．m8．如图，过△ABC的顶点A，作BC边上的高，以下作法正确的是（）A．B．C．D．二、填空题9．已知关于x的方程2x﹣3a﹣9=0的解是x=﹣3，则a的值为．10．已知方程2x+y﹣5=0用含y的代数式表示x为：x=．11．一元一次不等式3x﹣2＜0的解集为．12．在△ABC中，若∠A=80°，∠B=∠C，则∠C=度．13．方程组的解是．14．不等式组的整数解是．15．《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架．它的代数成就主要包括开方术、正负术和方程术．其中，方程术是《九章算术》最高的数学成就．《九章算术》中记载：“今有牛五、羊二，直金十两；牛二、羊五，直金八两．问：牛、羊各直金几何？”译文：“假设有5头牛、2只羊，值金10两；2头牛、5只羊，值金8两．问：每头牛、每只羊各值金多少两？”设每头牛值金x两，每只羊值金y两，可列方程组为．三、解答题（本大题共8个小题，满分65分）16．解下列方程（1）3（x﹣4）=12（2）．17．用指定的方法解下列方程组：（1）（代入法）（2）（加减法）18．解下列不等式或不等式组（1）2x﹣3≤5（x﹣3）（2）．19．若关于x，y的二元一次方程组的解也是二元一次方程2x+3y=6的解，求k的值．20．某商场投入13800元资金购进甲、乙两种矿泉水共500箱，矿泉水的成本价和销售价如表所示：类别/单价成本价销售价（元/箱）甲24 36乙33 48（1）该商场购进甲、乙两种矿泉水各多少箱？（2）全部售完500箱矿泉水，该商场共获得利润多少元？21．为了举行班级晚会，孔明准备去商店购买20个乒乓球做道具，并买一些乒乓球拍做奖品．已知乒乓球每个1.5元，球拍每个22元．如果购买金额不超过200元，且买的球拍尽可能多，那么孔明应该买多少个球拍？22．如图，BD是∠ABC的平分线，DE∥CB，交AB于点E，∠A=45°，∠BDC=60°，求△BDE各内角的度数．23．如图，O是△ABC内任意一点，连接OB、OC．（1）求证：∠B OC＞∠A；（2）比较AB+AC与OB+OC的大小，并说明理由．2015-2016学年某某省某某市太康县七年级（下）期中数学试卷参考答案与试题解析一、选择题下列各小题均有四个答案其中只有一个是正确的，将正确答案的代号字母填入题后括号内1．运用等式性质进行的变形，不正确的是（）A．如果a=b，那么a﹣c=b﹣cB．如果a=b，那么a+c=b+cC．如果a=b，那么D．如果a=b，那么ac=bc【考点】等式的性质．【分析】根据等式的基本性质可判断出选项正确与否．【解答】解：A、根据等式性质1，a=b两边都减c，即可得到a﹣c=b﹣c，故本选项正确；B、根据等式性质1，a=b两边都加c，即可得到a+c=b+c，故本选项正确；C、根据等式性质2，当c≠0时原式成立，故本选项错误；D、根据等式性质2，a=b两边都乘以c，即可得到ac=bc，故本选项正确；故选：C．【点评】主要考查了等式的基本性质．等式性质：1、等式的两边同时加上或减去同一个数或字母，等式仍成立；2、等式的两边同时乘以或除以同一个不为0数或字母，等式仍成立．2．若代数式4x﹣5与的值相等，则x的值是（）A．1B．C．D．2【考点】解一元一次方程．【专题】计算题．【分析】根据题意列出方程，求出方程的解即可得到x的值．【解答】解：根据题意得：4x﹣5=，去分母得：8x﹣10=2x﹣1，解得：x=，故选B．【点评】此题考查了解一元一次方程，其步骤为：去分母，去括号，移项合并，把未知数系数化为1，求出解．3．若单项式2x2y a+b与﹣x a﹣b y4是同类项，则a，b的值分别为（）A．a=3，b=1B．a=﹣3，b=1C．a=3，b=﹣1D．a=﹣3，b=﹣1【考点】同类项．【分析】根据同类项是字母相同且相同字母的指数也相同，可得方程，根据解方程，可得a、b的值．【解答】解：由2x2y a﹣b与﹣x ab y4是同类项，得a﹣b=2，a+b=4．解得：a=3，b=1，故选A．【点评】本题考查了同类项的知识，解答本题的关键是掌握同类项中的两个相同．4．不等式组的解集在数轴上可表示为（）A．B．C．D．【考点】在数轴上表示不等式的解集；解一元一次不等式组．【分析】先求出不等式组中每一个不等式的解集，再求出它们的公共部分，然后把不等式的解集表示在数轴上即可．【解答】解：由x+3＞0，解得x＞﹣3；由1﹣x≥0，解得x≤2，不等式组的解集为﹣3＜x≤2，故选：A．【点评】本题考查了在数轴上表示不等式的解集，每个不等式的解集在数轴上表示出来（＞，≥向右画；＜，≤向左画），数轴上的点把数轴分成若干段，如果数轴的某一段上面表示解集的线的条数与不等式的个数一样，那么这段就是不等式组的解集．有几个就要几个．在表示解集时“≥”，“≤”要用实心圆点表示；“＜”，“＞”要用空心圆点表示．5．一件夹克衫先按成本提高50%标价，再以8折（标价的80%）出售，结果获利28元，若设这件夹克衫的成本是x元，根据题意，可得到的方程是（）A．（1+50%）x×80%=x﹣28B．（1+50%）x×80%=x+28C．（1+50%x）×80%=x﹣28D．（1+50%x）×80%=x+28【考点】由实际问题抽象出一元一次方程．【专题】销售问题．【分析】根据售价的两种表示方法解答，关系式为：标价×80%=进价+28，把相关数值代入即可．【解答】解：标价为：x（1+50%），八折出售的价格为：（1+50%）x×80%；∴可列方程为：（1+50%）x×80%=x+28，故选B．【点评】考查列一元一次方程；根据售价的两种不同方式列出等量关系是解决本题的关键．6．为了开展阳光体育活动，某班计划购买毽子和跳绳两种体育用品，共花费35元，毽子单价3元，跳绳单价5元，购买方案有（）A．1种B．2种C．3种D．4种【考点】二元一次方程的应用．【分析】设毽子能买x个，跳绳能买y根，依据“某班计划购买毽子和跳绳两种体育用品，共花费35元，毽子单价3元，跳绳单价5元”列出方程，并解答．【解答】解：设毽子能买x个，跳绳能买y根，根据题意可得：3x+5y=35，y=7﹣x，∵x、y都是正整数，∴x=5时，y=4；x=10时，y=1；∴购买方案有2种．故选B．【点评】此题主要考查了二元一次方程的应用，根据题意得出正确等量关系是解题关键．7．已知，且x﹣y＜0，则m的取值X围为（）A．m B．m C．m D．m【考点】解二元一次方程组；解一元一次不等式．【专题】计算题；一次方程（组）及应用．【分析】方程组两方程相减表示出x﹣y，代入已知不等式求出m的X围即可．【解答】解：，②﹣①得：x﹣y=6m+1，代入已知不等式得：6m+1＜0，解得：m＜﹣．故选D．【点评】此题考查了解二元一次方程组，以及解一元一次不等式，熟练掌握运算法则是解本题的关键．8．如图，过△ABC的顶点A，作BC边上的高，以下作法正确的是（）A．B．C．D．【考点】三角形的角平分线、中线和高．【分析】根据三角形高线的定义：过三角形的顶点向对边引垂线，顶点和垂足之间的线段叫做三角形的高线解答．【解答】解：为△ABC中BC边上的高的是A选项．故选A．【点评】本题考查了三角形的角平分线、中线、高线，熟记高线的定义是解题的关键．二、填空题9．已知关于x的方程2x﹣3a﹣9=0的解是x=﹣3，则a的值为﹣5 ．【考点】一元一次方程的解．【分析】把x=﹣3代入方程计算即可求出a的值．【解答】解：把x=﹣3代入方程2x﹣3a﹣9=0得：﹣6﹣3a﹣9=0，解得：a=﹣5．故答案为：﹣5．【点评】此题考查了一元一次方程的解，掌握方程的解即为能使方程左右两边相等的未知数的值是解决问题的关键．10．已知方程2x+y﹣5=0用含y的代数式表示x为：x= \frac{5﹣y}{2} ．【考点】解二元一次方程．【分析】把x看做已知数求出y即可．【解答】解：2x+y﹣5=02x=5﹣y，x=．故答案为：．【点评】此题考查了解二元一次方程，解题的关键是把x看做已知数求出y．11．一元一次不等式3x﹣2＜0的解集为x＜\frac{2}{3} ．【考点】解一元一次不等式．【分析】把﹣2移的不等式的右边，然后不等式的两边同时除以3即可求解．【解答】解：3x﹣2＜0移项得3x＜2，系数化为1得，x＜；故答案为x＜．【点评】本题考查了解简单不等式的能力，解答这类题学生往往在解题时不注意移项要改变符号这一点而出错．解不等式要依据不等式的基本性质：（1）不等式的两边同时加上或减去同一个数或整式不等号的方向不变；（2）不等式的两边同时乘以或除以同一个正数不等号的方向不变；（3）不等式的两边同时乘以或除以同一个负数不等号的方向改变．12．在△ABC中，若∠A=80°，∠B=∠C，则∠C=50 度．【考点】三角形内角和定理．【分析】由三角形内角和定理可知．【解答】解：∵∠A=80°，∠B=∠C，∠A+∠B+∠C=180°，∴80°+2∠C=180°，∴∠C=50°．【点评】本题利用了三角形内角和定理求解．三角形的内角和是180°．13．方程组的解是\left\{\begin{array}{l}{x=﹣3}\\{y=﹣2.5}\end{array}\right. ．【考点】解二元一次方程组．【专题】计算题．【分析】方程组利用加减消元法求出解即可．【解答】解：，①﹣②得：2x=﹣6，即x=﹣3，把x=﹣3代入②得：y=﹣2.5，则方程组的解为．故答案为：．【点评】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．14．不等式组的整数解是﹣1，0 ．【考点】一元一次不等式组的整数解．【分析】首先解不等式组求得不等式的解集，然后确定解集中的整数解即可．【解答】解：，解①得：x≥﹣1，解②得：x＜1，则不等式组的解集是：﹣1≤x＜1，则整数解是：﹣1，0．故答案是：﹣1，0．【点评】本题考查了不等式组的整数解，正确解不等式组是解题的关键．15．《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架．它的代数成就主要包括开方术、正负术和方程术．其中，方程术是《九章算术》最高的数学成就．《九章算术》中记载：“今有牛五、羊二，直金十两；牛二、羊五，直金八两．问：牛、羊各直金几何？”译文：“假设有5头牛、2只羊，值金10两；2头牛、5只羊，值金8两．问：每头牛、每只羊各值金多少两？”设每头牛值金x两，每只羊值金y两，可列方程组为\left\{\begin{array}{l}{5x+2y=10}\\{2x+5y=8}\end{array}\right. ．【考点】由实际问题抽象出二元一次方程组．【分析】根据“假设有5头牛、2只羊，值金10两；2头牛、5只羊，值金8两”，得到等量关系，即可列出方程组．【解答】解：根据题意得：，故答案为：．【点评】本题考查了由实际问题抽象出二元一次方程组，解决本题的关键是找到题目中所存在的等量关系．三、解答题（本大题共8个小题，满分65分）16．解下列方程（1）3（x﹣4）=12（2）．【考点】解一元一次方程．【专题】计算题；一次方程（组）及应用．【分析】（1）方程去括号，移项合并，把x系数化为1，即可求出解；（2）方程去分母，去括号，移项合并，把x系数化为1，即可求出解．【解答】解：（1）去括号得：3x﹣12=12，移项合并得：3x=24，解得：x=8；（2）去分母得：3x+3﹣2+3x=6，解得：x=．【点评】此题考查了解一元一次方程，熟练掌握运算法则是解本题的关键．17．用指定的方法解下列方程组：（1）（代入法）（2）（加减法）【考点】解二元一次方程组．【分析】（1）利用代入消元法解方程组即可；（2）利用加减消元法解方程组．【解答】解：（1），由②得：x=4+y③，把③代入①得3（4+y）+4y=19，解得：y=1，将y=1代入①得：x=5，则方程组的解为：；（2），①﹣②×2得：x=2，把x=2代入①得：y=﹣1，方程组的解为：．【点评】本题考查的是二元一次方程组的解法，掌握代入消元法和加减消元法的一般步骤是解题的关键．18．解下列不等式或不等式组（1）2x﹣3≤5（x﹣3）（2）．【考点】解一元一次不等式组；解一元一次不等式．【分析】（1）根据不等式的性质直接求出x的取值X围，但要记得不等式的两边同乘于一个负数时不等式变号；（2）先解出不等式组中的每一个不等式的解集，再利用求不等式组解集的口诀来求得不等式的解集．【解答】解：（1）2x﹣3≤5（x﹣3）2x﹣3≤5x﹣152x﹣5x≤﹣15+3﹣3x≤﹣12x≥4；（2）解不等式①得：x＜2，解不等式②得：x≤6，所以不等式组的解集为x＜2．【点评】此题考查解一元一次不等式和一元一次不等式组；其简单的求法就是利用口诀求解，“同大取大，同小取小，大小小大中间找，大大小小找不到（无解）”．19．若关于x，y的二元一次方程组的解也是二元一次方程2x+3y=6的解，求k的值．【考点】二元一次方程组的解．【分析】首先解关于x的方程组，求得x，y的值，然后代入方程2x+3y=6，即可得到一个关于k的方程，从而求解．【解答】解：由方程组得：∵此方程组的解也是方程2x+3y=6的解∴2×7k+3×（﹣2k）=6k=．【点评】能使方程组中每个方程的左右两边相等的未知数的值即是方程组的解．解题的关键是要知道两个方程组之间解的关系．20．某商场投入13800元资金购进甲、乙两种矿泉水共500箱，矿泉水的成本价和销售价如表所示：类别/单价成本价销售价（元/箱）甲24 36乙33 48（1）该商场购进甲、乙两种矿泉水各多少箱？（2）全部售完500箱矿泉水，该商场共获得利润多少元？【考点】二元一次方程组的应用．【分析】（1）设商场购进甲种矿泉水x箱，购进乙种矿泉水y箱，根据投入13800元资金购进甲、乙两种矿泉水共500箱，列出方程组解答即可；（2）总利润=甲的利润+乙的利润．【解答】解：（1）设商场购进甲种矿泉水x箱，购进乙种矿泉水y箱，由题意得，解得：．答：商场购进甲种矿泉水300箱，购进乙种矿泉水200箱．（2）300×（36﹣24）+200×（48﹣33）=3600+3000=6600（元）．答：该商场共获得利润6600元．【点评】本题考查了二元一次方程组的实际应用．解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系列出方程，再求解．21．为了举行班级晚会，孔明准备去商店购买20个乒乓球做道具，并买一些乒乓球拍做奖品．已知乒乓球每个1.5元，球拍每个22元．如果购买金额不超过200元，且买的球拍尽可能多，那么孔明应该买多少个球拍？【考点】一元一次不等式的应用．【分析】设购买球拍x个，根据乒乓球每个1.5元，球拍每个22元，购买的金额不超过200元，列出不等式，求解即可．【解答】解：设购买球拍x个，依题意得：1.5×20+22x≤200，解之得：x≤7，由于x取整数，故x的最大值为7，答：孔明应该买7个球拍．【点评】此题考查了一元一次不等式的应用，解决问题的关键是读懂题意，依题意列出不等式进行求解．22．如图，BD是∠ABC的平分线，DE∥CB，交AB于点E，∠A=45°，∠BDC=60°，求△BDE各内角的度数．【考点】三角形内角和定理；平行线的性质．【专题】计算题．【分析】利用三角形的外角性质，先求∠ABD，再根据角平分线的定义，可得∠DBC=∠ABD，运用平行线的性质得∠BDE的度数，根据三角形内角和定理可求∠BED的度数．【解答】解：∵∠A=45°，∠BDC=60°，∴∠ABD=∠BDC﹣∠A=15°．∵BD是∠ABC的角平分线，∴∠DBC=∠EBD=15°，∵DE∥BC，∴∠BDE=∠DBC=15°；∴∠BED=180°﹣∠EBD﹣∠EDB=150°．【点评】本题综合考查了平行线的性质及三角形内角与外角的关系，三角形内角和定理．23．如图，O是△ABC内任意一点，连接OB、OC．（1）求证：∠BOC＞∠A；（2）比较AB+AC与OB+OC的大小，并说明理由．【考点】三角形三边关系；三角形的外角性质．【分析】（1）延长BO交AC于点D，首先利用三角形的外角性质得到∠BOC＞∠ODC，让根据∠ODC ＞∠A，证得∠BOC＞∠A；（2）根据三角形的三边关系证得AB+AD＞OB+OD，OD+CD＞OC，从而得到AB+AD+CD＞OB+OC，进而得到AB+AC＞OB+OC．【解答】解：（1）证明：延长BO交AC于点D，∴∠BOC＞∠ODC，又∠ODC＞∠A，∴∠BOC＞∠A；（2）AB+AC＞OB+OC，∵AB+AD＞OB+OD，OD+CD＞OC，∴AB+AD+CD＞OB+OC，即：AB+AC＞OB+OC．【点评】本题考出了三角形的三边关系及三角形的外角的性质，解题的关键是能够正确的构造三角形，难度不大．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2015-2016学年市防城区七年级（下）期中数学试卷一、选择题：每小题3分，共36分，每小题只有一个答案正确1．9的平方根是（）A．±3 B．± C．3 D．﹣32．如图，能判定EC∥AB的条件是（）A．∠B=∠ACE B．∠A=∠ECD C．∠B=∠ACB D．∠A=∠ACE3．如图，点A（﹣2，1）到y轴的距离为（）A．﹣2 B．1 C．2 D．4．如图，图中∠α的度数等于（）A．135° B．125° C．115° D．105°5．如图，AB∥CD，DE⊥CE，∠1=34°，则∠DCE的度数为（）A．34° B．56° C．66° D．54°6．如图，在直角坐标系中，卡片盖住的数可能是（）A．（2，3） B．（﹣2，1） C．（﹣2，﹣2.5） D．（3，﹣2）7．若|3﹣a|+=0，则a+b的值是（）A．2 B．1 C．0 D．﹣18．估算﹣2的值（）A．在1到2之间 B．在2到3之间 C．在3到4之间 D．在4到5之间9．已知点P位于y轴右侧，距y轴3个单位长度，位于x轴上方，距离x轴4个单位长度，则点P坐标是（）A．（﹣3，4） B．（3，4） C．（﹣4，3） D．（4，3）10．在平面直角坐标系中，将点B（﹣3，2）向右平移5个单位长度，再向下平移3个单位长度后与点A （x，y）重合，则点A的坐标是（）A．（2，5） B．（﹣8，5） C．（﹣8，﹣1） D．（2，﹣1）11．如图，已知棋子“车”的坐标为（﹣2，﹣1），棋子“马”的坐标为（1，﹣1），则棋子“炮”的坐标为（）A．（3，2） B．（﹣3，2） C．（3，﹣2） D．（﹣3，﹣2）12．如图，直线AC∥BD，AO、BO分别是∠BAC、∠ABD的平分线，那么∠BAO与∠ABO之间的大小关系一定为（）A．互余 B．相等 C．互补 D．不等二、填空题：每小题3分，共18分13．如图，直线a∥b，∠1=125°，则∠2的度数为．14．4的算术平方根是，9的平方根是，﹣27的立方根是．15．将实数，π，0，﹣6由小到大用“＜”号连起来，可表示为．16．如图，将周长为8的△ABC沿BC方向向右平移1个单位得到△DEF，则四边形ABFD的周长为．17．如图，在长20米，宽10米的长方形草地修建了宽2米的道路，则草地的面积为．18．观察下列各式： =2， =3， =4，…请你找出其中规律，并将第n（n≥1）个等式写出来．三、搜索相关资料解答题（共66分，要求写出解答过程）19．把下列各数的序号填在相应的横线上．①﹣0.3，②0，③，④π2，⑤|﹣2|，⑥，⑦3.1010010001…（2016春•防城区期中）如图，AB和CD相交于点O，∠C=∠1，∠D=∠2，求证：∠A=∠B．证明：∵∠C=∠1，∠D=∠2（已知）又∵∠1=∠2（）∴（等量代换）∴AC∥BD（）∴（两直线平行，错角相等）21．我们在学习“实数”时，画了这样一个图，即“以数轴上的单位长为‘1’的线段作一个正方形，然后以原点O为圆心，正方形的对角线长为半径画弧交x轴于点A”，请根据图形回答下列问题：（1）线段OA的长度是多少？（要求写出求解过程）（2）这个图形的目的是为了说明什么？（3）这种研究和解决问题的方式，体现了的数学思想方法．（将下列符合的选项序号填在横线上）A、数形结合；B、代入；C、换元；D、归纳．22．如图，已知：AB∥DE，∠1=∠2，直线AE与DC平行吗？请说明理由．23．如图，直线AB∥CD，BC平分∠ABD，∠1=65°，求∠2的度数．24．如图，△A1B1C1是△ABC向右平移4个单位长度后得到的，且三个顶点的坐标分别为A1（1，1），B1（4，2），C1（3，4）．（1）请画出△ABC，并写出点A，B，C的坐标；（2）求出△AOA1的面积．25．位于汉江沿岸的小明家、学校、医院、游乐场的平面图如图所示．（1）建立适当的平面直角坐标系，使医院的坐标为（3，0）并写出小明家、学校、游乐场的坐标；（2）根据蜀河大坝蓄水工程需要，小明家及学校、医院、游乐场需要等距离整体迁移，已知迁移后新的小明家、学校、游乐场、医院分别用A、B、C、D表示，且这四点的坐标分别用原来各地点的横坐标都减去5、纵坐标都加上2 得到，请先在图中描出A、B、C、D的位置，画出四边形ABCD，然后说明四边形ABCD是由以小明家、学校、游乐场、医院所在地为顶点的四边形经过怎样平移得到的？26．（12分）（2016春•防城区期中）如图，已知平面有两条直线AB、CD，且AB∥CD，P为一动点．（1）当点P移动到AB、CD之间时，如图（1），这时∠P与∠A、∠C有怎样的关系？证明你的结论．（2）当点P移动到如图（2）的位置时，∠P与∠A、∠C又有怎样的关系？请证明你的结论．2015-2016学年市防城区七年级（下）期中数学试卷参考答案与试题解析一、选择题：每小题3分，共36分，每小题只有一个答案正确1．9的平方根是（）A．±3 B．± C．3 D．﹣3【考点】平方根．【分析】根据平方根的含义和求法，可得9的平方根是：±=±3，据此解答即可．【解答】解：9的平方根是：±=±3．故选：A．【点评】此题主要考查了平方根的性质和应用，要熟练掌握，解答此题的关键是要明确：一个正数有两个平方根，这两个平方根互为相反数，零的平方根是零，负数没有平方根．2．如图，能判定EC∥AB的条件是（）A．∠B=∠ACE B．∠A=∠ECD C．∠B=∠ACB D．∠A=∠ACE【考点】平行线的判定．【分析】根据平行线的判定定理即可直接判断．【解答】解：A、两个角不是同位角、也不是错角，故选项错误；B、两个角不是同位角、也不是错角，故选项错误；C、不是EC和AB形成的同位角、也不是错角，故选项错误；D、正确．故选D．【点评】本题考查了判定两直线平行的方法，正确理解同位角、错角和同旁角的定义是关键．3．如图，点A（﹣2，1）到y轴的距离为（）A．﹣2 B．1 C．2 D．【考点】点的坐标．【分析】根据点到x轴的距离等于纵坐标的长度，到y轴的距离等于横坐标的长度解答．【解答】解：点A的坐标为（﹣2，1），则点A到y轴的距离为2．故选C．【点评】本题考查了点的坐标，熟记点到x轴的距离等于纵坐标的长度，到y轴的距离等于横坐标的长度是解题的关键．4．如图，图中∠α的度数等于（）A．135° B．125° C．115° D．105°【考点】对顶角、邻补角．【分析】根据邻补角互补解答即可．【解答】解：∠α的度数=180°﹣45°=135°．故选A．【点评】此题考查邻补角定义，关键是根据邻补角互补分析．5．如图，AB∥CD，DE⊥CE，∠1=34°，则∠DCE的度数为（）A．34° B．56° C．66° D．54°【考点】平行线的性质．【分析】根据平行线的性质得到∠D=∠1=34°，由垂直的定义得到∠DEC=90°，根据三角形的角和即可得到结论．【解答】解：∵AB∥CD，∴∠D=∠1=34°，∵DE⊥CE，∴∠DEC=90°，∴∠DCE=180°﹣90°﹣34°=56°．故选B．【点评】本题考查了平行线的性质，三角形的角和，熟记平行线的性质定理是解题的关键．6．如图，在直角坐标系中，卡片盖住的数可能是（）A．（2，3） B．（﹣2，1） C．（﹣2，﹣2.5） D．（3，﹣2）【考点】点的坐标．【分析】根据第四象限的点的横坐标大于零，纵坐标小于零，可得答案．【解答】解：A、（2，3）在第一象限，故A错误；B、（﹣2，1）在第二象限，故B错误；C、（﹣2，﹣2.5）在第三象限，故C错误；D、（3，﹣2）在第四象限，故D正确；故选：D．【点评】本题考查了点的坐标，记住各象限点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（﹣，+）；第三象限（﹣，﹣）；第四象限（+，﹣）．7．若|3﹣a|+=0，则a+b的值是（）A．2 B．1 C．0 D．﹣1【考点】非负数的性质：算术平方根；非负数的性质：绝对值．【分析】根据几个非负数的和为0时，这几个非负数都为0列出算式求出a、b的值，计算即可．【解答】解：由题意得，3﹣a=0，2+b=0，解得，a=3，b=﹣2，a+b=1，故选：B．【点评】本题考查的是非负数的性质，掌握几个非负数的和为0时，这几个非负数都为0是解题的关键．8．估算﹣2的值（）A．在1到2之间 B．在2到3之间 C．在3到4之间 D．在4到5之间【考点】估算无理数的大小．【分析】先估计的整数部分，然后即可判断﹣2的近似值．【解答】解：∵5＜＜6，∴3＜﹣2＜4．故选C．【点评】此题主要考查了无理数的估算能力，现实生活中经常需要估算，估算应是我们具备的数学能力，“夹逼法”是估算的一般方法，也是常用方法．9．已知点P位于y轴右侧，距y轴3个单位长度，位于x轴上方，距离x轴4个单位长度，则点P坐标是（）A．（﹣3，4） B．（3，4） C．（﹣4，3） D．（4，3）【考点】点的坐标．【分析】根据题意，P点应在第一象限，横、纵坐标为正，再根据P点到坐标轴的距离确定点的坐标．【解答】解：∵P点位于y轴右侧，x轴上方，∴P点在第一象限，又∵P点距y轴3个单位长度，距x轴4个单位长度，∴P点横坐标为3，纵坐标为4，即点P的坐标为（3，4）．故选B．【点评】本题考查了点的位置判断方法及点的坐标几何意义．10．在平面直角坐标系中，将点B（﹣3，2）向右平移5个单位长度，再向下平移3个单位长度后与点A （x，y）重合，则点A的坐标是（）A．（2，5） B．（﹣8，5） C．（﹣8，﹣1） D．（2，﹣1）【考点】坐标与图形变化-平移．【分析】让B的横坐标加5，纵坐标减3即可得到所求点A的坐标．【解答】解：∵将点B（﹣3，2）向右平移5个单位长度，再向下平移3个单位长度后与点A（x，y）重合，∴所求点A的横坐标为：﹣3+5=2，纵坐标为2﹣3=﹣1，∴所求点的坐标为（2，﹣1）．故选D．【点评】本题考查图形的平移变换，要牢记左右移动改变点的横坐标，左减，右加；上下移动改变点的纵坐标，下减，上加．11．如图，已知棋子“车”的坐标为（﹣2，﹣1），棋子“马”的坐标为（1，﹣1），则棋子“炮”的坐标为（）A．（3，2） B．（﹣3，2） C．（3，﹣2） D．（﹣3，﹣2）【考点】坐标确定位置．【专题】数形结合．【分析】先根据棋子“车”的坐标画出直角坐标系，然后写出棋子“炮”的坐标．【解答】解：如图，棋子“炮”的坐标为（3，﹣2）．故选C．【点评】本题考查了坐标确定位置：平面坐标系中的点与有序实数对一一对应；记住平面特殊位置的点的坐标特征．12．如图，直线AC∥BD，AO、BO分别是∠BAC、∠ABD的平分线，那么∠BAO与∠ABO之间的大小关系一定为（）A．互余 B．相等 C．互补 D．不等【考点】平行线的性质；余角和补角．【分析】根据平行线的性质得出∠CAB+∠ABD=180°，再根据角平分线的定义得出结论．【解答】解：∵AC∥BD，∴∠CAB+∠ABD=180°，∵AO、BO分别是∠BAC、∠ABD的平分线，∴∠CAB=2∠OAB，∠ABD=2∠ABO，∴∠OAB+∠ABO=90°，∴∠AOB=90°，∴OA⊥OB，故选A【点评】此题考查平行线的性质，关键是根据平行线的性质得出∠CAB+∠ABD=180°．二、填空题：每小题3分，共18分13．如图，直线a∥b，∠1=125°，则∠2的度数为55°．【考点】平行线的性质．【分析】先根据对顶角相等，∠1=65°，求出∠3的度数，再由两直线平行，同旁角互补得出∠2的度数．【解答】解：解：∵∠1=125°，∴∠3=∠1=125°，∵a∥b，∴∠2=180°﹣∠3=180°﹣125°=55°．故答案为：55°．【点评】本题考查了平行线的性质，对顶角的性质，熟记定理是解题的关键．14．4的算术平方根是 2 ，9的平方根是±3，﹣27的立方根是﹣3 ．【考点】立方根；平方根；算术平方根．【分析】根据算式平方根、平方根和立方根的定义求出即可．【解答】解：4的算术平方根是2，9的平方根是±3，﹣27的立方根是﹣3．故答案为：2；±3，﹣3．【点评】本题考查了对算术平方根、平方根和立方根的定义的应用，主要考查学生的理解能力和计算能力．15．将实数，π，0，﹣6由小到大用“＜”号连起来，可表示为﹣6．【考点】实数大小比较．【分析】正实数都大于0，负实数都小于0，正实数大于一切负实数，两个负实数绝对值大的反而小，据此判断即可．【解答】解：≈2.236，π≈3.14，∵﹣6＜0＜2.236＜3.14，∴﹣6．故答案为：﹣6．【点评】此题主要考查了实数大小比较的方法，要熟练掌握，解答此题的关键是要明确：正实数＞0＞负实数，两个负实数绝对值大的反而小．16．如图，将周长为8的△ABC沿BC方向向右平移1个单位得到△DEF，则四边形ABFD的周长为10 ．【考点】平移的性质．【分析】根据平移的基本性质解答即可．【解答】解：根据题意，将周长为8的△ABC沿边BC向右平移1个单位得到△DEF，则AD=1，BF=BC+CF=BC+1，DF=AC，又∵AB+BC+AC=8，∴四边形ABFD的周长=AD+AB+BF+DF=1+AB+BC+1+AC=10．故答案为：10．【点评】本题考查平移的基本性质：①平移不改变图形的形状和大小；②经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等．得到CF=AD，DF=AC是解题的关键．17．如图，在长20米，宽10米的长方形草地修建了宽2米的道路，则草地的面积为144米2．【考点】生活中的平移现象．【分析】将道路分别向左、向上平移，得到草地为一个长方形，分别求出长方形的长和宽，再用长和宽相乘即可．【解答】解：将道路分别向左、向上平移，得到草地为一个长方形，长方形的长为20﹣2=18（米），宽为10﹣2=8（米），则草地面积为18×8=144米2．故答案为：144米2．【点评】本题考查了平移在生活中的运用，将道路分别向左、向上平移，得到草地为一个长方形是解题的关键．18．观察下列各式： =2， =3， =4，…请你找出其中规律，并将第n（n≥1）个等式写出来．【考点】算术平方根．【专题】规律型．【分析】根据所给例子，找到规律，即可解答．【解答】解： =（1+1）=2，=（2+1）=3，=（3+1）=4，…，故答案为：．【点评】本题考查了实数平方根，解决本题的关键是找到规律．三、搜索相关资料解答题（共66分，要求写出解答过程）19．把下列各数的序号填在相应的横线上．①﹣0.3，②0，③，④π2，⑤|﹣2|，⑥，⑦3.1010010001…（2016春•防城区期中）如图，AB和CD相交于点O，∠C=∠1，∠D=∠2，求证：∠A=∠B．证明：∵∠C=∠1，∠D=∠2（已知）又∵∠1=∠2（对顶角相等）∴∠C=∠D（等量代换）∴AC∥BD（错角相等，两直线平行）∴∠A=∠B（两直线平行，错角相等）【考点】平行线的判定．【专题】推理填空题．【分析】根据对顶角相等可得∠1=∠2，再由∠C=∠1，∠D=∠2，等量代换可得∠C=∠D，然后根据错角相等，两直线平行可判断出AC∥DB，最后根据两直线平行，错角相等得出∠A=∠B．【解答】证明：∵∠C=∠1，∠D=∠2 （已知）又∵∠1=∠2 （对顶角相等）∴∠C=∠D（等量代换）∴AC∥BD （错角相等，两直线平行）∴∠A=∠B（两直线平行，错角相等）故答案为对顶角相等；∠C=∠D；错角相等，两直线平行；∠A=∠B．【点评】本题考查了平行线的判定与性质，对顶角的性质，熟练掌握平行线的判定方法和性质，并准确识图是解题的关键．21．我们在学习“实数”时，画了这样一个图，即“以数轴上的单位长为‘1’的线段作一个正方形，然后以原点O为圆心，正方形的对角线长为半径画弧交x轴于点A”，请根据图形回答下列问题：（1）线段OA的长度是多少？（要求写出求解过程）（2）这个图形的目的是为了说明什么？（3）这种研究和解决问题的方式，体现了 A 的数学思想方法．（将下列符合的选项序号填在横线上）A、数形结合；B、代入；C、换元；D、归纳．【考点】实数与数轴．【专题】数形结合．【分析】（1）首先根据勾股定理求出线段OB的长度，然后结合数轴的知识即可求解；（2）根据数轴上的点与实数的对应关系即可求解；（3）本题利用实数与数轴的对应关系即可解答．【解答】解：（1）∵OB2=12+12=2，∴OB=，∴OA=OB=；（2）数轴上的点和实数﹣一对应关系；（3）A．【点评】本题主要考查了实数与数轴之间的定义关系，此题综合性较强，不仅要结合图形，还需要熟悉平方根的定义．也要求学生了解数形结合的数学思想．22．如图，已知：AB∥DE，∠1=∠2，直线AE与DC平行吗？请说明理由．【考点】平行线的判定与性质．【分析】首先根据AB∥DE可得∠1=∠3，再由∠1=∠2可根据等量代换得到∠2=∠3，进而得到AE∥DC．【解答】答：AE∥DC；理由如下：∵AB∥DE（已知），∴∠1=∠3（两直线平行，错角相等），∵∠1=∠2（已知），∴∠2=∠3（等量代换），∴AE∥DC（错角相等，两直线平行）．【点评】此题主要考查了平行线的判定与性质，关键是掌握两直线平行，错角相等；错角相等，两直线平行．23．如图，直线AB∥CD，BC平分∠ABD，∠1=65°，求∠2的度数．【考点】平行线的性质．【分析】由平行线的性质得到∠ABC=∠1=65°，∠ABD+∠BDC=180°，由BC平分∠ABD，得到∠ABD=2∠ABC=130°，于是得到结论．【解答】解：∵AB∥CD，∴∠ABC=∠1=65°，∠ABD+∠BDC=180°，∵BC平分∠ABD，∴∠ABD=2∠ABC=130°，∴∠BDC=180°﹣∠ABD=50°，∴∠2=∠BDC=50°．【点评】本题考查了平行线的性质和角平分线定义等知识点，解此题的关键是求出∠ABD 的度数，题目较好，难度不大．24．如图，△A 1B 1C 1是△ABC 向右平移4个单位长度后得到的，且三个顶点的坐标分别为A 1（1，1），B 1（4，2），C 1（3，4）．（1）请画出△ABC，并写出点A ，B ，C 的坐标；（2）求出△AOA 1的面积．【考点】作图-平移变换．【分析】（1）直接把△A 1B 1C 1是向左平移4个单位，再写出点A ，B ，C 的坐标即可；（2）直接根据三角形的面积公式即可得出结论．【解答】解：（1）如图所示，A （﹣3，1），B （0，2），C （﹣1，4）；（2）S △AOA1=×4×1=2．【点评】本题考查的是作图﹣平移变换，熟知图形平移不变性的性质是解答此题的关键．25．位于汉江沿岸的小明家、学校、医院、游乐场的平面图如图所示．（1）建立适当的平面直角坐标系，使医院的坐标为（3，0）并写出小明家、学校、游乐场的坐标；（2）根据蜀河大坝蓄水工程需要，小明家及学校、医院、游乐场需要等距离整体迁移，已知迁移后新的小明家、学校、游乐场、医院分别用A、B、C、D表示，且这四点的坐标分别用原来各地点的横坐标都减去5、纵坐标都加上2 得到，请先在图中描出A、B、C、D的位置，画出四边形ABCD，然后说明四边形ABCD是由以小明家、学校、游乐场、医院所在地为顶点的四边形经过怎样平移得到的？【考点】坐标确定位置；坐标与图形变化-平移．【分析】（1）首先建立平面直角坐标系，进而得出小明家、学校、游乐场的坐标；（2）利用平移规律得出各对应点位置，进而得出答案．【解答】解：（1）如图所示：小明家的坐标为：（0，0）、学校的坐标为：（2，2）、游乐场的坐标为：（5，2）；（2）∵四点的坐标分别用原来各地点的横坐标都减去5、纵坐标都加上2 得到，∴A、B、C、D的位置如图所示，则四边形ABCD是由以小明家、学校、游乐场、医院所在地为顶点的四边形经过向左平移5个单位再向上平移2个单位得到的．【点评】此题主要考查了坐标确定位置以及平移变换，根据题意得出对应点位置是解题关键．26．（12分）（2016春•防城区期中）如图，已知平面有两条直线AB、CD，且AB∥CD，P为一动点．（1）当点P移动到AB、CD之间时，如图（1），这时∠P与∠A、∠C有怎样的关系？证明你的结论．（2）当点P移动到如图（2）的位置时，∠P与∠A、∠C又有怎样的关系？请证明你的结论．【考点】平行线的性质．【分析】（1）延长AP后通过外角定理可得出结论；（2）延长BA到E，延长DC到F，利用角和定理解答．【解答】证明：（1）∠P=∠A+∠C，如图（1）延长AP交CD与点E．∵AB∥CD，∴∠A=∠AEC．又∵∠APC是△PCE的外角，∴∠APC=∠C+∠AEC．∴∠APC=∠A+∠C；（2）∠P=360°﹣（∠A+∠C）．如图（2）延长BA到E，延长DC到F，由（1）得∠P=∠PAE+∠PCF．∵∠PAE=180°﹣∠PAB，∠PCF=180°﹣∠PCD，∴∠P=360°﹣（∠PAB+∠PCD）．【点评】本题考查平行线的性质，难度不大，注意图形的变化带来的影响，不要有惯性思维．。