北京市丰台区2016高三一模数学(理)教材

合集下载

2016丰台区高三(上)期末数学(理科)

2016丰台区高三（上）期末数学（理科）一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．（5分）复数（1+i）（1+ai）是实数，则实数a等于（）A．2 B．1 C．0 D．﹣12．（5分）x2＞0是x＞0的（）A．充分不必要条件 B．必要不充分条件C．充要条件D．既不充分也必要条件3．（5分）已知数列{a n}中，，若利用下面程序框图计算该数列的第2016项，则判断框内的条件是（）A．n≤2014 B．n≤2016 C．n≤2015 D．n≤20174．（5分）若点P为曲线（θ为参数）上一点，则点P与坐标原点的最短距离为（）A．B．C．D．25．（5分）函数在区间[0，π]上的零点之和是（）A．B．C．D．6．（5分）若，，，则a，b，c的大小关系是（）A．c＜b＜a B．b＜c＜a C．c＜a＜b D．a＜b＜c7．（5分）若F（c，0）为椭圆C：的右焦点，椭圆C与直线交于A，B 两点，线段AB的中点在直线x=c上，则椭圆的离心率为（）A． B．C．D．8．（5分）在下列命题中：①存在一个平面与正方体的12条棱所成的角都相等；②存在一个平面与正方体的6个面所成较小的二面角都相等；③存在一条直线与正方体的12条棱所成的角都相等；④存在一条直线与正方体的6个面所成的角都相等．其中真命题的个数为（）A．1 B．2 C．3 D．4二、填空题共6小题，每小题5分，共30分．9．（5分）在（2x﹣1）7的展开式中，x2的系数等于．（用数字作答）10．（5分）若x，y的满足，则z=2x﹣y的最小值为．11．（5分）设等差数列{a n}的前n项和为S n，若S7=42，则a2+a3+a7=．12．（5分）在△ABC中，，点M，N是线段AB上的动点，则的最大值为．13．（5分）某几何体的三视图如图所示，则该几何体的体积为．14．（5分）设函数其中a＞﹣1．①当a=0时，若f（x）=0，则x=；②若f（x）在（﹣∞，+∞）上是单调递增函数，则a的取值范围．二、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．15．（13分）如图，在△ABC中，AB=12，，，点D在边BC上，且∠ADC=60°．（Ⅰ）求cosC；（Ⅱ）求线段AD的长．16．（14分）如图，在四棱锥P﹣ABCD中，AD∥BC，AB⊥AD，E是AB的中点，AB=AD=PA=PB=2，BC=1，PC=．（Ⅰ）求证：CF∥平面PAB；（Ⅱ）求证：PE⊥平面ABCD；（Ⅲ）求二面角B﹣PA﹣C的余弦值．17．（14分）随着人们社会责任感与公众意识的不断提高，越来越多的人成为了志愿者．某创业园区对其员工是否为志愿者的情况进行了抽样调查，在随机抽取的10位员工中，有3人是志愿者．（Ⅰ）在这10人中随机抽取4人填写调查问卷，求这4人中恰好有1人是志愿者的概率P1；（Ⅱ）已知该创业园区有1万多名员工，从中随机调查1人是志愿者的概率为，那么在该创业园区随机调查4人，求其中恰有1人是志愿者的概率P2；（Ⅲ）该创业园区的A团队有100位员工，其中有30人是志愿者．若在A团队随机调查4人，则其中恰好有1人是志愿者的概率为P3．试根据（Ⅰ）、（Ⅱ）中的P1和P2的值，写出P1，P2，P3的大小关系（只写结果，不用说明理由）．18．（13分）已知函数．（Ⅰ）求函数y=f（x）的极值；（Ⅱ）若存在实数x0∈（﹣1，0），且，使得，求实数a的取值范围．19．（13分）已知定点M（1，0）和直线x=﹣1上的动点N（﹣1，t），线段MN的垂直平分线交直线y=t于点R，设点R的轨迹为曲线E．（Ⅰ）求曲线E的方程；（Ⅱ）直线y=kx+b（k≠0）交x轴于点C，交曲线E于不同的两点A，B，点B关于x轴的对称点为点P．点C关于y轴的对称点为Q，求证：A，P，Q三点共线．20．（13分）已知数列{a n}的各项均为正数，满足a1=1，a k+1﹣a k=a i．（i≤k，k=1，2，3，…，n﹣1）（Ⅰ）求证：；（Ⅱ）若{a n}是等比数列，求数列{a n}的通项公式；（Ⅲ）设数列{a n}的前n项和为S n，求证：．参考答案与试题解析一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．【解答】复数（1+i）（1+ai）=1﹣a+（1+a）i，因为复数是实数，所以1+a=0，解得a=﹣1．故选：D．2．【解答】由x2＞0得到：x≠0，而x≠0推不出x＞0，不是充分条件，由x＞0能推出x≠0，是必要条件，∴x2＞0是x＞0的必要不充分条件，故选：B．3．【解答】通过分析，本程序框图为“当型“循环结构，判断框内为满足循环的条件，第1次循环，A=，n=1+1=2，第2次循环，A==，n=2+1=3，…当执行第2016项时，n=2017，由题意，此时，应该不满足条件，退出循环，输出A的值．所以，判断框内的条件应为：n≤2016．故选：B．4．【解答】曲线的普通方程为（x﹣1）2+（y﹣1）2=1，∴曲线表示以（1，1）为圆心，以1为半径的圆．∴曲线的圆心到原点得距离为，∴点P与坐标原点的最短距离为．故选：A．5．【解答】由=0得sin2x=﹣cos2x，即tan2x=﹣，即2x=kπ﹣，即x=﹣，∵0≤x≤π，∴当k=1时，x=，当k=2时，x=，则函数f（x）的零点之和为+=，故选：C6．【解答】分别作出函数y=2x，（红色曲线），y=x（绿色曲线），y=log2x（蓝色曲线）的图象，则由图象可知当1≤x≤2时，对应的函数2x＞x＞log2x，即对应的平面的面积依次减小，即c＜b＜a，故选：A7．【解答】∵F（c，0）为椭圆C：的右焦点，椭圆C与直线交于A，B两点，∴A（a，0），B（0，b），∵线段AB的中点在直线x=c上，∴，∴椭圆的离心率e===．故选：B．8．【解答】①存在一个平面AB1D1与正方体的12条棱所成的角都相等，故①正确；②存在一个平面AB1D1与正方体的6个面所成较小的二面角都相等，故②正确；．．③存在一条直线AC1与正方体的12条棱所成的角都相等，故③正确；④存在一条直线AC1与正方体的6个面所成的角都相等，故④正确．故选：D．二、填空题共6小题，每小题5分，共30分．9．【解答】（2x﹣1）7的展开式中，通项公式为T r+1=•（2x）7﹣r•（﹣1）r，令7﹣r=2，解得r=5；所以展开式中x2的系数为•22•（﹣1）5=﹣84．故答案为：﹣84．10．【解答】由约束条件作出可行域如图，联立，解得A（1，4），化目标函数z=2x﹣y为y=2x﹣z．由图可知，当直线y=2x﹣z过A时，直线在y轴上的截距最大，z有最小值为﹣2．故答案为：﹣2．11．【解答】∵等差数列{a n}的前n项和为S n，S7=42，∴=42，解得a1+a7=12，∴2a1+6d=2（a1+3d）=12，即a1+3d=6，∴a2+a3+a7=a1+d+a1+2d+a1+6d=3（a1+3d）=3×6=18．故答案为：18．12．【解答】在△ABC中，，点M，N是线段AB上的动点，则=CM•CN•cos＜＞≤•=3，故答案为：3．13．【解答】如图，由三视圆得该几何体由直三棱柱ABC﹣A1B1C1与三棱锥B﹣B1C1D组合而成，其中A1B1DC1是边长为2的正方形，AA1=2，∴该几何体的体积为：V====．故答案为：．14．【解答】①当a=0时，f（x）=，由f（x）=0，可得lnx=0，解得x=1．②若f（x）在（﹣∞，+∞）上是单调递增函数，可得f（x）在x＜1为递增，在x≥1为递增函数，可得a＞﹣1；由增函数的定义可得e﹣1≤ln（1+a），解得a≥e e﹣1﹣1．综上可得a的范围是[e e﹣1﹣1，+∞）．故答案为：1，[e e﹣1﹣1，+∞）．二、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．15．【解答】（Ⅰ）∵AB=12，，，∴根据余弦定理：=．…（6分）（Ⅱ）∵0＜C＜π，∴sinC＞0，．∴根据正弦定理得：，即：=8．…（13分）16．【解答】证明：（Ⅰ）取AP的中点M，连接MF，MB，因为M是AP中点，F是PD中点，所以，又因为，所以四边形BCFM是平行四边形，所以FC∥BM，又FC⊄面ABP，BM⊂面ABP所以FC∥面ABP…（5分）（Ⅱ）连接CE，因为在△ABP中，AB=AP=BP，点E是边AB在的中点，所以PE⊥AB且，在Rt△BEC中，BE=EC=1，EB⊥BC，所以在△PEC中，，，，所以PE⊥EC又因为AB∩EC=E，AB⊂面ABCD，EC⊂面ABCD所以PE⊥面ABCD…（9分）（Ⅲ）取CD中点N，以EB，EN，EP分别为轴x，y轴，z轴，建立空间直角坐标系，各点坐标为：B（1，0，0），C（1，1，0），B（1，0，0），，A（﹣1，0，0），因为：BC⊥PE，AB⊥BC，所以BC⊥面ABP，面ABP的法向量为设面ABC的法向量为，，，取x0=1，得，由图可知二面角为锐二面角，设锐二面角为θ，cosθ==，二面角B﹣PA﹣C余弦值为．…（14分）17．【解答】（Ⅰ），所以这4人中恰好有1人是志愿者的概率为．（Ⅱ），所以这4人中恰好有1人是志愿者的概率为0.4116．（Ⅲ）由于A团队中，每个人是志愿者的概率为，P3 =•=0.4116，P1＞P3=P2 ．18．【解答】（Ⅰ）f′（x）=ax2+2x，令f′（x）=0得x2=0，．∴函数y=f（x）的极大值为；极小值为f（0）=0．…（8分）（Ⅱ）若存在，使得，则由（Ⅰ）可知，需要（如图1）或（如图2）（图1），（图2），于是可得．…（13分）19．【解答】（Ⅰ）解：由题意可知：RN=RM，即点R到直线x=﹣1和点M的距离相等．根据抛物线的定义可知：R的轨迹为抛物线，其中M为焦点．设R的轨迹方程为：y2=2px，，p=2所以R的轨迹方程为：y2=4x．…（5分）（Ⅱ证明：由条件可知，则．联立，消去y得k2x2+（2bk﹣4）x+b2=0，△=（2bk﹣4）2﹣4b2k2=16（1﹣bk）＞0．设A（x1，y1），B（x2，y2）（x1＜x2），则P（x2，﹣y2），，．因为，所以k AP=k AQ，所以A，P，Q三点共线．…（13分）20．【解答】（Ⅰ）证明：∵a k+1﹣a k=a i＞0（i≤k，k=1，2，3，…，n﹣1），∴数列{a n}是递增数列，即1＜a2＜a3＜…＜a n．﹣a k=a i≥1（i≤k，k=1，2，3，…，n﹣1），又∵a k+1﹣a k≥1（k=1，2，3，…，n﹣1）．∴a k+1（Ⅱ）解：∵a2﹣a1=a1，∴a2=2a1；∵{a n}是等比数列，∴数列{a n}的公比为2．∵a k﹣a k=a i（i≤k，k=1，2，3，…，n﹣1），∴当i=k时有a k+1=2a k．+1这说明在已知条件下，可以得到唯一的等比数列．∴．（Ⅲ）证明：∵1=a1=1，2=a2=2，，，…，，由上面n个式子相加，得到：，化简得，∴．。

北京市丰台区2016届高考一模理科综合试卷含解析

北京市丰台区2016届高考第一次模拟考试理科综合测试试题一、本部分共5小题，每小题6分，共120分．在每小题列出的四个选项中，选出最符合题目要求的一项．1．下列有关细胞的叙述．正确的是（）A．叶肉细胞中叶绿体产生的[H]可进入线粒体参与生成水B．内质网、高尔基体、核糖体都能进行蛋白质的合成和加工C．硝化细菌、酵母菌、颤藻的细胞体都含有核糖体、DNA和RNAD．抗原与抗体发生特异性结合的反应是在细胞质基质中完成的【知识点】原核细胞和真核细胞的形态和结构的异同．【试题解析】A、叶肉细胞中叶绿体产生的[H]只能用于暗反应，不能进入线粒体参与生成水，A错误；B、核糖体能进行蛋白质的合成、内质网能进行蛋白质的合成和加工、高尔基体只能进行蛋白质的加工，不能进行蛋白质的合成，B错误；C、所有细胞生物都含有核糖体这种细胞器，都含有核酸，硝化细菌、酵母菌、颤藻的细胞体都含有核糖体、DNA和RNA，C正确；D、抗原与抗体发生特异性结合的反应是在内环境中，D错误．【答案】C．2．如图是由3个圆所构成的概念关系图．符合这种概念关系的是（）A．Ⅰ抗体、Ⅱ受体、Ⅲ蛋白质B．Ⅰ递质、Ⅱ载体、Ⅲ信号分子C．Ⅰ排尿反射、Ⅱ体温调节、Ⅲ负反馈调节D．Ⅰ生殖隔离、Ⅱ地理隔离、Ⅲ物种形成【知识点】人体免疫系统在维持稳态中的作用；物种的概念与形成；神经冲动的产生和传导．【试题解析】A、抗体和受体的化学本质都是蛋白质，A正确；B、递质属于信号分子，载体不属于信号分子，B错误；C、排尿反射属于正反馈调节，体温调节属于负反馈调节，C错误；D、生殖隔离是物种形成的标志，地理隔离不是形成新物种的必须条件，如多倍体的形成，D错误．【答案】A．3．某家系的遗传系谱图及部分个体基因型如图所示，A1、A2、A3是位于X染色体上的等位基因．下列推断正确的是（）A．Ⅱ﹣2基因型为X A1X A2的概率是B．Ⅲ﹣1基因型为X A1Y的概率是C．Ⅲ﹣2基因型为X A1X A2的概率是D．Ⅳ﹣1基因型为X A1X A1的概率是【知识点】真题集萃；伴性遗传．【试题解析】父亲的X染色体一定能传递给女儿，Y染色体一定传递能儿子，母亲的两条X 染色体传递给后代的几率相等．Ⅱ﹣2和Ⅱ﹣3的基因型为X A1X A2、X A1X A3，产生配子为X A1：X A2：X A3，因此Ⅲ﹣1基因型为为X A1Y、X A2Y、X A3Y，产生含X的配子为为X A1：X A2：X A3，Ⅲ﹣2基因型为X A1X A2、X A2X A2、X A3X A2．A、由于Ⅱ﹣2基因型为X A1X A2、X A1X A3，所以基因型为X A1X A2的概率是，A错误；B、由于Ⅱ﹣2基因型为X A1X A2、X A1X A3，产生配子为X A1：X A2：X A3，Ⅱ﹣1提供Y配子，所以Ⅲ﹣1基因型为为X A1Y、X A2Y、X A3Y，X A1Y的概率是，B错误；C、由于Ⅱ﹣3基因型为X A1X A2或X A1X A3，产生配子为X A1：X A2：X A3，且Ⅱ﹣4基因型为X A2Y，又Ⅲ﹣2为女性，必有X A2，所以Ⅲ﹣2基因型为X A1X A2的概率是，C错误；D、由于Ⅲ﹣1基因型为X A1Y的概率是，Ⅲ﹣2基因型为X A1X A2、X A2X A2、X A3X A2，只有X A1X A2含X A1配子，X A1X A2的概率是，所以Ⅵ﹣1基因型为X A1X A1的概率是=，D正确．【答案】D．4．下列探究活动中，保证取样的随机性对于得出正确结论最为重要的是（）A．调查进行性肌营养不良在患者家系中的遗传方式B．探究融雪剂对于高速路边土壤小动物丰富度的影响C．获得分解纤维素效率最高的土壤微生物单个菌落D．通过根尖细胞计数比较细胞周期中各时期的时间长短【知识点】估算种群密度的方法．【试题解析】A、遗传方式的调查在患者家系中调查，不运用随机调查的方法，A错误；B、探究融雪剂对于高速路边土壤小动物丰富度的影响时，应随机选取样方进行调查，才能得出正确结论，B正确；C、获得分解纤维素效率最高的土壤微生物单个菌落使用选择培养基培养筛选，无需随机取样，C错误；D、通过根尖细胞计数比较细胞周期中各时期的时间长短中，需要多取样求平均值，取样的随机性并不是最重要的，D错误．【答案】B．5．烟盲蝽在烟草叶片上生活，以斜纹夜蛾幼虫等为食．研究人员观察并测定了烟盲蝽搜寻、刺吸猎物、刺吸植物、梳理、休息等行为的时间比例，结果如下．有关说法正确的是（）A．能量只能从烟草流向斜纹夜蛾，再流向烟盲蝽B．烟盲蝽对烟叶有害，而与斜纹夜蛾协同进化C．烟盲蝽对斜纹夜蛾幼虫的捕食效率与猎物密度无关D．利用烟盲蝽可以防治烟草上的斜纹夜蛾等害虫【知识点】种间关系．【试题解析】A、由图可知，烟盲蝽即可刺吸猎物（斜纹夜蛾），也可刺吸植物，因此能量可能直接从烟草流向烟盲蝽，A错误；B、烟盲蝽能刺吸植物（烟草），其与烟叶也是协同进化，B错误；C、由图可知，烟盲蝽对斜纹夜蛾幼虫的捕食效率与猎物密度有关，C错误；D 、烟盲蝽即可刺吸猎物（斜纹夜蛾），因此利用烟盲蝽可以防治烟草上的斜纹夜蛾等害虫，D 正确．【答案】D ．【知识点】金属与合金在性能上的主要差异．【专题】几种重要的金属及其化合物．【分析】合金是指在一种金属中加热熔合其它金属或非金属而形成的具有金属特性的物质．合金概念有三个特点：①一定是混合物；②合金中各成分都是以单质形式存在；③合金中至少有一种金属．【试题解析】A ．青铜是铜锡合金，故A 正确；B ．瓷器是硅酸盐产品，故B 错误；C ．石雕是碳酸盐或硅酸盐，故C 错误；D ．竹简的主要成分为纤维素，故D 错误．【答案】A ．7．下列物质性质的比较，不能用元素周期律解释的是（）A ．稳定性：H 2O ＞NH 3B ．碱性：NaOH ＞Al （OH ）3C ．氧化性：F 2＞Cl 2D ．酸性：CH 3COOH ＞H 2CO 3【知识点】元素周期律和元素周期表的综合应用；元素周期律的作用．【试题解析】A ．非金属性O ＞N ，稳定性：H 2O ＞NH 3，故A 正确；B ．金属性Na ＞Al ，最高价氧化物的水化物碱性为NaOH ＞Al （OH ）3，故B 正确；C ．非金属性F ＞Cl ，对应单质的氧化性为F 2＞Cl 2，故C 正确；D ．由醋酸可与碳酸钙反应生成碳酸判断酸性CH 3COOH ＞H 2CO 3，不能利用元素周期律解释，故D 错误；【答案】D ．8．下列用来解释事实的方程式中不合理的是（）A ．铁丝在氯气中燃烧：Fe+Cl 2FeCl 2B ．常温下，0.1mol/L 醋酸溶液pH ≈3 CH 3COOH ⇌CH 3COO ﹣+H +C ．铝片放入氢氧化钠溶液中有气体产生 2Al+2OH ﹣+2H 2O=2AlO 2﹣+3H 2↑D ．蔗糖与浓硫酸混合产生刺激性气味的气体 C+2H 2SO 4（浓）CO 2↑+2SO 2↑+2H 2O 【知识点】离子方程式的书写．【试题解析】A ．铁与氯气反应生成氯化铁：2Fe+3Cl 22FeCl 3，故A 错误；B．常温下，0.1mol/L醋酸溶液pH≈3，醋酸电离方程式：CH3COOH⇌CH3COO﹣+H+，故B 正确；C．铝片放入氢氧化钠溶液中有气体产生，离子方程式：2Al+2OH﹣+2H2O=2AlO2﹣+3H2↑，故C正确；D．蔗糖与浓硫酸混合产生刺激性气味的气体，化学方程式：C+2H2SO4（浓）CO2↑+2SO2↑+2H2O，故D正确；【答案】A．9．下列实验能够达到实验目的是（）A．用如图装置配制100 mL 0.1 mol/L的硫酸B．用如图装置提取碘水中碘C．用如图装置制取少量乙烯气体D．用如图装置验证溴乙烷发生消去反应【知识点】化学实验方案的评价；实验装置综合．【试题解析】A．不能将浓硫酸直接注入容量瓶中，应在烧杯中稀释、冷却后转移到容量瓶中，故A错误；B．碘不易溶于水，易溶于有机溶剂，则利用图中萃取分液可分离，故B正确；C．乙醇在170℃发生消去反应生成乙烯，则温度计应测定反应液的温度，故C错误；D．乙醇易挥发，乙醇、乙烯均与高锰酸钾反应，则不能验证溴乙烷的消去反应，故D错误；【答案】B．10．我国药学家屠呦呦因发现植物黄花蒿叶中含有抗疟疾的物质﹣青蒿素而荣获2015年诺贝尔奖．科学家对青蒿素的结构进行进一步改良，合成药效更佳的双氢青蒿素、蒿甲醚．下列说法正确的是（）A．利用黄花蒿叶研究青蒿素结构的基本步骤为：元素分析确定实验式→测定相对分子质量确定分子式→波谱分析确定结构式B．①、②的反应类型分别为还原反应、酯化反应C．双氢青蒿素在水中的溶解性大于青蒿素D．双氢青蒿素与蒿甲醚组成上相差﹣CH2﹣，二者互为同系物【知识点】有机物的结构和性质．【试题解析】A．研究有机物一般经过：分离、提纯→确定实验式→确定分子式→确定结构式，然后根据元素定量分析确定实验式、在测定相对分子质量确定分子式，最后通过波谱分析确定结构式，缺少分离、提纯过程，故A错误；B．蒿甲醚不含酯基，则②不是酯化反应，故B错误；C．双氢青蒿素含有羟基，可形成氢键，在水中溶解度较大，故C正确；D．双氢青蒿素与蒿甲醚结构不同，不是同系物，故D错误．【答案】C．11．如图是利用微生物燃料电池处理工业含酚废水的原理示意图，下列说法不正确的是（）A．该装置可将化学能转化为电能B．溶液中H+由a极移向b极C．电极b附近的pH降低D．电极a附近发生的反应是：C6H6O﹣28e﹣+11H2O6CO2+28H+【知识点】化学电源新型电池．【试题解析】A．根据图知，该装置没有外接电源，是原电池，是将化学能转化为电能装置，故A正确；B．放电时，电解质溶液中阳离子向正极移动，根据电子流向知，a是负极、b是正极，所以溶液中H+由a极移向b极，故B正确；C．b电极氧气得电子和氢离子反应生成水，导致溶液中氢离子浓度降低，溶液的pH升高，故C错误；D．a电极上苯酚失电子和水反应生成二氧化碳和氢离子，电极反应式为C6H6O﹣28e﹣+11H2O6CO2+28H+，故D正确；【答案】C．12．某同学探究溶液的酸碱性对FeCl3水解平衡的影响，实验方案如下：配制50mL0.001mol/L FeCl3溶液、50mL对照组溶液x，向两种溶液中分别滴加1滴1mol/L HCl溶液、1滴1mol/L NaOH 溶液，测得溶液pH随时间变化的曲线如图所示．下列说法不正确的是（）A．依据M点对应的pH，说明Fe3+发生了水解反应B．对照组溶液x的组成可能是0.003 mol/L KClC．依据曲线c和d说明Fe3+水解平衡发生了移动D．通过仪器检测体系浑浊度的变化，可表征水解平衡移动的方向【知识点】盐类水解的应用．【试题解析】A、FeCl3溶液的pH小于7，溶液显酸性，原因是氯化铁是强酸弱碱盐，Fe3+在溶液中发生了水解，故A正确；B、对照组溶液X加碱后溶液的pH的变化程度比加酸后的pH的变化程度大，而若对照组溶液x的组成是0.003 mol/L KCl，则加酸和加碱后溶液的pH的变化应呈现轴对称的关系，故B错误；C、在FeCl3溶液中加碱、加酸后，溶液的pH的变化均比对照组溶液X的变化小，因为加酸或加碱均引起了Fe3+水解平衡的移动，故溶液的pH的变化比较缓和，故C正确；D、FeCl3溶液水解出氢氧化铁，故溶液的浑浊程度变大，则水解被促进，否则被抑制，故D正确．【答案】B．13．关于分子间的作用力，下列说法正确的是（）A．分子间只存在引力B．分子间只存在斥力C．分子间同时存在引力和斥力D．分子间距离较小时，只存在斥力，分子间距离较大时，只存在引力【知识点】分子动理论的基本观点和实验依据【试题解析】分子间既有引力，也有斥力。

北京丰台区2016-2017高三期末数学(理)试卷

丰台区 2016~2017 学年度第一学期期末练习高三数学（理科）2017.01（本试卷满分共 150 分，考试时间120分钟）注意事项：1．答题前，考生务必先将答题卡上的学校、年级、班级、姓名、准考证号用黑色字迹签字笔填写清楚，并认真核对条形码上的准考证号、姓名，在答题卡的“条形码粘贴区”贴好条形码． 2．本次考试所有答题均在答题卡上完成．选择题必须使用 2B 铅笔以正确填涂方式将各小题对应选项涂黑，如需改动，用橡皮擦除干净后再选涂其它选项．非选择题必须使用标准黑色字迹签字笔书写，要求字体工整、字迹清楚．3．请严格按照答题卡上题号在相应答题区内作答，超出答题区域书写的答案无效，在试卷、草稿纸上答题无效．4．请保持答题卡卡面清洁，不要装订、不要折叠、不要破损．第一部分（选择题共 40 分）一、选择题共 8 小题，每小题 5 分，共 40 分．在每小题列出的四个选项中，选出符合题目要求的一项．1．已知集合 A x Zx 2x 1 0，B 2 1，，那么A B 等于（） A ． 2 1 0 1，，， B ． 2 1 0，，C ．2 1，D ．12．如果a b0 ，那么下列不等式一定成立的是（）abA ． a bB ． 1a b 1C ．1212D ．ln aln b3．如果平面向量a 2 0，，b 1 1，，那么下列结论中正确的是（）A ．a bB ．a b2 2C ．a b bD ．a b ∥4．已知直线m ，n 和平面，如果n，那么“m n ”是“m”的（）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件 5．在等比数列a n 中，a 1 3，a a a 1239，则a 4a a 56等于（） A ．9B ．72C ．9 或72D ．9 或726．如果函数 f xsinx 3cosx 的两个相邻零点间的距离为2 ，那么 f1f2f3 f 9的值为（） A ．1B ． 1CD ． 37．中国历法推测遵循以测为辅、以算为主的原则．例如《周髀算经》和《易经》里对二十四节气的晷（guĭ）影长的记录中，冬至和夏至的晷影长是实测得到的，其它节气的晷影长则是按照等差数列的规律计算得出的．下表为《周髀算经》对二十四节气晷影长的记录，其中115.1寸表示115寸1 分（ 1 寸=10 分）． 135.0125. 115.1 105.2 95.3 85.4 75.5 66.5 55.6 45.7 35.8 25.9蛰的晷影长应为（） A ．72.4 寸B ．81.4 寸C ．82.0 寸D ．91.6 寸8．对于任何集合S ，用S 表示集合S 中的元素个数，用n S 表示集合S 的子集个数．若集合A B ，满足条件：A 2017，且n A n B n AB ，则 A B 等于（） A ．2017B ．2016C ．2015D ．2014 第二部分（非选择题共 110 分）二、填空题共 6 小题，每小题 5 分，共 30 分． 2i9．设i 虚数单位，则复数 __________．1i 10．设椭圆C ：2x2y21a 0的左、右焦点分别为F F 1，2，点P 在椭圆C 上，如果 PF 1PF 2 10， a那么椭圆C 的离心率为___________．6 11．在1x x2的展开式中，常数项是__________（用数字作答）．x y2 0≤ ， 12．若x y ，满足2x y2 0≥ ，即z2x y的最大值为__________．y ≥0，13．如图，边长为 2 的正三角形ABC 放置在平面直角坐标系xOy 中，AC 在x 轴上，顶点 B 与y 轴上的定点 P 重合．将正三角形ABC 沿x 轴正方向滚动，即先以顶点C 为旋转中心顺时针旋转，当顶点 B 落在x 轴上时，再以顶点 B 为旋转中心顺时针旋转，如此继续．当△ABC 滚动到△ABC 1 1 1 时，顶点 B 运动轨迹的长度为_____________；在滚动过程中，OB OP 的最大值为____________．14．已知 f x 为偶函数，且 x ≥0 时， f xxx（x表示不超过 x 的最大整数）．设g x f xkx k kR，当k 1时，函数g x有___________个零点；若函数g x有三个不同的零点，则k 的取值范围是__________．三、解答题共 6 小题，共 80 分．解答应写出文字说明，演算步骤或证明过程．15．（本小题共 13 分）（Ⅰ）求角C 的大小；（Ⅱ）求边 AB 的长．16．（本小题共 14 分）如图所示的多面体中，面 ABCD 是边长为 2 的正方形，平面 PDCQ 平面 ABCD ，PD DC E F G，，，分别为棱BC AD P A ，，的中点．如图，在 ABC △ 中， D 是 BC 上的点，2 3 CD AC AD，， sinB ．（Ⅰ）求证：EG∥平面PDCQ；617．（本小题共14 分）数独游戏越来越受人们喜爱，今年某地区科技馆组织数独比赛，该区甲、乙、丙、丁四所学校的学生积极参赛，参赛学生的人数如下表所示：30 名参加问卷调查．（Ⅰ）问甲、乙、丙、丁四所中学各抽取多少名学生？（Ⅱ）从参加问卷调查的30名学生中随机抽取2 名，求这2 名学生来自同一所中学的概率；（Ⅲ）在参加问卷调查的30名学生中，从来自甲、丙两所中学的学生中随机抽取2 名，用X 表示抽得甲中学的学生人数，求X 的分布列．18．（本小题共13 分）已知函数f x xe x 与函数g x 1 x2 ax的图象在点0 0，处有相同的切线．2（Ⅰ）求a的值；（Ⅱ）设h x f x bg x b R，求函数h x在 1 2，上的最小值．19．（本小题共13分）已知抛物线C：y2 2px p0的焦点为F ，且经过点A 1 2，，过点F 的直线与抛物线C交于P Q，两点．（Ⅰ）求抛物线C的方程；p（Ⅱ）O为坐标原点，直线OP OQ，与直线x分别交于S T，两点，试判断FS FT是否为定2 值？若是，求出这个定值；若不是，请说明理由．（Ⅱ）已知二面角PBFC P ABCD的体积．20．（本小题共 13 分）已知无穷数列c n满足 c n11 1 2c n ．（Ⅰ）若c，写出数列c n的前 5 项；（Ⅱ）对于任意0≤c 1≤1，是否存在实数M ，使数列c n中的所有项均不大于M ？若存在，求M的最小值；若不存在，请说明理由．（Ⅲ）当c 1为有理数，且c 1≥0时，若数列c n自某项后是周期数列，写出c 1的最大值．（直接写出结果，无需证明）（考生务必交答案答在答题卡上，在试卷上作答无效）。

2016年北京个区一模立体几何理

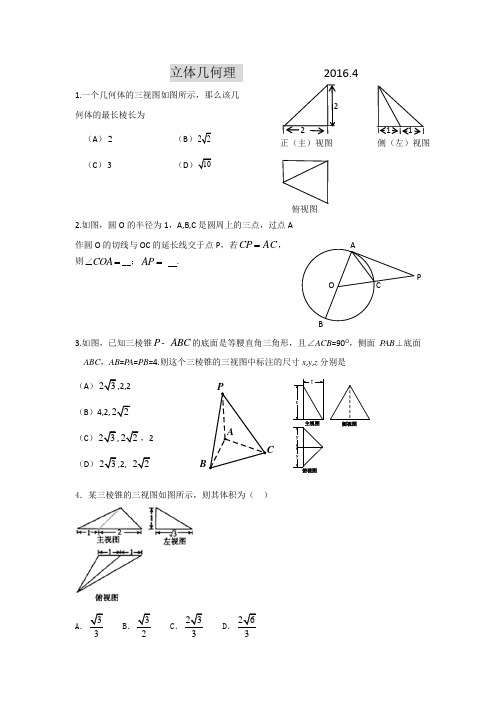
立体几何理2016.41.一个几何体的三视图如图所示，那么该几何体的最长棱长为（A）2（B ）22（C）3（D ）102.如图，圆O的半径为1，A,B,C是圆周上的三点，过点A作圆O的切线与OC的延长线交于点P，若ACCP=，则COA∠=__；AP=.3.如图，已知三棱锥P ABC-的底面是等腰直角三角形，且∠ACB=90O，侧面P AB⊥底面ABC，AB=P A=PB=4.则这个三棱锥的三视图中标注的尺寸x,y,z分别是（A ）23,2,2（B）4,2,22（C ）23,22，2（D ）23,2,224．某三棱锥的三视图如图所示，则其体积为（）A ．33B ．32C ．233D ．263俯视图侧（左）视图1 1正（主）视图22ABO CP俯视图侧视图主视图zyyxABPC5．某四面体的三视图如图所示，该四面体四个面的面积中最大的是( )A ．8B ．62C ．10D ．826.如图，已知平面αI 平面β=l ，⊥αβ.A B 、是直线l 上的两点，D C 、是平面β内的两点，且⊥DA l ，⊥CB l ，4,=DA 6=AB ，8=CB .P 是平面α上的一动点，且有∠=∠APD BPC ，则四棱锥-P ABCD 体积的最大值是（）（A ）48 （B ） 16 （C ）243 （D ）1447.已知某几何体的三视图如图,正（主）视图中的弧线是半圆，根据图中标出的尺寸，可得这个几何体的表面积是________（单位:2cm ）.8.一个棱长为4的正方体，被一个平面截去一部分后，所得几何体的三视图如图所示，则该截面的面积是.俯视图侧（左）视图正（主）视图229..如图，在棱长为()0a a >的正四面体ABCD 中，点B ，C ，D 分别在棱AB ，AC ，AD 上，且平面111B C D ∥平面BCD ，1A为AD CBD 1C 1B 1A 1BCD △内一点，记三棱锥1111A B C D -的体积为V ，设1AD x AD=，对于函数()V F x =，则 (A)当23x =时，函数()f x 取得最大值 (B)函数()f x 在1,12⎛⎫ ⎪⎝⎭上是减函数(C)函数()f x 的图像关于直线12x =对称 (D)存在0x ，使得()013A BCD f x V ->（其中A BCD V -为四面体ABCD 的体积）10.DC （本小题共14分）已知三棱柱111C B A ABC -中，1A A ⊥底面A B C ，90=∠BAC ，1A A 1=，3=AB ，2=AC ,E 、F 分别为棱C C 1、BC 的中点.（Ⅰ）求证 1AC A B ⊥；（Ⅱ）求直线EF 与B A 1所成的角；（Ⅲ）若G 为线段A A 1的中点，1A 在平面EFG 内的射影为H ，求A HA 1∠.11.FT （本小题共13分）如图，在五面体ABCDEF 中，四边形ABCD 为菱形，且∠BAD =60°，对角线AC 与BD 相交于O ；OF ⊥平面ABCD ，BC =CE =DE =2EF =2. (Ⅰ)求证： EF //BC ；(Ⅱ)求直线DE 与平面BCFE 所成角的正弦值.OCDABEF12．HD （本小题满分14 分）如图，在四棱锥P －ABCD 中，PA ⊥平面ABCD ，四边形ABCD 为正方形，点M ，N 分别为线段PB ，PC 上的点，MN ⊥PB ．（Ⅰ）求证： BC ⊥平面PAB ；（Ⅱ）求证：当点M 不与点P ，B 重合时，M ，N ，D ， A 四个点在同一个平面内；（Ⅲ）当PA ＝AB ＝2，二面角C －AN －D 的大小为3π时，求PN 的长．13.SJS （本小题共14分）如图，三棱柱111ABC A B C -中，1AA ⊥平面ABC ，BC AC ⊥，2BC AC ==，13AA =，D 为AC 的中点．（Ⅰ）求证：1AB ∥平面1BDC ；（Ⅱ）求二面角1C BD C --的余弦值；（Ⅲ）在侧棱1AA 上是否存在点P ，使得CP ⊥平面1BDC ？若存在，求出AP 的长；若不存在，说明理由．14.SY （本小题满分13分）如图，在四棱锥-P ABCD 中，等边 PAD 所在的平面与正方形ABCD 所在的平面互相垂直,O 为AD 的中点，E 为DC 的中点，且 2.=AD（Ⅰ）求证：⊥PO 平面ABCD ；（Ⅱ）求二面角--P EB A 的余弦值；（Ⅲ）在线段AB 上是否存在点M ，使线段PM 与 PAD 所在平面成30︒角.若存在，求出AM 的长,若不存在，请说明理由15．XC （本小题满分14分）如图，四边形为梯形ABCD ，DAD BC ∥，90BAD ∠=，四边形11CC D D 为矩形，已知1AB BC ⊥，4AD =，2AB =，1BC =. （Ⅰ）求证：1BC ∥平面1ADD ；（Ⅱ）若12DD =，求平面11AC D 与平面1ADD 所成的锐二面角的余弦值；（Ⅲ）设P 为线段1C D 上的一个动点（端点除外），判断直线1BC 与直线CP 能否垂直？并说明理由.D 1C 1DCBA16．（本小题满分14分）如图，在四棱锥P ABCD -中，底面ABCD 是平行四边形，135BCD ∠= ，侧面PAB ⊥底面ABCD ，90BAP ∠= ,2AB AC PA ===, ,E F 分别为,BC AD 的中点，点M 在线段PD 上.（Ⅰ）求证：EF ⊥平面PAC ；（Ⅱ）若M 为PD 的中点，求证：//ME 平面PAB ；（Ⅲ）如果直线ME 与平面PBC 所成的角和直线ME 与平面ABCD 所成的角相等，求PMPD的值.F CADPMB E17. （本小题满分14分）如图，在四棱锥P ABCD -中，PB ⊥底面ABCD ，底面ABCD 为梯形，AD BC ，AD AB ⊥，且3,1PB AB AD BC ====.（Ⅰ）若点F 为PD 上一点且13PF PD =，证明：CF 平面PAB ；（Ⅱ）求二面角B PD A --的大小；（Ⅲ）在线段PD 上是否存在一点M ，使得CM PA ⊥?若存在，求出PM 的长；若不存在，说明理由.FADCBP。

2016北京市丰台区高三(一模)数学(理)

2016北京市丰台区高三（一模）数学（理） 2016.3第一部分（选择题共40分）一.选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项． 1.已知全集U =R ，集合{}|23A x x x =≤-≥或，{}|14B x x x =<->或，那么集合()U C A B I 等于（）（A ）{}|24x x -<≤ （B ）{}|23x x -<<（C ）{}|21x x -<<-（D ）{}|2134x x x 或-<<-<<2．在下列函数中，是偶函数,且在0+∞（，）内单调递增的是（A ）||2x y = （B ）21y x =（C ）|lg |y x = （D ）cos y x =3.对高速公路某段上汽车行驶速度进行抽样调查，画出如下频率分布直方图.根据直方图估计在此路段上汽车行驶速度的众数和行驶速度超过80km/h 的概率（A ） 75，0.25 （B ）80,0.35 （C ）77.5,0.25 （D ）77.5,0.354. 若数列{}n a 满足*12(0,)N n n n a a a n +=刮，且2a 与4a 的等差中项是5，则12n a a a +++L 等于（A ）2n（B ）21n- （C ）12n - （D ）121n --5. 已知直线m ,n 和平面α，若n ⊥α，则“m ⊂α”是“n ⊥m ”的（A ）充分而不必要条件（B ）必要而不充分条件（C ）充分必要条件（D ）既不充分也不必要条件6. 有三对师徒共6个人，站成一排照相，每对师徒相邻的站法共有（A ） 72 （B ）54 （C ） 48 （D ） 87.如图，已知三棱锥P ABC -的底面是等腰直角三角形，且∠ACB =90O，侧面PAB ⊥底面ABC ，AB =PA =PB =4.则这个三棱锥的三视图中标注的尺寸x ,y ,z 分别是（A）（B ）4,2,侧视图（D）23,2,228. 经济学家在研究供求关系时，一般用纵轴表示产品价格(自变量)，而用横轴来表示产品数量（因变量）.某类产品的市场供求关系在不受外界因素（如政府限制最高价格等）的影响下，市场会自发调解供求关系：当产品价格P1低于均衡价格P0时，需求量大于供应量，价格会上升为P2；当产品价格P2高于均衡价格P0时，供应量大于需求量，价格又会下降，价格如此波动下去，产品价格将会逐渐靠进均衡价格P0.能正确表示上述供求关系的图形是（A）（B）（C）（D）第二部分（非选择题共110分）一、填空题共6小题，每小题5分，共30分．9.已知双曲线22221(0,0)x ya ba b-=>>的一条渐近线为3y x=，那么双曲线的离心率为_________.10. 如图，BC为⊙O的直径，且BC=6，延长CB与⊙O在点D处的切线交于点A，若AD=4，则AB=________.11. 在ABC∆中角A，B，C的对边分别是a，b，c，若3sin cos cosb Ac A a C=+，则sin A=________．12. 在梯形ABCD中，//AB CD,2AB CD=，E为BC中点，若AE x AB y ADu u u r u u u r u u u r=+,则x+y=_______.CBA DO 21单价需求曲线供应曲线21单价需求曲线供应曲线13. 已知,x y 满足0,,.x y x x y k ≥⎧⎪≤⎨⎪+≤⎩（k 为常数），若2z x y =+最大值为8，则k =________.14.已知函数1(1),()1).x x f x x +≤⎧⎪=>若()(1)f x f x >+，则x 的取值范围是______.二、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．15.（本小题共13分）已知函数(=cos (cos )f x x x x ）+ . (Ⅰ)求()f x 的最小正周期；(Ⅱ)当π[0,]2x ∈ 时，求函数(f x ）的单调递减区间.16.（本小题共13分）从某病毒爆发的疫区返回本市若干人，为了迅速甄别是否有人感染病毒，对这些人抽血，并将血样分成4组，每组血样混合在一起进行化验. （Ⅰ）若这些人中有1人感染了病毒.①求恰好化验2次时,能够查出含有病毒血样组的概率； ②设确定出含有病毒血样组的化验次数为X ，求E （X ）.(Ⅱ)如果这些人中有2人携带病毒，设确定出全部含有病毒血样组的次数Y 的均值E (Y )，请指出（Ⅰ）②中E （X ）与E (Y )的大小关系.（只写结论,不需说明理由）如图，在五面体ABCDEF 中，四边形ABCD 为菱形，且∠BAD =60°，对角线AC 与BD 相交于O ；OF ⊥平面ABCD ，BC =CE =DE =2EF =2.(Ⅰ)求证： EF //BC ；(Ⅱ)求直线DE 与平面BCFE 所成角的正弦值.18.（本小题共14分）已知函数()ln f x x x =.（Ⅰ）求曲线()y f x =在点(1,(1))f 处的切线方程；（Ⅱ）求证：()1f x x ≥-；（Ⅲ）若22()(0)f x ax a a≥+≠在区间(0,)+∞上恒成立，求a 的最小值.已知椭圆G1.（Ⅰ）求椭圆G 的方程；（Ⅱ）设椭圆G 的短轴端点分别为,A B ，点P 是椭圆G 上异于点,A B 的一动点，直线,PA PB 分别与直线4x =于,M N 两点，以线段MN 为直径作圆C . ① 当点P 在y 轴左侧时，求圆C 半径的最小值；② 问：是否存在一个圆心在x 轴上的定圆与圆C 相切？若存在，指出该定圆的圆心和半径，并证明你的结论；若不存在，说明理由.20.（本小题共13分）已知数列{}n a 是无穷数列，12=,a a a b =（,a b 是正整数），11111(1),=(1)n nn n n n n nn a a a a a a aa a --+--⎧>⎪⎪⎨⎪≤⎪⎩.（Ⅰ）若122,=1a a =，写出45,a a 的值；（Ⅱ）已知数列{}n a 中*1)k a k N （=∈，求证：数列{}n a 中有无穷项为1；（Ⅲ）已知数列{}n a 中任何一项都不等于1，记212=max{,}(1,2,3,;n n n b a a n L -=max{,}m n 为,m n 较大者）.求证：数列{}n b 是单调递减数列.数学试题答案一、选择题：本大题共8小题，每小题5分，共40分．9. 2 10. 2 11.14. (0,1] 三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．解：(Ⅰ) 2(cos cos f x x x x + 1cos2(=sin 222xf x x ）++ 1cos2(2)2x f x x ）++1(=sin(2)62f x x ）π++22||2T πππω===()f x 的最小正周期为π. ----------------------------------7分(Ⅱ)当3222,262k x k k Z πππππ+≤+≤+∈ 时，函数(f x ）单调递减, 即()f x 的递减区间为：2[,],63k k k Z ππππ++∈,由2[0,][,]263k k I πππππ++=[,]62ππ+,k Z ∈所以(f x ）的递减区间为：[,]62ππ. ------------------------------------13分16. 解：（Ⅰ）①恰好化验2次时,就能够查出含有病毒血样的组为事件A. 1()4P A =恰好化验2次时,就能够查出含有病毒血样的组的概率为14.-----4分②确定出含有病毒血样组的次数为X,则X 的可能取值为1，2，3.1(1)4P X ==, 1(2)4P X ==，1(3)2P X ==. 则X 的分布列为：所以：E （X ）=11191234424⨯+⨯+⨯=--------------------------------------11分 (Ⅱ) ()()E X E Y < ------------------------------------------------------------------13分 17. 解：(Ⅰ)因为四边形ABCD 为菱形所以AD ∥BC ，且BC ⊄面ADEF ，AD ⊂面ADEF所以BC ∥面ADEF 且面ADEF I 面BCEF EF =所以EF ∥BC . ----------------------------------------------------------6分 (Ⅱ)因为FO ⊥面ABCD 所以FO AO ⊥，FO OB ⊥ 又因为OB AO ⊥以O 为坐标原点，OA ，OB ，OF 分别为x 轴，y 轴，z 轴，建立空间直角坐标系，取CD 的中点M ，连,OM EM . 易证EM ⊥平面ABCD .又因为22BC CE DE EF ====，得出以下各点坐标：1(0,1,0),((0,1,0),(22B C D F E ---向量1(2DE u u u r =，向量(1,0)BC u u u r =-，向量(0,BF u u u r =- 设面BCFE 的法向量为：0000(,,)n x y z u u r=000,0n BC n BF u u u ru u ur ⎧⋅=⎪⎨⋅=⎪⎩得到000000y y ⎧-=⎪⎨-+=⎪⎩令0y =时0(n u u r=-设DF u u u r 与0n uu r 所成角为ϕ，直线DE 与面BCEF 所成角为θ.sin θ=|cos |ϕ=00||||||n DE n DE u u r u u u r uu r u u u r ⋅⋅1|((1)1|⨯-+=5 直线EF 与平面BCEF所成角的正弦值为5.--------------------------------------13分 18.设函数()ln f x x x =.（Ⅰ）求曲线()y f x =在点(1,(1))f 处的切线方程；（Ⅲ）若22()(0)f x ax a a≥+≠在区间(0,)+∞上恒成立，求a 的最小值. 解：（Ⅰ）设切线的斜率为k()ln 1f x x '=+ (1)ln111k f '==+=因为(1)1ln10f =⋅=，切点为(1,0).切线方程为01(1)y x -=⋅-，化简得：1y x =-.----------------------4分（Ⅱ）要证：()1f x x ≥-只需证明：()ln 10g x x x x =-+≥在(0,)+∞恒成立， ()ln 11ln g x x x '=+-=当(0,1)x ∈时()0f x '<，()f x 在(0,1)上单调递减；当(1,)x ∈+∞时()0f x '>，()f x 在(1,)+∞上单调递增；当1x =时min ()(1)1ln1110g x g ==⋅-+=()ln 10g x x x x =-+≥在(0,)+∞恒成立所以()1f x x ≥-.----------------------------------------------------------------10分（Ⅲ）要使：22ln x x ax a ≥+在区间在(0,)+∞恒成立，等价于：2ln x ax ax≥+在(0,)+∞恒成立，等价于：2()ln 0h x x ax ax=--≥在(0,)+∞恒成立因为212()h x a x ax '=-+=2222a x ax ax-++=2212()()a x x a a ax -+- ①当0a >时，2(1)ln10h a a=--<，0a >不满足题意②当0a <时，令'()0h x =，则1x a =-或2x a=（舍）.所以1(0,)x a ∈-时()0h x '<，()h x 在1(0,)a -上单调递减；1(,)x a ∈-+∞时()0h x '>，()h x 在1(,)a -+∞上单调递增；当1x a =-时min 11()()ln()12h x h a a =-=-++当1ln()30-+≥时，满足题意所以30e a -≤<，得到a 的最小值为 3e ------------------------------------14分19. 解：1.所以2221,2b ca abc =⎧⎪⎪=⎨⎪⎪=+⎩得到21,a b c ⎧=⎪=⎨⎪=⎩分（Ⅱ）① 设00(,)P x y ，(0,1),(0,1)A B - 所以直线PA 的方程为：0011y y x x --=令4x =，得到004(1)1M y y x -=+同理得到004(1)1N y y x +=-，得到08|||2|MN x =- 所以，圆C 半径004|1|(20)r x x =--≤< 当02x =-时，圆C 半径的最小值为3. -----------------------------------9分② 当P 在左端点时，圆C 的方程为：22(4)9x y -+= 当P 在右端点时，设(2,0)P ，(0,1),(0,1)A B - 所以直线PA 的方程为：112y x --=令4x =，得到1M y =-同理得到1N y =，圆C 的方程为：22(4)1x y -+=，易知与定圆22(2)1x y -+=相切, 半径1R =由前一问知圆C 的半径0000041,204|1|41,02x x r x x x ⎧--≤<⎪⎪=-=⎨⎪-<≤⎪⎩ 因为004(1)1M y y x -=+，004(1)1N y y x +=-，圆C 的圆心坐标为004(4,)y x圆心距d =000004,2044||,02x x x x x ⎧--≤<⎪⎪=⎨⎪<≤⎪⎩ 当020x -?时，C 内切；当002x <?时，C 外切；存在一个圆心在x 轴上的定圆与圆C 相切，该定圆的圆心为(2,0)和半径1R =.(注: 存在另一个圆心在x 轴上的定圆与圆C 相切，该定圆的圆心为(6,0)和半径1R =.得分相同) --------------------------------------------------------------14分20..解：（Ⅰ）452,1a a ==；-------------------------------------------------2分（Ⅱ）*1)k a k N （=∈，假设1k a m +=①当1m =时，依题意有231k k a a ++==⋅⋅⋅⋅⋅⋅= ②当1m >时，依题意有2k a m +=，31k a +=③当1m <时，依题意有21k a m +=，321k a m +=，41k a m +=，51k a m+=，61k a += 由以上过程可知：若*1)k a k N （=∈，在无穷数列{}n a 中，第k 项后总存在数值为1 的项，以此类推，数列{}n a 中有无穷项为1. -------------------------------6分（Ⅲ）证明：由条件可知1(1,2,3,)n a n >=L ，因为{}n a 中任何一项不等于1，所以+11,2,3,)n n a a n ≠=L （. ①若212n n a a ->，则21n n b a -=.因为212+12=n n na a a -，所以212+1n n a a ->. 若21221n n a a ->，则212+22122n n n n a a a a --=<，于是2-12+2n n a a >；若21221n na a -<，则22222+222212121212n n n n n n n n n n na a a a a a a a a a a ----===⋅<<，于是2-12+2n n a a >；若21221n n a a -=，则2+21n a =，于题意不符；所以212+12+2max{,}n n n a a a ->，即1n n b b +>. ②若212n n a a -<，则2n n b a =. 因为22+1=nn a a ，所以22+1n n a a >；2016北京市丰台区高三(一模)数学(理)11 / 11 11 / 11 因为22+22+1=n n n a a a ，所以22+2n n a a >；所以22+12+2max{,}n n n a a a >，即1n n b b +>. 综上所述，对于一切正整数n ，总有1n n b b +>，所以数列{}n b 是单调递减数列.。

2016丰台一模理科数学附答案

丰台区2015—2016学年度第二学期统一练习（一） 2016.3高三数学（理科）第一部分（选择题共40分）选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1.已知全集U =R ，集合{}|23A x x x =≤-≥或，{}|14B x x x =<->或，那么集合()U C A B I 等于（）（A ）{}|24x x -<≤ （B ）{}|23x x -<<（C ）{}|21x x -<<-（D ）{}|2134x x x 或-<<-<<2．在下列函数中，是偶函数,且在0+∞（，）内单调递增的是（A ）||2x y =（B ）21y x =（C ）|lg |y x =（D ）cos y x = 3.对高速公路某段上汽车行驶速度进行抽样调查，画出如下频率分布直方图.根据直方图估计在此路段上汽车行驶速度的众数和行驶速度超过80km /h 的概率（A ） 75，0.25（B ）80,0.35 （C ）77.5,0.25 （D ）77.5,0.35 4.若数列{}n a 满足*12(0,)N n n n a a a n+=刮，且2a 与4a 的等差中项是5，则12n a a a +++L 等于（A ）2n （B ）21n -（C ）12n -（D ）121n --5. 已知直线m ,n 和平面α，若n ⊥α，则“m ⊂α”是“n ⊥m ”的（A ）充分而不必要条件（B ）必要而不充分条件（C ）充分必要条件（D ）既不充分也不必要条件6. 有三对师徒共6个人，站成一排照相，每对师徒相邻的站法共有（A ）72（B ）54（C ）48（D ） 87.如图，已知三棱锥P ABC -的底面是等腰直角三角形，且∠ACB=90O ，侧面P AB ⊥底面ABC ，AB =P A =PB =4.则这个三棱锥的三视图中标注的尺寸x ,y ,z 分别是（A ）23,2,2 （B ）4,2,22（C ）23,22，2 （D ）23,2,228. 经济学家在研究供求关系时，一般用纵轴表示产品价格(自变量)，而用横轴来表示产品数量（因变量）.某类产品的市场供求关系在不受外界因素（如政府限制最高价格等）的影响下，市场会自发调解供求关系：当产品价格P 1低于均衡价格P 0时，需求量大于供应量，价格会上升为P 2；当产品价格P 2高于均衡价格P 0时，供应量大于需求量，价格又会下降，价格如此波动下去，产品价格将会逐渐靠进均衡价格P 0.能正确表示上述供求关系的图形是（A ）（B ）（C ）（D ）侧视图zyy xABPC210单价需求曲线供应曲线210单价需求曲线供应曲线第二部分（非选择题共110分）一、填空题共6小题，每小题5分，共30分．9.已知双曲线22221(0,0)x y a b a b -=>>的一条渐近线为y =，那么双曲线的离心率为_________.10.如图，BC 为⊙O 的直径，且BC =6，延长CB 与⊙O 在点D 处的切线交于点A ，若AD =4，则AB =________.11. 在ABC ∆中角A ，B ，C 的对边分别是a ，b ，c ，若3sin cos cos b A c A a C =+，则sin A =________．12. 在梯形ABCD 中，//AB CD ,2AB CD =，E 为BC 中点，若AE x AB y AD u u u r u u u r u u u r =+,则x +y =_______.13. 已知,x y 满足0,,.x y x x y k ≥⎧⎪≤⎨⎪+≤⎩（k 为常数），若2z x y =+最大值为8，则k =________.14.已知函数1(1),()1).x x f x x +≤⎧⎪=>若()(1)f x f x >+，则x 的取值范围是______.A二、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15.（本小题共13分）已知函数(=cos (cos )f x x x x ）+ . (Ⅰ)求()f x 的最小正周期；(Ⅱ)当π[0,]2x ∈时，求函数(f x ）的单调递减区间.16.（本小题共13分）从某病毒爆发的疫区返回本市若干人，为了迅速甄别是否有人感染病毒，对这些人抽血，并将血样分成4组，每组血样混合在一起进行化验. （Ⅰ）若这些人中有1人感染了病毒.①求恰好化验2次时,能够查出含有病毒血样组的概率； ②设确定出含有病毒血样组的化验次数为X ，求E （X ）.(Ⅱ)如果这些人中有2人携带病毒，设确定出全部含有病毒血样组的次数Y的均值E (Y )，请指出（Ⅰ）②中E （X ）与E (Y )的大小关系.（只写结论,不需说明理由）17.（本小题共13分）如图，在五面体ABCDEF 中，四边形ABCD 为菱形，且∠BAD =60°，对角线AC 与BD 相交于O ；OF ⊥平面ABCD ，BC =CE =DE =2EF =2. (Ⅰ)求证： EF //BC ；(Ⅱ)求直线DE 与平面BCFE 所成角的正弦值.18.（本小题共14分）已知函数()ln f x x x =.（Ⅰ）求曲线()y f x =在点(1,(1))f 处的切线方程；（Ⅱ）求证：()1f x x ≥-；（Ⅲ）若22()(0)f x ax a a≥+≠在区间(0,)+∞上恒成立，求a 的最小值.19.（本小题共已知椭圆G1.（Ⅰ）求椭圆G 的方程；（Ⅱ）设椭圆G 的短轴端点分别为,A B ，点P 是椭圆G 上异于点,A B 的一动点，直线,PA PB 分别与直线4x =于,M N 两点，以线段MN 为直径作圆C . ① 当点P 在y 轴左侧时，求圆C 半径的最小值；② 问：是否存在一个圆心在x 轴上的定圆与圆C 相切？若存在，指出该定圆的圆心和半径，并证明你的结论；若不存在，说明理由.20.（本小题共13分）已知数列{}n a 是无穷数列，12=,a a a b =（,a b 是正整数），11111(1),=(1)nnn n n n n nn a a a a a a aa a --+--⎧>⎪⎪⎨⎪≤⎪⎩.（Ⅰ）若122,=1a a =，写出45,a a 的值；（Ⅱ）已知数列{}n a 中*1)k a k N （=∈，求证：数列{}n a 中有无穷项为1；（Ⅲ）已知数列{}n a 中任何一项都不等于1，记212=max{,}(1,2,3,;n n n b a a n L -=max{,}m n 为,m n 较大者）.求证：数列{}n b 是单调递减数列.丰台区2016年高三年级第二学期数学统一练习（一）数学（理科）参考答案一、选择题：本大题共8小题，每小题5分，共40分．二、填空题：本大题共6小题，每小题5分，共30分．9. 2 10. 2(0,1]三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．解：(Ⅰ) 2(cos cos f x x x x +1cos2(22xf x x ）++1cos2(2)2x f x x ）++1(=sin(2)62f x x ）π++22||2T πππω===()f x 的最小正周期为π. ----------------------------------7分(Ⅱ)当3222,262k x k k Z πππππ+≤+≤+∈ 时，函数(f x ）单调递减, 即()f x 的递减区间为：2[,],63k k k Z ππππ++∈, 由2[0,][,]263k k I πππππ++=[,]62ππ+,k Z ∈ 所以(f x ）的递减区间为：[,]62ππ. ------------------------------------13分16. 解：（Ⅰ）①恰好化验2次时,就能够查出含有病毒血样的组为事件A. 1()4P A =恰好化验2次时,就能够查出含有病毒血样的组的概率为14.-----4分②确定出含有病毒血样组的次数为X,则X 的可能取值为1，2，3.1(1)4P X ==, 1(2)4P X ==，1(3)2P X ==. 则X 的分布列为：所以：E （X ）=11191234424⨯+⨯+⨯=--------------------------------------------11分(Ⅱ) ()()E X E Y < ------------------------------------------------------------------13分 17. 解：(Ⅰ)因为四边形ABCD 为菱形所以AD ∥BC ，且BC ⊄面ADEF ，AD ⊂面ADEF所以BC ∥面ADEF 且面ADEF I 面BCEF EF =所以EF ∥BC . ----------------------------------------------------------6分 (Ⅱ)因为FO ⊥面ABCD 所以FO AO⊥，FO OB ⊥ 又因为OB AO ⊥以O 为坐标原点，OA ，OB ， OF 分别为x 轴，y 轴，z 轴，建立空间直角坐标系，取CD 的中点M ，连,OM EM . 易证EM ⊥平面ABCD . 又因为22BC CE DE EF ====，得出以下各点坐标：1(0,1,0),((0,1,0),(2B C D F E --向量1(22DE u u u r =-，向量(1,0)BC u u u r =-，向量(0,BFu u u r =- 设面BCFE 的法向量为：0000(,,)n x y z u u r=000,0n BC n BF u u u ru u ur ⎧⋅=⎪⎨⋅=⎪⎩得到000000y y ⎧-=⎪⎨-+=⎪⎩令0y =时0(n u u r=-设DF uuu r 与0n u u r所成角为ϕ，直线DE 与面BCEF 所成角为θ.sin θ=|cos |ϕ=00||||||n DE n DE u u r u u u r uu r u u u r ⋅⋅1|((1)1|-⨯-+=5直线EF 与平面BCEF分18.设函数()ln f x x x =.（Ⅰ）求曲线()y f x =在点(1,(1))f 处的切线方程；（Ⅱ）求证：()1f x x ≥-；（Ⅲ）若22()(0)f x ax a a≥+≠在区间(0,)+∞上恒成立，求a 的最小值.解：（Ⅰ）设切线的斜率为k()ln 1f x x '=+ (1)ln111k f '==+=因为(1)1ln10f =⋅=，切点为(1,0).切线方程为01(1)y x -=⋅-，化简得：1y x =-.----------------------------4分（Ⅱ）要证：()1f x x ≥-只需证明：()ln 10g x x x x =-+≥在(0,)+∞恒成立， ()ln 11ln g x x x '=+-=当(0,1)x ∈时()0f x '<，()f x 在(0,1)上单调递减；当(1,)x ∈+∞时()0f x '>，()f x 在(1,)+∞上单调递增；当1x =时min ()(1)1ln1110g x g ==⋅-+=()ln 10g x x x x =-+≥在(0,)+∞恒成立所以()1f x x ≥-.--------------------------------------------------------------------------10分（Ⅲ）要使：22ln x x ax a ≥+在区间在(0,)+∞恒成立，等价于：2ln x ax ax≥+在(0,)+∞恒成立，等价于：2()ln 0h x x ax ax=--≥在(0,)+∞恒成立因为212()h x a x ax '=-+=2222a x ax ax-++=2212()()a x x a a ax -+- ①当0a >时，2(1)ln10h a a=--<，0a >不满足题意②当0a <时，令'()0h x =，则1x a =-或2x a=（舍）.所以1(0,)x a ∈-时()0h x '<，()h x 在1(0,)a -上单调递减；1(,)x a ∈-+∞时()0h x '>，()h x 在1(,)a -+∞上单调递增；当1x a =-时min 11()()ln()12h x h a a =-=-++当1ln()30a-+≥时，满足题意所以30e a -≤<，得到a 的最小值为 3e ------------------------------------14分19. 解：1.所以2221,b ca ab c=⎧⎪⎪=⎨⎪⎪=+⎩得到21,a b c ⎧=⎪=⎨⎪=⎩ 所以椭圆的方程为-----------------------------------------------------------3分（Ⅱ）① 设00(,)P x y ，(0,1),(0,1)A B - 所以直线PA 的方程为：0011y y x x --=令4x =，得到004(1)1M y y x -=+同理得到004(1)1N y y x +=-，得到08|||2|MN x =-所以，圆C 半径004|1|(20)r x x =--≤< 当02x =-时，圆C 半径的最小值为3. --------------------------------------9分② 当P 在左端点时，圆C 的方程为：22(4)9x y -+= 当P 在右端点时，设(2,0)P ，(0,1),(0,1)A B - 所以直线PA 的方程为：112y x --=令4x =，得到1M y =-同理得到1N y =，圆C 的方程为：22(4)1x y -+=，易知与定圆22(2)1x y -+=相切, 半径1R =由前一问知圆C 的半径0000041,204|1|41,02x x r x x x ⎧--≤<⎪⎪=-=⎨⎪-<≤⎪⎩因为004(1)1M y y x -=+，004(1)1N y y x +=-，圆C 的圆心坐标为004(4,)y x圆心距d ==000004,2044||,02x x x x x ⎧--≤<⎪⎪=⎨⎪<≤⎪⎩ 当020x -?时，C 内切；当002x <?时，C 外切；存在一个圆心在x 轴上的定圆与圆C 相切，该定圆的圆心为(2,0)和半径1R =.(注: 存在另一个圆心在x 轴上的定圆与圆C 相切，该定圆的圆心为(6,0)和半径1R =.得分相同)------------------------------------------------------------------------------------14分20..解：（Ⅰ）452,1a a ==；-----------------------------------------------------2分（Ⅱ）*1)k a k N （=∈，假设1k a m += ①当1m =时，依题意有231k k a a ++==⋅⋅⋅⋅⋅⋅=②当1m >时，依题意有2k a m +=，31k a +=③当1m <时，依题意有21k a m +=，321k a m +=，41k a m +=，51k a m +=，61k a += 由以上过程可知：若*1)k a k N （=∈，在无穷数列{}n a 中，第k 项后总存在数值为1 的项，以此类推，数列{}n a 中有无穷项为1. --------------------------------------------------6分（Ⅲ）证明：由条件可知1(1,2,3,)n a n >=L ，因为{}n a 中任何一项不等于1，所以+11,2,3,)n n a a n ≠=L （.①若212n n a a ->，则21n n b a -=. 因为212+12=n n n a a a -，所以212+1n n a a ->. 若21221n na a ->，则212+22122n n n n a a a a --=<，于是2-12+2n n a a >；若21221n na a -<，则22222+222212121212n n n n n n n n n n na a a a a a a a a a a ----===⋅<<，于是2-12+2n n a a >；若21221n n a a -=，则2+21n a =，于题意不符；所以212+12+2max{,}n n n a a a ->，即1n n b b +>.②若212n n a a -<，则2n n b a =.因为22+12-1=n n n a a a ，所以22+1n n a a >；因为22+22+1=n n n a a a ，所以22+2n n a a >；所以22+12+2max{,}n n n a a a >，即1n n b b +>.综上所述，对于一切正整数n ，总有1n n b b +>，所以数列{}n b 是单调递减数列.-------------------------------------------------------------------------------13分。

【高3】2016年北京市丰台区高考2模数学(理科)答案

丰台区2016年高三年级第二学期数学统一练习（二）数学（理科）参考答案一、选择题：本大题共8小题，每小题5分，共40分．二、填空题：本大题共6小题，每小题5分，共30分．9. 2-i 10. 49 11. 5 12.13 13. 12 14. 12三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．15.（本小题共13分）解：（Ⅰ）由正弦定理及1cos 2a C c b +=得：1sin cos sin sin 2A C C B +=， ----------------------2分化简1sin cos sin sin()2A C C A C +=+ ----------------------4分解得：1cos 2A =， ----------------------6分因为0o <A<180o ,所以60oA =. -----------------------7分（Ⅱ）由余弦定理得：221255c c =+-，即2540c c -+=.---------------------10分解得1c =和4c =， ---------------------12分经检验1，4都是解，所以c 的值是1和4. ---------------------13分 16.（本小题共13分）解：（Ⅰ）在编号为1、2、3的收案案件中随机取1件，共有2400+3000+4100=9500种取法，其中取到的是结案案件方法数为2400+2900+4000=9300种---—————-----—--3分设“在收案案件中取1件结案案件”为事件A ，则P （A ）=9395.——-——-----5分（Ⅱ）在该结案案件中任取一件共有2900种取法，其中是判决案件有1200种取法.—8分设“在该结案案件中取1件判决案件”为事件B ，则P （B ）=1229.-----------10分 (注：讲评时应告诉学生这个概率低是因为人民法院做了大量工作如法庭调解案件、使得当事人撤诉等工作，有时法律不能解决感情问题)（Ⅲ）21S >22S . --------------------------13分（可以简单直观解释，也可以具体：设4类案件的均值为X ，则34x xX x +==. 2222212342()()()()4x x x x x x x x S -+-+-+-=2222123()()()()4x x x x x x x x -+-+-+-=222123()()()4x x x x x x -+-+-=22221231()()()3x x x x x x S -+-+-<=）17.（本小题共14分）解：（Ⅰ）在图1中，因为AB ∥CD ，AB =CD ，所以ABCD 为平行四边形，所以AD ∥BC ,因为∠B =90O,所以AD ⊥BE ，当三角形EDA 沿AD 折起时，AD ⊥AB ，AD ⊥AE ，即：AD ⊥AB ，AD ⊥P A ， -----------------------3分又AB ∩P A =A .所以AD ⊥平面P AB ， -----------------------4分又因为PB 在平面P AB 上，所以AD ⊥PB . ---------------------5分（Ⅱ） ①以点A 为坐标原点，分别以AB ，AD ，AP 为x ,y ,z 轴建立空间直角坐标系，如图. -------6分则A （0,0,0），B （1,0,0），C （1,1,0），P （0,0,1）.即(1,1,1)PC =-，(0,1,0)BC =，(1,0,0)DC =—————-------———7分设平面PBC 的法向量为(,,)n x y z =，则0,PC n BC n ⎧⋅=⎪⎨⋅=⎪⎩，所以0,0x y z y +-=⎧⎨=⎩，取1z =，取1x =， —------———8分所以(1,0,1)n =；同理求得平面PCD 的法向量(0,1,1)m =--. 设二面角B-PC-D 为α，所以1cos 2||||n m n m α⋅-==⋅,————————9分所求二面角B-PC-D 为120o. —————————————10分图2图1②设AM 与面PBC 所成的角为ϕ.(0,0,1)(1,1,1)(,,1)AM AP PM λλλλ=+=+-=-，平面PBC 的法向量 1(1,0,1)n =, --------------12分sin ϕ=1|cos ,||2AM n <>==,---------------13分解得：20,3λλ==—————————————14分18.（本小题共13分）解：（Ⅰ）当2a =-时，22()exg x x -=，222'()e(22)=-2(1)e xx g x x x x x --=--—-2分x 与'()g x 、()g x 之间的关系如下表：函数在区间(0,)+∞内只有一个极大值点，所以这个极值点也是最大值点1x =，---4分最大值21(1)e g =. --------------------5分（Ⅱ）（1）当0a =时，2()1h x x =-，显然在区间(0,16)内没有两个零点，0a =不合题意. --------------------------------- ---6分(2)当0a ≠时，2()1e ax x h x =-，222()(2)e '()e e axax axax x x ax a h x ---==. --------8分①当0a <且(0,16)x ∈时，'()0h x >，函数()h x 区间(0,)+∞上是增函数，所以函数()h x 区间(0,16)上不可能有两个零点，所以0a <不合题意； ————9分 ②当0a >时，在区间(0,)+∞上x 与'()h x 、()h x 之间的关系如下表：分因为(0)1h =-，若函数()h x 区间(0,16)上有两个零点，则2()0,216,(16)0h a a h ⎧>⎪⎪⎪<⎨⎪<⎪⎪⎩，所以22816410,1,8210ae a a e ⎧->⎪⎪⎪>⎨⎪⎪-<⎪⎩，化简20,e 1,8ln 22a a a ⎧<<⎪⎪⎪>⎨⎪⎪>⎪⎩. ------------11分因为1ln 214ln 21ln161682e <⇔<⇔<⇔<，2ln 24eln 243eln 2e 2>⇔>⇔>>, ----------------------12分所以1ln 2282e<<. 综上所述，当ln 222ea <<时，函数2()1()x h x f x =-在区间(0,16)内有两个零点. —————————13分19.（本小题共14分）解：（Ⅰ）因为2,a b ==，所以1c =，离心率12e =. ————————3分（Ⅱ）22,3412y x m x y =+⎧⎨+=⎩，消去y 的并化简得22784120x mx m ++-=.------4分2226428(412)16(213)0m m m ∆=--=->，—————----------5分设1122(,),(,)M x y N x y，则||7MN ==，-------7分解得2m =±，且满足0∆>. —————————8分（Ⅲ）直线AB 的方程为11y y x x =，即110y x x y -=. 点22(,)P x y 到直线AB的距离d =，||AB =分21211||||2PAB S AB d y x x y ∆===-， -----—10分因为12120,0,0,0x x y y ><>>，2222112233(4),(4)44y x y x =-=-，12y y ==--12分所以21212112||||||y x x y y x y x -=+ -------------13分21|||)2x x =2221)x x =+，=所以当22124x x +=时，三角形△P AB的面积为定值 ---------------14分（Ⅲ）方法二：设直线AB 的方程为y kx =，即0kx y -=.220,3412kx y x y -=⎧⎨+=⎩，解得2121234x k =+. 1||2|AB x ==点22(,)P x y ）到直线AB的距离d =，11221|||||||2PAB S AB d x x kx y ∆===-，-------------10分因为12120,0,0,0x x y y ><>>，则0k >.所以1x =，2x ==，212y x ===， ----------------12分22kx y k -=⨯=122||||PAB S x kx y ∆=-==.所以三角形△P AB 的面积为定值. ---------------------14分20.（本小题共13分）解：（Ⅰ）1110,1,2,3(7)max {3}max{0,3,6,9}9x f x ====，当13x =时,1(7)9f =.-----4分（Ⅱ）222120,1,2(7)max{4(73)}x f x f x ==+-， 111max{0(7),4(4),8(1)}f f f =+++当21x =时，1110,1,2(4)max{3}max{0,3,6}6x f x ====,当12x =时1(4)6f =.当22x =时，1110(1)max{2}0x f x ===,即当10x =时,1(1)0f =.2(7)m a x {9,46,80}10f =++=，即当21x =，12x =时2(7)10f =.-----10分（Ⅲ）答：4 4.5p <<. ----- -----13分。

北京市丰台区2016-2017学年度第二学期一模练习高三数学文科试题Word版含答案

丰台区2017年高三年级第二学期综合练习(一)数学(文科)2017. 03(本试卷满分共150分，考试时间120分钟) 注意事项：1. 答题前，考生务必先将答题卡上的学校、年级、班级、姓名、准考证号用黑色字迹签字笔填写清楚，并认真核对条形码上的准考证号、姓名，在答题卡的“条形码粘贴区”贴好条形码。

2. 本次考试所有答题均在答题卡上完成。

选择题必须使用2B铅笔以正确填涂方式将各小题对应选项涂黑，如需改动，用橡皮擦除干净后再选涂其它选项。

非选择题必须使用标准黑色字迹签字笔书写，要求字体工整、字迹清楚。

3•请严格按照答题卡上题号在相应答题区内作答，超出答题区域书写的答案无效，在试卷、草稿纸上答题无效。

4•请保持答题卡卡面清洁，不要装订、不要折叠、不要破损。

第一部分(选择题共40分)一、选择题共8小题，每小题5分，共40分•在每小题列出的四个选项中，选出符合题目要求的一项.1. 如果集合A」..x Z - 2 空x：：:1^, B-—1,0,1｝，那么A B =(A)〈-2, -1,0,r ( B)〈-1,0,1? (C) \0,v( D)〈-1,0?2. 在平面直角坐标系xOy中，与原点位于直线(A) (-3,4)(D) (0, -3)3. 执行如图所示的程序框图，则输出的i值是(A ) 3(C) 54. 设命题p：一[0,二),e x -1，则一p 是(A)X。

订0, ：：) , e x0：：1(B)~x[0,：：) , e x：：1(C)X0[0,：：) , e x°-1(D)-x[0,：：) ,e x.13x+2y • 5=0同一侧的点是(B) (-3, -2) ( C ) (-3, -4) / 输/。

2016届北京市丰台区高三下学期统一练习(一模)数学(文科)

2016届北京市丰台区高三下学期统一练习（一模）数学（文科）一、选择题（共8小题；共40分）1. 已知全集，集合，集合，则集合A. B. C. D.2. 下列函数在其定义域上既是奇函数又是增函数的是A. B.C. D.3. 某赛季，甲、乙两名篮球运动员都参加了场比赛，他们每场比赛得分的情况用茎叶图表示，如图，则甲、乙两名运动员得分的中位数分别为A. ，B. ，C. ，D. ，4. 已知直线，和平面，，，那么“”是“”的A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件5. 已知双曲线的一个焦点，点在双曲线的一条渐近线上，点为双曲线的对称中心，若为等腰直角三角形，则双曲线的离心率为A. B. C. D.6. 已知等比数列{ }中，且，那么的值是A. B. C. D.7. 如图，已知三棱锥的底面是等腰直角三角形，且，侧面底面，.则这个三棱锥的三视图中标注的尺寸，，分别是A. ，B. ，，C. ，，D. ，，8. 经济学家在研究供求关系时，一般用纵轴表示产品价格（自变量），用横轴表示产品数量（因变量）．某类产品的市场供求关系在不受外界因素（如政府限制最高价格等）的影响下，市场会自发调解供求关系：当产品价格低于均衡价格时，则需求量大于供应量，价格会上升为；当产品价格高于均衡价格时，则供应量大于需求量，价格又会下降，价格如此继续波动下去，产品价格将会逐渐靠近均衡价格．能正确表示上述供求关系的图形是A. B.C. D.二、填空题（共6小题；共30分）9. 在锐角中，角，，所对应的边分别为，，，若，则 ______ .10. 已知中，，，，则 ______ .11. 已知圆，则圆被动直线所截得的弦长是______ .12. 已知，则函数的最小值为______ .13. 已知满足目标函数的最大值为，则的值为______ .14. 函数．①.当时，函数的零点个数是______；②.若函数有两个不同的零点，则的取值范围是______．三、解答题（共6小题；共78分）15. 已知函数．（1）求函数的最小正周期；（2）求在区间上的最大值和最小值.16. 下图是根据某行业网站统计的某一年 1 月到 12 月（共 12 个月）的山地自行车销售量（代表辆）折线图，其中横轴代表月份，纵轴代表销售量，由折线图提供的数据回答下列问题：（1）在一年中随机取一个月的销售量，估计销售量不足的概率；（2）在一年中随机取连续两个月的销售量，估计这连续两个月销售量递增（如 2 月到 3 月递增）的概率；（3）根据折线图，估计年平均销售量在哪两条相邻水平平行线线之间（只写出结果，不要过程）.17. 已知在中，，，分别为边，的中点，将沿翻折后，使之成为四棱锥（如图）.（1）求证：平面；（2）设平面平面，求证：；（3）若，，，为棱上一点，设，当为何值时，三棱锥的体积是?18. 已知函数，数列满足： .（1）求数列的通项公式；（2）设数列的前项和为，求数列的前项和 .19. 已知函数．（1）求曲线在处的切线的方程；（2）若函数在定义域内是单调函数，求的取值范围；（3）当时，（1）中的直线与曲线有且只有一个公共点，求的取值范围.20. 已知椭圆：过点，离心率，斜率为直线过点，与椭圆交于，两点（在，之间），与轴交于点 .（1）求椭圆的标准方程；（2）为轴上不同于点的一点，为线段的中点，设的面积为，面积为，求的取值范围.答案第一部分1. A2. A3. C4. A5. B6. B7. C8. D第二部分9.10.11.12.13.14. ；第三部分15. （1）；（2）因为，所以，即，由此得到：，此时；，此时．16. （1）设销售量不足为事件，这一年共有 12 个月，其中1 月，2 月，6 月，11 月共 4 个的销售量不足，所以．（2）设连续两个月销售量递增为事件，在这一年中随机取连续两个月的销售量，有 1，2 月；2，3 月；3，4 月；4，5 月；5，6 月；6，7 月；7，8 月；8，9 月；9，10 月；10，11 月；11，12 月共 11 种取法，其中2，3 月，3，4 月；4，5 月；6，7 月；7，8 月；8，9 月；11，12 月共种情况的销售量递增，所以．（3）在这两条水平线之间．17. （1）因为，，分别为，的中点，所以 .所以，．又因为，所以平面．（2）因为，面，面，所以面，又因为面，面面，所以．（3）因为，，，所以平面．因为，所以 .又因为，，，所以 .，解得．18. （1）因为，所以 .即，所以数列是以首项为，公差为的等差数列，所以 .（2）因为数列是等差数列，所以 .所以 .所以19. （1），因为，所以切点为（，）．又，所以切线，即 .（2）①当时，，所以在上单调递减，符合题意．②当时，设，该抛物线开口向上，且，过点，所以该抛物线与轴相交，交点位于原点两侧，不单调，不符合题意，舍去．综上．（3）因为直线与有且只有一个公共点，所以方程，即有且只有一个根．设，则，①当时，因为，所以，令，解得；令，解得；所以在上单调递增，在上单调递减，所以，所以符合条件．②当时，则令，解得；令，解得或；所以在上单调递增，在，上单调递减，因为，所以，．又，所以，即，所以．所以在上有一个零点，且，所以有两个零点，不符合题意．综上．20. （1）由已知得，又，所以，即，所以椭圆的标准方程为．（2）设，直线．由得：所以，即因为所以，即．因为，所以．又，而，，设，所以．。

北京市丰台区高三一模考(数学理)1

北京市丰台区2009年高三统一练习（一）数学（理科） 2009年3月本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

第Ⅰ卷1至2页，第Ⅱ卷3至9页，共150分。

考试时间120分钟。

考试结束，将本试卷和答题卡一并交回。

第Ⅰ卷（选择题共40分）注意事项：1. 答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。

2. 每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

不能答在试卷上。

一、选择题：本大题共8个小题，每小题5分，共40分。

在每个小题列出的四个选项中，选出符合题目要求的一项。

1. 在复平面内，复数2)21(i z +=所对应的点位于（A ）第一象限（B ）第二象限（C ）第三象限（D ）第四象限 2. 已知全集R U =，集合{}2≤=y y A ，集合{}x y y B 2==，那么集合)(B C A U 等于（A ）{}02≤≤-y y （B ）{}20≤≤y y （C ）{}2-≥y y （D ）{}0≤y y3. 已知直线m ⊂平面α ，直线n ⊂平面α ，“直线c ⊥m ，直线c ⊥n ”是“直线c ⊥平面α”的（A ）充分而不必要条件（B ）必要而不充分条件（C ）充要条件（D ）既不充分也不必要条件4. 以双曲线1322=-x y 的一个焦点为圆心，离心率为半径的圆的方程是（A ）4)2(22=+-y x (B ) 2)2(22=-+y x (C ) 2)2(22=+-y x (D ) 4)2(22=-+y x5. 已知函数)(x f y =的图像与函数)0(2≥=x x y 的图像关于直线x y =对称，那么下列情形不可能出现的是（A ）函数)(x f y =有最小值（B ）函数)(x f y =过点（4，2）（C ）函数)(x f y =是偶函数（D ）函数)(x f y =在其定义域上是增函数 6. 在平面直角坐标系xOy 中作矩形OABC ,已知3,4==AB OA ,则AC → ·OB →的值为（A ）0 （B ）7 （C ）25 （D ）7-7. 北京奥运会乒球男团比赛规则如下：每队3名队员，两队之间共需进行五场比赛，其中一场双打，四场单打，每名队员都需比赛两场（双打需两名队员同时上场比赛），要求双打比赛必须在第三场进行，若打满五场，则三名队员不同的出赛顺序安排共有（A ）144 （B ）72 （C ）36 （D ）188. 已知)(x f ，)(x g 都是定义在R 上的函数，且满足以下条件：①)(x f =x a ·)(x g （0,0≠>a a ）；②)(x g 0≠；③)()()()(''x g x f x g x f ⋅>⋅。

北京市丰台区高三数学第一次高考模拟考试(理)新人教版

北京市丰台区2010年高三年级第二学期统一练习（一）数学试题（理）注意事项： 1．答题前，考生务必先将答题卡上的学校、年级、班级、姓名、准考证号用黑色字迹签字笔填写清楚，并认真核对条形码上的准考证号、姓名，在答题卡的“条形码粘贴区”贴好条形码.2．本次考试所有答题均在答题卡上完成.选择题必须使用2B 铅笔以正确填涂方式将各小题对应选项涂黑，如需改动，用橡皮擦除干净后再选涂其它选项.非选择题必须使用标准黑色字迹签字笔书写，要求字体工整、字迹清楚.作图题用2B 铅笔作图，要求线条、图形清晰.3．请严格按照答题卡上题号在相应答题区内作答，超出答题区域书写的答案无效，在试题、草稿纸上答题无效.4．请保持答题卡卡面清洁，不要装订、不要折叠、不要破损.一、本大题共8小题，每小题5分共40分.在每小题列出的四个选项中，选出符合题目要求的一项. 1．如果aiaiz +-=11为纯虚数，则实数a 等于（）A ．0B ．-1C ．1D ．-1或12．设集合[)(]}1,0,log |{},,0,)21(|{2∈==+∞∈==x x y y N x y y M x，则集合N M 是（）A ．[)+∞-∞,1)0,(B ．[)+∞,0C ．(]1,∞-D ．)1,0()0,( -∞ 3．若,)21(2210n n n x a x a x a a x ++++=- 则2a 的值是（）A ．84B ．-84C ．280D ．-2804．奇函数)0,()(-∞在x f 上单调递增，若,0)1(=-f 则不等式0)(<x f 的解集是（） A ．)1,0()1,(⋃--∞ B ．),1()1,(+∞⋃--∞C ．)1,0()0,1( -D ．),1()0,1(+∞⋃-5．从0，2，4中取一个数字，从1，3，5中取两个数字，组成无重复数字的三位数，则所有不同的三位数的个数是（） A ．36 B ．48 C ．52 D ．54 6．在ABC ∆，|"||"""AC =⋅=⋅是的（）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件7．设,24,0,0=++>>ab b a b a 则（）A ．a+b 有最大值8B ．a+b 有最小值8C ．ab 有最大值8D ．ab 有最小值8 8．已知整数以按如下规律排成一列：（1，1）、（1，2）、（2，1）、（1，3）、（2，2），（3，1），（1，4），（2，3），（3，2），（4，1）……，则第60个数对是（） A ．（10，1） B ．（2，10） C ．（5，7） D ．（7，5）二、填空题：本大题共6小题，每小题5分，共30分.把答案填在题中横线上.9．在平行四边形ABCD 中，点E 是边AB 的中点，DE 与AC 交于点F ，若AE F ∆的面积是1cm 2，则CDF ∆的面积是 cm 2.10．若一个正三棱柱的三视图及其尺寸如下图所示（单位：cm ），则该几何体的体积是cm 3.11．样本容量为1000的频率分布直方图如图所示.根据样本的频率分布直方图计算，x 的值为，样本数据落在[)14,6内的频数为 . 12．在平面直角坐标系xOy 中，直线l 的参数方程为⎩⎨⎧+==11t y x （参数R t ∈），圆C 的参数方程为⎩⎨⎧=+==θθsin 1cos y x （参数[)πθ2,0∈），则圆心到直线l 的距离是 .13．在右边的程序框图中，若输出i 的值是4，则输入x 的取值范围是 .14．函数)10(12≤≤+=x x y 图象上点P 处的切线与直线1,0,0===x x y 围成的梯形面积等于S ，则S 的最大值等于，此时点P 的坐标是 .三、解答题：本大题共6小题，共80分.解答应写出文字说明，演算步骤或证明过程. 15．（12分）已知函数x b x a x f cos sin )(+=的图象经过点).1,3(),0,6(ππ（I ）求实数a 、b 的值；（II ）若]2,0[π∈x ，求函数)(x f 的最大值及此时x 的值.16．（13分）如图，在底面是正方形的四棱锥P —ABCD 中，PA ⊥面ABCD ，BD 交AC 于点E ，F 是PC 中点，G 为AC 上一点. （I ）求证：BD ⊥FG ；（II ）确定点G 在线段AC 上的位置，使FG//平面PBD ，并说明理由. （III ）当二面角B —PC —D 的大小为32π时，求PC 与底面ABCD 所成角的正切值. 17．（14分）某工厂师徒二人各加工相同型号的零件2个，是否加工出精品均互不影响.已知师父加工一个零件是精品的概率为32，师徒二人各加工2个零件都是精品的概率为.91 （I ）求徒弟加工2个零件都是精品的概率；（II ）求徒弟加工该零件的精品数多于师父的概率；（III ）设师徒二人加工出的4个零件中精品个数为ξ，求ξ的分布列与均值E ξ.18．（13分）已知函数.ln )(xax x f += （I ）当a<0时，求函数)(x f 的单调区间；（II ）若函数f （x ）在[1，e]上的最小值是,23求a 的值. 19．（13分）在直角坐标系xOy 中，点M 到点)0,3(),0,3(21F F -的距离之和是4，点M 的轨迹是C 与x 轴的负半轴交于点A ，不过点A 的直线b kx y l +=:与轨迹C 交于不同的两点P 和Q.（I ）求轨迹C 的方程；（II ）当0=⋅时，求k 与b 的关系，并证明直线l 过定点.20．（14分）设集合W 由满足下列两个条件的数列}{n a 构成： ①;212++<+n n n a a a ②存在实数M ，使.M a n ≤（n 为正整数）（I ）在只有5项的有限数列;5,4,3,2,1,}{},{54321=====a a a a a b a n n 其中中 1,4,5,4,154321=====b b b b b ；试判断数列}{},{n n b a 是否为集合W 的元素；（II ）设}{n c 是各项为正的等比数列，n S 是其前n 项和，,47,4133==S c 证明数列W S n ∈}{；并写出M 的取值范围；（III ）设数列,}{W d n ∈且对满足条件的M 的最小值M 0，都有)(*N n M d n n ∈≠. 求证：数列}{n d 单调递增.参考答案一、选择题（每小题5分，共40分） BCAABCBC二、填空题（每小题5分，共30分） 9．4 10．324 11．0.09,680 12．2 13．(]4,2 14．)45,21(,45 三、解答题：（本大题共6小题，共80分） 15．（12分）解：（I ）∵函数x b x a x f cos sin )(+=的图象经过点)1,3(),0,6(ππ，⎪⎪⎩⎪⎪⎨⎧=+=+∴1212302321b a b a …………4分解得：1,3==b a …………5分（II ）由（I ）知：)6sin(2cos sin 3)(π-=-=x x x x f…………8分 ],3,6[6],2,0[ππππ-∈-∴∈x x…………9分2,36πππ==-∴x x 即当时，)(x f 取得最大值.3…………12分16．（13分）证明：（I ）⊥PA 面ABCD ，四边形ABCD 是正方形，其对角线BD ，AC 交于点E ， ∴PA ⊥BD ，AC ⊥BD. ∴BD ⊥平面APC ， ⊂FG 平面PAC ， ∴BD ⊥FG …………7分（II ）当G 为EC 中点，即AC AG 43=时， FG//平面PBD ， …………9分理由如下：连接PE ，由F 为PC 中点，G 为EC 中点，知FG//PE ，而FG ⊄平面PBD ，PB ⊂平面PBD ，故FG//平面PBD. …………13分（III ）作BH ⊥PC 于H ，连结DH ，∵PA ⊥面ABCD ，四边形ABCD 是正方形， ∴PB=PD ，又∵BC=DC ，PC=PC ， ∴△PCB ≌△PCD ，∴DH ⊥PC ，且DH=BH ，∴∠BHD 主是二面角B —PC —D 的平面角，…………11分即,32π=∠BHD ∵PA ⊥面ABCD ，∴∠PCA 就是PC 与底面ABCD 所成的角 …………12分连结EH ，则PC EH BHE BD EH ⊥=∠⊥,3,π,,3tan EC BE EHBEBHE ===∠∴而 ,33sin ,3==∠∴=∴EC EH PCA EH EC ,22tan =∠∴PCA ∴PC 与底面ABCD 所成角的正切值是22 …………14分解：以A 为原点，AB ，AD ，PA 所在的直线分别为x ，y ，z 轴建立空间直角坐标系如图所示，设正方形ABCD 的边长为1，则A （0，0，0），B （1，0，0），C （1，1，0） D （0，1，0），P （0，0，a ）（a>0）,)20)(0,,(),2,21,21(),0,21,21(<<m m m G aF E（I ）),2,21,21(),0,1,1(a m m FG BD ---=-= 002121=+-++=⋅m m FG BD ⊥∴ …………5分（II ）要使FG//平面PBD ，只需FG//EP ，而),21,21(a -=，由λ=可得⎪⎪⎩⎪⎪⎨⎧-=-=-λλa a m 22121，解得,1=λ,43=m …………7分,43),0,43,43(AC AG G =∴∴故当AC AG 43=时，FG//平面PBD…………9分设平面PBC 的一个法向量为),,,(z y x u =则⎪⎩⎪⎨⎧=⋅=⋅00PC u ，而)0,1,0(),,1,1(=-=a ⎩⎨⎧==-+∴00y az y x ，取z=1，得)1,0,(a =，同理可得平面PBC 的一个法向量)1,,0(a v = 设v u ,所成的角为0，则,21|32cos||cos |==πθ ,21111,21||||22=+⋅+∴=a a v u 1=∴a…………12分∵PA ⊥面ABCD ，∴∠PCA 就是PC 与底面ABCD 所成的角，2221tan ===∠∴AC PA PCA …………14分17．（14分）解：（I ）设徒弟加工1个零件是精品的概率为p 1，则,419132322121==⨯p p 得所以徒弟加工2个零件都是精品的概率是41…………3分（II ）设徒弟加工零件的精品数多于师父的概率为p ，由（I ）知，211=p徒弟加工两个零件中，精品个数的分布列如下：所以364949492=⨯+⨯+⨯=p…………9分（III ）ξ的分布列为…………13分 ξ的期望为373644361233613236613610=⨯+⨯+⨯+⨯+⨯…………14分18．（13分）解：函数xax x f +=ln )(的定义域为),0(+∞ …………1分 221)('xax x a x x f -=-=…………3分（1）.0)(',0>∴<x f a故函数在其定义域),0(+∞上是单调递增的. …………5分（II ）在[1，e]上，发如下情况讨论：①当a<1时，,0)('>x f 函数)(x f 单调递增，其最小值为,1)1(<=a f这与函数在[1，e]上的最小值是23相矛盾； …………6分②当a=1时，函数(]e x f ,1)(在单调递增，其最小值为,1)1(=f 同样与最小值是23相矛盾； …………7分③当e a <<1时，函数[)a x f ,1)(在上有0)('<x f ，单调递减，在(]e a ,上有,0)('>x f 单调递增，所以，函数)(x f 满足最小值为1ln )(+=a a f 由,,231ln e a a ==+得 …………9分④当a=e 时，函数[),0)(',1)(<x f e x f 上有在单调递减，其最小值为,2)(=e f 还与最小值是23相矛盾； …………10分⑤当a>e 时，显然函数],1[)(e x f 在上单调递减，其最小值为,21)(>+=eae f 仍与最小值是23相矛盾； …………12分综上所述，a 的值为.e…………13分19．（13分）解：（1）)0,3(),0,3(-到点M 的距离之和是4，M ∴的轨迹C 是长轴为4，焦点在x 轴上焦中为32的椭圆，其方程为.1422=+y x …………3分（2）将b kx y +=，代入曲线C 的方程，整理得0428)41(22=+++kx x k…………5分因为直线l 与曲线C 交于不同的两点P 和Q ，所以.0)14(16)44)(41(464222222>+-=-+-=∆b k b k b k ①设),,(),,(2211y x Q y x P ，则221221414,4128k x x k k x x +=+-=+ ② …………7分且.)()())((2212122121b x x kb x x k b kx b kx y y +++=++=⋅③ 显然，曲线C 与x 轴的负半轴交于点A （-2，0），所以),,2(),,2(2211y x y x +=+= 由.0)2)(2(,02121=+++=⋅y y x x 得将②、③代入上式，整理得.05161222=+-b kb k …………10分所以,0)56()2(=-⋅-b k b k 即,562k b k b ==或经检验，都符合条件①当b=2k 时，直线l 的方程为.2k kx y += 显然，此时直线l 经过定点（-2，0）点.即直线l 经过点A ，与题意不符. 当k b 56=时，直线l 的方程为).65(56+=+=x k k kx y显然，此时直线l 经过定点)0,56(-点，且不过点A.综上，k 与b 的关系是：,56k b =且直线l 经过定点)0,56(-点…………13分20．（14分）解：（I ）对于数列}{n a ，取,22231a a a ==+显然不满足集合W 的条件，① 故}{n a 不是集合W 中的元素， …………2分对于数列}{n b ，当}5,4,3,2,1{∈n 时，不仅有,42,32342231b b b b b b <=+<=+,32433b b b <=+而且有5≤n b ，显然满足集合W 的条件①②，故}{n b 是集合W 中的元素. …………4分（II ）}{n c 是各项为正数的等比数列，n S 是其前n 项和，,47,4133==S c 设其公比为q>0，,473323=++∴c q c qc 整理得0162=--q q 1121,1,21-==∴=∴n n c c q 1212--=n n S …………7分对于,212212122,222*+++=-<--=+∈∀n n n n n n n S S S N 有且,2<n S 故W S n ∈}{，且[)+∞∈,2M …………9分（III ）证明：（反证）若数列}{n d 非单调递增，则一定存在正整数k ，使1+≥k k d d ，易证于任意的k n ≥，都有1+≥k k d d ，证明如下：假设1,)(+≥≥=k k d d k m m n 时当n=m+1时，由,221212m m m m m m d d d d d d -<<+++++得而0)2(11121≥-=-->-+++++m m m m m m m d d d d d d d 所以,21++>m m d d所以，对于任意的,,1+≥≥m m d d k n 都有显然k d d d ,,,21 这k 项中有一定存在一个最大值，不妨记为0n d ；所以.),(0*00M d N n d d n n n =∈≥从而与这题矛盾.所以假设不成立，故命题得证. …………14分。

北京市各城区2016届高三第一次统练(一模)数学理试题合集

北京市朝阳区2015-2016学年度第二学期高三年级统一考试数学答案（理工类） 2016．3一、选择题：（满分40分）题号1 2 3 4 5 6 7 8 答案 D D A B C D A C二、填空题：（满分30分）题号9 10 11 12 13 14 答案 10 21n a n =-,(3)(411)n n ++ (2,)4π 3(,]4-∞ 3(0,)4 121||i i i ab =-∑ 22（注：两空的填空，第一空3分，第二空2分）三、解答题：（满分80分）15．（本小题满分13分）解：（Ⅰ）当1ω=时，213()sin 3cos 222x f x x =+- 13sin cos 22x x =+ sin()3x π=+．令22,232k x k k ππππ-≤+≤π+∈Z ．解得22,66k x k k 5πππ-≤≤π+∈Z ．所以()f x 的单调递增区间是[2,2],66k k k 5πππ-π+∈Z .……………………7分（Ⅱ）由213()sin 3cos 222x f x x ωω=+- 13sin cos 22x x ωω=+ sin()3x ωπ=+．因为()13f π=，所以sin()133ωππ+=．则2332n ωπππ+=π+，n ∈Z ．解得162n ω=+．又因为函数()f x 的最小正周期2T ωπ=，且0ω>，所以当ω12=时，T 的最大值为4π． ………………………………………13分 16．（本小题满分13分）解：（Ⅰ）设事件A ：从这个班级的学生中随机选取一名男生，一名女生，这两名学生阅读本数之和为4 ．由题意可知， 13+417()=12896P A ⨯⨯=⨯．………………………………………4分（Ⅱ）阅读名著不少于4本的学生共8人，其中男学生人数为4人，故X 的取值为0,1,2,3,4．由题意可得44481(0)70C P X C ===； 134448168(1)7035C C P X C ====； 2244483618(2)7035C C P X C ====； 314448168(3)7035C C P X C ====；44481(4)70C P X C ===．所以随机变量X 的分布列为 X0 1 2 3 4 P 170 835 1835 835 170随机变量X 的均值116361610123427070707070EX =⨯+⨯+⨯+⨯+⨯=．…………10分（Ⅲ）21s >22s ．…………………………………………………………………………13分17．（本小题满分14分）解：（Ⅰ）由已知1190A AB A AC ∠=∠=︒，且平面11AA C C ⊥平面11AA B B ，所以90BAC ∠=︒，即AC AB ⊥．又因为1AC AA ⊥且1AB AA A =，所以AC ⊥平面11AA B B ．由已知11//A C AC ，所以11A C ⊥平面11AA B B ．因为AP ⊂平面11AA B B ，所以11AC AP ⊥．…………………………………………………………………………4分（Ⅱ）由（Ⅰ）可知1,,AC AB AA 两两垂直．分别以1,,AC AB AA 为x 轴、y 轴、z 轴建立空间直角坐标系如图所示．由已知 11111222AB AC AA A B AC =====，所以(0,0,0),(0,2,0),(2,0,0),A B C 1(0,1,2)B ，1(0,0,2)A ．因为M 为线段BC 的中点，P 为线段1BB 的中点，所以3(1,1,0),(0,,1)2M P ．易知平面ABM 的一个法向量(0,0,1)=m ．设平面APM 的一个法向量为(,,)x y z =n ， y x AMPCB A 1C 1B 1 z由 0,0,AM AP ⎧⋅=⎪⎨⋅=⎪⎩n n 得0, 30. 2x y y z +=⎧⎪⎨+=⎪⎩ 取2y =，得(2,2,3)=--n ．由图可知，二面角P AM B --的大小为锐角，所以3317cos ,1717⋅〈〉===⋅m nm n m n ．所以二面角P AM B --的余弦值为31717．………………………………9分（Ⅲ）存在点P ，使得直线1A C //平面AMP ．设111(,,)P x y z ，且1BP BB λ=，[0,1]λ∈，则111(,2,)(0,1,2)x y z λ-=-，所以1110,2,2x y z λλ==-=．所以(0,2,2)AP λλ=-．设平面AMP 的一个法向量为0000(,,)x y z =n ，由 000,0,AM AP ⎧⋅=⎪⎨⋅=⎪⎩n n 得00000, (2)20. x y y z λλ+=⎧⎨-+=⎩ 取01y =，得02(1,1,)2λλ-=-n （显然0λ=不符合题意）．又1(2,0,2)AC =-，若1A C //平面AMP ，则10AC ⊥n ．所以10220AC λλ-⋅=--=n ．所以23λ=．所以在线段1BB 上存在点P ，且12BP PB =时，使得直线1A C //平面AMP ．…………14分 18．（本小题满分13分）解：（Ⅰ）函数()f x 的定义域为{}0x x >．()1a x a f x x x+'=+=．（1）当0a ≥时，()0f x '>恒成立，函数()f x 在(0,)+∞上单调递增；（2）当0a <时，令()0f x '=，得x a =-．当0x a <<-时，()0f x '<，函数()f x 为减函数；当x a >-时，()0f x '>，函数()f x 为增函数．综上所述，当0a ≥时，函数()f x 的单调递增区间为(0,)+∞．当0a <时，函数()f x 的单调递减区间为(0,)a -，单调递增区间为(+)a -∞，． ……………………………………………………………………………………4分（Ⅱ）由（Ⅰ）可知，（1）当1a -≤时，即1a ≥-时，函数()f x 在区间[]1,2上为增函数，所以在区间[]1,2上，min ()(1)1f x f ==，显然函数()f x 在区间[]1,2上恒大于零；（2）当12a <-<时，即21a -<<-时，函数()f x 在[)1a -，上为减函数，在(],2a - 上为增函数，所以min ()()ln()f x f a a a a =-=-+-．依题意有min ()ln()0f x a a a =-+->，解得e a >-，所以21a -<<-．（3）当2a -≥时，即2a ≤-时，()f x 在区间[]1,2上为减函数，所以min ()(2)2+ln 2f x f a ==．依题意有min ()2+ln 20f x a =>，解得2ln 2a >-，所以22ln 2a -<≤-．综上所述，当2ln 2a >-时，函数()f x 在区间[]1,2上恒大于零．………………8分（Ⅲ）设切点为000,ln )x x a x +（，则切线斜率01a k x =+，切线方程为0000(ln )(1)()a y x a x x x x -+=+-．因为切线过点(1,3)P ，则00003(ln )(1)(1)a x a x x x -+=+-．即001(ln 1)20a x x +--=． ………………① 令1()(ln 1)2g x a x x =+-- (0)x >，则 2211(1)()()a x g x a x x x-'=-=．（1）当0a <时，在区间(0,1)上，()0g x '>， ()g x 单调递增；在区间(1,)+∞上，()0g x '<，()g x 单调递减，所以函数()g x 的最大值为(1)20g =-<．故方程()0g x =无解，即不存在0x 满足①式．因此当0a <时，切线的条数为0．（2）当0a >时, 在区间(0,1)上，()0g x '<，()g x 单调递减，在区间(1,)+∞上，()0g x '>，()g x 单调递增，所以函数()g x 的最小值为(1)20g =-<．取21+1e e a x =>，则221112()(1e 1)2e 0a a g x a a a----=++--=>．故()g x 在(1,)+∞上存在唯一零点．取2-1-21e<e a x =，则221122()(1e 1)2e 24a a g x a a a a ++=--+--=--212[e 2(1)]a a a +=-+．设21(1)t t a=+>，()e 2t u t t =-，则()e 2t u t '=-．当1t >时，()e 2e 20t u t '=->->恒成立．所以()u t 在(1,)+∞单调递增，()(1)e 20u t u >=->恒成立．所以2()0g x >．故()g x 在(0,1)上存在唯一零点．因此当0a >时，过点P (13)，存在两条切线．（3）当0a =时，()f x x =，显然不存在过点P (13)，的切线．综上所述，当0a >时，过点P (13)，存在两条切线；当0a ≤时，不存在过点P (13)，的切线．…………………………………………………13分19．（本小题满分14分）解：(Ⅰ)由题意可知，24a =，22b =，所以22c =．因为(2,1)P 是椭圆C 上的点，由椭圆定义得124PF PF +=．所以12PF F ∆的周长为422+．易得椭圆的离心率2=2c e a =．………………………………………………………4分 (Ⅱ)由22220,1,42x y m x y ⎧-+=⎪⎨+=⎪⎩得2242280x mx m ++-=．因为直线l 与椭圆C 有两个交点，并注意到直线l 不过点P ，所以22844(8)0,0.m m m ⎧-⨯->⎨≠⎩解得40m -<<或04m <<．设11(,)A x y ，22(,)B x y ，则1222x x m +=-，21284m x x -=, 1122x m y +=，2222x m y +=．显然直线PA 与PB 的斜率存在，设直线PA 与PB 的斜率分别为1k ，2k ，则1212121122y y k k x x --+=+-- 12211222(1)(2)(1)(2)22(2)(2)x m x m x x x x ++--+--=-- 122112(22)(2)(22)(2)2(2)(2)x m x x m x x x +--++--=-- 1212121222(4)()22422[2()2]x x m x x m x x x x +-+-+=-++ 2121222(8)(4)228216244442[2()2]m m m m x x x x ----+=-++ 2121222(8)(4)22821628[2()2]m m m m x x x x ----+=-++ 2212122216222828216208[2()2]m m m m x x x x --+-+==-++．因为120k k +=，所以PMN PNM ∠=∠．所以PM PN =． ………………………………………………………14分 20．（本小题满分13分）解：（Ⅰ）观察数列}{n a 的前若干项：2，5，8，11，14，17，20，23，26，29，32，35，…. 因为数列}{n a 是递增的整数数列，且等比数列以2为首项，显然最小公比不能是52，最小公比是4. （ⅰ）以2为首项,且公比最小的等比数列的前四项是2，8，32，128.（ⅱ）由（ⅰ）可知12b =，公比4q =，所以124n n b -=⋅.又31n n k n b a k ==-，所以13124,n n k n -*-=⋅∈N ，即11(241),3n n k n -*=⋅+∈N .再证n k 为正整数.显然11k =为正整数，2n ≥时，1222111(2424)24(41)2433n n n n n n k k ------=⋅-⋅=⋅⋅-=⋅，即2124(2)n n n k k n --=+⋅≥，故11(241),3n n k n -*=⋅+∈N 为正整数. 所以，所求通项公式为11(241),3n n k n -*=⋅+∈N . ……………………………………………………………………………6分（Ⅱ）设数列{}n c 是数列}{n a 中包含的一个无穷等比数列，且115k c a ==，22231k c a k ==-，所以公比2315k q -=.因为等比数列{}n c 各项为整数，所以q 为整数. 取252k m =+（m *∈N ），则13+=m q ，故15(31)n n c m -=⋅+.只要证15(31)n n c m -=⋅+是数列}{n a 的项，即证31n k -15(31)n m -=⋅+. 只要证11[5(31)1]3n n k m -=++()n *∈N 为正整数，显然12k =为正整数. 又2n ≥时，12215[(31)(31)]5(31)3n n n n n k k m m m m -----=+-+=+，即215(31)n n n k k m m --=++，又因为12k =，25(31)n m m -+都是正整数，故2n ≥时，n k 也都是正整数.所以数列{}n c 是数列}{n a 中包含的无穷等比数列，其公比13+=m q 有无数个不同的取值，对应着不同的等比数列，故数列}{n a 所包含的以52=a 为首项的不同无穷等比数列有无数多个.…………………………………………………………………………………………13分DABC海淀区高三年级第二学期期中练习参考答案数学（理科） 2016.4阅卷须知:1.评分参考中所注分数，表示考生正确做到此步应得的累加分数。

北京市丰台区2016-2017学年度第二学期一模练习高三数学理科试题Word版含答案

丰台区2017年高三年级第二学期综合练习(一)数学(理科)2017. 03(本试卷满分共150分，考试时间120分钟)注意事项：1. 答题前，考生务必先将答题卡上的学校、年级、班级、姓名、准考证号用黑色字迹签字笔填写清楚，并认真核对条形码上的准考证号、姓名，在答题卡的“条形码粘贴区”贴好条形码。

2. 本次考试所有答题均在答题卡上完成。

选择题必须使用2B铅笔以正确填涂方式将各小题对应选项涂黑，如需改动，用橡皮擦除干净后再选涂其它选项。

非选择题必须使用标准黑色字迹签字笔书写，要求字体工整、字迹清楚。

3•请严格按照答题卡上题号在相应答题区内作答，超出答题区域书写的答案无效，在试卷、草稿纸上答题无效。

4•请保持答题卡卡面清洁，不要装订、不要折叠、不要破损。

第一部分(选择题共40分)一、选择题共8小题，每小题5分，共40分•在每小题列出的四个选项中，选出符合题目要求的一项.1. 如果集合A J.X- Z -2 空x ：：:1^, B -「-1,0,1，那么A B =(A)〈-2, -1,0,r ( B) -1,0,1f-1,0?2. 已知a,b • R，则’b =0”是复数a bi是纯虚数”的(A)充分而不必要条件件(C)充分必要条件要条件3 13. 定积分「(2x )dx =1x(A) 10 —In 3「0,1?( D)(B)(D)(B)必要而不充分条既不充分也不必8—1n33 (D)6494.设E, F分别是正方形ABCD的边AB, BC上的点，且AE=- AB , BF = - BC ,2 3。

(优辅资源)北京市丰台区高三数学一模试卷(理科) Word版含解析

2017年北京市丰台区高考数学一模试卷（理科）一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．如果集合A={x∈Z|﹣2≤x＜1}，B={﹣1，0，1}，那么A∩B=（）A．{﹣2，﹣1，0，1}B．{﹣1，0，1}C．{0，1}D．{﹣1，0}2．已知a，b∈R，则“b≠0”是“复数a+bi是纯虚数”的（）A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件3．定积分=（）A．10﹣ln3 B．8﹣ln3 C．D．4．设E，F分别是正方形ABCD的边AB，BC上的点，且，，如果（m，n为实数），那么m+n的值为（）A．B．0 C．D．15．执行如图所示的程序框图，若输出的S的值为64，则判断框内可填入的条件是（）A．k≤3？B．k＜3？C．k≤4？D．k＞4？6．某几何体的三视图如图所示，则该几何体的体积为（）A．B．C．D．7．小明跟父母、爷爷奶奶一同参加《中国诗词大会》的现场录制，5人坐成一排．若小明的父母至少有一人与他相邻，则不同坐法的总数为（）A．60 B．72 C．84 D．968．一次猜奖游戏中，1，2，3，4四扇门里摆放了a，b，c，d四件奖品（每扇门里仅放一件）．甲同学说：1号门里是b，3号门里是c；乙同学说：2号门里是b，3号门里是d；丙同学说：4号门里是b，2号门里是c；丁同学说：4号门里是a，3号门里是c．如果他们每人都猜对了一半，那么4号门里是（）A．a B．b C．c D．d二、填空题共6小题，每小题5分，共30分．9．抛物线y2=2x的准线方程是．10．已知{a n}为等差数列，S n为其前n项和．若a2=2，S9=9，则a8=．11．在△ABC中，若b2=ac，，则∠A=．12．若x，y满足，则的取值范围是．13．在平面直角坐标系xOy中，曲线C1：x+y=4，曲线（θ为参数），过原点O的直线l分别交C1，C2于A，B两点，则的最大值为．14．已知函数f（x）=e x﹣e﹣x，下列命题正确的有．（写出所有正确命题的编号）①f（x）是奇函数；②f（x）在R上是单调递增函数；③方程f（x）=x2+2x有且仅有1个实数根；④如果对任意x∈（0，+∞），都有f（x）＞kx，那么k的最大值为2．三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．15．已知函数f（x）=Asin（ωx）（ω＞0）的图象如图所示．（Ⅰ）求f（x）的解析式；（Ⅱ）若，求g（x）在上的单调递减区间．16．如图1，平面五边形ABCDE中，AB∥CD，∠BAD=90°，AB=2，CD=1，△ADE 是边长为2的正三角形．现将△ADE沿AD折起，得到四棱锥E﹣ABCD（如图2），且DE⊥AB．（Ⅰ）求证：平面ADE⊥平面ABCD；（Ⅱ）求平面BCE和平面ADE所成锐二面角的大小；（Ⅲ）在棱AE上是否存在点F，使得DF∥平面BCE？若存在，求的值；若不存在，请说明理由．17．某公司购买了A，B，C三种不同品牌的电动智能送风口罩．为了解三种品牌口罩的电池性能，现采用分层抽样的方法，从三种品牌的口罩中抽出25台，测试它们一次完全充电后的连续待机时长，统计结果如下（单位：小时）：（Ⅰ）已知该公司购买的C品牌电动智能送风口罩比B品牌多200台，求该公司购买的B品牌电动智能送风口罩的数量；（Ⅱ）从A品牌和B品牌抽出的电动智能送风口罩中，各随机选取一台，求A 品牌待机时长高于B品牌的概率；（Ⅲ）再从A，B，C三种不同品牌的电动智能送风口罩中各随机抽取一台，它们的待机时长分别是a，b，c（单位：小时）．这3个新数据与表格中的数据构成的新样本的平均数记为μ1，表格中数据的平均数记为μ0．若μ0≤μ1，写出a+b+c 的最小值（结论不要求证明）．18．已知函数．（Ⅰ）求f（x）的单调区间；（Ⅱ）对任意，都有xln（kx）﹣kx+1≤mx，求m的取值范围．19．已知椭圆C：的离心率为，右焦点为F，点B（0，1）在椭圆C上．（Ⅰ）求椭圆C的方程；（Ⅱ）过点的直线交椭圆C于M，N两点，交直线x=2于点P，设，，求证：λ+μ为定值．20．对于∀n∈N*，若数列{x n}满足x n﹣x n＞1，则称这个数列为“K数列”．+1（Ⅰ）已知数列：1，m+1，m2是“K数列”，求实数m的取值范围；（Ⅱ）是否存在首项为﹣1的等差数列{a n}为“K数列”，且其前n项和S n满足？若存在，求出{a n}的通项公式；若不存在，请说明理由；（Ⅲ）已知各项均为正整数的等比数列{a n}是“K数列”，数列不是“K数列”，若，试判断数列{b n}是否为“K数列”，并说明理由．2017年北京市丰台区高考数学一模试卷（理科）参考答案与试题解析一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．如果集合A={x∈Z|﹣2≤x＜1}，B={﹣1，0，1}，那么A∩B=（）A．{﹣2，﹣1，0，1}B．{﹣1，0，1}C．{0，1}D．{﹣1，0}【考点】交集及其运算．【分析】先分别求出集合A和B，由此利用交集定义能求出A∩B．【解答】解：∵集合A={x∈Z|﹣2≤x＜1}={﹣2，﹣1，0}，B={﹣1，0，1}，∴A∩B={﹣1，0}．故选：D．2．已知a，b∈R，则“b≠0”是“复数a+bi是纯虚数”的（）A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断．【分析】a，b∈R，复数a+bi是纯虚数⇔，即可判断出结论．【解答】解：a，b∈R，复数a+bi是纯虚数⇔，∴“b≠0”是“复数a+bii是纯虚数”的必要不充分条件．故选：B．3．定积分=（）A．10﹣ln3 B．8﹣ln3 C．D．【考点】定积分．【分析】求出原函数，即可求出定积分．【解答】解： ==8﹣ln3，故选B ．4．设E ，F 分别是正方形ABCD 的边AB ，BC 上的点，且，，如果（m ，n 为实数），那么m +n 的值为（）A ．B ．0C ．D ．1【考点】平面向量的基本定理及其意义．【分析】如图所示，==﹣．即可求得m ，n 即可．【解答】解：如图所示， ==﹣．∴m=﹣，n=，∴，故选：C5．执行如图所示的程序框图，若输出的S 的值为64，则判断框内可填入的条件是（）A．k≤3？B．k＜3？C．k≤4？D．k＞4？【考点】程序框图．【分析】模拟执行程序框图，依次写出每次循环得到的k，S的值，当k=4时，退出循环，输出S的值为64，故判断框图可填入的条件是k≤3．【解答】解：模拟执行程序框图，可得：S=1，k=0满足条件，S=1，k=1，满足条件，S=2，k=2，满足条件，S=8，k=3，满足条件，S=64，k=4，由题意，此时应不满足条件，退出循环，输出S的值为64．结合选项可得判断框内填入的条件可以是：k≤3．故选：A．6．某几何体的三视图如图所示，则该几何体的体积为（）A．B．C．D．【考点】棱柱、棱锥、棱台的体积．【分析】根据已知中的三视图，可得该几何体是一个以俯视图为底面的三棱柱切去一个三棱锥得到的组合体，可得答案．【解答】解：根据已知中的三视图，可得该几何体是一个以俯视图为底面的三棱柱切去一个三棱锥得到的组合体，其底面面积S=×1×1=，柱体的高为：2，锥体的高为1，故组合体的体积V=×2﹣××1=，故选：A．7．小明跟父母、爷爷奶奶一同参加《中国诗词大会》的现场录制，5人坐成一排．若小明的父母至少有一人与他相邻，则不同坐法的总数为（）A．60 B．72 C．84 D．96【考点】排列、组合的实际应用．【分析】根据题意，分3种情况讨论：①、小明的父母的只有1人与小明相邻且父母不相邻，②、小明的父母的只有1人与小明相邻且父母相邻，③、小明的父母都与小明相邻，分别求出每一种情况下的排法数目，由分类计数原理计算可得答案．【解答】解：根据题意，分3种情况讨论：①、若小明的父母的只有1人与小明相邻且父母不相邻时，先在其父母中选一人与小明相邻，有C21=2种情况，将小明与选出的家长看成一个整体，考虑其顺序有A22=2种情况，当父母不相邻时，需要将爷爷奶奶进行全排列，将整体与另一个家长安排在空位中，有A22×A32=12种安排方法，此时有2×2×12=48种不同坐法；②、若小明的父母的只有1人与小明相邻且父母相邻时，将父母及小明看成一个整体，小明在一端，有2种情况，考虑父母之间的顺序，有2种情况，则这个整体内部有2×2=4种情况，将这个整体与爷爷奶奶进行全排列，有A33=6种情况，此时有2×2×6=24种不同坐法；③、小明的父母都与小明相邻，即小明在中间，父母在两边，将3人看成一个整体，考虑父母的顺序，有A22=2种情况，将这个整体与爷爷奶奶进行全排列，有A33=6种情况，此时，共有2×6=12种不同坐法；则一共有48+24+12=84种不同坐法；故选：C．8．一次猜奖游戏中，1，2，3，4四扇门里摆放了a，b，c，d四件奖品（每扇门里仅放一件）．甲同学说：1号门里是b，3号门里是c；乙同学说：2号门里是b，3号门里是d；丙同学说：4号门里是b，2号门里是c；丁同学说：4号门里是a，3号门里是c．如果他们每人都猜对了一半，那么4号门里是（）A．a B．b C．c D．d【考点】进行简单的合情推理．【分析】根据题意，条件“四人都只说对了一半”，若甲同学猜对了1﹣b，依次判断3﹣d，2﹣c，4﹣a，再假设若甲同学猜对了3﹣c得出矛盾．【解答】解：根据题意：若甲同学猜对了1﹣b，则乙同学猜对了，3﹣d，丙同学猜对了，2﹣c，丁同学猜对了，4﹣a，根据题意：若甲同学猜对了3﹣c，则丁同学猜对了，4﹣a，丙同学猜对了，2﹣c，这与3﹣c相矛盾，综上所述号门里是a，故选：A．二、填空题共6小题，每小题5分，共30分．9．抛物线y2=2x的准线方程是．【考点】抛物线的简单性质．【分析】先根据抛物线方程求得p，进而根据抛物线的性质，求得答案．【解答】解：抛物线y2=2x，∴p=1，∴准线方程是x=﹣故答案为：﹣10．已知{a n}为等差数列，S n为其前n项和．若a2=2，S9=9，则a8=16．【考点】等差数列的前n项和．【分析】利用等差数列的通项公式和前n项和公式列出方程组，求出首项和公差，由此能求出a8．【解答】解：{a n}为等差数列，S n为其前n项和．a2=2，S9=9，∴，解得∴a8=a1+7d=16．故答案为：16．11．在△ABC中，若b2=ac，，则∠A=．【考点】余弦定理．【分析】根据余弦定理求解出a，c的关系，即可判断角A的大小．【解答】解：由b2=ac，，根据余弦定理cosB=，可得a2+c2=2ac，即（a﹣c）2=0，∴a=c，由b2=ac，可得a=b=c．△ABC是等边三角形．∴A=故答案为：．12．若x，y满足，则的取值范围是[，6] ．【考点】简单线性规划．【分析】先画出约束条件的可行域，然后分析的几何意义，结合图象，用数形结合的思想，即可求解．【解答】解：满足约束条件的可行域，如下图所示：又∵表示的是可行域内一点与原点连线的斜率当x=，y=时，有最小值；当x=1，y=6时，有最大值6故答案为：[，6]13．在平面直角坐标系xOy中，曲线C1：x+y=4，曲线（θ为参数），过原点O的直线l分别交C1，C2于A，B两点，则的最大值为．【考点】参数方程化成普通方程．【分析】求出曲线（θ为参数）的普通方程，设直线方程为kx﹣y=0，求出|OA|，|OB|，即可求出的最大值．【解答】解：曲线（θ为参数），普通方程为（x﹣1）2+y2=1．设直线方程为kx﹣y=0，圆心到直线的距离d=，∴|OB|=2=，kx﹣y=0与x+y=4联立，可得A（，），∴|OA|=，∴=，设k+1=t（t＞0），则=≤=．∴的最大值为．故答案为．14．已知函数f（x）=e x﹣e﹣x，下列命题正确的有①②④．（写出所有正确命题的编号）①f（x）是奇函数；②f（x）在R上是单调递增函数；③方程f（x）=x2+2x有且仅有1个实数根；④如果对任意x∈（0，+∞），都有f（x）＞kx，那么k的最大值为2．【考点】函数恒成立问题；命题的真假判断与应用．【分析】根据题意，依次分析4个命题，对于①、由奇函数的定义分析可得①正确；对于②、对函数f（x）=e x﹣e﹣x求导，分析可得f′（x）＞0，分析可得②正确；对于③、g（x）=e x﹣e﹣x﹣x2﹣2x，分析可得g（0）=0，即方程f（x）=x2+2x 有一根x=0，进而利用二分法分析可得g（x）有一根在（3，4）之间，即方程f （x）=x2+2x至少有2跟，故③错误，对于④、由函数的恒成立问题的分析方法，分析可得④正确，综合可得答案．【解答】解：根据题意，依次分析4个命题：对于①、f（x）=e x﹣e﹣x，定义域是R，且f（﹣x）=e﹣x﹣e x=﹣f（x），f（x）是奇函数；故①正确；对于②、若f（x）=e x﹣e﹣x，则f′（x）=e x+e﹣x＞0，故f（x）在R递增；故②正确；对于③、f（x）=x2+2x，令g（x）=e x﹣e﹣x﹣x2﹣2x，令x=0可得，g（0）=0，即方程f（x）=x2+2x有一根x=0，g（3）=e3﹣﹣13＜0，g（4）=e4﹣﹣20＞0，则方程f（x）=x2+2x有一根在（3，4）之间，故③错误；对于④、如果对任意x∈（0，+∞），都有f（x）＞kx，即e x﹣e﹣x﹣kx＞0恒成立，令h（x）=e x﹣e﹣x﹣kx，且h（0）=0，若h（x）＞0恒成立，则必有h′（x）=e x+e﹣x﹣k＞0恒成立，若e x+e﹣x﹣k＞0，即k＜e x+e﹣x=e x+恒成立，而e x+≥2，若有k＜2，故④正确；综合可得：①②④正确；故答案为：①②④．三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．15．已知函数f（x）=Asin（ωx）（ω＞0）的图象如图所示．（Ⅰ）求f（x）的解析式；（Ⅱ）若，求g（x）在上的单调递减区间．【考点】由y=Asin（ωx+φ）的部分图象确定其解析式；正弦函数的图象．【分析】（Ⅰ）由图象求得A及周期，再由周期公式求得ω，则f（x）的解析式可求；（Ⅱ）把f（x）代入，整理后由复合函数的单调性求得g（x）在上的单调递减区间．【解答】解：（Ⅰ）由图象可知A=2，设函数f（x）的周期为T，则，求得T=π，从而ω=2，∴f（x）=2sin2x；（Ⅱ）===，∴，即，k∈Z．令k=0，得，∴g（x）在上的单调递减区间为．16．如图1，平面五边形ABCDE中，AB∥CD，∠BAD=90°，AB=2，CD=1，△ADE 是边长为2的正三角形．现将△ADE沿AD折起，得到四棱锥E﹣ABCD（如图2），且DE⊥AB．（Ⅰ）求证：平面ADE⊥平面ABCD；（Ⅱ）求平面BCE和平面ADE所成锐二面角的大小；（Ⅲ）在棱AE上是否存在点F，使得DF∥平面BCE？若存在，求的值；若不存在，请说明理由．【考点】二面角的平面角及求法；平面与平面垂直的判定．【分析】（Ⅰ）推导出AB⊥AD，AB⊥DE，从而AB⊥平面ADE，由此能平面ADE ⊥平面ABCD．（Ⅱ）设AD的中点为O，连接EO，推导出EO⊥AD，从而EO⊥平面ABCD．以O为原点，OA所在的直线为x轴，在平面ABCD内过O 垂直于AD的直线为y 轴，OE所在的直线为z轴，建立空间直角坐标系O﹣xyz，利用向量法能求出平面BCE和平面ADE所成的锐二面角大小．（Ⅲ）设BE的中点为G，连接CG，FG，推导出四边形CDFG是平行四边形，从而DF∥CG．由此能求出在棱AE上存在点F，使得DF∥平面BCE，此时．【解答】（本小题共14分）证明：（Ⅰ）由已知得AB⊥AD，AB⊥DE．因为AD∩DE=D，所以AB⊥平面ADE．又AB⊂平面ABCD，所以平面ADE⊥平面ABCD..…解：（Ⅱ）设AD的中点为O，连接EO．因为△ADE是正三角形，所以EA=ED，所以EO⊥AD．因为平面ADE⊥平面ABCD，平面ADE∩平面ABCD=AD，EO⊂平面ADE，所以EO⊥平面ABCD．以O为原点，OA所在的直线为x轴，在平面ABCD内过O 垂直于AD的直线为y轴，OE所在的直线为z轴，建立空间直角坐标系O﹣xyz，如图所示．由已知，得E（0，0，），B（1，2，0），C（﹣1，1，0）．所以=（1，﹣1，），=（2，1，0）．设平面BCE的法向量=（x，y，z）．则，令x=1，则=（1，﹣2，﹣）．又平面ADE的一个法向量=（0，1，0），所以cos＜＞==﹣．所以平面BCE和平面ADE所成的锐二面角大小为．…（Ⅲ）在棱AE上存在点F，使得DF∥平面BCE，此时．理由如下：设BE的中点为G，连接CG，FG，则FG∥AB，FG=．因为AB∥CD，且，所以FG∥CD，且FG=CD，所以四边形CDFG是平行四边形，所以DF∥CG．因为CG⊂平面BCE，且DF⊄平面BCE，所以DF∥平面BCE..…17．某公司购买了A，B，C三种不同品牌的电动智能送风口罩．为了解三种品牌口罩的电池性能，现采用分层抽样的方法，从三种品牌的口罩中抽出25台，测试它们一次完全充电后的连续待机时长，统计结果如下（单位：小时）：（Ⅰ）已知该公司购买的C品牌电动智能送风口罩比B品牌多200台，求该公司购买的B品牌电动智能送风口罩的数量；（Ⅱ）从A品牌和B品牌抽出的电动智能送风口罩中，各随机选取一台，求A 品牌待机时长高于B品牌的概率；（Ⅲ）再从A，B，C三种不同品牌的电动智能送风口罩中各随机抽取一台，它们的待机时长分别是a，b，c（单位：小时）．这3个新数据与表格中的数据构成的新样本的平均数记为μ1，表格中数据的平均数记为μ0．若μ0≤μ1，写出a+b+c 的最小值（结论不要求证明）．【考点】函数模型的选择与应用．【分析】（I）利用该公司购买的C品牌电动智能送风口罩比B品牌多200台，建立方程，即可求该公司购买的B品牌电动智能送风口罩的数量；（Ⅱ）根据古典概型概率计算公式，可求出A品牌待机时长高于B品牌的概率；（Ⅲ）根据平均数的定义，写出a+b+c的最小值．【解答】解：（Ⅰ）设该公司购买的B品牌电动智能送风口罩的数量为x台，则购买的C品牌电动智能送风口罩为台，由题意得，所以x=800．答：该公司购买的B品牌电动智能送风口罩的数量为800台..…（Ⅱ）设A品牌待机时长高于B品牌的概率为P，则．答：在A品牌和B品牌抽出的电动智能送风口罩中各任取一台，A品牌待机时长高于B品牌的概率为..…（Ⅲ）18．…18．已知函数．（Ⅰ）求f（x）的单调区间；（Ⅱ）对任意，都有xln（kx）﹣kx+1≤mx，求m的取值范围．【考点】利用导数求闭区间上函数的最值；利用导数研究函数的单调性．【分析】（Ⅰ）求出函数的导数，解关于导函数的不等式，求出函数的单调区间；（Ⅱ）问题转化为m≥f（x）max，通过讨论k的范围，求出f（x）的最大值，从而求出m的范围即可．【解答】解：由已知得，f（x）的定义域为（0，+∞）．（Ⅰ），．令f'（x）＞0，得x＞1，令f'（x）＜0，得0＜x＜1．所以函数f（x）的单调减区间是（0，1），单调增区间是（1，+∞），（Ⅱ）由xln（kx）﹣kx+1≤mx，得，即m≥f（x）max．由（Ⅰ）知，（1）当k≥2时，f（x）在上单调递减，所以，所以m≥0；．（2）当0＜k≤1时，f（x）在上单调递增，所以，所以；（3）当1＜k＜2时，f（x）在上单调递减，在上单调递增，所以．又，，①若，即，所以1＜k＜2ln2，此时，所以．②若，即，所以2ln2≤k＜2，此时f（x）max=0，所以m ≥0综上所述，当k≥2ln2时，m≥0；当0＜k＜2ln2时，．19．已知椭圆C：的离心率为，右焦点为F，点B（0，1）在椭圆C上．（Ⅰ）求椭圆C的方程；（Ⅱ）过点的直线交椭圆C于M，N两点，交直线x=2于点P，设，，求证：λ+μ为定值．【考点】直线与椭圆的位置关系．【分析】（Ⅰ）由题意b=1，利用椭圆的离心率即可求得a的值，求得椭圆方程；（Ⅱ）设直线MN的方程为y=k（x﹣1），代入椭圆方程，利用韦达定理及向量的坐标运算，即可证明λ+μ=0为定值．【解答】解：（Ⅰ）由点B（0，1）在椭圆C：上，则，即b=1．又椭圆C的离心率为，则，由a2=b2+c2，得．∴椭圆C的方程为…（Ⅱ）证明：由已知得F（1，0），直线MN的斜率存在．设直线MN的方程为y=k（x﹣1），M（x1，y1），N（x2，y2），则P（2，k）．由，，得，∴，．联立得（1+2k2）x2﹣4k2x+2k2﹣2=0．∴，．∴==0，∴λ+μ=0为定值…20．对于∀n∈N*，若数列{x n}满足x n﹣x n＞1，则称这个数列为“K数列”．+1（Ⅰ）已知数列：1，m+1，m2是“K数列”，求实数m的取值范围；（Ⅱ）是否存在首项为﹣1的等差数列{a n}为“K数列”，且其前n项和S n满足？若存在，求出{a n}的通项公式；若不存在，请说明理由；（Ⅲ）已知各项均为正整数的等比数列{a n}是“K数列”，数列不是“K数列”，若，试判断数列{b n}是否为“K数列”，并说明理由．【考点】数列的应用．【分析】（Ⅰ）由题意得（m+1）﹣1＞1，m2﹣（m+1）＞1，联立解出即可得出．（Ⅱ）假设存在等差数列{a n}符合要求，设公差为d，则d＞1，由题意，得对n∈N*均成立，化为（n﹣1）d＜n．对n分类讨论解出即可得出．（Ⅲ）设数列{a n}的公比为q，则，由题意可得：{a n}的每一项均为﹣a n=a n q﹣a n=a n（q﹣1）＞1＞0，可得a1＞0，且q＞1．由a n+1正整数，且a n+1﹣a n=q（a n﹣a n﹣1）＞a n﹣a n﹣1，可得在{a n﹣a n﹣1}中，“a2﹣a1”为最小项．同理，在中，“”为最小项．再利用“K数列”，可得a1=1，q=3或a1=2，q=2．进而得出．【解答】解：（Ⅰ）由题意得（m+1）﹣1＞1，①m2﹣（m+1）＞1，②解①得m＞1；解②得m＜﹣1或m＞2．所以m＞2，故实数m的取值范围是m＞2．（Ⅱ）假设存在等差数列{a n}符合要求，设公差为d，则d＞1，由a1=﹣1，得，．由题意，得对n∈N*均成立，即（n﹣1）d＜n．①当n=1时，d∈R；②当n＞1时，，因为，所以d≤1，与d＞1矛盾，故这样的等差数列{a n}不存在．（Ⅲ）设数列{a n}的公比为q，则，﹣a n=a n q﹣a n=a n（q﹣1）＞1＞0，因为{a n}的每一项均为正整数，且a n+1所以a1＞0，且q＞1．因为a n﹣a n=q（a n﹣a n﹣1）＞a n﹣a n﹣1，+1}中，“a2﹣a1”为最小项．所以在{a n﹣a n﹣1同理，在中，“”为最小项．由{a n}为“K数列”，只需a2﹣a1＞1，即a1（q﹣1）＞1，又因为不是“K数列”，且“”为最小项，所以，即a1（q﹣1）≤2，由数列{a n}的每一项均为正整数，可得a1（q﹣1）=2，所以a1=1，q=3或a1=2，q=2．①当a1=1，q=3时，，则，令，则，又=，所以{c n}为递增数列，即c n＞c n﹣1＞c n﹣2＞…＞c1，所以b n+1﹣b n＞b n﹣b n﹣1＞b n﹣1﹣b n﹣2＞…＞b2﹣b1．因为，所以对任意的n∈N*，都有b n+1﹣b n＞1，即数列{c n}为“K数列”．②当a1=2，q=2时，，则．因为，所以数列{b n}不是“K数列”．综上：当时，数列{b n}为“K数列”，当时，数列{b n}不是“K数列”．2017年4月25日。