北京版-数学-七年级上册-《角的度量与角的换算》同步练习1
七年级数学上册 4.4 角的比较同步练习1 (新版)北师大

4.4 角的比较一、选择题1.如图1,∠AOB 是直角,∠AOC=38°,∠COD=∠COB=1:2,则∠BOD=( ) A.38° B.52° C.26° D.64°C BADOECB DOCB A DO(1) (2) (3) 2.用一副三角尺,可以拼出小于180°的角有n 个,则n 等于( ) A.4 B.6 C.11 D.13 3.已知α、β都是钝角,甲、乙、丙、丁四人计算16(α+β)的结果依次是50°,26°,72•°,90°,那么结果正确的可能是( )A.甲B.乙C.丙D.丁4.点P 在∠MAN 内部,现在四个等式:①∠PAM=∠MAP;②∠PAN=12∠A;•③∠MAP=12∠MAN,④∠MAN=2∠MAP,其中能表示AP 是角平分线的等式有( ) A.1个 B.2个 C.3个 D.4个 二、填空题5.如图2,OD,OE 分别是∠AOC 和∠BOC 的平分线,∠AOD=40°,∠BOE=25°,求∠AOB 的度数.解:∵OD 平分∠AOC,OE•平分∠BOC(•已知)•,• ∴∠AOC=•2•∠AOD,•∠BOC=•2•∠_________( ), ∵∠AOD=40°,∠_______=25°(已知), ∴∠AOC=2×40°=80°(•等量代换). ∠BOC=2×( )°=( ), ∴∠AOB=________.6.270°=_______直角_______平角________周角.7.如图3,若∠AOC=∠DOB,则∠AOB=_______∠COD;•若∠AOB=•∠COD,•则∠AOC_____∠DOB. 8.已知∠AOB 和∠BOC 之和为180°,这两个角的平分线所成的角是_______. 三、解答题:9.如图所示,OE 平分∠BOC,OD 平分∠AOC,∠BOE=20°,∠AOD=40•°,•求∠DOE 的度数.ECBADO10.如图,点O 在直线AC 上,OD 平分∠AOB,∠EOC=2∠BOE,∠DOE=72°,•求∠EOC.ECB ADO11.如图,BO,CO 分别平分∠ABC 和∠ACB,•已知任何三角形的三个角的和都是180°,若∠A=60°,试求∠BOC 的度数.CBA2O112.如图,一副三角板的两个直角顶点重合在一起. (1)比较∠EOM 与∠FON 的大小,并说明为什么?(2)∠EON 与∠MOF 的和是多少度,为什么?FEM NO13.(1)如图,已知∠AOB=90°,∠BOC=30°,OM 平分∠AOC,ON 平分∠BOC,求∠MON 的度数. (2)如果(1)中的∠AOB=α,其它条件不变,求∠MON 的度数. (3)如果(1)中∠BOC=β(β为锐角),其它条件不变,求∠MON 的度数. (4)从(1)、(2)、(3)的结果中能得出什么结论?(“希望杯”试题)CB AM N O参考答案一、1.C(点拨:∠COD=∠BOD)2.C(点拨:拼出的角是15°的整数倍)3.A点拨:∵90°< <180°,90°< <180°)∴30°<16(α+β)<60°故甲正确 4.C二、5.EOC,角的平分线定义;BOE;25;50;130° 6.3;32;347.=;= 8.•直角或锐角。
角的度量与换算【北师大版】七年级数学(上册)-【完整版】

角的度量与换算北师大版七年级数学 上册-精 品课件 ppt(实 用版)
角的度量与换算北师大版七年级数学 上册-精 品课件 ppt(实 用版)
(2)32°17′53″+42°42′7″; (3)53°÷8. (2)原式=74°59′60″=75°. (3)原式=6°37′30″.
12.(1)将31.24°化为用度、分、秒表示的形式; 解:(1)31.24°=31°+0.24°, 0.24°=0.24×60′=14.4′, 0.4′=0.4×60″=24″,∴31.24°=31°14′24″.
角的度量与换算北师大版七年级数学 上册-精 品课件 ppt(实 用版)
角的度量与换算北师大版七年级数学 上册-精 品课件 ppt(实 用版)
角的度量与换算北师大版七年级数学 上册-精 品课件 ppt(实 用版)
10.下列计算错误的是( C ) A. 1.9°=6840″ B. 90′=1.5° C. 32.15°=32°15′ D. 2700″=45′
角的度量与换算北师大版七年级数学 上册-精 品课件 ppt(实 用版)
角的度量与换算北师大版七年级数学 上册-精 品课件 ppt(实 用版)
解:(1)2时15分时分针指向数字3,而时针从数字2开始 转动的角度为15×0.5°=7.5°,所以钟表上2时15分时, 时针与分针所成的锐角的度数为30°-7.5°=22.5°.
(2)若时针由2时30分走到2时55分,问分针转过多大 的角度?
(2)分针转过的角度为25×6°=150°.
重难易错
角的度量与换算北师大版七年级数学 上册-精 品课件 ppt(实 用版)
北京版-数学-七年级上册-《角的度量与角的换算》同步练习3
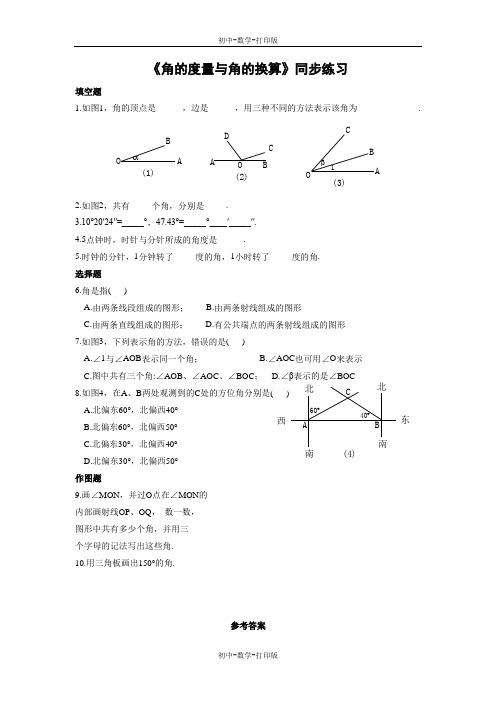
40︒60︒南北(4)北西南东CA B 《角的度量与角的换算》同步练习填空题1.如图1,角的顶点是______,边是______,用三种不同的方法表示该角为______________.α(1)OA B(2)CADβ(3)1OCAB2.如图2,共有_____个角,分别是_____.3.10°20′24″=_____°,47.43°=_____°____′_____″.4.5点钟时,时针与分针所成的角度是______.5.时钟的分针,1分钟转了_____度的角,1小时转了_____度的角. 选择题6.角是指( )A.由两条线段组成的图形;B.由两条射线组成的图形C.由两条直线组成的图形;D.有公共端点的两条射线组成的图形 7.如图3,下列表示角的方法,错误的是( )A.∠1与∠AOB 表示同一个角;B.∠AOC 也可用∠O 来表示C.图中共有三个角:∠AOB 、∠AOC 、∠BOC ;D.∠β表示的是∠BOC 8.如图4,在A 、B 两处观测到的C 处的方位角分别是( ) A.北偏东60°,北偏西40° B.北偏东60°,北偏西50° C.北偏东30°,北偏西40° D.北偏东30°,北偏西50° 作图题9.画∠MON ,并过O 点在∠MON 的 内部画射线OP 、OQ , 数一数, 图形中共有多少个角,并用三 个字母的记法写出这些角. 10.用三角板画出150°的角.参考答案填空题1.O;BO;AO ∠O;∠AOB;∠α2.6;∠AOD,∠AOC,∠AOB,∠DOC,∠DOB,∠COB3.10.34 47°25′48″4.150°5.6°360°选择题6.D7.B8.B作图题9.如答图,图中一共有6个角,分别是∠MOP,∠MOQ,∠MON,∠POQ,∠PON,∠Q ON.OPQN90︒60︒OCAB10.解:如答图所示,∠AOC=150°.。
北师大版七年级数学上册试题一课一练《角》同步练习(含答案)

4.3 《角》习题1一、填空题1.图书馆在餐厅的北偏东40°方向,那么餐厅在图书馆的________方向.2.若一个角的补角加上10º后等于这个角的4倍,则这个角的度数为____.3.过点O 引三条射线OA 、OB 、OC ,使2AOC AOB ∠=∠,如果32AOB ∠=︒,那么BOC ∠的度数是_______.二、选择题1.如图,能用∠1、∠ABC 、∠B 三种方法表示同一个角的是( )A .B .C .D .2.如图,甲从A 点出发向北偏东70°方向走到点B ,乙从点A 出发向南偏西15°方向走到点C ,则∠BAC 的度数是( )A .85°B .105°C .125°D .160°3.将一个直角分成1:2:3的三个角,那么这三个角中,最大的角与最小的角相差( )A .10°B .20°C .30°D .40°4.如图,射线OB 和OD 分别为AOC ∠和COE ∠的角平分线,45,20AOB DOE ∠=︒∠=︒,则AOE ∠=( )A .110°B .120°C .130°D .140°5.2019年4月12日我军在南海举行了建国以来海上最大的军事演习,位于点O 处的军演指挥部观测到军舰A 位于点O 的北偏东70°方向(如图),同时观测到军舰B 位于点O 处的南偏西15°方向,那么∠AOB 的大小是( )A .85°B .105°C .115°D .125°6.已知180αβ∠+∠=︒,且αβ∠>∠,那么β∠的余角一定是( )A .αβ∠-∠B .90α︒-∠C .90α∠-︒D .90β∠-︒7.如图所示,OC 是AOB ∠的平分线,OD 是BOC ∠的平分线,那么下列各式中正确的是( )A .23AOD AOB ∠=∠ B .13BOD AOB =∠∠ C .23BOC AOB ∠=∠ D .12∠=∠COD BOC 8.一个角的余角比它的补角的一半少30,则这个角的度数为( )A .20︒B .40︒C .60︒D .80︒9.如图,已知CO ⊥AB 于点O ,∠AOD =5∠DOB +6°,则∠COD 的度数( )A.58°B.59°C.60°D.61°10.下列语句中,正确的个数是( )①直线AB和直线BA是两条直线;②射线AB和射线BA是两条射线;③若∠1+∠2+∠3=90°,则∠1、∠2、∠3互余;④一个角的余角比这个角的补角小;⑤一条射线就是一个周角;⑥两点之间,线段最短.A.1个B.2个C.3个D.4个11.将一副三角尺按不同位置摆放,摆放方式中∠α与∠β互余的是( )A.B.C.D.12.如图,∠AOC和∠BOC互补,∠AOB=α,OM是∠AOC的平分线,ON是∠BOC的平分线,∠MON的度数是( )A.1802α-B.12a C.1902a+D.1902a-13.在同一平面内,已知∠AOB=70°,∠BOC=20°,如果OP是∠AOC的平分线,则∠BOP的度数为( )A.25°B.25°或35°C.35°D.25°或45°14.如图,已知点A,O,B在同一直线上,∠2是锐角,则∠2的余角是( )A .1122∠-∠B .()1123∠+∠C .()1122∠-∠ D .131222∠-∠三、解答题1.用一副三角尺画角. (1)135AOB ∠=︒. (2)150BOC ∠=︒.2.计算:(1)2027'3554'︒+︒; (2)90431836"'︒-°.3.完成推理填空:如图,直线AB 、CD 相交于O ,∠EOC =90°,OF 是∠AOE 的角平分线,∠COF =34°,求∠BOD 的度数.其中一种解题过程如下:请在括号中注明根据,在横线上补全步骤.解:∵∠EOC =90°,∠COF =34°( )∴∠EOF = °又∵OF 是∠AOE 的角平分线( )∴∠AOF = =56°( )∴∠AOC =∠ —∠ = °∴∠BOD=∠AOC=°( )4.如图,已知直线AB和CD相交于点O,∠COE= 90︒, OF平分∠AOE, ∠COF=28︒.求∠AOC 的度数.5.请仔细观察如图所示的折纸过程,然后回答下列问题:(1)2∠的度数为__________;∠有何数量关系:______;(2)1∠与3∠有何数量关系:__________;(3)1∠与AEC6.如图,已知直线和直线外三点A,B,C,按下列要求画图:(1)画线段AB(2)画出射线BC(3)以A 为顶点画出表示东西南北的十字线,再画出表示北偏西30的射线AD (注:D 为射线与直线l 的焦点,标注字母D 与30角)7.如图,OM ,ON 分别是BOC ∠和AOC ∠的平分线,且84AOB ∠=︒.(1)当OC 静止时,求MON ∠的度数;(2)当OC 在AOB ∠内转动时,MON ∠的大小是否会发生变化,简单说明理由.8.已知:AOB ∠和COD ∠是直角.(1)如图,当射线OB 在COD ∠内部时,请探究AOD ∠和BOC ∠之间的关系;(2)如图2,当射线,OA 射线OB 都在COD ∠外部时,过点О作射线OE ,射线OF ,满足13BOE BOC ∠=∠,23DOF AOD ∠=∠,求EOF ∠的度数.(3)如图3,在(2)的条件下,在平面内是否存在射线OG ,使得:2:3GOF GOE ∠∠=,若不存在,请说明理由,若存在,求出GOF ∠的度数.答案一、填空题1.南偏西40°(或西偏南50°).2.38°.3.32︒或96︒二、选择题1.A . 2.C .3.C .4.C .5.D.6.C .7.D .8.C .9.D.10.C .11.C .12.B .13.D .14.C .三、解答题1.(1)如图,∠AOB 为所求;(2)如图,∠BOC 为所求;2.(1)2027'3554'5581'5621'+=︒=°°°(2)904318'36"8959'60"4318'36"464124"︒-︒=︒-︒=︒′3.解:∵∠EOC=90°∠COF=34° (已知)∴∠EOF=90°-34°=56°,∵OF 是∠AOE 的角平分线∴∠AOF =∠EOF =56°(角平分线定义)∴∠AOC=∠AOF-∠COF=22°,∴∠BOD=∠AOC=22° (同角的余角相等),4.解:∵∠EOF=∠COE-∠COF=90°-28°=62°.又∵OF平分∠AOE,∴∠AOF=∠EOF=62°,∴∠AOC=∠AOF-∠COF=62°-28°=34°.5.解:(1)根据折叠的过程可知:∠2=∠1+∠3,∵∠1+∠2+∠3=∠BEC,B、E、C三点共线∴∠2=180°÷2=90°.故答案是:90°.(2)∵∠1+∠3=∠2,∴∠1+∠3=90°.故答案是:∠1+∠3=90°.(3)∵B、E、C三点共线,∴∠1+∠AEC=180°,故答案是:∠1+∠AEC=180°.6.解:(1)线段AB作图如下,(2)射线BC作图如下,(3)方向角作图如下,7.解:(1) OM ,ON 分别是BOC ∠和AOC ∠的平分线,11,,22MOC BOC NOC AOC ∴∠=∠∠=∠ ()11,22MON MOC NOC BOC AOC AOB ∴∠=∠+∠=∠+∠=∠ 84AOB ∠=︒,18442.2MON ∴∠=⨯︒=︒ (2)MON ∠的大小不会发生变化,理由如下:OM ,ON 分别是BOC ∠和AOC ∠的平分线,11,,22MOC BOC NOC AOC ∴∠=∠∠=∠()11,22MON MOC NOC BOC AOC AOB ∴∠=∠+∠=∠+∠=∠ 84AOB ∠=︒,18442.2MON ∴∠=⨯︒=︒ 所以只要∠AOB 的大小不变,无论OC 在∠AOB 内怎样转动,∠MON 的值都不会变.8.解:(1)180AOD BOC ∠+∠=︒ ,证明:AOB ∠和COD ∠是直角,90AOB COD ∴∠=∠=︒,BOD BOC COD ∠+∠=∠,90BOD BOC ∴∠=︒-∠,同理:90AOC BOC ∠=︒-∠,9090180AOD AOB BOD BOC BOC ∴∠=∠+∠=︒+︒-∠=-∠,180AOD BOC ∴∠+∠=︒;(2)解:设BOE α∠=,则3BOC α∠=,BOE EOC BOC ∠+∠=∠,2EOC BOC BOE α∴∠=∠-∠=,360AOD COD BOC AOB ∠+∠+∠+∠=︒,360AOD COD BOC AOB ∴∠=︒-∠-∠-∠360903901803a α=︒-︒--︒=︒-,23DOF AOD ∠=∠, 21803103(22DOF a a ∴∠=︒-=︒-), (1118036033AOF AOD a a ∴∠=∠=-=︒-), 9060150EOF BOE AOB AOF a α∴∠=∠+∠+∠=+︒+︒-=︒,答:EOF ∠的度数是150;(3)①如图,当射线OG 在EOF ∠内部时,:2:3GOF GOE ∠∠=,222150602355GOF EOF EOF ∴∠=∠=∠=⨯︒=︒+,②如图,当射线OG 在EOF ∠外部时,:2:3GOF GOE ∠∠=,()()222352360360150210845GOF EOF ︒∴∠=∠=+-︒-︒=⨯︒=︒,综上所述,GOF ∠的度数是60︒或84︒.。
京改版七年级上3.7《角度量与角换算》同步练习(含)

3.7 角的胸襟与角的换算一、夯实基础1、若∠ 1=75 °24',∠2=75.3 °,∠ 3=75.12 ,°则 ()A. ∠1=∠ 2B. ∠2=∠3C.∠ 1=∠ 3D.以上都不对2、.由 2 点 15分到 2 点 30 分 ,钟表的分针转过的角度是 ()A.30 °B.45 °C.60 °D.90 °3、 32.6 °=°'.4、 50° 25'12″=°.二、能力提升5、已知∠ MON=30° ,∠NOP=15°,则∠ MOP=().A.45 °B.15 °C.45 °或 15°D. 无法确定6、用一副三角板的内角(其中一个三角板的内角是45°,45 °,90 ,?°另一个是30°,60 °,90 °)可以画出大于 0°且小于 176°的不同样度数的角共有( )A.8 种B.9 种C.10 种D.11 种7、 10.145 =°°″;8、计算: 153 ° 19'42 ″ +26 ° 40'28 ″解:9、计算: 90° 3-″57° 21'44 ″解:10、计算: 33° 15'16 ″× 5.计算:三、课外拓展11、如图 ,∠1∶∠ 2∶∠ 3∶∠ 4=1∶ 1∶ 3∶ 4,求∠ 1,∠ 2,∠ 3,∠ 4 的度数 .解:四、中考链接12、(百色)以下关系式正确的选项是()A .35.5 ° =35° 5′B.35.5 ° =35° 50C′.35.5 °< 35° 5′D. 35.5 °> 35° 5′参照答案夯实基础1、 D2、 D3、 32 364、能力提升5、 C6、 D7、10 8 428、解 :153 ° 19'42 ″ +26 ° 40'28 ″ =179 ° 59'70 ″=179 ° 60'10 ″ =180 ° 10″.9、解: 90° 3-″57° 21'44 ″ =89 ° 59'6357-° 21'44″ ″=32 ° 38'19 ″.10、解: 33° 15'16 ″× 5=165 ° 75'80 ″=165 ° 76'20 ″ =166 ° 16'20 ″.课外拓展11、解 :设∠ 1=x °,则∠ 2=x°,∠3=3x°,∠ 4=4x°.依题意 ,得 x°+x°+3x°+4x°=360°,9x °=360 °,则 x°=40 °.故∠ 1=40°,∠2=40°,∠ 3=120°,∠ 4=160°.中考链接12、 D7、我们各种习惯中再没有一种象战胜骄傲那麽难的了。
七年级数学上册4.3 角的度量 同步练习(含答案)

ABC 4.3 角的度量一、选择:1.下列关于角的说法正确的个数是( )①角是由两条射线组成的图形;②角的边越长,角越大; ③在角一边延长线上取一点D;④角可以看作由一条射线绕着它的端点旋转而形成的图形. A.1个 B.2个 C.3个 D.4个2.下列4个图形中,能用∠1,∠AOB,∠O 三种方法表示同一角的图形是( )AA1BO BA1B OCA B OCDA 1BOD3.图中,小于平角的角有( )A.5个B.6个C.7个D.8个 二、填空:4.将一个周角分成360份,其中每一份是______°的角, 直角等于____°,平角等于______°.5.30.6°=_____°_____′=_______′;30°6′=_______′______°. 三、解答题:6.计算:(1)49°38′+66°22′; (2)180°-79°19′; (2)22°16′×5; (4)182°36′÷4.7.根据下列语句画图: (1)画∠AOB=100°;(2)在∠AOB的内部画射线OC,使∠BOC=50°;(3)在∠AOB的外部画射线OD,使∠DOA=40°;(4)在射线OD上取E点,在射线OA上取F,使∠OEF=90°.8.任意画一个三角形,估计其中三个角的度数,再用量角器检验你的估计是否准确.9.分别确定四个城市相应钟表上时针与分钟所成的角的度数.10.九点20分时,时钟上时钟与分钟的夹角a等于多少度?11.马路上铺的地砖有很多种图案,如图所示的图案是某街面方砖铺设的示意图,请你用量角器量一下其中出现的所有的角度?12.如图,在∠AOB的内部引一条射线OC,可得几个小于平角的角? 引两条射线OC、OD呢?引三条射线OC、OD、OE呢?若引十条射线一共会有多少个角?ABO13.请用直线、线段、角等图形设计成表示客观事物的图画,如图, 并为你的图画命名.一盏吊灯一帆风顺答案:1.A2.B3.D4.1,90,1805.30,36,1836;1806,30.16.(1)116°;(2)100°41′;(3)111°20′;(4)45°39′.9.30°;0°;120°;90°10.160°12. 引1条射线有2+1=3个角;引2条射线有3+2+1=6个角;引3条射线有4+3+2+1=10个角;引10条射线有11+10+9+……+3+2+1=66个角.。
新北师大版数学七上同步测试:4.3 角

4.3 角一、选择题(每题4分,共12分)1.下列关于角的说法正确的个数是(A)①角是由两条射线组成的图形;②角的边越长,角越大;③在角一边延长线上取一点D;④角可以看成由一条射线绕着它的端点旋转而形成的图形.A.1个B.2个C.3个D.4个解:①角是由有公共端点的两条射线组成的图形,故说法错误;②角的大小与开口大小有关,角的边是射线,没有长短之分,故说法错误;③角的边是射线,不能延长,故说法错误;④角可以看成由一条射线绕着它的端点旋转而形成的图形,说法正确.所以只有④一个说法正确.故选A.2.已知∠α=18°18′,∠β=18.18°,∠γ=18.3°,下列结论正确的是(C) A.∠α=∠βB.∠α<∠βC.∠α=∠γD.∠β>∠γ3.如图,OA是北偏东30°方向的一条射线,若射线OB与射线OA垂直,则OB的方位角是(B)A.北偏西30°B.北偏西60°C.东偏北30°D.东偏北60°二、填空题(每题4分,共12分)4.如图是一个时钟的钟面,8:00时时针及分针的位置如图所示,则此时分针与时针所成的∠α是120°.5.如图,∠1,∠2表示的角可分别用大写字母表示为∠ABC,∠BCN;∠A也可表示为∠BAC,还可以表示为∠MAN.6.甲从O点出发,沿北偏西30°方向走了50 m到达A点;乙也从O点出发,沿南偏东35°方向走了80 m到达B点,则∠AOB的度数为175°.解:如图所示:因为甲从O点出发,沿北偏西30°走了50 m到达A点,乙从O点出发,沿南偏东35°方向走了80 m到达B点,所以∠AOB=180°-35°+30°=175°.三、解答题(共26分)7.(8分)如图,以B为顶点的角有几个?把它们表示出来.以D为顶点且小于平角的角有几个?把它们表示出来.解:图中以B为顶点的角有∠ABD,∠ABC,∠DBC共3个;以D为顶点且小于平角的角有∠ADE,∠ADB,∠BDC,∠EDC共4个.8.(8分)如图,有五条射线与一条直线分别交于A,B,C,D,E五点.(1)请用字母表示出以OC为边的所有的角.(2)如果B是线段AC的中点,D是线段CE的中点,AB=2,AE=10,求线段BD的长.解:(1)∠AOC,∠BOC,∠COD,∠COE,∠OCA(∠OCB),∠OCE(∠OCD);(2)因为B是线段AC的中点,所以AB=BC=2,AC=4.所以CE=AE-AC=10-4=6.因为D是线段CE的中点,所以CD=DE=12CE=3.所以BD=BC+CD=2+3=5.9.(10分)如图,在∠AOB的内部引一条射线,能组成多少个角?引两条射线能组成多少个角?引三条射线呢?引五条射线呢?引n条射线呢?图1图2图3解:由图1可知,在∠AOB的内部引一条射线时,组成的角的个数为1+2=3;由图2可知,在∠AOB的内部引两条射线时,组成的角的个数为1+2+3=6;由图3可知,在∠AOB的内部引三条射线时,组成的角的个数为1+2+3+4=10,…,所以在∠AOB的内部引五条射线时,组成角的个数为1+2+3+4+5+6=21;因此可得规律:在∠AOB的内部引出n条射线时,组成角的个数为1+2+3+…+(n+1)=(n+1)(n+2)2.。
北师大版七年级数学(上册)4.3 角 同步练习

4.3 角1.在小学我们学过角吗?它是怎样来表示的?和我们前面所学的射线有什么相同之处?2.在生活中有哪些地方用到“角”?阅读教材完成下列问题:1.角的定义:角是由所组成的图形。
其中叫做角的边。
2.角的表示方法:角用符号:“____”表示,读作“____”,通常的表示方法有:①用三个大写字母表示,如图的角表示为∠____(或∠_____),中间字母B表示_____,其他两个字母A、C分别表示角的________上的点。
注意:顶点的字母必须写在_______。
②用一个数字或希腊字母(如α、β、γ)表示,如图的角分别可表示为∠1、∠α、∠β等。
③在不引起混淆的情况下,也可以用角的顶点字母表示。
如上图中的∠ABC 就可以表示为_________.注意:当________________________时,不能用一个大写字母.3. 角另一种定义:角也可以看作是由______________________而成的图形。
注意:角将平面分为三部分:即角的外部、角的内部、和角的两边.4.明确平角和周角的定义及画法.1.判断:①角就是两条射线()②平角就是一条直线()③周角就是一条射线()④射线是一个周角.( )2.如图所示,角的顶点是,边是,用三种不同的记法表示这个角为。
3. 如图所示,图中共有_____个角,并把它们表示出来:4.选择题①如下图,下列表示∠α的方法中,正确的是( )。
A. ∠CB. ∠ACBC. ∠ADCD. ∠ACD②如下图,小于平角的角的个数为( )。
A.3B.4C.5D.6③时钟2时整,时针与分针所夹的锐角度为数为( )。
A.10°B.30°C.40°D.60°5.如下图所示,写出所有以点O为顶点的角,写出所有以点B为顶点的角。
6.计算:已知,如图在∠AOE的内部从O引出3条射线,求图中共有多少个角?如果引出4条射线呢?99条射线呢?自我检测参考答案1.错错错错2.O OA、 OB ∠O 、∠α、∠AOB3.6个∠AOC ,∠AOB,∠AOD,∠COB,∠COD,∠BOD4.①D ②D ③D5.∠ABE,∠ABO,∠OBC,∠CBE6.10个角,15个角,5050个角;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《角的度量与角的换算》同步练习
基础能力训练
1.35.8°=_____°_____';
45°42'24":________°.
2.用计算器检验第1题的结论是否正确.
3.计算
(1)36°54'+143°6':
(2)50°20'36"+40°32'48":
(3)90°-25°41'39";
(4)182°27'12"-100°32'40";
(5)25°40'5"×4:
(6)30°÷8.
综合创新训练
4._____°<锐角<_____°,直角=_____°.
_____°<钝角<_____°,平角=_____°.
周角=_____°.
5. 某校七年级下午3:00开展“阳光体育”活动,下午3:00这一时刻,时钟上分针与时针所夹的角等于_______.
6.若∠A+∠B=180°,且∠A是锐角,则∠B是( )
A.锐角B直角 C.钝角 D.不能确定
7.一个角的2倍与16°6′的差是42°58',求这个角的大小.
8.回答下列问题:
(1)1点20分时,时钟的时针与分针的夹角是多少度?2点15分时,时钟的时针与分针的夹角是多少度?
(2)从1点15分到1点35分,时钟的分针与时针各转了多大角度?
(3)从3点45分到8点21分,时钟的时针转过了多大角度?
(4)时钟的分针从4点整的位置起,按顺时针方向旋转多少度时,才能与时针重合?
9. 度、分、秒的互化:
(1)用度、分、秒表示48.26°;
(2)用度表示30°9'36".
10.计算:
(1)90°-36°12'15";
(2) 32°17'53"+42°42'7";
(3)25°12'35"×5;
(4)53°÷6.
11.如图4—1—1,(1)钟表在下午3:00时,时钟的时针与分针的夹角是多少度?
(2)下午4:40时,时钟的时针与分针的夹角是多少度?
参考答案
基础能力训练
1答案:35 48 75
5345 2答案:解析:如果两种方法计算的答案不统一,请认真核对.
3答案:解:(1)36°54'+143°6'=179°60'=180°;
(2)50°20'36"+40°32'48"=90°52'84"=90°53'24"
(3)90°-25°41'39"=89°59'60"-25°41'39"=64°18'21";
(4)182°27'12"-100°32'40"=181°86'72"-100°32'40"=81°54'32";
(5)25°40'5"×4=100°160'20"=102°40'20";
(6)30°÷8=3°45'.
综合创新训练
4答案:0 90 90 90 180 180 360
5答案:90°
6答案:C
7答案:解:设这个角的度数为x ,根据题意得2x -16°6'=42°58',2x=59°4',x=29°32'.(本题可以不列方程,列算式求也可以)
8答案:解:因为时针I 小时走30°,分针1分走6°(或分针每分走1小格·时针每分走121小格),所以
(1)1点20分时,时针与分针的央角是[20-(5+12
1×20)]×6°=80°; 2点15分时,时针与分针的夹角是[15-(10+
121×15)]×6°=22.5°; (2)分针转过的角度是(35-15)×6°=120°, 时针转过的角度是 1012012
1=⨯; (3)时钟转过的角度是 1386)12
455201221(=⨯-++; (4)设分针需要按顺时针方向旋转x 度,才能与时针重合,则时针按顺时针方向旋转了
12x 度,根据题意得,12012=-
x x , 解得11
10130=x . 9.解:(1) ∵60'×0.26=15.6',60"×0.6=36",
∴48.26°=48°15'36";
(2)∵36"=(6036)'=0.6',9.6'=(60
6.9)°=0.16°, ∴30°9'36"=30.16°.
10. 解:(1)90°-36°12'15" (2)32°17'53"+42°42'7" =89°59'60"-36°12'15" =74°59'60"
=53°47'45"; =75°;
(3)25°12'35"×5 (4)53°÷6
=125°60'175" =8°50'
=126°2'55";
∵300'÷6=50',
∴53°÷6=8°50'
11. 解:(1)3×30°=90°;
(2)3×30°+(30°-30°×6040
)=100°.。
