九年级下册数学解直角三角形同步练习3
人教版九年级数学下册28.2 解直角三角形 同步练习附答案【新】

28.2 解直角三角形第3课时坡角、方向角与解直角三角形1. 如图,某水库堤坝横断面迎水坡AB的坡比是1:3,堤坝高BC=50 m,则迎水坡面AB的长度是()A.100 m B.1003 mC.150 m D.503 m2. 小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为30°,同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为()A.(6+3)米 B. 12米 C. (4-23)米 D. 10米3. 如图,小明要测量河内小岛B到河边公路l的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=50米,则小岛B到公路l的距离为米.4. 如图,某公园入口处原有三级台阶,每级台阶高为18 cm,深为30 cm,为方便残疾人士,拟将台阶改为斜坡,设台阶的起始点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是cm.5. 如图,在一次夏令营活动中,小明从营地A点出发,沿北偏东60°方向走了5003 m到达B点,然后再沿北偏西30°方向走了500 m到达目的地C点.(1)求A、C两点之间的距离;(2)确定目的地C在营地A的什么方向?参考答案1.A2.A3.4.2105.解:(1)过B 点作BE ∥AD ,如图,∴∠DAB =∠ABE =60°.∵30°+∠CBA +∠ABE =180°,∴∠CBA =90°, 即△ABC 为直角三角形.由已知可得:BC =500 m ,AB ,由勾股定理可得:AC 2=BC 2+AB 2,∴1000(m)=AC .(2)在Rt △ABC 中,∵BC =500 m ,AC =1000 m , ∴∠CAB =30°.∵∠DAB =60°,∴∠DAC =30°. 即点C 在点A 的北偏东30°的方向.。
九年级数学下册解直角三角形及其应用同步练习3(新版)新人教版

九年级数学下册解直角三角形及其应用同步练习3〖新版〗新人教版一﹨双基整合:1.轮船航行到C 处时,观测到小岛B 的方向是北偏西35°,那么同时从B•观测到轮船的方向是_________.2.如图1所示,在离地面高度为5m 的C 处引拉线固定电线杆,拉线和地面成α角,•则拉线AC 的长为_____m 〖用α的三角函数表示〗.(1) (2) (3)3.如图2所示,点B 在点A 北偏西60°方向,且AB=5km ,点C 在点B 北偏东30°方向,且BC=12km ,则A 到C 的距离为________.4.如图3,为了测量河对岸旗杆AB 的高度,在点C 处测得旗杆顶端A 的仰角为30°,•沿CB 方向前进20m 到达D 处,在点D 处测得旗杆顶端A 的仰角为45°,则旗杆AB 的高度为_______〖精确到0.1m ,参考数据:2=1.414,3=1.732〗5.如图4所示,在坡度为1:2的山坡上种树,要求株距〖相邻两树间的水平距离〗•是6米,则斜坡上相邻两树间的坡面距离是〖 〗A .6米B .35米C .3米D .12米(4) (5) (6)6.如图5所示,一架飞机在空中A 点处测得飞行高度为h 米,从飞机上看到地面指挥站B 的俯角为α,则飞机与地面指挥站间的水平距离为〖 〗A .h ·sin α米B .h ·cos α米C .h ·tan α米D .tan h米 7.如图6,在高为h 的山顶上,测得一建筑物顶端与底部的俯角分别为30°和60°,用h 表示这个建筑物的高度为〖 〗A .23hB .32h C 3h D 38.如图7,上午9时,一条船从A 处出发以20里/时的速度向正北航行,11时到达B 处,从A ﹨B 望灯塔C ,测得∠NAC=36°,∠NBC=72°,那么从B 处到灯塔C 的距离是〖 〗A .20里B .36里C .72里D .40里(7) (8)9.如图8所示,拦水坝的横断面为梯形ABCD,已知上底长CB=5米,迎水面坡度为1:3,背水面坡度为1:1,坝高为4米,求:〖1〗坡底宽AD的长;〖2〗迎水坡CD的长;〖3〗坡角α﹨β.二﹨探究创新10.如图,在一个坡角为15°的斜坡上有一棵树,•高为AB,•当太阳光与水平线成50°角时,测得该树在斜坡上的树影BC的长为7m,求树高.〖精确到0.1m〗三﹨智能升级11.如图,某市郊外景区内一条笔直的公路a经过三个景点A﹨B﹨C,•景区管委会又开发了风景优美的景点D,经测量,景点D位于景点A的北偏东30′方向8km处,•位于景点B 的正北方向,还位于景点C的北偏西75°方向上,已知AB=5km.〖1〗景区管委会准备由景点D向公路a修建一条距离最短的公路,不考试其他因素,求出这条公路的长.〖结果精确到0.1km〗.〖2〗求景点C与景点D之间的距离.〖结果精确到1km〗〖参考数据:3,5,sin53°=0.80,sin37°=0.60,tan53°=1.33,tan37°=0.75,sin38°=0.62,sin52°=0.79,tan38°=0.78,tan52°=1.28,sin75°=0.97,cos75°=0.26,tan75°=3.73〗.2.如图,海平面上灯塔O方圆100千米范围内有暗礁,•一艘轮船自西向东方向航行,在点A处测量得灯塔O在北偏东60°方向,继续航行100米后,在点B•处测量得灯塔O在北偏东37°方向.请你作出判断,为了避免触礁,这艘轮船是否要改变航向?〖参考数据:sin37°≈0.6018,cos37°≈0.7986,tan37°≈0.7536,cot37°≈1.327,3≈1.732〗答案:1.南偏东55° 2.5sin3.13km 4.27.3m 5.B 6.D 7.A 8.D9.〖1〗〖9+43〗m;〖2〗8m;〖3〗α=30°,β=45°10.解:如图,过点C作水平线与AB的延长线交于点D,则AD⊥CD,∴∠BCD=15°,∠ACD=50°,在Rt△CDB中,CD=7×cos15°,BD=7×sin15°,在Rt△CDA•中,•AD=•CD•×tan50°=7×cos15°×tan50°,∴AB=AD-BD=〖7×cos15°×tan50°-7×sin15°〗=7〖cos15°×tan50°-sin15°〗≈6.2〖m〗11.〖1〗约3.1km;〖2〗约4km12.解:如图过点O作OC垂直于AB的延长线于点C,在Rt△COB中,∠BOC=37°,BC=OC.tan37°,在Rt△AOC中,∠AOC=60°,AC=OCtan60°=3OC,又∵AC=AB+BC,AB=100千米,即3OC=100+•OC·tan37°,≈102.2〖千米〗,∴OC=-︒3tan37故OC>100千米,这艘轮船可以不改变航向,不会触礁.。
人教版九年级数学下册《解直角三角形》同步作业(含答案)

图28-3练习9 解直角三角形一、自主学习1.如图28-3所示,Rt △ABC 中 (1)它三边之间的关系是_________. (2)它两锐角之间的关系是________. (3)它的边角之间的关系是:___________________,____________________; ___________________,__________________; ___________________,____________________; 二、基础巩固2.等腰三角形的周长为2+3,腰长为1,则它的底角等于________.3.在离地面5 m 处引拉线固定电线杆,拉线和地面成60°角,则拉线的长为_______________.4.一个梯形的两个下底角分别为30°和45°,较大的腰长为10 cm ,则它另一腰长为________.5.△ABC 中,BC=2,AC=3+3,∠C=30°,则sinA=_________.6.在高度为93 m 的建筑物上,观察一楼房的顶端和底部的俯角分别为30°,60°,则这栋楼房的高度为___________m.7.Rt △ABC 中,∠C=90°,sinA=54,AB=10,则BC=________,cosB=________8.△ABC 中,若∠ABC=45°,∠ACB=30°,AB=22,则S △ABC =_________.9.如图28-4所示,△ABC 中,CD ⊥AB 于D 点,且BD=2AD ,若CD=34,tan ∠BCD=33,则高AE=____.10.Rt △ABC 中,CD 是斜边AB 上的高,AB=8 cm ,AC=34cm ,则AD=_____________cm.11.Rt △ABC 中,∠C=90°,∠A 、∠B 、∠c 所对的边分别为a 、b 、c ,若a=25,b=215,则c=________,∠A_______,∠B________.三、能力提高12.Rt △ABC 斜边上的中线CD 长为1,周长是2+6,则它的面积是( ) A.2B.21C.1D.)32(21+13.正方形ABCD 的边长为5,E 、F 分别在边BC 、CD 上,若△AEF 为等边三角形,则BE 的长是( ) A.3255-B.3310C.3510-D.23514.如图28-5所示,一束平行的光线从教室窗射入教室,测得光线与地面所成的∠AMC=30°,窗户的高在教室地面的图28-4影长MN=32m ,窗户的下檐到教室地面的距离BC=1 m ,(点M 、N 、C 在同一直线上),则窗户高AB 为( )图28-5 图28-6 图28-7A.3m B.3 m C.2 m D.1.5 m15.在平面直角坐标系内,坐标原点为O ,点M 在第四象限,且OM=1,∠MOx=30°,则点M 的坐标是( ) A.(21,23-) B.(21,23--) C.(21,23-) D.(23,21-)16.如图28-6所示,在山坡上种树,已知相邻两株树的坡面距离AB 为4 m ,∠B=60°,则这两株树的水平距离和高度差分别为( ) A.32m ,2 m B.2 m ,32m C.3 m ,1 mD.1 m,3m17.大风刮断一根废弃的木电线杆,如图28-7所示,杆的顶端B 落到地面离其底部A 的距离为3m处,若两截电线杆的夹角为30°,则电线杆刮断前的高度为( ) A.6 m B.33m C.3+32 m D.32 m18.Rt △ABC 中,∠C=90°,若AC 的长等于斜边上的中线长的34,则较大锐角的余弦值是( )A.35B.552C.553D.3219.如图28-8所示,将-矩形纸片ABCD 折起一个角,使点C 恰好落在AB 边,若AD=m ,∠CDE=α,则折痕DE=( )A.αα2sin cos •mB.ααcos sin 2•mC.ααcos sin •mD.ααsin cos 2•m图28-8 图28-920.已知平行四边形两邻边长分别是64cm和34cm ,一角为45°,则这个平行四边形的较长对角线长是( ) A.66cm B.68 cm C.38 cm D.154cm21.如图28-9所示,△ABC 中,D 为AB 的中点,∠ACB=135°,AC ⊥CD ,则sinA=( ) A.53B.55C.51 D.52四、模拟链接22.小明家在花园小区某栋楼AD 内,他家附近又新建了一座大厦BC ,已知两栋楼房间的水平距离为90 m ,AD 楼高60 m ,小明爬上自家所在楼房顶测得大厦顶部C 的仰角为30°,求大厦BC 的高.(精确到1 m ,如图28-10所示)图28-1023.小华所在的学校A位于某工地O的正西方向,如图28-11所示,且OA=200 m.一拖拉机从工地O出发,以5m/s的速度沿北偏西53°方向行驶,设拖拉机的噪音影响半径为130 m,问小华所在的学校A是否受拖拉机噪音影响?若受影响,请求出学校受拖拉机噪音影响的时间.(已知sin53°≈0.80、sin37°≈0.60)图28-1124.阅读下列材料,并解决后面的问题:在锐角△ABC 中,∠A 、∠B 、∠C 的对边分别为a 、b 、c ,作AD ⊥BC 于D(如图28-12),则sinB=cAD ,sinC=bAD ,即AD=c·sinB ,AD=b·sinC ,于是c·sinB=b·sinC ,即C cB b sin sin =,同理有A a C c sin sin =,即Cc B b A a sin sin sin == 即:在一个锐角三角形中,各边和它所对角的正弦的比相等.[来源:学+科+网Z+X+X+K](1)在锐角三角形中,若已知三个元素a 、b 、∠A ,运用上述结论和有关定理就可求出其余三个元素c 、∠B 、∠C ,请按照下列步骤填空,完成求解过程.第一步:由条件a 、b 、∠A −−−→−有关系式_________−−→−求出∠B ; 第二步:由条件∠A 、∠B −−−→−有关系式________−−→−求出∠C ; 第三步:由条件_______−−−→−有关系式__________−−→−求出∠c (2)一货轮在C 处测得灯塔A 在其北偏西30°的方向上,随后货轮以284海里/时的速度沿北偏东45°的方向航行,半小时后到达B 处,此时又测得灯塔在货轮的北偏西70°的方向上(如图28-13),求此时货轮距灯塔A 的距离AB(结果精确到0.1,参考数据:sin40°=0.643,sin65°=0.906,sin70°=0.940,sin75°=0.966).图28-12图28-13参考答案一、自主学习1.如图28-3所示,Rt△ABC中(1)它三边之间的关系是_________.(2)它两锐角之间的关系是________.(3)它的边角之间的关系是:__________________________,_______________________ ______;____________________________,__________________________;___________________________,_________________________;图28-3答案:(1)a 2+b 2=c 2 (2)∠A+∠B=90° (3)sinA=ca ,cosA=cb ,tanA=bacotA=ab ,sinB=cb ,cosB=ca ,tanB=ab ,cotB=ba二、基础巩固2.等腰三角形的周长为2+3,腰长为1,则它的底角等于________. 答案:30°3.在离地面5 m 处引拉线固定电线杆,拉线和地面成60°角,则拉线的长为_______________. 答案:3310m4.一个梯形的两个下底角分别为30°和45°,较大的腰长为10 cm ,则它另一腰长为________. 答案:255.△ABC 中,BC=2,AC=3+3,∠C=30°,则sinA=_________.答案:10106.在高度为93 m 的建筑物上,观察一楼房的顶端和底部的俯角分别为30°,60°,则这栋楼房的高度为___________m.答案:627.Rt △ABC 中,∠C=90°,sinA=54,AB=10,则BC=________,cosB=________ 答案:8548.△ABC 中,若∠ABC=45°,∠ACB=30°,AB=22,则S △ABC =_________. 答案:2329.如图28-4所示,△ABC 中,CD ⊥AB 于D 点,且BD=2AD ,若CD=34,tan ∠BCD=33,则高AE=__________.图28-4答案:3310.Rt △ABC 中,CD 是斜边AB 上的高,AB=8 cm ,AC=34cm ,则AD=_____________cm.答案:611.Rt △ABC 中,∠C=90°,∠A 、∠B 、∠c 所对的边分别为a 、b 、c ,若a=25,b=215,则c=________,∠A_______,∠B________. 答案:530° 60°三、能力提高12.Rt △ABC 斜边上的中线CD 长为1,周长是2+6,则它的面积是( ) A.2B.21 C.1D.)32(21+答案:B13.正方形ABCD 的边长为5,E 、F 分别在边BC 、CD 上,若△AEF 为等边三角形,则BE 的长是( ) A.3255-B.3310C.3510-D.235答案:C14.如图28-5所示,一束平行的光线从教室窗射入教室,测得光线与地面所成的∠AMC=30°,窗户的高在教室地面的影长MN=32m ,窗户的下檐到教室地面的距离BC=1 m ,(点M 、N 、C 在同一直线上),则窗户高AB 为( )图28-5A.3m B.3 m C.2 mD.1.5 m 答案:C15.在平面直角坐标系内,坐标原点为O ,点M 在第四象限,且OM=1,∠MOx=30°,则点M 的坐标是( )A.(21,23-) B.(21,23--) C.(21,23-)D.(23,21-)答案:A16.如图28-6所示,在山坡上种树,已知相邻两株树的坡面距离AB 为4 m ,∠B=60°,则这两株树的水平距离和高度差分别为( ) A.32m ,2 m B.2 m ,32 m C.3 m ,1 mD.1 m,3m图28-6答案:A17.大风刮断一根废弃的木电线杆,如图28-7所示,杆的顶端B 落到地面离其底部A 的距离为3m处,若两截电线杆的夹角为30°,则电线杆刮断前的高度为( ) A.6 m B.33 m C.3+32mD.32m图28-7答案:C18.Rt △ABC 中,∠C=90°,若AC 的长等于斜边上的中线长的34,则较大锐角的余弦值是( )A.35B.552 C.553D.32 答案:D19.如图28-8所示,将-矩形纸片ABCD 折起一个角,使点C 恰好落在AB 边,若AD=m ,∠CDE=α,则折痕DE=( )图28-8A.αα2sin cos •mB.ααcos sin 2•mC.ααcos sin •mD.ααsin cos 2•m 答案:A20.已知平行四边形两邻边长分别是64cm和34cm ,一角为45°,则这个平行四边形的较长对角线长是( ) A.66 cm B.68 cm C.38cmD.154cm答案:D21.如图28-9所示,△ABC 中,D 为AB 的中点,∠ACB=135°,AC ⊥CD ,则sinA=( ) A.53 B.55C.51 D.52图28-9答案:B 四、模拟链接22.小明家在花园小区某栋楼AD 内,他家附近又新建了一座大厦BC ,已知两栋楼房间的水平距离为90 m ,AD 楼高60 m ,小明爬上自家所在楼房顶测得大厦顶部C 的仰角为30°,求大厦BC 的高.(精确到1 m ,如图28-10所示)图28-10答案:112 m23.小华所在的学校A 位于某工地O 的正西方向,如图28-11所示,且OA=200 m.一拖拉机从工地O 出发,以5m/s 的速度沿北偏西53°方向行驶,设拖拉机的噪音影响半径为130 m ,问小华所在的学校A 是否受拖拉机噪音影响?若受影响,请求出学校受拖拉机噪音影响的时间.(已知sin53°≈0.80、sin37°≈0.60)图28-11答案:受影响的时间为20 s24.阅读下列材料,并解决后面的问题:在锐角△ABC 中,∠A 、∠B 、∠C 的对边分别为a 、b 、c ,作AD ⊥BC 于D(如图28-12),则sinB=cAD ,sinC=bAD ,即AD=c·sinB ,AD=b·sinC ,于是c·sinB=b·sinC ,即C cB b sin sin =,同理有A a C c sin sin =,即Cc B b A a sin sin sin == 即:在一个锐角三角形中,各边和它所对角的正弦的比相等.[来源:学+科+网Z+X+X+K](1)在锐角三角形中,若已知三个元素a 、b 、∠A ,运用上述结论和有关定理就可求出其余三个元素c 、∠B 、∠C ,请按照下列步骤填空,完成求解过程.第一步:由条件a 、b 、∠A −−−→−有关系式_________−−→−求出∠B ; 第二步:由条件∠A 、∠B −−−→−有关系式________−−→−求出∠C ; 第三步:由条件_______−−−→−有关系式__________−−→−求出∠c (2)一货轮在C 处测得灯塔A 在其北偏西30°的方向上,随后货轮以284海里/时的速度沿北偏东45°的方向航行,半小时后到达B 处,此时又测得灯塔在货轮的北偏西70°的方向上(如图28-13),求此时货轮距灯塔A 的距离AB(结果精确到0.1,参考数据:sin40°=0.643,sin65°=0.906,sin70°=0.940,sin75°=0.966).图28-12 图28-13答案:(1)略(2)约为21.3海里(提示:用题目中的结论)。
人教版九年级数学下册解直角三角形同步练习

人教版九年级数学下册解直角三角形同步练习基础训练知识点1 已知两边解三角形1‘在Rt△ABC中,∠C=90°‘(1)若c=6,a=6,则b=_________,∠B=_______,∠A=_______;(2)若a=4,b=4,则∠A=_______,∠B=_______,c=_______‘2‘如图,△ABC中,∠B=90°,BC=2AB,则cos A=( )A‘B‘ C‘D‘3‘如图,四边形ABCD是梯形,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,AB=4,AD=6,则tan B=( )A‘2B‘2C‘D‘知识点2 已知一边及一锐角解三角形4‘在Rt△ABC中,∠C=90°‘(1)若∠B=60°,BC=,则∠A=__________,AC=_________,AB=_________;(2)若∠A=45°,AB=2,则∠B=_________,AC=_________,BC=_________‘5‘在直角三角形ABC中,已知∠C=90°,∠A=40°,BC=3,则AC 等于( )A‘3sin 40°B‘3sin 50°C‘3tan 40°D‘3tan 50°6‘如图,△ABC中,∠C=90°,AC=3,∠B=30°,P是BC边上的动点,则AP长不可能是( )A‘3‘5 B‘4‘2 C‘5‘8 D‘77‘如图,在Rt△ABC中,∠C=90°, D为BC上一点,∠DAC=30°,BD=2,AB=2,则AC的长是( )A‘ B‘2 C‘3 D‘知识点3 已知一边及一锐角的三角函数值解三角形8‘如图,菱形ABCD的边长为15,sin∠BAC=,则对角线AC的长为‘9‘如图,△ABC中,AC=5,cos B=,sin C=,则△ABC的面积是( )A‘B‘12 C‘14 D‘2110‘如图,已知菱形ABCD中,AE⊥BC于点E‘若sin B=,AD=6,则菱形ABCD的面积为( )A‘12 B‘12C‘24 D‘5411‘如图,在四边形ABCD中,AD∥BC,AC⊥AB,AD=CD,cos ∠DCA=,BC=10,则AB的值是( )A‘3 B‘6 C‘8 D‘912‘在△ABC中,AB=2,AC=,∠B=30°‘求∠BAC的度数‘提升训练考查角度1 利用三角函数解直角三角形13‘如图,在Rt△ABC中,∠C=90°,AC=BC=3,解这个直角三角形‘14‘在Rt△ABC中,∠C=90°,已知b=10,∠B=60°,解这个直角三角形‘15‘如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sin B=,AD=1‘(1)求BC的长;(2)求tan ∠DAE的值‘考查角度2 利用三角函数解斜三角形问题(化斜为直法)16‘如图,在△ABC中,sin B=,∠A=105°,AB=2,求△ABC的面积‘考查角度3 利用三角函数解与相似有关的综合问题17‘如图,在△A BC中,∠ABC=90°,BC=3,D为AC延长线上一点,AC=3CD,过点D作DH∥AB,交BC的延长线于点H‘(1)求BD·cos∠HBD的值;(2)若∠CBD=∠A,求AB的长‘18‘如图,两个全等的△ABC和△DEF重叠在一起,固定△ABC,将△DEF进行如下变换:(1)如图①,△DEF沿直线CB向右平移(即点F在线段CB上移动),连接AF,AD,BD,请直接写出S△ABC与S四边形AFBD的关系‘(2)如图②,当点F平移到线段BC的中点时,若四边形AFBD为正方形,那么△ABC应满足什么条件?请给出证明‘(3)在(2)的条件下,将△DEF沿DF折叠,点E落在FA的延长线上的点G处,连接CG,请你画出图形,并求出sin∠CGF的值‘①②19‘如图,PB为☉O的切线,B为切点,过B作OP的垂线BA,垂足为C,交☉O于点A,连接PA,AO‘并延长AO交☉O于点E,与PB 的延长线交于点D‘(1)求证:PA是☉O的切线‘(2)若=,且OC=4,求PA的长和tan D的值‘参考答案1‘【答案】(1)6;45°;45°(2)60°;30°;82‘【答案】D 3‘【答案】B4‘【答案】(1)30°;;2(2)45°;;5‘【答案】D 6‘【答案】D 7‘【答案】A8‘【答案】249‘【答案】A解:如图,过点A作AD⊥BC‘因为cos B=,所以∠B=45°,所以AD=BD‘因为sin C==,所以=,所以AD=BD=3,所以DC===4,所以BC=BD+DC=7,所以S△BC·AD=×7×3=‘ABC=10‘【答案】C解:∵四边形ABCD是菱形,AD=6,∴AB=BC=6‘在Rt△ABE中,sin B=,∵sin B=,∴=,解得AE=4‘∴菱形ABCD的面积是6×4=24‘故选C‘11‘【答案】B解:∵AD∥BC,∴∠DAC=∠ACB‘∵AD=CD,∴∠DAC=∠DCA‘∴∠ACB=∠DCA‘∴cos∠ACB=cos∠DCA=,即==,∴AC=8,∴AB==6‘12‘解:(1)如图①,当∠BAC是钝角时,过点A作AD⊥BC,垂足为点D‘在Rt△ABD中,∵∠B=30°,∴∠BAD=60°,AD=AB·sin 30°=1‘在Rt△ACD中,CD===1,∴△ACD是等腰直角三角形,则∠CAD=45°,∴∠BAC=∠BAD+∠CAD=60°+45°=105°‘(2)如图②,当∠BAC是锐角时,过点A作AD⊥BC,交BC的延长线于点D‘∵∠B=30°,∴AD=AB·sin 30°=1,∠BAD=60°‘∴CD===1,∴∠DAC=45°,∴∠BAC=∠BAD-∠DAC=60°-45°=15°‘综上可知,∠BAC的度数为105°或15°‘常见错解:解题时只考虑了一种情况(∠BAC为钝角或∠BAC为锐角),而忽略了另一种情况(∠BAC为锐角或∠BAC为钝角),从而造成漏解‘13‘解:在Rt△ABC中,AB===6‘∵tan A===1,∴∠A=45°‘∴∠B=90°-∠A=90°-45°=45°‘14‘解:∵∠B=60°,∴∠A=90°-∠B=30°‘∵tan B=,∴a====‘∵sin B=,∴c====‘方法解:已知一个锐角时,可以先根据直角三角形的两锐角互余来计算另一个锐角的度数‘已知一个锐角及对边,常通过正切和正弦来解直角三角形‘15‘解:(1)在△ABC中,∵AD是BC边上的高,∴∠ADB=∠ADC=90°‘在△ADC中,∵∠ADC=90°,∠C=45°,AD=1,∴DC=AD=1‘在△ADB中,∵∠ADB=90°,sin B=,AD=1,∴AB==3,∴BD==2,∴BC=BD+DC=2+1‘(2)∵AE是BC边上的中线,∴CE=BC=+,∴DE=CE-CD=-,∴tan ∠DAE==-‘16‘解:过A作AD⊥BC于D‘在Rt△ABD中,易得∠B=45°,又AB=2,∴∠DAB=∠B=45°,AD=BD=2×=,∴∠CAD=105°-45°=60°‘在Rt△CAD中,tan∠CAD=,∴CD=AD·tan∠CAD=×tan 60°=‘∴BC=CD+BD=+‘∴S△ABC=·BC·AD=(+)×=+1‘17‘解:(1)∵DH∥AB,∴∠BHD=∠ABC=90°, ∴△ABC∽△DHC,∴=‘∵AC=3CD,BC=3,∴CH=1‘∴BH=BC+CH=4‘在Rt△BHD中,cos ∠HBD=‘∴BD·cos∠HBD=BH=4‘(2)方法一:∵∠A=∠CBD,∠ABC=∠BHD,∴△ABC∽△BHD,∴=‘∵△ABC∽△DHC,∴==,∴AB=3DH,∴=,DH=2,∴AB=6‘方法二:∵∠CBD=∠A,∠BDC=∠ADB,∴△CDB∽△BDA,∴=,BD2=CD·AD‘∴BD2=CD·4CD=4CD2‘∴BD=2CD‘∵△CDB∽△BDA,∴=‘∴=‘∴AB=6‘18‘解:(1)S△ABC=S四边形AFBD‘(2)△ABC为等腰直角三角形,即:AB=AC,∠BAC=90°‘理由如下:∵F为BC的中点,∴CF=BF‘∵CF=AD,∴AD=BF‘又∵AD∥BF,∴四边形AFBD为平行四边形‘∵AB=AC,F为BC的中点,∴AF⊥BC‘∴平行四边形AFBD为矩形‘∵∠BAC=90°,F为BC的中点,∴AF=BC=BF‘∴四边形AFBD为正方形‘(3)正确画出图形如图‘由(2)知,△ABC为等腰直角三角形,AF⊥BC,设CF=k,则GF=EF=CB=2k‘由勾股定理,得:CG=k‘sin ∠CGF===‘19‘(1)证明:如图,连接BO,∵PB为☉O的切线,B为切点,∴OB⊥PD,∠PBO=90°‘又∵OA=OB,OC⊥AB,∴∠AOC=∠BOC‘又∵OP=OP,∴△PAO≌△PBO,∴∠PAO=∠PBO=90°,PA=PB,∴PA是☉O的切线‘(2)解:∵∠ACO=∠PAO=90°,∠AOC=∠POA,∴△AOC∽△POA,∴==‘又∵OC=4,∴AC=6‘在Rt△AOC中,OA===2,∴PA=OA=3,∴PB=3‘在Rt△PAO中,PO===13‘如图,连接BE‘∵AE为直径,∴∠ABE=90°‘又∵OC⊥AB, ∴BE∥OP,∴△DBE∽△DPO,BE=2OC=8‘∴=‘即=‘解得BD=‘∴在Rt△DBO中,tan D===‘。
人教版九年级下册数学 28.2.1解直角三角形 同步练习
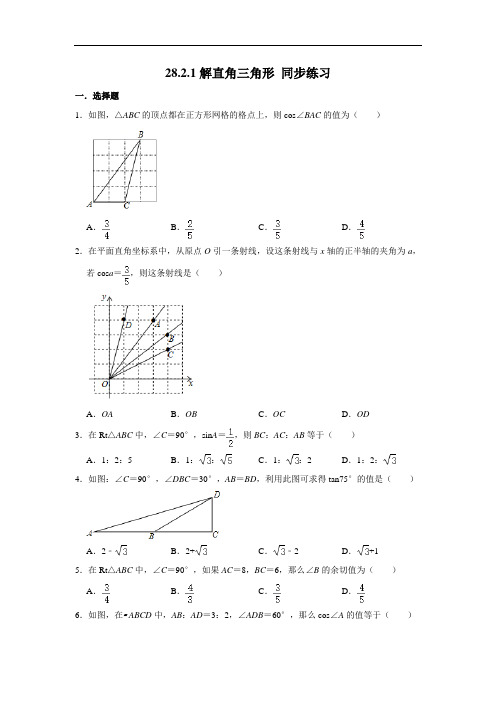
28.2.1解直角三角形同步练习一.选择题1.如图,△ABC的顶点都在正方形网格的格点上,则cos∠BAC的值为()A.B.C.D.2.在平面直角坐标系中,从原点O引一条射线,设这条射线与x轴的正半轴的夹角为a,若cos a=,则这条射线是()A.OA B.OB C.OC D.OD3.在Rt△ABC中,∠C=90°,sin A=,则BC:AC:AB等于()A.1:2:5B.1::C.1::2D.1:2:4.如图:∠C=90°,∠DBC=30°,AB=BD,利用此图可求得tan75°的值是()A.2﹣B.2+C.﹣2D.+15.在Rt△ABC中,∠C=90°,如果AC=8,BC=6,那么∠B的余切值为()A.B.C.D.6.如图,在▱ABCD中,AB:AD=3:2,∠ADB=60°,那么cos∠A的值等于()A.B.C.D.7.如图,在等腰△ABC中,AB=AC,BD是AC边上的高,cos C=,则△BCD与△ABD 的面积比是()A.1:3B.2:7C.2:9D.2:118.如图,△ABC在边长为1个单位的方格纸中,它的顶点在小正方形的顶点位置.如果△ABC的面积为10,且sin A=,那么点C的位置可以在()A.点C1处B.点C2处C.点C3处D.点C4处9.如图,在△ABC中,∠C=90°,AC=8cm,AB的垂直平分线MN交AC于D,连接BD,若cos∠BDC=,则BC的长是()A.4cm B.6cm C.8cm D.10cm10.如图,已知A、B两点的坐标分别为(8,0)、(0,8),点C、F分别是直线x=﹣5和x轴上的动点,CF=10,点D是线段CF的中点,连接AD交y轴于点E,当△ABE面积取得最小值时,tan∠BAD的值是()A.B.C.D.二.填空题11.如图,在△ABC中,∠ACB=90°,D是AB的中点,DE⊥AB,交AC于E,若=,则tan∠A=.12.如图,在△ABC中,AB=4,BC=7,∠B=60°,点D在边BC上,CD=3,连接AD.如果将△ACD沿直线AD翻折后,点C的对应点为点E,那么点E到直线BD的距离为.13.一副直角三角板如图放置,点C在FD的延长线上,已知AB∥FC,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=8,则CD的长为.14.如果三角形有一边上的高恰好等于这边长的,那么称这个三角形为“好玩三角形”,在Rt△ABC是“好玩三角形”,且∠C=90°,则tan A=.15.如图,平面上七个点A、B、C、D、E、F、G,图中所有的连线长均相等,则cos∠BAF =.三.解答题16.如图,已知:Rt△ABC中,∠ACB=90°,点E为AB上一点,AC=AE=3,BC=4,过点A作AB的垂线交射线EC于点D,延长BC交AD于点F.(1)求CF的长;(2)求∠D的正切值.17.已知:如图,在△ABC中,AB=AC=5,BC=8,D是边AB上一点,且tan∠DCB=.(1)试求cos B的值;(2)试求△BCD的面积.18.如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,点D是边AC的中点,CF⊥BD,垂足为点F,延长CF与边AB交于点E.求:(1)∠ACE的正切值;(2)线段AE的长.参考答案一.选择题1.解:过B作BH⊥AC交AC的延长线于H,∴AB===5,AH=3,∴cos∠BAC==,故选:C.2.解:∵点A的坐标为(3,4),∴OA=5,∴cos a=,则这条射线是OA.故选:A.3.解:∵在Rt△ABC中,∠C=90°,sin A==,∴∠A=30°,cos A==,∴BC:AC:AB=1::2.故选:C.4.解:∵AB=BD,∴∠A=∠ADB,∵∠DBC=∠A+∠ADB=30°,∴∠A=15°,∴∠ADC=75°,设CD=a,在Rt△BCD中,∵∠DBC=30°,∴BD=2a,BC=a,∴AC=AB+BC=BD+BC=2a+a=(2+)a,在Rt△ACD中,tan∠ADC=tan75°===2+.故选:B.5.解:如图,在Rt△ABC中,∵∠C=90°,AC=8,BC=6,∴cot B===,故选:A.6.解:作AF⊥DB于F,作DE⊥AB于E.设DF=x,则AD=2x,∵∠ADB=60°,∴AF=x,又∵AB:AD=3:2,∴AB=3x,于是BF=x,∴3x•DE=(+1)x•x,DE=x,sin∠A=,cos∠A==.故选:A.7.解:作AE⊥BC于E,∵AB=AC,∴BE=EC=BC,∵在Rt△AEC中,cos C==,∴AC=3EC,∴AC=BC,在Rt△BCD中,cos C==,∴BC=3CD,∴AC=CD,∴=,∴===,故选:B.8.解:过点C作CD⊥直线AB于点D,如图所示.∵AB=5,△ABC的面积为10,∴CD=4.∵sin A=,∴AC=4,∴AD==8,∴点C在点C4处.故选:D.9.解:∵∠C=90°,AC=8cm,AB的垂直平分线MN交AC于D,∴BD=AD,∴CD+BD=8,∵cos∠BDC==,∴=,解得:CD=3,BD=5,∴BC=4.故选:A.10.解:如图,设直线x=﹣5交x轴于K.由题意KD=CF=5,∴点D的运动轨迹是以K为圆心,5为半径的圆,∴当直线AD与⊙K相切时,△ABE的面积最小,∵AD是切线,点D是切点,∴AD⊥KD,∵AK=13,DK=5,∴AD=12,∵tan∠EAO==,∴=,∴OE=,∴AE==,作EH⊥AB于H.∵S△ABE=•AB•EH=S△AOB﹣S△AOE,∴EH=,∴AH==,∴tan∠BAD===,故选:B.二.填空题11.解:连接EB,∵D是AB的中点,DE⊥AB,∴DE是AB的垂直平分线,∴EA=EB,∵==,设EC=3k,则AE=BE=4k,AC=5k+3k=8k,在Rt△BCE中,BC==4k,在Rt△ABC中,tan∠A===,故答案为:.12.解:如图,过点E作EH⊥BC于H.∵BC=7,CD=3,∴BD=BC﹣CD=4,∵AB=4=BD,∠B=60°,∴△ABD是等边三角形,∴∠ADB=60°,∴∠ADC=∠ADE=120°,∴∠EDH=60°,∵EH⊥BC,∴∠EHD=90°,∵DE=DC=3,∴EH=DE•sin60°=,∴E到直线BD的距离为,故答案为.13.解:过点B作BM⊥FD于点M,在△ACB中,∠ACB=90°,∠A=60°,AC=8,∴∠ABC=30°,BC=AC×tan60°=8,∵AB∥CF,∴BM=BC×sin30°=8×=4,CM=BC×cos30°=12,在△EFD中,∠F=90°,∠E=45°,∴∠EDF=45°,∴MD=BM=4,∴CD=CM﹣MD=12﹣4.14.解:分三种情况:①如图1,高AC=BC,此时tan A===2;②如图2,高BC=AC,此时tan A===;③如图3,高CD=AB,设AC=x,BC=y,CD=a,则AB=2a,由三角形面积公式和勾股定理得:,解得:x=y=a(负数舍去),tan A==1;故答案为:或2或1.15.解:连接AC、AD,过点D作DM⊥AC,垂直为M.设AE的长为x,则AB=AG=BG=CG=CB=AF=AE=EF=x,∴△ABG、△AEF、△CBG和△DEF都是等边三角形,四边形ABCG、四边形AEDF是菱形,∴∠BAC=∠EAD=30°∴AC=AD=2×cos∠BAC×AB=2×x=x∵∠CAD=∠BAE﹣∠BAC﹣∠EAD=∠BAE﹣60°,∠BAF=∠BAE﹣∠EAF=∠BAE﹣60°,∴∠BAF=∠CAD在Rt△AMD中,因为DM=sin∠CAD×x,AM=coa∠CAD×x,CM=x﹣cos∠CAD×x,在Rt△CMD中,CD2=CM2+MD2,即x2=(x﹣cos∠CAD×x)2+(sin∠CAD×x)2整理,得5x2=6x2cos∠CAD∴cos∠CAD=∴cos∠BAF=.故答案为:三.解答题16.解:(1)∵∠ACB=90°,∴∠ACF=∠ACB=90°,∠B+∠BAC=90°,∵AD⊥AB,∴∠BAC+∠CAF=90°,∴∠B=∠CAF,∴△ABC∽△F AC,∴=,即=,解得CF=;(2)如图,过点C作CH⊥AB于点H,∵AC=3,BC=4,∴AB=5,则CH==,∴AH==,EH=AE﹣AH=,∴tan D=tan∠ECH==.17.解:(1)作AE⊥BC于E,如图,∵AB=AC,∴BE=CE=BC=×8=4,在Rt△ABC中,cos B==;(2)作DF⊥BC于F,如图,在Rt△CDF中,tan∠DCF==,设DF=3x,则CF=5x,在Rt△ABE中,AE==3,∴tan B==,在Rt△BDF中,tan B==,而DF=3x,∴BF=4x,∴BC=BF+CF=4x+5x=9x,即9x=8,解得x=,∴DF=3x=,∴S△BCD=×DF×BC=××8=.18.解:(1)∵∠ACB=90°,∴∠ACE+∠BCE=90°,又∵CF⊥BD,∴∠CFB=90°,∴∠BCE+∠CBD=90°,∴∠ACE=∠CBD,∵AC=4且D是AC的中点,∴CD=2,又∵BC=3,在Rt△BCD中,∠BCD=90°.∴tan∠CBD==,∴tan∠ACE=tan∠CBD=;(2)过点E作EH⊥AC,垂足为点H,在Rt△EHA中,∠EHA=90°,∴tan A=,∵BC=3,AC=4,在Rt△ABC中,∠ACB=90°,∴tan A==,∴=,设EH=3k,AH=4k,∵AE2=EH2+AH2,∴AE=5k,在Rt△CEH中,∠CHE=90°,∴tan∠ECA==,∴CH=k,∴AC=AH+CH=k=4,解得:k=,∴AE=.。
人教版九年级数学下册28.2 解直角三角形 同步练习3 含答案

28.2解直角三角形(3)一、选择题1. 一个人从山下沿30°角的坡路登上山顶,共走了500m,那么这山的高度是[ ]m.A.230B.240C.250D.2602. 一个人从A点出发向北偏东60°方向走了一段距离到达B点,再从B点出发向南偏东15°方向走了一段距离到C点,则∠ABC的度数为 [ ]A.15°B.75°C.105°D.45°3. 为了求河对岸建筑物AB的高,在地平面上测得基线CD=180米,在C点测得A点的仰角为30°,在地平面上测得∠BCD=∠BDC=45°,那么AB的高是[ ]米.4. 如图,一船向正北航行,看见正东有两个相距10海里的灯塔,船航行半小时后,一个灯塔在船的东南,另一个灯塔在船的东22°30′南,则船的速度(精确到0.1米)是[ ]米/时(tg22°30′=0.4142)A.12.1B.13.1C.14.1D.15.15. 一只船向正东航行,上午7时在灯塔A的正北C处,上午9时到达塔的北偏东60°B处,已知船的速度为每小时20千米,那么AB的距离是[ ]千米.6. 如图:B处有一船,向东航行,上午9时在灯塔A的西南58.4千米的B上午11时到达灯塔的南C处,那么这船航行的速度是[ ]千米/时.A.19.65B.20.65C.21.65D.22.657. 如图:一只船以每小时20千米的速度向正东航行,起初船在A处看见一灯塔B在船的北偏东60°,2小时后,船在C处看见这个灯塔在船的北偏东45°,则灯塔B到船的航海线AC的距离是 [ ]千米.二、填空题一只船向东航行,上午9点到一座灯塔的西南68海里处,上午11点到达这座灯塔的正南,这只船航行的速度是_____________.(答案可带根号)三、解答题1. 如图:已知一船以每小时20海里的速度向正南行驶,上午10时在A 处见灯塔P 在正东,1小时后行至B 处,观察灯塔P 的方向是北60°东.求正午12时船行驶至C 处距灯塔P 的距离.(答案可带根号)2.如图:东西方向的海岸线上有A 、B 两码头,相距100 )13(-千米,由码头A 测得海上船K 在北偏东30°,由码头B 测得船K 在北偏西15°,求船K 距海岸线AB 的距离(已知tan75°=32+-)参考答案一、选择题1. C2. B3. C4. C5. D6. B7. C二、填空题时海里/217三、解答题1.米7202.350千米。
新人教版九年级数学下册 28.2.1 解直角三角形同步测试(含答案)

解直角三角形1.△ABC 中,a ,b ,c 分别是∠A ,∠B ,∠C 的对边,如果a 2+b 2=c 2,那么下列结论正确的是( A )A .c sin A =aB .b cos B =cC .a ta n A =bD .c tan B =b2.在Rt △ABC 中,∠C =90°,若tan A =12,c =2,则b 的值等于( D )A.55 B.255 C.355 D.455【解析】 ∵tan A =a b =12,∴a =b 2,又∵a 2+b 2=c 2,∴⎝ ⎛⎭⎪⎫b 22+b 2=4,∴5b 24=4,∴b =45 5.3.如图28-2-1,小明为了测量其所在位置A 点到河对岸B 点之间的距离,沿着与AB 垂直的方向走了m 米,到达点C ,测得∠ACB =α,那么AB 等于( B ) A .m ·sin α米 B .m ·tan α米 C .m ·cos α米 D.mtan α米图28-2-1图28-2-24.如图28-2-2,△ABC 中,cos B =22,sin C =35,AC =5,则△ABC 的面积是( A ) A.212B .12C .14D .21 5.已知:在△ABC 中,AB =AC ,∠BAC =120°,AD 为BC 边上的高.则下列结论中,正确的是( B ) A .AD =32AB B .AD =12AB C .AD =BD D .AD =22BD 6.在Rt △ABC 中,∠C =90°,a =6,b =23,则∠B =__30°__.【解析】 本题是已知两直角边解直角三角形,由tan B =b a =236=33,得∠B =30°.7.已知Rt △ABC 中,∠C =90°,c =83,∠A =60°,则a =__12__,b =.【解析】 本题是已知一锐角和斜边解直角三角形,由sin A =a c ,得a =sin A ·c =32×83=12.由∠A =60°,得∠B =30°,所以b =12c =4 3.8.等腰三角形底边长为26,底边上的高为32,则底角为__60°__. 【解析】 底边上的高将等腰三角形分割成两个直角三角形,通过解直角三角形即可求底角. 9.在△ABC 中,∠C =90°,由下列条件解直角三角形. (1)已知∠A =60°,b =4,求a ; (2)已知a =13,c =23,求b ;(3)已知c =282,∠B =30°,求a ;(4)已知a =2,cos B =13,求b .解:(1)∵tan A =a b,∴a =b ·tan A =4·tan60°=4×3=43;(2)∵a 2+b 2=c 2, ∴b =c 2-a 2=⎝ ⎛⎭⎪⎫232-⎝ ⎛⎭⎪⎫132=13; (3)∵cos B =a c, ∴a =c ·cos B =282×32=146; (4)∵cos B =a c ,∴c =a cos B =213=6.又∵b 2=c 2-a 2,∴b =c 2-a 2=62-22=4 2. 10.在Rt △ABC 中,∠C =90°. (1)已知a =4,b =8,求c .(2)已知b =10,∠B =60°,求a ,c . (3)已知c =20,∠A =60°,求a ,b .解:(1)c =a 2+b 2=42+82=45;(2)a =b tan B =10tan60°=103=1033,c =b sin B =10sin60°=1032=2033;(3)a =c ×sin A =20×32=103,b =c ×cos A =20×12=10. 11.根据下列条件,解直角三角形:(1)在Rt △ABC 中,∠C =90°,a =8,∠B =60°; (2)在Rt △ABC 中,∠C =90°,∠A =45°,b = 6.解:(1)∠A =90°-∠B =30°,c =acos B=16,b =a ·tan B =83;(2)∠B =90°-∠A =45°,a =b ·tan A =6,c =bcos A=2 3.图28-2-312.如图28-2-3,在Rt △ABC 中,∠C =90°,AC =2,AB = 22,解这个直角三角形.解:∵∠C =90°,AC =2,AB =22,∴sin B =AC AB =12,∴∠B =30°, ∴∠A =60°.BC =AB 2-AC 2=8-2= 6.13.如图28-2-4,已知△ABC 中,∠C =90°,tan A =12,D 是AC 上一点,∠CBD =∠A ,则sin ∠ABD =( A )图28-2-4A.35B.105C.310D.4914.如图28-2-5,已知在Rt △ABC 中,∠BAC =90°,点D 在BC 边上,且△ABD 是等边三角形.若AB =2,求△ABC 的周长(结果保留根号). 解:∵△ABD 是等边三角形,∴∠B = 60°. 在Rt △ABC 中,∵cos B =AB BC ,sin B =AC BC,∴BC = AB cos B =2cos60°=4,∴AC =BC ·sin B =4×sin60°=23, ∴△ABC 的周长=AB +AC +BC =6+2 3.图28-2-5图28-2-615.如图28-2-6,△ABC 中,∠C =90°,点D 在AC 上,已知∠BDC =45°,BD =102,AB =20.求∠A 的度数.解:在Rt △BDC 中,因为sin ∠BDC =BC BD, 所以BC =BD ×sin ∠BDC =102×sin45°=102×22=10. 在Rt △ABC 中,因为sin A =BC AB =1020=12,所以∠A =30°. 16.如图28-2-7,在△ABC 中,∠A =30°,∠B =45°,AC =23,求AB 的长.图28-2-7第16题答图解:如图,过点C 作CD ⊥AB 于点D , ∴∠ADC =∠BDC =90°.∵∠B =45°,∴∠BCD =∠B =45°,∴CD =BD . ∵∠A =30°,AC =23,∴CD =12AC =3,∴BD =CD = 3.由勾股定理得:AD =AC 2-CD 2=3, ∴AB =AD +BD =3+ 3.17.某学校的校门是伸缩门(如图①),伸缩门中的每一行菱形有20个,每个菱形边长为30厘米.校门关闭时,每个菱形的锐角度数为60°(如图②);校门打开时,每个菱形的锐角度数从60°缩小为10°(如图③).问:校门打开了多少米?(结果精确到1米,参考数据:sin5°≈0.087 2,cos5°≈0.996 2,sin10°≈0.173 6,cos10°≈0.984 8).图28-2-8 解:如图,校门关闭时,取其中一个菱形ABC D.根据题意,得∠BAD=60°,AB=0.3米.∵在菱形ABCD中,AB=AD,∴△BAD是等边三角形,∴BD=AB=0.3米,∴大门的宽是:0.3×20≈6(米);校门打开时,取其中一个菱形A1B1C1D1.根据题意,得∠B1A1D1=10°,A1B1=0.3米.∵在菱形A1B1C1D1中,A1C1⊥B1D1,∠B1A1O1=5°,∴在Rt△A1B1O1中,B1O1=sin∠B1A1O1·A1B1=sin5°×0.3=0.02616(米),∴B1D1=2B1O1=0.05232米,∴伸缩门的宽是:0.05232×20=1.0464米;∴校门打开的宽度为:6-1.0464=4.9536≈5(米).故校门打开了5米.。
【新】人教版九年级数学下册: 解直角三角形及其应用 同步练习 (含答案)

解直角三角形及其应用同步练习一.选择题(共12小题)1.如图,在等腰△ABC中,AB=AC,BD是AC边上的高,cosC=,则△BCD与△ABD的面积比是()A.1:3B.2:7C.2:9D.2:112.如图,每个小正方形的边长都为1,点A、B、C都在小正方形的顶点上,则∠ABC的正弦值为()A.1B.C.0.5D.3.如图,在边长为1的正方形网格中,连接格点D、N和E、C,DN和EC相交于点P,tan∠CPN为()A.1B.2C.D.4.如图,在Rt△ABC中,∠C=90°,∠BAC=30°,延长CA到点D,使AD=AB,连接BD.根据此图形可求得tan15°的值是()A.B.C.D.5.如图,在莲花山滑雪场滑雪,需从山脚下乘缆车上山,缆车索道与水平线所成的角为31°,缆车速度为每分钟40米,从山脚下A到达山顶B缆车需要15分钟,则山的高度BC为()A.600•tan31°B.C.600•sin31°D.6.小明同学在数学实践课中测量路灯的高度.如图,已知他的目高AB为1.5米,他先站在A处看路灯顶端O的仰角为30°,向前走3米后站在C处,此时看灯顶端O的仰角为60°,则灯顶端O 到地面的距离约为()A.3.2米B.4.1米C.4.7米D.5.4米7.如图所示,小明所住高楼AB高为100米,楼旁有一座坡比为3:1的山坡CE,小明想知道山坡的高度,于是小明来到楼顶B俯视坡底C,测得俯角为45°,仰视坡项E,测得仰角为27°,请根据小明提供的信息,帮小明求出斜坡CE的高度ED的值.(结果均精确到0.1米.参考数据:sin27°≈0.45,cos37°≈0.89,tan27°≈0.51)()A.151.1米B.168.7米C.171.6米D.181.9米8.如图,要测量小河两岸相对的两点P、A之间的距离,可以在小河边PA的垂线PB上取一点C.测得PC=80米,∠PCA=32°,则PA的长为()A.80sin32°米B.80tan32°米C.D.9.如图,某“拓展训练营”的一个自行车爬坡项目有两条不同路线,路线一:从C到B,路线二:从D到A,AB为垂直升降梯.其中BC的坡度为i=1:2,BC=12米,CD=8米,∠D=36°(其中A,B,C,D均在同一平面内),则垂直升降梯AB的高度约为(精确到0.1米)()(参考数据:tan36°≈0.73,cos36°≈0.81,sin36°≈0.59)A.8.6B.11.4C.13.9D.23.410.如图,在一笔直的海岸线l上有A,B两个测点,AB=4km,从A处测得船C在北偏东45°的方向,从B 处得船C在北偏东22.5°的方向,则船C离海岸线l的距离CD的长为()A.4kmB.(4+2)kmC.(4+)kmD.(4-)km11.某游客乘坐“金碧皇宫号游船”在长江和嘉陵江的交汇处A点,测得来福土最高楼顶点F的仰角为45°,此时他头项正上方146米的点B处有架航拍无人机测得来福士最高楼顶点F的仰角为31°,游船朝码头方向行驶120米到达码头C,沿坡度i=1:2的斜坡CD走到点D,再向前走160米到达来福士楼底E,则来福士最高楼EF的高度约为()(结果精确到0.1,参考数据:sin31°≈0.52,cos31°≈0.87,tan31°≈0.60)A.301.3米B.322.5米C.350.2米D.418.5米12.诗人卞之琳的代表作《断章》:“你站在桥上看风景,看风景的人在楼上看你,明月装饰了你的窗子,你装饰了别人的梦”.2019年国庆,重庆来福士广场开业,吸引了全国各地游客前来,重庆又有了一张新的名片.10月2日,游客小王从南滨路的A处,沿坡度i=1:0.75的斜坡上行20米到达B处,再往正前方水平走8米到达C处,对来福士广场拍照.同时,小王身后的一栋居民楼里面的重庆市民小张在D处测得C处的俯角为42°,若居民楼底端E处与A处的距离是45米,A、B、C、D、E在同一平面内,DE⊥AE于点E.则DE的长约为()米.(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.9)A.74.5B.74.1C.61.2D.58.5二.填空题(共6小题)13.已知一段公路的坡度为1:20,沿着这条公路前进,若上升的高度为2m,则前进了.14.如图,l是一条笔直的公路,道路管理部门在点A设置了一个速度监测点,已知BC为公路的一段,B 在点A的北偏西30°方向,C在点A的东北方向,若AB=50米.则BC的长为米.(结果保留根号)15.如图,在Rt△ABC中,∠ACB=90°,AC=2,tanB=0.75,CD平分∠ACB交AB于点D,DE⊥BC,垂足为点E,则DE=.16.如图,渔船在A处看到灯塔C在北偏东60°方向上,渔船向正东方向航行了12km达B处,在B处看到灯塔C在正北方向上,则A处与灯塔C的距离是.17.在△ABC中,∠A=30°,AB=2,AC=6,则BC的长为18.如图,为了测量塔CD的高度,小明在A处仰望塔顶,测得仰角为30°,再往塔的方向前进60m至B处,测得仰角为60°,那么塔的高度是m.(小明的身高忽略不计,结果保留根号).三.解答题(共5小题)19.如图,正在海岛C西南方向20海里作业的海监船A,收到位于其正东方向渔船B发出的遇险求救信号,已知渔船B位于海岛C的南偏东30°方向,海岛C周围13海里内都有暗礁.(参考数据)(1)如果海监船A沿正东方向前去救援是否有触礁的危险?(2)求海监船A与渔船B的距离.(结果精确到0.1海里)20.某中学为数学实验“先行示范校”,一数学活动小组带上高度为1.5m的测角仪BC,对建筑物AO进行测量高度的综合实践活动,如图,在BC处测得直立于地面的AO顶点A的仰角为30°,然后前进40m至DE处,测得顶点A的仰角为75°.(1)求∠CAE的度数;(2)求AE的长(结果保留根号);(3)求建筑物AO的高度(精确到个位,参考数据:.21.如图是一种简易台灯的结构图,灯座为△ABC,A、C、D在同一直线上.量得∠ACB=90°,∠A=60°,AB=16cm,∠ADE=135°,灯杆CD长为40cm,灯管DE长为15cm.求台灯的高(即台灯最高点E到底盘AB 的距离).(结果取整,参考数据sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,22.某工厂生产某种多功能儿童车,根据需要可变形为图1的滑板车或图2的自行车,已知前后车轮半径相同,AD=BD=DE=30cm,CE=40cm,车杆AB与BC所成的∠ABC=53°,图1中B、E、C三点共线,图2中的座板DE与地面保持平行.问变形前后两轴心BC的长度有没有发生变化?若不变,请写出BC的长度;若变化,请求出变化量?(参考数据:sin53°)23.如图①是某小区入口实景图,图②是该入口抽象成的平面示意图,已知入口BC宽3.9米,门卫室外墙(灯罩长度忽略不计),∠AOM=60°.上的O点处装有一盏灯,点O与地面BC的距离为3.3米,灯臂OM长1.2米,(1)求点M到地面的距离,(2)某搬家公司一辆总宽2.55米,总高3.5米的货车能否从该入口安全通过?如果能安全通过,请直接写出货车离门卫室外墙AB的最小距离(精确到0.01米);如果不能安全通过,请说明理由.(参考数据:参考答案1-5:BDBAC 6-10:BDBBB 11-12:BA13、214、)15、16、17、18、19、20、21、22、在Rt△CEN中,∵CE=40cm,∴由勾股定理可得CN=32cm,则BC=18+30+32=80(cm),答:BC的长度发生了改变,增加了4cm23、(1)过点M作MN⊥OA于点N,∵OM长1.2米,∠AOM=60°.∴ON=0.6米,∴BN=OB+ON=3.3+0.6=3.9米.答:点M到地面的距离为3.9米.(2)一辆总宽2.55米,总高3.5米的货车能从该入口安全通过,理由如下:过点A作AE⊥BA,垂足为A,∵设货车高AB=3.5米,则OA=3.5-3.3=0.2∴AE=OAtan60°=≈0.35答:货车离门卫室外墙AB的最小距离为0.35米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
九年级下册数学解直角三角形同步
练习3
一·选择题
1. 一个人从山下沿30°角的坡路登上山顶,共走了500m,那么这山的高度是
[ ]m.
A.230
B.240
C.250
D.260
2. 一个人从A点出发向北偏东60°方向走了一段距离到达B点,再从B点出发向南偏东15°方向走了一段距离到C点,则∠ABC的度数为 [ ]
A.15°
B.75°
C.105°
D.45°
3. 为了求河对岸建筑物AB的高,在地平面上测得基线CD=180米,在C点测得A点的仰角为30°,在地平面上测得∠BCD=∠BDC=45°,那么AB的高是[ ]米
.
4. 如图,一船向正北航行,看见正东有两个相距10海里的灯塔,船航行半小时后,一个灯塔在船的东南,另一个灯塔在船的东22°30′南,则船的速度(精确到0.1米)是[ ]米/
时(tg22°30′=0.4142)
A.12.1
B.13.1
C.14.1
D.15.1
5. 一只船向正东航行,上午7时在灯塔A的正北C处,上午9时到达塔的北偏东60°B
处,已知船的速度为每小时20千米,那么AB的距离是[ ]千米.
6. 如图:B处有一船,向东航行,上午9时在灯塔A的西南58.4千米的B
上午11时到达灯塔的南C处,那么这船航行的速度是[ ]千米/时.
A.19.65
B.20.65
C.21.65
D.22.65
7. 如图:一只船以每小时20千米的速度向正东航行,起初船在A处看见一灯塔B在船的北偏东60°,2小时后,船在C处看见这个灯塔在船的北偏东45°,则灯塔B到船的航海线AC的距离是 [ ]千米.
二·填空题
一只船向东航行,上午9点到一座灯塔的西南68海里处,上午11点到达这座灯塔的正南,这只船航行的速度是_____________.(答案可带根号)
三·解答题
1. 如图:已知一船以每小时20海里的速度向正南行驶,上午10时在A 处见灯塔P 在正东,1小时后行至B 处,观察灯塔P 的方向是北60°东.求正午12时船行驶至C 处距灯塔P 的距离.(答案可带根号)
2.如图:东西方向的海岸线上有A ·B 两码头,相距100 )13(-千米,由码头A 测得海上船K 在北偏东30°,由码头B 测得船K 在北偏西15°,求船K 距海岸线AB 的距离(已知tan75°=32+-)
参考答案
一·选择题
1. C
2. B
3. C
4. C
5. D
6. B
7. C 二·填空题
时
海里/217 三·解答题
1.米720
2.350千米。
