悬臂梁—有限元ABAQUS线性静力学分析实例-精选.pdf
ABAQUS线性静力学分析实例

线性静力学分析实例线性静力学问题是简单且常见的有限元分析类型,不涉及任何非线性(材料非线性、几何非线性、接触等),也不考虑惯性及时间相关的材料属性。
在ABAQUS 中,该类问题通常采用静态通用(Static,General)分析步或静态线性摄动(Static,Linear perturbation)分析步进行分析。
线性静力学问题很容易求解,往往用户更关系的是计算效率和求解效率,希望在获得较高精度的前提下尽量缩短计算时间,特别是大型模型。
这主要取决于网格的划分,包括种子的设置、网格控制和单元类型的选取。
在一般的分析中,应尽量选用精度和效率都较高的二次四边形/六面体单元,在主要的分析部位设置较密的种子;若主要分析部位的网格没有大的扭曲,使用非协调单元(如CPS4I、C3D8I)的性价比很高。
对于复杂模型,可以采用分割模型的方法划分二次四边形/六面体单元;有时分割过程过于繁琐,用户可以采用精度较高的二次三角形/四面体单元进行网格划分。
一悬臂梁的线性静力学分析1.1 问题的描述一悬臂梁左端受固定约束,右端自由,结构尺寸如图1-1所示,求梁受载后的Mises应力、位移分布。
ν材料性质:弹性模量3=2eE=,泊松比3.0均布载荷:Mpa=p6.0图1-1 悬臂梁受均布载荷图1.2 启动ABAQUS启动ABAQUS有两种方法,用户可以任选一种。
(1)在Windows操作系统中单击“开始”--“程序”--ABAQUS 6.10 -- ABAQUS/CAE。
(2)在操作系统的DOS窗口中输入命令:abaqus cae。
启动ABAQUS/CAE后,在出现的Start Section(开始任务)对话框中选择Create Model Database。
1.3 创建部件在ABAQUS/CAE顶部的环境栏中,可以看到模块列表:Module:Part,这表示当前处在Part(部件)模块,在这个模块中可以定义模型各部分的几何形体。
ABAQUS实验报告

ABAQUS实验报告1.实验目的本次实验的主要目的是使用ABAQUS软件对一个具体的结构进行有限元分析,了解结构在受力情况下的变形情况,并通过分析结果评估结构的强度和稳定性。
2.实验对象本次实验选择了一个简单的悬臂梁结构作为分析对象,悬臂梁的尺寸为L=100mm,H=10mm,t=10mm,材料为钢材,杨氏模量为210GPa,泊松比为0.33.实验过程首先,使用ABAQUS软件建立了悬臂梁的有限元模型,包括结构的几何形状、材料性质和边界条件。
然后,施加一个向下的均布载荷在悬臂梁的自由端上,通过有限元分析得到了结构在受力后的应力分布、变形情况和位移等数据。
最终,对分析结果进行评估并提出改进建议。
4.实验结果通过ABAQUS软件进行有限元分析,得到了悬臂梁在受力后的应力分布、变形情况和位移等数据。
其中,悬臂梁在受力后的最大应力出现在悬臂梁的根部,并随着距离自由端的增加逐渐减小;结构的最大变形出现在梁的自由端,变形由中间向两侧逐渐减小;结构的最大位移也出现在梁的自由端。
5.结果分析通过对实验结果的分析,可以得出以下结论:(1)悬臂梁在受力后的应力、变形和位移分布符合结构力学的基本原理,最大应力、变形和位移出现在悬臂梁的根部和自由端。
(2)结构的受力情况对结构的强度和稳定性有重要影响,必须合理设计结构的几何形状和材料性质。
(3)通过有限元分析可以准确地预测结构在受力情况下的响应,为结构设计和优化提供了有效的工具和方法。
6.结论与建议根据实验结果的分析,可以得出以下结论和建议:(1)结构的几何形状、材料性质和受力情况对结构的强度和稳定性有重要影响,必须合理设计和选择结构的几何形状和材料性质。
(2)有限元分析是一种有效的工具,可以准确地预测结构在受力情况下的响应,为结构设计和优化提供了重要的参考。
(3)在进行结构设计和优化时,应该充分考虑结构的受力情况,避免结构出现应力集中和失稳现象。
综上所述,通过本次实验,我深刻认识到了结构在受力情况下的变形和破坏机制,对结构的强度和稳定性有了更深入的理解。
ABAQUS线性静力学分析实例

线性静力学分析实例线性静力学问题是简单且常见的有限元分析类型,不涉及任何非线性(材料非线性、几何非线性、接触等),也不考虑惯性及时间相关的材料属性。
在ABAQUS中,该类问题通常采用静态通用(Static,General)分析步或静态线性摄动(Static,Linear perturbation)分析步进行分析。
线性静力学问题很容易求解,往往用户更关系的是计算效率和求解效率,希望在获得较高精度的前提下尽量缩短计算时间,特别是大型模型。
这主要取决于网格的划分,包括种子的设置、网格控制和单元类型的选取。
在一般的分析中,应尽量选用精度和效率都较高的二次四边形/六面体单元,在主要的分析部位设置较密的种子;若主要分析部位的网格没有大的扭曲,使用非协调单元(如CPS4I、C3D8I)的性价比很高。
对于复杂模型,可以采用分割模型的方法划分二次四边形/六面体单元;有时分割过程过于繁琐,用户可以采用精度较高的二次三角形/四面体单元进行网格划分.一悬臂梁的线性静力学分析1。
1 问题的描述一悬臂梁左端受固定约束,右端自由,结构尺寸如图1—1所示,求梁受载后的Mises应力、位移分布。
ν材料性质:弹性模量3=E=,泊松比3.02e均布载荷:Mpa=p6.0图1-1 悬臂梁受均布载荷图1。
2 启动ABAQUS启动ABAQUS有两种方法,用户可以任选一种。
(1)在Windows操作系统中单击“开始”--“程序”-—ABAQUS 6。
10 -—ABAQUS/CAE。
(2)在操作系统的DOS窗口中输入命令:abaqus cae。
启动ABAQUS/CAE后,在出现的Start Section(开始任务)对话框中选择Create Model Database.1.3 创建部件在ABAQUS/CAE顶部的环境栏中,可以看到模块列表:Module:Part,这表示当前处在Part(部件)模块,在这个模块中可以定义模型各部分的几何形体.可以参照下面步骤创建悬臂梁的几何模型。
悬臂梁—有限元ABAQUS线性静力学分析报告实例

线性静力学分析实例——以悬臂梁为例线性静力学问题是简单且常见的有限元分析类型,不涉及任何非线性(材料非线性、几何非线性、接触等),也不考虑惯性及时间相关的材料属性。
在ABAQUS 中,该类问题通常采用静态通用(Static ,General )分析步或静态线性摄动(Static ,Linear perturbation )分析步进行分析。
线性静力学问题很容易求解,往往用户更关系的是计算效率和求解效率,希望在获得较高精度的前提下尽量缩短计算时间,特别是大型模型。
这主要取决于网格的划分,包括种子的设置、网格控制和单元类型的选取。
在一般的分析中,应尽量选用精度和效率都较高的二次四边形/ 六面体单元,在主要的分析部位设置较密的种子;若主要分析部位的网格没有大的扭曲,使用非协调单元(如CPS4I、C3D8I)的性价比很高。
对于复杂模型,可以采用分割模型的方法划分二次四边形/ 六面体单元;有时分割过程过于繁琐,用户可以采用精度较高的二次三角形/ 四面体单元进行网格划分。
悬臂梁的线性静力学分析1.1 问题的描述一悬臂梁左端受固定约束,右端自由,结构尺寸如图1-1 所示,求梁受载后的Mises 应力、位移分布。
材料性质:弹性模量 E 2e3 ,泊松比0.3均布载荷:F=103N图1-1 悬臂梁受均布载荷图1.2 启动ABAQUS启动ABAQUS有两种方法,用户可以任选一种1)在Windows 操作系统中单击“开始” -- “程序” --ABAQUS 6.10 -- ABAQUS/CA。
E(2)在操作系统的DOS窗口中输入命令:abaqus cae 。
启动ABAQUS/CA后E ,在出现的Start Section (开始任务)对话框中选择Create Model Database 。
1.3 创建部件在ABAQUS/CA顶E 部的环境栏中,可以看到模块列表:Module:Part ,这表示当前处在Part (部件)模块,在这个模块中可以定义模型各部分的几何形体。
ABAQUS线性静力学分析实例

线性静力学分析实例线性静力学问题是简单且常见的有限元分析类型,不涉及任何非线性(材料非线性、几何非线性、接触等),也不考虑惯性及时间相关的材料属性。
在ABAQUS 中,该类问题通常采用静态通用(Static,General )分析步或静态线性摄动(Static ,Linear perturbation)分析步进行分析.线性静力学问题很容易求解,往往用户更关系的是计算效率和求解效率,希望在获得较高精度的前提下尽量缩短计算时间,特别是大型模型.这主要取决于网格的划分,包括种子的设置、网格控制和单元类型的选取.在一般的分析中,应尽量选用精度和效率都较高的二次四边形/六面体单元,在主要的分析部位设置较密的种子;若主要分析部位的网格没有大的扭曲,使用非协调单元(如CPS4I 、C3D8I )的性价比很高.对于复杂模型,可以采用分割模型的方法划分二次四边形/六面体单元;有时分割过程过于繁琐,用户可以采用精度较高的二次三角形/四面体单元进行网格划分.一 悬臂梁的线性静力学分析1.1 问题的描述一悬臂梁左端受固定约束,右端自由,结构尺寸如图1-1所示,求梁受载后的Mises 应力、位移分布。
材料性质:弹性模量32e E =,泊松比3.0=ν均布载荷:Mpa p 6.0=图1—1 悬臂梁受均布载荷图1.2 启动ABAQUS启动ABAQUS 有两种方法,用户可以任选一种。
(1)在Windows操作系统中单击“开始”——“程序”——ABAQUS 6。
10 -—ABAQUS/CAE。
(2)在操作系统的DOS窗口中输入命令:abaqus cae。
启动ABAQUS/CAE后,在出现的Start Section(开始任务)对话框中选择Create Model Database。
1.3 创建部件在ABAQUS/CAE顶部的环境栏中,可以看到模块列表:Module:Part,这表示当前处在Part(部件)模块,在这个模块中可以定义模型各部分的几何形体.可以参照下面步骤创建悬臂梁的几何模型.(1)创建部件。
ABAQUS线性静力学分析实例

ABAQUS线性静力学分析实例ABAQUS(全称为Abaqus FEA)是一种广泛使用的有限元分析软件。
它可用于进行结构、热、电、磁、多物理场等各类工程问题的数值模拟和分析。
在本文中,我们将介绍一个ABAQUS线性静力学分析的实例。
假设我们要分析一个悬臂梁的变形和应力分布。
悬臂梁是一种常见的结构,通常由一根固定在一端的梁杆组成,另一端悬空。
我们将使用ABAQUS来计算这个悬臂梁的变形和应力。
首先,我们需要创建模型。
在ABAQUS中,可以通过几何建模或直接输入节点和单元的方式来创建模型。
这里我们使用几何建模来构建一个悬臂梁。
在ABAQUS的图形用户界面中,选择"Part",然后使用"Sketch"工具绘制悬臂梁的剖面。
在剖面绘制完成后,选择"Extrude"工具将其拉伸为所需长度。
接下来,我们需要定义材料特性。
在这个实例中,我们假设悬臂梁是由钢材料构成的。
在ABAQUS中,可以通过创建相应的材料属性来定义材料的性能。
选择"Material",然后创建一个具有适当材料属性的钢材料。
随后,我们需要定义悬臂梁的边界条件。
在这个实例中,我们将在悬臂梁的固定端施加一个约束,防止其发生位移。
在ABAQUS中,可以选择"Assembly",然后选择"Constraints"来设置边界条件。
在这里我们选择固定一个端点。
完成边界条件的设置后,我们需要划分网格。
在ABAQUS中,使用网格划分将悬臂梁划分成小的单元,以便数值计算。
选择"Mesh",然后选择适当的网格划分方式和单元类型。
然后,我们需要定义加载条件。
在这个实例中,我们将在悬臂梁的空悬端施加一个垂直向下的加载。
在ABAQUS中,可以选择"Loading",然后选择适当的加载类型和大小。
现在,所有的模型设置都完成了,我们可以进行分析。
悬臂梁有限元分析
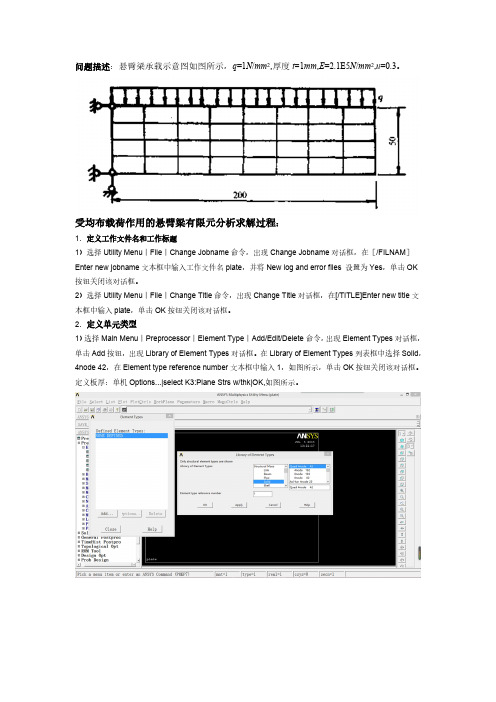
问题描述:悬臂梁承载示意图如图所示,q=1N/mm2,厚度t=1mm,E=2.1E5N/mm2,u=0.3。
受均布载荷作用的悬臂梁有限元分析求解过程:1.定义工作文件名和工作标题1)选择Utility Menu︱File︱Change Jobname命令,出现Change Jobname对话框,在[/FILNAM]Enter new jobname文本框中输入工作文件名plate,并将New log and error files 设置为Yes,单击OK 按钮关闭该对话框。
2)选择Utility Menu︱File︱Change Title命令,出现Change Title对话框,在[/TITLE]Enter new title文本框中输入plate,单击OK按钮关闭该对话框。
2.定义单元类型1)选择Main Menu︱Preprocessor︱Element Type︱Add/Edit/Delete命令,出现Element Types对话框,单击Add按钮,出现Library of Element Types对话框。
在Library of Element Types列表框中选择Solid,4node 42,在Element type reference number文本框中输入1,如图所示,单击OK按钮关闭该对话框。
定义板厚:单机Options...|select K3:Plane Strs w/thk|OK,如图所示。
3.定义材料性能参数1)选择Main Menu︱Preprocessor︱Material Props︱Material Models命令,出现Define Material Model Behavior对话框。
2)在Material Models Available一栏中依次单击Structural、Linear、Elastic、Isotropic选项(如图3.5所示),出现Linear Isotropic Properties for Material Number 1对话框,在EX文本框中输入2.1E5,在PRXY文本框中输入0.3,如图所示,单击OK按钮关闭该对话框。
有限元作业:悬臂梁

例一:悬臂梁在循环加载作用下的弹塑性计算(GUI)一、问题描述:一个左端固定的悬臂梁见图1-1(a),厚度为1cm,在它的右段中点上施加有一个集中力,该集中力为循环载荷见图1-1(b),悬臂梁的材料为多线性弹性材料,材料的弹性模量为20000,实验获得的该材料的非线性应力-应变行为见表1-2,分析该悬臂梁在循环载荷作用下的观测点P的水平方向上的应力应变历程。
(a)悬臂梁以及加载位置(cm)(b)所受的循环载荷(N)图1-1一个悬臂梁以及加载历程表1-2 〉材料的应力-应变行为实验数据二、问题分析解答:为考察悬臂梁根部P点的应力-应变历程,采用2D的计算模型,使用平面单元PLANE42,材料采用多线性弹塑性模型(mkin),进行循环加载过程的分析。
建模的要点如下:①设置几何以及材料参数,②输入材料的多线性弹塑性模型(包括:弹性模量、屈服极限),见图1-3;③通过设置time来给出加载历程,每次加载都输入当时的状态载荷值,不是增量加载,每次加载后,必须进行计算,再进入下一步的计算;④在时间后处理中,通过设置几何位置来查询对应的P观测点的节点编号,并设置观测点的应力显示变量(2号变量)以及塑性应变为显示变量(3号变量),最后将3号变量设置为横轴,画出2号变量随3号变量的变化曲线见图1-4,可以看出,该材料具有非常明显的Bauschinger效应(即正向屈服与反向屈服之和是单拉实验屈服极限的2倍)。
给出的基于图形界面(GUI)的交互式操作(step by step)过程如下:(1) 进入ANSYS(设定工作目录和工作文件)程序→ANSYS →ANSYS Interactive →Working directory(设置工作目录)→Initial jobname(设置工作文件名): Beams →Run →OK(2) 设置计算类型ANSYS Main Menu:Preferences… →Structural →OK(3) 设定不显示时间ANSYS Utility Menu:PlotCtrls→Window Controls →Window Options… →DATE:No Date or Time →OK(4) 定义单元类型ANSYS Main Menu:Preprocessor →Element Type →Add/Edit/Delete... →Add…→Solid: Quad 4node 42 →OK(返回到Element Types窗口)→Close(5) 定义材料参数ANSYS Main Menu: Preprocessor →Material Props →Material Models →Structural →Linear →Elastic →Isotropic →输入EX: 2E4, PRXY: 0.3 (定义弹性模量及泊松比) →OK →返回Define Material ModelBehavior 窗口Structural →NonLinear→Inelastic →Rate Independent →Kinematic Hardening Plasticity →Mises Plasticity →Multilinear (Fixed table) →在Strain一行中对应1至4号点输入0.004、0.015、0.03、0.08 →在Curve1中对应1至4号点输入80、160、210、280 →点击右下角Graph→OK →Close(关闭材料定义窗口),见图1-3,观察窗口中的多线性弹塑性模型(6) 构造模型生成关键点ANSYS Main Menu:Preprocessor →Modeling →Create →Keypoints→In Active CS →Keypoints number:1,X,Y,Z Location in active CS:0,0,0 →Apply →同样依次输入其他三个关键点(100,0,0)、(100,10,0)与(0,10,0)→OKANSYS Main Menu:Preprocessor →Modeling →Create →Areas →Arbitrary →Through KPs →用鼠标依次点击1、2、3、4关键点,生成面单元,见图1-5构造模型图(7) 网格划分ANSYS Main Menu:Preprocessor →Meshing →Mesher Opts →Mesher Type : Mapped →OK →2D Shape Key : Quad →OKANSYS Main Menu:Preprocessor →Meshing →size contrls→ManualSize→Lines →Picked Lines →选择上下两条横边线,Ok →NDIV 设置为20 →Apply →选择两条竖边线→Ok →NDIV设置为8 →OK ANSYS Main Menu:Preprocessor →Meshing →Mesh →Areas →Target Surf →点击生成面几何体的位置,显示矩形面被选中→OK,见图1-6网格划分图(8) 模型加约束ANSYS Main Menu: Solution →Define Loads →Apply →Structural →Displacement On Lines →选取左侧边线(L4)→OK →select Lab2: All DOF(施加全部约束) →OK,见图1-7模型加约束图(9)求解设置ANSYS Main Menu : Solution →Analysis Type →Sol’n Controls →在Basic标签下设置Analysis Options 为Large Displacement Satic,Number of substeps: 8, Max no. of substeps :25Min no. Of substeps:2, Frequency 设置为Write N number of substeps Where N = 10 →OK(10)按照时间步施加循环载荷ANSYS Main Menu : Solution →Analysis Type →Sol’n Controls →在Basic标签下设置Time at end of loadstep:1 →OKANSYS Main Menu : Solution →Define Loads →Apply →Structural →Force/Moment →On Nodes →选择右侧边缘中点(26号节点)→OK →Lab:Fy,Value:-40 →OK,结果见图1-8ANSYS Main Menu:Solution →Solve →Current LS →OK,结果见图1-9ANSYS Utility Menu : Plot →ReplotANSYS Main Menu : Solution →Analysis Type →Sol’n Controls →在Basic标签下设置Time at end of loadstep: 2 →OKANSYS Main Menu : Solution →Define Loads →Apply →Structural →Force/Moment →On Nodes →选择右侧边缘中点(26号节点)→OK→Lab:Fy,Value:0 →OK,结果见图1-10ANSYS Main Menu:Solution →Solve →Current LS →OK,ANSYS Utility Menu : Plot →ReplotANSYS Main Menu : Solution →Analysis Type →Sol’n Controls →在Basic标签下设置Time at end of loadstep: 3 →OKANSYS Main Menu : Solution →Define Loads →Apply →Structural →Force/Moment →On Nodes →选择右侧边缘中点(26号节点)→OK →Lab:Fy,Value:40 →OK,结果见图1-11ANSYS Main Menu:Solution →Solve →Current LS →OK,结果见图1-12ANSYS Utility Menu : Plot →ReplotANSYS Main Menu : Solution →Analysis Type →Sol’n Controls →在Basic标签下设置Time at end of loadstep: 4 →OKANSYS Main Menu : Solution →Define Loads →Apply →Structural →Force/Moment →On Nodes →选择右侧边缘中点(26号节点)→Lab:Fy,Value:0 →OK,结果见图1-13ANSYS Main Menu:Solution →Solve →Current LS →OK,结果见图1-14ANSYS Utility Menu : Plot →ReplotANSYS Main Menu : Solution →Analysis Type →Sol’n Controls →在Basic标签下设置Time at end of loadstep: 5 →OKANSYS Main Menu : Solution →Define Loads →Apply →Structural →Force/Moment →On Nodes →选择右侧边缘中点(26号节点)→Lab:Fy,Value:-40 →OK,结果见图1-15ANSYS Main Menu:Solution →Solve →Current LS →OK,结果见图1-16ANSYS Utility Menu : Plot →ReplotANSYS Main Menu : Solution →Analysis Type →Sol’n Controls →在Basic标签下设置Time at end of loadstep: 6 →OKANSYS Main Menu : Solution →Define Loads →Apply →Structural →Force/Moment →On Nodes →选择右侧边缘中点(26号节点)→Lab:Fy,Value:0 →OK,结果见图1-17ANSYS Main Menu:Solution →Solve →Current LS →OK,结果见图1-18(11) 计算结果ANSYS Main Menu:General Postproc→Read Results →Last SetANSYS Main Menu:General Postproc→Plot Results →Deformed Shape →Def + Undeformed→OK,观察最后变形情况,见图1-19ANSYS Main Menu:General Postproc→Plot Results →Contour Plot →Element solu→PlasticStrain →Equivalent plastic strain →OK,观察累计的等效塑性应变,见图1-20ANSYS Main Menu:TimeHistPostpro→关闭弹出窗口→Define Variables →Add… →Element Results →OK 在方框中输入2 →OK 在方框中输入4 →OK →在Item,Comp Data item 中选择Stress, X-direction SX →OK返回Define Time-History Variables →Add… →Element Results →OK 在方框中输入2 →OK 在方框中输入4 →OK →在Item,Comp Data item 中选择Strain-plastic, X-dir’n EPPL X →OK →Close ANSYS Main Menu:TimeHistPostpro→关闭弹出窗口→Settings →Graph →Single Variable No. 输入3 →OKANSYS Main Menu:TimeHistPostpro→关闭弹出窗口→Graph Variables →Nvar1中输入2 →OK观察观测点P上的应力应变历程(SX),见图1-4ANSYS Utility Menu:File →Exit →Save Everything →OK三、ANSYS分析结果:图1-3 多线性弹塑性模型图1-4 观测点P上的应力应变历程(SX)图1-5 构造模型图图1-6 网格划分图图1-7 模型加约束图图1-8图1-9 图1-10图1-11 图1-12图1-13 图1-14图1-15 图1-16图1-17图1-18图1-19 图1-20。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
线性静力学分析实例——以悬臂梁为例线性静力学问题是简单且常见的有限元分析类型,不涉及任何非线性(材料非线性、几何非线性、接触等),也不考虑惯性及时间相关的材料属性。
在ABAQUS 中,该类问题通常采用静态通用(Static ,General )分析步或静态线性摄动(Static ,Linear perturbation )分析步进行分析。
线性静力学问题很容易求解,往往用户更关系的是计算效率和求解效率,希望在获得较高精度的前提下尽量缩短计算时间,特别是大型模型。
这主要取决于网格的划分,包括种子的设置、网格控制和单元类型的选取。
在一般的分析中,应尽量选用精度和效率都较高的二次四边形/六面体单元,在主要的分析部位设置较密的种子;若主要分析部位的网格没有大的扭曲,使用非协调单元(如CPS4I 、C3D8I )的性价比很高。
对于复杂模型,可以采用分割模型的方法划分二次四边形/六面体单元;有时分割过程过于繁琐,用户可以采用精度较高的二次三角形/四面体单元进行网格划分。
悬臂梁的线性静力学分析1.1 问题的描述一悬臂梁左端受固定约束,右端自由,结构尺寸如图1-1所示,求梁受载后的Mises 应力、位移分布。
材料性质:弹性模量32e E,泊松比3.0均布载荷:F=103N 图1-1 悬臂梁受均布载荷图1.2 启动ABAQUS启动ABAQUS 有两种方法,用户可以任选一种。
(1)在Windows 操作系统中单击“开始”--“程序”--ABAQUS 6.10 --ABAQUS/CAE。
(2)在操作系统的DOS窗口中输入命令:abaqus cae。
启动ABAQUS/CAE后,在出现的Start Section(开始任务)对话框中选择Create Model Database。
1.3 创建部件在ABAQUS/CAE顶部的环境栏中,可以看到模块列表:Module:Part,这表示当前处在Part(部件)模块,在这个模块中可以定义模型各部分的几何形体。
可以参照下面步骤创建悬臂梁的几何模型。
(1)创建部件。
对于如图1-1所示的悬臂梁模型,可以先画出梁结构的二维截面(矩形),再通过拉伸得到。
单击左侧工具区中的(Create Part)按钮,或者在主菜单里面选择Part--Create,弹出如图1-2所示的Create Part对话框。
图1-2 Create Part对话框在Name(部件名称)后面输入Beam,Modeling Space(模型所在空间)设为3D,Shape选择Solid(实体),Type采用默认的Extrusion,在Approximate size 里面输入300。
单击Continue...按钮。
注意:如果无法输入字符,原因可能是当前正处于中文输入法的状态,应切换到英文输入法。
(2)绘制矩形。
ABAQUS/CAE自动进入绘图环境,左侧的工具区显示出绘图工具按钮,视图区内显示栅格,视图区正中两条相互垂直的点划线即当前二维区域的X轴和Y轴。
二者相交于坐标原点。
选择绘图工具箱中的工具,窗口提示区显示Pick a starting corner for the rectangle--or enter X,Y(选择矩形的一个角点,或输入X,Y的坐标),如图1-3所示。
图1-3 输入点坐标输入矩形的第一个点得坐标为(-100,10),移动光标选择与该店相对的点得坐标为(100,-10),单击鼠标左键,矩形就画出来了。
如果在绘制过程中操作有误,可以单击绘图工具箱的撤销工具来撤销上一步操作,也可以使用删除工具来删除错误的几何图形,具体操作步骤入校所示。
a 单击绘图工具箱中的删除工具。
b 在所绘图形中选择要删除的线或者图形,ABAQUS/CAE以红色高亮显示被选中的对象。
提示:如果想删除多个对象,可以在单击此对象的同时按住Shift键,或者按住鼠标左键不放,在视图区中画出一个矩形框,选中矩形框中的对象。
如果想取消对某对象的选择,可以在单击此对象的同时按住Ctrl键。
c 在视图区单击鼠标中键,或者单击提示区中的Done按钮,结束对删除工具的使用。
d 根据需要,重复a、b、c步骤。
注意:在确认结束某一步操作的时候,一般总是在视图区中单击鼠标中键,或者单击窗口底部提示区的Done按钮(完成),一下不再赘述。
(3)由于前面操作中,已经选择了Extrusion类型,在上一步退出后,ABAQUS即弹出“编辑基本拉伸”对话框。
在该窗口中,输入拉伸尺寸30,如图1-4所示。
然后单击OK按钮,视图区就出现了悬臂梁的结构图,如图1-5所示。
图1-4 “编辑基本拉伸”对话框图1-5 形成的悬臂梁结构图(4)保存模型。
在下一步之前,单击窗口顶部工具栏中的按钮来保存所建立的模型。
键入希望保存的文件名,ABAQUS/CAE会自动加上后缀.cae。
用户还可以在主菜单中选择File--Save对所建立的模型进行保存操作。
此处把该部件取名为beam。
说明:ABAQUS/CAE不会自动保存模型的数据,用户每隔一段时间自己保存模型。
如果由于意外造成系统死机或者无法自动退出ABAQUS/CAE,下次启动时就会显示自动恢复的对话框,选择Yes就可以自动恢复尚未保存的数据,但是有时会因为恢复文件中存在错误,出现自动恢复失败,所以建议用户养成经常保存模型的习惯。
1.4 创建材料和截面属性在窗口左上角Module(模块)列表中选择Property(特性)功能模块,按照以下步骤来定义材料。
(1)创建材料。
单击工具区左侧的(Create Material)按钮,或者在主菜单中选择Material--Create,弹出Edit Material对话框(也可以双击左侧模型树中的Material来完成此操作),如图1-6所示。
图1-6 Edit Material对话框在Name(材料名称)后面输入Steel,单击此对话框中的Mechanical(力学特性)--Elasticity(弹性)。
在数据表中设置Young’s Modulus(弹性模量)为2e3,Poisson’s Ratio(泊松比)为0.3,其余参数不变,如图1-7所示,单击OK按钮。
图1-7 输入弹性模量和泊松比说明:在ABAQUS/CAE中,如果希望修改或撤销已经完成的操作,可以在窗口左侧的模型树中找到此操作,在上面单击鼠标右键,选择Edit或者Delete。
在绘制二维平面图时,可以单击绘图工具箱中的按钮来撤销上一步操作。
(2)创建截面属性。
单击左侧工具区的(Create Section)按钮,或者在主菜单中选择Section--Create,弹出Create Section对话框(也可以双击左侧模型树中的Section来完成此操作),Name改为BeamSection,保持其他默认参数不变,单击Continue...按钮。
在弹出的Edit Section对话框(见图1-8)中,默认的参数(Material:Steel;Type:Solid,Homogeneous;Plane stress/strain thickness:1)不变,单击OK按钮。
图1-8 Edit Section对话框(3)给部件赋予截面属性。
单击左侧工具区中的(Assign Section)按钮,或者在主菜单中选择Assign--Section,单击视图区中的悬臂梁模型,ABAQUS/CAE以红色高亮显示被选中,在视图区单击鼠标中键,弹出Edit Section Assignment对话框,如图1-9所示,单击OK按钮。
图1-9 Edit Section Assignment对话框说明:ABAQUS/CAE不把材料属性直接赋予单元或者几何实体,而是首先在截面属性(Section)中定义材料特性,再为每个部件赋予相应的截面属性。
注意:ABAQUS/CAE推荐的建模方法是把整个数值模型(如材料、载荷、边界条件等)都直接定义在几何模型上,而不是像其他前处理器一样定义在单元或者节点上,这样在修改网格时不必重新定义材料和边界条件等模型参数。
这样在处理复杂问题时,可以首先简单地划分粗网格,得到初步的模型结果,然后再适当的区域细化网格。
1.5 定义装配件整个分析模型是一个装配件,前面的Part功能模型中创建的各个部件将在Assembly功能模块中装配起来。
具体的操作方式:在窗口左上角Module列表中选择Assembly(装配)功能模块。
单击左侧工具区的(Instance Part)按钮,或者在主菜单中选择Instance--Create(也可以直接单击左侧模型树中的Assembly左侧的+号,然后双击其下一层的Instance来完成此项操作)。
在弹出的Create Instance对话框中(见图1-10),前面创建的部件beam自动被选中,默认参数为Instance Type:Dependent(mesh on part),单击OK按钮。
1.6 设置分析步ABAQUS/CAE会自动创建一个初始分析步(Initial step),可以在其中施加边界条件,用户必须自己创建后续分析步(analysis step),用来施加载荷。
具体操作方法如下。
图1-10 Create Instance对话框(1)在窗口左上角的Module列表中选择Step(分析步)功能模块。
单击左侧工具区的(Create Step)按钮,或者在主菜单中选择Step--Create(也可以直接单击左侧模型树中的Steps来完成此项操作)。
(2)在弹出的Create Step对话框中,在Name后面输入分析步的名称,此处将默认值Step-1改为loadbeam。
其余参数如图1-11所示(Procedure type:General;选择Static General),单击Continue...按钮。
图1-11 Create Step对话框(3)在弹出的Edit Step对话框(见图1-12)中,Description后面改为Load the top of the beam,其余参数都保持默认值,单击OK按钮,完成操作。
图1-12 Edit Step对话框1.7 定义边界条件和载荷在窗口左上角的Module列表中选择Load(载荷)功能模块,定义边界条件和载荷。
1 施加载荷单击左侧工具区的(Create Load)按钮,或在主菜单中选择Load--Create (也可以直接单击左侧模型树中的Loads来完成此项操作)。
在弹出的Create Load对话框中(见图1-13),在Name 后输入Pressure;将Types for Selected Step (所选分析步的载荷类型)设为Pressure(单位面积上的压力),Step设为loadbeam,单击Continue...按钮。
