抗震与设计计算题目解析
抗震及设计练习题答案
1．从结构的体系上来分，常用的高层建筑结构的抗侧力体系主要有：＿框架结构，剪力墙结构，＿框架-剪力墙＿结构，＿筒体＿结构，悬挂结构和巨型框架结构。
2．一般高层建筑的基本风压取＿50＿年一遇的基本风压。
对于特别重要或对风荷载比较敏感的高层建筑，采用＿100＿年一遇的风压值；在没有＿100＿年一遇的风压资料时，可近视用取＿50＿年一遇的基本风压乘以1.1的增大系数采用。
3．震级――地震的级别，说明某次地震本身产生的能量大小地震烈度――指某一地区地面及建筑物受到一次地震影响的强烈程度基本烈度――指某一地区今后一定时期内，在一般场地条件下可能遭受的最大烈度设防烈度――一般按基本烈度采用，对重要建筑物，报批后，提高一度采用4．《建筑抗震设计规范》中规定，设防烈度为＿6＿度及＿6＿度以上的地区，建筑物必须进行抗震设计。
5．详细说明三水准抗震设计目标。
小震不坏：小震作用下应维持在弹性状态，一般不损坏或不需修理仍可继续使用中震可修：中震作用下，局部进入塑性状态，可能有一定损坏，修复后可继续使用大震不倒：强震作用下，不应倒塌或发生危及生命的严重破坏6．设防烈度相当于＿B＿A、小震 B 、中震 C、中震7．用《高层建筑结构》中介绍的框架结构、剪力墙结构、框架－剪力墙结构的内力和位移的近似计算方法，一般计算的是这些结构在＿＿下的内力和位移。
A 小震B 中震 C大震8.在建筑结构抗震设计过程中，根据建筑物使用功能的重要性不同，采取不同的抗震设防标准。
请问建筑物分为哪几个抗震设防类别？甲：高于本地区设防烈度，属于重大建筑工程和地震时可能发生严重次生灾害的建筑乙：按本地区设防烈度，属于地震时使用功能不能中断或需尽快恢复的建筑丙：除甲乙丁外的一般建筑丁：属抗震次要建筑，一般仍按本地区的设防烈度9.下列高层建筑需要考虑竖向地震作用。
（D）A 8°抗震设计时B 跨度较大时C 有长悬臂构件时D 9°抗震设计10.什么样的高层建筑结构须计算双向水平地震作用下的扭转影响？对质量和刚度不对称、不均匀的结构以及高度超过100m的高层建筑结构11.结构的自振周期越大，结构的刚度越＿小＿，结构受到的地震作用越＿小＿。
抗震结构设计要点及重要习题及答案
1、【地震烈度】：指某一地区的地面和各类建筑物遭受一次地震影响的强弱程度。
2、【抗震设防烈度】：一个地区作为抗震设防依据的地震烈度，应按国家规定权限审批或颁发的文件（图件）执行。
3、【场地土的液化：】饱和的粉土或砂土，在地震时由于颗粒之间的孔隙水不可压缩而无法排出，使得孔隙水压力增大，土体颗粒的有效垂直压应力减少，颗粒局部或全部处于悬浮状态，土体的抗剪强度接近于零，呈现出液态化的现象。
４、【等效剪切波速：】若计算深度范围内有多层土层，则根据计算深度范围内各土层剪切波速加权平均得到的土层剪切波速即为等效剪切波速。
5、【地基土抗震承载力】：地基土抗震承载力，其中ζa 为地基土的抗震承载力调整系数，f a 为深宽修正后的地基承载力特征值。
6、【场地覆盖层厚度】：我国《建筑抗震设计规范》（GB50011-2001）定义：一般情况下，可取地面到剪切波速大于500m/s 的坚硬土层或岩层顶的距离。
7、【重力荷载代表值：】结构抗震设计时的基本代表值，是结构自重（永久荷载）和有关可变荷载的组合值之和。
8、【强柱弱梁：】结构设计时希望梁先于柱发生破坏，塑性铰先发生在梁端，而不是在柱端。
9、【砌体的抗震强度设计值：】VE N V f f ς=，其中f v 为非抗震设计的砌体抗剪强度设计值，ζN 为砌体抗震抗剪强度的正应力影响系数。
10、【剪压比：】剪压比为c 0V/f bh ，是构件截面上平均剪力与混凝土轴心抗压强度设计值的比值，用以反映构件截面上承受名义剪应力的大小。
１、【简述两阶段三水准抗震设计方法。
】答：我国《建筑抗震设计规范》（GB50011-2001）规定：进行抗震设计的建筑，其抗震设防目标是：当遭受低于本地区抗震设防烈度的多遇地震影响时，一般不受损坏或不需修理可继续使用，当遭受相当于本地区抗震设防烈度的地震影响时，可能损坏，经一般修理或不需修理仍可继续使用，当遭受高于本地区抗震设防烈度预估的罕遇地震影响时，不致倒塌或发生危及生命的严重破坏。
抗震计算题整理
[2 0.2 1 (T 5Tg )]max
5Tg
6 .0
T ( s)
0.05 0.05 0.9 2 1 0.3 6 0.08 1.6
例：试用振型分解反应谱法计算图示框架多遇地震时的层间剪力。 抗震设防烈度为8度，Ⅱ类场地，设计地震分组为第二组。 解： （1）求体系的自振周期和振型 m 180t
K3 98MN/m
m2 270t
K 2 195MN/m
m1 270t K1 245MN/m
T1 0.467s T2 0.208s T3 0.134s
（2）计算各振型的地震影响系数 查表得 max 0.16
Tg 0.4s
2 max
T ( g ) 2 max T
K3 98MN/m
m2 270t
K 2 195MN/m
m1 270t K1 245MN/m
T1 0.467s T2 0.208s T3 0.134s
（2）计算各振型的地震影响系数 查表得 max 0.16
Tg 0.4s
地震影响系数最大值（阻尼比为0.05）
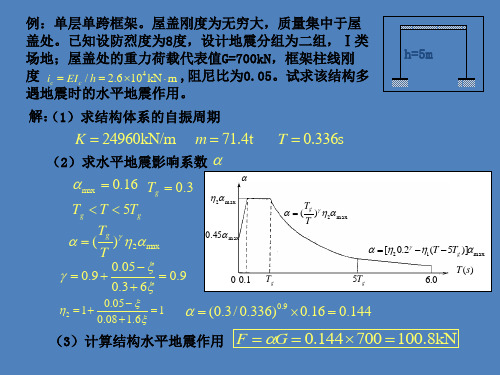
例：单层单跨框架。屋盖刚度为无穷大，质量集中于屋 盖处。已知设防烈度为8度，设计地震分组为二组，Ⅰ类 场地；屋盖处的重力荷载代表值G=700kN，框架柱线刚 度 ic EI c / h 2.6 104 kN m ,阻尼比为0.05。试求该结构多 遇地震时的水平地震作用。
h=5m
解： （1）求结构体系的自振周期
D2 (t ) 0.000534(1 cos 2t )
y1 (t ) 1 1 D1 (t ) D2 (t ) 1 / 2 y2 (t ) 2
抗震结构设计要点及重要习题及答案_考试必胜解析
二、填空题（每空1分，共25分）1、地震波包括在地球内部传播的体波和只限于在地球表面传播的面波，其中体波包括纵波（P）波和横（S）波，而面波分为瑞雷波和洛夫波，对建筑物和地表的破坏主要以面波为主。
2、场地类别根据等效剪切波波速和场地覆土层厚度划分为IV类。
3、在用底部剪力法计算多层结构的水平地震作用时，对于T1>1.4T g时，在结构顶部附加ΔF n，其目的是考虑高振型的影响。
4、《抗震规范》规定，对于烈度为8度和9度的大跨和长悬臂结构、烟囱和类似的高耸结构以及9度时的高层建筑等，应考虑竖向地震作用的影响。
5、钢筋混凝土房屋应根据烈度、建筑物的类型和高度采用不同的抗震等级，并应符合相应的计算和构造措施要求。
6、地震系数k表示地面运动的最大加速度与重力加速度之比；动力系数 是单质点最大绝对加速度与地面最大加速度的比值。
7、多层砌体房屋的抗震设计中，在处理结构布置时，根据设防烈度限制房屋高宽比目的是为了使多层砌体房屋有足够的稳定性和整体抗弯能力，根据房屋类别和设防烈度限制房屋抗震横墙间距的目的是避免纵墙发生较大出平面弯曲变形，造成纵墙倒塌。
８、用于计算框架结构水平地震作用的手算方法一般有反弯点法和D值法。
9、在振型分解反应谱法中，根据统计和地震资料分析，对于各振型所产生的地震作用效应，可近似地采用平方和开平方的组合方法来确定。
１０、为了减少判别场地土液化的勘察工作量，饱和沙土液化的判别可分为两步进行，即初步判别和标准贯入试验判别。
1、根据土层剪切波速的范围把土划分为坚硬土、中硬土、中软土、软弱土四类。
2、地震波中的纵波（P）是由震源向外传播的疏密波，横波（S）是由震源向外传播的剪切波。
用来反映一次地震本身强弱程度的大小和尺度的是震级，其为一种定量的指标。
３、在地基土的抗震承载力计算中，地基土的抗震承载力调整系数一般应>1.0 。
４、当建筑物的地基有饱和的砂土和粉土的土时，应经过勘察试验预测在地震时是否会出现液化现象。
建筑结构抗震设计习题及答案
结构地震反应分析与抗震验算计算题3.1 单自由度体系，结构自振周期T=0.5S，质点重量G=200kN，位于设防烈度为8 度的Ⅱ类场地上，该地区的设计基本地震加速度为0．30g，设计地震分组为第一组，试计算结构在多遇地霞作用时的水平地震作用。
3.2 结构同题3．1，位于设防烈度为8度的Ⅳ类场地上，该地区的设计基本地震加速度为0.20g，设计地设分组为第二组，试计算结构在多遇地震作用时的水平地震作用。
3.3 钢筋混凝土框架结构如图所示，横梁刚度为无穷大，混凝土强度等级均为C25，一层柱截面450mm×450mm，二、三层柱截面均为400mm×400mm，试用能量法计算结构的自振周期T1。
3.4 题3．2的框架结构位于设防烈度为8度的Ⅱ类场地上，该地区的设计基本地震加速度为0.20g，设计地震分组为第二组，试用底部剪力法计算结构在多遇地震作用时的水平地震作用。
3.5 三层框架结构如图所示，横梁刚度为无穷大，位于设防烈度为8度的Ⅱ类场地上，该地区的设计基本地震加速为0.30g, 设计地震分组为第一组。
结构各层的层间侧移刚度分别为k1=7.5×105kN／m，k2=9.1×105kN／m，k3=8.5×105 kN／m，各质点的质量分别为m1=2×106kg, m2=2×106kg, m3=1.5×105kg，结构的自震频率分别为ω1＝9.62rad/s, ω2=26.88 rad/s, ω3=39.70 rad/s, 各振型分别为：要求：①用振型分解反应谱法计算结构在多遇地震作用时各层的层间地震剪力；②用底部剪力法计算结构在多遇地震作用时各层的层间地震剪力。
3.6 已知某两个质点的弹性体系（图3-6），其层间刚度为k1=k2=20800kN／m，，质点质量为m1=m2=50×103kg。
试求该体系的自振周期和振型。
抗震原理计算题
抗震原理计算题1. 引言地震是一种常见的自然灾害，对建筑物的破坏造成了严重影响。
因此，在设计建筑物时需要考虑抗震能力。
本文将通过计算抗震原理来解决抗震设计中的问题。
2. 设计要求设计要求如下：•设计一个具有一定抗震能力的建筑物•给定地震条件：地震烈度为8.0级3. 计算方法首先，我们需要计算建筑物的质量。
假设建筑物的体积为V，密度为ρ，则质量可以通过以下公式计算：质量 = 密度 * 体积接下来，我们需要计算抗震结构的刚度。
刚度可以用弹性模量E和截面面积A 来表示。
假设建筑材料的弹性模量为E，截面面积为A，则刚度可以通过以下公式计算：刚度 = 弹性模量 * 截面面积然后，我们需要计算地震作用在建筑物上的力。
地震力可以根据地震烈度和建筑物的质量来计算。
根据结构物的质量和地震烈度，地震力可以通过以下公式计算：地震力 = 质量 * 加速度其中，加速度可以根据地震烈度来确定。
最后，我们需要计算建筑物的位移。
位移可以通过以下公式计算：位移 = 地震力 / 刚度4. 计算结果根据给定的地震条件和建筑物参数，我们可以进行计算。
假设建筑物的体积为1000 m^3，密度为2500 kg/m^3，弹性模量为20 GPa，截面面积为10 m^2，地震烈度为8.0级，加速度为10 m/s^2。
根据计算公式，我们可以得到以下结果：•建筑物的质量为：质量 = 2500 kg/m^3 * 1000 m^3 = 2.5 * 10^6 kg•抗震结构的刚度为：刚度 = 20 GPa * 10 m^2 = 200 GPa * m^2•地震力为：地震力 = 2.5 * 10^6 kg * 10 m/s^2 = 25 * 10^6 N•建筑物的位移为：位移 = 25 * 10^6 N / 200 GPa * m^2 = 125 * 10^-3 m = 125 mm5. 结论通过以上计算，我们得出以下结论：•建筑物的质量是2.5 * 10^6 kg•抗震结构的刚度是200 GPa * m^2•地震力是25 * 10^6 N•建筑物的位移是125 mm这些计算结果可以作为设计抗震结构的参考，从而提高建筑物的抗震能力，减少地震灾害造成的损失。
抗震结构设计经典计算题及答案
1、某两层钢筋混凝土框架，集中于楼盖和屋盖处的重力荷载代表值相等kN 120021==G G ，每层层高皆为4.0m ，各层的层间刚度相同m /kN 863021==S S ==S S D D ；Ⅱ类场地，设防烈度为7度，设计基本地震加速度为0.10g ，设计分组为第二组，结构的阻尼比为05.0=z 。
（1）求结构的自振频率和振型，并验证其主振型的正交性（2）试用振型分解反应谱法计算框架的楼层地震剪力解1）：（1）计算刚度矩阵）计算刚度矩阵m kN k k k /17260286302111=´=+= m kN k kk/863022112-=-== m kN k k /8630222==（2）求自振频率）求自振频率])(4)()[(21211222112121122211122212122,1k k k k m m k m k m k m k m m m --++= w ])8630(863017260[(1201204)172601208630120()172601208630120[(1201202122--´´´-´+´´+´´´= 28.188/47.27=s r a d/24.51=w s r a d /72.132=w（3）求主振型）求主振型 当s rad /24.51=w 1618.186301726024.5120212112111112=--´=-=k k m X X w 当s rad /72.132=w1618.086301726072.13120212112212122-=--´=-=k k m X X w （4）验证主振型的正交性）验证主振型的正交性质量矩阵的正交性质量矩阵的正交性0618.0000.112000120618.1000.1}]{[}{21=þýüîíì-úûùêëéþýüîíì=T T X m X 刚度矩阵的正交性刚度矩阵的正交性0618.0000.186308630863017260618.1000.1}]{[}{21=þýüîíì-úûùêëé--þýüîíì=T T X k X 解2）：由表3.2查得：Ⅱ类场地，第二组，T g =0.40s 由表3.3查得：7度多遇地震08.0max =a第一自振周期g g T T T T 5s,200.12111<<==w p 第二自振周期g g T T T T 5s,458.02122<<==w p（1）相应于第一振型自振周期1T 的地震影响系数：的地震影响系数：030.008.0200.140.09.0max 9.011=´÷øöçèæ=÷÷øöççèæ=a a T T g第一振型参与系数第一振型参与系数第一振型参与系数724.0618.11200000.11200618.11200000.11200222121111=´+´´+´==åå==i i i n i i i m m ffg 于是：kN 06.261200000.1724.0030.01111111=´´´==G F f g a kN 17.421200618.1724.0030.02121112=´´´==G F f g a第一振型的层间剪力：第一振型的层间剪力：第一振型的层间剪力：kN 17.421212==F V kN 23.68121111=+=F F V（（2）相应于第二振型自振周期2T 的地震影响系数：的地震影响系数：071.008.0458.040.09.0max 9.022=´÷øöçèæ=÷÷øöççèæ=a a T T g 第二振型参与系数第二振型参与系数第二振型参与系数276.0)618.0(1200000.11200)618.0(1200000.11200222122122=-´+´-´+´==åå==i i i ni i i m m f fg 于是：kN 52.231200000.1276.0071.01212221=´´´==G F f g a kN 53.141200)618.0(276.0071.02222222-=´-´´==G F f g a第二振型的层间剪力：第二振型的层间剪力：第二振型的层间剪力：kN 53.142222-==F VkN 99.8222121=+=F F V （（3）由SRSS 法，计算各楼层地震剪力：法，计算各楼层地震剪力：kN 60.44)53.14(17.422222222=-+==å=j j V V kN 821.6899.823.682222211=+==å=j j V V2重、某两层钢筋混凝土框架，集中于楼盖和屋盖处的重力荷载代表值相等力荷载代表值相等kN 120021==G G ，每层层高皆为 4.0m ，框架的自振周期s 028.11=T ；各层的层间刚度相同m /kN 863021=S =S D D ；Ⅱ类场地，7度第二组（)08.0 s,40.0max==a g T ，结构的阻尼比为05.0=z ，试按底部剪力法计算框架的楼层地震剪力，并验算弹性层间位移是否满足要求（[]450/1=e q ）。
抗震结构设计要点及重要习题及答案-考试必胜
1、《抗震规范》给出的设计反应谱中，当结构自振周期在~Tg 之间时，谱曲线为（A ）A ．水平直线B. 斜直线C. 抛物线D. 指数曲线2、实际地震烈度与下列何种因素有关（B ）A. 建筑物类型B. 离震中的距离C. 行政区划D. 城市大小3、规范规定不考虑扭转影响时，用什么方法进行水平地震作用效应组合的计算（ B ）A.完全二次项组合法（CQC法）B.平方和开平方法（SRSS法）C.杜哈米积分D. 振型分解反应谱法4、基底剪力法计算水平地震作用可用于下列何种建筑（ C ）米以上的高层建筑 B. 自振周期T i很长（T i>4s）的高层建筑C. 垂直方向质量、刚度分布均匀的多层建筑D. 平面上质量、刚度有较大偏心的多高层建筑5、地震系数k 与下列何种因素有关（ A ）A. 地震基本烈度B. 场地卓越周期C. 场地土类别D. 结构基本周期6、9度区的高层住宅竖向地震作用计算时，结构等效总重力荷载Gq为（C ）A.恒载标准值G+活载标准值Q）B. （G K+Q）C. （G K+D. （G K+7、框架结构考虑填充墙刚度时,T i与水平弹性地震作用F e有何变化（A ）J ,F e f f ,F e f f ,F e J J ,F e J8、抗震设防区框架结构布置时，梁中线与柱中线之间的偏心距不宜大于（ A ）A ．柱宽的1/4B ．柱宽的1/8C ．梁宽的1/4D ．梁宽的1/89、土质条件对地震反应谱的影响很大，土质越松软，加速度谱曲线表现为（ A ）A ．谱曲线峰值右移B ．谱曲线峰值左移C ．谱曲线峰值增大D ．谱曲线峰值降低10、震中距对地震反应谱的影响很大，在烈度相同的条件下，震中距越远，加速度谱曲线表现为（A ）A ．谱曲线峰值右移B．谱曲线峰值左移C ．谱曲线峰值增大D．谱曲线峰值降低11、为保证结构“大震不倒”，要求结构具有( C )A. 较大的初始刚度B.较高的截面承载能力C. 较好的延性D.较小的自振周期T112、楼层屈服强度系数沿高度分布比较均匀的结构，薄弱层的位置为（D ）A. 最顶层B. 中间楼层C. 第二层D. 底层13、多层砖房抗侧力墙体的楼层水平地震剪力分配（ B ）C. 仅与墙体刚度有关D.仅与墙体质量有关14、场地特征周期T g与下列何种因素有关( C )A. 地震烈度B.建筑物等级C. 场地覆盖层厚度D.场地大小15、关于多层砌体房屋设置构造柱的作用，下列哪句话是错误的（D ）A．可增强房屋整体性，避免开裂墙体倒塌B．可提高砌体抗变形能力C．可提高砌体的抗剪强度D．可抵抗由于地基不均匀沉降造成的破坏16、考虑内力塑性重分布，可对框架结构的梁端负弯矩进行调幅（B ）A ．梁端塑性调幅应对水平地震作用产生的负弯矩进行B ．梁端塑性调幅应对竖向荷载作用产生的负弯矩进行C ．梁端塑性调幅应对内力组合后的负弯矩进行D ．梁端塑性调幅应只对竖向恒荷载作用产生的负弯矩进行17、水平地震作用标准值F ek 的大小除了与质量, 地震烈度, 结构自振周期有关外, 还与下列何种因素有关（ B ）A.场地平面尺寸B.场地特征周期C.荷载分项系数D.抗震等级18、表征地震动特性的要素有三个，下列哪项不属于地震动要素（ B ）A.加速度峰值B.地震烈度C.频谱特性D.地震持时19、震级大的远震与震级小的近震对某地区产生相同的宏观烈度，则对该地区产生的地震影响是（B ）A．震级大的远震对刚性结构产生的震害大B．震级大的远震对柔性结构产生的震害大C．震级小的近震对柔性结构产生的震害大D.震级大的远震对柔性结构产生的震害小20、地震烈度主要根据下列哪些指标来评定（C ）A ．地震震源释放出的能量的大小B ．地震时地面运动速度和加速度的大小C. 地震时大多数房屋的震害程度、人的感觉以及其他现象D. 地震时震级大小、震源深度、震中距、该地区的土质条件和地形地貌21、一般情况下，工程场地覆盖层的厚度应按地面至剪切波速大于多少的土层顶面的距离确定（D ）A．200m/s B ．300m/s C ．400m/s D ．500m/s 22、关于地基土的液化，下列哪句话是错误的A．饱和的砂土比饱和的粉土更不容易液化B．地震持续时间长，即使烈度低，也可能出现液化C．土的相对密度越大，越不容易液化D．地下水位越深，越不容易液化23、某地区设防烈度为7 度，乙类建筑抗震设计应按下列要求进行设计（D ）A ．地震作用和抗震措施均按8 度考虑B ．地震作用和抗震措施均按7 度考虑C ．地震作用按8度确定，抗震措施按7度采用D.地震作用按7度确定，抗震措施按8度采用24、框架柱轴压比过高会使柱产生（B ）A .大偏心受压构件B.小偏心受压构件C .剪切破坏D .扭转破坏25、钢筋混凝土丙类建筑房屋的抗震等级应根据那些因素查表确定（B ）A .抗震设防烈度、结构类型和房屋层数B .抗震设防烈度、结构类型和房屋高度C .抗震设防烈度、场地类型和房屋层数D .抗震设防烈度、场地类型和房屋高度26、纵波、横波和面波（L 波）之间的波速关系为（A ）A. V P > V S > V LB. V S > V P > V LC. V L > V P > V S D . V P > V L> V S27、位于软弱场地上,震害较重的建筑物是: （A ）A. 木楼盖等柔性建筑B. 单层框架结构C.单层厂房结构D. 多层剪力墙结构28、强剪弱弯是指: （B ）A. 抗剪承载力Vu 大于抗弯承载力MuB. 剪切破坏发生在弯曲破坏之后C. 设计剪力大于设计弯矩D. 柱剪切破坏发生在梁剪切破坏之后29、下列结构延性哪个延性在抗震设计时要求最高（D ）A. 结构总体延性B.结构楼层的延性C. 构件的延性D. 关键杆件的延性30、强柱弱梁是指:（B ）A. 柱线刚度大于梁线刚度B. 柱抗弯承载力大于梁抗弯承载力C. 柱抗剪承载力大于梁抗剪承载力C. 柱配筋大于梁配筋1、工程结构抗震设防的三个水准是什么如何通过两阶段设计方法来实现答：抗震设防的三个水准：第一水准：当遭受低于本地区抗震设防烈度的多遇地震影响时，一般不受损坏或不需修理仍可继续使用；第二水准：当遭受相当于本地区抗震设防烈度的地震影响时，可能损坏，经一般修理或不需修理仍可继续使用；第三水准：当遭受高于本地区抗震设防烈度的罕遇地震影响时，不致倒塌或发生危及生命的严重破坏。
建筑结构抗震计算题及例题答案
《建筑结构抗震》（清华大学出版社）计算题及例题解答1. 某两层房屋计算简图如图1所示。
已知楼层集中质量为1100t m =，250t m=，每层层高均为h ，楼板平面内刚度无限大，沿某抗震主轴方向的层间剪切刚度为120000kN m k =，210000kN m k =。
求该结构体系在该抗震主轴方向的自振周期、振型和振型参与系数。
图1 动力模型计算简图【解】1m 100t =，2m 50t =，m /kN 20000k 1=，m /kN 10000k 2=（1）自振圆频率⎥⎥⎦⎤⎢⎢⎣⎡+++⎪⎪⎭⎫ ⎝⎛-±++=ω）（2212112222112212122,1m k 2m k k 2m k m k m k m k m k k 21⎥⎥⎦⎤⎢⎢⎣⎡⨯++⨯+⎪⎭⎫ ⎝⎛-±++=）（50100002100100002000021001000050100001002000050100001001000020000212）（30020030021±+==100400⎧⎨⎩s /rad 101=ω∴，s /rad 202=ω∴（2）自振周期628.01014.322T 11=⨯=ωπ=314.02014.322T 22=⨯=ωπ=（3）振型第一主振型：210000101001000020000k m k k X X 22211211112=⨯-+=ω-+=第二主振型：110000201001000020000k m k k X X 22221212122=⨯-+=ω-+=（4）振型参与系数3225011002501100X m X m X m X m Xm Xm 222122211112211121i 21ji21i 1ii1=⨯+⨯⨯+⨯=++==γ∑∑== 3115011001501100X m X m X m X m Xm X m 222222221122221121i 22ii21i 2ii2=-⨯+⨯-⨯+⨯=++==γ∑∑==）（）（2. 某三层钢筋混凝土框架，如图2和图3所示。
高层建筑结构抗震与设计补充题及解答
高层建筑结构抗震与设计(练习题1)1.表1为某建筑场地的钻孔资料，试确定该场地的类别。
表12.已知某6层、高度为20米的丙类建筑的场地地质钻孔资料如表2所示（无剪切波速数据），试确定该场地的类别。
3.某单跨单层厂房如图1所示，集中于屋盖的重力荷载代表值为G＝2800kN，柱抗侧移刚度系数k1=k2=2.0×104kN/m,结构阻尼比ζ＝0.03，Ⅱ类建筑场地，设计地震分组为第一组，设计基本地震加速度为0.15g。
分别求厂房在多遇地震和罕遇地震时水平地震作用。
图1单层厂房计算简图2k 1k kGG4. 图2为两层房屋计算简图，楼层集中质量分别为m1=120t,m2=80t,楼板刚度无穷大，楼层剪切刚度系数分别为k1= 5×104kN/m , k2= 3×104kN/m 。
求体系自振频率和振型，并验算振型的正交性。
图2 两层房屋计算简图1m 2m 1k 2k5. 钢筋混凝土3层框架计算简图如图3所示。
分别按能量法和顶点位移法计算结构的基本自振周期（取填充墙影响折减系数为0.6）。
图3 3层框架计算简图kgm 3310180⨯=kgm 3210270⨯=kgm 3110270⨯=mkN k /98003=mkN k /1950002=mkN k /2450001=6. 钢筋混凝土3层框架经质量集中后计算简图如图4所示。
各层高均为5米，各楼层集中质量代表值分别为：G1=G2=750kN ，G3=500kN ；经分析得结构振动频率和振型如图4所示。
结构阻尼比ζ＝0.05，Ⅰ类建筑场地，设计地震分组为第一组，设计基本地震加速度为0.10g 。
试按振型分解反应谱法确定结构在多遇地震时的地震作用效应，绘出层间地震剪力图。
s rad /22.101=ωsrad /94.272=ωsrad /37.383=ω12图4 计算简图7. 已知条件和要求同上题，试按底部剪力法计算。
1、表1为某建筑场地的钻孔资料，试确定该场地的类别。
建筑抗震习题及答案
建筑抗震习题及答案建筑抗震是确保建筑物在地震等自然灾害发生时能够保持结构安全和功能完整的重要设计原则。
以下是一些建筑抗震的习题及答案，供学习和参考。
习题一：某地区地震烈度为8度，若某建筑物的设计使用年限为50年，请根据《建筑抗震设计规范》计算该建筑物的抗震设防烈度。
答案：根据《建筑抗震设计规范》，设计使用年限为50年的建筑物，其抗震设防烈度应为基本烈度加上0.5度。
因此，该建筑物的抗震设防烈度为8.5度。
习题二：简述建筑物抗震设计中的“三水准”设防目标。
答案：建筑物抗震设计中的“三水准”设防目标包括：1. 小震不坏：在小震作用下，建筑物能够保持结构的完整性和使用功能，不出现严重损伤。
2. 中震可修：在中等强度地震作用下，建筑物可能遭受一定损伤，但损伤程度应限制在可修复范围内。
3. 大震不倒：在罕遇大震作用下，建筑物虽然可能遭受严重损伤，但应保证结构不发生整体倒塌，以保障人员安全。
习题三：某建筑物采用框架结构，其柱子的截面尺寸为600mm×600mm，柱子材料为C30混凝土。
若该建筑物位于地震烈度为7度的地区，请计算该柱子在设计时需要考虑的最小配筋率。
答案：根据《建筑抗震设计规范》，框架结构柱子的最小配筋率应满足以下公式：\[ \rho_{min} = 0.0045 + 0.000175 \times \text{烈度} \]将烈度7代入公式，得到：\[ \rho_{min} = 0.0045 + 0.000175 \times 7 = 0.00595 \]因此，该柱子在设计时需要考虑的最小配筋率为0.59%。
习题四：什么是“隔震减震”技术？请简述其工作原理。
答案：“隔震减震”技术是一种先进的抗震技术，其工作原理是在建筑物的基础与上部结构之间设置隔震层，该隔震层通常由橡胶隔震支座、滑动支座等组成。
在地震发生时，隔震层能够吸收和分散地震能量，减少传递到上部结构的地震力，从而保护建筑物的结构安全。
抗震设计有关计算例题
N j= 1
= &&g ( t ) ∑ γ j x ji = &&g ( t ) x x
j =1
& & & = m ∑ xjiγ j ∆ j (t) +γ j xji & g (t)] [ x i = ∑Fji (t)
j =1 N
3
0.334 {X}1 = 0.667 1.000
− 0.667 4.019 {X}2 = − 0.666 {X}3 = −3.035 1.000 1.000
K 3 = 98MN/m
m2 = 270t
K 2 = 195MN/m
i 质点相对于基底的位移与加速度为
xi (t) = ∑xji Dj (t)
j =1
N
N
= ∑xjiγ j ∆ j (t)
j =1 N
& & & i (t) = ∑xjiγ j ∆ j (t) & x
j =1
∑
n
j =1
γ j x ji &&g ( t ) = x
n
i 质点 t 时刻的水平地震作用为 时刻的水平地震作用为
M* = {X}j [m]{X}j ---j振型广义质量 ---j j
T
K* = {X}j [k]{X}j ---j振型广义刚度 ---j j
T
C* = {X}j [c]{X}j ---j振型广义阻尼系数 ---j j
T
C* & K* & (t) + j D + j D (t) = −{X}j [M]{I} & (t) & & Dj xg j j * * * Mj Mj Mj
建筑结构抗震习题及思考题
建筑结构抗震习题及思考题1.1 为什么要进行建筑抗震设计?我国《建筑抗震设计规范》规定对哪些建筑必须进行抗震设计?1. 2 地震按其成因分为哪几种类型?按其震源的深浅又分为哪几种类型?1. 3 地震灾害主要表现在哪几个方面?建筑物破坏的表现形式是什么?1.4 什么是地震波?地震波包含了哪几种波?1.5 什么是地震动的三要素?它们的作用是什么?1.6 什么是地震震级?什么是地震烈度、基本烈度和抗震设防烈度?1.7 简述众值烈度、基本烈度和罕遇烈度的划分标准及其关系。
1.8 我国规范依据建筑使用功能的重要性将建筑分为哪儿类?分类的作用是什么?1.9 抗震设防烈度和设计基本地层加速度的关系是什么?1.10 什么是三水准设防目标和两阶段设计方法?1.11 什么是建筑抗震概念设汁?它主要包括哪几方面内容?1.12 在选择建筑抗震结构体系时，应注意符合哪些要求?2.1 我国抗震规范将建筑场地类别划分为几类？为什么划分？主要考虑哪些因素？2.2 建筑场地类别与场地土类型是否相同？它们有何区别？2.3 什么是土层等效剪切波速？其作用是什么？如何计算？2.4 什么是场地覆盖层厚度?如何确定？2.5 什么是场地的卓越周期？确定卓越周期的意义是什么？2.6 哪些建筑可不进行天然地基及基础的抗震承载力验算？为什么？2.7 如何确定地基抗震承载力？简述天然地基抗震承载力的验算方法。
2.8什么是地基土的液化？液化会造成哪些震害？影响地基土液化的主要因素有哪些？2.9怎么样判别地基土的液化？如何确定地基土液化的严重程度？2.10 不同液化等级可能造成的震害如何？简述地基土的抗液化措施。
2.11 下表为某建筑场地的钻孔资料，试确定该场地的类别。
层底深度/m 土层厚度/m 岩土名称土层剪切波速/(m/s)3.00 3.00 杂填土1606.50 3.50 粉土18011.50 5.00 黏土22016.00 4.50 中沙23022.00 6.00 卵石290----- ----- 砾岩8002.12 已知某6层、高度为20cm的丙类建筑的场地地质钻孔资料如下表所示（无剪切波速数据），试确定该场地的类别。
建筑结构抗震设计试题及答案
建筑结构抗震设计试题一、名词解释(每题3分,共30分)1、地震烈度2、抗震设防烈度3、场地土得液化４、等效剪切波速5、地基土抗震承载力6、场地覆盖层厚度7、重力荷载代表值8、强柱弱梁9、砌体得抗震强度设计值10、剪压比二、填空题(每空1分,共25分)1、地震波包括在地球内部传播得体波与只限于在地球表面传播得面波,其中体波包括波与波,而面波分为波与波,对建筑物与地表得破坏主要以波为主。
2、场地类别根据与划分为类。
3、在用底部剪力法计算多层结构得水平地震作用时,对于T1>1、4T g时,在附加ΔF n,其目得就是考虑得影响。
4、《抗震规范》规定,对于烈度为8度与9度得大跨与结构、烟囱与类似得高耸结构以及9度时得等,应考虑竖向地震作用得影响。
5、钢筋混凝土房屋应根据烈度、与采用不同得抗震等级,并应符合相应得计算与构造措施要求。
6、地震系数表示与之比;动力系数就是单质点与得比值。
7、多层砌体房屋得抗震设计中,在处理结构布置时,根据设防烈度限制房屋高宽比目得就是,根据房屋类别与设防烈度限制房屋抗震横墙间距得目得就是。
８、用于计算框架结构水平地震作用得手算方法一般有与。
9、在振型分解反应谱法中,根据统计与地震资料分析,对于各振型所产生得地震作用效应,可近似地采用得组合方法来确定。
１０、为了减少判别场地土液化得勘察工作量,饱与沙土液化得判别可分为两步进行,即与判别。
三、简答题(每题６分,共30分)１、简述两阶段三水准抗震设计方法。
２、简述确定水平地震作用得振型分解反应谱法得主要步骤。
３、简述抗震设防烈度如何取值。
４、简述框架节点抗震设计得基本原则。
５、简述钢筋混凝土结构房屋得震害情况。
四、计算题(共15分)二质点体系如图所示,各质点得重力荷载代表值分别为m1=60t, m2=50t,层高如图所示。
该结构建造在设防烈度为8度、场地土特征周期T g=0、25s得场地上,其水平地震影响系数最大值分别为max =0、16(多遇地震)与max=0、90(罕遇地震)。
抗震结构设计重要习题及答案
抗震结构设计重要习题及答案1、《抗震规范》给出的设计反应谱中，当结构自振周期在~Tg之间时，谱曲线为A．水平直线 B.斜直线C.抛物线 D.指数曲线2、实际地震烈度与下列何种因素有关？A.建筑物类型B.离震中的距离C.行政区划D.城市大小3、规范规定不考虑扭转影响时，用什么方法进行水平地震作用效应组合的计算？ A.完全二次项组合法 B. 平方和开平方法 C.杜哈米积分 D. 振型分解反应谱法4、基底剪力法计算水平地震作用可用于下列何种建筑( C )米以上的高层建筑 B.自振周期T1很长(T1>4s)的高层建筑 C. 垂直方向质量、刚度分布均匀的多层建筑 D. 平面上质量、刚度有较大偏心的多高层建筑 5、地震系数k 与下列何种因素有关？( A )A.地震基本烈度B.场地卓越周期C.场地土类别D.结构基本周期6、9度区的高层住宅竖向地震作用计算时，结构等效总重力荷载Geq为 A. (恒载标准值GK+活载标准值QK) B. (GK+Qk) C. (GK+) D. (GK+)7、框架结构考虑填充墙刚度时,T1与水平弹性地震作用Fe有何变化( A ) ↓,Fe↑↑,Fe↑↑,Fe↓↓,Fe↓8、抗震设防区框架结构布置时，梁中线与柱中线之间的偏心距不宜大于A．柱宽的1/4 B．柱宽的1/8 C．梁宽的1/4 D．梁宽的1/89、土质条件对地震反应谱的影响很大，土质越松软，加速度谱曲线表现为A．谱曲线峰值右移B．谱曲线峰值左移C．谱曲线峰值增大D．谱曲线峰值降低10、震中距对地震反应谱的影响很大，在烈度相同的条件下，震中距越远，加速度谱曲线表现为A．谱曲线峰值右移B．谱曲线峰值左移C．谱曲线峰值增大D．谱曲线峰值降低 11、为保证结构“大震不倒”，要求结构具有( C )A.较大的初始刚度 B.较高的截面承载能力C.较好的延性D.较小的自振周期T1 12、楼层屈服强度系数沿高度分布比较均匀的结构，薄弱层的位置为A.最顶层B.中间楼层C. 第二层D. 底层13、多层砖房抗侧力墙体的楼层水平地震剪力分配( B ) A.与楼盖刚度无关 B.与楼盖刚度有关C.仅与墙体刚度有关D.仅与墙体质量有关14、场地特征周期Tg与下列何种因素有关( C )A.地震烈度B.建筑物等级C.场地覆盖层厚度D.场地大小15、关于多层砌体房屋设置构造柱的作用，下列哪句话是错误的A．可增强房屋整体性，避免开裂墙体倒塌 B．可提高砌体抗变形能力 C．可提高砌体的抗剪强度D．可抵抗于地基不均匀沉降造成的破坏16、考虑内力塑性重分布，可对框架结构的梁端负弯矩进行调幅A．梁端塑性调幅应对水平地震作用产生的负弯矩进行B．梁端塑性调幅应对竖向荷载作用产生的负弯矩进行C．梁端塑性调幅应对内力组合后的负弯矩进行D．梁端塑性调幅应只对竖向恒荷载作用产生的负弯矩进行17、水平地震作用标准值Fek的大小除了与质量,地震烈度,结构自振周期有关外,还与下列何种因素有关( B ) A.场地平面尺寸 B.场地特征周期 C.荷载分项系数 D.抗震等级 18、表征地震动特性的要素有三个，下列哪项不属于地震动要素A.加速度峰值B.地震烈度C.频谱特性D.地震持时19、震级大的远震与震级小的近震对某地区产生相同的宏观烈度，则对该地区产生的地震影响是A．震级大的远震对刚性结构产生的震害大 B．震级大的远震对柔性结构产生的震害大C．震级小的近震对柔性结构产生的震害大 D．震级大的远震对柔性结构产生的震害小20、地震烈度主要根据下列哪些指标来评定A．地震震源释放出的能量的大小B．地震时地面运动速度和加速度的大小C．地震时大多数房屋的震害程度、人的感觉以及其他现象D．地震时震级大小、震源深度、震中距、该地区的土质条件和地形地貌21、一般情况下，工程场地覆盖层的厚度应按地面至剪切波速大于多少的土层顶面的距离确定A．200m/s B．300m/s C．400m/s D．500m/s22、关于地基土的液化，下列哪句话是错误的A．饱和的砂土比饱和的粉土更不容易液化 B．地震持续时间长，即使烈度低，也可能出现液化 C．土的相对密度越大，越不容易液化 D．地下水位越深，越不容易液化23、某地区设防烈度为7度，乙类建筑抗震设计应按下列要求进行设计A．地震作用和抗震措施均按8度考虑B．地震作用和抗震措施均按7度考虑C．地震作用按8度确定，抗震措施按7度采用D．地震作用按7度确定，抗震措施按8度采用 24、框架柱轴压比过高会使柱产生A．大偏心受压构件 B．小偏心受压构件 C．剪切破坏 D．扭转破坏 25、钢筋混凝土丙类建筑房屋的抗震等级应根据那些因素查表确定 A．抗震设防烈度、结构类型和房屋层数B．抗震设防烈度、结构类型和房屋高度C．抗震设防烈度、场地类型和房屋层数D．抗震设防烈度、场地类型和房屋高度26、纵波、横波和面波之间的波速关系为A．VP > VS > VL B．VS > VP > VL C．VL > VP > VS D．VP > VL> VS27、位于软弱场地上,震害较重的建筑物是: A.木楼盖等柔性建筑 B.单层框架结构 C.单层厂房结构 D.多层剪力墙结构28、强剪弱弯是指: A.抗剪承载力Vu大于抗弯承载力Mu B.剪切破坏发生在弯曲破坏之后 C.设计剪力大于设计弯矩 D.柱剪切破坏发生在梁剪切破坏之后29、下列结构延性哪个延性在抗震设计时要求最高A.结构总体延性B.结构楼层的延性C.构件的延性D.关键杆件的延性30、强柱弱梁是指: A.柱线刚度大于梁线刚度 B.柱抗弯承载力大于梁抗弯承载力 C.柱抗剪承载力大于梁抗剪承载力 C.柱配筋大于梁配筋1、工程结构抗震设防的三个水准是什么？如何通过两阶段设计方法来实现？答：抗震设防的三个水准：第一水准：当遭受低于本地区抗震设防烈度的多遇地震影响时，一般不受损坏或不需修理仍可继续使用；第二水准：当遭受相当于本地区抗震设防烈度的地震影响时，可能损坏，经一般修理或不需修理仍可继续使用；第三水准：当遭受高于本地区抗震设防烈度的罕遇地震影响时，不致倒塌或发生危及生命的严重破坏。
抗震设计计算题_PPT课件
No Image
i V vb ( M b M br ) / ln VGb
M
c
c M b
第六章 多层砌体结构房屋的抗震设计 1、多层混合结构房屋的结构布置方案应优先采用 结构 布置方案，其次采用 _____结构布置方案。 2、多层砌体房屋的抗震设计中，在处理结构布置时，根据 设防烈度限制房屋高宽比目的是为了使多层砌体房屋有足 够的稳定性和整体抗弯能力，根据房屋类别和设防烈度限 制房屋抗震横墙间距的目的是避免纵墙发生较大出平面弯 曲变形，造成纵墙倒塌 。 3、砌体结构中设置钢筋混凝土构造柱和圈梁的作用？ 答：设置钢筋混凝土构造柱的作用：加强房屋的整体性，提 高砌体的受剪承载力(10%-30%)，对砌体有约束作用, 提高 砌体的变形能力，提高房屋的抗震性能。 设置圈梁的作用：增加纵横墙体的连接，加强整个房屋的整 体性；圈梁可箍住楼盖，增强其整体刚度；减小墙体的自 由长度，增强墙体的稳定性；可提高房屋的抗剪强度，约 束墙体裂缝的开展；抵抗地基不均匀沉降，减小构造柱计 算长度。
强柱弱梁梁端先于柱出现塑性铰同时塑性铰区段有较好的延性和耗能能力强剪弱弯梁形成塑性铰后仍有足够的受剪承载力强节点强锚固妥善解决梁纵筋锚固问题为保证强剪弱弯应使构件的受剪承载力大于构件弯曲屈服时实际达到的剪力值对一二三级框架梁梁端截面组合的剪力设计值调整为
抗震结构设计复习题
土木工程与建筑学院
G1 G2 1200kN
1、何谓“抗震概念设计”？“概念设计”与计算设计有何不同？ 答：指根据地震灾害和工程经验等所形成的基本设计原则和设计思想， 进行建筑和结构总体布置并确定细部构造的过程。与计算设计的不同： 计算设计是通过地震作用的取值进行结构的抗震验算，而概念设计强 调，在工程设计一开始，就应该把握好能量输入、房屋体型、结构体 系、刚度分布，构件延性等几个主要方面，从根本上消除建筑中的抗 震薄弱环节，概念设计需要辅以必要地计算设计。 2、抗震设计中为什么要限制各类结构体系的最大高度和高宽比？ 答：随着多层和高层房屋高度的增加，结构在地震作用以及其他荷载作 用下产生的水平位移迅速增大，要求结构的抗侧移刚度必须随之增大。 不同类型的结构体系具有不同的抗侧移刚度，因此具有各自不同的合 理使用高度。 房屋的高宽比是对结构刚度、整体稳定、承载能力和 经济合理性的宏观控制。 震害表明，房屋高宽比大，地震作用产生的倾覆力矩会造成基础转动， 引起上部结构产生较大侧移，影响结构整体稳定。同时倾覆力矩会在 混凝土框架结构两侧柱中引起较大轴力，使构件产生压曲破坏；会在 多层砌体房屋墙体的水平截面产生较大的弯曲应力，使其易出现水平 裂缝，发生明显的整体弯曲破坏。
建筑结构抗震设计课后习题解答
1、震级和烈度有什么区别和联系？震级是表示地震大小的一种度量，只跟地震释放能量的多少有关，而烈度则表示某一区域的地表和建筑物受一次地震影响的平均强烈的程度。
烈度不仅跟震级有关，同时还跟震源深度、距离震中的远近以及地震波通过的介质条件等多种因素有关。
一次地震只有一个震级，但不同的地点有不同的烈度。
3.怎样理解小震、中震与大震？小震就是发生机会较多的地震，50年年限，被超越概率为63.2%； 中震，10%； 大震是罕遇的地震，2%。
4、概念设计、抗震计算、构造措施三者之间的关系？建筑抗震设计包括三个层次：概念设计、抗震计算、构造措施。
概念设计在总体上把握抗震设计的基本原则；抗震计算为建筑抗震设计提供定量手段；构造措施则可以在保证结构整体性、加强局部薄弱环节等意义上保证抗震计算结果的有效性。
他们是一个不可割裂的整体。
1、场地土的固有周期和地震动的卓越周期有何区别和联系？；由于地震动的周期成分很多，而仅与场地固有周期T 接近的周期成分被较大的放大，因此场地固有周期T 也将是地面运动的主要周期，称之为地震动的卓越周期。
3、影响土层液化的主要因素是什么？⑴土的类型、级配和密实程度⑵土的初始应力状态（地震作用时，土中孔隙水压力等于固结水压力是产生土体液化的必要条件）⑶震动的特性（地震的强度和持续时间）⑷先期振动历史或者：土层地质年代；土的颗粒组成及密实程度；埋置深度、地下水；地震烈度和持续时间。
1、结构抗震设计计算有几种方法？各种方法在什么情况下采用？底部剪力法、振型分解反应谱法、时程分析法、静力弹塑性法⑴高度不超过40m 、以剪切变形为主且质量和刚度沿高度分布比较均匀的结构，以及近似于单质点体系的结构，可采用底部剪力法等简化方法。
⑵除⑴外的建筑结构，宜采用振型分解反应谱法。
⑶特别不规则的建筑、甲类建筑和表3—10所列高度范围的高层建筑，应采用时程分析法进行多遇地震下的补充计算，可取多条时程曲线计算结果的平均值与振型分解反应谱法计算结果的较大值。
建筑结构抗震设计习题解答李国强版
4. a 中软场地上的建筑物抗震性能比中硬场地上的建筑物抗震性能要差 （建筑物条件均同）。 b. 粉土中粘粒含量百分率愈大,则愈容易液化. c．液化指数越小，地震时地面喷水冒砂现象越轻微。 d．地基的抗震承载力为承受竖向荷载的能力。
土层厚度：第 i 实测标贯点所代表的土层厚度的上界取上部非液化土层的底面或第
i 1实测标贯点所代表土层的底面；其下界取下部非液化土层的顶面或相邻实测标贯点
的深度的均值。
测点
测点深度 （m）
土层厚度
标准贯入度
土层中点 权函数 液化指数
（m） 实测值 临界值 深度（m） wi
I IE
0
－
1.0
未测 不计算
i 1
6950 0.3329 12606.72
T1 2
6
Giui2
i 1 6
2
Gi u
i 1
3308.05 1.0245s 12606.72
第四章的习题解答
1．见教材。
2．多层砌体结构一般不考虑垂直地震作用。 3．a.增强纵横墙的连接；b.加强楼盖的整体性；c.约束墙体裂缝的开展；
5．a.正确；b. 正确；c. 正确；d.错误，因两方向的ξ不一定相同。 6．a.500mm，2Ф6，1m；b.端部，拐角；c. 主拉应力理论，剪摩擦理论；
d.小于，小于，等于；e.芯柱
7．解：楼梯间的楼层剪力 V 82.8kN
2.08 2.08 5
2
10
4
0
即： 5 2 2 6.24 5 2 4.3264 0
12 31.2
2 2
31.2
抗震与设计计算题目解析
高层建筑结构抗震与设计（练习题1）1.某单跨单层厂房如图1所示，集中于屋盖的重力荷载代表值为G= 2800kN，柱抗侧移刚度系数k1=k2=2.0 xi04kN/m,结构阻尼比Z=0.03 , n类建筑场地，设计地震分组为第一组，设计基本地震加速度为0.15g。
分别求厂房在多遇地震和罕遇地震时水平地震作用。
GG2.图2为两层房屋计算简图，楼层集中质量分别为m1=120t,m2=80t,楼板刚度无穷大，楼层剪切刚度系数分别为k1= 5 xi04kN/m , k2= 3 xi04kN/m。
求体系自振频率和振型, 并验算振型的正交性。
m2k2 k1图2两层房屋计算简图3.钢筋混凝土3层框架计算简图如图3所示。
分别按能量法和顶点位移法计算结构的基本自振周期（取填充墙影响折减系数为0.6 ）。
3图3 3层框架计算简图4.钢筋混凝土 3层框架经质量集中后计算简图如图4所示。
各层高均为5米，各楼层集中质量代表值分别为：G1=G2=750kN，G3=500kN ;经分析得结构振动频率和振型如图4所示。
结构阻尼比Z= 0.05 , I 类建筑场地，设计地震分组为第一组，设计基本地震加速度为0.10g 。
试按振型分解反应谱法确定结构在多遇地震时的地震作用效应，绘出层间 地震剪力图。
图4计算简图5. 已知条件和要求同上题，试按底部剪力法计算。
1、表1为某建筑场地的钻孔资料，试确定该场地的类别。
m 3180 10 kgm 2270 103kgk39800kN / mm 1270 103kgn/" / / 才k 2195000kN/mk 1245000kN / m• G3-1.."10.22rad /s338.37rad / s[./x'J..227.94rad /s3层底深度土层厚度岩土名称土层剪切波速/(m/s)20米的丙类建筑的场地地质钻孔资料如表 2所示（无剪切波速解: 覆盖层厚度达22m ，故取20m 深度计算,共有五个土层:t3d 3V s3 V 5d 5 V s5V sl5 220 4 290平均剪切波速:—0.01875 160 0.022730.01379V sed 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
高层建筑结构抗震与设计(练习题1)1. 某单跨单层厂房如图1所示，集中于屋盖的重力荷载代表值为G ＝2800kN ，柱抗侧移刚度系数k1=k2=2.0×104kN/m,结构阻尼比ζ＝0.03，Ⅱ类建筑场地，设计地震分组为第一组，设计基本地震加速度为0.15g 。
分别求厂房在多遇地震和罕遇地震时水平地震作用。
图1单层厂房计算简图2k 1k kGG2. 图2为两层房屋计算简图，楼层集中质量分别为m1=120t,m2=80t,楼板刚度无穷大，楼层剪切刚度系数分别为k1= 5×104kN/m , k2= 3×104kN/m 。
求体系自振频率和振型，并验算振型的正交性。
图2 两层房屋计算简图1m 2m 1k 2k3. 钢筋混凝土3层框架计算简图如图3所示。
分别按能量法和顶点位移法计算结构的基本自振周期（取填充墙影响折减系数为0.6）。
图3 3层框架计算简图kgm 3310180⨯=kgm 3210270⨯=kgm 3110270⨯=mkN k /98003=mkN k /1950002=mkN k /2450001=4. 钢筋混凝土3层框架经质量集中后计算简图如图4所示。
各层高均为5米，各楼层集中质量代表值分别为：G1=G2=750kN ，G3=500kN ；经分析得结构振动频率和振型如图4所示。
结构阻尼比ζ＝0.05，Ⅰ类建筑场地，设计地震分组为第一组，设计基本地震加速度为0.10g 。
试按振型分解反应谱法确定结构在多遇地震时的地震作用效应，绘出层间地震剪力图。
s rad /22.101=ωsrad /94.272=ωsrad /37.383=ω12图4 计算简图5. 已知条件和要求同上题，试按底部剪力法计算。
1、表1为某建筑场地的钻孔资料，试确定该场地的类别。
表1解：覆盖层厚度达22m ，故取20m 深度计算，共有五个土层： s 01944.01805.3 s 01875.01603222111======s s v d t v d t s 01957.02305.4 s 02273.022********======s s v d t v d t s 01379.02904555===s v d v s 09428.0==∑i t t 平均剪切波速： m/s 2120.09428200===t d v se 由于v se 在140m/s~250m/s 之间，故该场地土为中软场地土。
2、已知某6层、高度为20米的丙类建筑的场地地质钻孔资料如表2所示（无剪切波速数据），试确定该场地的类别。
解：覆盖层厚度为15.5m ，小于20m ，故取15.5m 深度计算，共有四个土层： s 02051.01954 s 01667.01202222111======s s v d t v d t s 01867.03757 s 0119.02105.2444333======s s v d t v d t s 06775.0==∑i t t 平均剪切波速： m/s 2290.067755.150===t d v se 由于v se 在140m/s~250m/s 之间，故该场地土为中软场地土。
3、某单跨单层厂房如图1所示，集中于屋盖的重力荷载代表值为G ＝2800kN ，柱抗侧移刚度系数k1=k2=2.0×104kN/m,结构阻尼比ζ＝0.03，Ⅱ类建筑场地，设计地震分组为第一组，设计基本地震加速度为平地震作用。
解：(1)求周期561086.28.9108.2⨯=⨯==g G m kg721100.4⨯=+=k k k N/m53.0100.41086.214.32275=⨯⨯⨯==k m T π s (2)查表得αmax 、T g ：查表3.1知 设防为七度；查表3.2知，多遇地震：αmax =0.12，罕遇地震：αmax =0.72 ； 查表3.3知 T g =0.35(3)计算α值：因T g ‹T=0.53s ‹5T g ，所以计算公式如下 max 2)(αηαγTT g =其中 18.103.07.106.003.005.017.106.005.012=⨯+-+=+-+=ξξη93.003.055.003.005.0155.005.09.0=⨯+-+=+-+=ξξγ多遇地震： 096.012.018.1)53.035.0()(93.0max 2=⨯⨯==αηαγT T g 罕遇地震： 576.072.018.1)53.035.0()(93.0max 2=⨯⨯==αηαγTT g(4)求水平地震作用多遇地震：8.2682800096.0=⨯==G F EK α kN 罕遇地震：8.16122800576.0=⨯==G F EK α kN 4、图2为两层房屋计算简图，楼层集中质量分别为m 1=120t,m 2=80t,楼板刚度无穷大，楼层剪切刚度系数分别为k 1= 5×104kN/m , k 2= 3×104kN/m 。
求体系自振频率和振型，并验算振型的正交性。
解: (1)刚度矩阵和质量矩阵[]kg 108.0002.100521⨯⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=m m m k 11=k 1+k 2=8×104 kN/m k 12=k 21=-k 2=-3×104 kN/m k 22=k 2=3×104 kN/m []kN/m 103338422211211⨯⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡=k kk k K (2)频率方程为：080103103103120108244424222221122111=-⨯⨯-⨯--⨯=--ωωωωm k k k m k0109)80103)(120108(82424=⨯--⨯-⨯ωω 展开后，得01562507.104124=+-ωω解方程，得 ω1=13.47 rad/s ω2=29.33 rad/s (3)求振型：ω1=13.47 rad/s 对应的振型：194.11031087.1811204412112111112=⨯-⨯-⨯=-=k k m X X ω ω1=29.33 rad/s 对应的振型：177.01031088601204412112212122-=⨯-⨯-⨯=-=k k m X X ω (4)验算振型的正交性：{}[]{}{}{}06.6194.11206.6112094.1177.01800012094.1121=⨯-=⎭⎬⎫⎩⎨⎧-=⎭⎬⎫⎩⎨⎧-⎥⎦⎤⎢⎣⎡=X m X T{}[]{}{}{}031.594.131.1031.531.1094.1177.01333894.1121=⨯-=⎭⎬⎫⎩⎨⎧-=⎭⎬⎫⎩⎨⎧-⎥⎦⎤⎢⎣⎡--=X K X T5、钢筋混凝土3层框架计算简图如图3所示。
分别按能量法和顶点位移法计算结构的基本自振周期（取填充墙影响折减系数为0.6）。
图3 3层框架计算简图kgm 3310180⨯=kgm 3210270⨯=kgm 3110270⨯=mkN k /98003=mkN k /1950002=mkN k /2450001=解: (1)将各楼层重力荷载假定为水平荷载作用于结构楼层处时，计算结构侧移(2)按能量法计算s278.00294.027000524.027000708.018000294.027000524.027000707.018006.02222221121121=⨯+⨯+⨯⨯+⨯+⨯⨯=∆∆=∆∆=∑∑∑∑====ni iini iiTn i ii ni iiTG G G g G T ϕπϕ(3)按顶点位移计算s 319.00708.06.027.11=⨯=∆=T T ϕ6、钢筋混凝土3层框架经质量集中后计算简图如图4所示。
各层高均为5米，各楼层集中质量代表值分别为：G 1=G 2=750kN ，G 3=500kN ；经分析得结构振动频率和振型如图4所示。
结构阻尼比ζ＝0.05，Ⅰ类建筑场地，设计地震分组为第一组，设计基本地震加速度为0.10g 。
试按振型分解反应谱法确定结构在多遇地震时的地震作用效应，绘出层间地震剪力图。
s rad /22.101=ωsrad /94.272=ωsrad /37.383=ω12图4 计算简图解: (1)计算地震影响系数αj 结构侧移I 类场地土，设计地震分组为第一组，T g =0.25 s ，αmax =0.08 阻尼比 ξ=0.05，η2=1.0，γ=0.9自振周期： T 1=0.614 s , T 2=0.225 s , T 3=0.164 s ∵ T g ﹤T 1﹤5 T g ， ∴ 0356.008.00.1)614.025.0()(9.0max 211=⋅⋅=⋅⋅=αηαγT T g ∵ 0.1﹤T 2﹤T g ， ∴ 08.0max 2==αα ∵ 0.1﹤T 3﹤T g ， ∴ 08.0max 3==αα (2)计算振型参数232.15000.175085.075049.05000.175085.075049.022212111121111=⨯+⨯+⨯⨯+⨯+⨯===∑∑∑∑====ni ii ni ii ni ii ni ii G XG X m Xm X γ 275.05000.1750)12.0(750)02.1(5000.1750)12.0(750)02.1(22212212122122-=⨯+⨯-+⨯-⨯+⨯-+⨯-===∑∑∑∑====ni ii ni ii ni ii ni ii G XG X m Xm X γ 113.05000.1750)12.1(75073.05000.1750)12.1(75073.022212313123133=⨯+⨯-+⨯⨯+⨯-+⨯===∑∑∑∑====ni ii ni ii ni ii ni ii G XG X m Xm X γ (3)计算水平地震作用标准值 第一振型：F 11=α1γ1x 11G 1=0.0356×1.232×0.49×750=16.11 kN F 21=α1γ1x 21G 2=0.0356×1.232×0.85×750=27.96 kN F 31=α1γ1x 31G 3=0.0356×1.232×1.00×500=21.9 kN 第二振型：F 12=α2γ2x 12G 1=0.08×(-0.275)×(-1.02)×750=16.83 kN F 22=α2γ2x 22G 2=0.08×(-0.275)×(-0.12)×750=1.98 kN F 32=α2γ2x 32G 3=0.08×(-0.275)×1.00×500=-11.0 kN 第三振型：F 13=α3γ3x 13G 1=0.08×0.113×0.73×750=4.95 kN F 23=α3γ3x 23G 2=0.08×0.113×(-1.12)×750=-7.59 kN F 33=α3γ3x 33G 3=0.08×0.113×1.00×500=4.52 kN (4)计算结构地震作用效应S EK92.2452.4)11(9.212221=+-+=EK S kN 76.50)07.3()02.9(86.492222=-+-+=EK S kN 46.6688.181.797.652223=++=EK S kN7、 已知条件和要求同上题，试按底部剪力法计算。