3.3Fluent紊流模型
fluent湍流模型
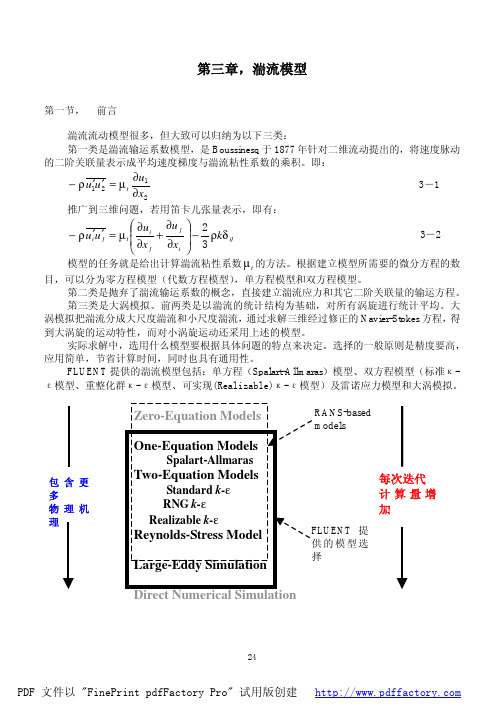
第三节,
湍流模型
3.3.1 单方程(Spalart-Allmaras)模型 ~ ,表征出了近壁(粘性影响)区域以外的湍流运动粘 Spalart-Allmaras 模型的求解变量是ν ~ 的输运方程为: 性系数。ν
~ ~ ~ ∂ν Dν 1 ∂ ∂ν ~ − Yν ρ = Gν + 3-9 ( µ + ρν ) + Cb 2 ρ Dt σ ν~ ∂ x ∂ x ∂ x j j j 其中,Gν 是湍流粘性产生项;Yν 是由于壁面阻挡与粘性阻尼引起的湍流粘性的减少;σ ν ~
ρu y u = τ uτ µ ρuτ y u 1 = ln E µ uτ k
其中,k=0.419,E=9.793。
3-18
如果网格粗错不能用来求解层流底层,则假设与壁面近邻的网格质心落在边界层的对数 区,则根据壁面法则: 3-19
对流传热传质模型 在 FLUENT 中,用雷诺相似湍流输运的概念来模拟热输运过程。给出的能量方程为:
3-11
壁面的距离;S ≡
Ω ij =
∂u 1 j − ∂u i 2 ∂xi ∂x j
由于平均应变率对湍流产生也起到很大作用,FLUENT 处理过程中,定义 S 为:
S ≡ Ω ij + C prod min(0, S ij − Ω ij )
Байду номын сангаас其中, C prod = 2.0 , Ω ij ≡
率ε两个方程,湍流粘性系数用湍动能 k 和耗散率ε的函数。Boussinesq 假设的缺点是认为湍 流粘性系数 µ t 是各向同性标量,对一些复杂流动该条件并不是严格成立,所以具有其应用限 制性。 另外的方法是求解雷诺应力各分量的输运方程。这也需要额外再求解一个标量方程,通常 是耗散率ε方程。这就意味着对于二维湍流流动问题,需要多求解 4 个输运方程,而三维湍流 问题需要多求解 7 个方程,需要比较多的计算时间,对计算机内存也有更高要求。 在许多问题中,Boussinesq 近似方法可以得到比较好的结果,并不一定需要花费很多时间 来求解雷诺应力各分量的输运方程。但是,如果湍流场各向异性很明显,如强旋流动以及应力 驱动的二次流等流动中,求解雷诺应力分量输运方程无疑可以得到更好的结果。
如何在fluent中设置多相流讲解

3 设置一般的多相流问题(Setting Up a General Multiphase Problem)3.1使用一般多相流模型的步骤(Steps for Using the General Multiphase Models)设置和求解一般多相流问题的步骤的要点如下,各个子部分详细的讲述在随后的章节中。
记住这里给出的仅是与一般多相流计算相关的步骤。
有关你使用的其它模型和相关的多相流模型的输入的详细信息,将在这些模型中合适的部分给出。
1)选中你想要使用的多相流模型(VOF, mixture, or Eulerian)并指定相数。
Define Models Multiphase...2)从材料库中复制描述每相的材料。
Define Materials...如果你使用的材料在库中没有,应创建一种新材料。
!!如果你的模型中含有微粒(granular)相,你必须在fluid materials category中为它创建新材料(not the solid materials category.)3)定义相,指定相间的相互作用(interaction)(例如,使用欧拉模型时的drag functions)Define Phases...4)(仅对欧拉模型)如果流动是紊流,定义多相紊流模型。
Define Models Viscous...5)如果体积力存在,turn on gravity and specify the gravitational acceleration.Define Operating Conditions...6)指定边界条件,包括第二相体积份额在流动边界和壁面上的接触角。
Define Boundary Conditions...7)设置模拟具体的解参数Solve Controls Solution...8)初始化解和为第二相设定初始体积份额。
Solve Initialize Patch...9)计算求解和检查结果*欧拉多相流模拟的附加指南(Additional Guidelines for Eulerian Multiphase Simulations)一旦你决定了欧拉多相流模型适合你的问题,你应当考虑求解你的多相流问题的需求计算能力。
总结紊流模型

总结紊流模型引言紊流模型是研究流体力学中的一种重要模型。
紊流是流体运动中的一种不规则且无序的状态,其对流体的输运和混合过程具有重要影响。
紊流模型是为了研究和描述紊流行为而开发的一套数学模型和数值方法。
在本文中,我们将对紊流模型进行总结和介绍。
紊流模型的背景紊流是指流体运动中出现的一种混乱、不规则且无序的状态。
紊流行为对于理解和描述自然界中很多现象具有重要意义。
例如,在地球大气层中,气象学家需要研究和预测风场的紊流行为,以便预测天气和气候变化。
此外,在工程领域中,了解和控制液体和气体的紊流行为对于设计有效的流体输运系统和减小能量损耗也是至关重要的。
紊流模型的发展可以追溯到19世纪。
著名的物理学家奥斯特里奇尔首先提出了紊流的描述方法,他认为紊流是由无数个不同尺度的涡旋组合而成的。
随后,许多学者对紊流进行了深入研究,并提出了不同的理论和模型。
这些模型主要包括雷诺平均纳维-斯托克斯(RANS)方程模型、大涡模拟(LES)模型和直接数值模拟(DNS)模型等。
雷诺平均纳维-斯托克斯方程模型雷诺平均纳维-斯托克斯方程模型是最常用的紊流模型之一。
该模型基于平均流动场的假设,将流场分解为平均部分和涨落部分。
该模型利用雷诺应力项来描述涨落部分的影响,并采用一系列经验公式来计算涨落部分的动力学行为。
尽管RANS 模型已经广泛应用于各个领域,但由于其对涡旋的统计特性进行了平均化处理,因此无法准确描述流体中小尺度涡旋的空间和时间演化。
大涡模拟模型大涡模拟模型是一种介于RANS模型和DNS模型之间的紊流模型。
该模型利用滤波方法将流体运动分解为大尺度运动和小尺度运动,并采用过滤后的雷诺平均纳维-斯托克斯方程对大尺度运动进行求解,对小尺度运动进行模型化处理。
大涡模拟模型具有较好的精度和计算效率,因此在工程领域中得到了广泛应用。
直接数值模拟模型直接数值模拟模型是对紊流行为进行最准确描述的一种模型。
该模型通过离散化流体运动方程,并采用数值方法对其进行求解,可以直接获得流体中各个尺度的涡旋的空间和时间演化。
(word完整版)fluent湍流模型总结,推荐文档

一般来说,DES和LES是最为精细的湍流模型,但是它们需要的网格数量大,计算量和内存需求都比较大,计算时间长,目前工程应用较少。
S-A模型适用于翼型计算、壁面边界层流动,不适合射流等自由剪切流问题。
标准K-Epsilon模型有较高的稳定性、经济性和计算精度,应用广泛,适用于高雷诺数湍流,不适合旋流等各相异性等较强的流动。
RNG K-Epsilon模型可以计算低雷诺数湍流,其考虑到旋转效应,对强旋流计算精度有所提供。
Realizable K-Epsilon模型较前两种模型的有点是可以保持雷诺应力与真实湍流一致,可以更加精确的模拟平面和圆形射流的扩散速度,同时在旋流计算、带方向压强梯度的边界层计算和分离流计算等问题中,计算结果更符合真实情况,同时在分离流计算和带二次流的复杂流动计算中也表现出色。
但是此模型在同时存在旋转和静止区的计算中,比如多重参考系、旋转滑移网格计算中,会产生非物理湍流粘性。
因此需要特别注意。
专用于射流计算的Realizable k-ε模型。
标准K-W模型包含了低雷诺数影响、可压缩性影响和剪切流扩散,适用于尾迹流动、混合层、射流、以及受壁面限制的流动附着边界层湍流和自由剪切流计算。
SST K-W模型综合了K-W模型在近壁区计算的优点和K-Epsilon模型在远场计算的优点,同时增加了横向耗散导数项,在湍流粘度定义中考虑了湍流剪切应力的输运过程,适用更广,可以用于带逆压梯度的流动计算、翼型计算、跨声速带激波计算等。
雷诺应力模型没有采用涡粘性各向同性假设,在理论上比前面的湍流模型要精确的多,直接求解雷诺应力分量(二维5个,三维7个)输运方程,适用于强旋流动,如龙卷风、旋流燃烧室计算等。
!!!!!所以在选择湍流模型时要注意各个模型是高雷诺数模型还是低雷诺数模型,前者采用壁面函数时,应该避免使用太好(对壁面函数方法)或太粗劣(对增强函数处理方法)的网格。
而对于低雷诺数模型,壁面应该有好的网格。
fluent中常见的湍流模型及各自应用场合

标题:深入探讨fluent中常见的湍流模型及各自应用场合在fluent中,湍流模型是模拟复杂湍流流动的重要工具,不同的湍流模型适用于不同的流动情况。
本文将深入探讨fluent中常见的湍流模型及它们各自的应用场合,以帮助读者更深入地理解这一主题。
1. 简介湍流模型是对湍流流动进行数值模拟的数学模型,通过对湍流运动的平均值和湍流运动的涡旋进行描述,以求解湍流运动的平均流场。
在fluent中,常见的湍流模型包括k-ε模型、k-ω模型、LES模型和DNS模型。
2. k-ε模型k-ε模型是最常用的湍流模型之一,在工程领域有着广泛的应用。
它通过求解两个方程来描述湍流场,即湍流能量方程和湍流耗散率方程。
k-ε模型适用于对流动场变化较为平缓的情况,如外流场和边界层内流动。
3. k-ω模型k-ω模型是另一种常见的湍流模型,在边界层内流动和逆压力梯度流动情况下有着良好的适用性。
与k-ε模型相比,k-ω模型对于边界层的模拟更加准确,能够更好地描述壁面效应和逆压力梯度情况下的流动。
4. LES模型LES(Large Ey Simulation)模型是一种计算密集型的湍流模拟方法,适用于对湍流细节结构和湍流的大尺度结构进行同时模拟的情况。
在fluent中,LES模型通常用于对湍流尾流、湍流燃烧和湍流涡流等复杂湍流流动进行模拟。
5. DNS模型DNS(Direct Numerical Simulation)模型是一种对湍流流动进行直接数值模拟的方法,适用于小尺度湍流结构的研究。
在fluent中,DNS模型常用于对湍流的微观结构和湍流的小尺度特征进行研究,如湍流能量谱和湍流的空间分布特性等。
总结与回顾通过本文的介绍,我们可以看到不同的湍流模型在fluent中各有其适用的场合。
从k-ε模型和k-ω模型适用于工程领域的实际流动情况,到LES模型和DNS模型适用于研究湍流细节结构和小尺度特征,每种湍流模型都有其独特的优势和局限性。
《fluent湍流模型》课件

Fluent湍流模型的常见问题
常见的问题包括模型精度不够、 计算量太大、计算时间过长等。
解决法
可以通过减小网格尺寸、改变模 拟设置、使用高性能计算机等方 法来解决问题。
常见错误示范
常见错误包括不合理的边界条件、 不准确的物理参数设定等。
总结
通过本课程的学习,您已了解Fluent湍流模型的基本概念、原理和应用。希望您可以将所学应用到实际工作中, 并继续跟踪湍流模型的发展趋势。
工业中的应用
在飞机、汽车、火箭等工业 制造领域中广泛应用,可以 用于优化产品设计、性能测 试和流体控制等方面。
实际案例分析
使用Fluent湍流模型成功预 测了风力发电机转子的性能, 为风力发电技术的发展做出 了重要贡献。
优缺点
具有高精度、高可靠性和可 灵活扩展等优点,但对计算 资源要求较高。
常见问题与解决方法
通过求解雷诺应力方程来描述湍流过程,
精度更高但计算量更大。
3
Large Eddy Simulation
通过将湍流流场分解成大尺度和小尺度
Detached Eddy Simulation
4
来模拟流体运动。
相对于LES模拟时间更短,适合处理具有 湍流特性的旋转流和湍流边界层等问题。
Fluent湍流模型应用
质量守恒方程
描述流体中物质的流 动规律,保证物质质 量不会凭空消失或凭 空增加。
模拟方法
计算流体力学(CFD) 模拟的方法,如有限 元方法、有限体积法 和边界元方法等。
湍流模型原理
1
k-ε模型
在工程实践中应用广泛,许多气动工程
Reynolds Stress Model
2
和水动力学模拟都基于该模型进行。
第三章紊流模型知识分享

①零方程模型:常系数模型,混合长模型,剪力模型等 ②单方程模型:k方程模型
③双方程模型:k- 模型
4、评价紊流模型优劣的标准
①适用于多种类型的水流现象; ②具有足够的精度; ③人力和计算机费用适度; ④复杂程度适当。
第三章 紊流模型
五、 紊流的数学描述
紊流是满足连续性条件的,因此对于连续介质流体所导出的连续 性方程和Navier-Stokes方程组可以用于描述紊流的瞬时流态。
从20世纪40年代开始,采用一些紊动量的微分输运方程,例如 紊动动能的输运方程、雷诺应力的输运方程等。这类模型的特 点是理论严谨、概念完整,其中某些模型中提出的基本概念仍 作为目前最先进的紊流模型的理论基础。
第三章 紊流模型
在20世纪60年代中期,计算机的威力已足够强大,才有可能 求解时均流偏微分方程,也才有可能检验、应用和发展这一 类紊流模型。
涡度脉动的三维性 紊流是涡度的脉动强度很大的有
旋三维运动。
第三章 紊流模型
第三章 紊流模型
二、紊流现象及相应的研究课题
②河流中的淡水注人海洋,与 咸水混合,在河口区域内,水 中含盐量的分布规律如何?是 否影响水中动植物的生长?
①热电厂的废气排人大气层中,这 些废气在风的作用下如何运动?是 否有可能触及地面,地面上废气的 浓度如何?
第三章 紊流模型
③管流中的突然放大段,通常 在突然放大处形成涡旋,使流 态复杂,涡旋的尺寸和流速分 布如何确定?局部阻力系数如 何计算?
④溢流坝反弧段的高速水流有可 能在反弧段末端引起空蚀破坏, 如何计算反弧段紊流的速度场。 压力场,预测空泡在水中的发生、 发展和溃灭,从而寻求减免空蚀 破坏的合理措施。
作为紊流的通解,纳维埃-斯 托克斯方程描述了流体运动的 一切细节
FLUENT算例 (3)三维圆管紊流流动状况的数值模拟分析

三维圆管紊流流动状况的数值模拟分析在工程和生活中,圆管内的流动是最常见也是最简单的一种流动,圆管流动有层流和紊流两种流动状况。
层流,即液体质点作有序的线状运动,彼此互不混掺的流动;紊流,即液体质点流动的轨迹极为紊乱,质点相互掺混、碰撞的流动。
雷诺数是判别流体流动状态的准则数。
本研究用CFD 软件来模拟研究三维圆管的紊流流动状况,主要对流速分布和压强分布作出分析。
1 物理模型三维圆管长2000mm l =,直径100mm d =。
流体介质:水,其运动粘度系数62110m /s ν-=⨯。
Inlet :流速入口,10.005m /s υ=,20.1m /s υ= Outlet :压强出口Wall :光滑壁面,无滑移2 在ICEM CFD 中建立模型2.1 首先建立三维圆管的几何模型Geometry2.2 做Blocking因为截面为圆形,故需做“O ”型网格。
2.3 划分网格mesh注意检查网格质量。
在未加密的情况下,网格质量不是很好,如下图因管流存在边界层,故需对边界进行加密,网格质量有所提升,如下图2.4 生成非结构化网格,输出fluent.msh等相关文件3 数值模拟原理紊流流动当以水流以流速20.1m /s υ=,从Inlet 方向流入圆管,可计算出雷诺数10000υdRe ν==,故圆管内流动为紊流。
假设水的粘性为常数(运动粘度系数62110m /s ν-=⨯)、不可压流体,圆管光滑,则流动的控制方程如下:①质量守恒方程:()()()0u v w t x y zρρρρ∂∂∂∂+++=∂∂∂∂ (0-1)②动量守恒方程:2()()()()()()()()()()[]u uu uv uw u u ut x y z x x y y z z u u v u w p x y z xρρρρμμμρρρ∂∂∂∂∂∂∂∂∂∂+++=++∂∂∂∂∂∂∂∂∂∂'''''∂∂∂∂+----∂∂∂∂ (0-2)2()()()()()()()()()()[]v vu vv vw v v v t x y z x x y y z z u v v v w px y z yρρρρμμμρρρ∂∂∂∂∂∂∂∂∂∂+++=++∂∂∂∂∂∂∂∂∂∂'''''∂∂∂∂+----∂∂∂∂ (0-3)2()()()()()()()()()()[]w wu wv ww w w w t x y z x x y y z z u w v w w px y z zρρρρμμμρρρ∂∂∂∂∂∂∂∂∂∂+++=++∂∂∂∂∂∂∂∂∂∂'''''∂∂∂∂+----∂∂∂∂ (0-4)③湍动能方程:()()()()[())][())][())]t t k k t k k k ku kv kw k k t x y z x x y yk G z zμμρρρρμμσσμμρεσ∂∂∂∂∂∂∂∂+++=+++∂∂∂∂∂∂∂∂∂∂+++-∂∂ (0-5)④湍能耗散率方程:212()()()()[())][())][())]t t k k t k k u v w t x y z x x y y C G C z z k kεεμμρερερερεεεμμσσμεεεμρσ∂∂∂∂∂∂∂∂+++=+++∂∂∂∂∂∂∂∂∂∂+++-∂∂ (0-6)式中,ρ为密度,u 、ν、w 是流速矢量在x 、y 和z 方向的分量,p 为流体微元体上的压强。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• Classical models. Based on Reynolds Averaged Navier-Stokes (RANS) equations (time averaged):
• The number of equations denotes the number of additional PDEs that are being solved. • Large eddy simulation. Based on space-filtered equations. Time dependent calculations are performed. Large eddies are explicitly calculated. For small eddies, their effect on the flow pattern is taken into account with a “subgrid model” of which many styles are available.
• Using the suffix notation where i, j, and k denote the x-, y-, and zdirections respectively, viscous stresses are given by: ui u j ij eij x j xi • Similarly, link Reynolds stresses to the mean rate of deformation:
t ( m 2 / s ) ( m / s ) ( m)
• If we then assume that the velocity scale is proportional to the length scale and the gradients in the velocity (shear rate, which has dimension 1/s): U y we can derive Prandtl’s (1925) mixing length model: 2 U t m y • Algebraic expressions exist for the mixing length for simple 2-D flows, such as pipe and channel flow.
• Its unit is the same as that of the molecular viscosity: Pa.s. • It is also called the eddy viscosity. • We can also define a kinematic turbulent viscosity: t = t/. Its unit is m2/s. • The turbulent viscosity is not homogeneous, i.e. it varies in space. • It is, however, assumed to be isotropic. It is the same in all directions. This assumption is valid for many flows, but not for all (e.g. flows with strong separation or swirl).
– 1. Zero equation model: mixing length model. – 2. One equation model: Spalart-Almaras. – 3. Two equation models: k- style models (standard, RNG, realizable), k- model, and ASM. – 4. Seven equation model: Reynolds stress model.
• Disadvantages:
– Completely incapable of describing flows where the turbulent length scale varies: anything with separation or circulation. – Only calculates mean flow properties and turbulent shear stress.
• Many turbulence models are based upon the Boussinesq hypothesis.
– It was experimentally observed that turbulence decays unless there is shear in isothermal incompressible flows. – Turbulence was found to increase as the mean rate of deformation increases. – Boussinesq proposed in 1877 that the Reynolds stresses could be linked to the mean rate of deformation.
9
Spalart-Allmaras one-equation model
• Solves a single conservation equation (PDE) for the turbulent viscosity:
– This conservation equation contains convective and diffusive transport terms, as well as expressions for the production and dissipation of t. – Developed for use in unstructured codes in the aerospace industry.
• Because of its relatively narrow use we will not discuss this model in detail.
10
The k-ε model
• The k-ε model focuses on the mechanisms that affect the turbulent kinetic energy (per unit mass) k. • The instantaneous kinetic energy k(t) of a turbulent flow is the sum of mean kinetic energy K and turbulent kinetic energy k:
• We will discuss these one by one.
7
Mixing length model
• On dimensional grounds one can express the kinematic turbulent viscosity as the product of a velocity scale and a length scale:
• A turbulence model is a computational procedure to close the system of mean flow equations. • For most engineering applications it is unnecessary to resolve the details of the turbulent fluctuations. • Turbulence models allow the calculation of the mean flow without first calculating the full time-dependent flow field. • We only need to know how turbulence affected the mean flow. • In particular we need expressions for the Reynolds stresses. • For a turbulence model to be useful it:
3
Prediction Methods
l Direct numerical simulation (DNS)
h = l/ReL3/4
Large eddy simulation (LES)
Reynolds averaged Navier-Stokes equations (RANS)
4
Boussinesq hypothesis
• Use:
– Sometimes used for simple external aero flows. – Pretty much completely ignored in commercial CFD programs today.
• Much better models are available.
Lecture 10 - Turbulence Models
Applied Computational Fluid Dynamics
Instructor: André Bakker
© André Bakker (2002-2005) © Fluent Inc. (2002)
1
Turbulence models
U i U j ij ui ' u j ' t x x i j
