高中数学知识结构框图(人教版)
2020秋新人教版高中数学必修二第八章立体几何初步复习课题型课知识框架思维导图
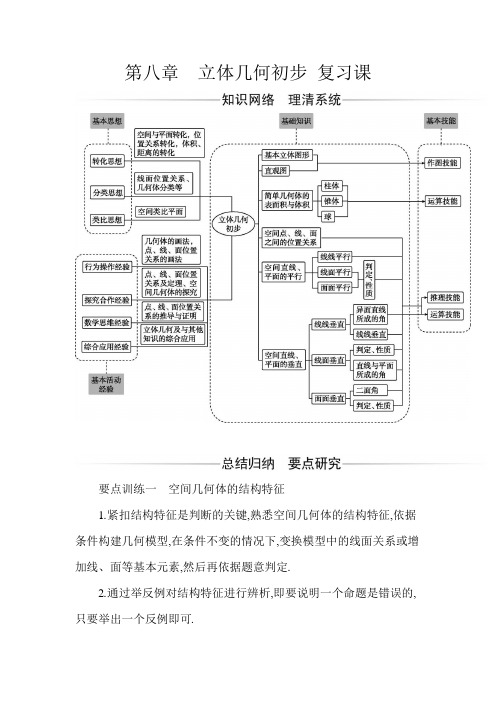
第八章立体几何初步复习课要点训练一空间几何体的结构特征1.紧扣结构特征是判断的关键,熟悉空间几何体的结构特征,依据条件构建几何模型,在条件不变的情况下,变换模型中的线面关系或增加线、面等基本元素,然后再依据题意判定.2.通过举反例对结构特征进行辨析,即要说明一个命题是错误的,只要举出一个反例即可.1.设有四个命题:①底面是矩形的平行六面体是长方体;②棱长都相等的直四棱柱是正方体;③侧棱垂直于底面两条边的平行六面体是直平行六面体;④对角线相等的平行六面体是直平行六面体.其中真命题的个数是()A.1B.2C.3D.4解析:底面是矩形的直平行六面体是长方体,①错误;棱长都相等的直四棱柱是正方体,②正确;侧棱垂直于底面两条相邻边的平行六面体是直平行六面体,③错误;任意侧面上两条对角线相等的平行六面体是直平行六面体,④错误.故命题正确的个数是1.答案:A2.在四棱锥的四个侧面中,直角三角形最多可有()A.1个B.2个C.3个D.4个解析:如图所示,在长方体ABCD-A1B1C1D1中,取四棱锥A1-ABCD,则此四棱锥的四个侧面都是直角三角形.答案:D要点训练二空间几何体的表面积与体积1.空间几何体表面积的求法(1)以三视图为载体的几何体的表面积问题,关键是分析三视图确定几何体中各元素之间的位置关系及数量.(2)多面体的表面积是各个面的面积之和;组合体的表面积问题注意衔接部分的处理.(3)旋转体的表面积问题,应注意其侧面展开图的应用.2.空间几何体体积问题的常见类型及解题策略(1)若所给定的几何体问题是可直接用公式求解的柱体、锥体或台体,则可直接利用公式进行求解.(2)若所给定的几何体的体积不能直接利用公式得出,则常用转换法、分割法、补形法等进行求解.(3)若以三视图的形式给出几何体,则应先根据三视图得到几何体的直观图,再根据条件求解.1.已知一个六棱锥的体积为2√3 ,其底面是边长为2的正六边形,侧棱长都相等,则该六棱锥的侧面积为12.解析:由题意可知,该六棱锥是正六棱锥.设该六棱锥的高为h ,则13×6×√34×22×h =2√3,解得h =1.由题意,得底面正六边形的中心到其边的距离为√3,所以侧面等腰三角形底边上的高为√(√3)2+1=2,所以该六棱锥的侧面积为6×12×2×2=12. 2.如图所示,三棱锥O -ABC 为长方体的一角,其中OA ,OB ,OC 两两垂直,三个侧面OAB ,OAC ,OBC 的面积分别为1.5 cm 2,1 cm 2,3 cm 2,求三棱锥O -ABC 的体积.解:设OA ,OB ,OC 的长依次为x cm,y cm,z cm,由已知可得12xy =1.5,12xz =1,12yz =3,解得x =1,y =3,z =2. 将三棱锥O -ABC 看成以C 为顶点,以OAB 为底面,易知OC 为三棱锥C -OAB 的高.故V 三棱锥O -ABC =V C -OAB =13S △OAB ·OC =13×1.5×2=1(cm 3). 3.如图所示,已知三棱柱ABC -A'B'C',侧面B'BCC'的面积是S ,点A'到侧面B'BCC'的距离是a ,求三棱柱ABC -A'B'C'的体积.解:连接A'B ,A'C ,如图所示,这样就把三棱柱ABC -A'B'C'分割成了两个棱锥,即三棱锥A'-ABC 和四棱锥A'-BCC'B'.设所求体积为V ,显然三棱锥A'-ABC 的体积是13V. 而四棱锥A'-BCC'B'的体积为13Sa , 故有13V +13Sa =V ,所以V =12Sa. 要点训练三 与球有关的切、接问题与球相关问题的解题策略(1)作适当的截面(如轴截面等)时,对于球内接长方体、正方体,则截面一要过球心, 二要过长方体或正方体的两条体对角线,才有利于解题.(2)对于“内切”和“外接”等问题,首先要弄清几何体之间的相互关系,主要是指特殊的点、线、面之间的关系,然后把相关的元素放到这些关系中来解决.1.正四棱锥的顶点都在同一球面上,若该棱锥的高为6,底面边长为4,则该球的表面积为( )A.443πB.4849πC.814πD.16π 解析:如图所示,设PE 为正四棱锥P -ABCD 的高,则正四棱锥P -ABCD 的外接球的球心O 必在其高PE 所在的直线上,延长PE 交球面于一点F ,连接AE ,AF.由球的性质可知△PAF 为直角三角形,且AE ⊥PF.因为该棱锥的高为6,底面边长为4,所以AE =2√2,PE =6,所以侧棱长PA =√PE 2+AE 2=√62+(2√2)2=√44=2√. 设球的半径为R ,则PF =2R. 由△PAE ∽△PFA ,得PA 2=PF ·PE ,即44=2R ×6,解得R =113,所以S =4πR 2=4π×(113)2=484π9.答案:B2.一个球与一个正三棱柱的三个侧面和两个底面都相切,如果这个球的体积是323π,那么这个正三棱柱的体积是( ) A.96√3 B.16√3 C.24√3 D.48√3解析:由球的体积公式可求得球的半径R =2. 设球的外切正三棱柱的底面边长为a ,高即侧棱长,为h ,则h =2R =4. 在底面正三角形中,由正三棱柱的内切球特征,得a 2×√33=R =2,解得a =4√3. 故这个正三棱柱的体积V =12×√32×(4√3)2×4=48√3.答案:D要点训练四 空间中的平行关系1.平行问题的转化关系2.直线与平面平行的主要判定方法(1)定义法;(2)判定定理;(3)面与面平行的性质.3.平面与平面平行的主要判定方法(1)定义法;(2)判定定理;(3)推论;(4)a ⊥α,a ⊥β⇒α∥β.1.如图所示,三棱柱ABC -A'B'C'中,M ,N 分别为BB',A'C'的中点.求证:MN ∥平面ABC'.证明:取B'C'的中点P ,连接MP ,NP (图略),则MP ∥BC',NP ∥A'B'. 因为A'B'∥AB ,所以NP ∥AB.因为AB ⊂平面ABC',NP ⊄平面ABC',所以NP ∥平面ABC'.同理MP∥平面ABC'.因为NP∩MP=P,所以平面MNP∥平面ABC'.因为MN⊂平面MNP,所以MN∥平面ABC'.2.两个全等的正方形ABCD和ABEF所在平面相交于AB, M∈AC,N∈FB,且AM=FN,过点M作MH⊥AB于点H.求证:平面MNH∥平面BCE.证明:因为正方形ABCD中,MH⊥AB,BC⊥AB,所以MH∥BC.因为BF=AC,AM=FN,所以FNBF =AM AC.因为MH∥BC,所以AMAC =AH AB,所以FNBF =AH AB,所以NH∥AF∥BE.因为MH⊂平面MNH,NH⊂平面MNH,MH∩NH=H, BC⊂平面BCE,BE⊂平面BCE,BC∩BE=B,所以平面MNH∥平面BCE.要点训练五空间中的垂直关系1.空间中垂直关系的相互转化2.判定线线垂直的方法(1)平面几何中证明线线垂直的方法.(2)线面垂直的性质:a⊥α,b⊂α⇒a⊥b;a⊥α,b∥α⇒a⊥b.3.判定线面垂直的常用方法(1)利用线面垂直的判定定理.(2)利用“两平行线中的一条与平面垂直,则另一条也与这个平面垂直”.(3)利用“一条直线垂直于两平行平面中的一个,则与另一个平面也垂直”.(4)利用面面垂直的性质.4.判定面面垂直的方法(1)利用定义:两个垂直平面相交,所成的二面角是直二面角.(2)判定定理:a⊂α,a⊥β⇒α⊥β.1.如图所示,Rt△AOC可以通过Rt△AOB以直角边AO所在直线为轴旋转得到,且二面角B-AO-C是直二面角,D是AB上任意一点.求证:平面COD⊥平面AOB.证明:由题意,得CO⊥AO,BO⊥AO,所以∠BOC是二面角B-AO-C 的平面角.因为二面角B-AO-C是直二面角,所以∠BOC=90°,所以CO⊥BO.因为AO∩BO=O,所以CO⊥平面AOB.因为CO⊂平面COD,所以平面COD⊥平面AOB.2.如图所示,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=BC=2, AD=CD=√7,PA=√3,∠ABC=120°,G为线段PC上的点,O为AC,BD交点.(1)证明:BD⊥平面APC;(2)若G满足PC⊥平面BGD,求PG的值.GC(1)证明:由AB=BC,AD=CD,得BD垂直平分线段AC.所以O为AC的中点,BD⊥AC.因为PA⊥平面ABCD,BD⊂平面ABCD,所以PA⊥BD.因为AC∩PA=A,AC⊂平面APC,PA⊂平面APC,所以BD⊥平面APC.(2)解:连接OG,如图所示.因为PC⊥平面BGD,OG⊂平面BGD,所以PC⊥OG.在△ABC中,由余弦定理,得AC=√22+22-2×2×2×cos120°=2√3.在Rt△PAC中,得PC=√AC2+PA2=√12+3=√所以由△GOC∽△APC可得GC=AC·OCPC =2√155.从而PG=3√155,所以PGGC=32.要点训练六空间角的求解方法1.找异面直线所成角的三种方法(1)利用图中已有的平行线平移.(2)利用特殊点(线段的端点或中点)作平行线平移.(3)补形平移.2.线面角求斜线与平面所成的角关键是找到斜线在平面内的射影,即确定过斜线上一点向平面所作垂线的垂足.通常是解由斜线段、垂线段、斜线在平面内的射影所组成的直角三角形.3.求二面角的两种常用方法(1)定义法:在二面角的棱上找一个特殊点,在两个半平面内分别过该点作垂直于棱的射线.(2)垂面法:过棱上一点作棱的垂直平面,该平面与二面角的两个半平面产生交线,这两条交线所成的角,即为二面角的平面角.1.如图所示,在三棱锥P-ABC中,PA⊥平面ABC,∠BAC=90°, AB≠AC,D,E分别是BC,AB的中点,AC>AD,设PC与DE所成的角为α,PD与平面ABC所成的角为β,二面角P-BC-A的平面角为γ,则α,β,γ的大小关系是α<β<γ.解析:因为D,E分别是BC,AB的中点,所以DE∥AC,所以PC与DE所成的角为∠PCA,即α.因为PA⊥平面ABC,所以PD与平面ABC所成的角为∠PDA,即β.如图所示,过点A作AH⊥BC,垂足为H,连接PH,易证BC⊥平面PAH,所以∠PHA是二面角P-BC-A的平面角,即γ.因为AB≠AC,所以AD>AH.因为AC >AD,所以AC >AD >AH,所以PAAC <PAAD<PAAH,所以tan α<tan β<tan γ,所以α<β<γ.2.如图所示,AB是☉O的一条直径,PA垂直于☉O所在的平面,C 是圆周上不同于A, B的一动点.(1)证明:△P BC是直角三角形;(2)若PA=AB=2,且当直线PC与平面ABC所成角的正切值为√2时,求直线AB与平面PBC所成角的正弦值.(1)证明:因为AB是☉O的一条直径, C是圆周上不同于A,B的一动点,所以BC⊥AC.因为PA⊥平面ABC,所以BC⊥PA.因为PA∩AC=A,PA⊂平面PAC,AC⊂平面PAC,所以BC⊥平面PAC,所以BC⊥PC,所以△BPC是直角三角形.(2)解:如图所示,过点A作AH⊥PC于点H,连接BH.因为BC⊥平面PAC,所以BC⊥AH.因为PC∩BC=C,PC⊂平面PBC,BC⊂平面PBC,所以AH⊥平面PBC,所以∠ABH是直线AB与平面PBC所成的角.因为PA⊥平面ABC,所以∠PCA即是PC与平面ABC所成的角.因为tan∠PCA=PAAC=√2,PA=2, 所以AC=√2.在Rt△PAC中,AH=√PA2+AC2=23√3,在Rt△ABH中,sin∠ABH=23√32=√33,即AB与平面PBC所成角的正弦值为√33.要点训练七转化思想转化思想是指在解决数学问题时,一个数学对象在一定条件下转化为另一种数学对象的思想.它包括从未知到已知的转化,从一般到特殊的转化等,折叠问题中体现了转化思想.解决折叠问题的关键在于认真分析折叠前后元素的位置变化情况,看看哪些元素的位置变了,哪些元素的位置没有变,基本思路是利用“不变求变”,一般步骤如下:(1)平面→空间:根据平面图形折出满足条件的空间图形,想象出空间图形,完成平面图形与空间图形在认识上的转化.(2)空间→平面:为解决空间图形问题,要回到平面上来,重点分析元素的变与不变.1.如图所示,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°.若将△ADB沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A-BCD,则在三棱锥A-BCD中,下列结论正确的是()A.平面ABD⊥平面ABCB.平面ADC⊥平面BDCC.平面ABC⊥平面BDCD.平面ADC⊥平面ABC解析:因为在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°, ∠BAD=90°,所以BD⊥CD.因为平面ABD⊥平面BCD,且平面ABD∩平面BCD=BD,所以CD⊥平面ABD,所以CD⊥AB.因为AD⊥AB,AD∩CD=D,AD⊂平面ADC,CD⊂平面ADC,故AB⊥平面ADC.因为AB⊂平面ABC,所以平面ABC⊥平面ADC.答案:D2.如图所示,在矩形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC(端点除外)上一动点.现将△AFD沿AF折起,使平面ABD⊥平面ABC.在平面ABD内过点D作DK⊥AB,垂足为K.设AK=t,则t的取值范围是(1,1).2→解析:如图所示,过点K作KM⊥AF于M点,连接DM,易得DM⊥AF,与折前的图形对比,可知在折前的图形中D,M,K三点共线,且DK⊥AF, 于是△DAK∽△FDA,所以AKAD =ADDF.所以t1=1DF.所以t=1DF.因为DF∈(1,2),所以t∈( 12,1).3.如图①所示,在等腰梯形CDEF中,DE=CD=√2,EF=2+√2,将它沿着两条高AD,CB折叠成四棱锥E-ABCD(E,F两点重合),如图②所示.①②(1)求证:BE⊥DE;(2)设M为线段AB的中点,试在线段CE上确定一点N,使得MN∥平面DAE.(1)证明:因为AD⊥EF,所以AD⊥AE,AD⊥AB.因为AB∩AE=A,AB⊂平面ABE,AE⊂平面ABE,所以AD⊥平面ABE,所以AD⊥BE.由题图①和题中所给条件知,AE=BE=1,AB=CD=√2,所以AE2+BE2=AB2,即AE⊥BE.因为AE∩AD=A,AE⊂平面ADE,AD⊂平面ADE,所以BE⊥平面ADE,所以BE⊥DE.(2)解:如图所示,取EC的中点G,BE的中点P,连接PM,PG,MG, 则MP∥AE,GP∥CB∥DA,所以MP∥平面DAE,GP∥平面DAE.因为MP∩GP=P,所以平面MPG∥平面DAE.因为MG⊂平面MPG,所以MG∥平面DAE,即存在点N与G重合满足条件,使得MN∥平面DAE.。
人教版高中数学知识框架思维导图(04)-按章节整理(含目录高清版)

公式的变形、逆用、
“1”的替换
cos
诱导公式:奇变偶不变,符号看象限
和角、差角公式,辅助角公式(sin ± cos)
二倍角公式,降幂公式(cos2 α =
1+cos2α
2
, sin2 α =
1−cos2α
2
化简、求值、
证明(恒等变形)
)
和角、差角公式,二倍角公式,降幂公式,辅助角公式
⑴sin( ± ) = sincos ± cossin;⑵cos( ± ) = coscos ∓ sinsin;⑶tan( ± ) =
⑴sin2 = 2sincos;⑵cos2 = cos2 − sin2 = 2cos2 − 1 = 1 − 2sin2 ;⑶tan2 =
1
1+cos2α
2
2
⑴sincos = sin2;⑵cos2 α =
⑴sin ± cos =
√2
+ 2 sin(
;⑶sin2 α =
互逆
原命题:若 p 则 q
关系
命题
互否
简易逻辑
互否
等价关系
否命题:若p 则q
充分条件、必要条件、充要条件
复合命题
逆命题:若 q
若 ⇒ ,则是的充分条件,是的必要条件
或:p q
一真便真
否定: p q
且:p q
一假则假
否定: p q
对称变换: = () → = −(), = () → = (−), = () → = −(−)
函数图象
及其变换
翻折变换: = () → = |()|, = () → = (||)
伸缩变换: = () → = (), = () → = ()
人教版 高中数学 第一章 循环结构的程序框图(共16张PPT)教育课件
凡 事都 是多棱 镜, 不同 的角 度会
凡 事都是 多棱 镜, 不同 的角度 会看 到不 同的 结果 。若 能把一 些事 看淡 了, 就会 有个好 心境 ,若 把很 多事 看开 了 ,就会 有个 好心 情。 让聚散 离合 犹如 月缺 月圆 那样 寻常, 让得 失利 弊犹 如花 开花谢 那样 自然 ,不 计较 ,也 不 刻意执 着; 让生 命中 各种的 喜怒 哀乐 ,就 像风 儿一 样,来 了, 不管 是清 风拂 面,还 是寒 风凛 冽, 都报 以自 然 的微笑 ,坦 然的 接受 命运的 馈赠 ,把 是非 曲折 ,都 当作是 人生 的
i<100? 否 是 i=i+1
S=S+ i
输出S 结束
开始 i=0,S=0
i=i+1 S=S+ i 否 i>=100?
是 输出S 结束
当型循环与直到循环的区别:
①当型循环可以不执行循环体,直到 循环至少执行一次循环体. ②当型循环先判断后执行,直到型循 环先执行后判断. ③对同一算法来说,当型循环和直到 循环的条件互为反条件.
开始 i=0,S=0
否 i<100? 是 i=i+1 S=S+ i
输出S 结束
思考:将步骤A和步骤B交换位 置,结果会怎样?能达到预期结果 吗?为什么?要达到预期结果,还 需要做怎样的修改?
步骤A
步骤B 答:达不到预期结果;
当i = 100时,退出循环,i 的值未能加入到S中;修 改的方法是将判断条件改 为i<101
i=i+1 S=S+ i
i=i+1 S=S + i
当型结构
i<100? 是
否
i=i+1
人教版高中数学必修3课件程序框图

结束
否 否
d=d+1
否 n不是质数
程序框图:又称流程图,是一种用规定的图形、指向线及文字说明来准确、
直观的表示算法的图形.
名称
作用 终端框或起止框
表示算法的 起始和结束
名称
输入、输出框 作用 表示算法的输入 和输出的信息
名称
作用
处理框或执行框
赋值、计算
名称 判断框 作用
判断某一条件是否成立, 成立在出口处标明“是”或“Y” 不成立标明“否”或“N”
5;
结束
指向②处时,输出 sum 15 .
5.下图为求1~1000的所有的偶数的和而设计的一个程 序框图,将空白处补上,并指明它是循环结构中的哪一 种类型,并画出它的另一种循环结构框图.
开始
i=2
sum=0 i<=1000
i=i+2 sum=sum+i
输出sum 结束
课堂小结:
1.要掌握程序框的作用; 2.掌握三种逻辑结构,并能正确使用这三种结构画流程图; 3.在循环结构中,一定有条件结构,通常都有一个起到循环计数作用的变量; 4.确实明确当型和直到型的区别和联系,不要混用。
输出S 结束
输出S 结束
练习:
1.就(1)、(2)两种逻辑结构,说出各自的算法功能 ຫໍສະໝຸດ 1)开始(2) 开始
输入a,b
输入a,b
2.已知梯形上底为2,下底为4, 高为5,求其面积,设计出该 问题的流程图.
开始
d a2 b2
sum=a+b
a 2,b 4, h 5
c d
输出c
结束
输出sum 结束
S 1 (a b)h 2
高二数学流程图及结构图

探究:
双线流程图:
某“儿童之家”开展亲子活动, 儿童与家长如约来到“儿童之家” 计划活动步骤如下: 首先,儿童与家长按事先约定时 接待家长交 接待儿童做 间来到“儿童之家”。 流本周表现 活动前准备 然后,一部分工作人员接待儿童, 做活动前准备;同时,另一部分 工作人员接待家长,交儿童本周 按亲子活动方案活动” 表现。 第三步,按照亲子活动方案进行 启导员填写亲子 家长填写亲子 动。 活动总结记录 活动反馈卡 第四步,启导员填写亲子活动总 结记录;同时 家长填写亲子活 动反馈卡。 启导员填写服务跟踪表 最后,启导员填写服务跟踪表。
第六步:两鬼过河
流程图:
开始 一人一鬼过河,一人划回 两鬼过河,一鬼划回
两人过河,一鬼一人回
两人过河,一鬼回 两鬼过河,一鬼回 两鬼过河 结束
工序流程 图(统筹 图)
流程图概念:
像这样由一些图形符号和文字说明构成,用来表示 动态过程的图示称为流程图。
1. 流程图有哪几部分组成?
图形符号和文字说明。
动手
绘制流程图:
2.单线流程图 咨询考试事宜 是否新考生
是 否
1.用自然语言描述考试流程
第一步:咨询考试事宜 第二步:新生填写考生注册表, 并领取考生号;老生出示考号。 第三步:明确考试科目和时间 第四步:交纳考试费 第五步:按规定时间参加考试 第六步:领取成绩单 第七步:领取证书
填写考生注册表 领取考生号 明确考试科目和时间 交纳考试费
必修3 P3例2
举例说明
2、怎样用程序框 图表达算法步骤 中的“第一步?”
f(x) x 2
2
输入精确度
的初值1、2
x1 , x2
举例说明:
3、第二步中有哪些操作?其中包 含了哪些逻辑结构?怎样用程序 框图表达?
高中数学(必修5)知识结构框图
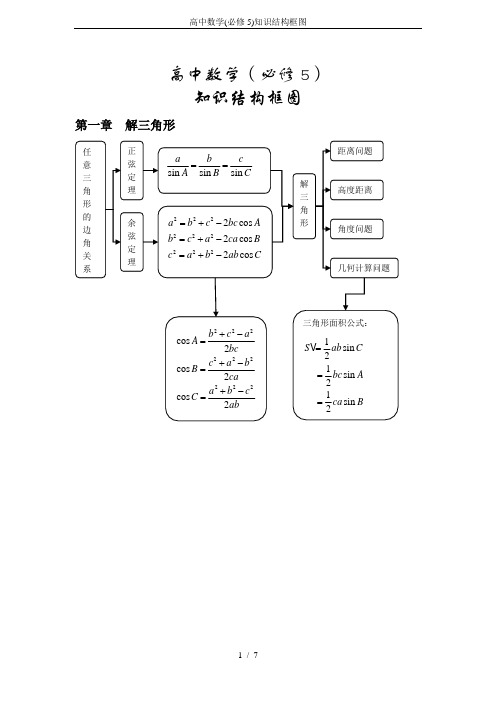
高中数学(必修5) 知识结构框图第一章 解三角形1sin 21sin 2S ab bc == 第二章数列第三章不等式¤例题精讲:【例1】在四棱锥的四个侧面中,直角三角形最多可有( ).A. 1个B. 2个C. 3个D. 4个 选D. 【例2】已知球的外切圆台上、下底面的半径分别为,r R ,求球的半径.解:圆台轴截面为等腰梯形,与球的大圆相切,由此得梯形腰长为R +r ,梯形的高即球的直径为=.第4讲 §1.2.3 空间几何体的直观图¤知识要点:“直观图”最常用的画法是斜二测画法,由其规则能画出水平放置的直观图,其实质就是在坐标系中确定点的位置的画法. 基本步骤如下:(1) 建系:在已知图形中取互相垂直的x 轴和y 轴,得到直角坐标系xoy ,直观图中画成斜坐标系'''x o y ,两轴夹角为45︒.(2)平行不变:已知图形中平行于x 轴或y 轴的线段,在直观图中分别画成平行于x ’或y ’轴的线段.(3)长度规则:已知图形中平行于x 轴的线段,在直观图中保持长度不变;平行于y 轴的线段,长度为原来的一半.第5讲 §1.3.1 柱体、锥体、台体的表面积¤学习目标:了解棱柱、棱锥、台的表面积的计算公式(不要求记忆公式);能运用柱、锥、台的表面积进c 直截面周长h 高S h 底高2. 当台体的上底面逐渐扩展到与下底面全等时,它就成了柱体. 因而体积会有以下的关系:13V S h =锥 '0S =←−−− 1(')3V S S h =台 'S S=−−−→ V S h =柱. 第7讲 §1.3.2球的体积和表面积¤知识要点:1. 表面积:24S R π=球面 (R :球的半径). 2. 体积:343V R π=球面. 第8讲 §2.1.1 平面¤知识要点:1. 点A 在直线上,记作A a ∈;点A 在平面α内,记作A α∈;直线a 在平面α内,记作a α⊂.ll β=∈推论1 经过一条直线和这条直线外的一点,有且只有一个平面; 推论2 经过两条相交直线,有且只有一个平面; 推论3 经过两条平行直线,有且只有一个平面. 第9讲 §2.1.2 空间中直线与直线之间的位置关系¤知识要点:1.空间两条直线的位置关系:⎧⎧⎪⎨⎨⎩⎪⎩相交直线:同一平面内,有且只有一个公共点;共面直线平行直线:同一平面内,没有公共点;异面直线:不同在任何一个平面内,没有公共点.2. 已知两条异面直线,a b ,经过空间任一点O 作直线//,//a a b b '',把,a b ''所成的锐角(或直角)叫异面直线,a b 所成的角(或夹角). ,a b ''所成的角的大小与点O 的选择无关,为了简便,点O 通常取在异面直线的一条上;异面直线所成的角的范围为(0,90]︒,如果两条异面直线所成的角是直角,则叫两条异面直线垂直,记作a b ⊥. 求两条异面直线所成角的步骤可以归纳为四步:选点→平移→定角→计算.第19讲 §3.1.2 两条直线平行与垂直的判定¤知识要点:1. 对于两条不重合的直线1l 、2l ,其斜率分别为1k 、2k ,有:(1)12//l l ⇔12k k =;(2)12l l ⊥⇔121k k ⋅=-.2. 特例:两条直线中一条斜率不存在时,另一条斜率也不存在时,则它们平行,都垂直于x 轴;….第20讲 §3.2.1 直线的点斜式方程¤知识要点:1. 点斜式:直线l 过点000(,)P x y ,且斜率为k ,其方程为00()y y k x x -=-.2. 斜截式:直线l 的斜率为k ,在y 轴上截距为b ,其方程为y kx b =+.3. 点斜式和斜截式不能表示垂直x 轴直线. 若直线l 过点000(,)P x y 且与x 轴垂直,此时它的倾斜角为90°,斜率不存在,它的方程不能用点斜式表示,这时的直线方程为00x x -=,或0x x =.4. 注意:y y k x x -=-与00()y y k x x -=-是不同的方程,前者表示的直线上缺少一点000(,)P x y ,后者才是整条直线.第21讲 §3.2.2 直线的两点式方程¤知识要点:1. 两点式:直线l 经过两点111222(,),(,)P x y P x y ,其方程为112121y y x x y y x x --=--, 2. 截距式:直线l 在x 、y 轴上的截距分别为a 、b ,其方程为1x ya b+=.3. 两点式不能表示垂直x 、y 轴直线;截距式不能表示垂直x 、y 轴及过原点的直线.4. 线段12P P 中点坐标公式1212(,)22x x y y ++. 第22讲 §3.2.3 直线的一般式方程¤知识要点:1. 一般式:0Ax By C ++=,注意A 、B 不同时为0. 直线一般式方程0(0)Ax By C B ++=≠化为斜截式方程A Cy x B B=--,表示斜率为A B -,y 轴上截距为C B -的直线.2 与直线:0l Ax By C ++=平行的直线,可设所求方程为'0Ax By C ++=;与直线0Ax By C ++=垂直的直线,可设所求方程为'0Bx Ay C -+=. 过点00(,)P x y 的直线可写为00()()0A x x B y y -+-=.经过点0M ,且平行于直线l 的直线方程是00()()0A x x B y y -+-=; 经过点0M ,且垂直于直线l 的直线方程是00()()0B x x A y y ---=.3. 已知直线12,l l 的方程分别是:1111:0l A x B y C ++=(11,A B 不同时为0),2222:0l A x B y C ++=(22,A B 不同时为0),则两条直线的位置关系可以如下判别: (1)1212120l l A A B B ⊥⇔+=; (2)1212211221//0,0l l A B A B AC A B ⇔-=-≠; (3)1l 与2l 重合122112210,0A B A B AC A B ⇔-=-=; (4)1l 与2l 相交12210A B A B ⇔-≠. 如果2220A B C ≠时,则11112222//A B C l l A B C ⇔=≠;1l 与2l 重合111222A B CA B C ⇔==;1l 与2l 相交1122A B A B ⇔≠. 第23讲 §3.3.1 两条直线的交点坐标¤知识要点:1. 一般地,将两条直线的方程联立,得到二元一次方程组1112220A x B y C A x B y C ++=⎧⎨++=⎩. 若方程组有惟一解,则两条直线相交,此解就是交点的坐标;若方程组无解,则两条直线无公共点,此时两条直线平行;若方程组有无数解,则两条直线有无数个公共点,此时两条直线重合.2. 方程111222()()0A x B y C A x B y C λ+++++=为直线系,所有的直线恒过一个定点,其定点就是1110A x B y C ++=与2220A x B y C ++=的交点.第24讲 §3.3.2 两点间的距离两点111(,)P x y ,222(,)P x y ,则两点间的距离为:.特别地,当12,P P 所在直线与x 轴平行时,1212||||PP x x =-;当12,PP 所在直线与y 轴平行时,1212||||PP y y =-;当12,PP 在直线y kx b =+上时,1212|||PP x x -. 2. 坐标法解决问题的基本步骤是:(1)建立坐标系,用坐标表示有关量;(2)进行有关代数运算;(3)把代数运算的结果“翻译”成几何关系.第25讲 §3.3.3 点到直线的距离及两平行线距离¤知识要点:1. 点00(,)P x y 到直线:0l Ax By C ++=的距离公式为d .2. 利用点到直线的距离公式,可以推导出两条平行直线11:0l Ax By C ++=,22:0l Ax By C ++=之间的距离公式d =,推导过程为:在直线2l 上任取一点00(,)P x y ,则0020A x B y C ++=,即002A x B y C +=-. 这时点00(,)P x y 到直线11:0l Ax By C ++=的距离为d ==第26讲 第4章 §4.1.1 圆的标准方程¤知识要点:1. 圆的标准方程:方程222()()(0)x a y b r r -+-=>表示圆心为A (a ,b ),半径长为r 的圆.2. 求圆的标准方程的常用方法:(1)几何法:根据题意,求出圆心坐标与半径,然后写出标准方程;(2)待定系数法:先根据条件列出关于a 、b 、r 的方程组,然后解出a 、b 、r ,再代入标准方程.第27讲 §4.1.2 圆的一般方程¤知识要点:1. 圆的一般方程:方程220x y Dx Ey F ++++= (2240D E F +->)表示圆心是(,)22D E --的圆. 2. 轨迹方程是指点动点M 的坐标(,)x y 满足的关系式.第28讲 §4.2.1 直线与圆的位置关系¤知识要点:1. 直线与圆的位置关系及其判定: 方法一:方程组思想,由直线与圆的方程组成的方程组,消去x 或(y ),化为一元二次方程,由判别式符号进行判别;方法二:利用圆心(,a b )到直线0Ax By C ++=的距离d =,比较d 与r 的大小.(1)相交d r ⇔<⇔ 0∆>;(2)相切d r ⇔=⇔0∆=;(3)相离d r ⇔>⇔0∆<.2. 直线与圆的相切研究,是高考考查的重要内容. 同时,我们要熟记直线与圆的各种方程、几何性质,也要掌握一些常用公式,例如点线距离公式d =第29讲 §4.2.2 圆与圆的位置关系¤知识要点:两圆的位置关系及其判定: 设两圆圆心分别为12,O O ,半径分别为12,r r ,则: (1)两圆相交121212||||r r O O r r ⇔-<<+;(2)两圆外切1212||O O r r ⇔=+;(3)两圆内切1212||||O O r r ⇔=-;第30讲 §4.2.3 直线与圆的方程的应用¤知识要点:坐标法:建立适当的直角坐标系后,借助代数方法把要研究的几何问题,转化为坐标之间的运算,由此解决几何问题。
高中数学知识点框图
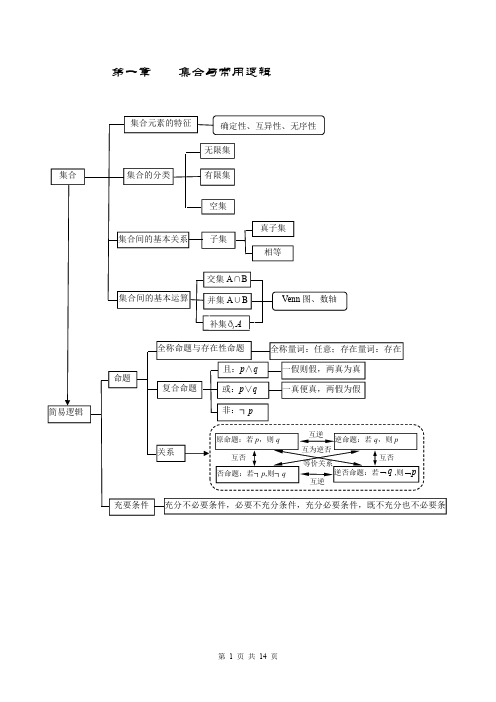
相交 平行
平行 相交
只有一个公共点 没有公共点 没有公共点
有公共点
平行关系的 相互转化
线线 平行
线面 平行
面面 平行
空间直角坐标系
垂直关系的 相互转化
线线 垂直
线面 垂直
面面 垂直
空间的角 空间的距离
异面直线所成的角 直线与平面所成的角 二面角
点到面的距离 直线与平面的距离 平行平面之间的距离
第九章 直线与圆的方程
本章知识结构图
倾斜角和斜率
k
tan
y2 x2
y1 x1
,
0,
2
2
,
,当
=
2
时,k不存在
直线的方程
位置关系
重合 平行
A1B2-A2B1=0
截距
相交
A1B2-A2B1≠0
注意:截距可正、可负,也可为 0.
点斜式:y-y0=k(x-x0) 斜截式:y=kx+b
②图象也可以用五点作图法;③用整体代换求单调区间(注意的符号);
④最小正周期
T= |
2 ;⑤对称轴 |
x=(2k+1)-2,对称中心为(k-,b)(k∈Z).
2
解三角形
正弦定理 余弦定理
面积
实际应用
解的个数的讨论 三角形形状的判定
S△=1ah=1absinC= p(p-a)(p-b)(p-c)(其中 p=a+b+c)
逐差累加法 逐商累积法 构造等比数列{an+ q }
p-1
④pan+1an=an-an+1
构造等差数列
人教版高中数学必修三第1章程序框图与算法的基本逻辑结构教学课件

或
流程线
连接程序框
连接点
连接程序框图的两部分
顺序结构 循环结构
条件结构
开始 输入n
i=2
n除以i的余数r
i=i+1
i>n-1或r=0? 是
r=0?
是 n不是质数
否 否
n是质数
结束
知识探究(二):算法的顺序结构
1.顺序结构:按照步骤依次执行的一个算法 2.顺序结构的流程图
语句A 语句B
例1(1)写出图中程序框图的运行结果:
你能画出这个算法的程序框图吗?
开始 输入a,b,c
a+b>c,b+c>a,c+a>b是否
否
同时成立?
是
存在这样的三角形
不存在这样的三角 形
结束
课堂练习
画出求函数y
x x
( x 0) ( x 0)
的 函数值的程序框图.
理论迁移
例5 设计一个求解一元二次方程ax2+bx+c=0 的算法,并画出程序框图表示.
算法分析:
第一步,输入三个系数a,b,c.
第二步,计算△=b2-4ac.
第三步,判断△≥0是否成立.若是,则计
程没有
p =算- b ,q = V
;否则,输出“方
实数2a 根”2,a 结束算法.
第四步,判断△=0是否成立.若是,则输出 x1=x2=p,否则,计算x1=p+q,x2=p-q, 并输出x1,x2.
我们可以将上述算法用下面的图形表示:
开始
输入n i=2
求n除以i的余数 i的值增加1,仍用i表示
i>n-1或r=0? 是
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学知识结构框图(必修1)第一章集合与函数概念第二章基本初等函数(Ⅰ)第三章函数的应用函数的应用函数与方程函数模型及其应用方程的根与函数零点的关系用二分法求方程的近似解几种不同增长的函数模型用已知函数模型解决问题建立实际问题的函数模型函数零点的存在性直线上升指数爆炸对数增长指数函数,对数函数,幂函数增长速度的比较。
见教材P98~100数学二第一章空间几何体的知识结构框架第二章点、直线、平面之间的位置关系的知识结构框架第三章直线与方程的知识结构框架第四章圆与方程的知识结构框架数学三数学四本章知识结构如下:本章知识结构如下:本章知识结构如下:英语(课程)书信的常见写作模板开头部分:How nice to hear from you again. Let me tell you something about the activ ity. I’m glad to have received your letter of Apr. 9th. I’m pleased to hear that you’re coming to China for a visit. I’m writing to thank you for your help during my stay in America.结尾部分:With best wishes. I’m looking forward to your reply. I’d apprec iate it if you could reply earlier.口头通知常见写作模板开场白部分:Ladies and gentlemen, May I have your attention, please? I have an announcement to make.正文部分:All the teachers and students are required to attend it. Please take your notebooks and make note s. Please listen carefully and we’ll have a discussion in groups. Please come on time and don’t be late.结束语部分:Please come and join in it. Everybody is welcome to attend it. I hope you’ll have a nice time here. That’s all. Thank you.议论文模板1.正反观点式议论文模板:导入:第1段:Recently we’ve had a discussion about whether we should... (导入话题) Our opinions are divided on this topic.(观点有分歧) 正文:第2段:Most of the students are in favour of it.(正方观点) Here are the reasons. First... Second... Finally...(列出2~3个赞成的理由) 第3段:However, the others are strongly against it. (反方观点) Their reasons are as follows. In the first place... What’s more... In addition...(列出2~3个反对的理由) 结论:第4段:Personally speaking, the advantages overweigh the disadvantages, for it will do us more harm than good, so I supportit.(个人观点)2.“A或者B”类议论文模板:导入:第1段:Some people hold the opinion that A is superior to B in many ways. Others, however, argue that B is much better. Personally, I would prefer A because I think A has more advantages. 正文:第2段:There are many reasons why I prefer A. The main reason is that ... Another reason is that...(赞同A的原因) 第3段: Of course, B also has advantages to some extent... (列出1~2个B的优势) 结论:第4段: But if all these factors are considered, A is much better than B. From what has been discussed above, we may finally draw the conclusion that ...(得出结论)3.观点论述类议论文模板:导入:第1段:提出一种现象或某个决定作为议论的话题 As a student, I am strongly in favour of the decision. (亮明自己的观点是赞成还是反对) The reasons for this may be listed as follows. (过渡句,承上启下) 正文:第2段:First of all... Secondly... Besides...(列出2~3个赞成或反对的理由) 结论:第3段:In conclusion, I believe that... (照应第1段,构成"总—分—总"结构)4."How to"类议论文模板:导入:第1段:提出一种现象或某种困难作为议论的话题正文:第2段:Many ways can help to solve this serious problem, but the following may be most effective. First of all... Another way to solve the problem is ... Finally...(列出2~3个解决此类问题的办法) 结论:第3段:These are not the best but the only two/ three measures we can take. But it should be noted that we should take action to...(强调解决此类问题的根本方法)图表作文写作模板The chart gives us an overall picture of the 图表主题.The first thing we notice is that 图表最大特点 .This means that as 进一步说明.We can see from the statistics given that 图表细节图表细节一 . After 动词-ing :细节一中的第一个变化, the动词-ed+幅度+时间(紧跟着的变化) .The figures also tell us that图表细节二 .In the column, we can see that accounts for (进一步描述).Judging from these figures, we can draw the conclusion that (结论).The reason for this, as far as I am concerned is that (给出原因). b或是It is high time that we (发出倡议).图画类写作模板1.开头Look at this picture./The picture shows that.../From this picture, we can see.../As is shown in the picture.../As is seen in the picture...2.衔接句 As we all know, .../As is known to all,.../It is well known that.../In my opinion,.../As far as I am concerned,.../This sight reminds me of something in my daily life.3.结尾句 In conclusion.../In brief.../On the whole.../In short.../In a word.../Generally speaking.../As has been stated..一、有关语言修辞的题型描绘类提问方式:某句话中某个词换成另一个行吗?为什么?或:文章的某个句子说成另一个句子好不好?为什么?答题模式:不行。
因为该词生动具体(形象、准确)地写出了+对象+效果,换了后就变成+不好的效果。
或:不行,因为该词比另一词的感情更强烈(或该词比另一词更切合对象的性格特征)。
动词:不行。
因为该词准确生动具体地写出了……形容词:不行。
因为该词生动形象地描写了……副词(如都,大都,非常只有等):不行。
因为该词准确地说明了……的情况(表程度,表限制,表时间,表范围等),换了后就变成……,与事实不符。
答题示例:山间林密,泉隐其中,有时,泉水在林木疏朗处闪过亮亮的一泓,再向前寻,已不可得。
那半含半露、欲近故远的娇态,使我想起?诩疑⒉绞保3H莆蚁ハ碌陌C考疑焓钟科浣埃卦对兜嘏芸銎鹦α扯何?;待我佯作冷淡而不顾,她却又悄悄跑近,偎我腰间。
好一个调皮的孩子!(节选自谢大光《鼎湖山听泉》)问:“好一个调皮的孩子”,为什么不说成“真是可爱的孩子”?答:因为“好一个”比“真是”感情更强烈,“调皮”比“可爱”更切合爱女的性格特征。
结构类提问方式:某两个或三个词的顺序能否调换?为什么?答题模式:不能。
因为(1)与人们认识事物的规律(由浅入深、由表入里、由现象到本质)不一致(2)该词与上文是一一对应的关系(3)这些词是递进关系,环环相扣,表达了…答题示例:“记住:想占便宜的人,往往占不到便宜!”父亲指着碗里的荷包蛋告诫儿子……“记住,想占便宜的人,可能要吃亏!”父亲指着蛋教训儿子说……“不想占便宜的人,生活也不会让他吃亏!”父亲意味深长的对儿子说。
