新三年级奥数速算与巧算
三年级奥数 速算与巧算(修正后)

1、加减法巧算在进行加减法计算时,“先计算括号中的部分,再从左往右依次计算”是基本的运算法则,但除此之外,还有许多运算技巧,熟练掌握各种运算技巧可以使你算得更快更准。
“凑整法”是最常用的巧算方法,就是在计算时优先计算可以得到整十、整百、整千的部分,从而达到巧算的目的,要想凑出整十,两个数的末位相加应该得0,这样的情况除了0+0外,还有1+9,2+8,3+7,4+6,5+5,同学们在作题时要注意观察各加数的个位,看能不能找到合适的凑法,除了加法可以凑整以外,减法同样可以凑整,个位相同的两个数相减后便能得到整十的数。
在进行加减法混合运算时,经常会遇到能够巧算的数不在一起的情况,这时候就需要通过调整运算顺序,把能巧算的放在一起先算,但需要注意的是,在调整的过程中,每个数都必须带着自己左边的符号一起移动,这种调整可以形象地称作“带符号搬家”,如果搬家的是算式中的第一个数,前面没有符号,在这个数之前添上一个加号即可。
例题1(1)计算:73+45+17+55;(2)计算:73+119+231+69+381+17(3)计算:375-138+247-175+139-237。
分析(1)通过个位凑十来配对;(2)加法配对看末位,减法应该如何配对?练习1、(1)计算:45+67+33+55+84(2)计算:36+97+32+64+168+103;(3)计算:2468-192+532+392-224+1234。
除了“带符号搬家”可以调整运算次序外,“脱括号”与“添括号”也是改变运算顺序的常用手段,加减法算式中“脱括号”要遵循下面的规则:例题2(1)计算:4723-(723+189)(2)计算:162-(162-135)-35-19(3)计算:163-(50-18)-(153-76)+(124-18)分析:去掉括号会变成什么样?练习:(1)计算123-(23-45)-(45-67)(2)计算:437-(200-83)+(63-53)………………………………………………笑话………………………………………………从前,山东省有个大军阀,他横行霸道,却不学无术,经常闹笑话。
三年级奥数加减法的速算与巧算.

又如:11+89=100,33+67=100, 22+78=100,44+56=100, 55+45=100, 在上面算式中,
1叫9的“补数”;89叫11的“补数”,11
凑整法 〔补数法〕
例1 计算: (1) 1+2+3+4+5+6+7+8+9+10
= ( 1+9)+ ( 2+8)+ ( 3+7)+ ( 4+6)+5+10 =10+10+10+10+10+5 =55
(2) 1+3+5+7+9+11+13+15+17+19 =(1+19)+(3+17)+(5+15)+(7+13)+(9+11) =20+20+20+20+20 =100
凑整法 〔补数法〕
如:43+(38+45)+(55+62+57) =43+38+45+55+62+57 =〔43+57〕+〔38+62〕 +〔45+55〕 =100+100+100 =300
去括号添括号法则
2.在加、减法混合运算中,添括号时:假设添加的括号前 面是“+”号,那么括号内的数的原运算符号不变;假设 添加的括号前面是“-”号,那么括号内的数的原运算符 号“+”变为“-”,“-”变为“+”。
小学三年级数学奥数知识点速算与巧算

1.快速计算乘法口诀表在小学三年级,学生已经开始学习乘法口诀表。
熟练掌握乘法口诀表是进行速算和巧算的基础。
学生应该掌握1乘以任意数等于该数本身,以及0乘以任意数等于0的原则。
另外,在计算乘法的过程中,还可以利用一些巧妙的方法,如利用乘法交换律和结合律,简化计算的步骤。
2.快速计算除法在小学三年级,学生已经开始学习除法运算。
为了进行快速计算除法,学生需要熟悉乘法和除法之间的关系。
例如,学生可以通过将除法问题转化为乘法问题来进行计算。
另外,学生还需要熟悉常见的除法口诀,如9除以任意数的口诀。
3.快速计算加法与减法在小学三年级,学生已经开始学习加法和减法运算。
为了进行速算和巧算,学生可以借助一些技巧。
例如,学生可以利用补数进行计算,将加法问题转化为减法问题或将减法问题转化为加法问题。
另外,在计算的过程中,学生还可以利用进位和借位的方法简化计算的步骤。
4.快速计算小数在小学三年级,学生已经开始学习小数的运算。
为了进行快速计算小数,学生需要熟悉小数的基本概念,如小数点的意义和小数的大小比较。
另外,在计算小数的过程中,学生还可以利用近似计算和适当舍入的方法简化计算的步骤。
5.快速计算整数问题在小学三年级,学生已经开始学习整数的运算。
为了进行速算和巧算,学生需要熟悉整数的基本概念,如正数、负数和零的概念。
另外,在计算整数的过程中,学生还可以利用相反数的概念简化计算的步骤。
6.快速计算组合问题在小学三年级,学生已经开始学习组合的概念。
为了进行快速计算组合问题,学生需要熟悉排列组合的基本原理,如乘法原理和加法原理。
另外,在计算组合的过程中,学生还可以利用化简问题和分类讨论的方法简化计算的步骤。
7.快速计算面积和周长问题在小学三年级,学生已经开始学习面积和周长的计算。
为了进行速算和巧算,学生需要熟悉面积和周长的基本公式,如长方形的面积和周长的计算公式。
另外,在计算面积和周长的过程中,学生还可以利用化简问题和近似计算的方法简化计算的步骤。
三年级奥数速算巧算经典题目

三年级奥数速算巧算经典题目一、加法中的速算巧算1. 凑整法题目:计算199 + 298+397 + 496。
解析:把199看作200 1,298看作300 2,397看作400 3,496看作500 4。
原式=(200 1)+(300 2)+(400 3)+(500 4)去括号得:200 1+300 2 + 400 3+500 4重新组合:(200+300 + 400+500)-(1 + 2+3+4)先计算括号里的数,200+300+400 + 500 = 1400,1+2+3+4 = 10。
所以结果为1400 10 = 1390。
2. 带符号搬家题目:计算134 + 297 34。
解析:根据带符号搬家的原则,把+297和 34的位置交换。
原式=134 34+297先计算134 34 = 100,再计算100+297 = 397。
二、减法中的速算巧算1. 凑整法题目:计算472 97。
解析:把97看作100 3。
原式=472-(100 3)去括号得:472 100+3先计算472 100 = 372,再计算372+3 = 375。
2. 一个数连续减去几个数题目:计算568 123 77。
解析:根据一个数连续减去几个数等于这个数减去这几个数的和。
原式=568-(123 + 77)先计算123+77 = 200,再计算568 200 = 368。
三、乘法中的速算巧算1. 乘法分配律题目:计算25×(40 + 4)。
解析:根据乘法分配律a×(b + c)=a×b+a×c。
这里a = 25,b = 40,c = 4。
原式=25×40+25×425×40 = 1000,25×4 = 100。
所以结果为1000+100 = 1100。
2. 乘法结合律题目:计算25×125×4×8。
解析:根据乘法结合律(a×b)×(c×d)=(a×c)×(b×d)。
三年级奥数速算、巧算方法及习题
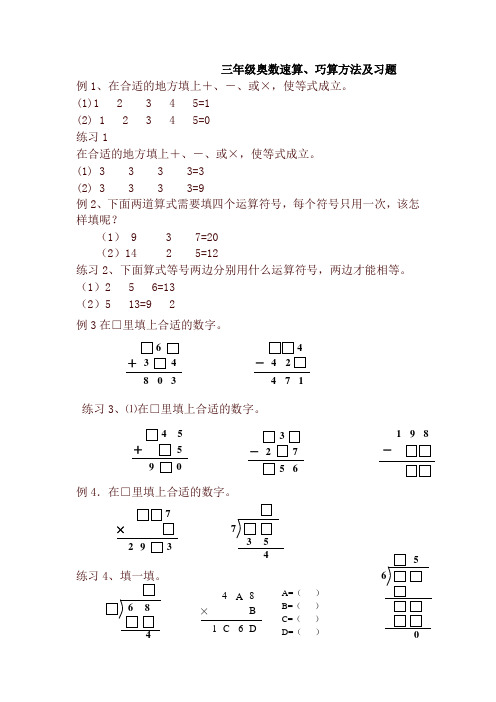
三年级奥数速算、巧算方法及习题例1、在合适的地方填上+、-、或×,使等式成立。
(1)1 2 3 4 5=1 (2) 1 2 3 4 5=0 练习1在合适的地方填上+、-、或×,使等式成立。
(1) 3 3 3 3=3 (2) 3 3 3 3=9例2、下面两道算式需要填四个运算符号,每个符号只用一次,该怎样填呢?(1) 9 3 7=20 (2)14 2 5=12练习2、下面算式等号两边分别用什么运算符号,两边才能相等。
(1)2 5 6=13 (2)5 13=9 2例3在□里填上合适的数字。
练习3、⑴在□里填上合适的数字。
例4.在□里填上合适的数字。
练习4、填一填。
4- 44 7 1+ 3648 0 34 +5 9 54427× 93 1 8×C D4 A B 6 A=( ) B=( ) C=( ) D=( )3- 275 689 - 1课后练习1、在相同的图形里填上相同的整十数,使等式成立。
×3=1 ×6=2 ×6=42、在下面的方格里填上合适的数字,使它横看成为两道算式,竖看成为五个成语。
3、把1~9这9个数字分别填入下面的○中,正好组成一道算式。
4、把494、495、496、497、498、499、501、502、503、504、505、506这十二个数分别填入下面的方格中,使等式成立。
(每个数只能用一次)5、在同样的图形中填入同样的数字。
6、在数字之间填上合适的运算符号或括号,使等式成立。
□÷□×□ + □=□(□+□-□)×□=□上 下面 方生 死花 门 拿 稳+3 14 6+=+==+ ==++ = +仔细观察这些数!8 8+ - 4 9 5 找准入手点!(1)1 2 3 4=1(2)1 1 1 1=1(3)5 5 5 5=15(4)5 5 5 5=25(5)1 2 3 4 5 6 =127、算式8×5-42÷7+25,计算时()可以同时计算。
小学三年级奥数万以内加减法的速算与巧算

加、减法的速算与巧算知识要点:“凑整”先计算,认真审题,灵活分组。
两个数相加,若能恰好凑成整十、整百、整千、整万...则先计算。
如: 1+9=10,3+7=10,2+8=10,4+6=10,5+5=10。
又如:12+88=100,35+65=100,21+79=100,44+56=100,55+45=100。
在上面算式中,1叫9的“补数”;79叫21的“补数”,44也叫56的“补数”,也就是说两个数互为“补数”。
对于不能直接凑整的数,可以把其中一个数拆分后再凑整。
找基准数几个相接近的数相加,可以用找基准数法,进行移多补少计算。
找基准数的方法:整十、整百、整千等等。
本节课需要掌握:移数凑整法,拆数凑整法,借数凑整法,分组凑整法。
例1:换位凑整,快速计算。
(提示:看个位凑整,巧用小括号)(1)34+53+66 (2)679+27+321 (3)63+294+37+54+9 =34+66+53 =679+321+27 =63+37+(294+6)+3+54 =100+53 =1000+27 =100+300+3+54=153 =1027 =457练习1:(1)491+273+209+27 (2)882+356+18+55+44 (3)49+38+51+62+162+38 =1000 =1355 =400拓展题:(提示:巧用小括号,移数凑整法)(1350+249+468)+(251+332+1650)=1350+1650+(249+251)+(468+332)=3000+500+800=4300(2549+385+739)+(61+15+451)=4200例2: 先观察,再速算。
199999+19999+1999+199+19法1:拆数凑整法=(200000-1)+(20000-1)+(2000-1)+(200-1)+(20-1)= 200000+20000+2000+200+20-(1+1+1+1+1)=222220-5=222215法2:借数凑整法=199999+19999+1999+199+15+1+1+1+1=200000+20000+2000+200+15=222215练习2:28+208+2008+20008+200008=28+200+8+2000+8+20000+8+200000+8=200000+20000+2000+200+20+(8+8+8+8+8)=222220+40=222260例3:先观察,再速算。
三年级奥数乘法速算与巧算

乘法速算与巧算乘法的速算与巧算前面我们已经学习了加、减法中的巧算,大家学会了运用“凑整”的方法进行计算,实际上这种凑整的方法也同样可以运用在乘除计算中。
为了更好地凑整,要牢记以下几对补数:乘法中常用的三对补数:2×5=10,4×25=100,8×125=1000在乘法的巧算中,经常要用到一些运算定律,例如乘法交换律、乘法结合律、乘法分配律等等,善于运用运算定律,是提高巧算能力的关键。
乘法交换律:b c a c b a ⨯⨯=⨯⨯乘法结合律:)()(c b a c b a ⨯⨯=⨯⨯乘法分配律:c a b a c b a ⨯±⨯=±⨯)(乘法分配律的反用:)(c b a c a b a ±⨯=⨯±⨯乘法分配律在除法中的应用:a c b a c a b ÷±=÷±÷)(除法的性质:a ÷(b ×c)=a ÷b ÷c乘除混合运算中还可以利用倍数关系巧算,涉及到去括号和添括号。
在乘法的巧算中同样会用到三个技巧:补数先算、凑整再算、拆数凑整补数先算:2×54×258×125常用的补数要记得:2×5=104×25=1008×125=1000凑整再算:99=100-1102=100+2在做乘除法巧算时,要运用这些规律,先凑整得出10、100、1000……再进行简便计算。
拆数凑整:4=2×2、8=2×4、12=4×3、16=4×4、24=6×4、32=8×4、28=4×7……例题1:简便计算下列各题。
(1)25×17×4(2)125×77×8练习1:(1)5×41×2(2)8×18×125(3)8×25×4×125(4)125×25×8×5×2×4例题2:简便计算下列各题(1)125×32(2)25×48(3)5×25×16(4)5×25×125×64练习2:简便计算下列各题(1)125×56(2)25×5×32(3)45×25×2×4(4)125×25×72×4例题3:简算下列各题。
巧算与速算小学三年级奥数题及详解

巧算与速算小学三年级奥数题及详解
巧算与速算小学三年级奥数题及详解
巧算与速算试题:
41×49=
详解:
相乘的两个数都是两位数,且十位上的数字相同,个位上的数字之和正好是10,这就可以运用“头同尾合十”的巧算法进行简便计算。
“头同尾合十”的巧算方法是:用十位上的数字乘十位上的数字加1的积,再乘100,最后加上个位上2个数字的乘积。
41×49,先用(4+1)×4=20,将20作为积的前两位数字,再用1×9=9,可以发现末位数字相乘的'积是一位数,那就在9的前面补一个0,作为积的后两位数字。
这样答案很简单的就求出了,即41×49=(4+1)×4×100+1×9=2009。
科学的学习方法和合理的复习资料能帮助大家更好的学好数学这门课程。
希望为大家准备的奥数题及答案巧算与速算,对大家有所帮助!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1讲速算与巧算专题简析:
在进行加减运算时,除了要熟练地掌握计算法则外,还需要掌握一些巧算的方法。
加减法的巧算主要是运用“凑整”的方法,把接近整十、整百、整千.......的数看作所接近的整数进行简算。
进行加减巧算时,凑整之后,对于原数与整十、整百、整千......相差的数,要根据“多加要再加,多减要再减”的原则进行处理。
另外可以结合加法交换律、加法结合律以及减法的性质进行凑整,从而达到简算的目的。
知识点、重点、难点:
1、加法的简便运算:
(1)A+B=B+A(加法交换律)
(2)(A+B)+C=A+(B+C)(加法结合律)
2、减法的简便运算:
(1)A-B-C=A-(B+C)
(2)A-B+C=A-(B-C)
注意:加减法同级运算,括号外面是减号的,添上或去掉括号,括号里的符号:加号要变成减号、减号要变成加号。
当所有括号都去掉后,可以将数与前面的符号一起移动,第一个数前面为加号。
王牌例题1
在小学奥数中计算中,凑整是一种方法,更是一种解题思想。
凑整只是手段,简算才是目的。
凑整法:
1、你有好方法迅速算出下面各题的结果吗?
(1)23+45+67=(2)25+53+75+78+47=
(3)872+284-272=(4)537-142-58=
思路导航:先把加在一起为整十、整百、整千......的数相加,再与其他数相加。
举一反三1
用简便方法计算下面各题。
1、(1)487+321+113+479=(2)723-251+177=
(3)773+368+227=(4)34+47+53+66=
2、(1)89+123+11+177=(2)235-125+65=
(3)483+254-183=(4)271+97-171=
(5)425-172-28=
王牌例题2
你有好办法迅速算出下面各题的结果吗?
(1)199+74(2)347+102
(3)784-297(4)1384-501
思路导航:计算时,先将接近整十、整百、整千的数看作整十、整百、整千来计算,对于原数与整十、整百、整千......相差的数,要根据“多加要再加,多减要再减”的原则进行处理。
比如:(1)计算199+74时,把199看作200来计算比较简便,这样计算的结果就比原来多1,再减去多加的1就能得到正确的结果。
举一反三2
1、简便计算
(1)398+64(2)336+502
(3)876-198(4)2825-1003
2、想一想,怎样计算最简便。
(1)903+297(2)903-297
3、你有好办法迅速算出下题的结果吗?
502+499-398-97
王牌例题3(基准法)
简便运算
(1)83+78+80+77+84+79(2)9999+999+99+9
思路导航:(1)这道题的六个加数都接近80,先把它们看作80来计算,这样计算结果就是80x6=480,然后把少算的“零头”数加上,把多算的“零头”数减去,这样计算比较简便。
举一反三3
用简便方法计算下面各题的和。
(1)42+38+45+39+41+37
(2)66+57+65+53+60+59+62
(3)1999+199+19
王牌例题4
计算下面各题。
(1)372-(54+72)(2)432-(154-68)
(3)321+(279-155)
思路导航:通过减法的运算法则来计算,括号外面是减号的,添上或去掉括号,括号里的符号:加号要变成减号、减号要变成加号。
举一反三4
用简便方法计算下面各题。
(1)421+(179-125)(2)375+(125-47)
(3)523-(175+123)(4)785-(231+285)
三年级数学课课练拓展题
1、红豆和蓝豆共有50本练习本,红豆的练习本比蓝豆的2倍多2本。
红豆和蓝豆各有几本练习本?
2、有两盘苹果共有25个,其中一盘比另一盘多7个,问两盘各有多少个苹果?
数学小趣味:
定理:喝醉的酒鬼总能找到回家的路,喝醉的小鸟则可能永远也回不了家。
假设有一条水平直线,从某个位置出发,每次有50%的概率向左走1米,有50%的概率向右走1米。
按照这种方式无限地随机游走下去,最终能回到出发点的概率是多少?
答案是100%。
在一维随机游走过程中,只要时间足够长,我们最终总能回到出发点。
现在考虑一个喝醉的酒鬼,他在街道上随机游走。
假设整个城市的街道呈网格状分布,酒鬼每走到一个十字路口,都会概率均等地选择一条路(包括自己来时的那条路)继续走下去。
那么他最终能够回到出发点的概率是多少呢?答案也还是100%。
刚开始,这个醉鬼可能会越走越远,但最后他总能找到回家路。
不过,醉酒的小鸟就没有这么幸运了。
假如一只小鸟飞行时,每次都从上、下、左、右、前、后中概率均等地选择一个方向,那么它很有可能永远也回不到出发点了。
事实上,在三维网格中随机游走,最终能回到出发点的概率只有大约34%。
这个定理是着名数学家波利亚(GeorgePólya)在1921年证明的。
随着维度的增加,回到出发点的概率将变得越来越低。
在四维网格中随机游走,最终能回到出发点的概率是19.3%,而在八维空间中,这个概率只有7.3%。
