矩阵的秩及其求法-求秩的技巧
矩阵求秩方法

矩阵求秩方法
求矩阵的秩是线性代数中常见的问题,以下是关于矩阵求秩的10条方法及其详细描述:
1. 奇异值分解法:通过对矩阵进行奇异值分解,将矩阵变换为一个对角矩阵,其中非零元素的个数即为矩阵的秩。
2. 初等变换法:利用矩阵的初等行(列)变换,将矩阵化简为行简化阶梯型矩阵,其中非零行的个数即为矩阵的秩。
3. 极大线性无关组法:通过逐步选择矩阵中的列,构建一个极大线性无关组,其中向量的个数即为矩阵的秩。
4. 秩-零空间法:矩阵的秩与其零空间的维数之和为矩阵的列数。
可以通过计算矩阵的零空间 (null space) 的维数来求解矩阵的秩。
5. 行列式法:矩阵的行列式非零的最大子阵的阶数就是矩阵的秩。
6. 直接检验法:将矩阵转换为梯形矩阵或行阶梯矩阵,其中非零行的个数即为矩阵的秩。
7. 特征值法:矩阵的秩等于其特征值不为零的个数。
8. 与单位矩阵求秩法:通过将矩阵与单位矩阵进行连接,得到一个增广矩阵,进而将其化简为行简化阶梯型矩阵,其中非零行的个数即为矩阵的秩。
9. Gauss-Jordan消元法:通过高斯消元法和高斯约当消元法将矩阵化简为行简化阶梯型矩阵,其中非零行的个数即为矩阵的秩。
10. 极大线性无关组与生成组比较法:利用极大线性无关组与生成组的关系来求解矩阵的秩,其中生成组的个数等于矩阵的秩。
线性代数:矩阵秩的求法

6/44
定理 Ax=0 的解的情况:
1.Ax=0 有非零解 r(A)<n 只有零解 r(A)=n
2.若A是方阵,Ax 0有非零解 A 0 只有零解 A 0
3.Ax 0,若m n,则一定有非零解。 m :方程个数 n :未知量个数
k
2
1 2
0
3 2
1
.
其中k1
,
k
为任意常数。
2
12/44
定理 3 线性方程组 Ax=b 有解 r(A)=r(Ab)
定理 4 设线性方程组 Ax=b 有解。 若A为方阵,
如果 r(A)=n,则它有唯一解; A 0,唯一解
如果
r(A)<n,则它有无穷多解。
A
0,无穷解
13/44
x1 x2 a1
a4
x5 x1 a5
RA RB
5
ai 0
i 1
15/44
5
方程组有解的充要条件是 ai 0.
i 1
x1 x2 a1
由于原方程组等价于方程组
x2 x3
x3 x4
a2 a3
例4
证明方
程组
x2 x3
x3 x4
a2 a3
x4
x5
a4
x5 x1 a5
有解的充要条件
是a1 a2 a3 a4 a5 0.在有解的情况下,
求出它的一切解.
解证 对增广矩阵B进行初等变换, 方程组的增广矩阵为
14/44
1 1 0 0 0 a1
0 1 1 0 0 a2
第十-十一次
2.5 矩阵的秩及其求法

求 R( A).
1 0 2 −4 1 0 2 −4 −4 → 0 1 −1 2 r 2r , 解 A 2 − 0 1 −1 2 r1 → r3 + 1 0 −1 1 − 2 0 0 0 0
R(A) = 2
13
1 −1 1 2 例5 设A = 3 λ −1 2, 且R(A) 2 = ,求λ, µ 5 3 µ 6
∴ R( A) = 3
A为满秩方阵。
19
若求A 若求 的标准型矩阵
1 − 2 1 − 4 0 −1 −1 3 → 0 0 1 9 0 0 0 0
2 1 1 0 →0 2 0 0
0 −1 2 1 0 0
4 0 12 3 1 9 2 0 0 0
矩阵A 的第一、三行,第二、四列相交处的元素 所构成的二阶子式为
2 −1 D2 = 0 −1
3 5 为 A 的一个三阶子式。
而
1 2 D3 = 4 6
1 0 −1
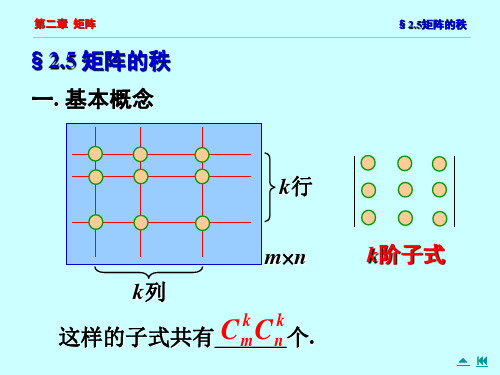
k k m× n 矩阵 A 共有 cmcn 个 k 阶子式。 显然,
4
设
A = (aij )m×n 当 A=0 时,它的任何子式都为零。
⑤ R(AB)≤ min{R(A),R(B)} ⑥ 若 Am×nBn×s=0,则 R(A)+R(B)≤n
24
例8
设A为n阶矩阵,证明R(A+E)+R(A-E)≥n 证: ∴ 而 ∴ ∵ (A+E)+(E-A)=2E r(A+E)+ r( E-A )≥ r(2E)=n r( E-A )= r( A-E ) r(A+E)+r(A-E)≥n
7
矩阵秩的求法 二、矩阵秩的求法 1、子式判别法 定义 。 、子式判别法(定义 定义)。
矩阵的秩求法

4 3 9 12
1 1 7 8
4 1 11 12
上页 下页
返回
1 0 0 0
6 4 12 16
4 3 9 12
1 1 7 8
4 1 11 12
1 r3 3r2 0 ~ 0 r4 4r2 0
6 4 0 0
4 3 0 0
1 1 4 4
4 1 8 8
上页 下页
返回
1 0 0 0 1 r4 3r3 0 ~ 0 0
6 4 0 0 6 4 0 0
4 3 0 0 4 3 0 0
1 1 4 4 1 1 4 0
2 0 0 1 3 0 3 2 24 0, 4
因此R(B)= 3 。
上页 下页 返回
从本例可知,由矩阵A 的秩的定义求秩,关键在 于找 A 中不等于 0 的子式的最高阶数。 一般当行数与列数都较高时,按定义求秩是很麻 烦的。 对于行阶梯形矩阵,显然它的秩就等于非零行的 行数。 因此自然想到用初等变换把矩阵化为行阶梯形矩 阵,但两个等价的矩阵的秩是否相等呢?
上页 下页 下页 返回 上页
2.6-矩阵的秩
1 0 5 1 0 5 1 0 5 1 0 0
E(1, 3(5)) = 0 1 0 , 0 1 0 0 1 0 = 0 1 0 .
00 1 001 00 1 001
第二章 矩阵
§2.6 方阵的逆矩阵
2. 可逆矩阵的分解
***
(1) * * *
** * ***
***
= ***
10 0
010.
000 *** 000 001
第二章 矩阵
2 0 4 1
0 1 3 2 的3阶子式有14个:
4 0 8 2
§2.5矩阵的秩
2 0 4 2 0 1 2 4 1 0 4 1
0 1 3 = 0 1 2 = 0 3 2 = 1 3 2 = 0. 4 0 8 4 0 2 4 8 2 0 8 2
第二章 矩阵
§2.5矩阵的秩
问题: 假若一个56的矩阵中所有3阶子式都等
1 0
0 1
3/2 1
3 1
5/2 1
1 3 2 故A1 = 3/2 3 5/2 .
1 1 1
第二章 矩阵
§2.6 方阵的逆矩阵
三. 用初等变换解矩阵方程
设A可逆, 则A可以经过有限次初等行变换化为 行最简形——单位矩阵E.
下面用初等变换解矩阵方程AX = B. 注意到X = A1B.
(A B) … (E ?)
第二章 矩阵
§2.5 矩阵的秩
定理2. 设A是满秩方阵,则存在初等方阵
P1, P2, , Ps. 使得 Ps Ps1 , P2P1A E
第二章 矩阵
§2.5 矩阵的秩
定理3. mn矩阵A, m阶初等矩阵
P1, P2, …, Ps 及m阶初等矩阵
矩阵的秩及其求法矩阵秩求法演示文稿

5 3 6
0
8
5
4
1 1 1 2
0 3 4 4 0 5 1 0
R(A) 2, 5 0, 1 0
5, 1
三、满秩矩阵 定义3 A 为 n 阶方阵时,
RA n, 称 A 是满秩阵,(非奇异矩阵)
RA n, 称 A 是降秩阵,(奇异矩阵) 可见:RA n A 0
RA n A ~ E
RA n A ~ En
例如 1 A 2 3
2 1 1
3 2 2
1 0 0
2 3 2
3 1 4 0 3 0
0 1 2
0 1 3
1 0 0
0 0
1 0 E 0 1
RA 3
A为满秩方阵。
关于矩阵的秩的一些重要结论:
定理5
R(AB) R(A), R(AB) R(B),即
对于满秩方阵A施行初等行变换可以化为单位阵E, 又根据初等阵的作用:每对A施行一次初等行变换, 相当于用一个对应的初等阵左乘A, 由此得到下面的 定理
定理3 设A是满秩方阵,则存在初等方阵
P1, P2,, Ps. 使得 Ps Ps1 , P2P1A E
对于满秩矩阵A,它的行最简形是 n 阶单位阵 E .
2 1 所构成的二阶子式为 D2 0 1
12 3 而 D3 4 6 5 为 A 的一个三阶子式。
1 0 1
显然, m n 矩阵 A 共有 cmk cnk 个 k 阶子式。
2. 矩阵的秩
定义2 设 A aij mn ,有r 阶子式不为0,任何r+1阶
子式(如果存在的话)全为0 , 称r为矩阵A的秩,
0 1
2 3
4 6
求 RA.
1 1 1 2
线性代数-矩阵的秩

设A
=
2 −2 3
−4 4 −6
8 −2 0
−036 , b
=
2 43
求矩阵A及矩阵B = ( A b)的秩. 解 分析:设 B 的行阶梯形矩阵为 B~ = ( A~,b~),
则 A~ 就是 A 的行阶梯形矩阵, 故从 B~ = ( A~,b~) 中可同时看出 R( A) 及 R(B).
1 − 2 2 − 1 1
故 R(AT A) = R(A).
又由于 B 也可经一次初等变换变为 A, 故也有 R(B) ≤ R( A).
因此 R( A) = R(B).
经一次初等行变换矩阵的秩不变,即可知经 有限次初等行变换矩阵的秩仍不变.
设A经初等列变换变为 B,也有R( A) = R(B).
设 A 经初等列变换变为 B, 则 AT 经初等行变换变为 BT , R( AT ) = R(BT ),
6 11
则这个子式便是A 的一个最高阶非零子式.
设 n 阶可逆矩阵 A, A ≠ 0, ∴ A 的最高阶非零子式为 A, R( A) = n, 故 A 的标准形为单位阵 E, A ~ E.
可逆矩阵的秩等于阶数 ,故称可逆矩阵 为满秩矩阵. 奇异矩阵为降秩矩阵 .
1 − 2 2 − 1 1
例5
− 2 0 1 5
解
13 02 −2 0
1 0
3 = 2 ≠ 0, 2
计算A的3阶子式,
−2
1 3 2 1 −2 2
− 1 = 0, 0 2 3 = 0, 0 − 1 3 = 0,
1
−2 0 5 −2 1 5
3 −2 2
2 − 1 3 = 0, ∴ R(A) = 2.
015
1 3 − 2 2 另解 对矩阵 A = 0 2 − 1 3 做初等变换,
求矩阵的秩的三种方法

求矩阵的秩的三种方法矩阵是线性代数中的一个重要概念,它由一个数域中的矩形阵列组成,是线性变换的一种表现形式。
矩阵的秩是矩阵的重要性质之一,它可以告诉我们矩阵中行向量或列向量之间的关系。
在实际应用中,求解矩阵的秩是非常常见的问题。
本文将介绍矩阵的三种求解秩的方法。
方法一:高斯消元法高斯消元法是求解矩阵秩的一种基础方法。
对于一个矩阵A,如果它的秩为r,则A必然存在一个大小为r的非零行列式。
我们可以通过对矩阵A进行初等行变换将矩阵转化为行简化阶梯矩阵,然后统计矩阵中非零行的个数来确定矩阵的秩。
具体步骤如下:1. 对矩阵A进行高斯列变换,将A转化为行简化阶梯矩阵形式。
2. 统计矩阵中非零行的个数,即为矩阵的秩。
对于下面的矩阵A,我们可以通过高斯消元法求解矩阵的秩:$$A=\begin{bmatrix}1 &2 & 3\\4 &5 & 6\\7 & 8 & 9\end{bmatrix}$$按照高斯消元法的步骤对A进行初等行变换,得到行简化阶梯矩阵:方法二:矩阵的列空间对于一个矩阵A,其列空间是由A中所有列向量所张成的向量空间。
矩阵的秩等于它的列空间的维度。
我们可以先求解矩阵A的列空间的维度,然后确定矩阵A的秩。
具体步骤如下:2. 取矩阵A中与非零列对应的列向量,将它们作为张成列空间的一组基。
3. 求解列空间的维度,即为矩阵A的秩。
阶梯矩阵中非零列的位置分别是1和2,因此取A中的第1列和第2列作为列空间的一组基。
可以看出,这组基中存在一个线性关系:第2列 = 2*第1列。
矩阵A的列空间实际上只由A中的第1列张成,其维度为1,因此矩阵A的秩为1。
总结:本文介绍了求解矩阵秩的三种方法:高斯消元法、矩阵的列空间和矩阵的行空间。
对于一般的矩阵,三种方法的求解结果并不一定相同。
但无论采用哪种方法,都能够有效地求解矩阵的秩。
还有一些特殊的矩阵,它们的秩具有一些特殊性质:1. 对于一个n阶矩阵A,如果它是一个可逆矩阵,那么它的秩为n。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五节:矩阵的秩及其求法之迟辟智美创作
一、矩阵秩的概念 1. k 阶子式 界说1 设 在A 中任取k 行k 列交叉处元素按原相对
位置组成的
阶行列式,称为A 的一个k 阶子式.
例如共有个二阶子式,有 个三阶子式
矩阵 A 的第一、三行,第二、四列相交处的元素所构成的二阶子式为 而
为 A 的一个三阶子式.显然, 矩阵 A 共有 个k 阶子式. 2. 矩阵的秩
界说2 设 有r 阶子式不为0,任何r +1阶子式(如果存在的话)全为0 ,称r 为矩阵A 的秩,记作R (A )或秩(A ).
规定: 零矩阵的秩为 0 .
注意:(1) 如 R ( A ) = r ,则 A 中至少有一个 r 阶子式
所有 r + 1 阶子式为 0,且更高阶子式均为 0,r 是 A 中不为零的子式的最高阶数,是唯一的 .
(2) 有行列式的性质,
(3) R(A ) ≤m , R (A ) ≤n , 0 ≤R (A ) ≤min { m , n } .
(4) 如果An ×n , 且 则 R ( A ) = n .反之,如 R ( A ) = n ,则
()
n
m ij a A ⨯={})
,min 1(n m k k ≤≤4
3
334=C C 1
015
643
213-=D n
m ⨯()
n
m ij
a A ⨯=0,
r D ≠()().
T R A R A =0,A ≠0.
A ≠
因此,方阵 A 可逆的充沛需要条件是 R ( A ) = n . 二、矩阵秩的求法 1、子式判别法(界说).
例1 设 为阶梯形矩阵,求R (B ).
解 由于 存在一个二阶子式不为0,而任何三阶子式全为0,则R (B ) = 2.
结论:阶梯形矩阵的秩=台阶数.
例如
一般地,行阶梯形矩阵的秩即是其“台阶数”——非零行的行数. 例2 设 如果 求
a .
解 或
例3
则
2、用初等变换法求矩阵的秩
定理2矩阵初等变换不改变矩阵的秩. 即则
注: 只改变子行列式的符号. 是 A 中对应子式的k 倍.
是行列式运算的性质.
0202
1≠⎪⎪⎪⎭⎫ ⎝⎛=010*********A ⎪⎪⎪⎭⎫ ⎝⎛=001021B ⎪⎪⎪⎭
⎫ ⎝⎛=100010011C 125034000D ⎛⎫ ⎪
= ⎪ ⎪⎝⎭212350815300072000
0E ⎛⎫ ⎪
⎪= ⎪ ⎪⎝⎭
⎪⎪⎪
⎭
⎫ ⎝⎛=a a a A 111111(),3<A R ()3
<A R 1=∴a 2
-=a ()3
=A R =K 3
-B
A →)
()(B R A R =j i r r ↔.1i r k .2j i kr r +.3
求矩阵A 的秩方法:
1)利用初等行变换化矩阵A 为阶梯形矩阵B 2)数阶梯形矩阵B 非零行的行数即为矩阵A 的秩.
例4求 解
R(A ) = 2
例
5
三、满秩矩阵
界说3A 为n 阶方阵时,
称 A 是满秩阵,(非奇异矩阵)
称 A 是降秩阵,(奇异矩阵)
可见:
对满秩方阵A 施行初等行变换可以化为单元阵E ,又根据初等阵的作用:每对A 施行一次初等行变换,相当于用一个对应的初等阵左乘A,由此获得下面的定理. 定理3设A 是满秩方阵,则存在初等方阵 使得
对满秩矩阵A ,它的行最简形是n 阶单元阵 E . 例如
A 为满秩方阵.
关于矩阵的秩的一些重要结论:
定理5R (AB )R (A ),R (AB )R (B ),即R (AB )min{R (A ),R (B )}
().
A R μλμλ
,2,63
521321
1
1,求)(且设=⎪⎪⎪
⎭
⎫ ⎝
⎛--=A R A (),
n A R =(),n A R <()0
≠⇔=A n A R E
A P P P P s s =-121, ≤
设A 是 矩阵,B 是 矩阵, 性质1
性质2 如果 A B = 0 则
性质3 如果 R (A )= n, 如果A B = 0 则 B = 0. 性质4 设A,B 均为矩阵,则
例8 设A 为n 阶矩阵,证明R (A+E )+R (A-E )≥n 证: ∵ (A+E )+(E-A )=2E
∴R (A+E )+ R ( E-A )≥ R (2E )=n
而 R ( E-A )=R ( A-E ) ∴ R (A+E )+R (A-E )≥n
n
m ⨯t
n ⨯).
()()(AB R n B R A R ≤-+.
)()(n B R A R ≤+n
m ⨯).
()()(B R A R B A R +≤±。
