2015年清华自主选拔数学试题及答案
清华大学自主招生数学试题解析
清华大学自主招生数学试题解析一、引言近年来，自主招生考试逐渐成为高等教育选拔的重要方式之一。
作为中国顶尖的学府之一，清华大学在自主招生中具有极高的影响力和标准制定地位。
数学作为基础学科，是清华大学自主招生考试的重要科目。
本文将对清华大学自主招生数学试题进行解析，探讨其考察内容、特点及应对策略。
二、考察内容1、基础知识：清华大学自主招生数学试题中，基础知识考察占据较大比例。
包括但不限于高中数学中的函数、数列、三角函数、概率与统计等。
2、知识运用：除了基础知识外，试题还注重考察考生对数学知识的运用能力。
例如，通过实际应用题或几何题的形式，要求考生运用数学知识解决实际问题。
3、思维能力：清华大学自主招生数学试题注重考察考生的思维能力，包括逻辑推理、归纳分类、化归等能力。
这类题目通常需要考生灵活运用数学知识，通过猜想、归纳、推理等方式寻找解题思路。
4、创新精神：自主招生数学试题还注重考察考生的创新精神和实践能力。
这类题目通常以开放式问题的形式出现，要求考生从不同角度思考问题，寻找独特的解题方法。
三、特点分析1、覆盖面广：清华大学自主招生数学试题涉及的知识面较广，要求考生具备扎实的数学基础和广泛的知识储备。
2、难度适中：试题难度适中，既考察了考生的基础知识，又对其思维能力、创新能力进行了充分挑战。
3、突出重点：试题突出对重点知识的考察，如函数与方程、数列与不等式、平面几何等，要求考生对重点知识有深入理解和掌握。
4、强调应用：试题强调对数学知识的应用能力，通过设置实际应用题等方式，引导考生数学在实际生活中的应用价值。
四、应对策略1、巩固基础知识：针对清华大学自主招生数学试题中基础知识的考察，考生应注重巩固高中阶段的基础知识，尤其是函数、数列、三角函数等重点内容。
2、提高运用能力：在掌握基础知识的前提下，考生应注重提高对数学知识的运用能力。
通过练习实际应用题、几何题等类型，提高解决实际问题的能力。
3、培养思维能力：考生应在平时的学习中注重培养逻辑推理、归纳分类、化归等思维能力。
2015清华大学金秋营数学试题及其解答(2)
2015清华大学金秋营数学试题及其解答 (2)(2)" title="2015清华大学金秋营数学试题及其解答(2)" action-data="http%3A%2F%%2Fmw690 %2F001omMDwzy6WiczvzFdbf%26690"action-type="show-slide">(2)" title="2015清华大学金秋营数学试题及其解答(2)">(2)" title="2015清华大学金秋营数学试题及其解答(2)" style="max-width: 650px;">2015年华中科技大学理科实验班选拔数学试题(2)" title="2015清华大学金秋营数学试题及其解答(2)" style="max-width: 650px;">(2)" title="2015清华大学金秋营数学试题及其解答(2)" style="max-width: 650px;">(2)" title="2015清华大学金秋营数学试题及其解答(2)"style="max-width: 650px;">(2)" title="2015清华大学金秋营数学试题及其解答(2)" style="max-width: 650px;">2014年华中科技大学理科实验班选拔试题—数学(2)" title="2015清华大学金秋营数学试题及其解答(2)"style="max-width: 650px;">(2)" title="2015清华大学金秋营数学试题及其解答(2)" style="max-width: 650px;">(2)"title="2015清华大学金秋营数学试题及其解答(2)"style="max-width: 650px;">(2)" title="2015清华大学金秋营数学试题及其解答(2)" style="max-width: 650px;">(2)"title="2015清华大学金秋营数学试题及其解答(2)">2015清华大学金秋营试题第1题的解">熊昌进2015清华大学金秋营试题第1题的解2015清华大学金秋营试题第1题的解" title="[转载]熊昌进2015清华大学金秋营试题第1题的解"action-data="/DownloadImg/20 16/08/2419/78630869_13" action-type="show-slide"style="margin: 0px; padding: 0px; list-style: none; text-align: center; display: block;">参考文献:宋庆(2)"href="/s/blog_4c1131020102vvk7.ht ml" target="_blank">2015清华大学金秋营数学试题及其解答(2)作者：sqing55熊昌进2015清华大学金秋营试题第5题的证明(2)" title="2015清华大学金秋营数学试题及其解答(2)">参考文献:宋庆(2)"href="/s/blog_4c1131020102vvk7.ht ml" target="_blank">2015清华大学金秋营数学试题及其解答(2)作者：sqing55熊昌进2015清华大学金秋营试题第4题的解(2)" title="2015清华大学金秋营数学试题及其解答(2)"> (2)" title="2015清华大学金秋营数学试题及其解答(2)">参考文献:宋庆(2)"href="/s/blog_4c1131020102vvk7.ht ml" target="_blank">2015清华大学金秋营数学试题及其解答(2)作者：sqing55(2)" title="2015清华大学金秋营数学试题及其解答(2)" style="max-width: 650px;">(2)"action-data="http%3A%2F%%2Fmw690 %2F001omMDwzy6WfcIpXWP63%26690"action-type="show-slide">。
清华大学高考自主招生领军计划历年面试真题(2015年—2018年)
清华大学高考自主招生领军计划历年面试真题(2015年—2018年)同样，小北也为大家准备了清华近4年的综合评价招生面试真题。
清华也是从2015年才开始在全国范围开展综合评价招生！清华大学2018年领军计划面试题学科面试：1.建筑系：7位考官面试一个学生，不仅考查学生的综合素质，还考查他们对于各省市建筑的理解和表达。
2.数学系：给出4道题目让考生现场在黑板上作答，考官根据考生的解答思路或提问或追问。
清华大学2017年领军计划面试题1.材料阅读：影响你选择大学以及专业志愿的有哪些因素？请列举出来并说明理由。
可以借鉴但不局限于所给三则材料：第一则选择大学更重要还是选择专业更重要，第二则选择专业有哪些影响因素，第三则大学排名，包括US NEWS、泰晤士、QS、软科世界大学排名、毕业生就业力排名等等。
2.对人才培养的看法3.对清华理念的理解清华大学2016年领军计划面试题1.时政题是南京一个母亲盗窃超市为给自己的女儿过儿童节，警察赶到后宽大处理并帮助筹集善款，你怎么看？反映了什么社会问题？2.如果你在清华创立社团，你会创建什么社团？怎样让它发展得更好？3.大学应该无微不至地照顾学生，宽容对待他们的小错误还是应该训练学生适应社会？4.关于考生个人，被问到为什么选择这个专业清华大学2015年领军计划面试题1.你对“中国式过马路”怎么看?2.你对“中国梦”怎么理解?3.2012年度的五大新闻是什么，如果你是新闻评论员，请对这些新闻事件作出评论。
4.你对“钓鱼岛事件”怎么看?清华大学与北大相似，题目涉及范围较广，与经济、社会的各个方面相关。
童鞋们在做好充分准备的同时也要大方主动的展示自己的想法，不要太过于谨慎，甚至羞于表达。
清华大学2015年自主招生数学试题及答案解析
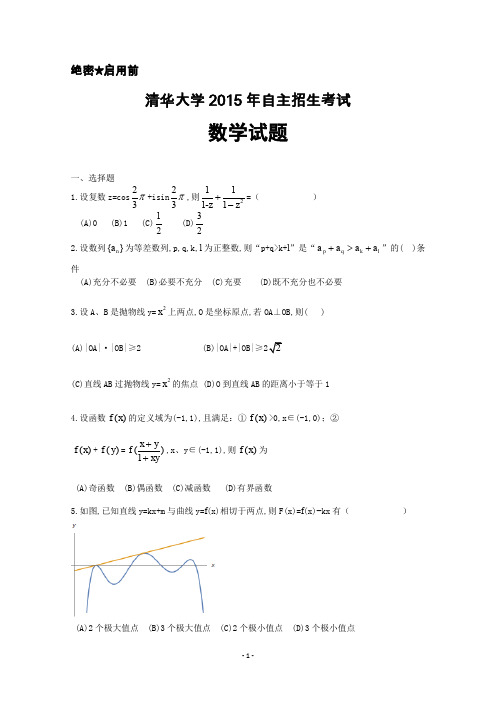
绝密★启用前清华大学2015年自主招生考试数学试题一、选择题1.设复数z=cos 23π+isin 23π,则2111-1z z +-=（ ） (A)0 (B)1 (C)12 (D)32 2.设数列{}n a 为等差数列,p,q,k,l 为正整数,则“p+q>k+l ”是“p q k l a a a a +>+”的( )条件(A)充分不必要 (B)必要不充分 (C)充要 (D)既不充分也不必要3.设A 、B 是抛物线y=2x 上两点,O 是坐标原点,若OA ⊥OB,则( )(A)|OA|·|OB|≥2 (B)|OA|+|OB|≥(C)直线AB 过抛物线y=2x 的焦点 (D)O 到直线AB 的距离小于等于1 4.设函数()f x 的定义域为(-1,1),且满足：①()f x >0,x ∈(-1,0)；②()f x +()f y =()1x y f xy++,x 、y ∈(-1,1),则()f x 为 (A)奇函数 (B)偶函数 (C)减函数 (D)有界函数5.如图,已知直线y=kx+m 与曲线y=f (x)相切于两点,则F(x)=f (x)−kx 有（ ）(A)2个极大值点 (B)3个极大值点 (C)2个极小值点 (D)3个极小值点6.△ABC 的三边分别为a 、b 、c ．若c=2,∠C=3π,且sinC+sin(B −A)−2sin2A=0,则有（ ）(A)b=2a (B)△ABC 的周长为 (C)△ABC (D)△ABC 的外接圆半径为7.设函数2()(3)x f x x e =-,则（ ）(A)()f x 有极小值,但无最小值 (B) ()f x 有极大值,但无最大值(C)若方程()f x =b 恰有一个实根,则b>36e (D)若方程()f x =b 恰有三个不同实根,则0<b<36e 8.已知A={(x,y)∣222x y r +=},B={(x,y)∣222()()x a y b r -+-=,已知A∩B={(11,x y ),(22,x y )},则（ ）(A)0<22a b +<22r (B)1212()(y )0a x x b y -+-=(C)12x x +=a ,12y y +=b (D)22a b +=1122ax by +9.已知非负实数x,y,z 满足22244x y z +++2z=3,则5x+4y+3z 的最小值为（ ）(A)1 (B)2 (C)3 (D)410.设数列{n a }的前n 项和为n S ,若对任意正整数n,总存在正整数m,使得n S =m a ,则（ ）（A ）{n a }可能为等差数列 （B ）{n a }可能为等比数列（C ）{n a }的任意一项均可写成{n a }的两项之差(D)对任意正整数n,总存在正整数m,使得n a =m S11.运动会上,有6名选手参加100米比赛,观众甲猜测：4道或5道的选手得第一名；观众乙猜测：3道的选手不可能得第一名；观众丙猜测：1,2,6道选手中的一位获得第一名；观众丁猜测：4,5,6道的选手都不可能获得第一名．比赛后发现没有并列名次,且甲、乙、丙、丁中只有1人猜对比赛结果,此人是（ ）(A)甲 (B)乙 (C)丙 (D)丁12.长方体ABCD −1111A B C D 中,AB=2,AD=A 1A =1,则A 到平面1A BD 的距离为（ ）。
2015年《高校自主招生考试》数学真题分类解析之9、排列、组合与二项式定理
专题之9、排列、组合与二项式定理一、选择题。
1．(2009年复旦大学)设X是含n(n>2)个元素的集合,A,B是X中的两个互不相交的子集,分别含有m,k(m,k≥1,m+k≤n)个元素,则X中既不包含A也不包含B的子集的个数是A.2n−m+2n−k−2n−m−kB.2n−m−kC.2n−2n−m−2n−k+2n−m−kD.2n+1−2n−m−2n−k+2n−m−k 2．(2009年复旦大学)设有n+1个不同颜色的球,放入n个不同的盒子中,要求每个盒子中至少有一个球,则不同的放法有A.(n+1)!种B.n(n+1)!种C.(n+1)!种D.n(n+1)!种3．(2011年复旦大学)用字母a、b、c组成字长为5个字母的码字,要求每码字中a至多出现2次,b至多出现1次,c至多出现3次,则这种码字的个数是A.50B.52C.60D.62 4．(2011年复旦大学)设平面上有100条直线,其中无两条直线相互平行,无三条直线相交于一点,则这些直线将平面分成块互异的区域.A.5 050B.5 051C.5 052D.5 053 5．(2011年复旦大学)小于1 000的正整数中不能被3和5所整除的整数的个数是A.530B.531C.532D.5336．(2011年复旦大学)从1到100这100个正整数中任取两个不同的整数,要求其和大于100,则取法总数为A.2 450B.2 500C.2 525D.5 050 7．(2012年复旦大学)记2 012!=1×2×3×…×2 012,则2 012!的值的尾部连续的0(从个位往前计数)的个数是A.504B.503C.502D.5018．(2011年同济大学等九校联考)数列{a n}共有11项,a1=0,a11=4,且|a k+1−a k|=1,k=1,2,…,10,满足这种条件的不同数列的个数为A.100B.120C.140D.1609．(2010年清华大学等五校联考)欲将正六边形的各边和各条对角线都染成n 种颜色之一,使得以正六边形的任何3 个顶点作为顶点的三角形有3 种不同颜色的边,并且不同的三角形使用不同的3 色组合,则n 的最小值为A.6B.7C.8D.910．(2012年清华大学等七校联考)红蓝两色车、马、炮棋子各一枚,将这6枚棋子排成一列,其中每对同字的棋子中,均为红棋子在前,蓝棋子在后,满足这个条件的不同排列方式共有A.36种B.60种C.90种D.120种二、解答题。
2015年清华大学数理体验营数学考试试题
n12n i 对于A=(a1,a2,⋯,an)∈Sn,B=(b1,b2,⋯,bn)∈Sn,定义A与B的差为A−B=(|a1−b1|,|a2−b2|,⋯,|an−bn|),且A与B之间的距离为(,)ni id A B a b=∑-2015清华大学数理体验营数学试题解答即可，解得综上所述，若不等式f(x)>0对∀x∈[1,+∞)恒成立，则a的取值范围是(−∞,（2）根据二项分布的计算方式，可得分布列为4、（1）椭圆L 的方程为2212x y +=（2）设A 点坐标为(x 1,y 1)，B 点坐标为(x 2,y 2)，C 点坐标为(x 3,y 3)．由可得由椭圆的焦准性质可知，112+2=2x x λ+，将1211=1x x λ+--代入上式，可得λ1=2x 1+3；同理，1232=2x x λ--，将1321=1x x λ-+代入上式，可得λ2=−2x 1+3． 所以λ1+λ2=6．（3）当直线AC 的方程为x=1时，△F 1AC 的面积S 取到最大值2．5、（1）若∃k ∈N+，使得0<a k ⩽a k+1，则矛盾．所以a n >a n+1(n=1,2,⋯)． （2）显然0<an<1(n=1,2,⋯)，故有所以a n >1/3．由于数列{a n }单调递减有下界，所以n →∞时，数列{a n }的极限存在．设则所以对于任意给定的0<ε<1，总存在正整数m，当n>m时，0<an −13<ϵ．6、(1)d(A−C,B−C)=d(A,B)显然成立．因为(ai−bi)+(bi−ci)+(ci−ai)=0，而(ai−bi)+(bi−ci)+(ci−ai)与|ai−bi|+|bi −ci|+|ci−ai|的奇偶性相同，故d(A,B)+d(A,C)+d(B,C))是偶数．所以d(A,B),d(A,C),d(B,C)三个数中至少有一个是偶数．（2）其中表示P中所有两个元素间距离的总和．设P中所有元素的第i个位置的数字中共有ti 个1，m−ti个0，则（3）S3中含有8个元素，可将其看成正方体的8个顶点．易知集合M中的元素所对应的点，应该两两位于该正方体面对角线的两个端点处．所以集合M={(0,0,0),(1,1,0),(1,0,1),(0,1,1)}，或M={(0,0,1),(0,1,0),(1,0,0),(1,1,1)}．。
2015年《高校自主招生考试》数学真题分类解析之7、解析几何
专题之7、解析几何一、选择题。
1．(2009年复旦大学)设△ABC三条边之比AB∶BC∶CA=3∶2∶4,已知顶点A的坐标是(0,0),B的坐标是(a,b),则C的坐标一定是2．(2009年复旦大学)平面上三条直线x−2y+2=0,x−2=0,x+ky=0,如果这三条直线将平面划分成六个部分,则k可能的取值情况是A.只有唯一值B.可取二个不同值C.可取三个不同值D.可取无穷多个值3．(2010年复旦大学)已知常数k1,k2满足0<k1<k2,k1k2=1.设C1和C2分别是以y=±k1(x−1)+1和y=±k2(x−1)+1为渐近线且通过原点的双曲线,则C1和C2的离心率之比等于5．(2011年复旦大学)A.ρsin θ=1B.ρcos θ=−1C.ρcos θ=1D.ρsin θ=−1 6．(2011年复旦大学)设直线L过点M(2,1),且与抛物线y2=2x相交于A,B两点,满足|MA|=|MB|,即点M(2,1)是A,B的连接线段的中点,则直线L的方程是A.y=x−1B.y=−x+3C.2y=3x−4D.3y=−x+5 7．(2011年复旦大学)设有直线族和椭圆族分别为x=t,y=mt+b(m,b为实数,t为参数)和(a是非零实数),若对于所有的m,直线都与椭圆相交,则a,b应满足A.a2(1−b2)≥1B.a2(1−b2)>1C.a2(1−b2)<1D.a2(1−b2)≤1 8．(2011年复旦大学)极坐标表示的下列曲线中不是圆的是A.ρ2+2ρ(cos θ+sin θ)=5B.ρ2−6ρcos θ−4ρsin θ=0C.ρ2−ρcos θ=1D.ρ2cos 2θ+2ρ(cos θ+sin θ)=19.10.(2012年复旦大学)B.抛物线或双曲C.双曲线或椭圆D.抛物线或椭圆A.圆或直线线11．(2011年同济大学等九校联考)已知抛物线的顶点在原点,焦点在x轴上,△ABC的三个顶点都在抛物线上,且△ABC的重心为抛物线的焦点,若BC边所在直线的方程为4x+y−20=0,则抛物线方程为A.y2=16xB.y2=8xC.y2=−16xD.y2=−8xA.2B.2C.4D.413．(2011年清华大学等七校联考)AB为过抛物线y2=4x焦点F的弦,O为坐标原点,且∠OFA=135°,C为抛物线准线与x轴的交点,则∠ACB的正切值为14．(2012年清华大学等七校联考)椭圆长轴长为4,左顶点在圆(x−4)2+(y−1)2=4上,左准线为y 轴,则此椭圆离心率的取值范围是二、解答题。
《北大清华自主招生数学试题的分析与解》试读本
兰琦 毕业于清华大学计算机系 " # # . 年高考数学满分 邮箱 6 9 K 6 6 9 A @ @ $$ / -! 6 7 8 L 博客地址 9 : : H G M K ! 7 @ ; 5 N
" #
三测 高考难度 $ " # $ % 年清华大学 OPQ ( ( R O 测试文科数学 三测 高考难度 $ " # $ % 年清华大学 OPQ ( ( R O 测试理科数学 # 二测 高考难度 " " # $ + 年清华大学 OPQ ( ( R O 测试理科数学 " 一测 高考难度 " # $ + 年清华大学 OPQ ( ( R O 测试理科数学 " 二测 . " # $ + 年清华大学 OPQ ( ( R O 附加科目测试数学部分 " # $ + 年清华大学自主招生暨领军计划试题 / " " # $ + 年清华大学 . " & 学术能力测试数学试题 + 4 " # $ + 年清华大学暑期学校测试 % + " # $ + 年北京大学自主招生数学试题 & 数学测试试题 $ " # $ + 年北京大学优特 Q , O A B : # # " # $ + 年北京大学优秀中学生夏令营数学试题 $ # & " # $ + 年北京大学博雅计划数学试题 $ $ " # $ / 年清华大学自主招生暨领军计划试题 $ " " # $ / 年清华大学夏令营数学试题 $ & " # $ / 年北京大学自主招生数学试题 $ . . " # $ / 年北京大学数学学科夏令营初赛试题 $ 4 # " # $ / 年北京大学生命科学冬令营试卷数学部分试题 $ 4 " # $ / 年北京大学全国优秀中学生暑期夏令营试题 $ / # " # $ / 年北京大学博雅计划试题 $ / " " # $ 4 年清华大学自主招生暨领军计划试题 $ / + " # $ 4 年清华大学金秋营基础部分试题 $ + % " # $ 4 年北京大学博雅计划数学试卷 $ % " " # $ 4 年北京大学化学体验营数学试题 $ % . " # $ 4 年北京大学生命科学冬令营试卷数学部分试题 $ % / " # $ 4 年北京大学优秀中学生体验营综合测试数学科目试题 $ % & " # $ 4 年北京大学自主选拔录取考试试题 $ & $ " # $ . 年清华大学等五校联考自主招生试题 $ & . " # $ . 年北京大学全国优秀中学生体验营数学试卷 $ & %
2015北大自主招生数学试题文件.doc
一.选择题1.整数x,y,z满足xy+yz+zx=1 ，则(1+ 2x )(1+2y )(1+2z )可能取到的值为（）A．16900 B．17900 C．18900 D．前三个答案都不对2.在不超过99 的正整数中选出50 个不同的正整数，已知这50 个数中任两个的和都不等于99，也不等于100．这50 个数的和可能等于（）A．3524 B．3624 C．3724 D．前三个答案都不对3.已知x∈[0,2 ]，对任意实数a，函数y= 2cos x - 2 a cosx+1 的最小值记为g(a)，则当 a 取遍所有实数时，g( a)的最大值为（）A．1 B．2 C．3 D．前三个答案都不对4.已知2010 -20n 的整数倍，则正整数n 的最大值为（）2 是2A．21 B．22 C．23 D．前三个答案都不对5.在凸四边形ABCD 中，BC=4 ，∠ADC=60 °，∠BAD=90 °，四边形ABCD 的面积等于则C D 的长（精确到小数点后 1 位）为（）A B CD BC AD2，A．6.9 B．7.1 C．7.3 D．前三个答案都不对二.填空题1 1x 1 20156.满足等式（1+ ) (1 ) 的整数x 的个数是_______ ．x 20152( ab cd)7.已知a,b,c,d ∈[2,4] ，则2 2 2 2(a d )(b c ) 的最大值与最小值的和为___________8.对于任意实数x∈[1,5],| 2x +px+q| ≤2,不超过2 2p q 的最大整数是__________9.设x=2 2 2b c a2bc,y=2 2 2a c b2ac,z=2 2 2b a c2ba2015 2015 2015x y z 的值为___,且x+y+z=1 ，则10.设A1 ,A2,..., A n 都是9 元集合{1,2,3, ⋯,9} 的子集，已知| A i |为奇数，1≤i≤n,| A i A j |为偶数，1≤i ≠j≤n ，则n的最大值为____________三．解答题11.已知数列{ a}为正项等比数列，且a3 a4 a1 a2 =5,求n a a 的最小值5 612.已知f(x)为二次函数，且a,f(a),f (f(a)), f(f (f(a)))成正项等比数列，求证：f( a)= a13.称四个顶点都在三角形边上的正方形为此三角形的内接正方形。
2015年普通高等学校招生全国统一考试数学试题及答案(全word可编辑版,全解全析)
2015年普通高等学校招生全国统一考试课标全国Ⅰ理科数学注意事项:1.本试题分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至3页,第Ⅱ卷3至5页.2.答题前,考生务必将自己的姓名、准考证号填写在本试题相应的位置.3.全部答案在答题卡上完成,答在本试题上无效.4.考试结束后,将本试题和答题卡一并交回.第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.(2015课标全国Ⅰ,理1)设复数z满足1+z=i,则|z|=()A.1B.2C.3D.2答案:A解析:∵1+z=i,∴z=i−1=(i−1)(−i+1)=i,∴|z|=1.2.(2015课标全国Ⅰ,理2)sin 20°cos 10°-cos 160°sin 10°=()A.-32B.32C.-12D.12答案:D解析:sin20°cos10°-cos160°sin10°=sin20°cos10°+cos20°sin10°=sin(10°+20°)=sin30°=12.3.(2015课标全国Ⅰ,理3)设命题p:∃n∈N,n2>2n,则p为()A.∀n∈N,n2>2nB.∃n∈N,n2≤2nC.∀n∈N,n2≤2nD.∃n∈N,n2=2n答案:C解析:∵p:∃n∈N,n2>2n,∴p:∀n∈N,n2≤2n.故选C.4.(2015课标全国Ⅰ,理4)投篮测试中,每人投3次,至少投中2次才能通过测试.已知某同学每次投篮投中的概率为0.6,且各次投篮是否投中相互独立,则该同学通过测试的概率为()A.0.648B.0.432C.0.36D.0.312答案:A解析:由条件知该同学通过测试,即3次投篮投中2次或投中3次.故P=C320.62(1-0.6)+C330.63=0.648.5.(2015课标全国Ⅰ,理5)已知M(x0,y0)是双曲线C:x 22-y2=1上的一点,F1,F2是C的两个焦点.若MF1·MF2<0,则y0的取值范围是()A. −3,3B. −3,3C. −22,22D. −23,23答案:A解析:由条件知F1(-3,0),F2(3,0),∴MF1=(-3-x0,-y0),MF2=(3-x0,-y0),∴MF1·MF2=x02+y02-3<0.①又∵x022−y02=1,∴x02=2y02+2.代入①得y02<13,∴-3<y0<3. 6.(2015课标全国Ⅰ,理6)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有( ) A .14斛 B .22斛 C .36斛 D .66斛 答案:B解析:设底面圆半径为R ,米堆高为h.∵米堆底部弧长为8尺,∴14·2πR=8,∴R=16π.∴体积V=1×1·πR 2h=1×π× 16 2×5.∵π≈3,∴V ≈3209(尺3). ∴堆放的米约为3209×1.62≈22(斛).7.(2015课标全国Ⅰ,理7)设D 为△ABC 所在平面内一点,BC =3CD ,则( )A .AD =-1AB +4AC B .AD =1AB −4AC C .AD =43AB +13AC D .AD=43AB −13AC 答案:A解析:如图:∵AD =AB +BD,BC =3CD , ∴AD =AB +43BC =AB +43(AC −AB )=-13AB +43AC. 8.(2015课标全国Ⅰ,理8)函数f (x )=cos(ωx+φ)的部分图像如图所示,则f (x )的单调递减区间为( ) A . kπ−1,kπ+3 ,k ∈Z B . 2kπ−1,2kπ+3 ,k ∈Z C . k −14,k +34 ,k ∈Z D . 2k −1,2k +3 ,k ∈Z 答案:D解析:不妨设ω>0,由函数图像可知,其周期为T=2× 54−14=2,所以2πω=2,解得ω=π. 所以f (x )=cos(πx+φ).由图像可知,当x=12 14+54=34时,f (x )取得最小值,即f 3 =cos3π+φ =-1,解得3π4+φ=2k π+π(k ∈Z ),解得φ=2k π+π4(k ∈Z ).令k=0,得φ=π,所以f (x )=cos πx +π.令2k π≤πx+π≤2k π+π(k ∈Z ),解得2k-14≤x ≤2k+34(k ∈Z ).所以函数f (x )=cos πx +π4的单调递减区间为 2k−14,2k +34(k ∈Z ).结合选项知应选D .9.(2015课标全国Ⅰ,理9)执行下面的程序框图,如果输入的t=0.01,则输出的n=( )A .5B .6C .7D .8答案:C解析:∵S=1,n=0,m=1,t=0.01,∴S=S-m=12,m=m 2=14,n=n+1=1,S>0.01,∴S=14,m=18,n=2,S>0.01,∴S=1,m=1,n=3,S>0.01,∴S=1,m=1,n=4,S>0.01,∴S=132,m=164,n=5,S>0.01,∴S=1,m=1,n=6,S>0.01,∴S=1,m=1,n=7,S<0.01,∴n=7.10.(2015课标全国Ⅰ,理10)(x 2+x+y )5的展开式中,x 5y 2的系数为( ) A .10 B .20 C .30 D .60 答案:C解析:由于(x 2+x+y )5=[(x 2+x )+y ]5,其展开式的通项为T r+1=C 5r (x 2+x )5-r y r (r=0,1,2,…,5),因此只有当r=2,即T 3=C 52(x 2+x )3y 2中才能含有x 5y 2项.设(x 2+x )3的展开式的通项为S i+1=C 3i (x 2)3-i ·x i =C 3i x 6-i(i=0,1,2,3),令6-i=5,得i=1,则(x 2+x )3的展开式中x 5项的系数是C 31=3,故(x 2+x+y )5的展开式中,x 5y 2的系数是C 52·3=10×3=30. 11.(2015课标全国Ⅰ,理11)圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16+20π,则r=( ) A .1 B .2 C .4 D .8 答案:B解析:由条件知,该几何体是由一个圆柱被过圆柱底面圆直径的平面所截剩下的半个圆柱及一个半球拼接而成,其表面积是一个矩形面积、两个半圆面积、圆柱侧面积的一半、球表面积的一半相加所得,所以表面积为S 表=2r×2r+2×12πr 2+πr×2r+12×4πr 2=5πr 2+4r 2=16+20π,解得r=2.12.(2015课标全国Ⅰ,理12)设函数f (x )=e x (2x-1)-ax+a ,其中a<1,若存在唯一的整数x 0使得f (x 0)<0,则a 的取值范围是( )A. −32e ,1B. −32e,34C.32e ,34D.32e,1答案:D解析:设g(x)=e x(2x-1),h(x)=a(x-1),则不等式f(x)<0即为g(x)<h(x).因为g'(x)=e x(2x-1)+2e x=e x(2x+1),当x<-12时,g'(x)<0,函数g(x)单调递减;当x>-12时,g'(x)>0,函数g(x)单调递增.所以g(x)的最小值为g −1.而函数h(x)=a(x-1)表示经过点P(1,0),斜率为a的直线.如图,分别作出函数g(x)=e x(2x-1)与h(x)=a(x-1)的大致图像.显然,当a≤0时,满足不等式g(x)<h(x)的整数有无数多个.函数g(x)=e x(2x-1)的图像与y轴的交点为A(0,-1),与x轴的交点为D1,0.取点C −1,−3e.由图可知,不等式g(x)<h(x)只有一个整数解时,须满足k PC≤a<k PA.而k PC=0−−3e=3,k PA=0−(−1)=1,所以32e ≤a<1.故选D.第Ⅱ卷本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须做答.第22题~第24题为选考题,考生根据要求做答.二、填空题:本大题共4小题,每小题5分.13.(2015课标全国Ⅰ,理13)若函数f(x)=x ln(x+ a+x2)为偶函数,则a=.答案:1解析:∵f(x)是偶函数,∴f(-1)=f(1).又f(-1)=-ln(-1+a+1)=ln a+1+1a,f(1)=ln(1+a+1),因此ln(a+1+1)-ln a=ln(a+1+1),于是ln a=0,∴a=1.14.(2015课标全国Ⅰ,理14)一个圆经过椭圆x 2+y2=1的三个顶点,且圆心在x轴的正半轴上,则该圆的标准方程为.答案: x−32+y2=25解析:由条件知圆经过椭圆的三个顶点分别为(4,0),(0,2),(0,-2),设圆心为(a,0)(a>0),所以(a−0)2+(0−2)2=4-a,解得a=32,故圆心为32,0,此时半径r=4-32=52,因此该圆的标准方程是 x−322+y2=254.15.(2015课标全国Ⅰ,理15)若x,y满足约束条件x−1≥0,x−y≤0,x+y−4≤0,则yx的最大值为.答案:3解析:画出约束条件对应的平面区域(如图),点A为(1,3),要使y最大,则y−0最大,即过点(x,y),(0,0)两点的直线斜率最大,由图形知当该直线过点A时,yx max =3−01−0=3.16.(2015课标全国Ⅰ,理16)在平面四边形ABCD 中,∠A=∠B=∠C=75°,BC=2,则AB 的取值范围是 . 答案:( 6− 2, 6+ 2) 解析:如图.作CE ∥AD 交AB 于E ,则∠CEB=75°,∠ECB=30°. 在△CBE 中,由正弦定理得,EB= − 延长CD 交BA 的延长线于F ,则∠F=30°. 在△BCF 中,由正弦定理得,BF= 6+ 2, 所以AB 的取值范围为( 6− 2, 6+ 2).三、解答题:解答应写出文字说明、证明过程或演算步骤.17.(本小题满分12分)(2015课标全国Ⅰ,理17)S n 为数列{a n }的前n 项和.已知a n >0,a n 2+2a n =4S n +3. (1)求{a n }的通项公式; (2)设b n =1a n a n +1,求数列{b n }的前n 项和.解:(1)由a n 2+2a n =4S n +3,可知a n +12+2a n+1=4S n+1+3.可得a n +12−a n 2+2(a n+1-a n )=4a n+1,即2(a n+1+a n )=a n +12−a n 2=(a n+1+a n )(a n+1-a n ). 由于a n >0,可得a n+1-a n =2.又a 12+2a 1=4a 1+3,解得a 1=-1(舍去),a 1=3.所以{a n }是首项为3,公差为2的等差数列,通项公式为a n =2n+1. 6分(2)由a n =2n+1可知b n =1n n +1=1=11−1.设数列{b n }的前n 项和为T n ,则 T n =b 1+b 2+…+b n=12 13−15 + 15−17 +⋯+12n +1−12n +3=n . 12分18.(本小题满分12分)(2015课标全国Ⅰ,理18)如图,四边形ABCD 为菱形,∠ABC=120°,E ,F 是平面ABCD 同一侧的两点,BE ⊥平面ABCD ,DF ⊥平面ABCD ,BE=2DF ,AE ⊥EC.(1)证明:平面AEC ⊥平面AFC ;(2)求直线AE 与直线CF 所成角的余弦值. 解:(1)连结BD ,设BD ∩AC=G ,连结EG ,FG ,EF.在菱形ABCD 中,不妨设GB=1. 由∠ABC=120°,可得AG=GC=由BE ⊥平面ABCD ,AB=BC ,可知AE=EC. 又AE ⊥EC ,所以EG= 3,且EG ⊥AC. 在Rt △EBG 中,可得BE= 2,故DF= 2. 在Rt △FDG 中,可得FG= 62.在直角梯形BDFE 中,由BD=2,BE= 2,DF= 22,可得EF=3 22. 从而EG 2+FG 2=EF 2,所以EG ⊥FG. 又AC ∩FG=G ,可得EG ⊥平面AFC.因为EG ⊂平面AEC ,所以平面AEC ⊥平面AFC. 6分(2)如图,以G 为坐标原点,分别以GB ,GC 的方向为x 轴、y 轴正方向,|GB |为单位长,建立空间直角坐标系G-xyz.由(1)可得A (0,- E (1,0, F −1,0,2,C (0, 3,0),所以AE =(1, 3, 2),CF= −1,− 3, 2 . 10分故cos <AE ,CF >=AE ·CF|AE ||CF|=- 33. 所以直线AE 与直线CF 所成角的余弦值为 3.12分19.(本小题满分12分)(2015课标全国Ⅰ,理19)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x (单位:千元)对年销售量y (单位:t)和年利润z (单位:千元)的影响.对近8年的年宣传费x i 和年销售量y i (i=1,2,…,8)数据作了初步处理,得到下面的散点图及一些统计量的值.表中w i = x i ,w =18∑i =18w i. (1)根据散点图判断,y=a+bx 与y=c+d x 哪一个适宜作为年销售量y 关于年宣传费x 的回归方程类型?(给出判断即可,不必说明理由)(2)根据(1)的判断结果及表中数据,建立y 关于x 的回归方程;(3)已知这种产品的年利润z 与x ,y 的关系为z=0.2y-x.根据(2)的结果回答下列问题: ①年宣传费x=49时,年销售量及年利润的预报值是多少? ②年宣传费x 为何值时,年利润的预报值最大?附:对于一组数据(u 1,v 1),(u 2,v 2),…,(u n ,v n ),其回归直线v=α+βu 的斜率和截距的最小二乘估计分别为β^=∑i =1n(u i −u )(v i −v )∑i =1n(u i −u )2,α^=v −β^u .解:(1)由散点图可以判断,y=c+d x 适宜作为年销售量y 关于年宣传费x 的回归方程类型.2分(2)令w= x ,先建立y 关于w 的线性回归方程.由于d ^=∑i =18(w i −w )(y i −y )∑i =18(w i −w )2=108.81.6=68, c ^=y −d ^w =563-68×6.8=100.6,所以y 关于w 的线性回归方程为y ^=100.6+68w ,因此y 关于x 的回归方程为y ^=100.6+68 x . 6分(3)①由(2)知,当x=49时,年销售量y 的预报值y ^=100.6+68 49=576.6,年利润z 的预报值z ^=576.6×0.2-49=66.32. 9分②根据(2)的结果知,年利润z 的预报值z ^=0.2(100.6+68 x )-x=-x+13.6 x +20.12.所以当 x =13.6=6.8,即x=46.24时,z ^取得最大值.故年宣传费为46.24千元时,年利润的预报值最大.12分20.(本小题满分12分)(2015课标全国Ⅰ,理20)在直角坐标系xOy 中,曲线C :y=x 24与直线l :y=kx+a (a>0)交于M ,N两点.(1)当k=0时,分别求C 在点M 和N 处的切线方程;(2)y 轴上是否存在点P ,使得当k 变动时,总有∠OPM=∠OPN ?说明理由. 解:(1)由题设可得M (2 a ,a ),N (-2 a ,a ),或M (-2 a ,a ),N (2 a ,a ).又y'=x 2,故y=x 24在x=2 a 处的导数值为 a ,C 在点(2 a ,a )处的切线方程为y-a= a (x-2 a ),即 a x-y-a=0. y=x 2在x=-2 a 处的导数值为- a ,C 在点(-2 a ,a )处的切线方程为y-a=- a (x+2 a ),即 a x+y+a=0. 故所求切线方程为 a x-y-a=0和 a x+y+a=0. 5分(2)存在符合题意的点,证明如下:设P (0,b )为符合题意的点,M (x 1,y 1),N (x 2,y 2),直线PM ,PN 的斜率分别为k 1,k 2. 将y=kx+a 代入C 的方程得x 2-4kx-4a=0. 故x 1+x 2=4k ,x 1x 2=-4a.从而k 1+k 2=y 1−b x 1+y 2−bx 2=2kx 1x 2+(a−b )(x 1+x 2)x 1x 2=k (a +b )a.当b=-a 时,有k 1+k 2=0,则直线PM 的倾角与直线PN 的倾角互补,故∠OPM=∠OPN ,所以点P (0,-a )符合题意. 12分21.(本小题满分12分)(2015课标全国Ⅰ,理21)已知函数f (x )=x 3+ax+1,g (x )=-ln x.(1)当a 为何值时,x 轴为曲线y=f (x )的切线;(2)用min{m ,n }表示m ,n 中的最小值,设函数h (x )=min{f (x ),g (x )}(x>0),讨论h (x )零点的个数. 解:(1)设曲线y=f (x )与x 轴相切于点(x 0,0),则f (x 0)=0,f'(x 0)=0,即 x 03+ax 0+1=0,3x 02+a =0.解得x 0=1,a=-3.因此,当a=-34时,x 轴为曲线y=f (x )的切线. 5分(2)当x ∈(1,+∞)时,g (x )=-ln x<0,从而h (x )=min{f (x ),g (x )}≤g (x )<0,故h (x )在(1,+∞)无零点. 当x=1时,若a ≥-54,则f (1)=a+54≥0,h (1)=min{f (1),g (1)}=g (1)=0,故x=1是h (x )的零点;若a<-54,则f (1)<0,h (1)=min{f (1),g (1)}=f (1)<0,故x=1不是h (x )的零点.当x ∈(0,1)时,g (x )=-ln x>0.所以只需考虑f (x )在(0,1)的零点个数.(ⅰ)若a ≤-3或a ≥0,则f'(x )=3x 2+a 在(0,1)无零点,故f (x )在(0,1)单调.而f (0)=14,f (1)=a+54,所以当a ≤-3时,f (x )在(0,1)有一个零点;当a ≥0时,f (x )在(0,1)没有零点.(ⅱ)若-3<a<0,则f (x )在 0, −3单调递减,在 −3,1 单调递增,故在(0,1)中,当x= −3时,f (x )取得最小值,最小值为f −a =2a −a +1. ①若f −a >0,即-3<a<0,f (x )在(0,1)无零点; ②若f −a =0,即a=-3,则f (x )在(0,1)有唯一零点;③若f −3 <0,即-3<a<-34,由于f (0)=14,f (1)=a+54,所以当-54<a<-34时,f (x )在(0,1)有两个零点;当-3<a ≤-54时,f (x )在(0,1)有一个零点.10分综上,当a>-3或a<-5时,h (x )有一个零点;当a=-3或a=-5时,h (x )有两个零点;当-5<a<-3时,h (x )有三个零点. 12分请考生在第22、23、24三题中任选一题做答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分,做答时请用2B 铅笔在答题卡上将所选题号后的方框涂黑.22.(本小题满分10分)(2015课标全国Ⅰ,理22)选修4—1:几何证明选讲如图,AB是☉O的直径,AC是☉O的切线,BC交☉O于点E.(1)若D为AC的中点,证明:DE是☉O的切线;(2)若OA=3CE,求∠ACB的大小.解:(1)连结AE,由已知得,AE⊥BC,AC⊥AB.在Rt△AEC中,由已知得,DE=DC,故∠DEC=∠DCE.连结OE,则∠OBE=∠OEB.又∠ACB+∠ABC=90°,所以∠DEC+∠OEB=90°,故∠OED=90°,DE是☉O的切线.5分(2)设CE=1,AE=x,由已知得AB=2,BE=2.由射影定理可得,AE2=CE·BE,所以x2=12−x2,即x4+x2-12=0.可得x=3,所以∠ACB=60°.10分23.(本小题满分10分)(2015课标全国Ⅰ,理23)选修4—4:坐标系与参数方程在直角坐标系xOy中,直线C1:x=-2,圆C2:(x-1)2+(y-2)2=1,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.(1)求C1,C2的极坐标方程;(2)若直线C3的极坐标方程为θ=π4(ρ∈R),设C2与C3的交点为M,N,求△C2MN的面积.解:(1)因为x=ρcosθ,y=ρsinθ,所以C1的极坐标方程为ρcosθ=-2,C2的极坐标方程为ρ2-2ρcosθ-4ρsinθ+4=0.5分(2)将θ=π4代入ρ2-2ρcosθ-4ρsinθ+4=0,得ρ2-32ρ+4=0,解得ρ1=22,ρ2= 2.故ρ1-ρ2=2,即|MN|= 2.由于C2的半径为1,所以△C2MN的面积为1.10分24.(本小题满分10分)(2015课标全国Ⅰ,理24)选修4—5:不等式选讲已知函数f(x)=|x+1|-2|x-a|,a>0.(1)当a=1时,求不等式f(x)>1的解集;(2)若f(x)的图像与x轴围成的三角形面积大于6,求a的取值范围.解:(1)当a=1时,f(x)>1化为|x+1|-2|x-1|-1>0.当x≤-1时,不等式化为x-4>0,无解;当-1<x<1时,不等式化为3x-2>0,解得2<x<1;当x≥1时,不等式化为-x+2>0,解得1≤x<2.所以f(x)>1的解集为 x2<x<2.5分(2)由题设可得,f(x)=x−1−2a,x<−1,3x+1−2a,−1≤x≤a,−x+1+2a,x>a.所以函数f(x)的图像与x轴围成的三角形的三个顶点分别为A2a−13,0,B(2a+1,0),C(a,a+1),△ABC的面积为2(a+1)2.由题设得23(a+1)2>6,故a>2.所以a的取值范围为(2,+∞).10分。
2015年《高校自主招生考试》数学真题分类解析之5、概率
专题之5、概率一、选择题。
1、(2009年华中科技大学)从0,1,2,…,9这十个数码中不放回地随机取n(2≤n≤10)个数码,能排成n位偶数的概率记为Pn,则数列{Pn}A.既是等差数列又是等比数列B.是等比数列但不是等差数列C.是等差数列但不是等比数列D.既不是等差数列也不是等比数列2、(2009年华中科技大学)5张票中有1张奖票,5个人按照排定的顺序从中各抽1张以决定谁得到其中的奖票,且后抽的人不知道先抽的人抽出的结果,则第3个人抽到奖票的概率是A. B. C. D.3、(2009年复旦大学)某种细胞如果不能分裂则死亡,并且一个细胞死亡和分裂为两个细胞的概率都为,现有两个这样的细胞,则两次分裂后还有细胞存活的概率是A. B. C. D.4、(2012年复旦大学)随机任取一个正整数,则它的3次方的个位和十位上的数字都是1的概率是A. B. C. D.二、填空题。
5、(2009年南京大学)有一个1,2,…,9的排列,现将其重新排列,则1和2不在原来位置的概率是.三、解答题。
6、(2010年中南财经政法大学)某市在36位“政协委员”候选人中任选2名,其中来自教育界的候选人共有6人,求:(1)至少有1名来自教育界的人当选的概率是多少?(2)候选人中任何人都有当选的可能性,若选得同性别委员的概率等于,则男女候选人相差几名?(注:男候选人多于女候选人)7、(2011年同济大学等九校联考)一袋中有a个白球和b个黑球,从中任取一个球,如果取出白球,则把它放回袋中;如果取出黑球,则该黑球不再放回,另补一个白球放到袋中.在进行n次这样的操作后,记袋中白球的个数为Xn.(1)求E;(2)设P(=a+k)=,求P(=a+k),k=0,1,…,b;(3)证明:EX n+1=(1)EX n+1.8、(2009年清华大学)12名职工(其中3名为男性)被平均分配到3个部门.(1)试求3名男员工分配到不同部门的概率;(2)试求3名男员工分配到相同部门的概率;(3)试求1名男员工指定到某一部门,另两名不在同部门的概率.9、(2009年清华大学)M为三位的自然数,求:(1)M含因子5的概率;(2)M中恰有两位数码相同的概率.10、(2010年清华大学)12个人玩一个游戏,游戏开始后每个人被随机地戴上红、黄、蓝、绿四种颜色之一的帽子,每个人都可以看到其余11个人帽子的颜色,游戏开始后12个人不能再交流,并被要求猜出自己帽子的颜色,请为这12个人在游戏前商定一个方案,使得他们同时猜对自己帽子的颜色的概率尽可能大.11、(2010年清华大学等五校联考)假定亲本总体中三种基因型式:AA,Aa,aa的比例为u∶2v∶w(u>0,v>0,w>0,u+2v+w=1)且数量充分多,参与交配的亲本是该总体中随机的两个.(1)求子一代的三种基因型式的比例;(2)子二代的三种基因型式的比例与子一代的三种基因型式的比例相同吗?并说明理由.12、(2011年清华大学等七校联考)将一枚均匀的硬币连续抛掷n次,以表示未出现连续三次正面的概率.(1)求、、和;(2)探究数列{}的递推公式,并给出证明(3)讨论数列{}的单调性及其极限,并阐述该极限的概率意义.13、(2012年清华大学等七校联考)系统内有2k−1(k∈N*)个元件,每个元件正常工作的概率为p(0<p<1),各个元件独立工作.若系统有超过一半的元件正常工作,则系统正常工作,系统正常工作的概率称为系统的可靠性.(1)求该系统正常工作的概率;(2)试讨论的单调性,并讨论增加两个元件后,能否提高系统的可靠性.因此两次分裂后还有细胞存活的概率为1−P(E)=.4.D【解析】首先,一个正整数的3次方的个位数是1,则这个正整数的个位数也必须是1.其次可试得1~100中只有71符合要求,而且末两位是71的均符合要求.故选D.5..【解析】2+=57×或+7×7×,∴P=.6.(1) . (2) 6【解析】(1)任意选取2人的选法为,其中2人都不是来自教育界的选法为,因此所求概率为p==.(2)设男候选人为x(x>18)人,则女候选人为36−x人,选出两人都是男性的概率为p 1=,选出两人都是女性的概率为=,+=,∴x2−36x+35×9=0,∴x=21(x>18),p2∴男女相差6人.=a+k)=p k·+p k−1·(k≥1).7.(1) . (2) P(X(3)第n次白球个数的数学期望为EX n,由于白球和黑球的总个数为a+b,则将第n+1次白球个数的数学期望分为两类:第n+1次取出来的是白球,这种情况发生的概率是,此时白球的个数为EX n;第n+1次取出来的是黑球,这种情况发生的概率是,此时白球的个数是EX n+1,数的数学期望分为两类:第n+1次取出来的是白球,这种情况发生的概率是,此时白球的个数为EX n ;第n+1次取出来的是黑球,这种情况发生的概率是,此时白球的个数是EX n +1, 故EX n+1=EX n +·(EX n +1)=+(1)(EX n +1)=+EX n+1=(1)EX n +1. 8.(1(2)(3)【解析】(1)P 1==;(2)P 2==;(3)P3==.9.(1) (2).【解析】(1)当个位数字为0时,有9×10=90个符合题意的三位数;当个位数字为5时,有9×10=90个符合题意的三位数,故M含因子5的概率为=.(2)当M中含有数字0,且0是重复数码时,有9个符合题意的三位数;当M中含有数字0,且0不是重复数码时,有9×=18个符合题意的三位数;当M中不含数字0时,有9×8×3=216个符合题意的三位数,故M中恰有两位数码相同的概率为=.10.12个人同时猜对的概率一定不大于单独一个人猜对的概率,即.【解析】首先将问题数学化,将红、黄、蓝、绿四种颜色分别用数字0、1、2、3代表.策略是每个人将其余11人的帽子的颜色所对应的数字求和,记为S,S除以4的余数设为d,(4−d)对应的颜色即为他所猜的颜色.例如,若12个人都戴黄帽子,每个人看到其余11个人的帽子颜色对应数字和均为11,11除以4余3,4−3=1对应黄色,全都猜对.这样的策略使得同时猜对头上帽子颜色的概率为.当且仅当12个人的帽子颜色所对应数字之和为4的倍数时,12个人能够同时猜对.不然,12个人会同时猜错.这12个人或者同时猜对,或者同时猜错,同时猜对的概率与一个人随机猜测正确的概率相等,为.而多个人猜测时,由于不能由他人的帽子颜色推断出有关自己帽子颜色的信息,因此12个人同时猜对的概率一定不大于单独一个人猜对的概率,即.因此上述方案是最优的.11.(1)AA,Aa,aa的比例为p2∶2pq∶q2.(2) 相同可知子二代的基因型式AA,Aa,aa的比例为α2∶2αβ∶β2,其中α=p2+pq,β=pq+q2.由p+q=1,可得α=p,β=q.故子二代的三种基因型式AA,Aa,aa的比例为p2∶2pq∶q2,与子一代的三种基因型式的比例相同.【解析】(1)参与交配的两个亲本(一个称为父本,一个称为母本)的基因型式的情况,及相应情p 1=u2×1+2uv×+2uv×+4v2×=(u+v)2.由对称性知子一代的基因型式为aa的概率为p3=(v+w)2.子一代的基因型式为Aa的概率为p 2=2uv×+uw×1+2uv×+4v2×+2vw×+uw×1+2vw×=2(uv+uw+v2+vw)=2(u+v)(v+w).若记p=u+v,q=v+w,则p>0,q>0,p+q=1,子一代的三种基因型式AA,Aa,aa的比例为p2∶2pq∶q2.(2)由(1)可知子二代的基因型式AA,Aa,aa的比例为α2∶2αβ∶β2,其中①×②,有p=p n−1p n−4(n≥5).(3)n≥4时,{p n}单调递减.又p1=p2>p3>p4,∴n≥2时,数列{p n}单调递减,且有下界0.∴p的极限存在记为a,对p n=p n−1p n−4两边同时取极限可得a=a a,a=0,故p n=0.其概率意义:当投掷的次数足够多时,不出现连续三次正面的概率非常小.【解析】(1)显然p 1=p2=1,p3=1=;又投掷四次出现连续三次正面的情况只有:正正正正或正正正反或反正正正,故p 4=1=.(2)共分三种情况:1)如果第n次出现反面,那么前n次不出现连续三次正面和前n−1次不出现连续三次正面是相同的,所以这个时候不出现连续三次正面的概率是×p n−1;2)如果第n次出现正面,第n−1次出现反面,那么前n次不出现连续三次正面和前n−2次不出现连续三次正面是相同的,所以这个时候不出现连续三次正面的概率是×p n−2;增加两个元件时,系统可靠性降低;当p>时,P k+1>P k,函数P k单调递增,增加两个元件时,系统可靠性提高.【解析】(1)当系统有2k−1(k∈N*)个元件时,恰有k个元件正常工作的概率为·p k(1−p)k−1,恰有k+1个元件正常工作的概率为·p k+1(1−p)k−2,…,恰有2k−1个元件正常工作的概率为·p2k−1(1−p)0,P k=·p k(1−p)k−1+·p k+1(1−p)k−2+…+·p2k−1(1−p)0。
2015年《高校自主招生考试》数学真题分类解析之4、创新与综合题
专题之4、创新与综合题一、选择题。
1．(2011年复旦大学)设正整数n可以等于4个不同的正整数的倒数之和,则这样的n的个数是A.1B.2C.3D.42．(2011年同济大学等九校联考)设σ是坐标平面按顺时针方向绕原点做角度为的旋转,τ表示坐标平面关于y轴的镜面反射,用τσ表示变换的复合,先做τ,再做σ,用σk表示连续做k 次σ的变换,则στσ2τσ3τσ4是A.σ4B.σ5C.σ2τD.τσ2二、解答题。
3．(2009年南京大学)求所有满足tan A+tan B+ta n C≤[tan A]+[tan B]+[tan C]的非直角三角形.4．(2010年浙江大学)如图,一条公路两边有六个村庄,要建一个车站,要求到六个村庄的距离之和最小,应该建在哪里最合适?如果再在边上增加一个村庄呢?5．(2009年清华大学)A、B两人玩一个游戏,A选择n枚硬币,B根据自己的策略将这些硬币全部摆放在位点上,之后A选取一个至少有2枚硬币的位点,取走一枚硬币,再将另一枚硬币移动到相邻位点,A若在有限步内根据规则在指定点P处放上一个硬币则获胜.问在一条有5个位点的线段和7个位点的圆环上,A分别至少选择多少枚硬币时,无论点P的位置如何均可保证获胜?6．(2009年清华大学)有64匹马,每匹马的速度保持不变且各不相同,现通过比赛来完成排名,若每场比赛最多只能有8匹马参赛,问理想状态下能否在50场比赛内完成排名?7．(2009年清华大学)有100个集装箱,每个集装箱装有两件货物.在取出来的过程中货物的顺序被打乱了,现在按一定的规则将货物依次放入集装箱中.集装箱的体积都是1,且每个集装箱最多放两件货物,若装了一件货物后装不下第二件货物,那么就将这个集装箱密封,把第二件货物装到下一个集装箱中.问在最坏情况下需要多少个集装箱?8．(2009年清华大学)请写出一个整系数多项式f(x),使得+是其一根.9．(2010年清华大学)将长为n的棒锯开,要求锯成的每段长都是整数,且任意时刻,锯成的所有棒中最长的一根严格小于最短的一根的2倍,如6只能锯一次,6=3+3,而7能锯2次,7=4+3,4又能锯为2+2,问长为30的棒最多能锯成几段?若a,b,c中没有1,则a≥2,b≥2,c≥2,a+b+c=abc化为++=1,而1=++≤++=,显然不成立.∴三角形三内角的正切值分别为1,2,3.即满足三内角的正切值分别为1,2,3的三角形,即为所求.【解析】无4.1.首先设六个村庄到达公路的距离之和为S0,车站P到六个村庄的距离之和为S,下面我们根据车站所建的位置来讨论它到六个村庄的距离之和.(1)建在A、B之间(包括端点A),则S=AP+2PB+PC+PD+PE+S0=AE+BC+BD+S0+4PB.(2)建在B、C之间(包括两端点B、C),则S=PA+2PB+PC+PD+PE+S0=AE+BC+BD+S0.(3)建在C、D之间(包括端点D),则S=PA+2PB+PC+PD+PE+S0=AE+BC+BD+S0+2PC.(4)建在D、E之间(包括端点E),则S=PA+2PB+PC+PD+PE+S0=AE+BC+BD+S0+2PC+2PD.(5)建在A的左侧或E的右侧,则S均比情况(2)中的大.综合以上各种情况,我们可以发现:当车站建在B、C之间(包括端点B、C)时最合适.币.于是由结论①可知A可获胜.③对于4个位点线段的情况,A只要选择8枚硬币,不妨设点P为P1,P2,P3三点中的一点,并设点P 4处有硬币S枚,则点P4处的硬币尽可能移到点P3处后,点P1,P2与P3处共有:8−S+[]≥4②左半环内有7枚硬币.a.若这7枚硬币全在点P7处,则看右半环内的4枚硬币,若点P1处有2枚,则将其移动到点P7处后,点P7处就有8枚硬币,就能保证通过左半环的通路移动硬币,最终让点P处有硬币;若点P1处仅有1枚或没有硬币,则可将点P7处的硬币移动3枚到点P1处,再将点P1处的硬币移动到点P2处后,点P2与点P3处的硬币就不少于4枚.这样,通过右半环的通路,最终可将至少1枚硬币移动到点P4处.b.若这7枚硬币不全在点P7处,则将点P7处的硬币移到点P6处后,在点P5与点P6两处的硬币就不少于4枚.于是通过左半环的通路,最终也可保证有硬币移动到点P4处.③左半环有6枚硬币,则右半环就有5枚硬币.a.左半环内的6枚硬币全在点P7处,将它们移动到点P1处后,右半环内就有了8枚硬币,则通过右半环的通路,可最终保证至少移动1枚硬币到点P4处.b.左半环内的6枚硬币,点P7处有5枚,则再看点P1处,若点P1处的硬币数不足2枚,则在点P2与点P3处就有4枚硬币,则从右半环的通路,就能移动硬币到点P4;若点P1处的硬币数有2枚或2枚以上,则至少可从点P1处移动1枚硬币到点P7处.这样,点P7处就有6枚硬币,于是可移3枚到点P6处.这样点P5与点P6处就有4枚硬币,通过左半环可移动硬币到点P4处.c.左半环内的6枚硬币,点P7处有4枚或不足4枚,则在点P6与点P5处就有2枚或2枚以上,则将点P7处的硬币移动到点P6处以后,在点P6与点P5处的硬币数就不少于4枚,于是通过左半环可移动硬币到点P4处.④若左半环内的硬币数不足6枚,则右半环内的硬币就在6枚或6枚以上,则对右半环内硬币的分布情况进行相同的讨论,亦可发现必可将硬币移动到点P4处.各自的前4名,共8匹马进行一场比赛.这8匹马中的前4名,就是A组与B组32匹马中的前4名;接下来,又在A组与B组中分别扣除32匹马中的前4名后,再分别按照A组与B组中的排名,再各取4匹马,这8匹马进行一场比赛,它们中的前4名,就是A组与B组32匹马中的第5名到第8名;重复上述过程,又可分别确定第9名到第12名;……;最后留下的8匹马,只需进行一场比赛,就能确定第25名到第32名的排名.这样进行了7场比赛,就将A组与B组中的32匹马进行了排名.同理进行7场比赛,又可将C组与D组中的32匹马进行排名.这样第三步共进行14场比赛.第四步:要来完成AB组的32匹马与CD组的32匹马(它们各自内部的排名已经完成)共计64匹马的排名.采用第三步中的方法,每次分别选择AB组与CD组中留下的前4名进行一场比赛,都能确定其中4匹马在总体中的排名,这样14场比赛后,就确定了前56匹马的排名,最后留下的8匹马,只需进行一场比赛,就确定了第57名到第64名的排名.因此,只需15场比赛就能完成这两大组64匹马的排名.综观以上四个步骤,一共进行:8+12+14+15=49(场).所以,可以在50场比赛内完成排名.【解析】无7.由题意知共有200件货物.设a1≤a2≤…≤a99≤a100,b1≥b2≥…≥b99≥b100,令a i+b i=1,a i≥b i,则将它们按如下顺序排列:a1,a2,b1,a3,b2,a4,b3,…,a99,b98,a100,b99,b100,则a 1+a2>1,a2+b1>1,b1+a3>1,…,a100+b99>1,+<1,a1到a100,b1到b98各在一个箱中,b99,b100在一个箱子中,则在最坏情况下需要199个箱子.换个角度考虑,无论200件货物如何排列,体积最小的货物总能与它前面的或后面的货物合装进一个集装箱的,故有199个集装箱就一定能将200件货物全部装下.【解析】无8.设x=+,则(x)3=3,即x3−3x2·+3x·2−2=3,∴x3+6x−3=(3x2+2)·,∴(x3+6x−3)2=2·(3x2+2)2,整理得:x6−6x4−6x3+12x2−36x+1=0,则f(x)=x6−6x4−6x3+12x2−36x+1即为所求的一个整系数多项式.【解析】无9.首先,由题意可知:当我们锯了若干次之后,产生若干根棒,它们中有长度相等与仅差一个单位的棒(例如:7,8,9;6,6,7;5,5,6,6等),这些棒除了2k−2,2k−1,2k与2k−1,2k−1,2k这两种情况,其他无论锯开哪一根,均不能符合最长的一根严格小于最短一根的2倍,有了这样的认识,我们就可以用枚举法来解本题了.(1)30=11+19=11+7+12=11+7+6+6=5+6+7+6+6,。
清华大学2016年自主招生与领军计划数学试题
清华大学2016年自招、领军试题选择题：本卷共40小题，共100分。
在每小题给出的四个选项中，有一个或多个选项是正确的。
（1）若函数()y f x =具有下列两个性质：①在区间,63ππ⎡⎤-⎢⎥⎣⎦上单调递增；②其图像关于3x π=对称.则()f x =（ ）（A ）5sin 26x π⎛⎫-⎪⎝⎭ （B ）cos 23x π⎛⎫+ ⎪⎝⎭ （C ）sin 26x π⎛⎫- ⎪⎝⎭ （D ）2cos 23x π⎛⎫-⎪⎝⎭ 【答案】CD解析：由②可知13f π⎛⎫=± ⎪⎝⎭，再结合①可知13f π⎛⎫= ⎪⎝⎭，由①还可知22T π≥，即T π≥，而选项中所有函数的周期都是π，可知此题最好的方法是代入法. 因此只需要检验四个选项中哪个符合这个条件即可. （A ）132f π⎛⎫= ⎪⎝⎭；（B ）13f π⎛⎫=- ⎪⎝⎭；（C ）13f π⎛⎫= ⎪⎝⎭；（D ）13f π⎛⎫= ⎪⎝⎭. 因此答案为CD.（2）曲线21y x =-与ln y x =（ ）ACD（A ）在点(1,0)处相交 （B ）在点(1,0)处相切 （C ）存在相互平行的切线 （D ）有两个交点 【答案】ACD解析：令2()1f x x =-，()ln g x x =，2()ln 1h x x x =--，()2f x x '=，1()g x x '=，1()2h x x x'=-. 其中()g x 和()h x 的定义域都是(0,)+∞.对于（A ）（B ），(1)(1)0f g ==，(1)2f '=，(1)1g '=，可知两条曲线在点(1,0)处相交. （A ）正确.令()()f x g x ''=，可得2x =；122f ⎛=- ⎝⎭，1ln ln 2g ==->-=-⎝⎭，所以f g ≠⎝⎭⎝⎭，因此两条曲线在2x =处存在相互平行的切线.令()0h x '=，可得x =()h x '和()h x 的变化如下表：由上述分析可知()h x 在0,2⎛ ⎝⎭上单调递减，且02h ⎛< ⎝⎭，2110h e e ⎛⎫=> ⎪⎝⎭，并且12e <，可知()h x 在⎛ ⎝⎭上只有有一个零点，因此两条曲线在⎛ ⎝⎭上只有一个交点.而()h x 在2⎛⎫+∞ ⎪ ⎪⎝⎭上单调递增，并且(1)0h =，()h x 在2⎛⎫+∞ ⎪ ⎪⎝⎭上只有一个零点1，可知两条曲线在2⎛⎫+∞ ⎪ ⎪⎝⎭上只有一个交点.因此答案为ACD.（3）“ABC 为锐角三角形”是“sin sin sin cos cos cos A B C A B C ++>++”的（ ）（A ）充分不要条件 （B ）必要不充分条件 （C ）充要条件 （D ）既不充分也不必要条件 【答案】A解析：若ABC ∆为锐角三角形，则222A B A C B C πππ⎧+>⎪⎪⎪+>⎨⎪⎪+>⎪⎩， 且0,,2A B C π<<，可得022022022A B C A B C ππππππ⎧>>->⎪⎪⎪>>->⎨⎪⎪>>->⎪⎩，又()sin f x x =在0,2π⎛⎫ ⎪⎝⎭上单调递增，所以sin cos sin cos sin cos A B C A B C >⎧⎪>⎨⎪>⎩， 因此可得sin sin sin cos cos cos A B C A B C ++>++，所以“ABC 为锐角三角形”是“sin sin sin cos cos cos A B C A B C ++>++”的充分条件.考虑直角ABC ∆，其中,,236A B C πππ===，则1sin sin sin 122A B C ++=++，1cos cos cos 2A B C ++=+，则sin sin sin cos cos cos A B C A B C ++>++，而显然ABC ∆是不是锐角三角形，因此“ABC ∆为锐角三角形”不是“sin sin sin cos cos cos A B C A B C ++>++”的必要条件.（4）设函数()f x 在区间(1,1)-内有定义，则（ ）（A ）当导数(0)f '存在时，曲线()y f x =在点(0,(0))f 处存在切线 （B ）当曲线()y f x =在点(0,(0))f 处存在切线时，导数(0)f '存在 （C ）当导数(0)f '存在时，函数2()f x 在0x =时的导数等于零 （D ）当函数2()f x 在0x =时的导数等于零时，导数(0)f '存在 【答案】ABC解析：（A ）显然正确；（B ）函数13()f x x =，在在点(0,(0))f 处的切线为y 轴，但是231()3f x x -'=-， (0)f '不存在；（C ）()22()2()f x xf x ''=，因为(0)f '存在，所以()20()20(0)0x f x f =''=⨯⨯=，所以(C)正确；（D ）令 ()f x x =，则222()f x x x ==，所以函数2()f x 在0x =时的导数等于零，但是()f x x =在0x =处的导数(0)f '不存在，因此（D ）错误. （5）设22cos sin 33z i ππ=+，则2322z z z z +=++（ ） （A）122-+ （B）122i -（C）122- （D）122i -+【答案】C解析：易得31z =，2z z =，210z z ++=，23211111212222z z z z i z z +=+=+=--=-++，因此答案选C.（6）甲、乙、丙、丁四人进行网球比赛，首先是甲与乙比，丙与丁比，这两场比赛的胜者再争夺冠军. 他们之间相互获胜的概率如下：则甲获得冠军的概率为（ ）（A ）0.165 （B ）0.245（C ）0.275 （D ）0.315 【答案】A解析：甲与乙比甲获胜为事件A ，则()0.3P A =， 丙与丁比，丙获胜为事件B ，则()0.5,P B =()0.5,P B = 甲与丙比甲获胜为事件C ，则()0.3,P C = 甲与丁比甲获胜为事件D ，则()0.8,P D = 甲获胜的概率为()()()P ABC ABD P ABC P ABD +=+ ()()()()()()P A P B P C P A P B P D =+0.30.50.30.30.50.80.165=⨯⨯+⨯⨯=. 因此答案选A.（7）设函数2()()x f x x a e =+在R 上存在最小值，则函数2()g x x x a =++的零点个数为（ ） （A ）0 （B ）1 （C ）2 （D ）无法确定 【答案】C解析：2()(2)x f x x x a e '=++①当1a ≥时，220x x a ++≥在R 上恒成立，所以()0f x '≥在R 上恒成立，所以函数()f x 在R 上单调递增，因此()f x 在R 上无最小值；②当1a <时，令()0f x '=，则11x =，21x =，且21x x <，()f x '和()f x 的变化情况如下表：x →-∞时，()0f x →，因为()f x 在2(,)x -∞上单调递增，在21(,)x x 上单调递减，在1(,)x +∞上单调递增，所以若()f x 有最小值，只需要1()0f x ≤.11()(2)0x f x e =-≤2⇔≤11a ⇔≤-0a ⇔≤. 20x x a ++=的判别式为141a ∆=-≥，所以()g x 有两个零点. 因此选C.（8）设随机变量ξ的分布列如下：则 （ ）（A ）当{}n a 为等差数列时，5615a a += （B ）数列{}n a 的通项公式可能为1110(1)n a n n =+（C ）当数列{}n a 满足12n n a =(1,2,,9)n =时，10912a =（D ）当数列{}n a 满足2()k P k k a ξ≤=(1,2,,10)k =时，1110(1)n a n n =+【答案】ABCD解析：由题目可知12101a a a +++=；（A ）若{}n a 为等差数列，1210565()1a a a a a +++=+=，所以5615a a +=； （B ）11111110(1)101n a n n n n ⎛⎫==- ⎪++⎝⎭，则0n a ≥，且121011111111111111022310111011a a a ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+++=-+-++-=-= ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦，符合分布列的定义，因此B 正确； （C ）129991111222a a a +++=++=-，又由分布列的定义可知12101a a a +++=，所以10912a =，C 正确； （D ）2()k P k k a ξ≤=，则10(10)1001P a ξ≤==，所以10111100101011a ==⨯⨯，满足题意， 当2k ≥时，221()(1)(1)k k k a P k P k k a k a ξξ-=≤-≤-=--，则221(1)(1)(1)(1)k k k k a k a k k a --=-=-+，因为2k ≥，所以1(1)(1)k k k a k a --=+，即111k k k a a k -+=-. 91011111119910010910a a ==⋅=⨯⨯，满足题意. 当29n ≤≤时，1110112121110111111119(1)10010(1)n n n n n n n n a a a a n n n n nn n n n-++++++⨯==⋅=⋅⋅=⋅=-----则当18n ≤≤时，1110(1)n a n n =+. 因此D 正确.（9）棱长为1的正方体1111ABCD A B C D -中，O 为正方体的中心，E 在11B C 上，11113B E BC =，F 在1AA 上，1114A F AA =，则四面体B EFO -的体积为（ ）（A ）11144 （B ）17144（C ）1138 （D ）1738【答案】A解析：以A 为原点建立空间直角坐标系，则(0,0,0)A ，111(,,)222O ，(1,0,0)B ，1(1,0,1)B ，1(1,1,1)C ，1(1,,1)3E ,3(0,0,)4F ,则111(,,)222BO =-,1(1,0,)4BF =-,1(0,,1)3BF =,四面体B EFO -的体积为111222131110641441013--=（10）设定义在R 上的函数()f x ，()g x 满足：①(0)1g =；②对任意实数12,x x ，121212()()()()()g x x f x f x g x g x -=+；③存在大于零的常数λ，使得()1f λ=，且当(0,)x λ∈时，()0f x >，()0g x > 则（A ）()(0)0g f λ== （B ）当(0,)x λ∈时，()()1f x g x +> （C ）函数()f x ()g x 在R 上无界 （D ）任取x R ∈，()()f x g x λ-= 【答案】ABD解析：令120x x ==，代入②得22(0)(0)(0)g f g =+，因为(0)1g =，所以(0)0f =；令12x x λ==，代入②得22(0)()()g f g λλ=+，因为()1f λ=，所以()0g λ=，因此()(0)0g f λ==；A 正确对于任意实数x ，令12x x x ==代入②得22(0)()()1g f x g x =+=，可得2()1f x ≤，2()1g x ≤，进而()1f x ≤，()1g x ≤，因此C 错误；当(0,)x λ∈时，()0f x >，()0g x >，所以20()1f x <<，20()1g x <<，进而0()1f x <<，0()1g x <<，故22()(),()()f x f x g x g x <<，因此22()()()()f x g x f x g x +<+，又22()()1f x g x +=，故()()1f x g x +>，所以B 正确；令1x λ=，2x x λ=-，代入②得()()()()()g x f f x g g x λλλλ=-+-，又()(0)0g f λ==，()1f λ=，所以()()g x f x λ=-，故D 正确.（11）设,,A B C 是随机事件，A 与C 互不相容，1()2P AB =，1()3P C =，则()P AB C = （ ） （A ）16 （B ）12（C ）13 （D ）34【答案】D解析：因为A 与C 互不相容，所以A C ⊂，则AB C ⊂，因此ABC AB =，可得1()()32()2()()43P ABC P AB P AB C P C P C ====，所以该题选D.（12）甲、乙、丙、丁四人参加数学竞赛，四人在成绩公布前作出如下预测：甲预测说：获奖者在乙、丙、丁三人中； 乙预测说：我不会获奖，丙获奖； 丙预测说：甲和丁中有一人获奖； 丁预测说：乙的猜测是对的.成绩公布后表明，四人的猜测中有两人的预测与结果相符. 另外两人的预测与结果不相符，已知有两人获奖，则获奖的是（ ）（A ）甲和丁 （B ）乙和丁 （C ）乙和丙 （D ）甲和丙 【答案】B解析：因为乙和丁的预测一样，则根据题干可知四人的猜测有两种情况：①乙和丁的预测与结果相符，甲和丙的预测与结果不相符，那么丙获奖，因为丙的预测与结果不相符，所以丙和乙获奖，与甲的预测相符了，矛盾；②乙和丁的预测与结果不相符，甲和丙的预测与结果相符，那么乙获奖，丙不获奖，结合甲预测可知丁获奖，与丙的预测相符，因此获奖者是乙和丁.该题选B. （13）设24πα=，则sin sin sin sin cos 4cos3cos3cos 2cos 2cos cos ααααααααααα+++=（A）6 （B）3 （C）2 （D ）12【答案】B 解析：sin sin((1))cos cos(1)cos cos(1)n n n n n n ααααααα--=--sin cos(1)cos sin(1)tan tan(1)cos cos(1)n n n n n n n n αααααααα---==---所以sin sin sin sin cos 4cos3cos3cos 2cos 2cos cos ααααααααααα+++tan 4tan3tan3tan 2tan 2tan tan ααααααα=-+-+-+tan 4tan63πα===. 因此该题选B（14）设正三棱锥P ABC -的高为h ，底面三角形的边长为1. 设异面直线AB 与PC 的距离为()d h ，则lim ()h d h →∞=（A ）1 （B ）12（C （D ）【答案】C解析：在APC ∆内，过A 向PC 做垂线，垂足为Q ，即AQ PC ⊥，连结BQ ，根据对称性，显然BQ PC ⊥，且BQ AQ =，取AB 中点D ，连结DQ ，DQ ⊂平面AQBAQ PC BQ PC ⊥⎫⇒⎬⊥⎭PC ⊥平面AQB ，又DQ ⊂平面AQB DQ PC ⇒⊥，在AQB 中，BQ AQ =，D 为AB 中点，所以DQ AB ⊥， 因此DQ 为AB 与PC 的公垂线；设点P 在平面ABC 的投影为O ，则AO BO CO ===,AP BP CP ===在APC 中，112APCS=⋅=又12APCSPC AQ AQ =⋅⋅=，所以AQ =，在等腰三角形AQB ∆中，DQ ===()d h =lim ()h h h d h →∞====（15）设,,αβγ分别为1,61,121︒︒︒，则（A ）tan tan tan 3tan tan tan αβγαβγ++=- （B ）tan tan tan tan tan tan 3αββγγα++=-（C ）tan tan tan 3tan tan tan αβγαβγ++=- （D ）tan tan tan tan tan tan 3αββγγα++=【答案】AB解析：22tan (tan 3)tan(60)tan tan(60)tan (13tan )βββββββ--︒+︒==-tan(60)tan tan(60)tan ββββ-︒+++︒=+3228tan 9tan 3tan tan tan 13tan 13tan βββββββ-=+=+=-- 223tan (3tan )13tan βββ-=- 所以tan tan tan tan(60)tan tan(60)3tan tan tan tan(60)tan tan(60)αβγβββαβγβββ++-︒+++︒==--︒+︒，A 正确.tan tan tan tan tan tan αββγγα++tan(60)tan tan tan(60)tan(60)tan(60)ββββββ=-︒++︒++︒-︒tan (tan(60)tan(60))tan(60)tan(60)βββββ=+︒+-︒++︒-︒ tan (tan(60)tan(60))tan(60)tan(60)βββββ=+︒+-︒++︒-︒22228tan tan 313tan 13tan ββββ-=+-- 229tan 313tan ββ-=- 3=-. 所以B 正确.（16）设函数7(,)6()22f x y xy x y =-++-，则[0,1][0,1]max{min{(,)}}y x f x y ∈∈=（A ）0 （B ）124（C ）124- （D ）[0,1][0,1]min{max{(,)}}y x f x y ∈∈【答案】BD解析：77(,)6222f x y x y x ⎛⎫=-+- ⎪⎝⎭求[0,1]min{(,)y f x y ∈把(,)f x y 看成y 的一次函数，[0,1]77(,0) 2 212min (,)357(,1) 2212y f x x x f x y f x x x ∈⎧⎛⎫=-≤ ⎪⎪⎪⎝⎭=⎨⎛⎫⎪=-> ⎪⎪⎝⎭⎩则[0,1]min (,)y f x y ∈在[0,1]x ∈上的最大值在712x =处取得， 所以[0,1][0,1]771max{min{(,)}}221224y x f x y ∈∈=⨯-=. 选项B 正确.[0,1]357(1,) 2212max{(,)}77(0,) 2 212x f y y y f x y f y y y ∈⎧⎛⎫=-≤ ⎪⎪⎪⎝⎭=⎨⎛⎫⎪=-> ⎪⎪⎝⎭⎩， 则[0,1]max{(,)}x f x y ∈在[0,1]y ∈的最小值在712y =处取得， 所以[0,1][0,1]771min{max{(,)}}221224y x f x y ∈∈=⨯-=，故[0,1][0,1][0,1][0,1]max{min{(,)}}min{max{(,)}}y y x x f x y f x y ∈∈∈∈=.所以D 正确.（17）椭圆2222:1x y C a b+=的左、右焦点分别为1F 和2F ，P 为C 上的动点，则（A）当a =时，满足1290F PF ∠=︒的点P 有两个 （B）当a <时，满足1290F PF ∠=︒的点P 有四个（C ）12F PF 面积的最大值为22a（D ）12F PF 的周长小于4a 【答案】AD解析：求满足1290F PF ∠=︒的点的个数只需要求22222221x y a b x y c ⎧+=⎪⎨⎪+=⎩的交点的个数，将222y c x =-代入椭圆可得222221x c x a b -+=，化简得22222222221c c b a x a b b b --=-=，即222222a b x a c-=.当a =时，0x =，因此满足1290F PF ∠=︒的点P 有两个，为短轴两个端点，A 正确；当a <时，20x <，因此满足1290F PF ∠=︒的点P 不存在，B 错误； 显然，当点P 位于短轴端点时，12F PF 面积最大，此时12122F PF Sc b bc =⋅⋅=，C 错误； 12F PF 的周长为224a c a +<，D 正确.（18）设复数z 使得10z 及10z的实部和虚部都是小于1的正数. 记z 在复平面上对应的点的集合是图形C ，则C 的面积是（A ）25752π- （B ）25702π- （C ）15752π- （D ）15702π-【答案】A解析：令z x iy =+，则101010z x y i =+，22101010()x iy z x iy x y ==+-+由题意可知22220,1101010100,1x y x y x y x y ⎧<<⎪⎪⎨⎪<<++⎪⎩，则22220,101010x y x y x x y y <<⎧⎪+>⎨⎪+>⎩，图中的阴影部分就是所求的图形C ，两圆相交部分的面积为252542π-，所以 C 的面积是25252510025275422S πππ⎡⎤⎛⎫=---⨯=-⎪⎢⎥⎝⎭⎣⎦. 选A. （19）设n 是正整数，则定积分22120()(1sin )d n n x x x ππ--+⎰的值（A ）等于0 （B ）等于1 （C ）等于π （D ）与n 的取值有关 【答案】A解析：令x y π-=，则22122120()(1s i n )d (1s i n )d n nn nx x x y yyππππ----+=+⎰⎰，因为212(1sin )n n y y -+是奇函数，则积分的上下限关于原点对称，所以212(1sin )d 0n n y y y ππ--+=⎰.（20）过点(1,0)F 的直线交抛物线24y x =于,A B 两点，则（A ）以AB 为直径的圆与直线32x =-没有公共点（B ）以FB 为直径的圆与y 轴只有一个公共点（C ）AB 的最小值为4（D ）AF 的最小值为2【答案】ABC解析：AB 时抛物线的焦点弦，焦点弦与准线1x =-相切，与32x =-相离，A 项正确；由抛物线定义知B 项也正确；当AB 垂直x 轴时，其长度最短为2p=4（此时称为通径），C 正确；||||1AF AO >=，即AF 可无限接近于1，最小值不存在，D 错误。
清华大学自主招生考试数学试题研究
B.有 2析：设直线 l1 , l2 , l3 分别与直线 y kx m 平行且与 函数 y f ( x) 相切，则三条直线 y kx m ， l1 , l2 , l3 和函数 y f ( x) 的切点设为
A( x A , f ( x A )), B ( xB , f ( xB )), C ( xC , f ( xC )), D( xD , f ( xD )), E ( xE , f ( xE ))
2
3.2 试题考点分布统计 2006 年－2016 年自主招生数学试题主要考点分布统计表 2006 三角函数 复数 函数与方程 概率与统计 数列、不等式 向量 平面几何 立体几何 解析几何 排列与组合 数论与推理 1 1 0 1 0 0 0 1 1 0 1 2007 0 0 1 1 1 0 0 0 1 0 0 2008 1 0 1 1 1 0 0 1 1 0 2 2009 0 2 1 2 1 0 0 1 2 7 2 2010 2 1 1 1 1 1 1 3 2 1 0 2011 2 1 2 1 2 1 2 2 2 1 0 2012 2 1 1 1 1 1 1 1 2 2 1 2013 1 0 1 1 1 0 0 0 1 2 1 2014 1 0 1 1 1 0 0 0 1 0 1 2015 3 2 5 1 6 2 1 1 4 2 3 合计 13 8 14 11 15 5 5 10 17 14 11
1 1 ， cos x cos y ，求 sin( x y ), cos( x y ) 的值. 2 5
分析： 解决数学问题就是要建立已知与未知之间的联系， 本题的已知条件与问题之间很容易 发现下面的这个关系：
x y x y x , 2 2 y x y x y . 2 2
2015年清华大学自主招生数学试题
2015年清华大学自主招生试题注所有选择题均为不定项选择题．1、已知非负实数\(x,y,z\)满足\(4x^2+4y^2+z^2+2z=3\)，求\(5x+4y+3z\)的最大值．2、已知\(x^2+y^2\leqslant 1\)，求\(\left|x^2+2xy-y^2\right|\)的最大值．3、如图所示，已知函数\(f(x)\)与直线\(y=kx+m\)有两个切点，则\(g(x)=kx-f(x)\)有（）A．\(3\)个极大值点B．\(2\)个极小值点C．\(2\)个极大值点D．\(4\)个极小值点4、已知\(x,y,z\in\mathcal Z\)，且\(xy+yz+zx=1\)，则\(\left(1+x^2\right)\left(1+y^2\right)\left(1+z^2\right)\)的值可能是（）A．\(16900\)B．\(17900\)C．\(18900\)D．以上都不对5、一个以\(O\)为圆心的圆上的整数格点（横纵坐标都是整数）的点的个数可能是（）A．\(4\)B．\(6\)C．\(8\)D．\(12\)6、已知\(2x+y=1\)，求\(x+\sqrt{x^2+y^2}\)的最值．7、\(50\)个黑球和\(49\)个白球排成一排，则（）A．必有一个黑球右侧白球的数量等于黑球的数量B．必有一个白球右侧白球的数量等于黑球的数量C．必有一个黑球右侧黑球的数量比白球的数量多\(1\)D．必有一个白球右侧黑球的数量比白球的数量多\(1\)8、已知\(P=\left\{(x,y)\left|x^2+y^2=r^2\right.\right\}\)，\(Q=\left\{(x,y)\left|(x-a)^2+(y-b)^2=r^2\right.\right\}\)，已知\(P\capQ=\left\{(x_1,y_1),(x_2,y_2)\right\}\)，则（）A．\(a(x_1-x_2)+b(y_1-y_2)=0\)B．\(2ax_1+2by_1=a^2+b^2\)C．\(0<a^2+b^2<2r^2\)D．\(x_1+x_2=a\)，\(y_1+y_2=b\)9、一个正十五边形，任取其三个顶点构成三角形，可构成多少个钝角三角形？10、已知\(\overrightarrow{a}=\left(m\cos\theta_1,m\sin\theta_1\right)\)，\(\overrightarrow{b}=\left(m\cos\theta_2,m\cos\theta_2\right)\)，定义\(\overrightarrow{a}^{\frac 12}=\left(\sqrt m\cos\dfrac{\theta_1}{2},\sqrt m\sin\dfrac{\theta_1}{2}\right)\)，\(\overrightarrow{b}^{\frac12}=\left(\sqrt m\cos\dfrac{\theta_2}{2},\sqrtm\sin\dfrac{\theta_2}{2}\right)\)，则（）A．\(\left|\overrightarrow{a}^{\frac 12}\cdot \overrightarrow{b}^{\frac 12}\right|\)B．\(\left|\overrightarrow{a}^{\frac 12}+\overrightarrow{b}^{\frac12}\right|\geqslant 4\sqrt{mn}\cos^2\dfrac{\theta}{2}\)C．\(\left|\overrightarrow{a}^{\frac 12}-\overrightarrow{b}^{\frac12}\right|\geqslant 4\sqrt{mn}\sin^2\dfrac{\theta}{2}\)D．11、一个抛物线\(y^2=2px\)上有两个点\(A\)、\(B\)，则（）A．\(AB\)过抛物线焦点B．\(OA\cdot OB\leqslant ?\)C．\(OA^2+OB^2\leqslant ?\)D．\(O\)到\(AB\)的距离小于\(1\)12、点集\(A=\left\{(x,y)\left|\dfrac{\sin\pi x}{x^2-x+1}=y\right.\right\}\)，则（）A．曲线有对称轴B．\(A\subseteq \left\{(x,y)\left|-\dfrac 12\leqslant y\leqslant \dfrac12\right.\right\}\)C．曲线有对称中心。
2015年全国高校自主招生数学模拟试卷2
∴所求值=log2．
三、（本题满分20分）
设x≥y≥z≥，且x+y+z=，求乘积cosxsinycosz的最大值和最小值．
解：由于x≥y≥z≥，故≤x≤－×2=．
∴cosxsinycosz=cosx×[sin(y+z)+sin(y－z)]=cos2x+cosxsin(y－z)≥cos2=．即最小值．
(A)x100a，S100=2ba(B)x100b，S1002ba
(C)x100b，S100=ba(D)x100a，S100ba
解：x1=a，x2=b，x3=b－a，x4=－a，x5=－b，x6=a－b，x7=a，x8=b，…．易知此数列循环，xn+6=xn，于是x100=x4=－a，
又x1+x2+x3+x4+x5+x6=0，故S100=2b－a．选A．
(由于≤x≤，y≥z，故cosxsin(y－z)≥0)，当y=z=，x=时，cosxsinycosz=．
∵cosxsinycosz=cosz×[sin(x+y)－sin(x－y)]=cos2z－coszsin(x－y)．
三、（20分）
设x≥y≥z≥，且x+y+z，求乘积cosxsinycosz的最大值和最小值．
四、(20分)
设双曲线xy1的两支为C1，C2(如图)，正三角形PQR的三顶点位于此双曲线上．
(1)求证：P、Q、R不能都在双曲线的同一支上；
(2)设P(1，1)在C2上，Q、R在C1上，求顶点Q、R的坐标．
解：f(x)的对称轴为x=，
易得，0<α<<<β<<<γ<<<δ<．选B．
北京市清华大学附中2015届全国高校自主招生考试数学复习讲义：平面几何(无答案)
平面几何一、考试要求：平面几何是自主招生考试中北约、华约、卓越共同考查的内容，主要考查平 面图形中三边角关系以及长度、角度、面积的计算；考查学生逻辑思维能力，推理认证 能力及计算能力.二、知识准备：定理：梅涅劳斯定理：设△ABC 的三边BC 、CA 、AB 或他们的延长线与一条不经过其 顶点的直线交于P 、Q 、R 三点，则1=∙∙RBAR QA CQ PC BP . 梅涅劳斯逆定理：设P 、Q 、R 分别是△ABC 的三边BC 、CA 、AB 或他们的延 长线上三点，若有1=∙∙RBAR QA CQ PC BP ，则P 、Q 、R 三点在同一条直线上. 三、题型训练：类型一：凸多边形有关的计算或证明例1：（2012北约）求证：若圆内接五边形的两个角都相等，则它为正五边形.例2：（2008北约）求证：边长为1的正五边形对角线长为215+.例4：（2013北约）如果锐角△ABC 的外接圆圆心为O ，求O 到三角形三边距离比.例5：（2009北大）圆内接四边形ABCD 中，AB=1，BC=2，CD=3，DA=4.求圆的半径.例6：（2011北约）在△ABC 中，若c b a 2≥+，证明60≤∠c .其中∠A,∠B,∠C 的对 边 分别为c b a ,,. 例7：（2009中国科技大）如图：已知D ，E ，F 分别为BC ，AC ，AB 的三等分点.且EC ＝ ２AE ，BD ＝２CD ，AF ＝２BF ，若1=∆ABC S ，试求PQR S ∆.例８：（２０１１华约）如图，已知△ABC 的面积为２，D ，E 分别为边AB ，AC 上的点， F 为线段DE 上一点，设z DEDF y AC AE x AB AD ===,,，且1=-+x z y .则△BD 下面 积的最大值为（ ）A.278 B. 2710 C. 2714 D. 2716例9：（2010五校）如图，△ABC 的两条交线AD ，BE 交于H ，其外接圆圆心为O ，过O OF 垂直BC 于F ，OH 与AF 相交于G ，则△OFG 与△GAH 面积之比为（ ）A. 1:4B. 1:3C. 2:5D. 1:2例10：（2011北大保送）在△ABC 内有一点P ，满足PCA PAC PAB PBC ∠=∠=∠=∠. 求证：△ABC 的三边边长成等比数列.例11：（2009南京大学）P 为△ABC 内一点，它到三边BC ，CA ，AB 的距离分别为321,,d d d ，S 为△ABC 的面积.求证：sc b ad c d b d a 2)(2321++≥++（这里c b a ,,分别表示BC ， CA ，AB 的长）.例14：（2007克罗地亚国家采训队）已知：S 为△ABC 内一点，证明：当S 到△ABC 三边 距离的积取最大值时，S 为△ABC 的重心.例15：在锐角△ABC 中，111,,C B A 分别为BC ，CA ，AB 的中点，O 为△ABC 外接圆的圆 心，若外接圆半径为1，证明：6111111≥++OC OB OA .。
2015年清华大学自主招生试题数学试卷含解析
2015年清华⼤学⾃主招⽣试题数学试卷含解析2015年清华⼤学⾃主招⽣考试数学试卷⼀．选择题1.设复数z=cos 23π+isin 23π，则2111-1z z +-=（） (A)0 (B)1 (C)12 (D)322.设数列{}n a 为等差数列，p,q,k,l 为正整数，则“p+q>k+l ”是“p q k l a a a a +>+”的( )条件(A)充分不必要 (B)必要不充分 (C)充要 (D)既不充分也不必要3.设A 、B 是抛物线y=2x 上两点，O 是坐标原点，若OA ⊥OB,则( )(A)|OA|·|OB|≥2 (B)|OA|+|OB|≥(C)直线AB 过抛物线y=2x 的焦点 (D)O 到直线AB 的距离⼩于等于14.设函数()f x 的定义域为(-1,1)，且满⾜：①()f x >0,x ∈(-1,0)；②()f x +()f y =()1x y f xy++，x 、y ∈(-1,1)，则()f x 为 (A)奇函数 (B)偶函数 (C)减函数 (D)有界函数5.如图，已知直线y=kx+m 与曲线y=f (x)相切于两点，则F(x)=f (x)?kx 有（）(A)2个极⼤值点 (B)3个极⼤值点 (C)2个极⼩值点 (D)3个极⼩值点6.△ABC 的三边分别为a 、b 、c ．若c=2，∠C=3π，且sinC+sin(B ?A)?2sin2A=0,则有（）(A)b=2a (B)△ABC 的周长为△ABC 的⾯积为3(D)△ABC 的外接圆半径为7.设函数2()(3)x f x x e =-，则（）(A)()f x 有极⼩值，但⽆最⼩值 (B) ()f x 有极⼤值，但⽆最⼤值(C)若⽅程()f x =b 恰有⼀个实根，则b>36e(D)若⽅程()f x =b 恰有三个不同实根，则06e 8.已知A={(x,y)∣222x y r +=}，B={(x,y)∣222()()x a y b r -+-=，已知A∩B={(11,x y ),(22,x y )}，则（）(A)0<22a b +<22r (B)1212()(y )0a x x b y -+-=(C)12x x +=a ，12y y +=b (D)22a b +=1122ax by +9.已知⾮负实数x,y,z 满⾜22244x y z +++2z=3，则5x+4y+3z 的最⼩值为（）(A)1 (B)2 (C)3 (D)410.设数列{n a }的前n 项和为n S ，若对任意正整数n ，总存在正整数m ，使得n S =m a ，则（）（A ）{n a }可能为等差数列（B ）{n a }可能为等⽐数列（C ）{n a }的任意⼀项均可写成{n a }的两项之差(D)对任意正整数n ，总存在正整数m ，使得n a =m S11.运动会上，有6名选⼿参加100⽶⽐赛，观众甲猜测：4道或5道的选⼿得第⼀名；观众⼄猜测：3道的选⼿不可能得第⼀名；观众丙猜测：1,2,6道选⼿中的⼀位获得第⼀名；观众丁猜测：4,5,6道的选⼿都不可能获得第⼀名．⽐赛后发现没有并列名次，且甲、⼄、丙、丁中只有1⼈猜对⽐赛结果，此⼈是（）(A)甲 (B)⼄ (C)丙 (D)丁12.长⽅体ABCD ?1111A B C D 中，AB=2，AD=A 1A =1，则A 到平⾯1A BD 的距离为（）(A)13 (B)23 (C)2。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
）
A．奇函数 C．减函数
B．偶函数 D．有界函数
5、如图，已知直线 y kx m 与曲线 y f x 相切于两点，则 F x f x kx 有（
）
A．2 个极大值点 C．2 个极小值点
B．3 个极大值点 D．3 个极小值点
6、ABC 的三边分别为 a,b, c ．若 c 2 ，C ，且 sin C sinB A 2sin 2A 0 ,
D．若方程
f
x
b 恰有三个不同实根，则
0
b
6 e3
8 、 已 知 A x, y| x2 y2 r 2 ， B x, y| x a2 y b2 r 2 , 已 知
A B x1, y1, x2, y2 ，则（
A． 0 a2 b2 2r 2
）
B． ax1 x2 by1 y2 0
3
则（
）
A． b 2a
B． ABC 的周长为 2 2 3
C． ABC 的面积为 2 3 3
7、设函数 f x x2 3 ex ，则（
D． ABC 的外接圆半径为 2 3 3
）
A． f x 有极小值，但无最小值
B． f x 有极大值，但无最大值
C．若方程
f
x
b 恰有一个实根，则 b
6 e3
4
21、设数列 an满足：
a1
6
，
an1
n
n
3
an
，则（
）
A． n N , an n 13
B． n N , an 2015
C． n N ， an 为完全平方数
D． n N ， an 为完全立方数
22、在极坐标系中，下列方程表示的图形是椭圆的有（
）
A．
1
cos sin
C． 1 2 cos
C． x1 x2 a , y1 y2 b
D． a2 b2 2ax1 2by1
9、已知非负实数 x, y, z 满足 4x2 4 y2 z2 2z 3 ，则 5x 4 y 3z 的最小值为（ ）
A．1 C．3
B．2 D．4
10、设数列 an的前 n 项和为 Sn ，若对任意正整数 n ，总存在正整数 m ，使得 Sn am ，
3
D．
2
2、设 an为等差数列， p, q, k, l 为正整数，则“ p q k l ”是“ ap aq ak al ”的
（
）
A．充分不必要条件
C．充分必要条件
B．必要不充分条件 D．既不充分也不必要条件
3、设 A, B 是抛物线 y x2 上的两点， O 是坐标原点．若 OA OB ，则（ ）
23、设函数 f x sin x ，则（
x2 x 1
A． f x 4
3
B． 1 2 sin
D． 1 2 2sin
）
B． f x 5 x
C．曲线 y f x 存在对称轴
D．曲线 y f x 存在对称中心
24、 ABC 的三边分别为 a, b, c ，若 ABC 为锐角三角形，则（
B． L 是中心对称图形
C． L x, y| x2 y2 1
D．
L
x,
y|
1 2
y
1
2
题号
1
答案
B
题号 11
答案
D
题号 21
答案 AB
参考答案
2
3
4
5
6
7
8
9
10
D
ABD
AC
BC
BCD
BD
BCD
C
AC
12
13
14
15
16
17
18
19
20
B
ABD
D
ABC
BD
C
ACD ACD BCD
22
23
则（
）
A． an可能为等差数列
B． an可能为等比数列
C． an的任意一项均可写成 an的两项之差
D．对任意正整数 n ，总存在正整数 m ，使得 an Sm
11、运动会上，有 6 名选手参加 100 米比赛，观众甲猜测：4 道或 5 道的选手得第一名；观 众乙猜测：3 道的选手不可能得第一名；观众丙猜测：1,2,6 道选手中的一位获得第一名；
）
A． sin A cos B
B． tan A cot B
C． a2 b2 c2
D． a3 b3 c3
25、设函数 f x 的定义域是 1,1 ，若 f 0 f '0 1 ，则存在实数 0,1 ，使得（ ）
A． f x 0, x ,
B． f x 在 , 上单调递增
C． f x 1, x 0,
）
3
A．最小值为
4
4
B．最小值为
5
4
C．最大值为
3
5
D．最大值为
4
17、从正十五边形的顶点中选出 3 个构成钝角三角形，则不同的选法有（
）
A．105 种
B．225 种
C．315 种
D．420 种
18、已知存在实数 r ，使得圆周 x2 y2 r 2 上恰好有 n 个整点，则 n 可以等于（ ）
A．4
2015 年清华大学自主选拔数学试题
说明：本试卷共 30 小题，共 100 分．在每小题给出的四个选项中，有一个或多个选项是符
合题目要求的．全部选对的，得满分；选对但不全的，得部分分；有选错的，得 0 分．
1、设复数 z
cos
2 3
i sin
2 3
1
，则
1 z
1 1 z2
（
）
A．0
B．1
1
C．
2
观众丁猜测：4,5,6 道的选手都不可能获得第一名．比赛后发现没有并列名次，且甲、乙、
丙、丁中只有 1 人猜对比赛结果，此人是（
）
A．甲
B．乙
C．丙
D．丁
12、长方体 ABCD A1B1C1D1 中， AB 2 ， AD AA1 1，则 A 到平面 A1BD 的距离为
（）
1
A．
3
2
B．
3
2
C．
2
6
D．
3
x y 2,
13、设不等式组
y
2
k
x
1,
所表示的区域为ຫໍສະໝຸດ D，其面积为S
，则（
）
A．若 S 4 ，则 k 的值唯一 B．若 S 12 ，则 k 的值有 2 个 C．若 D 为三角形，则 0 k 2
3 D．若 D 为五边形，则 k 4
14、 ABC 的三边长是 2,3,4，其外心为 O ，则 OA AB OB BC OC CA （ ）
29、从 1,2,3,4,5 中挑出三个不同数字组成五位数，其中有两个数字各用两次，例如 12231，
则能得到的不同的五位数有（
）
A．300 个
B．450 个
C．900 个
D．1800 个
30、设曲线 L 的方程为 y4 2x2 2 y2 x4 2x2 0 ，则（
）
A． L 是轴对称图形
A．0
B．−15
C． 21
D． 29
2
2
15、设随机事件 A 与 B 互相独立，且 PB 0.5 ， PA B 0.2 ，则（ ）
A． PA 0.4 B． PB A 0.3 C． PAB 0.2 D． PA B 0.9
16、过 ABC 的重心作直线将 ABC 分成两部分，则这两部分的面积之比的（
B．6
C．8
D．12
19、设复数 z 满足 2 z z 1 ，则（
）
A． z 的最大值为 1 2
C． z 的虚部的最大值为 3
1 B． z 的最小值为
3 1
D． z 的实部的最大值为 3
20、设 m, n 是大于零的实数，向量 a m cos , m sin ， b n cos , n sin ，其中
）
4
A．最小值为
5
2
B．最小值为
5
C．最大值为 1
1 2
D．最大值为
3
28、对于 50 个黑球和 49 个白球的任意排列（从左到右排成一行），则（
）
A．存在一个黑球，它右侧的白球和黑球一样多
B．存在一个白球，它右侧的白球和黑球一样多
C．存在一个黑球，它右侧的白球比黑球少一个
D．存在一个白球，它右侧的白球比黑球少一个
24
25
26
27
28
29
30
BC
ABC ABC
AC
B
AC
A
C
ABD
,
1
0,2 ．定义向量 a 2
m cos ,
m sin
1
，b 2
n cos ,
n sin ，记
2
2
2
2
，则（
）
11
A． a 2 a 2 a
11
B． a 2 b 2
mn cos
2
1
12
C． a 2 b 2 4
mn sin2
4
1
12
D． a 2 b 2 4
mn cos2
A． OA OB 2
B． OA OB 2 2
C．直线 AB 过抛物线 y x2 的焦点 D． O 到直线 AB 的距离小于等于 1
4、设函数 f x 的定义域为 1,1 ，且满足：
① f x 0 ， x 1,0 ；② f x f y f 1xxyy , x, y 1,1.
则 f x 为（
D． f x 1, x ,0