堆芯一维中子扩散方程的数值解法(通用型)
合集下载
CANDU反应堆物理数值计算技术
RFSP 程序中使用的是 POWDERPUFS-V 的栅元程序 。 2． 超栅元计算
由 于 CANDU 反 应 堆 的 堆 芯 内 部 存 在 的 一 系 列 反 应 性 控制装置和结构材料与燃 料 通道 成 正 交 垂 直方 位 ， 因 此 在对 基 本 栅 元 计 算 时 ，无 法 考 虑 它 们 的 影 响 ，必 须 建 立 一 种 反 应 堆 基 本 单 元 模 型 ：使 用 笛 卡 儿 坐 标 ，采 用 一 种 超 栅 元 计 算 模 型 （ 参见图 2 ）。 该模型由基本栅元和垂直于栅元的反应性装 置组成 ， 然后计算反应性 装 置 对最 接 近 的 相邻 网 格 区 域中 基 本的栅元特性的改变 （ 增 加 的 截 面 ）， 最 后 得 到 反应 性 装 置 相 应对基本栅元造成的增量截 面 ， 用 于 堆 芯模 拟 中 的 反应 性 装 置的反应性计算 。 栅元的综合截面＝栅元的基本截面＋反应性设备增量截面 计算程序 ：MUTICELL （ 扩散程序 ） 此外 ，DRAGON 也可计算反应性装置的反应性 。
1. RFSP 中的节点模型 RFSP 程序采用有限差分法求解中子扩散方程 。 首先 ，要引
入一系列网格点将堆芯离散化 ，这里使用全堆芯 48×32×40（X,Y,
Z）网格模型 。 所有的反应性控制装置和结构材料都被包含在模
型中 ，诸如 ：调节棒和调节棒导向管 、停堆棒和停堆棒导向管 、轻 水区域控制器、2 号停堆系统的毒物喷嘴等。
量分布：
●求解两群三维的有限差分中子扩散方程 ●使用通量绘图的方法进行谐波拟合 RFSP 能进行燃料管理计算，按照给定的时间步长和该时间
段的换料通道 ，模拟反应堆的运行历史 ，这就是 RFSP 命名的由 来。
赞 Fi(t)， 所以 堆芯棒束 i 的燃耗为 ωi(t) ， 棒束所在位置的通量为 Φ 赞 Fi(t)△t。 然后调用 当前堆芯中每个棒束的燃耗 ωi(t+△t)=ωi(t)+Φ
第四章：均匀反应堆的临界理论
一、反射层节省
在芯部包有反射层以后，芯部临界大小尺寸的减少量通常可以用
反射层节省 来表示。 对于圆柱形反应堆，反射层节省通常分别用径向和轴向的反射层节 省来表示，即
反射层对临界的影响可以用反射层节省这个量来表示。它表示反应堆由 于加上反射层所引起的临界尺寸的减少。因此，可以把有反射层反应堆 的几何曲率用芯部外形尺寸增大2δ 后的等效裸堆的几何曲率来表示。
1 2 2 1 L Bg
不泄漏几率
k k P
1
L
1
再次说明，k1是有效增殖系数
1 B: PL 2 2 1 L Bg
反应堆的中子泄漏不仅与扩散长度有关，而且与
几何曲率有关。从前面平板状反应堆的例子中可以看 到，当反应堆体积增大时，Bg2就减小，因而正如所预 料的那样，不泄漏几率也就增大。 同样，扩散长度 L 愈大，意味着中子自产生到 被吸收所穿行的距离也愈大，因而从反应堆中泄漏出 去的几率也就增大，不泄漏几率PL就要减小
2 对于给定的曲率 Bg ，对芯部半径为 R0 的球形裸堆有
2 Bg R0
2
R B g
2 0
2
设具有反射层时芯部的临界半径为R，则
Bg
R
R
对有反射层的球形堆有
2 Bg (
)2
可以把有反射层的球形堆的几何曲率用一个尺寸等于 R 的等效 裸堆的几何曲率来表示
芯部
反 射 层 反 射 层
k<1，调整k∞使 其临界
① 带有反射层的球形堆
考虑一个芯部半径为R，带有厚度为T（包括外推距离在内）的反射层 的球形堆。采用球坐标系，并把坐标远点取在球心上。根据中子通量 密度在堆内处处为有限值的条件，得到芯部方程
核反应堆物理基础第3章
中子从dV内泄漏的总数应等于以上三项之和，这样，单位时间， 单位体积泄漏出去的中子数
L D D D x x y y z z
（3-15）
若护散系数D与空间位置无关，那么便得到
u Ae
r / L
Ce
r/L
因此
er / L er / L (r ) A C r r
式中A，C为两个待定常数，可以由边界条件确定 C必须为零，否则当r趋于无限大时，φ便变为无限大 常数A由中子源条件求出
r 0
J (r ) D
d 1 1 DA 2 e r / L dr rL r
s dA 2 2 J dA (r )e s r cos sin drd d 4 0 0 0
z
s dA 2 2 J dA (r )e s r cos sin drd d 4 0 0 0
z
其中， J z
得
A
SL 2D
最后得中子通量密度
( x)
SL x / L e 2D
根据对称性，只需将式中的x用 x 代替，源平面 左边介质内的中子通量密度即可得到。
第三章 单速中子扩散
§3.1 单速中子扩散方程
§3.2
§3.3
非增殖介质内中子扩散方程的解 扩散长度
§3.4 与能量相关的中子扩散方程
基本概念
中子角密度:
n(t , r, v, )
中子角通量密度:
n(t , r, v, )v (t , r, v, )
稳态情况
中子角密度: 中子角通量密度: 一、中子流密度:
如果之间有一夹角
第三章 中子扩散理论
J z (r ) J z (r ) J z (r )
s (r )
3 z
J z (r ) 叫做z方向的中子流密度或净中子流密度，若dA的取向
与x轴垂直，沿着x方向穿过dA平面单位面积净中子数Jx为
J x (r )
s ( r )
3 x
同样，沿着y方向穿过dA平面单位面积净中子数Jy为
推导中并没有考虑中子源的贡献，中子流密度的贡献只 是来自中子与介质核的散射碰撞 在强中子源两三个平均自由程的区域内，斐克定律不 适用。
3.2 非增殖介质内中子扩散方程的解
稳态单能的中子扩散方程
D2 (r ) a (r ) S (r ) 0
无源情况下，即除中子源所在的位置以外的无源区域,扩散 方程有以下形式: 1 D (r ) 2 2 2 2 L ( r ) 0 (r ) (r ) 0 或 k2 L2
第三章 中子扩散理论
中子在介质中的输运过程中 的运动状态由位置矢量r(x,y,z), 能量 E, 和运动方向Ω表示。 Ω通过极角θ 和方位角φ 来 表示
dS r 2 sin dd d 2 sin dd 2 r r
中子角密度函数n(r,E, Ω)定义： 方向 Ω的表示 在r处单位体积内和能量为E的 单位能量间隔内，运动方向为 Ω的单位立体角内的中子数目。 中子角通量密度定义为: ( r, E, ) n( r , E, )v( E ) 对中子角密度和中子角通量密度积分便可得到与运动方向无 关的标量中子密度和标量中子通量密度
4
tr d
6 dx
0
d dx
x 0
30 2tr
应用输运理论和扩散理论的 外推距离求得的扩散方程的解
s (r )
3 z
J z (r ) 叫做z方向的中子流密度或净中子流密度，若dA的取向
与x轴垂直，沿着x方向穿过dA平面单位面积净中子数Jx为
J x (r )
s ( r )
3 x
同样，沿着y方向穿过dA平面单位面积净中子数Jy为
推导中并没有考虑中子源的贡献，中子流密度的贡献只 是来自中子与介质核的散射碰撞 在强中子源两三个平均自由程的区域内，斐克定律不 适用。
3.2 非增殖介质内中子扩散方程的解
稳态单能的中子扩散方程
D2 (r ) a (r ) S (r ) 0
无源情况下，即除中子源所在的位置以外的无源区域,扩散 方程有以下形式: 1 D (r ) 2 2 2 2 L ( r ) 0 (r ) (r ) 0 或 k2 L2
第三章 中子扩散理论
中子在介质中的输运过程中 的运动状态由位置矢量r(x,y,z), 能量 E, 和运动方向Ω表示。 Ω通过极角θ 和方位角φ 来 表示
dS r 2 sin dd d 2 sin dd 2 r r
中子角密度函数n(r,E, Ω)定义： 方向 Ω的表示 在r处单位体积内和能量为E的 单位能量间隔内，运动方向为 Ω的单位立体角内的中子数目。 中子角通量密度定义为: ( r, E, ) n( r , E, )v( E ) 对中子角密度和中子角通量密度积分便可得到与运动方向无 关的标量中子密度和标量中子通量密度
4
tr d
6 dx
0
d dx
x 0
30 2tr
应用输运理论和扩散理论的 外推距离求得的扩散方程的解
一维对流扩散方程的数值解法
一维对流扩散方程的数值解法对流-扩散方程是守恒定律控制方程的一种模型方程，它既是能量方程的表示形式，同时也可以认为是把压力梯度项隐含到了源项中去的动量方程的代表。
因此，以对流-扩散方程为例，来研究数值求解偏微分方程的相容性、收敛性和稳定性具有代表性的意义。
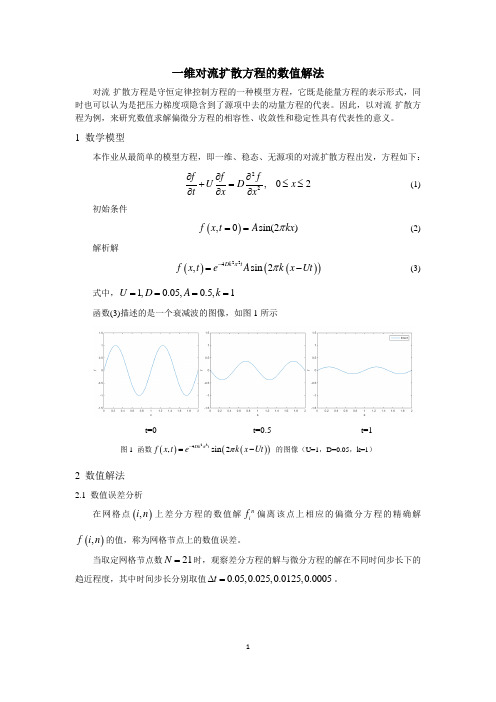
1 数学模型本作业从最简单的模型方程，即一维、稳态、无源项的对流扩散方程出发，方程如下： 22, 02f f fU D x t x x∂∂∂+=≤≤∂∂∂ (1)初始条件 (),0sin(2)f x t A kx π==(2)解析解()()()224,sin 2Dk tf x t eA k x Ut ππ-=-(3)式中，1,0.05,0.5,1U D A k ====函数(3)描述的是一个衰减波的图像，如图1所示t=0 t=0.5 t=1图1 函数()()()224,sin 2Dk tf x t ek x Ut ππ-=- 的图像（U=1，D=0.05，k=1）2 数值解法2.1 数值误差分析在网格点(),i n 上差分方程的数值解ni f 偏离该点上相应的偏微分方程的精确解(),f i n 的值，称为网格节点上的数值误差。
当取定网格节点数21N =时，观察差分方程的解与微分方程的解在不同时间步长下的趋近程度，其中时间步长分别取值0.05,0.025,0.0125,0.0005t ∆=。
（a ）21,0.05N t =∆= （b ）21,0.025N t =∆=（c ）21,0.0125N t =∆= （d ）201,0.0005N t =∆=图2 数值误差随步长的变化情况从图2的(a)~(d)可以定性的看出，数值误差与步长的大小有关。
在满足稳定性条件的前提下，数值误差随着时间步长的减小而减小，同时，图（d ）表示增大网格的分辨率也有助于减小网格误差。
为了对数值误差有一个定量的认识，接下来取定时间步长为0.0005t ∆=，分别算出11,21,41,61,81,101,121,161N =时，指标E =1所示。
第3章反应堆物理设计计算
常用的反射层材料有：水、重水、石墨和铍等。
19
反射层节省
在芯部包有反射层以后，芯部临界大小的减少量称为反射层 节省，用δ表示。 对圆柱形反应堆： 径向反射层 节省：
2.405 2 2 Bc Br2 Bz R H eff eff
2 2
r Reff R
29
压水堆的非均匀化计算
（1）堆芯最基本单元的栅元均匀化。 空间均匀化：将栅元等效成简单的一维圆柱，能 量和能群简并，采用多群近似。 计算方法：输运方程→碰撞概率法；Sn直接离散 →中子通量按能量的分布φn,i。 （2）利用栅元均匀化结果对燃料组件进行均匀化、并 群计算。 计算方法：穿透概率法、直接离散。按通量-体积 权重，并群求出组件的均匀化少群常数。 （3）利用得到的少群常数，做全堆芯的扩散计算， 求出keff和功率、中子通量分布。 计算方法：有限差分、节块法。 少群常数并非不变，受燃料密度影响很大。 30
(r, z) r R 0
z
z 0
(r , z )
z
H 2
0
0
r
r 0
0
8
有限高圆柱形均匀裸堆
几何曲率：
2 B2 R H
临界时其高度H与半径R须满足：
B2 k 1 2.405 2 ( ) ( )2 R H L2
中子通量密度分布不均匀系数
中子通量密度分布不均匀系数定义为堆芯最大热中子通量密 度与堆芯平均热中子通量密度的比值，即：
max KV
最大中子通量密度 平均中子通量密度
(r, z)dv 1 (r, z)dv V dv
V V V
哈尔滨工业大学计算传热学第四章扩散方程的数值解法及其应用资料重点
1
y
xw
TP
aETE
aNTN
aSTS
1
y
xw
Tf
Scxy
kB
kB
所以对第三类边界条件不仅有附加常数源项，而且还有 附加源项的斜率项
aPTP aETE aNTN aSTS (Sc•ad Sc )xy
aP aE 0 aN aS (Sp•ad Sp )xy
Sp•ad
y xy
a)算术平均线性分布
ke
kp
xe+ xe
kE
xe xe
e
••
•
W
Pxe xe E
xe
b)调和平均
qe
TE TP
xe
ke
TE Te
xe
kE
Te Tp
xe
kp
TE
xe
kE
TP
xe
kP
ke
kP kExe xek p xekE
当 xe xe
kP kE
算术平均
ke
kP
kE 2
kP 2
第四章 扩散方程的数值解法及其应用
§4.1 一维稳态导热
1 • d [kF(x) dT ] S 0
F (x) dx
dx
F(x)：与坐标系和截面形状有关的计算因子
S：内热源。
w
e
△x
e d
dT
[kF (x) ]dx
w dx
dx
e
F (x) • Sdx 0
w
•
W
xw
•
P
xe
•
E
keFe
W PE
ap
Fe k e
xe
反应堆物理数值计算
核科学与技术学院
25
Harbin Engineering University
四个节块共32个系数，需32个方程。 1. 四个相邻节块平均中子通量密度，可建立四个方程。
2. 节块间平均偏通通量密，可建立四个方程。
核科学与技术学院
26
Harbin Engineering University
3. 交界面上平均偏中子通量密度对应的净中子流，确定 四个方程
从而得
（5-158）
（5-159）
核科学与技术学院 12
Harbin Engineering University
则（5-159）式可表示为
（5-161）
（5-162）
核科学与技术学院
13
Harbin Engineering University
比较上述两式，可知
（5-163）
上式结合双曲函数定义及（5-135）式通过更复杂的运算， 由（5-138）及（5-140）可得（5-145）式，其系数矩阵为
4. 节块界面偏中子通量连续，确定四个方程
核科学与技术学院
27
Harbin Engineering University
5. 交界面上偏净中子流连续，确定四个方程
核科学与技术学院
28
Harbin Engineering University
6. 角点处连续性条件，确定七个方程。
核科学与技术学院
29
令 则
同理可得v、w方向上类似的横向积分中子通量密度方程。 （5-177）式是非齐次方程，对泄漏项源，采用二次函 数逼近。
核科学与技术学院
18
Harbin Engineering University
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
10-11-17 下午1:11
F:\my_matlab\core_1D.m
3 of 3
flux_fast=tdma(a1,b1,c1,d1);%解出快群. %慢群 d2=[]; for i=1:N for j=1:n d2(j+(i-1)*n)=E12(m(i))*flux_fast(j+(i-1)*n)*dx; end end d2(1)=d2(1)+2*f_left*D(m(1),2)/dx; d2(N*n)=d2(N*n)+2*f_right*D(m(N),2)/dx; flux_slow=tdma(a2,b2,c2,d2);%解出慢群. for i=1:N for j=1:n Q_new(j+(i-1)*n)=flux_fast(j+(i-1)*n)*vEf(m(i),1)+flux_slow(j+(i-1)*n)*vEf(m(i),2); end end %更新源项. keff_new=sum(Q_new)*dx/(sum(Q_old)*dx/keff_old);%更新keff. e_keff=abs((keff_new-keff_old)/(keff_new+eps)); keff_old=keff_new; e_Q=max(abs((Q_new-Q_old)./(Q_new+eps))); Q_old=Q_new; cycle=cycle+1;%记录循环次数. if e_keff<error_keff && e_Q<error_Q break; end end %归一化. flux_fast=flux_fast/(sum(flux_fast)); flux_slow=flux_slow/(sum(flux_slow)); Q=Q_new'; Q=N*L*Q/(dx*sum(Q)); keff=keff_new; end
10-11-17 下午1:11
F:\my_matlab\core_1D.m
2 of 3
end a1(1)=3*D(m(1),1)/dx+Ea(m(1),1)*dx+E12(m(1))*dx; a1(N*n)=3*D(m(N),1)/dx+Ea(m(N),1)*dx+E12(m(N))*dx; for i=1:N b1=[b1,-(D(m(i),1)/dx)*ones(1,n)]; end for i=1:N-1 b1(i*n)=-2*D(m(i),1)*D(m(i+1),1)/((D(m(i),1)+D(m(i+1),1))*dx); end for i=1:N c1=[c1,(-D(m(i),1)/dx)*ones(1,n)]; end for i=1:N-1 c1(i*n+1)=-2*D(m(i),1)*D(m(i+1),1)/((D(m(i),1)+D(m(i+1),1))*dx); end %三对角矩阵系数的对角系数向量计算-慢群 a2=[];b2=[];c2=[]; for i=1:N a2=[a2,(Ea(m(i),2)*dx+2*D(m(i),2)/dx)*ones(1,n)]; end for i=1:N-1 a2(i*n)=Ea(m(i),2)*dx+(D(m(i),2)^2+3*D(m(i),2)*D(m(i+1),2))/((D(m(i),2)+D(m(i+1),2))*dx); a2(i*n+1)=Ea(m(i+1),2)*dx+(D(m(i+1),2)^2+3*D(m(i),2)*D(m(i+1),2))/((D(m(i),2)+D(m(i+1),2))*dx); end a2(1)=3*D(m(1),2)/dx+Ea(m(1),2)*dx; a2(N*n)=3*D(m(N),2)/dx+Ea(m(N),2)*dx; for i=1:N b2=[b2,(-D(m(i),2)/dx)*ones(1,n)]; end for i=1:N-1 b2(n*i)=-2*D(m(i),2)*D(m(i+1),2)/((D(m(i),2)+D(m(i+1),2))*dx); end for i=1:N c2=[c2,(-D(m(i),2)/dx)*ones(1,n)]; end for i=1:N-1 c2(i*n+1)=-2*D(m(i),2)*D(m(i+1),2)/((D(m(i),2)+D(m(i+1),2))*dx); end %迭代计算 while(1) %快群 d1=[]; d1=Q_old*dx/keff_old; d1(1)=d1(1)+2*f_left*D(m(1),1)/dx; d1(N*n)=d1(N*n)+2*f_right*D(m(1),1)/dx;
10-11-17 下午1:11
F:\my_matlab\core_1D.m
1 of 3
function [keff flux_fast flux_slow Q]=core_1D(m) %m为燃料排布,L为结块长度,N为结块数目,n为每个结块划分份额. %材料参数. Ea=[1.071240E-02 9.389003E-02 8.915481E-03 9.007146E-02 1.033911E-02 9.685340E-02 9.920272E-03 9.850721E-02 1.033911E-02 9.685340E-02 9.616552E-03 9.824058E-02 3.064667E-03 4.777252E-02 8.603110E-03 7.853440E-02]; vEf=[4.334360E-03 1.029336E-01 6.260639E-03 1.217170E-01 4.769662E-03 1.141428E-01 5.251954E-03 1.232079E-01 4.769662E-03 1.141428E-01 5.555385E-03 1.264411E-01 0.000000E+00 0.000000E+00 6.160544E-03 1.207603E-01]; E12=[1.771023E-02 1.812268E-02 1.770407E-02 1.776033E-02 1.770407E-02 1.785182E-02 2.090091E-02 1.708523E-02]; D=[1.378098E+00 3.437887E-01 1.373819E+00 3.542306E-01 1.376979E+00 3.443704E-01 1.376071E+00 3.457435E-01 1.376979E+00 3.443704E-01 1.375501E+00 3.472169E-01 1.134501E+00 2.587405E-01 1.407447E+00 0.3670093E+0]; L=20;n=20;N=length(m); dx=L/n;%等边距划分,dx为每份宽度. Q_old=10*ones(1,N*n);keff_old=1.7;%设置初始值. error_keff=1e-6;error_Q=1e-5;%方程收敛验收系数. cycle=0;%存储计算循环次数. f_left=0;f_right=0;%边界条件. %三对角矩阵系数的对角系数向量计算-快群. a1=[];b1=[];c1=[]; for i=1:N a1=[a1,(Ea(m(i),1)*dx+E12(m(i))*dx+2*D(m(i),1)/dx)*ones(1,n)]; end for i=1:N-1 a1(i*n)=(Ea(m(i),1)+E12(m(i)))*dx+(D(m(i),1)^2+3*D(m(i),1)*D(m(i+1),1))/((D(m(i),1)+D(m(i+1),1)) *dx); a1(i*n+1)=(Ea(m(i+1),1)+E12(m(i+1)))*dx+(D(m(i+1),1)^2+3*D(m(i),1)*D(m(i+1),1))/((D(m(i),1)+D(m (i+1),1))dx);