一维扩散方程数值解法
扩散方程的数值解法及应用-热流问题的数值计算-课件-04

a PTP a E TE aW TW a N TN a S TS b
其中
r aE re ( ) e / e
r aW rw ( ) w / w
0 P
rn aN (r ) n / n
rs aS (r ) s / s
( c) P V a V 0.5(rn rs )r t
因为离散方程都可表示为
a PTP anbTnb b
aP anb S P V
线性代数方程迭代求解收敛的一个充分必 要条件是对角占优,即:
a P anb
要求
SP 0
4. 由代数方程迭代求解的公式
TP
a a
nb nb
T b
nb
S P V
SP绝对值的大小影响到迭代过程中温度的 变化速度,SP的绝对值越大,系统的惯性越大, 相邻两次迭代之间TP的变化越小,收敛速度下 降,但有利于克服迭代过程的发散;SP的绝对 值小,可使变化率加快,但容易引起发散。
由式(5),可得
0 TP aP (1 f )aE (1 f )aW 1 2(1 f ) FO 0 TP aP 1 2 fFO
FO
at 2 x
为网格Fourier数。
从物理概念上,TP与前一时层的温度 之比应永远为正值,并随时间的增长而 0 趋近于0。在不同的f下, P / TP随 FO T 的变化如图所示:图4-3。 只有全隐格 式才能满足要求,任何f<1的格式, 当 FO大于一定值后都会出现物理 上不真 实的解。
(1)
4.1.2 用控制容积积分法导出通用方程的 离散形式
假定源项S在任一控制容积内中的值可以表 示温度的线性函数:
扩散方程的数值差分解法

扩散方程的数值差分解法作者:刘浩庭来源:《价值工程》2019年第29期摘要:扩散现象是其初始密度不均匀分布引起的,它会对物质粒子的分布状态产生影响,最终达到物质在空间均匀分布状态。
本研究通过分离变量法对给定条件的粒子浓度在一维空间分布下的扩散现象的解析解进行计算,同时结合使用欧拉法利用计算物理的方法对扩散过程进行了数值模拟。
通过对比理论数据与模拟实验数据对等离子体一维扩散现象进行阐释与讨论。
Abstract: The diffusion phenomenon is caused by the difference of the initial density. It affects the motion of the particles and finally make all the particles into the uniformly distribution. In this study, the analytical solution of the diffusion phenomenon of a given particle concentration in a one-dimensional space is calculated by using the method of separation of variables, and the diffusion process is simulated numerically by using the computational physics method combined with Euler's polygonal arc method. The one-dimensional plasma diffusion phenomenon is explained by comparing the theoretical data with the simulated experimental data.關键词:一维扩散;分离变量法;欧拉法Key words: one-dimensional diffusion;the method of separation of variables;Euler's polygonal arc method中图分类号:O122.2; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ;文献标识码:A; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; 文章编号:1006-4311(2019)29-0272-041; 简介受控热核聚变是受世人瞩目的前沿重要课题,其目的便是探索清洁可持续的新能源。
土体一维传热方程解析解及热扩散系数测定

T (t) = D + A ⋅ sin(ωt) ,
(22)
式中,D 表示平均温度,A 为温度波动幅度,即振幅。
下面将证明,在地下深度为 z 处的温度是深度 z 的函
数。由式(22),该式对应的傅里叶级数系数分别为
a0 = D, ⎫
a1
=
1 2j
当土体中有水分存在时,表示热导率比空气大 30 倍的水(参见表 2)在一定程度上取代了空气,这样, 土体热导率将随土体湿度的增加而增大,其增长速度
在湿度比较小时比较显著,然后随着湿度的继续增加,
热导率增长速度慢慢降低。
表 2 不同物质的热导率λ
Table 2 Thermal conductivity of some materials 单位: W/(m·k)
绍了该方法的应用效果。 关键词:热导率;热扩散系数;传热方程;地温梯度
中图分类号:TU441
文献标识码:A
文章编号:1000–4548(2008)05–0652–06
作者简介:涂新斌(1971– ),湖北孝感人,博士,主要从事工程地质、岩土工程研究。E-mail: tuxinbin@。
物质 λ
物质
λ
物质
λ
纯铜 398.00 大理石 2.700 水(0℃) 0.5510
黄铜 109.00 壤土 1.256 水(20℃) 0.6280
钢
36.70 砂土 1.172
蒸汽
0.0183
铁
29.10 冰
2.093 空气(0℃) 0.0244
花岗岩 4.06 冰(0℃) 2.220 空气(20℃) 0.0260
其边界条件为
T (0,t) = T (t) 。
(12)
第四章扩散方程的数值求解

非线性代数方程组的求解流程
给定节点上的温度值T* aPTP = aETE + aW TW + b
计算差分方程的系数和源项 a*PTP = a*ETE + a*WTW + b*
求解线性代数方程组,得到新的温度分布T
T → T*
Max T − T * < ε? Y 结束
N
例子
d2T d2x
+
f
(
x)
=
0
x
中国科学院研究生院2010年春季
3
T(K) T(K)
T(K) T(K)
x= 0 ∆x
1
i= 1 2 … i-1 i i+1 … ∆x=1/(n-1)
…
n
中国科学院研究生院2010年春季
500
prediction accuracy solution D-D,T(1)=300,T(100)=500,f(x)=600x
aPTP = aETE + a W TW + b
系数是待 求温度的 函数
线性代数方程组
线性代数 方程组的 求解方法
非线性代数方程组 线化
温度场
假定温度场
中国科学院研究生院2010年春季
非线性代数方程组的求解步骤
1、在所有各个网格节点上,猜测或估计或假定一个T值 2、用这些估计的T值去计算差分方程中的所有系数,从而差 分方程中的所有系数变成了已知量,而使差分方程变成了线性 方程。 3、求解上边的线性方程组,得到各离散点新T值。 4、用新得到的T值去计算差分方程中的所有系数,并返回第 3步求解系数发生了变化的线性差分方程。重复3、4这个过程, 直到重复计算不在引起T值任何有意义的变化为止。
一维对流扩散方程的数值解法
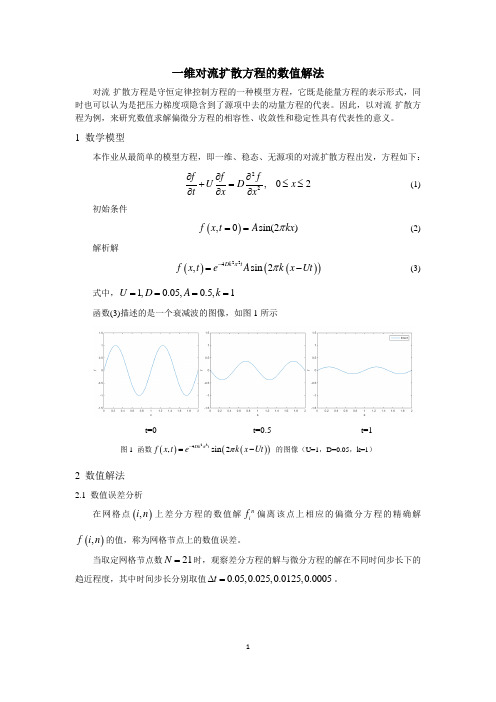
一维对流扩散方程的数值解法对流-扩散方程是守恒定律控制方程的一种模型方程,它既是能量方程的表示形式,同时也可以认为是把压力梯度项隐含到了源项中去的动量方程的代表。
因此,以对流-扩散方程为例,来研究数值求解偏微分方程的相容性、收敛性和稳定性具有代表性的意义。
1 数学模型本作业从最简单的模型方程,即一维、稳态、无源项的对流扩散方程出发,方程如下: 22, 02f f fU D x t x x∂∂∂+=≤≤∂∂∂ (1)初始条件 (),0sin(2)f x t A kx π==(2)解析解()()()224,sin 2Dk tf x t eA k x Ut ππ-=-(3)式中,1,0.05,0.5,1U D A k ====函数(3)描述的是一个衰减波的图像,如图1所示t=0 t=0.5 t=1图1 函数()()()224,sin 2Dk tf x t ek x Ut ππ-=- 的图像(U=1,D=0.05,k=1)2 数值解法2.1 数值误差分析在网格点(),i n 上差分方程的数值解ni f 偏离该点上相应的偏微分方程的精确解(),f i n 的值,称为网格节点上的数值误差。
当取定网格节点数21N =时,观察差分方程的解与微分方程的解在不同时间步长下的趋近程度,其中时间步长分别取值0.05,0.025,0.0125,0.0005t ∆=。
(a )21,0.05N t =∆= (b )21,0.025N t =∆=(c )21,0.0125N t =∆= (d )201,0.0005N t =∆=图2 数值误差随步长的变化情况从图2的(a)~(d)可以定性的看出,数值误差与步长的大小有关。
在满足稳定性条件的前提下,数值误差随着时间步长的减小而减小,同时,图(d )表示增大网格的分辨率也有助于减小网格误差。
为了对数值误差有一个定量的认识,接下来取定时间步长为0.0005t ∆=,分别算出11,21,41,61,81,101,121,161N =时,指标E =1所示。
一维扩散偏微分方程

一维扩散偏微分方程一维扩散偏微分方程(PDE)是一类常见的微分方程,它表达了某种物理现象的变化。
举个例子,它可以用来描述热的传导、浓度的变化、电场的强度以及气体的压力等等。
PDES 的形式可以用更抽象的方法表达,可以为应用程序设计者提供更多的自由度。
一维扩散偏微分方程的形式可以用通用的微积分方式来描述,其基本形式可以表述为:u_t=k(u_xx),其中u表示变量,t表示时间,x表示空间,k表示扩散系数。
该方程描述了当变量因扩散作用而随时间发生变化时,随着空间单位变化量的变化率,变量会发生变化。
一维扩散偏微分方程有几个典型的形式,具体可以分为以下几类:一、静态扩散型方程:这种方程的形式为:u_t=k(u_xx),其中u表示变量,t表示时间,x表示空间,k表示扩散系数。
它描述了由于变量的扩散作用而发生变化的系统,而不考虑任何外部影响因素。
二、动态扩散型方程:它的形式为:u_t=k(u_xx)+f(u,x,t),其中f(u,x,t)表示变量受外部影响因素的作用,由外部影响决定变量的波动。
三、热扩散型方程:这种方程的形式为:u_t=a(u_xx)+b(u_xxxx),其中a和b分别表示传热系数和热容系数。
当变量受到外部热源的影响时,可以使用这种方程来描述。
四、声学扩散型方程:它的形式为:u_t=c(u_xx)+v(u_xxxx),其中c和v分别表示声学场的传播速度和声学场的波动速度。
它通常用来描述声音在空间上的传播。
五、湍流扩散型方程:它的形式为:u_t=p(u_xxx)+q(u_xxxx),其中p和q分别表示湍流的传播速度和湍流的波动速度。
它通常用来描述边界层的湍流场的变化。
一维扩散偏微分方程在物理上反映了某些物理现象的变化,是一类经典的微分方程,广泛应用于物理,工程和数学领域,如工程热力学、传热学、流体动力学等。
值得一提的是,一维扩散偏微分方程也可以用一般的微分方法来求解,求解过程相对简单,求解结果可靠,值得我们学习和应用。
哈尔滨工业大学计算传热学第四章扩散方程的数值解法及其应用资料重点

1
y
xw
TP
aETE
aNTN
aSTS
1
y
xw
Tf
Scxy
kB
kB
所以对第三类边界条件不仅有附加常数源项,而且还有 附加源项的斜率项
aPTP aETE aNTN aSTS (Sc•ad Sc )xy
aP aE 0 aN aS (Sp•ad Sp )xy
Sp•ad
y xy
a)算术平均线性分布
ke
kp
xe+ xe
kE
xe xe
e
••
•
W
Pxe xe E
xe
b)调和平均
qe
TE TP
xe
ke
TE Te
xe
kE
Te Tp
xe
kp
TE
xe
kE
TP
xe
kP
ke
kP kExe xek p xekE
当 xe xe
kP kE
算术平均
ke
kP
kE 2
kP 2
第四章 扩散方程的数值解法及其应用
§4.1 一维稳态导热
1 • d [kF(x) dT ] S 0
F (x) dx
dx
F(x):与坐标系和截面形状有关的计算因子
S:内热源。
w
e
△x
e d
dT
[kF (x) ]dx
w dx
dx
e
F (x) • Sdx 0
w
•
W
xw
•
P
xe
•
E
keFe
W PE
ap
Fe k e
xe
扩散方程的数值解法

扩散方程的应用例子
• 多孔介质渗流
• 二维无旋流
• 充分发展的管流 • 电磁场理论
4.1 一维导热
• • • • • • 1. 一维导热问题的通用控制方程 2. 控制容积积分法离散 3. 控制容积界面当量导热系数的确定方法 4. 源项的线化处理 5. 边界条件的引入 6. 线化代数方程组的三对角阵解法
源项
0 0 a (1 f ) a (1 f ) a (1 f ) S A ( x ) T E W P P P P SC AP ( x ) P P
• 显式
aPTP a T a T b
0 E E 0 W W
• 全隐式
aPTP aETE aW TW b
• C-N格式
aE aW aPTP TE TW b 2 2
区别在于系数的表达式不同
稳态一维导热情况:没有时间积分
• 整理为:
aPTP aETE aW TW b
• 其中:
aP aE aW SP AP (x)P , b SC AP (x) P
源项
4.1.3 控制容积界面当量导热系数的 确定方法
木头
铜
(1) 加权平均法:
( x )e ( x )e e P E ( x )e ( x )e
(2) 调和平均法
TE TP 整体 qe ( x )e
e
TE TP qe ( x )e ( x ) e
w e t t
T dx
t
t t
t
e t t T T A( x ) x A( x ) x dt A( x ) Sdxdt e w w t
