中学物理竞赛培训讲义第四讲电磁感应
合集下载
高二物理竞赛课件：电磁感应
安培的分子电流假设：电与磁是同一体，它们的同一性 在电流方面反映出来，即磁由电流产生。
Faraday认为电与磁是一对和谐的对称现象，若认为磁 由电流产生，反而破坏了这种对称和谐，
因而Faraday推理：磁也可产生电流！
在什么条件下，磁场才能产生电流？ 感应电动势——动生电动势、感生电动势。
1831年夏， Faraday再次回到磁产生电的课题 上来，终于获得突破，发现了期待已久的电磁 感应现象。
向相同。
电磁感应现象：当穿过一个闭合导体回路的磁通量发生变
化时（不论这种变化是由什么原因引起的），在导体回路中 就有感应电流产生。（感只产生确定的感应电动势
2)当回路不闭合时，没有感应电流，仍存在感应电动势。
电磁感应现象：当穿过一个闭合导体回路的磁通量发生变
化时，在导体回路中就有感应电动势产生。
1831年8月29日，Faraday改用磁铁插入和拉出。 发现电流表的指针偏转。
电磁感应(Electromagnetic Induction)
1831年法拉第总结出以下五种情况都可产生感应电流： 变化着的电流，运动着的恒定电流，在磁场中运动着的导体， 变化着的磁场，运动着的磁铁。
电磁感应的共同规律
电动势的方向由楞次定理给出： 闭合回路中感应电流的方向，总是使得它所激
发的磁场来阻止引起磁感应电流的磁通量的变化。
楞次定理的另一种表述： 当导体在磁场中运动时，导体中由于出现感
应电流而受到的磁场力必然阻碍此导体的运动。 阻碍的意思： （1）磁通增加时，感应电流的磁通与原来磁通
方向相反。 （2）磁通减少时，感应电流的磁通与原磁通方
楞次定理的实质：能量守恒律
线圈中产生感应电流而产生焦耳 热，能量何来？
感应电流的方向服从楞次定律是能量守恒 和转化定律的必然结果
Faraday认为电与磁是一对和谐的对称现象，若认为磁 由电流产生，反而破坏了这种对称和谐，
因而Faraday推理：磁也可产生电流！
在什么条件下，磁场才能产生电流？ 感应电动势——动生电动势、感生电动势。
1831年夏， Faraday再次回到磁产生电的课题 上来，终于获得突破，发现了期待已久的电磁 感应现象。
向相同。
电磁感应现象：当穿过一个闭合导体回路的磁通量发生变
化时（不论这种变化是由什么原因引起的），在导体回路中 就有感应电流产生。（感只产生确定的感应电动势
2)当回路不闭合时，没有感应电流，仍存在感应电动势。
电磁感应现象：当穿过一个闭合导体回路的磁通量发生变
化时，在导体回路中就有感应电动势产生。
1831年8月29日，Faraday改用磁铁插入和拉出。 发现电流表的指针偏转。
电磁感应(Electromagnetic Induction)
1831年法拉第总结出以下五种情况都可产生感应电流： 变化着的电流，运动着的恒定电流，在磁场中运动着的导体， 变化着的磁场，运动着的磁铁。
电磁感应的共同规律
电动势的方向由楞次定理给出： 闭合回路中感应电流的方向，总是使得它所激
发的磁场来阻止引起磁感应电流的磁通量的变化。
楞次定理的另一种表述： 当导体在磁场中运动时，导体中由于出现感
应电流而受到的磁场力必然阻碍此导体的运动。 阻碍的意思： （1）磁通增加时，感应电流的磁通与原来磁通
方向相反。 （2）磁通减少时，感应电流的磁通与原磁通方
楞次定理的实质：能量守恒律
线圈中产生感应电流而产生焦耳 热，能量何来？
感应电流的方向服从楞次定律是能量守恒 和转化定律的必然结果
高二物理竞赛电磁感应课件(共45张PPT)
2 一 般 情 况 B 常 矢 量 ， v 常 矢 量 ， 且 导 体 为
任 意 形 状 d， ii则 LvdiBLdlvB dl
3当导体为闭合回路则时 ， iL diLv B d l
二、洛仑兹力传递能量
电子的速度：
v
—随导体运动的速度
u—相对导体的定向运度动速
电子所受到的总的洛仑兹力为
(2)若为铜盘转动， 视为铜棒并联;
(3)用法拉第定律直接求解：
i
d dt
设想回路Oab（如图）
ioab ioa
v a
O
S
b
法二 选l如图所示
S 1 L2
2
BS
ioab
d dt
L
a
o
l S b
1 BL2 d
2 dt
1 BL2
0 随时间减小d/dt0
0 随 时 间 增 大d/dt0
0 随 时 间 减 小 d/dt0
B
nl
N
v
S
d/dt0
(4)由 i d/dt 确定 i 正负
i 0
i方 向 与 l方 向 一 致
i 0 i方 向 与 l方 向 相 反
n
l
B
i i
NN SS v
id/dt0
例：利用法拉第电磁感应定律判断感应电动势 的方向。
三、法拉第电磁感应定律
实验给出 Ii ：dd t (磁通量随时间的变
说明有
(感应电动势)存在,
i
即
i
d dt
i
d dt
SI制
i与ddt有关， 无 与关，与回路关 的。 材料
i的存在与回路无 是关 否， 闭 Ii的 而 合 存在
高二物理竞赛电磁感应定律课件(共14张PPT)
i ,电磁与感应反现向象(2)
R dt 引6．起磁导场体对回载路流中导产线生的感作应用电流的原因，是由于电磁感应在回路中建立了感应电动势，比感应电流更本质，即使由于回路中的电阻无限大而电流为零，感应电动势依然存在。
引第六起章导电体磁回感路应中与产暂态生过感程应电流的原因，是由于电磁感应在回路中建立了感应电动势，比感应电流更本质，即使由于回路中的电阻无限大而电流为零，感应电动势依然存在。
引18起20导年体，回奥路斯中特产(生丹感麦应) ，电电流流的磁原效因应，。是由于电磁感应在回路中建立了感应电动势，比感应电流更本质，即使由于回路中的电阻无限大而电流为零，感应电动势依然存在。
1 dΦ 13．顺电磁磁质感抗应磁定质律铁磁质
电第五磁章感应电现磁象感(应2和) 暂态过程
I 他1 是电电磁磁理感论应的定创律始人之一，于1831年发现电磁感应现象。
t t 2 1电线,1电（,法感第2．2磁拉圈磁生六）电感 第 法电不与与感感电章磁应（拉应磁动应动感现M电，电感电应i现势象动c同同磁h磁定应磁势(象a2向 向感铁律大e感定感)(l小插生3F应律应与a)入电r定与磁a或场d通津暂a拔量y态,变出1化过时7的9程，1快-慢18有6关7；），伟大的英国物理学家和化学家。
v
v
D
导体切割磁力线运动时产生感应电流
结论：闭合回路磁通量变化时产生感应电动势
1 电磁感应定律
法拉第定律(1)
法拉第通过各种实验发现了电磁感应现象，并总结了电磁感应的共同规律：
（1）通过导体回路的磁通量随时间发生变化时，回路中就有感应电动势产生， 从而产生感应电流。磁通量的变化可以是磁场变化引起的，也可以是导体在 磁场中运动或导体回路中的一部分切割磁力线的运动产生的，
R dt 引6．起磁导场体对回载路流中导产线生的感作应用电流的原因，是由于电磁感应在回路中建立了感应电动势，比感应电流更本质，即使由于回路中的电阻无限大而电流为零，感应电动势依然存在。
引第六起章导电体磁回感路应中与产暂态生过感程应电流的原因，是由于电磁感应在回路中建立了感应电动势，比感应电流更本质，即使由于回路中的电阻无限大而电流为零，感应电动势依然存在。
引18起20导年体，回奥路斯中特产(生丹感麦应) ，电电流流的磁原效因应，。是由于电磁感应在回路中建立了感应电动势，比感应电流更本质，即使由于回路中的电阻无限大而电流为零，感应电动势依然存在。
1 dΦ 13．顺电磁磁质感抗应磁定质律铁磁质
电第五磁章感应电现磁象感(应2和) 暂态过程
I 他1 是电电磁磁理感论应的定创律始人之一，于1831年发现电磁感应现象。
t t 2 1电线,1电（,法感第2．2磁拉圈磁生六）电感 第 法电不与与感感电章磁应（拉应磁动应动感现M电，电感电应i现势象动c同同磁h磁定应磁势(象a2向 向感铁律大e感定感)(l小插生3F应律应与a)入电r定与磁a或场d通津暂a拔量y态,变出1化过时7的9程，1快-慢18有6关7；），伟大的英国物理学家和化学家。
v
v
D
导体切割磁力线运动时产生感应电流
结论：闭合回路磁通量变化时产生感应电动势
1 电磁感应定律
法拉第定律(1)
法拉第通过各种实验发现了电磁感应现象，并总结了电磁感应的共同规律：
（1）通过导体回路的磁通量随时间发生变化时，回路中就有感应电动势产生， 从而产生感应电流。磁通量的变化可以是磁场变化引起的，也可以是导体在 磁场中运动或导体回路中的一部分切割磁力线的运动产生的，
第4讲电磁感应物理竞赛市公开课获奖课件省名师示范课获奖课件
k
E(t) d B0l ( kv){cos[t k(x d )] cos(t kx)}
dt k
i(t) E B0l ( kv){cos[t k(x d )] cos(t kx)}
R kR
f (t) i(t)B(x,t)l i(t)B(x d,t)l
f
(t)
b02
2
2 0
ri
ri
Bi
k
Ii ri
k
2 0ri
ri2
注意到
ri ri2
ri ri1 ri ri 1
1 ri1
1 ri
riri1 r i(ri ri ) ri2
B 2k 0(a2a1)
a1a 2
BS
2k 0(a2a1)
a1a 2
a02
E
t
2k
0 (a a1a
2 2
a1
)
a02
t
2k
0 (a2 a1a2
1 3
k
n i1
(r
3 i
r3
i1
)
1 3
k[(r13
r03) (r23
r13) (rn3
r3
n1
)
1 ka3
(3)
3
I ka3
(4)
R 3R
f Ai BIri kIriri
M i f Ai ri kIri2ri
M
n i 1
M i
kI
n i 1
ri2ri
1 kI 3
属框旳电阻为R，不计金属框旳电感。
解法二：通量法则
t
B B0 cos(t kr)
d B ds B0 cos(t kr)ldr
E(t) d B0l ( kv){cos[t k(x d )] cos(t kx)}
dt k
i(t) E B0l ( kv){cos[t k(x d )] cos(t kx)}
R kR
f (t) i(t)B(x,t)l i(t)B(x d,t)l
f
(t)
b02
2
2 0
ri
ri
Bi
k
Ii ri
k
2 0ri
ri2
注意到
ri ri2
ri ri1 ri ri 1
1 ri1
1 ri
riri1 r i(ri ri ) ri2
B 2k 0(a2a1)
a1a 2
BS
2k 0(a2a1)
a1a 2
a02
E
t
2k
0 (a a1a
2 2
a1
)
a02
t
2k
0 (a2 a1a2
1 3
k
n i1
(r
3 i
r3
i1
)
1 3
k[(r13
r03) (r23
r13) (rn3
r3
n1
)
1 ka3
(3)
3
I ka3
(4)
R 3R
f Ai BIri kIriri
M i f Ai ri kIri2ri
M
n i 1
M i
kI
n i 1
ri2ri
1 kI 3
属框旳电阻为R，不计金属框旳电感。
解法二：通量法则
t
B B0 cos(t kr)
d B ds B0 cos(t kr)ldr
电磁感应物理竞赛课件
感应电动机结构简单、维护方 便、成本低廉，广泛应用于工 业、农业、交通运输等领域。
电磁炉
电磁炉是利用电磁感应原理加热 食物的厨房电器，主要由加热线 圈、铁磁性锅具和控制系统组成
。
当加热线圈中通入交变电流时， 会在周围产生交变磁场，该磁场 与铁磁性锅具的相互作用产生热
量，使食物加热。
电磁炉具有高效节能、安全环保 、使用方便等优点，已成为现代
楞次定律
总结词
楞次定律是关于感应电流方向的规律，它指出感应电流的方向总是阻碍引起感应 电流的磁通量的变化。
详细描述
楞次定律是电磁感应中感应电流方向的判断依据。当磁通量增加时，感应电流的 磁场方向与原磁场方向相反；当磁通量减少时，感应电流的磁场方向与原磁场方 向相同。这个定律是能量守恒定律在电磁感应现象中的具体体现。
变压器在电力系统、电子设备和工业自动化等领域 有广泛应用，是实现电能传输和分配的重要设备。
感应电动机
感应电动机是利用电磁感应原 理实现电能和机械能转换的电 动机，主要由定子、转子和气 隙组成。
当定子绕组中通入三相交流电 时，会在气隙中产生旋转磁场 ，该磁场与转子导体的相互作 用产生转矩，使转子转动。
总结词
掌握解决物理竞赛中电磁感应问题的技巧
详细描述
解决物理竞赛中的电磁感应问题需要一定的技巧 和经验。例如，利用楞次定律判断感应电流的方 向、利用法拉第电磁感应定律计算感应电动势的 大小等。通过多做练习和总结经验，提高解决这 类问题的能力。
05
电磁感础题目主要考察学生对电磁感应基本概念的掌握情况，包括法拉第电磁感应定 律、楞次定律等核心知识点。通过解答这些题目，学生可以加深对电磁感应现象 的理解，为解决更复杂的问题打下基础。
厨房中不可或缺的电器之一。
电磁炉
电磁炉是利用电磁感应原理加热 食物的厨房电器，主要由加热线 圈、铁磁性锅具和控制系统组成
。
当加热线圈中通入交变电流时， 会在周围产生交变磁场，该磁场 与铁磁性锅具的相互作用产生热
量，使食物加热。
电磁炉具有高效节能、安全环保 、使用方便等优点，已成为现代
楞次定律
总结词
楞次定律是关于感应电流方向的规律，它指出感应电流的方向总是阻碍引起感应 电流的磁通量的变化。
详细描述
楞次定律是电磁感应中感应电流方向的判断依据。当磁通量增加时，感应电流的 磁场方向与原磁场方向相反；当磁通量减少时，感应电流的磁场方向与原磁场方 向相同。这个定律是能量守恒定律在电磁感应现象中的具体体现。
变压器在电力系统、电子设备和工业自动化等领域 有广泛应用，是实现电能传输和分配的重要设备。
感应电动机
感应电动机是利用电磁感应原 理实现电能和机械能转换的电 动机，主要由定子、转子和气 隙组成。
当定子绕组中通入三相交流电 时，会在气隙中产生旋转磁场 ，该磁场与转子导体的相互作 用产生转矩，使转子转动。
总结词
掌握解决物理竞赛中电磁感应问题的技巧
详细描述
解决物理竞赛中的电磁感应问题需要一定的技巧 和经验。例如，利用楞次定律判断感应电流的方 向、利用法拉第电磁感应定律计算感应电动势的 大小等。通过多做练习和总结经验，提高解决这 类问题的能力。
05
电磁感础题目主要考察学生对电磁感应基本概念的掌握情况，包括法拉第电磁感应定 律、楞次定律等核心知识点。通过解答这些题目，学生可以加深对电磁感应现象 的理解，为解决更复杂的问题打下基础。
厨房中不可或缺的电器之一。
高二物理竞赛课件：电磁感应定律
Ψ NΦm
B
i
N
d Φm dt
步骤： 1）确定回路所在空间的磁场的分布；
dS n
2）选择回路的绕行方向，所围曲面
的正法向方向与回路绕行方向
满足右手螺旋法则；
3）计算回路所围曲面的磁通量Φm；
L
4）根据电磁感应定律： i
dΦm dt
，计算感应电动势。
i＞0 时，电动势的方向与回路绕行方向相同。 i＜0 时，电动势的方向与回路绕行方向相反；
实验与探究 1
检流计
N
S
A
现象： 1）当条形磁铁插入螺线管或从螺线管中抽出时， 灵敏检流计的指针偏转，说明闭合回路中产生了电流。 2）当条形磁铁与螺线管保持相对静止时， 灵敏检流计的指针不偏转，说明闭合回路中没有电流。
实验与探究 2
电源
A
A
检流计
现象: 1) 开关接通或断开瞬间, 2) 开关接通，变阻器滑片不动, 3) 开关接通，变阻器滑片移动,
电磁感应定律
一、电磁感应定律
奥斯特在1820年发现的电流磁效应，使整个科学界 受到了极大的震动，它证实电现象与磁现象是有联系的。
1) 既然电能生磁，那么，磁是否能生电呢？ 2) 如果磁能生电，那么，怎样才能实现呢？
法拉第经过十年的不懈 努力终于在1831年发现了
－－－电磁感应现象。
法拉第（Michael Faraday）
例 : 一长直导线通以电流 i I0 sin t (ω、I0为常数)，
近旁共面有一个边长分别为l1和l2的单匝矩形线圈abcd， ab边距直导线的距离为r，求矩形线圈中的感应电动势。
解： 当 i 0 时，设电流方向如图
建立坐标系Ox如图,
x处的磁感应强度为： B 0i , 方向 2x
高二物理竞赛资料——电磁感应(学生)
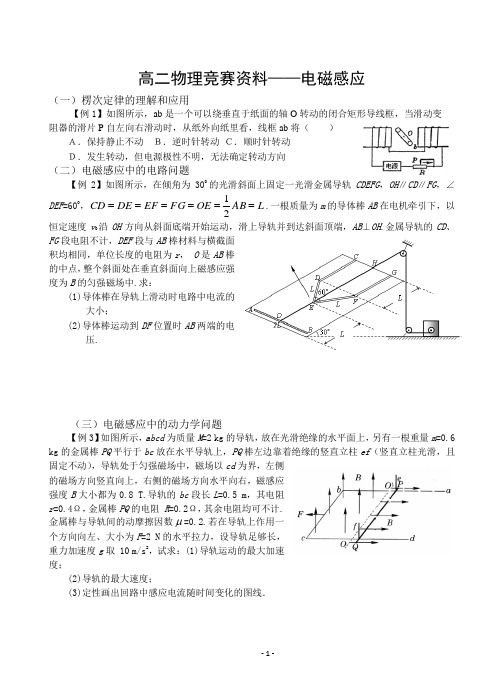
高二物理竞赛资料——电磁感应（一）楞次定律的理解和应用【例1】如图所示，ab 是一个可以绕垂直于纸面的轴O 转动的闭合矩形导线框，当滑动变阻器的滑片P 自左向右滑动时，从纸外向纸里看，线框ab 将（ ）Ａ．保持静止不动 Ｂ．逆时针转动 Ｃ．顺时针转动Ｄ．发生转动，但电源极性不明，无法确定转动方向（二）电磁感应中的电路问题【例2】如图所示，在倾角为300的光滑斜面上固定一光滑金属导轨CDEFG ，OH ∥CD ∥FG ，∠DEF =600，L AB OE FG EF DE CD ======21.一根质量为m 的导体棒AB 在电机牵引下，以恒定速度v 0沿OH 方向从斜面底端开始运动，滑上导轨并到达斜面顶端，AB ⊥OH .金属导轨的CD 、FG 段电阻不计，DEF 段与AB 棒材料与横截面积均相同，单位长度的电阻为r ， O 是AB 棒的中点，整个斜面处在垂直斜面向上磁感应强度为B 的匀强磁场中.求：(1)导体棒在导轨上滑动时电路中电流的大小；(2)导体棒运动到DF 位置时AB 两端的电压.（三）电磁感应中的动力学问题【例3】如图所示，abcd 为质量M =2 kg 的导轨，放在光滑绝缘的水平面上，另有一根重量m =0.6 kg 的金属棒PQ 平行于bc 放在水平导轨上，PQ 棒左边靠着绝缘的竖直立柱ef （竖直立柱光滑，且固定不动），导轨处于匀强磁场中，磁场以cd 为界，左侧的磁场方向竖直向上，右侧的磁场方向水平向右，磁感应强度B 大小都为0.8 T.导轨的bc 段长L =0.5 m ，其电阻r =0.4Ω，金属棒PQ 的电阻 R =0.2Ω，其余电阻均可不计.金属棒与导轨间的动摩擦因数μ=0.2.若在导轨上作用一个方向向左、大小为F =2 N 的水平拉力，设导轨足够长，重力加速度g 取 10 m/s 2，试求：(1)导轨运动的最大加速度；(2)导轨的最大速度；(3)定性画出回路中感应电流随时间变化的图线．（四）电磁感应中的能量问题【例4】如图所示，固定的水平光滑金属导轨，间距为L，左端接有阻值为R的电阻，处在方向竖直、磁感应强度为B的匀强磁场中，质量为m的导体棒与固定弹簧相连，放在导轨上，导轨与导体棒的电阻均可忽略.初始时刻，弹簧恰处于自然长度，导体棒具有水平向右的初速度v0.在沿导轨往复运动的过程中，导体棒始终与导轨垂直并保持良好接触.(1)求初始时刻导体棒受到的安培力。
2020年人大附中高中物理竞赛辅导课件(电磁感应)麦克斯韦电磁场理论(共14张PPT)
位移电流
对于变化的磁场，麦克斯韦提出了“有旋电场”假
说，根据法拉第电磁感应定律可以得到普遍情况下电场
的环路定理
B
L E涡 • dl S t • dS
另外，当时的理论和实验都表明电场的高斯定理和磁
场的高斯定理在变化的电、磁场中理在变化的电、磁场中
存 在什么样的关系呢？
如充电时
q
D
D
t
同向
D
t 同向
D +q+++0
D
q0
I
I
+++++
I
如放电时 q
D
D
t 反向
D
D
t 同向
I
+q+++0
D
q0
I
+++++
I
结论：
充电时，极板间变化电场 D 的方向和传导电流同向。
t
放电时，极板间变化电场 D 的方向仍和传导电流同向。 t
通过演示现象观察可知：回路中的传导电流和极板间的电
是否连续？
I
++++++
I
对L所围攻成的S1面
LH
dl
S1
j
dS
iI
对L所围攻成的S2面 矛盾
S1 L
++ +
++
+
I
S2
I
LH dl
S2
j dS
0
显然，H 的环流不再是唯一确定的了。 这说明安培环路定律在非恒定场中须加以修正。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
I
ε动
M
ε动=[UMN(R+r)-εR]/r=2 (V) (或 1V)
ε, r
R
N
(或: UMN= ε-Ir=ε动+IR, ε动=2 (V) )
又根据电磁感应规律, 有 ε动= Blu,
因此求得磁感应强度为 B=1 (T) (或 0.5 T)
(用已知量字母表示: B=-[mgD(R+r)+qεR]/(qlur)=1 T 或 0.5T)
例1：某人在地球的北半球某处向北水平抛出一 直导体棒，初速为v0，棒长为l，东西取向。已 知该处地磁场的磁感应强度为B，且与水平方向 夹角为θ，略去磁偏角的影响，问抛出t 秒后棒 端的电势差为何？哪端电势高？
解：棒在重力场中作平抛运动，设 t 秒时速度为V
水平方向：Vxv0, 1B0 lsvin, 由东指向西
即棒的东端电势高。
例2.相距l=0.4m的两根光滑平行金属导轨(不计电
阻), 左端接一电池(电动势ε=12V, 内阻r =2Ω), 右端接
有两个上下放置相距D=0.2m的平行金属板M和N(D远
小于板面的线度), 导轨上有电阻R=8Ω的金属杆ab(=l),
整个系统垂直放在均匀磁场B中(见图). 当ab以u=5m/s
性质不同, 静电场是有源场, 有势场无旋场, 电场线 有头有尾；感生电场是无源场, 有旋场无势场, 电场 线无头无尾(涡旋电场).
三. 感生电动势和感生电场
3. 感生电动势的计算:
(1) 法拉第定律直接计算: -Δ ΔΦ t
B(t) → Φ=Φ(t) → △t内的△Φ →
由楞次定律确定 ع的方向.
ΔΦ Δt
仅在长直 ,通常感生电场不易求的 :由感生电场计算 (2)
. 载流螺线管情形下磁场变化产生的感生电场方便求得
,R <r
E 感 2 r Δ Δ Φ Δ t Δr B t 2 ,E 感 2 r Δ ΔB t
,R >r
E 感 2 r Δ Δ r Φ t R Δ ΔB R t2 ,
E R2 ΔB 感 2r Δt
.在半径方向放置的导线上电动势为零 .方向沿圆周切向
因 任此一，导任线一上小，段有导线上的 感生 电i 动 势为E 感 l iiE 感 li
四. 自感与互感
1. 自感系数和自感电动势:
Φ=LI, L为自感系数； 自感电动势
由于重力与电场力平衡, 带电粒子等效于在磁场B中作匀速圆周 运动, 故有
d/2=mv/(-qB), v=-qBd/(2m)=0.01 (m/s) (或: v=5×10-3 m/s)
2. 计算: 导体线运动时产生的动生电动势等于导体单
位时间内扫过面积上的磁通.
均匀磁场中直导线且B, v, l 三者互垂时, 有
vBl
均匀磁场中直导线且B, v, l 三者不一定互垂时, 有 (vB )l
一般情况下, 有
(v B ) l
三. 感生电动势和感生电场
当线圈不动磁场随时间变化而产生的感应电动势
1. 感生电场力是与感生电动势对应的非静电力:
麦克斯韦提出一个假设: 随时间变化的磁场在其周围激 发一种（感生）电场, 它对带电粒子作用使其运动
2. 感生电场:
感生电动势的本质是时变磁场激发感生电场 感生电场与静电场的同异 同: 都对带电粒子作用，且 F=qE 异: 产生不同, 静电场由电荷产生的, 感生电场是由变化 的磁场产生的;
竖直方向：Vy g,t2Blgtco,s由西指向东
抛出t秒后棒两端的电势差为 1 2 B ( v 0 s l i n g cto ),s
由东指向西为动生电动势的正方向，
讨论：当
t
v0 g
tan
时，
0,
即棒的西端电势高；
当
t
v0 g
tan
时，
0,
2. 互感系数和互感电动势:
L -LΔ ΔIt
Φ12=MI1, 或 Φ21=MI2, M为互感系数
互感电动势 1 2-M Δ Δ 1,I t 2 1-M Δ Δ 2I t
3. 磁场的能量：
（1）自感磁能：自感线圈自感为L ，通有电流 I 时的储能
WL
1 2
LI2
（2）磁场能量密度：
章:电磁感应
一.电磁感应定律
ε-ΔΔΦ t, iε R
法拉第电磁感应定律:
2.楞次定律:感应电动势(电流)的方向判断
(1)感应电动势(电流)的方向,使它的磁场 阻止引起感应电流的磁通量的变化
二. 动生电动势
导线或线圈在磁场中运动时产生的感应电动势
1. 洛仑兹力是与动生电动势对应的非静电力:
导体内自由电子受洛仑兹力作用而运动就出现了电动势.
wm
1
2
B2
（3）磁场能量： W mw m V21 B2 V, W m 21B2V
五. 电磁振荡与电磁波
1. 振荡电路:
LC并联振荡, 固有频率
1 0 2 LC
有阻尼时，RL与C并联振荡（R较小），
则 0, 能量、振幅均减小，维持振荡外加源提供能量，受迫振荡
D
下,带电粒子在重力, 电场力和磁场
N
力作用下作匀速圆周运动, 必有
b
-q E=mg , UMN= -m g D /q =10 (V) (或9.8V)
即这便是维持粒子这种运动所需的电压, 而UMN是靠电池和金属 杆内动生电动势配合达到的, 其等效电路如右下图所示, 由直流
电路的欧姆定律, 有
UMN= ε-Ir, I=(ε-ε动)/(R+r),
2. 电磁辐射、电磁波 开放电路→电磁场辐射→电磁波
a. 电磁波是横波，电场和磁场方向均垂直传播方向
b.
电场与磁场方向互相垂直，EB 的方向 k的 沿 方 波 向
c. 与同相位, 振幅满足
E B
v , v是波速，真空中波速为 vc
1
00
六. 例题
的速度向右运动时, MN间有一质量m=2×10-6kg、电荷
q=－4×10-7C的质点可在竖直平面内作直径d=0.1m的
匀速圆周运动, 求磁感应强度B的量值和粒子运动的速
率v . (重力加速度取g=10 m/s2) a
解：设平行金属板M和N电压为UMN,
u
M
则其间电场为 E=UMN/D, 方向向 ع, r l