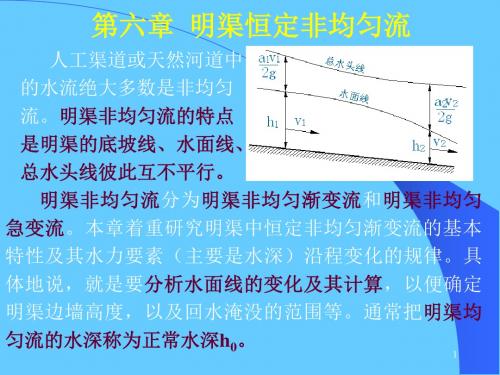
第六章明渠恒定非均匀流
水力学-第六章明渠恒定非均匀流
非
定
常
p2 p1dp
过
21d
程
T2 T1dT
3
6-1 明渠水流的三种流态
注意：波速与流体质
点速度的区别。
波驻 行波 波： ：静 运止 动的 的波 波
波膨 压胀 缩波 波： ：波 波后 后压 压强 强降 升的 的低 高波 波
4
6-1 明渠水流的三种流态 在t=0、1、2、3、4s， 分别有水滴滴入o点， 研究t=4s的流动图象
明渠水流有和大气接触的自由表面，与有压流不同， 具有独特的水流流态，即缓流、临界流和急流三种。
静水中传播的微波速度vw称为相对波速。 当v=0时，水流静止，干扰波能向四周以一定的速度传播。
当v＜vw时，水流为缓流，干扰波能向上游和下游传播。 当v＝vw时，水流为临界流， 当向下v＞游vw传时播，（水马流赫为椎急内流），。干扰波不能向上游传播，只能
K
点
dE s dh
0 临界流
下支
dE s 0 急流 dh
19
二、临界水深
相应于断面单位能量最小值的水深称为临界水深，
以hk表示。 由临界流方程
dEs dh
Q2B
1 gA3
0
Q2 AK3 (6.15)
g BK
注以脚标表示临界水深 时的水力要素
当流量和过水断面形状及尺寸给定时，利用上式 即可求解临界水深 hK 。
明渠中水流的流态也可从能量的角度来分析。
一、断面比能、比能曲线
如图所示渐变流， 若以0-0为基准面， 则过水断面上单位 重量液体所具有的 总能量为：
Ez2vg2 z0hcos2vg2
15
如果我们把参考基准面选在渠底这一特殊位置，把对
水力学 第六章课后题答案
思考题
6.6 明渠水流有哪三种流态，是如何定义的，判别标准是什么？ 明渠恒定均匀流 、明渠恒定非均匀流 、明渠非恒定非均匀流。 明渠恒定均匀流：流速的大小和方向均不随时间及距离而变的明渠水流。 明渠恒定非均匀流：流速不随时间变化，但其大小和方向或二者之一沿程变化 的明渠水流。 明渠非恒定非均匀流：流动要素随时间变化且其大小和方向或二者之一沿程变 化的明渠水流。
2
2
R A 41.8 2.43m
17.24
C
1
1
R6
1
1
2.436 82.8m0.5 / s
n 0.014
Q CA Ri 82.8 41.8 2.43 0.002 241.3m3 / s
6.2 一梯形混凝土渠道，按均匀流设计。已知Q为35m3/s，b为8.2m，m为1.5 ，n为0.012及i为0.00012，求h（用试算——图解法和迭代法分别计算）。
6.10 何谓断面比能曲线？比能曲线有哪些特征？ 答 水：深由的函Es 数h ，2g即QA22 知Es ，f (当h)，流按量此Q和函过数水绘断出面的的断形面状比及能尺随寸水一深定变时化，的断关面系比曲能线仅即仅是是断 面比能曲线。 特征：是一条下端以水平线为渐近线，上端以过原点的 45o直线为渐近线的二次 抛物线；在K点有最小Esmin ，K点上部Es 随h增加而增大，K点下部 Es随h增加而减 小。
23
v Q 23 1.25m / s A 18.4
第6章 水力学明渠恒定流动
d h
五、棱柱形渠道与非棱柱形渠道
• 棱柱形渠道：A=f ( h) • 非棱柱形渠道：A=f ( h, s).渠流动。 明渠具有自由表面，不存在非恒定明渠均匀流，明 渠均匀流必定为恒定流。 一、明渠均匀流的特性： 过水断面形状、大小、水深沿程不变。
G sin F f
二、 明渠均匀流的产生条件
恒定流 流量沿程不变（无分叉和汇流情况） 渠道为长、直的棱柱体顺坡渠，糙率沿程不变 渠中无闸、坝、跌水等建筑物的局部干扰
均匀流是对明渠流动的一种概化。多数明渠流是非均匀流。 近似符合这些条件的人工渠、河道中一些流段可认为是均匀流。
三、 明渠均匀流的基本计算公式
6 明渠恒定流动
学习重点 §6-1 概述 §6-2 明渠均匀流
• §6-3 明渠恒定非均匀流基本概念 • §6-4 明渠水流的两种急变流现象
学习重点
明渠的几何形态 明渠流动的特点 明渠恒定均匀流的特性、形成条件、基本 计算公式及水力计算。 明渠恒定非均匀流的基本概念、流动状态 及其判别。
§6.1 概述
不冲允许流速 [v ]max v [v ]min 不淤流速
六、 明渠均匀流的水力计算
V C Ri
Q AC Ri
f (m,b, h,i, n)
6个变量：Q，b，h，i，m，n 明渠均匀流的计算类型：校核和设计
（一）校核：校核渠道的过水能力和流速
已知 b、h、m、n、i ，求 Q
Q AC Ri
恒定流连续性方程： Q Av
谢才公式：
v C RJ
明渠均匀流
J=i
Q Av AC Ri K i
K---流量模数， K AC R
C---谢才系数。曼宁公式：C
1 n
第六章 明渠恒定非均匀流1
1一、缓流、急流、临界流二、Fr 得数三、断面单位能量四、临界水深五、临界底坡第六章明渠恒定非均匀流2•明渠非均匀流的水力特点：渠道底坡i ，水面坡度J z 和水力坡度J 不相等，即：p J J i≠≠•明渠非均匀流主要讨论的问题：计算各过水断面的水深h 的沿程变化，即分析和计算渠道的水面曲线，以便确定明渠边墙高度及回水淹没范围。
明渠非均匀流：当在渠道中修建了任意形式的水工建筑物，或任一均匀流的产生条件被改变，就会造成明渠中流速、水深的沿程变化，从而产生明渠非均匀流流动。
•产生明渠非均匀流流动的渠道形式有（1）i ≤0的渠道；（2）非棱柱形渠道；（3）边界突然变化的棱柱形渠道。
非均匀流（壅水曲线）h 0原均匀流水面3一、缓流、急流、临界流——明渠水流的三种流态（2）缓流：当明渠中水流受到干扰微波后，如干扰微波既能顺水流方向朝下游传播，又能逆水流方向朝上游传播，造成在障碍物前长距离的水流壅起，这时渠中水流就称为缓流。
此时水流流速小于干扰微波的流速，即i>0wv wv wv v （1）微波的产生(v =0)4(4)临界流：当明渠中水流受到干扰微波后，如干扰微波向上游传播的速度为零，这正是急流与缓流这两种流动状态的分界，称为临界流。
此时有(3)急流：当明渠中水流受到干扰后，如干扰微波只能顺水流方向朝下游传播，不能逆水流方向朝上游传播，水流只在障碍物处壅起，这种明渠水流称为急流。
此时水流流速大于干扰微波的流速，即。
w v v >wv v =w A v g ghB==由微小扰动波的传播理论可推导：急流临界流5明渠水流的流态缓流：水流流速小，水势平稳，遇到干扰，干扰的影响既能向下游传播，又能向上游传播急流：水流流速大，水势湍急，遇到干扰，干扰的影响只能向下游传播，而不能向上游传播6二、佛汝德数22322][][Fr glv gl v l ===ρρ重力惯性力222wvv v g Fr v h gh ===说明：（1）当Fr >1 时，v > v w ，水流为急流，惯性力起主导作用，水流中动能占主要部分。
6.明恒定非均匀流（总结）
第六章明槽恒定非均匀流一、判断题1、缓变流一定是缓流，急变流一定是急流。
( )2、棱柱形明渠中形成S2型水面曲线时，其弗劳德数F r 沿程减小。
( )二、填空题1、S2 型水面曲线是发生在( )(1) 缓坡渠道中的缓流(2) 陡坡渠道中的缓流(3) 缓坡渠道中的急流(4) 陡坡渠道中的急流2、在明渠渐变流中( )(1)总水头线一定平行于底坡线(2)总水头线与自由水面相重合(3)测压管水头线与自由水面一致(4)水面线与底坡线平行3、发生水跃的充分必要条件是( ) (1)从层流过渡到紊流(2)从陡坡过渡到缓坡(3)从缓流过渡到急流(4)从急流过渡到缓流4、已知某水闸下游收缩断面水深h c0 = 0.6 m (相应的跃后水深h c0 = 3.5 m) ,临界水深h c = 1.6 m，下游河道水深t = 1.4 m ,则闸下将发生( )(1)远离水跃(2) 临界水跃(3) 淹没水跃(4) 急流5、有两条梯形断面渠道1和2，已知其流量、边坡系数、糙率和底宽均相同，但底坡i1 > i2 ,则其均匀流水深h01和h02的关系为( )(1)h01> h02(2)h01< h02(3)h01= h02(4)无法确定6、有两条梯形断面渠道 1 和2，已知其流量、边坡系数、底坡和糙率均相同，但底宽b1 > b2,则其均匀流水深h01和h02的关系为( )(1)h01大于h02(2)h01小于h02(3)相等(4)无法确定7、有两条梯形断面渠道 1 和2，其流量、边坡系数、底宽及底坡均相同，但糙率n1 > n2，则其均匀流水深h01和h02的关系为( )(1)h01大于h02(2)h01小于h02(3)相等(4) 无法确定8、有四条矩形断面棱柱形渠道，其过水断面面积、糙率、底坡均相同，其底宽b与均匀流水深h。
有以下几种情况，则通过流量最大的渠道是( )(1) b1 =4 m ，h01 =1m (2) b2 =2 m ，h02 = 2m(3) b3 = 2.83 m ，h03 = 1.414m (4) b4 = 2.67 m ，h04 = 1.5m9、矩形明渠水流中，断面单位能量E s与势能h 之比值E s/h =1.8时，水流的弗劳德数F r为( )(1) F r >1.0 (2) F r <1.0 (3) F r =1.0 (4) 不定三、空题1、M2型水面曲线发生在____坡上，其水流属于_____流。
6 课堂测试-第六章 明渠恒定流
第六章明渠恒定流一、判断题1 在正坡非棱柱渠道内可以形成明渠均匀流。
（× ）2 陡坡上出现均匀流必为均匀急流，缓坡上出现均匀流必为均匀缓流。
（√ ）3 均匀流一定是恒定流，急变流一定是非恒定流。
（× ）4 矩形断面水力最佳断面的宽深比β=2。
（√ ）5 缓坡上可能发生急流。
（√ ）6. 缓流过渡到急流，可产生水跃现象。
（× ）7 在正坡明渠上，有可能产生均匀流。
（√ ）8 在恒定流中流线一定互相平行。
（× ）9 在i < i c的棱柱形明渠中发生非均匀流时，不可能是急流。
（× ）10 明渠水流中，底坡i = i c（临界底坡），则水深h = h c（临界水深）。
这个判别式只适用于明渠均匀流。
（√ ）11 明渠的临界水深与底坡无关。
（√ ）12 临界底坡上的非均匀流必定为临界流。
（× ）13 缓流时断面单位能量随水深的增大而增加，急流时断面单位能量随水深的增大而减小。
（√ ）14 均匀缓流只能在缓坡上发生，均匀急流只能在陡坡上发生。
（√ ）15 临界水深随流量、糙率的增大而增大，随底坡增大而减小。
（× ）16 临界底坡是明渠中发生临界流时相应的底坡。
（× ）17 断面单位能量随水深变化的规律取决于断面上临界水深的大小。
（× ）18 明渠正常水深h0与明渠底坡i无关。
（× ）19 平坡渠道中不可能发生均匀流。
（√ ）20 明渠的12种水面线中，凡M1、S1、C1型和M3、S3、C3型曲线一定是壅水曲线，M2、S2、C2型曲线一定是降水曲线。
（√ ）二、单选题1 棱柱体缓坡明渠中的水面曲线可能有（ B ）种。
A 2B 3C 4D 122 对于梯形断面的水力最佳断面，（ A ）。
A 边坡系数m确定，则水力最佳宽深比唯一确定B 底宽b确定，则水力最佳宽深比唯一确定C 水深h确定，则水力最佳宽深比唯一确定D 以上答案都不对3. 明渠均匀流的流量模数是（ A ）。
水力学课件 第六章_明渠恒定流
Gsinθ=F
2020/3/13
Gsinθ=F
上式表明： 1）明渠均匀流中 阻碍水流运动的摩擦阻力 F 与 使水流运动的 重力在水流方向上的分力(即推力)Gsinθ 相平衡。 2）说明了 反映水流推力的底坡sinθ= i 和 反映对水流的摩擦 阻力的粗糙系数n 必须沿程不变 才能维持明渠均匀流。
对于小型渠道，一般按水力最优设；
h(b h)h2( 1m2m)
对于大型土渠的计算，则要考虑经济条件，常作成宽浅断面。 例如取β=3—4 。
按水力最优断面设计的断面过于深窄。 例：m=1.5, b=10m,
则 βh=b/h=0.6055, h= 16.51m
对通航渠道则按特殊要求设计。
2020/3/13
当明渠断面形状、尺寸和流量一定 时，断面单位能量e为水深h的函数，它 在沿程的变化随水深h的变化而变。
（1）当h→0时，ω→0， Q2/2g2 ，则此时e→∞，
横坐标轴是函数曲线e=f(h)的渐近线，
（2）当h→∞时，ω→∞,则
，此时e=h→∞，
Q2/2g2 0
另一渐近线为通过坐标原点与横坐标轴成夹角45 0的直线。
如果把基准面0-0提到z1使其经过断面的最低点，则单位重量 液体对新基准面O1-O1的机械能为 e
eez1(zp 2 v g 2)z1h 2 v g 2
2020/3/13
断面单位能量或断 面比能 e ：基准面选在 断面最低点时 单位重量 液体的机械能。
E z p v2
2．临界水深
临界水深 是断面形式和流量给定的条件下，相应于断 面单位能量为最小值时的水深。
第六章明渠恒定非均匀流
第16讲（2课时）第六章 明渠恒定非均匀流明渠非均匀流特点：明渠大的底坡线、水面线、总水头线彼此互不平行。
产生非均匀流的原因：断面几何形状或尺寸沿流程改变，粗糙度或底坡沿流程改变，或有局部干扰。
分为渐变流和急变流。
分析水深的变化规律，)(s f h =；为区别将均匀流的水深称为正常水深，并以0h 表示。
★6-1 明渠水流的三种流态微波波速（相对速度）w V ，断面平均流速V 。
w V V <时，水流为缓流，干扰波能向上游传播； w V V =时，水流为临界流，干扰波不能向上游传播； w V V >时，水流为急流，干扰波不能向上游传播。
由连续方程2)(V h h hV w ∆+=及能量方程gV h h gV h w 2222221αα+∆+=+，可得：gh h h h h gh V w ≈∆+∆+=)2/1()/1(2，若为任意断面时，h g V w =，B A h /=平均水深。
定义佛汝德数（Froude ）, hg V Fr =则：当Fr<1时，水流为缓流；当Fr=1时，水流为临界流；当Fr>1时，水流为急流。
佛汝德数的物理意义是，一单位动能与单位势能之比的两倍开方；二惯性力与重力的对比。
★6-2 断面比能与临界水深一、断面比能、比能曲线断面比能：以渠底为基准面，所计算得到的单位总能量，以s E 表示。
2222222cos gAQ h gV h gV h E s αααθ+=+≈+=当流量和过水断面的形状尺寸一定时，断面比能仅是水深的函数。
即)(h f E s =。
比能曲线：断面比能随水深变化的关系曲线。
以h 为纵坐标，以比能为横坐标。
比能曲线特征：当0→h 时，0→A ，则∞→222gAQ α，故∞→s E ；当∞→h 时，∞→A ，则0222→gA Q α，故∞→s E 。
比能曲线是一支二次抛物线，曲线的下端以水平线为渐进线，上端以过原点的45度直线为渐进线。
有一最小值，将曲线分为两支。
这种水流称为明渠恒定非均匀渐变流
2.急流
当明渠中水流受到干扰后,若干扰微波
只能顺水流方向朝下游传播,不能逆水流方
向朝上游传播，这种明渠水流称为急流。 此时水流流速＞干扰微波的流速。 3.临界流
当明渠中水流受到干扰微波后，若干 扰微波向上游传播的速度为零，这正是急 流与缓流这两种流动状态的分界，称为临 界流。此时水流流速=干扰微波的流速。 明渠水流流态的判别依据是佛汝德数
（3）取跃前、跃后两过水断面的动量修正
系数相等
Q2
Q2
A1hc1 gA1 A2hc2 gA2
明渠恒定非均匀流
即:
J（h1）=J（h2）
A1、A2 —分别为跃前、跃后断面的面积；
1.临界水深的基本公式
Q 2 AK3
g
BK
明渠恒定非均匀流
由公式可知，临界水深的大小仅取决于 流量和过水断面的形状、大小，而与渠道的 底坡、糙率无关。
2.临界水深的计算
（1）矩形断面明渠临界水深的计算
hK
3
q2
g
临界流时， 断面比能为
ES min
h
K
hK 2
3 2
hK
明渠恒定非均匀流
当断面的形状、尺寸 和流量一定的时候，
Es只是水深h的函数。
dEs
Q2B 1
1 Fr2
dh
gA3
明渠恒定非均匀流
从上式可知：
当右端＞0，必定Fr＜l，水流是缓流。 当右端＜0，则Fr＞l，水流是急流。 当右端＝0，Fr＝1，是临界流。
二.临界水深
相应于断面单位能量最小值的水深称为
临界水深，以hk表示。
hK
明渠恒定非均匀流
第六章明渠恒定流解读
【解】 梯形断面最佳宽深比
m
b h
2(
1 m2 m) 0.61
根据已知的Q, i, n, m和 b = 0.61h, 得:
K Q 49.6m3 / s
i
水力最佳断面
1 Rm 2 hm
A (0.61h 1.5h)h 2.11h2
C
1
1
R6
1
1
(0.5h) 6
n 0.025
一、明渠横断面
1.天然河道的横断面 呈不规则形状，分主槽和滩地
枯水期：水流过主槽 丰水期：水流过主槽和滩地
主槽
滩地
一、明渠横断面
2.人工明渠的横断面 据渠道的断面形状分:
梯形、矩形、圆形、抛物线形等
断面确定：根据地质条件
岩石中开凿或条石砌筑或混
凝土渠或木渠
— 矩形
排水管道或无压隧道 — 圆形
土质地基
明渠水流分类：
明渠恒定流 明渠非恒定流
明渠均匀流 明渠非均匀流 无 明渠非均匀流
人工渠道、天然河道以及未被液流所充满的管道都是明渠流.
明渠流与有压流区别
有压管流： ① 具有封闭的湿周； ② 压力是流动的主要动力。
明渠流： ① 具有自由水面（即水面压强为大气压）； ② 重力是流动的主要动力； ③ 渠道的坡度影响水流的流速、水深。 坡度增大，则流速增大 ，水深减小； ③ 边界突然变化时，影响范围大。
2. 必须是长而直的棱柱形渠道。
（避免象弯管、阀门、滚水坝、桥孔等局部阻力对水流产生影响，而导 致非均匀流）
3. 渠道表面的粗糙系数应沿程不变。
（因为粗糙系数决定了阻力的大小，变化，阻力变化，有可能成为非均 匀流。）
明渠恒定流(均匀流与非均匀流)
水力学教案第六章明槽恒定流动【教学基本要求】1、了解明槽水流的分类与特征,了解棱柱体渠道的概念,掌握明槽底坡的概念与梯形断面明渠的几何特征与水力要素。
2、了解明槽均匀流的特点与形成条件,熟练掌握明槽均匀流公式,并能应用它来进行明渠均匀流水力计算。
3、理解水力最佳断面与允许流速的概念,掌握水力最佳断面的条件与允许流速的确定方法,学会正确选择明渠的糙率n值。
4、掌握明槽均匀流水力设计的类型与计算方法,能进行过流能力与正常水深的计算,能设计渠道的断面尺寸。
5、掌握明渠水流三种流态(急流、缓流、临界流)的运动特征与判别明渠水流流态的方法,理解佛汝德数Fr的物理意义。
6、理解断面比能、临界水深、临界底坡的概念与特性,掌握矩形断面明渠临界水深h k的计算公式与其它形状断面临界水深的计算方法。
7、了解水跃与水跌现象,掌握共轭水深的计算,特别就是矩形断明渠面共轭水深计算。
8、能进行水跃能量损失与水跃长度的计算。
9、掌握棱柱体渠道水面曲线的分类、分区与变化规律,能正确进行水面线定性分析,了解水面线衔接的控制条件。
10、能进行水面线定量计算。
11、了解缓流弯道水流的运动特征。
【内容提要与教学重点】这一章就是工程水力学部分内容最丰富也就是实际应用最广泛的一章。
本章有4个重点:明渠均匀流水力计算;明渠水流三种流态的判别;明渠恒定非均匀渐变流水面曲线分析与计算,这部分也就是本章的难点;水跃的特性与共轭水深计算。
学习中应围绕这4个重点,掌握相关的基本概念与计算公式。
明渠水流的复杂性在于有一个不受边界约束的自由表面,自由表面能随上下游的水流条件与渠道断面周界形状的变化而上下变动,相应的水流运动要素也发生变化,形成了不同的水面形态。
6、1 明槽与明槽水流的几何特征与分类（1）明槽水流的分类明槽恒定均匀流明槽恒定非均匀流(包括渐变流与急变流)明槽非恒定流明槽非恒定流一定就是非均匀流。
明槽非均匀流根据其流线不平行与弯曲的程度,又可以分为渐变流与急变流。
明渠恒定非均匀流
解 ： （ 一 ） 用 查 图 法 求 均 匀 流 水 深 h：
K Q 4.8 214.66m 3 / s i 0.0005
b 2.67
3 2.67
3.98
nK 0.022 214.66
由 m 0，b 2.67 3 .9 8查 附 图 可 得 ： nK
h / b 0.6 h 0.6b 0.6 3 1.8m
6-4 证明：当断面比能Es以及渠道断面形式、尺寸(b、m)一 定时，最大流量相应的水深是临界水深。
思路：
Q2
2g
Es h2gA2 QA (Es h)
其中A： (bmh)h
由dQ0，此 h对 时应 Q最 的大。 dh
证明：
Q 2
2g
E s h 2 gA 2 Q A ( E s h )
h ~ A3 B
2、由q查hK’，由hK’m/b查hK /hK’，求得hK 3、比较均匀流水深h与hK
（一） Q12 /g182 /9.816.53 假设一系列的h水 ，深 计算值列于下表：
h (m) B (m) A (m2) A3/B
0.20 8.40 1.64 0.53
0.40 8.80 3.36 4.30
A
(h 2 gA
2 h) 1
gA 3 1
Q 2 A 3 — —临界水深的方程式 gB
6.6 试分析并定性绘出图中三种底坡变化情况时，上下游渠道 水面线的形式。已知上下游渠道断面形状，尺寸及粗糙系数均 相同并为长直棱柱体明渠。
a1
b2
b1 b2
6.14 如图所示矩形渠道设置一潜坎，试证明缓流通 过潜坎时，水面要下降，而急流通过潜坎时，水 面要上升（不计损失）。
6-2 一梯形断面渠道，b为8m，m为1，n为0.014，i为0.0015 ，当流量分别为Q1=8m3/s，Q2=16m3/s时，求（一）用试算法 计算流量为Q1时临界水深；（二）用图解法计算流量为Q2时 临界水深；（三）流量为Q1及Q2时，判别明渠水流作均匀流 的流态。
水力学第6章明渠恒定流.
七.水跃发生的位置
分为:
临界式水跃 -- h’ 与 h” 共轭时发生水跃,从底坡发生转折时开始. 淹没式水跃 -- h’ 与 h” 不共轭,水跃向上游推,淹没了两渠道相接的断面.
(h1 h )
"
h1 为下游水深
远驱式水跃 -- h’ 与 h” 不共轭,水跃向下游推.待新的h’与h’共轭时水面跃
记为 ik.临界底坡的值是在流量、渠道断面形状及尺寸一定的前提下确定的。
ik f (Q, b, h, m, n)
当
可作为判别流态的依据. 为急流,陡坡. 为临界流,临界底坡
i ik i ik i ik
为缓流,缓坡
Q2 g k i i k k 临界底坡的计算公式为: 或 2 2 2 C K BK AK CK RK Ck , Rk , Bk 为临界水深对应的谢齐系数，水力半径,水面宽度.
i0 i0
2. 明渠的横断面
明渠的横断面通常有矩形,梯形,圆形和半圆形. 梯形断面水力要素: 底宽 b 边坡系数 水深为h h b B
m ctg
B b 2m h A (b m h)h
工程上最常用的是梯形断面,其过水断面的水力 要素关系为:
水面宽度 过水断面面积 湿周 水力半径
V>C 时为急流,干扰波只能向下游传播.
对临界流引入一个无量纲的数,称弗劳德数 Fr
V 1 ghm
则弗劳德数就成为急流、缓流和临界流的另一判别标准. Fr<1 为缓流。Fr=1 为临界流。Fr>1为急流. 7.8 断面单位能量与临界水深
一.断面单位能量
以0-0为基准面.取水面上的点为代表点. 单位重量液体总的机械能为: P V 2 V 2 EZ Z 0 h cos g 2 g 2g 0
水力学教程第6章
第六章明渠恒定均匀流人工渠道、天然河道以及未充满水流的管道等统称为明渠。
明渠流(OpenChannel Flow) 是一种具有自由表面的流动，自由表面上各点受当地大气压的作用，其相对压强为零，所以又称为无压流动。
与有压管流不同，重力是明渠流的主要动力，而压力是有压管流的主要动力。
明渠水流根据其水力要素是否随时间变化分为恒定流和非恒定流动。
明渠恒定流动又根据流线是否为平行直线分为均匀流和非均匀流。
明渠流动与有压管流的一个很大区别是：明渠流的自由表面会随着不同的水流条件和渠身条件而变动，形成各种流动状态和水面形态，在实际问题中，很难形成明渠均匀流。
但是，在实际应用中，如在铁路、公路、给排水和水利工程的沟渠中，其排水或输水能力的计算，常按明渠均匀流处理。
此外，明渠均匀流理论对于进一步研究明渠非均匀流也具有重要意义。
§6-1 概述1．明渠的分类由于过水断面形状、尺寸与底坡的变化对明渠水流运动有重要影响，因此在水力学中把明渠分为以下类型。
(1) 棱柱形渠道和非棱柱形渠道凡是断面形状及尺寸沿程不变的长直渠道，称为棱柱形渠道，否则为非棱柱形渠道。
前者的过水断面面积A仅随水深h变化，即A=f(h);后者的过水断面面积不仅随水深变化，而且还随着各断面的沿程位置而变化，即A=f(h, s) , s为过水断面距其起始断面的距离。
(2) 顺坡(正坡) 、平坡和逆坡(负坡)渠道明渠渠底线(即渠底与纵剖面的交线)上单位长度的渠底高程差，称为明渠的底坡(Bottom slope)，用i表示，如图6-1a，1-1和2-2两断面间，渠底线长度为A s,该两断面间渠底高程差为(a i-a2)= △ a,渠底线与水平线的夹角为B ,则底坡i 为。
(6-1-1)在水力学中，规定渠底高程顺水流下降的底坡为正，因此，以导数形式表示 时应为i=si n所以，在上述情况下，两断面间的距离△ s 可用水平距离△ l 代替，并且，过 水断面可以看作铅垂平面，水深 h 也可沿铅垂线方向量取。
第六章 明渠水流分析
彭文波 编著
6-3 明渠均匀流基本公式
明渠水力最佳断面（形状、尺寸）
梯形及矩形断面
定义：当A、n、i 一定时，流量 Q 最大的断面形状，称 为水力最佳断面。
1 1 C R6 n 1 Q AC Ri AR i n
2 1 3 2
5 i A3 1 2 n 3
（6-1）
A 水力半径 R
边坡系数
5
水力学与桥涵水文叶镇国
彭文波 编著
6-1 明渠几何特征与容许流速
明渠断面水力要素
圆形断面
过水面积 水面宽度 湿 周
d2 A ( sin ) 8
B d sin
2 h( d h) 2
（6-2）
水力半径 充满度
水力学与桥涵水文叶镇国
彭文波 编著
6-1 明渠几何特征与容许流速
（图6-3）
给排水教研室吴洪华
11
水力学与桥涵水文叶镇国
彭文波 编著
6-1 明渠几何特征与容许流速
渠道容许流速
定义——不冲刷、不淤积的渠中流速。
容许流速类型（试验研究成果，附录Ⅰ）
vmax——容许不冲刷流速（附录Ⅰ）
(b mb)h
（6-16）
经济最佳断面 小型渠道造价只取决于土方量，水力最佳可符合经济最 佳条件。 当m > 0.75时，b<h，断面形状窄而深，取土造价高，虽 为水力最佳但非经济最佳。 大型渠道取决于取土条件，常取β=3~4，成宽而浅形状。
给排水教研室吴洪华 21
水力学与桥涵水文叶镇国
给排水教研室吴洪华 1
水力学与桥涵水文叶镇国
第六章 明渠恒定非均匀流
第六章 明渠恒定非均匀流考点一 明渠恒定非均匀流产生的条件及特点1、明渠恒定非均匀流的产生当明渠底坡或粗糙系数沿程变化，或渠道的横断面形状（或尺寸）沿程变化，或在明渠中修建水工建筑物（闸、桥梁、涵洞等）使明渠中的流速和水深发生变化，这些均会在明渠中形成非均匀流。
2、非均匀流的特点非均匀流的特点是明渠的底坡、水面线、总水头线彼此互不平行。
也就是说，水深和断面平均流速v 沿程变化，流线间互不平行，水力坡度线、测压管水头线和底坡线彼此间不平行。
3、主要任务研究明渠恒定非均匀流的主要任务是：（1）定性分析水面线；（2）定量计算水面线。
考点二 明渠水流的三种流态及其判别1、明渠水流的三种流态一般明渠水流有三种流态，即缓流、临界流和急流。
（1）缓流：当水深较大，流速较小，渠道中有障碍物时将会产生干扰波，这时干扰波既能向上游传播也能向下游传播，这种水流流态称为缓流。
（2）急流：当水深较浅，流速较大，渠道中遇障碍物时，同样也产生干扰波，但这种干扰波只能向下游传播，这种水流流态称为急流。
（3）临界流：在缓流和急流之间还存在另一种流动，那就是水流流速与干扰波的波速相等，此时干扰波只能向下游传播，这种水流流态称为临界流，临界流的流动形态不稳定。
2、明渠水流流态的判断方法 （1）微波流速法波速法是只要比较水流的断面平均流速v 与微波的相对速度w v 的大小，就可以判断干扰波是否会向上游传播，也可以判断水流是属于哪一种流态。
当 w v v <时，水流为缓流，干扰波能向上游传播w v v =时，水流为临界流，干扰波不能向上游传播 w v v >时，水流为急流，干扰波不能向上游传播明渠中波速的计算公式为矩形渠道 gh v w =其他渠道 h g B gA v w ==/在断面平均流速为v 的水流中，微波传播的绝对速度绝w v 应是静水中的相对波速w v 与水流速度的代数和，即h g v v v w w ±=±=v 绝式中，微波顺水流方向传播的绝对速度用“+”号，微波逆水流方向传播的绝对速度用“-”号。
均匀流--《水力学》第六章
1． 明渠均匀流特性和形成条件由受力平衡推得f F G =θsin说明均匀流中重力分力与摩阻力平衡。
由能量方程推得21-=f h z ∆说明势能的减少等于克服摩阻力产生的能耗。
均匀流产生的条件：恒定、流量不变、糙率不变的长直正坡棱柱形渠。
2． 基本公式（谢才公式、曼宁公式）K ——流量模数，即底坡为1时通过的流量。
Ri C v =611R n C =i K Ri AC Av Q ===21321i R nv =3． 计算类型正常水深h 0：即均匀流水深，以区别于非均匀流水深。
1) 校核过水能力计算已知渠道边界条件（b 、m 、n 、i ）和实际水深(h)，求流量Q 。
Ri AC Q =2) 渠道设计计算——常用试算和图算✧ 底坡设计：已知渠道断面条件（b 、h 、m 、n ）以及流量Q ，求底坡i 。
R AC K =22KQ i = ✧ 底宽设计：已知流量Q 、底坡i 、边坡系数m 及糙率n ，水深h 另由通航、防洪或施工条件限定作为已知值，求底宽b 。
设不同b 值，由R AC K =作)(b f K =曲线，根据已知条件，由iQ K =实际值查对应的底宽b 。
✧ 渠深设计：水深h 加上一定超高就是渠深。
此类设计相当于已知流量Q 、底坡i 、边坡系数m 及糙率n ，底宽b 另由地形或施工条件限定，求水深h 。
与上相似，作)(h f K =曲线，查已知的实际K 值对应的水深h 。
✧ 宽深比hb =β已定，设计相应的b 、h ：流量Q 、底坡i 、边坡系数m 及糙率n 已知，宽深比β由水力最优或综合技术经济条件给出，此时b 、h 中只有一个独立未知量，可用前述方法计算。
✧ 限定最大允许流速[v]max ，求相应b 、h ：流量Q 、底坡i 、边坡系数m 及糙率n 为已知，此时渠道过水断面面积和水力半径为定值。
m ax][v Q A = 2/32/1m ax )][(i v n R = 由几何关系h mh b )(+=A212)(m h b h mh b A +++==χR联立可解b 、h 。
水力学教程 第6章
第六章明渠恒定均匀流人工渠道、天然河道以及未充满水流的管道等统称为明渠。
明渠流(Open Channel Flow)是一种具有自由表面的流动，自由表面上各点受当地大气压的作用，其相对压强为零，所以又称为无压流动。
与有压管流不同，重力是明渠流的主要动力，而压力是有压管流的主要动力。
明渠水流根据其水力要素是否随时间变化分为恒定流和非恒定流动。
明渠恒定流动又根据流线是否为平行直线分为均匀流和非均匀流。
明渠流动与有压管流的一个很大区别是：明渠流的自由表面会随着不同的水流条件和渠身条件而变动，形成各种流动状态和水面形态，在实际问题中，很难形成明渠均匀流。
但是，在实际应用中，如在铁路、公路、给排水和水利工程的沟渠中，其排水或输水能力的计算，常按明渠均匀流处理。
此外，明渠均匀流理论对于进一步研究明渠非均匀流也具有重要意义。
§6-1 概述1．明渠的分类由于过水断面形状、尺寸与底坡的变化对明渠水流运动有重要影响，因此在水力学中把明渠分为以下类型。
(1)棱柱形渠道和非棱柱形渠道凡是断面形状及尺寸沿程不变的长直渠道，称为棱柱形渠道，否则为非棱柱形渠道。
前者的过水断面面积A仅随水深h变化，即A=f(h)；后者的过水断面面积不仅随水深变化，而且还随着各断面的沿程位置而变化，即A=f(h,s)，s为过水断面距其起始断面的距离。
(2)顺坡(正坡)、平坡和逆坡(负坡)渠道明渠渠底线(即渠底与纵剖面的交线)上单位长度的渠底高程差，称为明渠的底坡(Bottom slope)，用i表示，如图6-1a，1-1和2-2两断面间，渠底线长度为Δs，该两断面间渠底高程差为(a1-a2)=Δa，渠底线与水平线的夹角为θ，则底坡i为。
图6-1θsin 21=∆∆=∆-=sas a a i (6-1-1) 在水力学中，规定渠底高程顺水流下降的底坡为正，因此，以导数形式表示时应为dsdai -= (6-1-2) 当渠底坡较小时，例如i ＜0.1或θ＜6°时，因两断面间渠底线长度Δs ，与两断面间的水平距离Δl ，近似相等，Δs ≈Δl ，则由图6-1a 可知θtan =∆∆≈∆∆=la s a ii=sin θ≈tg θ (6-1-3) 所以，在上述情况下，两断面间的距离Δs 可用水平距离Δl 代替，并且，过水断面可以看作铅垂平面，水深h 也可沿铅垂线方向量取。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第六章 明渠恒定非均匀流明渠中由于水工建筑物的修建、渠道底坡的改变、断面的扩大或缩小等都会引起非均匀流动。
非均匀流动是断面水深和流速均沿程改变的流动。
非均匀流的底坡线、水面线、总水头线三者互不平行。
根据流线不平行的程度，同样可将水流分为渐变流和急变流。
明渠非均匀流的水面曲线有雍水和降水之分，即渠道的水深沿程可升可降。
解决明渠非均匀流问题的思路：建立微分方程，进行水面曲线的定性分析和定量计算。
第一节 明渠水流的两种流态及其判别一、从运动学观点研究缓流和急流1、静水投石，以分析干扰波在静水中的传播干扰波在静水中的传播速度称为干扰波波速和微波波速，以w v表示。
如果投石子于流水之中，此时干扰所形成的波将随着水流向上、下游移动，干扰波传播的速度应该是干扰波波速wv 与水流速度v 的矢量和。
此时有如下三种情况。
（1）wv v <，此时，干扰波将以绝对速度0<-='w v v v 上向上游传播（以水流速度v的方向为正方向讨论），同时也以绝对速度0>+='w v v v 下向下游传播，由于下上v v '<'，故形成的干扰波将是一系列近似的同心圆。
（2）wv v =，此时，干扰波将向上游传播的绝对速度0=-='w v v v 上，而向下游传播的绝对速度02>=+='w w v v v v 下，此时，形成的干扰波是一系列以落入点为平角的扩散波纹向下游传播。
（3）wv v >，此时，干扰波将不能向上游传播，而是以绝对速度0>-='w v v v 上向下游传播，并与向下游传播的干扰波绝对速度0>+='w v v v 下相叠加，由于下上v v '<'，此时形成的干扰波是一系列以落入点为顶点的锐角形扩散波纹。
这样一来，我们就根据干扰波波速wv 与水流流速v 的大小关系将明渠水流分为如下三种流态——缓流、急流、临界流。
具体来讲，wv v <的水流称为缓流；wv v =的水流称为临界流；w vv >的水流称为急流。
临界流是缓流和急流的分界点。
上述分析说明了外界对水流的扰动（如投石水中、闸门的启闭等）有时能传至上游，而有时则不能的原因。
实际上，设置于水流中的各种建筑物可以看作是对水流连续不断的扰动，如闸门、水坝、桥墩等，上述分析结论仍然是适用的。
2、干扰波的波速由连续方程和能量方程可推导出干扰波波速公式：h g v w ±=式中，h 为平均水深。
对矩形平面，平均水深就等于渠道水深h 。
对静水而言，上式中的±只有数学上意义。
对于运动水流，设其流速为v ，则干扰波波速的绝对速度可表示为ww v v v ±='，顺流方向取“+”，逆流方向取“－”。
这样一来，流态的判别为 ωv <h g 水流为缓流ωv =h g 临界流ωv >h g 急流3、流态判别数——佛汝得数佛汝得数Fr 可定义为 hg v v v Fr w==显然，缓流1<Fr ；急流1>Fr ；临界流1=Fr 。
从上式可以看到佛汝得数Fr 的运动学意义是断面平均流速与干扰波波速的比值。
如果将佛汝得数的表达式稍作变形，可以得到h gv Fr 222=，该式表达的佛汝得数的物理意义是过水断面上单位重量液体平均动能与平均势能之比的2倍开平方。
从液体质点的受力情况分析，可以得到佛汝得数的力学意义是惯性力和重力的比值。
可用量纲关系来分析。
惯性力量纲 [][][][][][]2223v L LTL a M F ρρ=⋅==- 重力 [][][][][][]g L g L M g G 33ρρ===[][][][]⎥⎥⎦⎤⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡=gL v g L v LL G F 213232121ρρ二、断面比能（断面单位能量）1、断面比能（断面单位能量）的定义：以过渠道最低点的水平面O ＇—O ＇为基准面，计算得到的该断面上单位重量液体所具有的机械能，称为断面比能。
可表示为g v h E s 2cos 2αθ+=式中，sE 称为断面单位能量或断面比能。
2、断面总能量E 与断面比能Es 的区别与联系区别：1） E 在整个流程上为同一基准面 所以 E 沿程总是减小；Es 在整个流程上，针对不同的过水断面其计算比能的基准面不同， 即 断面比能Es 沿程可升可降可不变。
2） E 的基准面任意选；Es 的基准面是渠道横断面的最低点 。
3） 两者 之间差一个基准面高差。
联系：断面比能sE 是断面单位重量的液体具有的总机械能中反映水流运动状态的那一部分，断面比能计算公式中的水深h 及流速水头g v 22α都是水流运动状态的直接反映。
3、比能曲线在断面形状尺寸及流量一定的条件下，断面比能sE 只是水深h 的函数。
如果以纵坐标表示水深h ，以横坐标表示断面比能sE ,则一定流量下所讨论断面的断面比能sE 随水深h 的变化规律可以用h ～sE 曲线来表示，这个曲线称为比能曲线，见图。
可以证明，23211Fr B gA Q dh dE s -=-=α对于极值点，0=dh dE s，1=Fr ，即断面比能s E 最小时对应的水流为临界流，相应的水深称为临界水深，以符号kh 表示。
比能曲线的特点：①比能曲线是一条二次抛物线，曲线下端以sE 轴为渐进线，上端以45°直线为渐进线，曲线两端向右方无限延伸，中间必然存在极小点。
②断面比能sE 最小时对应的水深为临界水深；③曲线上支，随着水深h 的增大，断面比能sE 值增大，为增函数，0>dh dE s，1<Fr ，表示水流为缓流，即比能曲线的上支代表着水流为缓流。
在曲线下支，随着水深h 的增大，断面比能s E 值减小，为减函数，0〈dh dE s，则有1>Fr ，表示水流为急流，即比能曲线的下支代表着水流为急流。
而极值点对应的水流就为临界流。
④比能曲线的上支和下支分别代表不同的水流流态，而比能曲线上上支和下支的分界点处的水深又为临界水深，显然，也可以用临界水深来判别水流流态。
kh h >，相当于比能曲线的上支，水流为缓流；k hh <，相当于比能曲线的下支，水流为急流；kh h =，相当于比能曲线的极值点，水流为临界流。
三、 临界水深流量及断面形状尺寸一定的条件下，相应于断面比能最小时的水深称为临界水深kh 。
断面比能最小时，0=dh dE s，由此条件即可求得临界水深计算公式。
k k B A g Q 32=α在临界水深计算公式中，下标k 表示相应于临界水深时的水力要素。
在流量及断面形状尺寸一定的条件下，可由此时求解临界水深。
由于k k B A 3一般是水深h 的隐函数，对一般形式的断面需要试算求解。
临界水深与流量、断面形状尺寸有关，与渠道的底坡和粗糙系数无关。
1、矩形断面临界水深的计算对矩形断面而言，b B k =，k kbhA =，将其代入临界水深计算的一般公式，化简整理可得矩形断面临界水深的直接计算公式。
32322gq gbQ h k αα==式中，q 为单宽流量，b Q q =。
g v h gv h gh v gq h k k k k k k k22)(22223αααα=⇒=⇒==上式说明，在临界流时，矩形断面的临界水深等于其流速水头的2倍，此时相应的断面比能：k k k k k s s h h h gv h E E 232122min =+=+==α2、任意断面临界水深的计算任意断面临界水深的计算只能采取试算法。
当流量Q 给定之后，gQ 2α为一常数。
于是可假定不同的水深，求得相应的k k B A 3，当求得的某一水深时的k k B A 3值恰好等于g Q 2α时，该水深即为所求的临界水深。
任意断面临界水深的计算也可在用试算——图解法。
假定3～5个不同的水深，求得相应的k k B A 3，当求得的k k B A 3把g Q 2α包含在中间时，可作出k k B A h 3~曲线，由已知的g Q 2α值可从曲线上查得相应的水深值，该水深即为所求的临界水深。
3、等腰梯形断面临界水深的计算若明渠的过水断面为等腰梯形断面，则临界水深的计算除了可用试算法和试算——图解法外，还可采用查图法。
四、临界底坡在流量和断面形状尺寸一定的棱柱体正坡明渠中，当水流作均匀流动时，如果改变渠道的底坡，则相应的均匀流正常水深0h 也会相应地改变。
当变至某一底坡ki 时，其均匀流的正常水深0h恰好等于临界水深kh ，此时的底坡ki 就称为临界底坡。
临界底坡的计算公式。
k k kk B C g i 2αχ=临界底坡只取决于流量及断面形状尺寸，并与粗糙系数有关，而与渠道的实际底坡无关。
它并不是实际存在的渠道底坡，只是与某一流量、断面形状尺寸及粗糙系数相对应的某一特定坡度，是为便于分析非均匀流动而引入的一个概念。
事实上，实际渠道的底坡只可能在某一流量下为临界底坡，而在其它流量下则不是。
引入临界底坡之后，可将正坡明渠再分为缓坡、陡坡、临界坡三种类型。
如果渠道的实际底坡k i i <，我们称它为缓坡，ki i >称为陡坡，ki i =称为临界坡。
对明渠均匀流而言，当底坡k i i <时，k h h >0；k ii >时，k h h <0；k i i =时，k hh =0。
这就是说可以利用临界底坡判断明渠均匀流的水流流态，即缓坡上的均匀流是缓流，陡坡上的均匀流是急流，临界坡上的均匀流是临界流。
第二节 明渠恒定非均匀渐变流基本方程明渠恒定非均匀流是一种流速沿程变化的流动，伴随着流速变化，水位（或水深）、过水断面面积等水力要素也将沿程变化。
许多明渠非均匀流问题都可归结为探求水位或水深的沿程变化规律，即求出函数)(s z z =或)(s h h =的具体形式，其中，s 为流程坐标。
这里讲的明渠非均匀流水深或水位的沿程变化规律包括两方面的含义：一是水面曲线的定性分析，即探求水面曲线大致是什么形状的曲线；二是水面曲线的定量计算，即需要知道沿程的水深或水位。
为解决这两个问题，必须首先建立描述水深或水位沿程变化规律的微分方程。
一、明渠恒定非均匀渐变流的基本微分方程应用能量方程可建立明渠恒定非均匀渐变流的基本微分方程dsK Q g v d dh ids 222)2()(+++=ζα二、水深沿程变化的微分方程1、非棱柱体明渠323222)(1)(gA BQ s A gA Q K Q i ds dh ζαζα+-∂∂++-=2、棱柱体明渠222322211Fr K Q i gA B Q K Q i ds dh --=--=α上式可用于明渠恒定非均匀渐变流水面曲线的定性分析和定量计算。