3简明材料力学习题解答第三章 2
第三章材料的力学行为习题参考答案

第三章材料的力学行为习题参考答案第三章材料的力学行为一、解释下列名词1、加工硬化2、回复3、再结晶4、热加工5、冷加工答:1、加工硬化:随着塑性变形的增加,金属的强度、硬度迅速增加;塑性、韧性迅速下降的现象。
2、回复:加热温度较低时,变形金属中的一些点缺陷和位错,在某些晶内发生迁移变化的过程。
3、再结晶:被加热到较高的温度时,原子也具有较大的活动能力,使晶粒的外形开始变化。
从破碎拉长的晶粒变成新的等轴晶粒。
和变形前的晶粒形状相似,晶格类型相同,把这一阶段称为“再结晶”。
4、热加工:将金属加热到再结晶温度以上一定温度进行压力加工。
5、冷加工:在再结晶温度以下进行的压力加工。
二、填空题1、塑性变形的方式主要有滑移和孪生,而大多数情况下是滑移。
2、滑移常沿晶体中原子密度最大的晶面及晶向发生。
3、在体心立方晶格中, 原子密度最大的晶面是{110},有 6 个,原子密度最大的晶向是<111>,有2个;在面心立方晶格中, 原子密度最大的晶面是{111},有4 个,原子密度最大的晶向是<110>,有3个。
两者比较,具有面心立方晶格的金属塑性较好,其原因是滑移系和滑移方向多。
4、多晶体金属的塑性变形由于受到晶界和晶粒位向的影响,与单晶体金属相比,塑性变形抗力增大。
5、金属在塑性变形时,随变形量的增加,变形抗力迅速增大,即强度、硬度升高,塑性、韧性下降,产生所谓加工硬化现象。
这种现象可通过再结晶加以消除。
6、变形金属在加热时,会发生回复、再结晶和晶粒长大三个阶段的变化。
7、冷绕成形的钢质弹簧,成形后应进行回复退火,温度约为250~300℃。
8、回复退火也称去应力退火。
9、冷拉拔钢丝, 如变形量大, 拉拔工序间应穿插再结晶退火,目的是消除加工硬化。
10、热加工与冷加工的划分应以再结晶温度为界线。
在再结晶温度以下的塑性变形称为冷加工;在再结晶温度以上的塑性变形称为热加工。
三、简答题1、产生加工硬化的原因是什么?加工硬化在金属加工中有什么利弊?答:⑴随着变形的增加,晶粒逐渐被拉长,直至破碎,这样使各晶粒都破碎成细碎的亚晶粒,变形愈大,晶粒破碎的程度愈大,这样使位错密度显著增加;同时细碎的亚晶粒也随着晶粒的拉长而被拉长。
材料力学习题及答案

材料力学-学习指导及习题答案第一章绪论1-1 图示圆截面杆,两端承受一对方向相反、力偶矩矢量沿轴线且大小均为M的力偶作用。
试问在杆件的任一横截面m-m上存在何种内力分量,并确定其大小。
解:从横截面m-m将杆切开,横截面上存在沿轴线的内力偶矩分量M x,即扭矩,其大小等于M。
1-2 如图所示,在杆件的斜截面m-m上,任一点A处的应力p=120 MPa,其方位角θ=20°,试求该点处的正应力ζ与切应力η。
解:应力p与斜截面m-m的法线的夹角α=10°,故ζ=p cosα=120×cos10°=118.2MPaη=p sinα=120×sin10°=20.8MPa1-3 图示矩形截面杆,横截面上的正应力沿截面高度线性分布,截面顶边各点处的正应力均为ζmax=100 MPa,底边各点处的正应力均为零。
试问杆件横截面上存在何种内力分量,并确定其大小。
图中之C点为截面形心。
解:将横截面上的正应力向截面形心C简化,得一合力和一合力偶,其力即为轴力F N=100×106×0.04×0.1/2=200×103 N =200 kN其力偶即为弯矩M z=200×(50-33.33)×10-3 =3.33 kN·m1-4 板件的变形如图中虚线所示。
试求棱边AB与AD的平均正应变及A点处直角BAD的切应变。
解:第二章轴向拉压应力2-1试计算图示各杆的轴力,并指出其最大值。
解:(a) F N AB=F, F N BC=0, F N,max=F(b) F N AB=F, F N BC=-F, F N,max=F(c) F N AB=-2 kN, F N2BC=1 kN, F N CD=3 kN, F N,max=3 kN(d) F N AB=1 kN, F N BC=-1 kN, F N,max=1 kN2-2 图示阶梯形截面杆AC,承受轴向载荷F1=200 kN与F2=100 kN,AB段的直径d1=40 mm。
材料力学简明教程(景荣春)课后答案第三章

E 。 2(1 + μ )
3-5 圆轴扭转时如何确定危险截面、危险点及强度条件? 答 等截面圆轴扭转时的危险截面为扭矩最大的横截面,变截面圆轴扭转时的危险截面 在其扭矩与扭转截面系数比值最大的横截面;其危险点在该横截面的外边缘。强度条件为
τ max =
Tmax ≤ [τ ] Wp
3-6 金属材料圆轴扭转破坏有几种形式? 答 塑性金属材料和脆性金属材料扭转破坏形式不完全相同。塑性材料试件在外力偶作 用下,先出现屈服,最后沿横截面被剪断,如图 a 所示;脆性材料试件受扭时,变形很小, 最后沿与轴线约 45°方向的螺旋面断裂,如图 b 所示。
ϕ = ∫ dϕ = ∫
l l
T (x ) dx GI p ( x )
上式适用于等截面圆轴和截面变化不大的圆锥截面轴。对等截面圆轴,若在长 l 的两横截面 间的扭矩 T 为常量,则
ϕ=
圆轴扭转的刚度条件为
Tl GI p
⎟ ≤ [θ ] θ max = ⎜ ⎜ GI ⎟ ⎝ p ⎠ max
⎛ T ⎞
对于等截面圆轴为 或
50 ⎛ ⎞ 8 × 1.5 × 10 3 × 50 × 10 −3 ⎜ 4 × + 2 ⎟ 8 FD(4c + 2) 8 ⎝ ⎠ = 458 MPa = 解 (1) τ max = 3 50 ( ) πd 4c − 3 ⎛ ⎞ π × 8 3 × 10 −9 × ⎜ 4 × − 3 ⎟ 8 ⎝ ⎠ τ max − [τ ] 8 = × 100% = 1.78% < 5% [τ ] 450
材料力学第三章答案

材料力学第三章答案材料力学第三章答案【篇一:材料力学习题册答案-第3章扭转】是非判断题二、选择题0 b 2t?d316?1?? ? b wp??d316?1?? ?2c wp??d316?1?? ? d w3p??d316?1?? ?46.对于受扭的圆轴,关于如下结论:①最大剪应力只出现在横截面上;②在横截面上和包含杆件的纵向截面上均无正应力;③圆轴内最大拉应力的值和最大剪应力的值相等。
现有四种答案,正确的是( a )a ②③对b①③对c①②对d 全对7.扭转切应力公式?mnp?i?适用于(d)杆件。
pa 任意杆件;b 任意实心杆件;c 任意材料的圆截面;d 线弹性材料的圆截面。
9.若将受扭实心圆轴的直径增加一倍,则其刚度是原来的( d a 2倍; b 4倍; c 8倍; d 16倍。
三、计算题1.试用截面法求出图示圆轴各段内的扭矩t,并作扭矩图2.图示圆轴上作用有四个外力偶矩me1 =1kn/m, me2 =0.6kn/m,)me3= me4 =0.2kn/m, ⑴试画出该轴的扭矩图;⑵若me1与me2的作用位置互换,扭矩图有何变化?(1)(2)解:me1与me2的作用位置互换后,最大扭矩变小。
3.如图所示的空心圆轴,外径d=100㎜,内径d=80㎜,m=6kn/m,m=4kn/m.请绘出轴的扭矩图,并求出最大剪应力解:扭矩图如上,则轴面极惯性矩id4?d4)(1004?804)(10?3)4p=?(32??32?5.8?10?6m4㎜,l=500tr4?103?50?103ip5.8?104.图示圆形截面轴的抗扭刚度为g ip,每段长1m,试画出其扭矩图并计算出圆轴两端的相对扭转角。
ab+ad=cdab=t1l?90?gipgipad=bc=t2l100gipgipcd=t3l40gipgip?90?100?4050?gipgip【篇二:《材料力学》第3章扭转习题解】[习题3-1] 一传动轴作匀速转动,转速n?200r/min,轴上装有五个轮子,主动轮ii输入的功率为60kw,从动轮,i,iii,iv,v依次输出18kw,12kw,22kw和8kw。
材料力学第3章 (2)

2 2
FN 2 3F A2 4 b 2d 3 80 103 N 4 0.08m 2 0.016m 0.01m 125Mpa<[]
铆钉和板的强度都符合要求。
10
材料力学
出版社 科技分社
小结 (1) 连接件的破坏形式主要有剪切和挤压破坏。
7
材料力学
出版社 科技分社
例题 图示两块钢板用四个直径相同的钢铆钉连接一起。 已知载荷F = 80 KN,板宽b =80 mm,板厚 =10 mm,铆 钉 d =16 mm,许用切应力[] =100 MPa,铆钉和钢板许用 挤压应力[jy] = 300MPa,钢板的许用拉应力 [] =160Mpa 。试校核该钢板连接处的强度。
等直圆杆在扭转时,杆内各点均处于纯剪切应力状 态。最大切应力发生在最大扭矩所在横截面,即危 险截面的周边上任一点处,其强度条件是横截面最 大工作切应力不超过材料的许用切应力 。即
Tmax max Wp
根据该式可对空心或实心圆截面的轴进 行强度计算,即强度校核、选择截面或 计算许可荷载三种类型的问题。
T2 M 2 M 3 9.56kN m
材料力学
出版社 科技分社
AD段:沿3-3截面将轴截开 ,取右边分析,假设为正 值扭矩,则由平衡方程
M
x
0
T3 M 4 0
T3 M 4 6.37kN m
。
(3)作扭矩图。 根据以上计算结果 即可做出扭矩图。
Tmax 9.56kN m
材料力学
出版社 科技分社
(2)计算各段轴上的扭矩。 BC段:沿1-1截面将轴截开,取左边分析,假设 为正值扭矩,则由平衡方程得
M
简明材料力学习题解答第三章
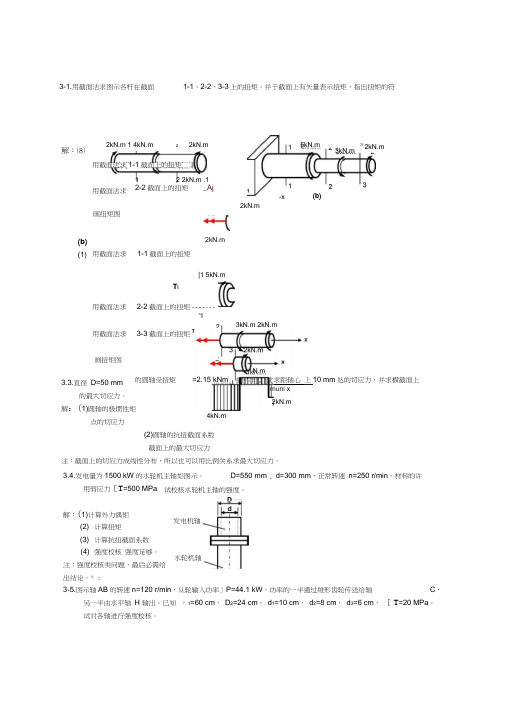
3-1.用截面法求图示各杆在截面 1-1、2-2、3-3上的扭矩。
并于截面上有矢量表示扭矩,指岀扭矩的符2kN.m3.4.发电量为1500 kW 的水轮机主轴如图示。
D=550 mm , d=300 mm ,正常转速 n=250 r/min 。
材料的许用剪应力[T =500 MPa 解:(1)计算外力偶矩(2) 计算扭矩(3) 计算抗扭截面系数 (4) 强度校核 强度足够。
注:强度校核类问题,最后必需给岀结论。
^ ;3-5.图示轴AB 的转速n=120 r/min ,从轮输入功率]P=44.1 kW ,功率的一半通过锥形齿轮传送给轴C ,另一半由水平轴 H 输岀。
已知 。
1=60 cm , D 2=24 cm , d 1=10 cm , d 2=8 cm , d 3=6 cm , [ T =20 MPa 。
试对各轴进行强度校核。
解:⑻用截面法求1-1截面上的扭矩用截面法求 32kN.m画扭矩图(b)(1) 用截面法求 1-1截面上的扭矩|1 5kN.mT i用截面法求 2-2截面上的扭矩 ------- '1 用截面法求 3-3截面上的扭矩T 2画扭矩图3.3.直径 D=50 mm的最大切应力。
解:(1)圆轴的极惯性矩点的切应力(2)圆轴的抗扭截面系数截面上的最大切应力注:截面上的切应力成线性分布,所以也可以用比例关系求最大切应力。
的圆轴受扭矩=2.15 kNm:求距轴心 上10 mm 处的切应力,并求横截面上 muni x 试校核水轮机主轴的强度。
D 一2kN.m 22kN.m 1 4kN.m12 2kN.m .12-2截面上的扭矩_Aj 5kN.m3kN.m(b)-x2kN.m2kN.m4kN.m3kN.m 2kN.m2xN.m发电机轴水轮机轴实心轴和空心轴由牙嵌式离合器连接在一起,如图所示。
已知轴的转速为n=100 r/min ,传递的功率P=7.5 kW ,材料的许用剪应力[T =40 MPa 。
材料力学第三章习题答案

第三章 轴向拉压变形
题号 页码 3-2 .........................................................................................................................................................1 3-4 .........................................................................................................................................................2 3-5 .........................................................................................................................................................2 3-7 .........................................................................................................................................................3 3-8 .........................................................................................................................................................5 3-10 .......................................................................................................................................................6 3-11 .......................................................................................................................................................7 3-13 .......................................................................................................................................................8 3-15 .....................................................................................................................................................10 3-16 .....................................................................................................................................................10 3-18 .....................................................................................................................................................11 3-19 .....................................................................................................................................................13 3-20 .....................................................................................................................................................14 3-24 .....................................................................................................................................................15 3-25 .....................................................................................................................................................16 3-27 .....................................................................................................................................................17 3-28 .....................................................................................................................................................18 3-29 .....................................................................................................................................................20 3-30 .....................................................................................................................................................21 3-32 .....................................................................................................................................................22
《工程力学(工程静力学与材料力学)(第3版)》习题解答:第3章 力系的平衡
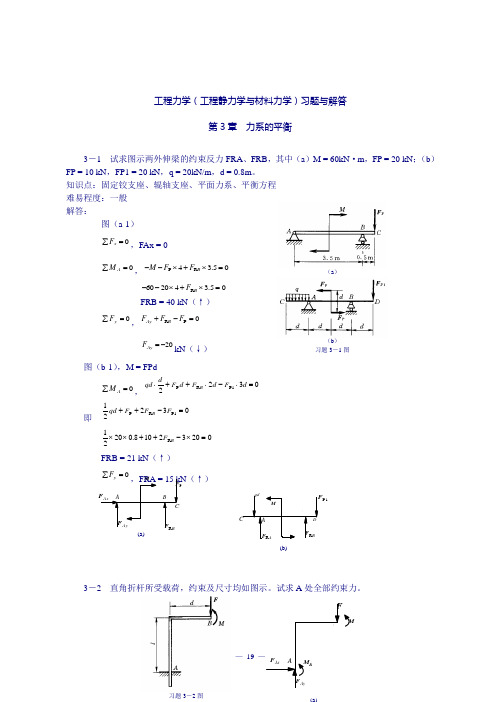
工程力学(工程静力学与材料力学)习题与解答第3章 力系的平衡3-1 试求图示两外伸梁的约束反力FRA 、FRB ,其中(a )M = 60kN ·m ,FP = 20 kN ;(b )FP = 10 kN ,FP1 = 20 kN ,q = 20kN/m ,d = 0.8m 。
知识点:固定铰支座、辊轴支座、平面力系、平衡方程 难易程度:一般 解答:图(a-1) 0=∑x F ,FAx = 00=∑A M ,05.34R P =⨯+⨯--B F F M 05.342060R =⨯+⨯--B F FRB = 40 kN (↑)=∑y F ,0P R =-+F F F B Ay20-=Ay F kN (↓)图(b-1),M = FPd 0=∑A M ,03221P R P =⋅-⋅++⋅d F d F d F dqd B即 032211P R P =-++F F F qd B 02032108.02021R =⨯-++⨯⨯B FFRB = 21 kN (↑)=∑y F ,FRA = 15 kN (↑)3-2 直角折杆所受载荷,约束及尺寸均如图示。
试求A 处全部约束力。
A MB Ay F B R F CAx F PF(a) M A B B R F A R F P 1F C qdBD(b)(a )(b ) 习题3-1图FMB习题3-3图sF W A F ABF BF AN F(a)知识点:固定端约束、平面力系、平衡方程 难易程度:一般 解答: 图(a ): 0=∑x F ,0=Ax F=∑y F ,=Ay F (↑)0=∑A M ,0=-+Fd M M AM Fd M A -=3-3 图示拖车重W = 20kN ,汽车对它的牵引力FS = 10 kN 。
试求拖车匀速直线行驶时,车轮A 、B 对地面的正压力。
知识点:固定端约束、平面力系、平衡方程 难易程度:一般解答: 图(a ):0)(=∑F A M 08.214.1NB S =⨯+⨯-⨯-F F W6.13NB =F kN=∑y F ,4.6NA =F kN3-4 图示起重机ABC 具有铅垂转动轴AB ,起重机重W = 3.5kN ,重心在D 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3-1. 用截面法求图示各杆在截面1-1、2-2、3-3上的扭矩。
并于截面上有矢量表示扭矩,指出扭矩的符号。
作出各杆扭矩图。
解: (a)(1) 用截面法求1-1截面上的扭矩110 202 .xmT T kN m=-+=∴=∑(2) 用截面法求2-2截面上的扭矩220 202 .xmT T kN m=--=∴=-∑(3) 画扭矩图(b)(1) 用截面法求1-1截面上的扭矩110 53204 .xmT T kN m=--+-=∴=-∑(2) 用截面法求2-2截面上的扭矩(a)xxxxx220 3201 .xmT T kN m=-+-=∴=∑(3) 用截面法求3-3截面上的扭矩330 202 .xmT T kN m=--=∴=-∑(4) 画扭矩图3.3. 直径D =50 mm 的圆轴受扭矩T =2.15 kN.m 的作用。
试求距轴心10 mm 处的切应力,并求横截面上的最大切应力。
解: (1) 圆轴的极惯性矩4474320.05 6.1410 3232P D I m π-⨯===⨯点的切应力372.15100.0135.0 6.1410p T MPa I ρτ-⨯⨯===⨯(2) 圆轴的抗扭截面系数7536.1410 2.45610 /20.05/2pt I W m D --⨯===⨯截面上的最大切应力3max52.151087.5 2.45610t T MPa W τ-⨯===⨯ 注:截面上的切应力成线性分布,所以也可以用比例关系求最大切应力。
max /20.05/235.087.5 0.01D MPa ττρ=⨯=⨯= 3.4. 发电量为1500 kW 的水轮机主轴如图示。
D =550 mm ,d =300 mm ,正常转速n =250 r/min 。
材料的许用剪应力[τ]=500 MPa 。
试校核水轮机主轴的强度。
x解:(1) 计算外力偶矩15009549954957.29 .250P m kN m n ==⨯= (2) 计算扭矩57.29 .T m kN m ==(3) 计算抗扭截面系数4433()29.810 16t W D d m Dπ-=-=⨯(4) 强度校核3357.291019.2[]29.810t T MPa W τσ-⨯===⨯强度足够。
注:强度校核类问题,最后必需给出结论。
3-5. 图示轴AB 的转速n =120 r/min ,从B 轮输入功率P =44.1 kW ,功率的一半通过锥形齿轮传送给轴C ,另一半由水平轴H 输出。
已知D 1=60 cm ,D 2=24 cm ,d 1=10 cm ,d 2=8 cm ,d 3=6 cm ,[τ]=20 MPa 。
试对各轴进行强度校核。
解:(1)计算外力偶矩1244.1954995493509 .12011755 .244.12295499549701.9 .6012024H C P m N m n m m N m P m N mD n D ==⨯======⨯⨯(2)计算内力扭矩3509 . 1755701.9.AB H H C C T m N m T m Nm T m N m======(3)计算抗扭截面系数3363133632336330.119610 16160.0810010 16160.0642.410 1616tAB tH tC W d m W d m W d m ππππππ---==⨯=⨯==⨯=⨯==⨯=⨯ (4)强度校核max 6max 6max 6350917.9[]19610175517.55[]10010701.916.55[]42.410AB AB tAB H H tH C C tC tCT MPa W T MPa W T MPa W ττττττ---===⨯===⨯===⨯ 强度足够。
3-6. 图示阶梯形圆轴直径分别为d 1=40 mm ,d 2=70 mm ,轴上装有三个带轮。
已知由轮3输入的功率为P 3=30 kW ,轮1输出的功率为P 1=13 kW ,轴作匀速转动,转速n =200 r/min ,材料的许用剪应力[τ]=60 MPa ,G=80 GPa ,许用扭转角[θ]=2 o /m 。
试校核轴的强度和刚度。
解:(1) 计算外力偶矩11331395499549620.720030954995491432.4200P m Nm n P m Nmn ==⨯===⨯=(2) 计算扭矩121233620.7 . 1432.4 .T m N m T m N m =-=-=-=-(3) 计算抗扭截面系数3363113363220.0412.561016160.0767.31101616t t W d m W d m ππππ--==⨯=⨯==⨯=⨯(4) 强度校核[][]12max16123max 262620.749.4212.56101432.421.2867.3110t t T MPa W T MPa W ττττ--===≤⨯===≤⨯强度足够。
(5) 计算截面极惯性矩6841116732220.0412.561025.1210 220.0767.311023.5610 22p t p t d I W m d I W m ----=⨯=⨯⨯=⨯=⨯=⨯⨯=⨯(6) 刚度校核12max198123max 2972180620.7180 1.77/[]801025.12101801432.41800.435/[]801023.5610o oo p o oop T m GI T m GI θθππθθππ--=⨯=⨯=⨯⨯⨯=⨯=⨯=⨯⨯⨯刚度足够。
注:本题中扭矩的符号为负,而在强度和刚度计算中,扭矩用其数值代入。
3.9. 实心轴和空心轴由牙嵌式离合器连接在一起,如图所示。
已知轴的转速为n =100r/min ,传递的功率P =7.5 kW ,材料的许用剪应力[τ]=40 MPa 。
试选择实心轴直径d 1和内外径比值为1/2的空心轴外径D 2。
解:(1) 计算外力偶矩7.595499549716.2.100P m N m n ==⨯= (2) 计算内力-扭矩716.2.T m N m ==(3) 计算抗扭截面系数3113422161(1) 162t t W d W D ππαα==-=(4) 设计截面311342216[]45 (1)16[]46 T d d mm TD D mm πτπατ≥===-≥===注:也可以用比例关系求直径D 2。
12246 d D mm D ====3.11. 图示传动轴的转速为n =500 r/min ,主动轮1输入功率P 1=368 kW ,从动轮2、3分别输出功率P 2=147 kW ,P 3=221 kW 。
已知[τ]=70 MPa ,[θ]=1 o /m ,G =80 GPa 。
(1) 确定AB 段的直径d 1和BC 段的直径d 2;(2) 若AB 和BC 两段选用同一直径,试确定其数值。
(3) 主动轮和从动轮的位置如可以重新安排,试问怎样安置才比较合理?解:(1) 计算外力偶矩112233368954995497028 .500147954995492807.500221954995494221 .500P m N m n P m N m n P m N mn ==⨯===⨯===⨯=(2) 计算内力-扭矩1212337028 .4221.T m N m T m N m=-=-=-=-(3) 计算AB 段的直径d 1和BC 段的直径d 2 根据强度条件设计31211116[]80 t T W d d mm πτ=≥≥==32322216[]67 t T W d d mm πτ=≥≥==根据刚度条件设计41211118032[]84.6 p T I d G d mmπθπ=≥⨯∴≥==42322218032[]74.5 p T I d G d mm πθπ=≥⨯∴≥==综合强度和刚度条件,取mm d mm d 5.74 6.8421==(4) 若AB 和BC 两段选用同一直径,则取mm d d 6.84 21==(5) 将A 轮和B 轮对调位置,则T12=2807N.m ,最大扭矩减小,轴的扭转强度提高了,所以主动轮放在中间更合理。
3.13. 设圆轴横截面上的扭矩为T ,试求四分之一截面上内力系的合力的大小、方向及作用点。
解:(1) 取微元dA ,上面的切应力是τρ,则微力为τρdA :4432 32T T T dA d d d I d ρρρρρϕρτππ====(2) 将四分之一截面上的力系向O点简化222400222400324sin sin3324cos cos33dxAdyAOT TQ dA d dd dT TQ dA d dd dRdπρπρτϕϕϕρρππτϕϕϕρρπππ========⎰⎰⎰⎰⎰⎰⎰⎰322400324dOAT TM dA d ddπρτρϕρρπ===⎰⎰⎰⎰(3) R o与x轴之间的夹角4πQQarctgαxy==(4) 将R o和M o进一步简化为一合力R,即将R o向左方平移一段距离d:2163dπRMdoo==3.14. 图示圆截面杆的左端固定,沿轴线作用集度为t的均布力偶矩。
试导出计算截面B的扭转角的公式。
解:(1) 用截面法求x截面上的扭矩:()()T x t l x=-(2) dx微段的扭转角()()p pT x t l xd dx dxGI GIϕ-==(3) 截面B 的扭转角()22lBA ppt l x tl dx GI GI ϕ-==⎰3.15. 将钻头简化成直径为20mm 的圆截面杆,在头部受均布阻抗扭矩t 的作用,许用剪应力为[τ]=70 MPa ,G =80 GPa 。
(1)求许可的m ;(2)求上、下两端的相对扭转角。
解:(1) 画扭矩图由扭矩图知max 0.1T m t ==(2) 确定许可载荷:336max [][]0.027010110 .1616t m T W d N m ππττ=≤==⨯⨯⨯=(3) 求上、下两端的相对扭转角:()()0.20.100249100.1/20.20.250.251100.022 1.260.02801032p pp p pomtx dx dxGI GI m m m GI GI GI rad ϕπ=+⨯=+=⨯===⨯⨯⨯⎰⎰3.17. AB 和CD 两轴的B 、C 两端以凸缘相连接,A 、D 两端则都是固定端。
由于两个凸缘的螺钉孔的中心线未能完全生命形成一个角度为的误差。
当两个凸缘由螺钉联接后,试度求两轴的装配扭矩。
解:(1) 整体受力分析,列平衡方程:tT0D A m m -=这是一次静不定问题。
