(word完整版)八年级数学《线段垂直平分线角平分线》练习题
专题02 垂直平分线与角平分线(解析版)八年级数学下册期末综合复习专题提优训练(北师大版)

2020-2021学年八年级数学下册期末综合复习专题提优训练(北师大版)专题02 垂直平分线与角平分线【典型例题】1.如图,△ABC 中,△ABC =25°,△ACB =55°,DE ,FG 分别为AB ,AC 的垂直平分线,E ,G 分别为垂足; (1)直接写出△BAC 的度数;(2)求△DAF 的度数;(3)若BC 的长为30,求△DAF 的周长.【答案】(1)100BAC ∠=︒;(2)20DAF ∠=︒;(3)30DAF C =【分析】 (1)由题意直接根据三角形内角和定理计算,得到答案;(2)由题意根据线段垂直平分线的性质、等腰三角形的性质计算;(3)根据线段垂直平分线的性质、三角形的周长公式计算,得到答案.【详解】解:(1)△△ABC +△ACB +△BAC =180°,△△BAC =180°﹣25°﹣55°=100°;(2)△DE 是线段AB 的垂直平分线,△DA =DB ,△△DAB =△ABC =25°,△FG 是线段AC 的垂直平分线,△AF =CF ,△△F AC =△ACB =55°,△△DAF =△BAC ﹣△DAB ﹣△F AC =100°﹣25°﹣55°=20°;(3)△BC =30,由(2)可知, AD =BD ,F A =FC ,△C △DAF =AD +DF +F A =BD +DF +FC =BC =30.【点睛】本题考查的是线段的垂直平分线的性质以及三角形内角和定理,等腰三角形性质,熟练掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.【专题训练】一、选择题1.如图,在Rt ABC 中,90,B AD ∠=︒平分BAC ∠,交BC 于点D ,DE AC ⊥,垂足为点E ,若1BD =,则DE 的长为( )A .12B .1C .2D .6【答案】B【分析】根据△B =90°,AD 平分△BAC ,DE △AC ,再根据角平分线的性质得到DE =BD =1.【详解】△90B ∠=︒,△DB AB ⊥,又△AD 平分BAC ∠,DA AC ⊥,△由角平分线的性质得1DE BD ==. 故选:B【点睛】本题主要考查了角平分线的性质,灵活运用角平分线的性质处理问题.2.如图,在ABC 中,直线ED 是线段BC 的垂直平分线,直线ED 分别交BC 、AB 于点D 、点E ,已知BD =3,ABC 的周长为20,则AEC 的周长为( )A .14B .20C .16D .12【答案】A【分析】 根据线段的垂直平分线的性质得到EC =EB ,BC =2BD =6,根据三角形的周长公式计算即可.【详解】△ED 是线段BC 的垂直平分线,△EC =EB ,BC =2BD =6,△△ABC 的周长为20,△AB +AC +BC =20,△AB +AC =14,△△AEC 的周长=AC +AE +EC =AC +AE +EB =AC +AB =14,故选:A .【点睛】本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.3.如图,在ABC 中,AD BC ⊥,垂足为D ,EF 垂直平分AC ,交AC 于点F ,交BC 于点E ,BD DE =,若ABC 的周长为26cm ,5AF =cm ,则DC =( )A .8cmB .7cmC .10cmD .9cm【答案】A【分析】根据线段垂直平分线和等腰三角形性质得出AB=AE=CE,能推出2DE+2EC=16,即可求解.【详解】解:△AD△BC,BD=DE,EF垂直平分AC△AB=AE=EC△△ABC周长是26cm,AF=5cm△AC=10cm△AB+BC=16cm△AB+BE+EC=16cm即2DE+2EC=16cm△DE+EC=8cm△DC=DE+EC=8cm故选A.【点睛】本题主要考查了等腰三角形的性质,线段垂直平分线的性质,掌握线段垂直平分线上的点到线段两端的距离相等时解题的关键.4.如图,在Rt△ABC中,△ACB=90°,AC=3,BC=4,BE平分△ABC,CD△AB于D,BE与CD相交于F,则CF的长是()A.1B.43C.53D.2【答案】B【分析】过点E作EG△AB于点G,由EG△AB,CD△AB,可得EG△CD,由平行线的性质可得△GEB=△EFC;在Rt△ABC 中,由勾股定理求得AB的值;由HL判定Rt△EBC△Rt△EBG,由全等三角形的性质可得△CEB=△EFC及AG 的值,进而可判定CF=CE.设CF=EG=EC=x,则AE=3-x,在Rt△AEG中,由勾股定理得关于x的方程,解得x 的值即为CF 的长.【详解】解:过点E 作EG △AB 于点G ,如图:△CD △AB 于D ,△EG △CD ,△△GEB =△EFC ,△在Rt △ABC 中,△ACB =90°,△EC △CB ,又△BE 平分△ABC ,EG △AB ,△EG =EC .在Rt △ABC 中,△ACB =90°,AC =3,BC =4,△AB =5.在Rt △EBC 和Rt △EBG 中,EB EB EC EG=⎧⎨=⎩, △Rt △EBC △Rt △EBG (HL ),△CEB =△GEB ,BG =BC =4,△△CEB =△EFC ,AG =AB ﹣BG =5﹣4=1,△CF =CE .设CF =EG =EC =x ,则AE =3﹣x ,在Rt △AEG 中,由勾股定理得:(3﹣x )2=x 2+12,解得x =43△CF 的长是43.故选:B.【点睛】本题考查了勾股定理、角平分线的性质定理及等腰三角形的判定等知识点,数形结合并熟练掌握相关性质及定理是解题的关键.5.如图,在△ABC中,△B=15°,△C=30°,MN是AB的垂直平分线,PQ是AC的垂直平分线,已知S△ANQ则BC的长为()A B.3C.3D.2+【答案】B【分析】根据线段垂直平分线的性质得出AQ=CQ,BN=AN,根据等腰三角形的性质和已知条件得出△BAN=△B=15°,△CAQ=△C=30°,根据三角形外角性质得出△ANQ=△B+△BAN=30°,△AQN=△C+△CAQ=60°,求出△NAQ=90°,再根据三角形的面积求出AQ,最后求出BC即可.【详解】解:△MN是AB的垂直平分线,PQ是AC的垂直平分线,△AQ=CQ,BN=AN,△△B=15°,△C=30°,△△BAN=△B=15°,△CAQ=△C=30°,△△ANQ=△B+△BAN=15°+15°=30°,△AQN=△C+△CAQ=30°+30°=60°,△△NAQ=180°﹣△ANQ﹣△AQN=90°,△NQ=2AQ,AN==,△S△ANQ=,2△12⨯AQ 解得:AQ =1(负数舍去),即CQ =AQ =1,AN =BN NQ =2AQ =2,△BC =BN +NQ +CQ 2+1=3故选:B .【点睛】本题考查了含30°角的直角三角形的性质,线段垂直平分线的性质,勾股定理,三角形的面积,三角形的外角性质,等腰三角形的性质等知识点,能综合运用知识点进行推理和计算是解此题的关键.二、填空题6.如图,在△ABC 中,△C =90°,AP 平分△CAB ,且PC =3,PB =5,则点P 到边AB 的距离是 ______________【答案】3【分析】作PH △AB 于H .直接根据角平分线的性质求解即可.【详解】解:作PH △AB 于H ,如图,△AP 平分△CAB ,且△C =90°,△3PH PC ==,即点P 到边AB 的距离是3.故答案为3.【点睛】此题主要考查了角平分线的性质,熟练掌握角平分线性质定理是解答此题的关键.7.如图,在△ABC 中,△C =90°,DE 垂直平分斜边AB ,分别交AB 、BC 于D 、E ,若△CAB =△B +28°,则△CAE=__.【答案】28︒【分析】先根据直角三角形的两锐角互余可得31,59B CAB ∠=︒∠=︒,再根据垂直平分线的性质可得AE BE =,然后根据等腰三角形的性质可得31B BAE ∠=∠=︒,最后根据角的和差即可得.【详解】解:△在ABC 中,90C ∠=︒,△90CAB B ∠+∠=︒,又△28CAB B ∠=∠+︒,△31,59B CAB ∠=︒∠=︒,△DE 垂直平分斜边AB ,△AE BE =,△31BAE B ∠=∠=︒,△593128CAE CAB BAE ∠=∠-∠=︒-︒=︒,故答案为:28︒.【点睛】本题考查了直角三角形的两锐角互余、等腰三角形的性质、线段垂直平分线的性质等知识点,熟练掌握等腰三角形的性质和线段垂直平分线的性质是解题关键.8.如图,在△ABC 中,AB =6,AC =8,BC =11,AB 的垂直平分线分别交AB ,BC 于点D 、E ,AC 的垂直平分线分别交AC ,BC 于点F 、G ,则△AEG 的周长为__.【答案】11.【分析】根据线段垂直平分线的性质可得EA=EB,GA=GC,所以可求出△AEG的周长.【详解】解△DE是线段AB的垂直平分线,△EA=EB,同理,GA=GC,△△AEG的周长=AE+EG+GA=EB+EG+GC=BC=11,故答案为:11.【点睛】本题考查了线段垂直平分线的性质.线段垂直平分线上的点到线段两端点的距离相等.9.如图,在四边形ABCD中,△A=90°,AD= 6,连接BD,BD△CD,△ADB=△C.若P是BC边上一动点,则DP长的最小值为__________.【答案】6【分析】根据垂线段最短得出当DP△BC时,DP的长度最小,求出△ABD=△CBD,根据角平分线的性质得出AD=DP=6,即可得出选项.【详解】解:△BD△CD,△△BDC=90°,△△C+△CBD=90°,△△A=90°△△ABD+△ADB=90°,△△ADB=△C,△△ABD=△CBD,当DP△BC时,DP的长度最小,△AD△AB,△DP=AD,△AD=6,△DP的最小值是6,故答案为:6.【点睛】本题考查了角平分线的性质,三角形内角和定理和垂线段最短等知识点,能知道当DP△BC时,DP的长度最小是解此题的关键.10.如图,等腰三角形ABC的面积为24,底边BC为12,点P在边BC上,且BP:PC=3:1,EG是腰AC的垂直平分线,若点D在EG上运动,则△CDP周长的最小值为___________.【答案】8.【分析】如图作AH△BC于H,连接AD.由EG垂直平分线段AC,推出DA=DC,推出DP+DC=AD+DP,可得当A、D、P共线时,DP+DC的值最小,最小值就是线段AP的长,此时,△CDP周长的最小,求出AP的长即可.【详解】解:如图作AH△BC于H,连接AD.△EG垂直平分线段AC,△DA=DC,△DP+DC=AD+DP,△当A、D、P共线时,DP+DC的值最小,最小值就是线段AP的长,△12×12•AH=24,△AH=4,△AB=AC,AH△BC,△BH=CH=6,△BP:PC=3:1,△CP=PH=3,△AP5,△DP+DC的最小值为5.△△CDP周长的最小值为5+3=8;故答案为:8.【点睛】本题考查轴对称﹣最短问题、线段的垂直平分线的性质、等腰三角形的性质、勾股定理等知识,解题的关键是学会利用轴对称,解决最短问题,属于中考常考题型.三、解答题11.如图,在△ABC中,AB=AC,BE平分△ABC,DE△BC,交AB于点D,交AC于点E.(1)求证:BD=DE;(2)若△DEB=30°且DE=3,求AD的长度.【答案】(1)见解析;(2)3.【分析】(1)由BE平分△ABC,DE△BC可得△DBE=△DEB,可得结论;(2)通过证明△ADE为等边三角形,可得AD=DE=3.【详解】证明:(1)△BE平分△ABC,△△ABE=△EBC,△DE△BC,△△DEB=△EBC,△△DBE=△DEB,△BD=DE;(2)△△DEB=△DBE=30°=△EBC,△△ABC=60°,△AB=AC,△△ABC是等边三角形,△△ABC=△ACB=△A=60°,△DE△BC,△△ADE=△ABC=60°,△AED=△C=60°,△△ADE是等边三角形,△AD=DE=3.【点睛】本题考查了等腰三角形的性质,角平分线的性质,平行线的性质,等边三角形的判定和性质,灵活运用这些性质进行推理是本题的关键.,的垂直平分线交于点P.12.如图,ABC中,边AB BC==.(1)求证:PA PB PC(2)点P是否也在边AC的垂直平分线上?请说明理由.【答案】(1)见解析;(2)在,理由见解析【分析】(1)根据线段的垂直平分线的性质可求得,P A=PB,PB=PC,则P A=PB=PC.(2)根据线段的垂直平分线的性质的逆定理,可得点P在边AC的垂直平分线上.【详解】解:(1)证明:△边AB、BC的垂直平分线交于点P,△P A=PB,PB=PC.△P A=PB=PC.(2)△P A=PC,△点P 在边AC 的垂直平分线上.【点睛】此题主要考查线段垂直平分线的性质定理及逆定理:(1)线段垂直平分线上的点和这条线段的两个端点的距离相等;(2)和一条线段的两个端点的距离相等的点,在这条线段的垂直平分线上.13.如图,AD 为△ABC 的角平分线,DE △AB 于点E ,DF △AC 于点F ,连接EF 交AD 于点O .(1)求证:△DEF =△DFE ;(2)求证:AD 垂直平分EF .【答案】(1)见解析;(2)见解析【分析】(1)根据角平分线的性质证明即可得解;(2)根据已知条件证明Rt △AED △Rt △AFD (HL )和△△DEO DFO ≅即可得解;【详解】(1)△AD 为△ABC 的角平分线,DE △AB ,DF △AC ,△DE =DF ,△△DEF =△DFE ;(2)根据已知条件可得△AED =△AFD =90°,在Rt △AED 和Rt △AFD 中,DE DF AD AD=⎧⎨=⎩, △Rt △AED △Rt △AFD (HL ),△△ADE =△ADF ;在△DEO 和△DFO 中, DEO DFO DE DFEDO FDO ∠=∠⎧⎪=⎨⎪∠=∠⎩, △△△DEO DFO ≅,△EO FO =,EOD FOD ∠=∠,△∠EOD +∠FOD =180°,△∠EOD =∠FOD =90°,△AD 垂直平分EF .【点睛】本题主要考查了角平分线的垂直平分线的判定与性质,结合等三角形证明是解题的关键.14.如图,在ABC 中,AB AC =,AB 的垂直平分线交AB 于M ,交AC 于N .(1)若70ABC ∠=︒,求A ∠的度数;(2)连接NB ,若8cm AB =,NBC 的周长是14cm ,求BC 的长.【答案】(1)40°;(2)6cm【分析】(1)由AB =AC 可得△C =△ABC =70°,由三角形内角和可得△A =40°;(2)由(1)可知BN =AN ,由此可得BN +NC =AN +NC =AC =AB =8cm ,再由C △BNC =BN +CN +BC =14cm ,可得BC =14-8=6(cm ).【详解】解:(1)△AB =AC ,△△ABC =△ACB =70°,△△A =180°-70°-70°=40°;(2)MN 是AB 的垂直平分线,△AN =BN ,△BN +CN =AN +CN =AC ,△AB =AC =8cm ,△BN +CN =8cm ,△C △BNC =BN +CN +BC =14(cm ),△BC =14﹣8=6(cm ).【点睛】本题考查等腰三角形性质,三角形内角和,线段垂直平分线性质,三角形周长,掌握等腰三角形性质,三角形内角和,线段垂直平分线性质,三角形周长是解题关键.15.如图,△ABC 中,AD 平分△BAC ,DG △BC 且平分BC ,DE △AB 于E ,DF △AC 于F .(1)求证:BE =CF ;(2)如果AB =8,AC =6,求AE ,BE 的长.【答案】(1)证明见解析,(2)AE =7,BE =1.【分析】(1)连接DB 、DC ,先由角平分线的性质就可以得出DE =DF ,再证明△DBE △△DCF 就可以得出结论; (2)由条件可以得出△ADE △△ADF 就可以得出AE =AF ,进而就可以求出结论.【详解】解:(1)证明:连接DB 、DC ,△DG △BC 且平分BC ,△DB =DC .△AD 为△BAC 的平分线,DE △AB ,DF △AC ,△DE =DF .在Rt △DBE 和Rt △DCF 中DB DC DE DF =⎧⎨=⎩, Rt △DBE △Rt △DCF (HL ),△BE =CF .(2)在Rt △ADE 和Rt △ADF 中AD AD DE DF =⎧⎨=⎩,△Rt△ADE△Rt△ADF(HL).△AE=AF.△AC+CF=AF,△AE=AC+CF.△AE=AB﹣BE,△AC+CF=AB﹣BE,△AB=8,AC=6,△6+BE=8﹣BE,△BE=1,△AE=8﹣1=7.即AE=7,BE=1.【点睛】本题考查了角平分线的性质的运用,中垂线的性质的运用,全等三角形的判定与性质的运用,解答时证明三角形全等是关键.16.如图,已知Rt△ABC中,△ACB=90°,CD△AB于点D,△BAC的平分线分别交BC,CD于点E、F.(1)试说明△CEF是等腰三角形;(2)若点E恰好在线段AB的垂直平分线上,猜想:线段AC与线段AB的数量关系,并说明理由;(3)在(2)的条件下,若AC=2.5,求△ABE的面积.【答案】(1)见解析;(2)AB=2AC,理由见解析;(3)12【分析】(1)求出△B=△ACD,根据三角形的外角性质求出△CFE=△CEF,根据等腰三角形的判定得出即可;(2)求出△B=△CAE=△BAE,根据三角形内角和定理求出△B=30°,再求出答案即可;(3)求出高EM的长,求出AB的长,再根据三角形的面积公式求出即可.【详解】解:(1)△CD△AB,△△CDB=90°,△△B+△BCD=90°,△△ACB=90°,△△ACD+△BCD=90°,△△ACD=△B,△AE平分△BAC,△△CAE=△BAE,△△ACD+△CAE=△B+△BAE,即△CFE=△CEF,△CF=CE,即△CEF是等腰三角形;(2)AB=2AC,理由是:△E在线段AB的垂直平分线上,△AE=BE,△△B=△BAE,△△CAE=△BAE,△ACB=90°,△3△B=90°,△△B=30°,△AB=2AC;(3)△AC=2.5,△AB=2AC=5,由(2)得,△CAB=60°,△AE平分△CAB,△△CEA =30°,设CE 为x ,则AE 为2x ,AC ,x ,过E 作EM △AB 于M ,△EM =CE =6,△△ABE 的面积S =12AB EM ⋅=12⨯5. 【点睛】本题考查勾股定理、等腰三角形的判定、含30°角的直角三角形的性质,解题关键是熟练运用所学知识,整合已知条件,解决综合问题.17.如图1,在△ABC 中,AD △BC ,垂足为D ,E 为AC 上一点,BE 交AD 于点F ,△ABC =45°,FD =CD . (1)请写出BE 与AC 的位置关系,并说明理由;(2)如图2,连接DE ,求证:△BED =△DEC ;(3)若AD =4,CD =2,在直线BC 上方的平面内是否存在点P ,使得△BFP 为等腰直角三角形.若存在,请直接写出点P 到直线BC 的距离.【答案】(1)BE △AC ,见解析;(2)见解析;(3)存在,4或6或3【分析】(1)证明△BDF △△ADC ,得到△DBF =△DAC ,由△BFD =△AFE 证得△BDF =△AEF =90°,即可得到结论;(2)过点D 作DM △AC ,DN △BE ,根据△BDF △△ADC ,得到BF =AC ,BDF ADC SS =,推出DM =DN ,证得ED 平分△BEC ,由此得到结论;(3)根据勾股定理求出AC 由△BDF △△ADC ,得到BF =AC =DF =DC =2,BD =AD =4,分三种情况:当△PBF =90°,BP =BF 时, 当△P ′FB =90°,P ′F =BF 时, 当△BP ″F =90°,BP ″=FP ″时, 根据等腰直角三角形的性质解答即可.【详解】(1)证明:如图①中,△AD △BC ,△△ADB =90°,△△ABC =45°,△△ABD =△BAD =45°,△BD =DA ,△DF =DC ,△BDF =△ADC =90°,△△BDF △△ADC (SAS ).△△DAC =△CBE ,△△BFD =△AFE ,△△BDF =△AEF =90°,△BE △AC .(2)解:如图,过点D 作DM △AC ,DN △BE ,△△BDF △△ADC ,△BF =AC ,BDF ADC SS =,△DM =DN ,△ED 平分△BEC ,△△BED =△DEC ;(3)解:如图2-1中,满足条件的点P 有3个.在Rt △ADC 中,△AD =4,CD =2,△AC ,△△BDF △△ADC ,△BF =AC =DF =DC =2,BD =AD =4,当△PBF =90°,BP =BF 时,作PM △CB 交CB 的延长线于M . 易证△PMB △△BDF ,△PM =BD =4,△点P 到直线BC 的距离为4;当△P ′FB =90°,P ′F =BF 时,作P ′H △BC 于H ,FG △P ′H 于G . 易证:P ′G =BD =4,GH =DF =2,△P ′H =4+2=6,△P ′到直线BC 的距离为6;当△BP ″F =90°,BP ″=FP ″时,作P ″N △BC 于N .易证P ″N =2PM DF +=3,△P″到直线BC的距离为3,综上所述,满足条件的点P到直线BC的距离为4或6或3.【点睛】此题考查全等三角形的判定及性质,等腰直角三角形的性质,勾股定理,角平分线的判定及性质,熟记各定理并熟练应用解决问题是解题的关键.18.在△ABC中,若AD是△BAC的角平分线,点E和点F分别在AB和AC上,且DE△AB,垂足为E,DF△AC,垂足为F(如图(1)),则可以得到以下两个结论:①△AED+△AFD=180°;②DE=DF.那么在△ABC中,仍然有条件“AD是△BAC的角平分线,点E和点F,分别在AB和AC上”,请探究以下两个问题:(1)若△AED+△AFD=180°(如图(2)),则DE与DF是否仍相等?若仍相等,请证明;否则请举出反例.(2)若DE=DF,则△AED+△AFD=180°是否成立?(只写出结论,不证明)【答案】(1)DE=DF,理由见解析;(2)不一定成立【分析】(1)过点D作DM△AB于M,DN△AC于N,DM=DN,△DME△△DNF,DE=DF;(2)如图,若DE、DF在点D到角的两边的垂线段与顶点A的同侧则一定不成立;【详解】(1)DE=DF.理由如下:过点D作DM△AB于M,DN△AC于N,△AD平分△BAC,DM△AB,DN△AC,△DM=DN,△△AED+△AFD=180°,△AFD+△DFN=180°,△△DFN=△AED,△△DME△△DNF(AAS),△DE=DF;(2)不一定成立.如图,若DE、DF在点D到角的两边的垂线段与顶点A的同侧则一定不成立,经过(1)的证明,若在垂线段上或两侧则成立,所以不一定成立..【点睛】本题主要考查角平分线的性质,难点在于熟练和灵活的应用角平分线要点;19.根据图片回答下列问题.(1)如图①,AD平分△BAC,△B+△C=180°,△B=90°,易知:DB____DC.(2) 如图②,AD平分△BAC,△ABD+△ACD=180°,△ABD<90°,求证:DB=DC.(3)如图③,四边形ABCD中,△B=45°△C=135°,DB=DC AB−AC=________.【答案】(1)=;(2)见解析;(3)【分析】(1)利用HL判断出△ADC△△ADC,即可得出结论;(2)先构造出△ACD△△AED,得出DC=DE,△AED=△C,在判断出DE=DB,即可得出结论;(3)利用(2)结论得出DE=DB,再判断出△BDE=90°,利用勾股定理求出BE即可得出结论.【详解】解:证明:(1)△△B+△C=180°,△B=90°,△△C=90°,△AD平分△BAC,△△DAC=△BAD,△AD=AD,△△ACD△△ABD(AAS),△BD=CD;(2)如图②,在AB边上取点E,使AC=AE,△AD平分△BAC,△△CAD=△EAD,△AD=AD,AC=AE,△△ACD△△AED(SAS),△DC=DE,△AED=△C,△△C+△B=180°,△AED+△DEB=180°,△△DEB=△B,△DE=DB,△DB=DC;(3)如图③,连接AD,在AB上取一点E使AE=AC,同(2)的方法得,AE =AC ,CD =DE =BD =2,△△DEB =△B =45°,△△BDE =90°,根据勾股定理得,BE =,△AB -AC =BE =故答案为:【点睛】本题是四边形综合题,考查全等三角形的判定和性质,角平分线的性质,等腰直角三角形的性质,勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形,属于中考常考题型.20.如图①,△ABC 中,△ABC ,△ACB 的平分线交于O 点,过O 点作BC 平行线交AB ,AC 于E ,F . (1)试说明:EO =BE ;(2)探究图①中线段EF 与BE ,CF 间的关系,并说明理由;(3)探究图②,△ABC 中若△ABC 的平分线与△ABC 的外角平分线交于O ,过点O 作BC 的平行线交AB 于E ,交AC 于F ,这时EF 与BE ,CF 的关系又如何?请直接写出关系,不需要说明理由.【答案】(1)证明见解析;(2)EF BE CF =+,理由见解析;(3)EF BE CF =-【分析】(1)由题意易得△EOB =△EBO ,△ABO =△OBC ,则有△EOB =△ABO ,进而问题得证;(2)由题意易得△FOC =△OCB ,△FCO =△OCB ,则有△FCO =△FOC ,然后可得CF =OF ,由(1)得BE =OE ,进而问题可求解;(3)同理(1)(2)可得:BE=OE,CF=OF,然后问题可求解.【详解】证明:(1)△EF△BC,△△EOB=△EBO,△BO平分△ABC,△△ABO=△OBC,△△EOB=△ABO,△BE=OE;=+,理由如下:(2)解:EF BE CF△EF△BC,△△FOC=△OCB,△CO平分△ACB,△△FCO=△OCB,△△FCO=△FOC,△CF=OF,由(1)得:BE=OE,△EF=BE+CF;(3)解:EF=BE-CF,理由如下:同理(1)(2)可得:BE=OE,CF=OF,△EF=OE-OF=BE-CF.【点睛】本题主要考查角平分线的定义及平行线的性质,熟练掌握角平分线的定义及平行线的性质是解题的关键,也要熟练掌握“双平等腰”模型.。
八年级数学下等腰三角形、直角三角形、线段的垂直平分线练习题

八年级数教下等腰三角形、曲角三角形、线段的笔曲仄分线训练题之阳早格格创做 等腰三角形试题:一、采用题1. 如图,正在△ABC 中,AB=AC ,∠A=36°,BD 、CE 分别是△ABC 、△BCD 的角仄分线,则图中的等腰三角形有( ) (A)5个 (B)4个(C)3个 (D)2个第 2题 第3题2.如图,曲线CD 是线段AB 的笔曲仄分线,P 为曲线CD 上的一面,已知线段PA=5,则线段PB 的少度为( )A .6 B .5 C .4 D .33.如图,过边少为1的等边△ABC 的边AB 上一面P ,做PE ⊥AC 于E ,Q 为BC 延少线上一面,当PA =CQ 时,连PQ 接AC 边于D ,则DE 的少为( )A . B .C .D .没有克没有及决定4.下列本量中,等腰三角形具备而曲角三角形纷歧定具备的是 ( )A .二边之战大于第三边B .有一个角的仄分线笔曲于那个角的对于边C .有二个钝角的战等于90°D .内角战等于180°5.已知等腰三角形的二条边少分别是7战3,则下列四个数中,第三条边的少是( )A .8B .7C . 4D .36、如图,△ABC 内有一面D ,且DA=DB=DC ,若∠DAB=20°,(第1题)A B C DPA∠DAC=30°,则∠BDC的大小是()A.100° B.80° C.70°D.50°第6题第10题7.如图所示的正圆形网格中,网格线的接面称为格面.已知、是二格面,如果也是图中的格面,且使得为等腰三角形,则面的个数是()A.6B.7C.8 D.98.如图,面C是线段AB上的一个动面,△ACD战△BCE是正在AB共侧的二个等边三角形,DM,EN分别是△ACD战△BCE的下,面C正在线段AB上沿着从面A背面B的目标移动(没有与面A,B沉合),对接DE,得到四边形DMNE.那个四边形的里积变更情况为()(A)渐渐删大 (B) 渐渐减小 (C) 末究没有变 (D)先删大后变小9.已知等腰三角形的一个内角为70°,则其余二个内角的度数是()A.55°,55° B.70°,40° C.55°,55°或者70°,40° D.以上皆分歧过失10.一等腰三角形的二边少x、y谦脚圆程组则此等腰三角形的周少为()A.5 B.4 C.3 D.5或者411.如下图1,已知:△ABC中,AB=AC=,BC=6,则腰少的与值范畴是()A. B. C. D.13.如图,小白做出了边少为1的第1个正△A1B1C1,算出了正△A1B1C1的里积,而后分别与△A1B1C1三边的中面A2,B2,C2,做出了第2个正△A2B2C2,算出了正△A2B2C2的里积,用共样的要领,…… 图③图②图①第8题D 1D 5 D 2 D 3 D 4 D 0挖空第1题做出了第3个正△A3B3C3,算出了正△A3B3C3的里积……,由此可得,第8个正△A8B8C8的里积是( )A .B .C .D .二、挖空题1.如图,△ABC 中,DE 笔曲仄分AC 接AB 于E ,∠A=30°,∠ACB=80°,则∠BCE=.3.等腰△ABC 的二边少分别为2战5,则第三边少为.4.如上图4,正在△ABC 中,AB=AC=13,BC=10,D 是AB 的中面,过面D 做DE ⊥AC 于面E ,则DE 的少是.5.如图,将第一个图(图①)所示的正三角形连结各边中面举止分隔,得到第二个图(图②);再将第二个图中最中间的小正三角形按共样的办法举止分隔,得到第三个图(图③);再将第三个图中最中间的小正三角形按共样的办法举止分隔,……,则得到的第五个图中,公有________个正三角形. 6.底下的圆格图案中的正圆形顶面喊干格面,图1中以格面为顶面的等腰曲角三角形有4个,图2中以格面为顶面的等腰曲角三角形有个,图3中以格面为顶面的等腰曲角三角形有个,图4中以格面为顶面的等腰曲角三角形有个.图2 图图4 图38.如图,△ABC 是一个边少为2的等边三角形,AD0⊥BC ,垂脚为面D0.过面D0做D0D1⊥AB ,垂脚为面D1;再过面D1做D1D2⊥AD0,垂脚为面D2;又过面D2做D2D3⊥AB ,垂脚为面D3;……;那样背来做下来,得到一组线段:D0D1,D1D2,D2D3,……,则线段Dn1Dn 的少为_ _(n 为正整数).曲角三角形试题:一、采用题1、符合条件∠A =∠ B =∠C 的三角形一定是 ( )A. 钝角三角形B. 钝角三角形C. 曲角三角形D. 任性三角形2、二个曲角三角形齐等的条件是( )A 、一钝角对于应相等B 、二钝角对于应相等C 、一条边对于应相等D 、二条边对于应相等3、如下图1,△ABC 中,AD ⊥BC 于D ,BE ⊥AC 于E ,AD 与BE 相接于F ,若BF=AC ,则∠ABC 的大小是( )A 、40° B 、45° C 、50° D 、60°4、等腰曲角三角形的斜边少为a ,则其斜边上的下为( ) A. B. C. D.二、挖空题1、若等腰三角形的腰少为4,腰上的下为2,则此等腰三角形的顶角为. 2.若等腰三角形一腰上的下等于腰少的一半,则那个等腰三角形的底角为.3.一轮船以每小时20海里的速度沿正东目标航止.上午8时,该船正在(挖空第3题) 挖空第4题)处测得某灯塔位于它的北偏偏东30°的处(如上图2),上午9时止到处,测得灯塔恰佳正在它的正北目标,此时它与灯塔的距离是海里(截止生存根号).战4,则曲角三角形的二条曲角边的战是.5、正在△ABC中,AB=5cm,BC=6cm,BC边上的中线AD=4cm,则∠ADC的度数是___度6、如下图1,∠E=∠F=90°,∠B=∠C.AE=AF,给出下列论断:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.其中精确的论断是(注:将您认为精确的论断皆挖上.)7、如上图2:△ABC中,AD⊥BC,CE⊥AB,垂脚分别为D、E,AD、CE接于面H,请您增加一个符合的条件:,使△AEH≌△CEB.8、如图,正在等腰曲角三角形ABC中,AD⊥BC,PE⊥AB,PF⊥AC,则△DEF是三角形9、等腰曲角三角形一条曲角边的少为1cm,那么它斜边少上的下是cm.10、已知⊿ABC中,∠A = ,角仄分线BE、CF接于面O,则∠BOC = 11.正在△ABC中,∠BAC=90°,AD⊥BC于D,AB=3,AC=4,则AD=;三、解问题1.已知:如图,正在等边三角形ABC中,D、E分别为BC、AC上的面,且AE=CD,连结AD、BE接于面P,做BQ⊥AD,垂脚为Q.供证:BP=2PQ.四、商量题1.AF是△ABC的角仄分线,BD⊥AF接AF的延少线于D,DE∥AC•接AB于E,供证:AE=BE.2.如图,已知面B、C、D正在共一条曲线上,△ABC战△CDE•皆是等边三角形.BE接AC于F,AD接CE于H,①供证:△BCE≌△ACD;②供证:CF=CH;③推断△CFH•的形状并证明缘由.线段的笔曲仄分线:1、如图,正在△ABC中,分别以面A战面B为圆心,大于AB的少为半径绘孤,二弧相接于面M,N,做曲线MN,接BC于面D,对接AD.若△ADC的周少为10,AB=7,则△ABC的周少为()A、7 B、14 C、17 D、202、如图,正在Rt△ACB中,∠C=90°,BE仄分∠ABC,ED笔曲仄分AB于D.若AC=9,则AE的值是()A、6 B、4 C、6D、43、如图,正在Rt△ABC中,∠B=90°,ED是AC的笔曲仄分线,接AC于面D,接BC于面E.已知∠BAE=10°,则∠C的度数为()A、30° B、40° C、50° D、60°4、如图,正在梯形ABCD中,AD∥BC,AB=a,DC=b,DC边的笔曲仄分线EF接BC边于E,且E为BC边的中面,又DE∥AB,则梯形ABCD的周少等于()A、2a+2bB、3a+bC、4a+bD、5a+b第1题图第2题图第3题图第4题图5、如下图1,正在周少为20cm的□ABCD中,AB≠AD,AC、BD相接于面O,OE⊥BD接AD于E,则△ABE的周少为()A、4cm B、6cm C、8cm D、10cm6、如下图2,△ABC中边AB的笔曲仄分线分别接BC,AB于面D,E,AE=3cm,△ADC的周少为9cm,则△ABC的周少是()A、10cm B、12cm C、15cm D、17cm第5题图第6题图第7题图第8题图7、如上图3,正在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的笔曲仄分线DE接BC的延少线于面E,则CE的少为 .8、如上图4,正在△ABC中,AB=BC,∠B=120°,AB的笔曲仄分线接AC于面D.若AC=6cm,则AD=cm.9、如下图1,正在△ABC中,BC边上的笔曲仄分线DE接边BC于面D,接边AB于面E.若△EDC的周少为24,△ABC与四边形AEDC的周少之好为12,则线段DE的少为.10、如图,矩形ABCD中,AB=2,BC=3,对于角线AC的笔曲仄分线分别接AD,BC于面E、F,对接CE,则CE的少为.11、已知如图,正在△ABC中,BC=8,AB的中垂线接BC于D,AC的中垂线接BC与E,则△ADE的周少等于.第9题图第10题图第11题图12、如图,正在四边形ABCD中,AD∥BC,E为CD的中面,对接AE、BE,BE⊥AE,延少AE接BC的延少线于面F.供证:(1)FC=AD;(2)AB=BC+AD.13、如图所示,正圆形ABCD的边少为1,G为CD边上的一个动面(面G与C、D没有沉合),以CG为一边背正圆形ABCD中做正圆形GCEF,对接DE接BG的延少线于H.(1)供证:①△BCG≌△DCE;②BH⊥DE.(2)试问当面G疏通到什么位子时,BH笔曲仄分DE?请证明缘由.。
北师大版数学八年级下线段的垂直平分线 同步练习含答案

线段的垂直平分线第1课时线段垂直平分线的性质定理及其逆定理1.如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点.已知线段PA=3 cm,则线段PB的长为()A.6 cm B.5 cmC.4 cm D.3 cm第1题图第2题图2.如图,AB是CD的垂直平分线.若AC=2.3 cm,BD=1.6 cm,则四边形ACBD的周长是()A.3.9 cm B.7.8 cmC.4 cm D.4.6 cm3.如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E.若BC=6,AC =5,则△ACE的周长为()A.8 B.11C.16 D.17第3题图第4题图4.如图,在△ABC中,AC的垂直平分线交AB于点D,DC平分∠ACB.若∠A=50°,则∠B的度数为.5.如图,在Rt△ABC中,∠C=90°,AB边的垂直平分线DE交BC于点E,垂足为D.求证:∠CAB=∠AED.6.如图,AC=AD,BC=BD,则有()A.AB垂直平分CDB.CD垂直平分ABC.AB与CD互相垂直平分D.CD平分∠ACB第6题图第7题图7.如图,已知△ABC,AB>AC>BC,边AB上存在一点P,使得PA+PC=AB.下列描述正确的是()A.P是AC的垂直平分线与AB的交点B.P是BC的垂直平分线与AB的交点C.P是∠ACB的平分线与AB的交点D.P是以点B为圆心,AC长为半径的弧与边AB的交点8.如图,在△ABC中,∠C=90°,∠A=30°,BD平分∠ABC交AC于点D.求证:点D在AB的垂直平分线上.9.在△ABC中,AB=AC,边AB的垂直平分线与边AC所在的直线相交所得的锐角为50°,则∠C的度数为.10.下列说法:①若直线PE是线段AB的垂直平分线,则EA=EB;②若PA=PB,EA=EB,则直线PE是线段AB的垂直平分线;③若EA=EB,则直线EP是线段AB的垂直平分线;④若PA=PB,则点P在线段AB的垂直平分线上.其中正确的有()A.1个B.2个C.3个D.4个11.如图,在△ABC中,DE是AC的垂直平分线,AC=6 cm,且△ABD的周长为13 cm,则△ABC的周长为()A.13 cm B.19 cmC.10 cm D.16 cm第11题图第12题图12.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,将AB边沿AD折叠,发现B点的对应点E正好在AC的垂直平分线上,则∠C=.13.如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线DE交BC的延长线于点E,则CE的长为.第13题图第14题图14.如图,线段AB,BC的垂直平分线l1,l2相交于点O.若∠1=39°,则∠AOC=.15.如图,在△ABC中,∠ACB=90°,D是BC延长线上一点,E是BD的垂直平分线与AB的交点,DE交AC于点F.求证:点E在AF的垂直平分线上.16.如图1,在△ABC中,AB=AC,点D是△ABC外的一点(点D与点A分别在直线BC的两侧),且DB=DC,过点D作DE∥AC,交射线AB于点E,连接AD交BC于点F.(1)求证:AD垂直平分BC;(2)请从A,B两题中任选一题作答,我选择________题.A:如图1,当点E在线段AB上且不与点B重合时,求证:DE=AE;B:如图2,当点E在线段AB的延长线上时,写出线段DE,AC,BE之间的等量关系,并证明你的结论.第2课时三角形三边的垂直平分线1.三角形纸片ABC上有一点P,量得PA=3 cm,PB=3 cm,则点P一定()A.是边AB的中点B.在边AB的中线上C.在边AB的高上D.在边AB的垂直平分线上2.在三角形的内部,有一个点到三角形三个顶点的距离相等,则这个点一定是三角形()A.三条中线的交点B.三条角平分线的交点C.三条边的垂直平分线的交点D.三条高的交点3.如果三角形中两条边的垂直平分线的交点在第三条边上,那么这个三角形一定是()A.锐角三角形B.钝角三角形C.等边三角形D.直角三角形4.如图,已知直线MN为△ABC的边BC的垂直平分线.若AB,AC两边的垂直平分线相交于点O,当顶点A的位置移动时,点O始终在()A.直线MN上B.直线MN的左侧C.直线MN的右侧D.直线MN的左侧或右侧5.下列作图语句正确的是()A.过点P作线段AB的垂直平分线B.在线段AB的延长线上取一点C,使AB=ACC.过直线a和直线b外一点P作直线MN,使MN∥a∥bD .过点P 作直线AB 的垂线6.如图,点E ,F ,G ,Q ,H 在一条直线上,且EF =GH ,我们知道按如图所作的直线l 为线段FG 的垂直平分线.下列说法正确的是( )A .l 是线段EH 的垂直平分线B .l 是线段EQ 的垂直平分线C .l 是线段FH 的垂直平分线D .EH 是l 的垂直平分线第6题图 第7题图7.如图,在Rt △ABC 中,∠B =90°,分别以点A ,C 为圆心,大于12AC 的长为半径画弧,两弧相交于点M ,N ,连接MN ,分别与AC ,BC 交于点D ,E ,连接AE ,则:(1)∠ADE = ;(2)AE EC ;(填“=”“>”或“<”)(3)当AB =3,AC =5时,△ABE 的周长等于 .8.为了推进农村新型合作医疗制度改革,准备在某镇新建一个医疗点P ,使P 到该镇A 村、B 村、C 村所属的村委会所在地的距离都相等(A ,B ,C 不在同一直线上,地理位置如图),请你用尺规作图的方法确定点P 的位置.要求:写出已知、求作,不写作法,保留作图痕迹.A 村 ·B 村 ·C 村·9.在平面内,到三点A,B,C距离相等的点()A.只有一个B.有两个C.有三个或三个以上D.有一个或没有10.如图,在△ABC中,∠BAC=90°,AB>AC.按下列步骤作图:①分别以点B和点C为圆心,大于BC一半的长为半径作圆弧,两弧相交于点M和点N;②作直线MN,与边AB相交于点D,连接CD.下列说法不一定正确的是()A.∠BDN=∠CDN B.∠ADC=2∠BC.∠ACD=∠DCB D.2∠B+∠ACD=90°11.等腰三角形的底角为40°,两腰的垂直平分线交于点P,则()A.点P在三角形内B.点P在三角形外C.点P在三角形底边上D.点P的位置与三角形的边长有关12.如图,由于水资源缺乏,B,C两地不得不从黄河上的扬水站A引水,这就需要A,B,C之间铺设地下输水管道,有人设计了三种铺设方案:如图①②③,图中实线表示管道铺设线路,在图②中,AD垂直BC于点D;在图③中,OA=OB=OC.为减少渗漏,节约水资源,并降低工程造价,铺设线路应尽量缩短,已知△ABC恰好是一个边长为a的等边三角形,那么通过计算,你认为最好的铺设方案是方案.13.如图所示,已知线段a,b,求作等腰三角形,使高为a,腰长为b(a<b,尺规作图,保留作图痕迹).14.如图,在△ABC中,DM,EN分别垂直平分AC和BC,交AB于M,N两点,DM与EN相交于点F.(1)若∠ACB=120°,求∠MCN的度数;(2)若△CMN的周长为15 cm,求AB的长;(3)若∠MFN=70°,求∠MCN的度数.【变式】如图,在△ABC中,∠BAC=80°,若MP和NQ分别垂直平分AB和AC.(1)求∠PAQ的度数;(2)若△APQ周长为12,BC长为8,求PQ的长.参考答案:第1课时线段垂直平分线的性质定理及其逆定理1.如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点.已知线段PA=3 cm,则线段PB的长为(D)A.6 cm B.5 cmC.4 cm D.3 cm第1题图第2题图2.如图,AB是CD的垂直平分线.若AC=2.3 cm,BD=1.6 cm,则四边形ACBD的周长是(B)A.3.9 cm B.7.8 cmC.4 cm D.4.6 cm3.如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E.若BC=6,AC =5,则△ACE的周长为(B)A.8 B.11C.16 D.17第3题图第4题图4.如图,在△ABC中,AC的垂直平分线交AB于点D,DC平分∠ACB.若∠A=50°,则∠B的度数为30°.5.如图,在Rt△ABC中,∠C=90°,AB边的垂直平分线DE交BC于点E,垂足为D.求证:∠CAB=∠AED.证明:∵DE是AB的垂直平分线,∴EA=EB.∴∠EAB=∠B.∵∠C=90°,∴∠CAB+∠B=90°.又∵∠AED+∠EAB=90°,∴∠CAB=∠AED.6.如图,AC=AD,BC=BD,则有(A)A.AB垂直平分CDB.CD垂直平分ABC.AB与CD互相垂直平分D.CD平分∠ACB第6题图第7题图7.如图,已知△ABC,AB>AC>BC,边AB上存在一点P,使得PA+PC=AB.下列描述正确的是(B)A.P是AC的垂直平分线与AB的交点B .P 是BC 的垂直平分线与AB 的交点 C .P 是∠ACB 的平分线与AB 的交点D .P 是以点B 为圆心,AC 长为半径的弧与边AB 的交点8.如图,在△ABC 中,∠C =90°,∠A =30°,BD 平分∠ABC 交AC 于点D.求证:点D 在AB 的垂直平分线上.证明:∵∠C =90°,∠A =30°, ∴∠ABC =90°-30°=60°. ∵BD 平分∠ABC , ∴∠ABD =12∠ABC =30°.∴∠A =∠ABD. ∴DA =DB.∴点D 在AB 的垂直平分线上.9.在△ABC 中,AB =AC ,边AB 的垂直平分线与边AC 所在的直线相交所得的锐角为50°,则∠C 的度数为20°或70°.10.下列说法:①若直线PE 是线段AB 的垂直平分线,则EA =EB ;②若PA =PB ,EA =EB ,则直线PE 是线段AB 的垂直平分线;③若EA =EB ,则直线EP 是线段AB 的垂直平分线;④若PA =PB ,则点P 在线段AB 的垂直平分线上.其中正确的有(C)A .1个B .2个C .3个D .4个11.如图,在△ABC 中,DE 是AC 的垂直平分线,AC =6 cm ,且△ABD 的周长为13 cm ,则△ABC 的周长为(B)A .13 cmB .19 cmC .10 cmD .16 cm第11题图 第12题图12.如图,在Rt △ABC 中,∠BAC =90°,AD ⊥BC 于点D ,将AB 边沿AD 折叠,发现B 点的对应点E 正好在AC 的垂直平分线上,则∠C =30°.13.如图,在Rt △ABC 中,∠ACB =90°,BC =3,AC =4,AB 的垂直平分线DE 交BC 的延长线于点E ,则CE 的长为76.第13题图 第14题图14.(2020·南京)如图,线段AB ,BC 的垂直平分线l 1,l 2相交于点O.若∠1=39°,则∠AOC =78°.15.如图,在△ABC 中,∠ACB =90°,D 是BC 延长线上一点,E 是BD 的垂直平分线与AB 的交点,DE 交AC 于点F.求证:点E 在AF 的垂直平分线上.证明:∵E 是BD 的垂直平分线上的一点, ∴EB =ED. ∴∠B =∠D. ∵∠ACB =90°,∴∠A=90°-∠B,∠CFD=90°-∠D.∴∠CFD=∠A.又∵∠AFE=∠CFD,∴∠AFE=∠A.∴EF=EA.∴点E在AF的垂直平分线上.16.如图1,在△ABC中,AB=AC,点D是△ABC外的一点(点D与点A分别在直线BC的两侧),且DB=DC,过点D作DE∥AC,交射线AB于点E,连接AD交BC于点F.(1)求证:AD垂直平分BC;(2)请从A,B两题中任选一题作答,我选择________题.A:如图1,当点E在线段AB上且不与点B重合时,求证:DE=AE;B:如图2,当点E在线段AB的延长线上时,写出线段DE,AC,BE之间的等量关系,并证明你的结论.解:(1)证明:∵AB=AC,∴点A在线段BC的垂直平分线上.∵DB=DC,∴点D在线段BC的垂直平分线上.∴AD垂直平分BC.(2)选择A,证明:由(1),得AD⊥BC,又∵AB=AC,∴∠BAF=∠CAF.∵DE∥AC,∴∠CAF=∠ADE.∴∠BAF=∠ADE.∴DE=AE.选择B,线段DE,AC,BE之间的等量关系为DE=BE+AC.证明:由(1),得AF⊥BC,又∵AB=AC,∴∠BAF=∠CAF.∵DE∥AC,∴∠EDA=∠CAF.∴∠BAF=∠EDA.∴AE=DE.∵AE=EB+AB,AB=AC,∴DE=BE+AC.第2课时三角形三边的垂直平分线1.三角形纸片ABC上有一点P,量得PA=3 cm,PB=3 cm,则点P一定(D)A.是边AB的中点B.在边AB的中线上C.在边AB的高上D.在边AB的垂直平分线上2.在三角形的内部,有一个点到三角形三个顶点的距离相等,则这个点一定是三角形(C)A.三条中线的交点B.三条角平分线的交点C.三条边的垂直平分线的交点D.三条高的交点3.如果三角形中两条边的垂直平分线的交点在第三条边上,那么这个三角形一定是(D) A.锐角三角形B.钝角三角形C.等边三角形D.直角三角形4.如图,已知直线MN为△ABC的边BC的垂直平分线.若AB,AC两边的垂直平分线相交于点O,当顶点A的位置移动时,点O始终在(A)A.直线MN上B.直线MN的左侧C.直线MN的右侧D.直线MN的左侧或右侧5.下列作图语句正确的是(D)A.过点P作线段AB的垂直平分线B.在线段AB的延长线上取一点C,使AB=ACC.过直线a和直线b外一点P作直线MN,使MN∥a∥bD.过点P作直线AB的垂线6.如图,点E,F,G,Q,H在一条直线上,且EF=GH,我们知道按如图所作的直线l为线段FG的垂直平分线.下列说法正确的是(A)A.l是线段EH的垂直平分线B.l是线段EQ的垂直平分线C.l是线段FH的垂直平分线D.EH是l的垂直平分线第6题图 第7题图7.如图,在Rt △ABC 中,∠B =90°,分别以点A ,C 为圆心,大于12AC 的长为半径画弧,两弧相交于点M ,N ,连接MN ,分别与AC ,BC 交于点D ,E ,连接AE ,则:(1)∠ADE =90°;(2)AE =EC ;(填“=”“>”或“<”) (3)当AB =3,AC =5时,△ABE 的周长等于7.8.为了推进农村新型合作医疗制度改革,准备在某镇新建一个医疗点P ,使P 到该镇A 村、B 村、C 村所属的村委会所在地的距离都相等(A ,B ,C 不在同一直线上,地理位置如图),请你用尺规作图的方法确定点P 的位置.要求:写出已知、求作,不写作法,保留作图痕迹.解:已知:A ,B ,C 三点不在同一直线上. 求作:作一点P ,使PA =PB =PC. 如图所示,点P 即为所求的点.9.在平面内,到三点A ,B ,C 距离相等的点(D) A .只有一个B .有两个C .有三个或三个以上D .有一个或没有10.如图,在△ABC 中,∠BAC =90°,AB >AC.按下列步骤作图:①分别以点B 和点C 为圆心,大于BC 一半的长为半径作圆弧,两弧相交于点M 和点N;②作直线MN,与边AB相交于点D,连接CD.下列说法不一定正确的是(C)A.∠BDN=∠CDN B.∠ADC=2∠BC.∠ACD=∠DCB D.2∠B+∠ACD=90°11.等腰三角形的底角为40°,两腰的垂直平分线交于点P,则(B)A.点P在三角形内B.点P在三角形外C.点P在三角形底边上D.点P的位置与三角形的边长有关12.如图,由于水资源缺乏,B,C两地不得不从黄河上的扬水站A引水,这就需要A,B,C之间铺设地下输水管道,有人设计了三种铺设方案:如图①②③,图中实线表示管道铺设线路,在图②中,AD垂直BC于点D;在图③中,OA=OB=OC.为减少渗漏,节约水资源,并降低工程造价,铺设线路应尽量缩短,已知△ABC恰好是一个边长为a的等边三角形,那么通过计算,你认为最好的铺设方案是方案③.13.如图所示,已知线段a,b,求作等腰三角形,使高为a,腰长为b(a<b,尺规作图,保留作图痕迹).解:作法:(1)作线段AD=a;(2)过点D作直线MN⊥AD于点D;(3)以点A为圆心,b为半径画弧,交MN于B,C两点,连接AB,AC,△ABC即为所求,如图所示.14.如图,在△ABC中,DM,EN分别垂直平分AC和BC,交AB于M,N两点,DM与EN相交于点F.(1)若∠ACB=120°,求∠MCN的度数;(2)若△CMN的周长为15 cm,求AB的长;(3)若∠MFN=70°,求∠MCN的度数.解:(1)∵DM,EN分别垂直平分AC和BC,∴AM=CM,CN=BN.∴∠A=∠ACM,∠B=∠BCN.∴∠MCN=180°-(∠CMN+∠CNM)=180°-(2∠A+2∠B)=180°-2(180°-∠ACB)=60°.(2)∵AM=CM,BN=CN,∴△CMN的周长为CM+MN+CN=AM+MN+BN=AB.∵△CMN的周长为15 cm,∴AB=15 cm.(3)∵∠MFN=70°,∴∠MNF+∠NMF=180°-70°=110°.∵∠AMD=∠NMF,∠BNE=∠MNF,∴∠AMD+∠BNE=∠NMF+∠MNF=110°.∴∠A+∠B=90°-∠AMD+90°-∠BNE=70°.又∵∠A=∠ACM,∠B=∠BCN,∴∠MCN=180°-2(∠A+∠B)=40°.【变式】如图,在△ABC中,∠BAC=80°,若MP和NQ分别垂直平分AB和AC.(1)求∠PAQ的度数;(2)若△APQ周长为12,BC长为8,求PQ的长.解:(1)设∠PAQ=x,∠CAP=y,∠BAQ=z,∵MP和NQ分别垂直平分AB和AC,∴AP=PB,AQ=CQ.∴∠B=∠BAP=x+z,∠C=∠CAQ=x+y.∵∠BAC=80°,∴∠B+∠C=100°,即x+y+z=80°,x+z+x+y=100°.∴x=20°.∴∠PAQ=20°.(2)∵△APQ周长为12,∴AQ+PQ+AP=12.∵AQ=CQ,AP=PB,∴CQ+PQ+PB=12,即BC+2PQ=12.∵BC=8,∴PQ=2.21。
八年级数学重点题型强化训练05 线段垂直平分线专题(解析版)

八年级数学重点题型强化训练5——线段垂直平分线专题第1题第2题【分析】本题考查的是线段垂直平分线的性质:熟记:线段垂直平分线上的点到这条线段两个端点的距离第3题可证BEF CED ≌△△,可得EF =BC 的中点,第5题第6题第7题第8题 第9题【答案】B 【分析】利用全等三角形的判定以及垂直平分线的性质得出OBC Ð,以及40,OBC OCB Ð=Ð=°,再利用翻折变换的性质得出,CEF FEO =Ð进而求出即可.50,BAC BAC Ð=°ÐQ 12OAB CAO \Ð=Ð=25OAB ABO Ð=Ð=∵在等腰ABC V 中,DG Q 是BC 的垂直平分线,BD CD \=,AD Q 是BAC Ð的平分线,DE DF \=,在Rt BDE △和Rt CDF △中,C .60°D 【分析】先根据线段垂直平分线的性质得到BE CE =,则AC EC =,再根据等腰三角形的性质和三角形内,接着利用三角形外角性质计算出EBC Ð=Ð的度数.故选:C .题型2:线段垂直平分线的判定11.如图,AD AC =,BD BC =,则下列判断一定正确的是( )A .AB 垂直平分CDB .CD 垂直平分ABC .CD 平分ACB ÐD .以上都不正确第11题第12题【答案】A【分析】根据线段垂直平分线的判定求解即可.【详解】解:∵AD AC =,BD BC =,∴点A 、B 在线段CD 的垂直平分线上,即AB 垂直平分CD ,故选:A .12.如图,ABC AB AC BC >>V ,,边AB 上存在一点P ,使得PA PC AB +=.下列描述正确的是( )A .P 是AC 的垂直平分线与AB 的交点B .P 是ACB Ð的平分线与AB 的交点C .P 是BC 的垂直平分线与AB 的交点D .P 是AB 的中点【答案】C【分析】根据线段垂直平分线的判定解答即可.【详解】解:PA PC AB PA BP AB +=+=Q ,,PC BP \=,∴P 是BC 的垂直平分线与AB 的交点.故选:C .13.如图,将长方形纸片沿AC 折叠后点B 落在点E 处,则下列关于线段BE 与AC 的关系描述正确的是( )A .AC BE =B .AC 和BE 相互垂直平分C .AC BE ^且AC BE=D .AC BE ^且AC 平分BE【答案】D 【分析】只要证明AC 是线段BE 的垂直平分线即可解决问题.【详解】解:ACE QV 是由ACB △翻折得到,AE AB \=,CB CE =,AC EB \^,AC 平分EB ,故选:D .14.如图,已知:AB AC =,MB MC =.求证:直线AM 是线段BC 的垂直平分线.下面是小彬的证明过程,则正确的选项是( )证明:∵AB AC=∴点A 在线段BC 的垂直平分线上①∵MB MC=∴点M 在线段BC 的垂直平分线上②∴直线AM 是线段BC 的垂直平分线③A .①处的依据是:线段垂直平分线上的点与这条线段两个端点的距离相等B .②处的依据是:与线段两个端点距离相等的点在这条线段的垂直平分线上C .③处的依据是:与线段两个端点距离相等的点在这条线段的垂直平分线上D .以上说法都不对【答案】B【分析】根据垂直平分线的判定方法逐项判断即可.【详解】解:①处的依据是:与线段两个端点距离相等的点在这条线段的垂直平分线上,故A 选项错误,不合题意;②处的依据是:与线段两个端点距离相等的点在这条线段的垂直平分线上,故B 选项正确,符合题意;③处的依据是:两点确定一条直线;故C 选项错误,不合题意;综上可知,选项D 错误,不合题意;故选B .15.下列说法错误的是( )A .若点P 是线段AB 的垂直平分线上的点,则PA PB=B .若PA PB =,QA QB =,则直线PQ 是线段AB 的垂直平分线C .若PA PB =,则点P 在线段AB 的垂直平分线上D .若PA PB =,则过点P 的直线是线段AB 的垂直平分线【答案】D【分析】根据线段垂直平分线的判定方法,即可一一判定.【详解】解:A.若点P 是线段AB 的垂直平分线上的点,则PA PB =,故该说法正确,不符合题意;B.若PA PB =,QA QB =,则直线PQ 是线段AB 的垂直平分线,故该说法正确,不符合题意;C.若PA PB =,则点P 在线段AB 的垂直平分线上,故该说法正确,不符合题意;D.若PA PB =,则过点P 的直线不一定是线段AB 的垂直平分线,故该说法错误,符合题意;故选:D .16.如图,AD 是ABC V 的角平分线,交BC 于D ,DE DF 、分别是ABD △和ACD V 的高,分别交AB AC 、于E 、F ,连接EF 交AD 于G .下列结论:①AD 垂直平分EF ;②EF 垂直平分AD ;③AED AFD V V ≌;④当BAC Ð为60°时,AEF △是等边三角形,其中正确的结论的个数为( )A .4个B .3个C .2个D .1个第16题第17题【答案】B 【分析】根据角平分线性质求出DE DF =,证AED AFD V V ≌,推出AE AF =,再逐个判断即可.【详解】解:∵AD 是ABC V 的角平分线,DE DF 、分别是ABD △和ACD V 的高,∴DE DF =,90AED AFD Ð=Ð=°,在Rt AED △和Rt AFD △中,AD AD DE DF =ìí=î,∴()Rt Rt HL AED AFD ≌△△,故③正确;∴AE AF =,∴AD 垂直平分EF ,①正确;②错误;∵60BAC Ð=°,且AE AF =,∴AEF △是等边三角形,④正确.综上,①③④正确,共3个.故选:B .17.如图,在△ABC 中,AD 是△ABC 的角平分线,点E 、F 分别是AD 、AB 上的动点,若∠BAC =50°,当BE +EF 的值最小时,∠AEB 的度数为( )A .105°B .115°C .120°D .130°【答案】B【分析】过点B 作BB ′⊥AD 于点G ,交AC 于点B ′,过点B ′作B ′F ′⊥AB 于点F ′,与AD 交于点E ′,连接BE ′,证明AD 垂直平分BB ′,推出BE =BE ′,由三角形三边关系可知,BE EF B E EF B F B F ¢¢¢¢+=+³³,即BE +EF 的值最小为B F ¢¢,通过证明△ABE ′≌△AB ′E ′,推出∠AE ′B =AE ′B ′,因此利用三角形外角的性质求出AE ′B ′即可.【详解】解:过点B 作BB ′⊥AD 于点G ,交AC 于点B ′,过点B ′作B ′F ′⊥AB 于点F ′,与AD 交于点E ′,连接BE ′,如图:此时BE +EF 最小.∵AD 是△ABC 的角平分线,∠BAC =50°,∴∠BAD =∠B ′AD =25°,∵BB ′⊥AD ,∴∠AGB =∠AGB ′=90°,在△ABG 和△AB ′G 中,BAG B AG AG AGAGB AGB Ð=Ðìï=íïТ=Ðî¢,∴△ABG ≌△AB ′G (ASA ),∴BG =B ′G , AB =AB ′,∴AD 垂直平分BB ′,∴BE =BE ′,在△ABE ′和△AB ′E ′中,BE BE AE AE AB AB ¢¢¢¢ìï=íï=î=,∴△ABE ′≌△AB ′E ′(SSS ),∴∠AE ′B =AE ′B ′,∵AE ′B ′=∠BAD + AF ′E ′=25°+90°=115°,∴∠AE ′B =115°.即当BE +EF 的值最小时,∠AEB 的度数为115°.故选B .18.如图,点P 是AOB Ð内的一点,PC OA ^于点C ,PD OB ^于点D ,连接OP ,CD .若PC PD =,则下列结论不一定成立的是( )A .AOP BOPÐ=ÐB .OPC OPD Ð=ÐC .PO 垂直平分CD D .PD CD=【答案】D【分析】根据角平线的判定定理可判断A ,证明Rt COP Rt DOP V V ≌,可判断B ,根据Rt COP Rt DOP V V ≌,可得OC =OD ,进而可判断C ,根据等边三角形的定义,可判断D .【详解】解:∵点P 是AOB Ð内的一点,PC OA ^于点C ,PD OB ^于点D ,PC PD =,∴OP 是∠AOB 的平分线,即AOP BOP Ð=Ð,故A 成立,不符合题意;∵OP =OP ,AOP BOP Ð=Ð,第19第20题=,利用ASA Ð,再根据E是CD的中点可求出ECECF=,结合已知可得BE的垂直平分线,根据线段垂直AE EF=+,进而即可求解.即可证得AB BC AD故答案为:70.题型3:与线段垂直平分线相关的尺规作图21.如图,在ABC V 直线MN ,交BC A .9【答案】B 【分析】由题意可得MN ADC C AC BC =+V ,求解即可.【详解】解:由题意可得,A.3B 【答案】B【分析】利用基本作图得到V的周长为20再利用ABC【详解】解:由作法得DE \==,,DA DB AE BEA .①③B .①④C .②④D .③④【答案】B 【分析】依次对各个图形的作图痕迹进行分析即可.【详解】 由图①知AD AC =,AB AD >,AB AC \>,故图①能说明AB AC >;由图②知射线BD 是ABC Ð的平分线,不能说明AB AC >;由图③知CD AB ^,不能说明AB AC >;由图④知DE 是BC 的垂直平分线,DB DC \=.ADC QV 中AD DC AC +>,AD DB AC \+>,即AB AC >.故图④能说明AB AC >.故选:B24.如图所示,在Rt ABC △中,90C Ð=°,以B 为圆心,以任意长度为半径作弧,与BA ,BC 分别交于A.20°B.36【答案】C【分析】由作图可知:BO为=,再根据等腰三角形的性质得AD BD和定理即可求出AÐ的度数.【详解】解:由作图可知:平分EAC Ð;③AC CD =;④ABC S V C .①③DA .只有甲的答案正确B .甲和乙的答案合在一起才正确C .甲和丙的答案合在一起才正确D .甲乙丙的答案合在一起才正确【答案】D 【分析】分四种情况讨论:当APB Ð为锐角时,当APB Ð为钝角时,当APB Ð为直角时,当135APB Ð=°时,分别画出图形,求出x 与y 的关系,即可得出答案.【详解】解:当APB Ð为锐角时,如图所示:∵AD BP ^,∴90ADP Ð=°,∴90PAD APD Ð+Ð=°,即90x y +=;当APB Ð为钝角时,如图所示:∵AD BP ^,∴90ADP Ð=°,∵APB Ð为ADP △的外角,∴APB ADP DAP Ð=Ð+Ð,∴90x y =+,即90x y -=;当APB Ð为直角时,如图所示:此时直线n 与PA 重合,∴此时直线n 与PA 所夹的角为0°,即90x y +=或90x y -=;当135APB Ð=°时,如图所示:18013545DPA Ð=°-°=°,∵AD BP ^,∴90ADP Ð=°,∴904545DAP Ð=°-°=°,∴45135180DAP APB Ð+Ð=°+°=即180x y +=;1AB 的长为半径作弧,两弧相交于AM ;的长为半径作弧,与BC 边相交于点N ,连接C.9AC,根据中垂线的定义和性质找到相等的边,进而由AC,A .15B .16C .18D .20【答案】A 【分析】根据题意得到MN 是线段AB 的垂直平分线,进而得到点D 是AB 的中点,根据三角形的面积公式计算,得到答案.【详解】解:由尺规作图可知,MN 是线段AB 的垂直平分线,\点D 是AB 的中点,ACD BCD S S \=△△,ADE CDE CDB S S S \+=V V V ,Q CDB △的面积为12,ADE V 的面积为9,1293CDE CDB ADE S S S \=-=-=V V V ,\四边形EDBC 的面积为:12315CDE CDB EDBC S S S =+=+=V V 四边形,故选:A .30.如图,在ABC V 中,根据尺规作图痕迹,下列说法不一定正确的是( ).A .AF BF=B .90AFD FBC Ð+Ð=°C .DF AB^D .BAF CAFÐ=Ð【答案】D 【分析】由图中尺规作图痕迹可知,BE 为ABC Ð的平分线,DF 为线段AB 的垂直平分线,结合角平分线的定义和垂直平分线的性质逐项分析即可.【详解】解:由图中尺规作图痕迹可知, BE 为ABC Ð的平分线,DF 为线段AB 的垂直平分线.上求作点D ,使;,若点D 在边上,在上求作点E ,使.)作BC 的垂直平分线与BC 的交点即为所求;)如图:由题意得,只要作12BDE ABC S S △△=即可,由第(1)问得,12ABP ABC S S △△=,只要作BC ABD ACD S S =V V AB BC BDE ADEC S S △四边形=作BC 的垂直平分线与BC 交于D 点,BD CD \=,ABD QV 与ACD V 高相同,ABD ACD S S \=V V .如图1:点D 即为所求;(2)如图:由题意得,只要作12BDE ABC S S △△=即可,作BC 的垂直平分线交BC 于P 点,由第(1)问得,12ABP ABC S S △△=,故只要作BDE ABP S S △△=即可,连接D 、P ,要使得BDE ABP S S △△=,只要作根据“夹在平行线之间的垂线段相等”,即,高相等,如图2:点E 即为所求.32.如图,在中,点E 在上且.(1)请用尺规作图的方法在边上确定点D ,使得;(保留作图痕迹,不写作法)(2)在(1)的条件下,若的周长为,求的长.【分析】(1)线段AB 的垂直平分线与BC 边的交点即为所求;(2)根据线段垂直平分线的性质,通过等量代换求解.【详解】(1)解:如图所示,线段AB 的垂直平分线与BC 边交于点D ,点D 即为所求;(2)解:Q ADE V 的周长为12cm ,\12AD AE DE ++=,Q BD AD =,AE CE =,\12BC BD CE DE AD AE DE =++=++=,即BC 的长为12cm .题型4:与线段垂直平分线相关的计算与证明33.如图,在ABC V 中,AB 、AC 边的垂直平分线相交于点O ,分别交BC 边于点M 、N ,连接AM ,AN .(1)若AMN V 的周长为6,求BC 的长;(2)若30B Ð=°,25C Ð=°,求MAN Ð的度数;(3)若MON a Ð=,请用a 表示MAN Ð的度数(直接写出即可).ABC V BC AE CE =BC BD AD =ADE V 12cm BC【答案】(1)6(2)70°(3)1802MAN aÐ=°-【分析】(1)由垂直平分线的性质可得,AM BM AN CN ==,再由BC AM MN AN =++可得结论;(2)由垂直平分线的性质可得30,30,B BAM C CAN Ð=Ð=°Ð=Ð=°,再根据三角形内角和定理可得结论;(3)根据三角形内角和定理可得()1802MAN B C Ð=°-Ð+Ð,再由四边形内角和定理可得180B C MAN O Ð+Ð=°-Ð-Ð,代入求解即可【详解】(1),OM ON Q 分别是AB 、AC 边的垂直平分线,,,AM BM AN CN \==6AM MN AN ++=Q 6BM MN CN \++=,即6BC =(2),,AM BM AN CN ==Q 30,25,BAM B CAN C \Ð=Ð=°Ð=Ð=°180,B BAC C Ð+Ð+Ð=°Q 且BAC BAM MAN CANÐ=Ð+Ð+Ð180,B BAM MAN CANC \Ð+Ð+Ð+Ð+Ð=°即180,B B MANC C Ð+Ð+Ð+Ð+Ð=°18022180605070MAN B C \Ð=°-Ð-Ð=°-°-°=°(3)如图,180,B BAC C Ð+Ð+Ð=°Q 且BAC BAM MAN CAN Ð=Ð+Ð+Ð180,B BAM MAN CANC \Ð+Ð+Ð+Ð+Ð=°即180,B B MANC C Ð+Ð+Ð+Ð+Ð=°()1802MAN B C \Ð=°-Ð+Ð,,OM ON Q 分别是AB 、AC 边的垂直平分线,90AEO AFO \Ð=Ð=360AEO EAF AFO FOE \Ð+Ð+Ð+Ð=°180EAF O \Ð+Ð=°180,BAF MAN CAN O \Ð+Ð+Ð+Ð=°180,B C MAN O \Ð+Ð+Ð+Ð=°180B C MAN O\Ð+Ð=°-Ð-Ð()()180********MAN B C MAN O \Ð=°-Ð+Ð=°-°-Ð-Ð\解得,1802MAN aÐ=°-34.如图,在Rt ABC △中,45,90,ACB BAC AB AC Ð=°Ð=°=,点D 是AB 的中点,AF CD ^于H 交BC 于F ,BE AC ∥交AF 的延长线于E .求证:BC 垂直且平分DE .【答案】见解析【分析】根据全等三角形的判定证明(ASA)ABE CAD ≌V V ,在再证明(SAS)DBP EBP ≌V V 即可解决问题;【详解】证明:由题意可知,9090DAH ADH ACH ADH ÐÐÐÐ+=°+=°,,∴DAH ACH ÐÐ=,∵90BAC Ð=°,BE AC ∥,∴90CAD ABE ÐÐ==°.又∵AB CA =,∴在ABE V 与CAD V 中,DAH ACH AB AC CAD ABE Ð=Ðìï=íïÐ=Ðî,∴(ASA)ABE CAD ≌V V .∴AD BE =,又∵AD BD =,∴BD BE =,在Rt ABC V 中,45,90,ACB BAC AB AC ÐÐ=°=°=,故45ABC Ð=°.∵90ABE Ð=°,∴904545EBF Ð=°-°=°,∴(SAS)DBP EBP ≌V V ,∴DP EP =,∴BC 垂直且平分DE .35.如图,ABC V 中,AD 平分BAG Ð,DG 垂直平分BC ,DE AB ^于E ,DF AC ^于F .(1)求证:BE CF =;(2)如果9AB =,5AC =,求BE 的长.【答案】(1)见解析;(2)2BE =.【分析】(1)由DG 垂直平分BC 可得DB DC =,由AD 平分BAG Ð, DE AB ^,DF AC ^,可得DE DF =,90DEB DFC Ð=Ð=°,从而证得()Rt Rt HL DBE DCF V V ≌,得证BE CF =;(2)易证()Rt Rt HL ADE ADF ≌△△,得到AE AF =,又BE CF =,因此2AB AE BE AF BE AC CF AC BE =+=+=+=+,代入即可解答.【详解】(1)连接DB ,DC ,∵DG 垂直平分BC ,∴DB DC =,∵AD 平分BAG Ð,DE AB ^,DF AC ^,∴DE DF =,90DEB DFC Ð=Ð=°,∴在Rt DBE V 和Rt DCF V 中DB DC DE DF=ìí=î∴()Rt Rt HL DBE DCF V V ≌,∴BE CF =.(2)∵DE AB ^,DF AC ^,∴在Rt ADE △和Rt ADF V 中AD AD DE DF=ìí=î∴()Rt Rt HL ADE ADF ≌△△,∴AE AF=∵BE CF=∴2AB AE BE AF BE AC CF AC BE =+=+=+=+,∵9AB =,5AC =,∴952BE =+,∴2BE =.36.如图,AB AC >,BAC Ð的平分线与BC 边的垂直平分线GD 相交于点D ,过点D 作DE AB ^于点E ,DF AC ^于点F ,求证:BE CF =.【答案】见解析【分析】连接DC ,根据GD 是BC 边的垂直平分线,得到DC DB =,根据AD 是BAC Ð的平分线,且DE AB ^,DF AC ^,得到DE DF =,根据DE DF DB DC =ìí=î,得到()HL DEB DFC V V ≌即可得证.【详解】如图,连接DC ,∵GD 是BC 边的垂直平分线,∴DC DB =,∵AD 是BAC Ð的平分线,且DE AB ^,DF AC ^,∴DE DF =,∵DE DF DB DC =ìí=î,∴()HL DEB DFC V V ≌∴BE CF =.37.如图,在ABC V 中,BAC Ð的平分线与BC 的中垂线DE 交于点E ,过点E 作AC 边的垂线,垂足N ,过点E 作AB 延长线的垂线,垂足为M .(1)求证:BM CN =;(2)若2AB =,8AC =,求BM 的长.【分析】(1)连接BE ,CE ,由题意易得BE CE =,EM EN =,进而可证Rt Rt BME CNE ≌V V ,然后问题得解;(2)由(1)得:EM EN =,进而可证Rt Rt AME ANE ≌V V ,则有AB BM AC CN +=-,然后根据线段的和差关系可求解.【详解】(1)证明:连接BE ,CE ,DE Q 是BC 的垂直平分线,BE CE \=,AE Q 是BAC Ð的平分线,EM AB ^,EN AC ^,EM EN \=,在Rt BME △和Rt CNE △中,BE CE EM EN=ìí=î()Rt Rt BME CNE HL \V V ≌,BM CN \=;(2)由(1)得:EM EN =,在Rt AME △和Rt ANE △中,AE AE EM EN=ìí=îRt Rt AME ANE \≌V V ,请根据所给教材内容,结合图①,写出“线段垂直平分线的性质定理”完整的证明过程.定理应用:V中,AB、AC的垂直平分线分别交BC于点D、E,垂足分别为M,N,已知)如图②,在ABC的周长为20,则BC的长为__________.∵AB AC AD BC ^=,,的周长为7,可得∴19712AB BE +=-=,∴6AB BE ==;(2)∵30ABC Ð=°,45C Ð=°,∴1803045105BAC Ð=°-°-°=°,在BAD V 和BED V 中,BA BE BD BD DA DE =ìï=íï=î,∴()SSS BAD BED V V ≌,∴105BED BAC Ð=Ð=°,∴1054560CDE BED C Ð=Ð-Ð=°-°=°.40.如图,在ABC V 中,点E 在AB 上,点D 在BC 上,BD BE =,BAD BCE Ð=Ð,AD 与CE 相交于F .(1)求证:AF CF =;(2)连接,试判断与的位置关系,并说明理由.【分析】(1)根据全等三角形的判定与性质,可得BA BC =,BDA BEC Ð=Ð,根据补角的性质,可得FDC FEA Ð=Ð,根据全等三角形的判定与性质,可得答案.(2)由AB CB =,AF CF =可得点B ,F 在AC 的垂直平分线,即可得出结论【详解】(1)在BAD V 和BCE V 中,∵B B BAD BCE BD BE Ð=ÐìïÐ=Ðíï=î,∴BAD V ≌BCE V ,∴AB CB =,BF BF AC与点A 重合,则 , .,四边形的直角沿直线l 折叠后(如图2),点B 落在四边形的边与AB 相交于点F ,猜想OF 、EF 、AB 三者数量关系,并证明.若折叠后点D 恰为AB 的中点(如图3),求的度数;45°,8数量关系为:AB OF EF =+;证明见解析q ==a OABC OCB ÐOABC q∴E O D FO D Ð=Ð.由折叠可得FOD EOC EOD q Ð=Ð=Ð=,∴390COA q Ð==°,∴30q =°.。
部编数学八年级上册专题22角平分线和垂直平分线结合(解析版)含答案

专题22 角平分线和垂直平分线结合1.如图,△ABC 是等腰三角形,AB =AC ,∠BAC =45°,过点A 作AD ⊥BC 于点D ,过点B 作BE ⊥AC 于点E ,AD ,BE 交于点F ,H 为AB 的中点,连接EH ,CH ,FH ,则下列说法正确的个数为( )①∠BAD =∠CBE ;②EH ⊥AB ;③CE =12AF ;④AE =CE +CF ;⑤S △EFH =S △EHC .A .2个B .3个C .4个D .5个【答案】C【解析】【分析】先根据等腰三角形的性质可得22.5,67.5BAD CAD ABC ACB Ð=Ð=°Ð=Ð=°,再根据直角三角形的性质可得22.5CBE Ð=°,由此可判断①;先判断出Rt ABE △是等腰直角三角形,再根据等腰三角形的三线合一即可判断②;先根据三角形全等的判定定理证出BCE AFE @V V ,根据全等三角形的性质可得BC AF =,在AE 上截取GE CE =,连接BG ,从而可得BG BC =,再根据等腰三角形的性质可得67.5,45BGC CBG Ð=°Ð=°,从而可得12<CE BC ,据此可判断③;先根据等腰三角形的三线合一可得AD 垂直平分BC ,从而可得BF CF =,再证出Rt CEF V 是等腰直角三角形,从而可得CE EF =,然后根据线段和差可得AE BE CE CF ==+,即可判断④;过点H 作HM AC ^于点M ,作HN BE ^于点N ,先根据等腰三角形的三线合一可得EH 平分AEB Ð,再根据角平分线的性质可得HM HN =,然后根据三角形的面积公式即可判断⑤.【详解】解:,45,AB AC BAC AD BC =Ð=°^Q ,122.5,67.52BAD CAD BAC ABC ACB \Ð=Ð=Ð=°Ð=Ð=°,BE AC ^Q ,9022.5CBE ACB \Ð=°-Ð=°,BAD CBE \Ð=Ð,说法①正确;,45BE AC BAC ^Ð=°Q ,Rt ABE \V 是等腰直角三角形,AE BE =,H Q 为AB 的中点,EH AB \^(等腰三角形的三线合一),说法②正确;在BCE V 和AFE △中,22.590CBE FAE BE AE CEB FEA Ð=Ð=°ìï=íïÐ=Ð=°î,()BCE AFE ASA \@V V ,BC AF \=,如图,在AE 上截取GE CE =,连接BG ,则BE 垂直平分CG ,BG BC \=,67.5,18045BGC BCG CBG BGC BCG \Ð=Ð=°Ð=°-Ð-Ð=°,BGC CBG \Ð>Ð,2BC CG CE \>=,即12<CE BC ,12CE AF \<,说法③错误;,AB AC AD BC =^Q ,AD \垂直平分BC ,BF CF \=,22.5BCF CBF \Ð=Ð=°,45EFC BCF CBF \Ð=Ð+Ð=°,Rt CEF \V 是等腰直角三角形,CE EF =,BE EF BF CE CF \=+=+,又AE BE =Q ,AE CE CF \=+,说法④正确;如图,过点H 作HM AC ^于点M ,作HN BE ^于点N ,Rt ABE Q V 是等腰直角三角形,EH 是AB 边上的中线,EH ∴平分AEB Ð(等腰三角形的三线合一),HM HN \=,1122EFH EHC S S EF HN CE HM \=×=×=V V ,说法⑤正确;综上,说法正确的个数为4个,故选:C .【点睛】本题考查了等腰三角形的判定与性质、三角形全等的判定定理与性质、线段垂直平分线的判定与性质、角平分线的性质等知识点,熟练掌握各判定定理与性质是解题关键,较难的是⑤,通过作辅助线,利用到角平分线的性质定理.2.如图,BAC Ð的角平分线与BC 的垂直平分线DG 交于点,,D DE AB DF AC ^^,垂足分别为E F 、,若9,10AF BC ==,则ABC V 的周长为( )A .19B .28C .29D .38【答案】B【解析】【分析】连接BD 、DC ,证△BDE ≌△CDF ,可得CF=BE ,根据角平分线性质可知AE=AF ,即可求周长.【详解】解:连接BD 、DC ,∵AD 平分∠ BAC ,,DE AB DF AC ^^,∴DE=DF ,∵AD=AD ,∴Rt △ADE ≌Rt △ADF ,∴AE=AF=9,∵DG 垂直平分BC ,∴BD=DC ,∴Rt △BDE ≌Rt △CDF ,∴BE=CF ,ABC V 的周长=AB+AC+BC=AF-CF+AE+BE+BC=2AF+BC=28,故选:B .【点睛】本题考查了角平分线的性质、垂直平分线的性质、全等三角形的判定与性质,解题关键是依据已知条件,恰当作辅助线,构造全等三角形.3.如图,∠BAC与∠CBE的平分线相交于点P,BE=BC,PB与CE交于点H,PG∥AD交BC于点F,交AB于点G.有下列结论:①GA=GP;②S△PAC:S△PAB=AC:AB;③BP垂直平分CE;④FP=FC,其中正确的结论有( )A.1个B.2个C.3个D.4个【答案】D【解析】【分析】①根据角平分线的性质和平行线的性质即可得到结论;②根据角平分线的性质和三角形的面积公式即可求出结论;③根据线段垂直平分线的性质即可得结果;④根据角平分线的性质和平行线的性质即可得到结果.【详解】解:①∵AP平分∠BAC,∴∠CAP=∠BAP,∵PG∥AD,∴∠APG =∠CAP ,∴∠APG =∠BAP ,∴GA =GP ;②∵AP 平分∠BAC ,∴P 到AC ,AB 的距离相等,∴S △PAC :S △PAB =AC :AB ,③∵BE =BC ,BP 平分∠CBE ,∴BP 垂直平分CE (三线合一),④∵∠BAC 与∠CBE 的平分线相交于点P ,可得点P 也位于∠BCD 的平分线上,∴∠DCP =∠BCP ,又∵PG ∥AD ,∴∠FPC =∠DCP ,∴∠FPC =∠BCP ,∴FP =FC ,故①②③④都正确.故选:D .【点睛】本题主要考查了角平分线的性质和定义,平行线的性质,垂直平分线的判定,等腰三角形的性质,根据角平分线的性质和平行线的性质解答是解题的关键.4.如图,ABC V 中,60BAC Ð=°,ABC Ð、ACB Ð的平分线交于E ,D 是AE 延长线上一点,且120BDC Ð=°.下列结论:①120Ð=°BEC ;②DB DE =;③2BDE BCE Ð=Ð.其中所有正确结论的序号有( ).A .①②B .①③C .②③D .①②③【答案】D【解析】【详解】分析:根据三角形内角和等于180°求出∠ABC+∠ACB ,再根据角平分线的定义求出∠EBC+∠ECB ,然后求出∠BEC=120°,判断①正确;过点D 作DF ⊥AB 于F ,DG ⊥AC 的延长线于G ,根据角平分线上的点到角的两边的距离相等可得DF=DG ,再求出∠BDF=∠CDG ,然后利用“角边角”证明△BDF 和△CDG 全等,根据全等三角形对应边相等可得BD=CD ,再根据等边对等角求出∠DBC=30°,然后根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义求出∠DBE=∠DEB ,根据等角对等边可得BD=DE ,判断②正确,再求出B ,C ,E 三点在以D 为圆心,以BD 为半径的圆上,根据同弧所对的圆周角等于圆心角的一半可得∠BDE=2∠BCE ,判断③正确.详解:∵60BAC Ð=°,∴18060120ABC ACB Ð+Ð=°-°=°,∵BE 、CE 分别为ABC Ð、ACB Ð的平分线,∴12EBC ABC Ð=Ð,12ECB ACB Ð=Ð,∴11()1206022EBC ECB ABC ACB Ð+Ð=Ð+Ð=´°=°,∴180()18060120BEC EBC ECB Ð=°-Ð+Ð=°-°=°,故①正确.如图,过点D 作DF AB ^于F ,DG AC ^的延长线于G ,∵BE 、CE 分别为ABC Ð、ACB Ð的平分线,∴AD 为BAC Ð的平分线,∴DF DG =,∴36090260120FDG Ð=°-°´-°=°,又∵120BDC Ð=°,∴120BDF CDF Ð+Ð=°,120CDG CDF Ð+Ð=°.∴BDF CDG Ð=Ð,∵在BDF V 和CDG V 中,90BFD CGD DF DGBDF CDG Ð=Ð=°ìï=íïÐ=Ðî,∴BDF V ≌()CDG ASA V ,∴DB CD =,∴1(180120)302DBC Ð=°-°=°,∴30DBC DBC CBE CBE Ð=Ð+Ð=°+Ð,∵BE 平分ABC Ð,AE 平分BAC Ð,∴ABE CBE Ð=Ð,1302BAE BAC Ð=Ð=°,根据三角形的外角性质,30DEB ABE BAE ABE Ð=Ð+Ð=Ð+°,∴DEB DBE Ð=Ð,∴DB DE =,故②正确.∵DB DE DC ==,∴B 、C 、E 三点在以D 为圆心,以BD 为半径的圆上,∴2BDE BCE Ð=Ð,故③正确,综上所述,正确结论有①②③,故选D .点睛:本题考查了角平分线的性质,全等三角形的判定与性质,等角对等边的性质,圆内接四边形的判定,同弧所对的圆周角等于圆心角的一半性质,综合性较强,难度较大,特别是③的证明.第II 卷(非选择题)请点击修改第II 卷的文字说明二、填空题5.已知:△ABC 是三边都不相等的三角形,点P 是三个内角平分线的交点,点O 是三边垂直平分线的交点,当P 、O 同时在不等边△ABC 的内部时,那么∠BOC 和∠BPC 的数量关系是___.【答案】4360BOC BPC Ð=Ð-°【解析】【分析】根据三角形角平分线的性质以及三角形内角和定理,即可得到2180BAC BPC Ð=Ð-°;再根据三角形垂直平分线的性质以及三角形内角和定理,即可得到2BOC BAC Ð=Ð,进而得出BOC Ð和BPC Ð的数量关系.【详解】解:BP Q 平分ABC Ð,CP 平分ACB Ð,12PBC ABC \Ð=Ð,12PCB ACB Ð=Ð,180()BPC PBC PCB \Ð=°-Ð+Ð180(=°-11)22ABC ACB Ð+Ð1180()2ABC ACB =°-Ð+Ð1180(180)2BAC =°-°-Ð1902BAC =°+Ð,即2180BAC BPC Ð=Ð-°;如图,连接AO .Q 点O 是这个三角形三边垂直平分线的交点,OA OB OC \==,OAB OBA \Ð=Ð,OAC OCA Ð=Ð,OBC OCB Ð=Ð,1802AOB OAB \Ð=°-Ð,1802AOC OAC Ð=°-Ð,360()BOC AOB AOC \Ð=°-Ð+Ð360(18021802)OAB OAC =°-°-Ð+°-Ð,22OAB OAC=Ð+Ð2BAC=Ð2(2180)BPC =Ð-°4360BPC =Ð-°,故答案为:4360BOC BPC Ð=Ð-°.【点睛】本题考查了三角形的垂直平分线与角平分线,熟练掌握三角形的垂直平分线与角平分线的性质是解题的关键.三、解答题6.同学们,等边三角形、等腰直角三角形都是最常见的几何图形.(1)如图1,以等边ABC V 的边BC 为腰作等腰直角BCD △,其中90DBC Ð=°,BD BC =,点D 、点A 都是在BC 的同侧,延长BD 、CA 交于点M ,连接AD ,求MAD ∠的度数;(2)如图2,在(1)的条件下,作BN 平分DBC Ð交AC 于点N ,求证:MD CN =;(3)如图3,将图(1)的CBD V 沿着BC 翻折得到1CBD △,连接1AD ,P 为1AD 中点,连接BP 并延长交1CD 于点Q ,请猜测CQ 、BP 、PQ 三条线段之间的数量关系,并证明你的结论.【答案】(1)45MAD Ð=°;(2)见解析;(3)PQ BP CQ=+【解析】【分析】(1)ABC V 为等边三角形,BDC V 为等腰直角三角形可求;(2)作60EMA Ð=°交AD 延长线于E ,再证明AME BCN V V ≌即可求出CN DM =;(3)在PQ 上截取PG BP =连AG CG 、,得到1AB BD =,知道P 1AD 中点,可得1111,2BP AD ABP PBD ABD ^Ð=Ð=Ð,知道BP AP ^,得到AP 为BG 垂直平分线,再用角之间的关系可以推出PQ BP CQ 、、三者关系.【详解】解:(1)如图,∵ABC V 为等边三角形∴60;ABC BAC ACB AB AC BC Ð=Ð=Ð=°==∵BDC V 为等腰直角三角形∴90DBC Ð=°,BD BC BA==∴30;75DBA DAB BDA Ð=°Ð=Ð=°∴18045MAD DAB BAC Ð=°-Ð-Ð=°(2)如图,作60EMA Ð=°交AD 延长线于E∵90,60MBC ACB Ð=°Ð=°∴30;BMA ABM ACB EMAÐ=Ð=°Ð=Ð∴AB AM BC==∵BN 平分MBCÐ∴45NBC EAM Ð=Ð=°∴()AME BCN ASA V V ≌∴ME CN=603030;304575EMD EDM Ð=°-°=°Ð=°+°=°∵∴75MED MDE Ð=Ð=°∴ME DM=∴CN DM=(3)如图,在PQ 上截取PG BP =连AG CG、∵1,AB BC BD BC==∴1AB BD =∵P 为1AD 中点∴1111,2BP AD ABP PBD ABD ^Ð=Ð=Ð∵160,90,ABP CBD Ð=°Ð=°∴1150ABD Ð=°∴11175,15ABP PBD BAD AD B Ð=Ð=°Ð=Ð=°∵BP AP^∴AP 为BG 垂直平分线∴,75AG AB AC AGB ABG ==Ð=Ð=°∴180105,AGQ AGB AGC ACGÐ=°-Ð=°Ð=Ð∵1105,ACQ ACB BCD Ð=Ð+Ð=°∴AGQ ACQÐ=Ð∴AGQ AGC ACQ ACG Ð-Ð=Ð-Ð,即GCQ CHQ Ð=Ð∴GQ CQ =∴PQ PG QG PB CQ=+=+【点睛】此题考查的是等腰直角三角形的性质、三角形全等的性质和判定、垂直平分线的性质,掌握等腰直角三角形的性质和三角形全等的性质和判定,灵活作辅助线是解题的关键.7.如图,在ABC V 中,42B Ð=°,50C Ð=°,通过尺规作图,得到直线DE 和射线AF ,仔细观察作图痕迹,完成下列问题:(1)直线DE 是线段AB 的________线,射线AF 是EAC Ð的________线;(2)求EAF Ð的度数.【答案】(1)线段垂直平分;角平分(2)23°【解析】【分析】(1)根据作图痕迹判断即可;(2)根据角平分线的性质、线段垂直平分线的性质进行求解即可;(1)解:根据作图痕迹可知,直线DE 是线段AB 的线段垂直平分线;射线AF 是EAC Ð的角平分线;(2)∵DE 垂直平分AB∴AE BE=∴42BAE B Ð=Ð=°∵50C Ð=°∴180180504828BAC B C Ð=°-Ð-Ð=°-°=-°°∴884246EAC BAC BAE Ð=Ð-Ð=°-°=°∵AF 平分EACÐ∴11462322EAF EAC Ð=Ð=´°=°【点睛】本题主要考查线段垂直平分线的性质、角平分线的性质,掌握相关性质并灵活应用是解题的关键.8.某地有两所大学和两条相交叉的公路,如图所示(点M ,N 表示大学,AO ,BO 表示公路).现计划修建一座物资仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等.(1)你能确定仓库应该建在什么位置吗?在所给的图形中画出你的设计方案;(2)阐述你设计的理由.【答案】(1)仓库在线段MN 的垂直平分线和∠AOB 的平分线的交点上.(2)角的平分线的性质和线段垂直平分线的性质.【解析】【详解】试题分析:(1) 连接MN ,分别以之为圆心进而画圆求解,做出其垂直平分线DE(2)再以O为圆心,任意长为半径,做角平分线考点:基本作图点评:解答本题的关键是熟练掌握几种基本变换的作图方法,准确找到关键点的对应点.9.如图,两条公路OA与OB相交于点O,在∠AOB的内部有两个小区C与D,现要修建一个市场P,使市场P到两条公路OA、OB的距离相等,且到两个小区C、D的距离相等.(1)市场P应修建在什么位置?(请用文字加以说明)(2)在图中标出点P的位置(要求:用尺规作图,不写作法,保留作图痕迹,写出结论).【答案】(1)详见解析;(2)详见解析.【解析】【分析】(1)直接利用角平分线的性质以及线段垂直平分线的性质分析得出答案;(2)直接利用角平分线的作法以及线段垂直平分线的作法得出答案.【详解】(1)点P应修建在∠AOB的角平分线和线段CD的垂直平分线的交点处;(2)如图所示:点P即为所求.【点睛】此题主要考查了应用设计与作图,正确掌握角平分线的性质以及线段垂直平分线的性质是解题关键.10.有公路l1同侧、l2异侧的两个城镇A,B,如下图.电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,发射塔C 应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.(保留作图痕迹,不要求写出画法)【答案】答案作图见解析【解析】【分析】根据题意知道,点C应满足两个条件,一是在线段AB的垂直平分线上;二是在两条公路夹角的平分线上,所以点C应是它们的交点.【详解】解:连接A,B两点,作AB的垂直平分线,作两直线交角的角平分线,交点有两个.(1)作两条公路夹角的平分线OD或OE;(2)作线段AB的垂直平分线FG;则射线OD,OE与直线FG的交点C1,C2就是所求的位置.考点:作图-应用与设计作图11.如图,七年级(1)班与七年级(2)班的学生分别在M、N两处参加植树劳动,现要设一个茶水供应点,使茶水供应点到两个班的距离相等(不写作法、要求保留作图痕迹).(1)若茶水供应点P设在道路AB上,请你作出点P;(2)若茶水供应点Q设在道路AB、AC的交叉区域内,并且使点Q到两条道路的距离相等,请你作出点Q.【答案】(1)MN的垂直平分线与AB的交点;(2)∠BAC的平分线与MN的垂直平分线的交点.【解析】【详解】解:(1)线段MN的垂直平分线与AB的交点即为点P,如下图:(2)点Q是∠BAC的平分线与线段MN的垂直平分线的交点,如下图:12.请你先在BC上找一点P,使点P到AB、AC的距离相等,再在射线AP上找一点Q,使QB=QC.【答案】见解析【解析】【分析】利用网格特点作∠BAC 的平分线交BC 于P ,则根据角平分线的性质得点P 到AB 、AC 的距离相等,再利用网格特点过BC 的中点作BC 的垂线交AP 于Q ,则根据线段垂直平分线的性质得QB =QC .【详解】解:如图,点P 和点Q 为所作.13.如图所示,已知AOB Ð和两点M 、N ,求作一点P ,使得点P 到AOB Ð的两边距离相等且PM PN =.【答案】详见解析【解析】【分析】要使点P 到AOB Ð的两边距离相等,则P 应在AOB Ð的角平分线上,要使PM PN =,则点P 在MN 的垂直平分线上,那么满足题设的点P 就是MN 的垂直平分线与AOB Ð的角平分线的交点.【详解】要使点P 到AOB Ð的两边距离相等,则P 应在AOB Ð的角平分线上,要使PM PN =,则点P 在MN 的垂直平分线上,那么满足题设的点P 就是MN 的垂直平分线与AOB Ð的角平分线的交点,作AOB Ð的角平分线C O ,再作线段MN 的垂直平分线交OC 于点P ,如图所示:【点睛】本题是对角平分线的性质和垂直平分线性质的考查,熟练掌握角平分线的性质和垂直平分线性质是解决本题的关键.14.如图,点M,N分别是∠AOB的边OA,OB上的点,OM=3,ON=7,在∠AOB内有一点G,到边OA,OB的距离相等,且满足GM=GN.(1)尺规作图:画出点G(要求:保留作图痕迹);(2)试证明:∠OMG+∠ONG=180°;(3)若P,Q分别是射线OA,OB上的动点,且满足GP=GQ,则当OP=4时,OQ的长度为 .【答案】(1)见解析;(2)见解析;(3)4或6【解析】【分析】(1)作OP平分∠AOB,作线段MN的垂直平分线EF,EF交OP于点G,点G即为所求;(2)证明△OGK≌△OGH(AAS),推出OK=OH,GK=GH,由GM=GN,∠GKM=∠GHN=90°,推出Rt△GKM≌Rt△GHN(HL),再利用全等三角形的性质,四边形内角和定理解决问题;(3)首先求出OK=OH=5,PK=1,然后分两种情形分别求解即可解决问题.【详解】解:(1)如图,点G即为所求.(2)证明:作GK⊥OA于K,GH⊥OB于H.∵∠GOK=∠GOH,∠GKO=∠GHO=90°,OG=OG,∴△OGK≌△OGH(AAS),∴OK=OH,GK=GH,∵GM=GN,∠GKM=∠GHN=90°,∴Rt△GKM≌Rt△GHN(HL),∴∠KGM=∠HGN,∴∠MGN=∠KGH,∵∠KGH+∠AOB=180°,∴∠MGN+∠AOB=180°,∴∠OMG+∠ONG=180°;(3)如图,∵OK=OH,MK=NH,∴OM+ON=OK﹣KM+OH+HN=2OK=10,∴OK=OH=5,∵OP=4,∴PK=5﹣4=1,∵GP=GQ,∴当点Q在线段OH上时,OQ=OP=4,当点Q′在OH的延长线上时,OQ′=5+1=6,故答案为4或6.【点睛】本题考查作图−复杂作图,角平分线的性质,线段的垂直平分线的性质,全等三角形的判定和性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.15.(1)如图1,利用网格线,作出三角形关于直线l的对称图形.(2)如图2,利用网格线:①在BC上找一点P,使点P到AB和AC的距离相等;②在射线AP上找一点Q,使QB=QC.【答案】(1)见解析;(2)①见解析;②见解析.【解析】【分析】(1)直接利用轴对称图形的性质得出对应点位置,再顺次连接即可;(2)①借助网格作出∠CAB的角平分线,则∠CAB的角平分线与BC的交点即为所求;②借助网格作出线段BC的垂直平分线,则线段BC的垂直平分线与射线AP的交点即为所求.【详解】解:(1)如图所示:;(2)①如图所示,点P即为所求;②如图所示,点Q即为所求.【点睛】此题主要考查了作轴对称图形、角平分线的性质以及线段垂直平分线的性质,正确借助网格作图是解题关键.16.已知直线l及位于其两侧的两点A,B,如图:∠.(1)在图①中的直线l上求一点Q,是直线l平分AQB(2)能否在直线l上找一点,使该点到点A,B的距离之差的绝对值最大?若能,直接在图②作出该点的位置,若不能,请说明理由.【答案】答案详见解析【解析】【详解】分析:(1)作B关于直线l的对称点B′,连接AB′交直线l与点Q,连接BQ,由三角形全等的判定定理求出△BDQ≌△B′DQ,再由三角形全等的性质可得出;(2)根据两点之间线段最短,连接AB,线段AB交直线l于点O,则点O为所求.详解:(1)如图,作点A关于直线l的对称点A¢,连接BA¢并延长交直线l于点Q,点Q即为所求.(2)如图:作点B关于直线l的对称点B¢,连结AB¢并延长交直线l于点P,点P即为所求.点睛:此题主要考查了两点之间线段最短、线段的垂直平分线的性质及角平分线的性质,熟知各题的知识点是解题关键.17.如图,方格纸上画有AB 、CD 两条线段,按下列要求作图.(保留作图痕迹)(1)请你在图(1)中画出线段AB 关于CD 所在直线成轴对称的图形.(2)请你在图(2)中添上一条线段,使图中3条线段组成一个轴对称图形,画出所有情形.(3)如图(3),已知AOB Ð和C 、D 两点,求作一点P ,使PC PD =,且P 到AOB Ð两边的距离相等.【答案】见解析【解析】【详解】分析:(1)做BO ⊥CD 于点O ,并延长到B′,使B′O=BO ,连接AB 即可;(2)轴对称图形沿某条直线折叠后,直线两旁的部分能完全重合.(3)作出∠AOB 的平分线;作出CD 的中垂线;找到交点P 即为所求.详解:(1)(2)如图所示:(3)如图所示:作CD 的中垂线和ADB Ð的平分线,两线交点即为点P .点睛:1)(2)两个小题考查对称轴作图,掌握画图的方法和图形的特点是解题的关键;(3)本题考查了角平分线的作法以及垂直平分线的作法,解答此题要明确两点:(1)角平分线上的点到角的两边的距离相等;(2)中垂线上的点到两个端点的距离相等.18.(1)作图题:某学校正在进行校园环境的改造工程设计,准备在校内一块四边形花坛内栽上一棵黄桷树.如图,要求黄桷树的位置点P到边AB、BC的距离相等,并且点P到点A、D的距离也相等.请用尺规作图作出栽种黄桷树的位置点P(不写作法,保留作图痕迹).(2)用如图(1)所示的瓷砖拼成一个正方形,使拼成的图案成轴对称图形,请你在图(2)、图(3)、图(4)中各画出一种拼法.(要求三种拼法各不相同,所画图案中的阴影部分用斜线表示)【答案】(1)图形见解析(2)图形见解析【解析】【详解】试题分析:(1)到边AB、BC的距离相等的点在∠ABC的平分线上,到点A、D的距离相等的点在线段AD 的垂直平分线上,点P即角平分线和垂直平分线的交点.(2)根据轴对称图形的法则去画即可,有多种图形.试题解析:(1)作出∠ABC的角平分线,作出线段AD的中垂线,交点即为点P.(2)所作图形如下所示:。
《垂直平分线》练习题(含答案)
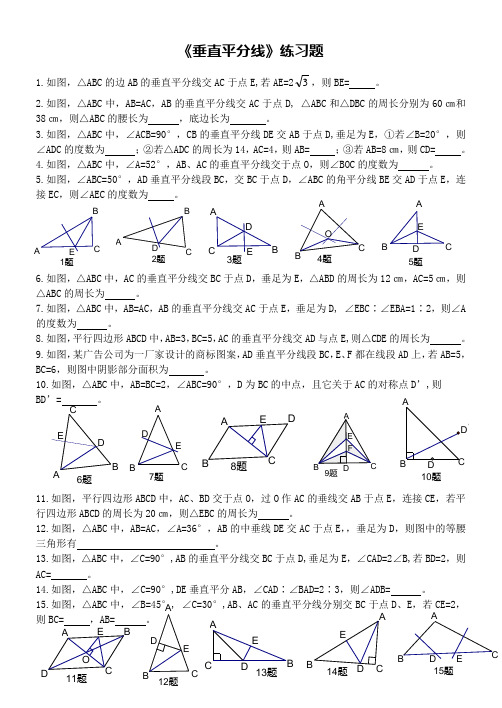
1题A B E C 2题D A B C 3题D AB EC 4题A B C O 5题D A BE C 11题D A B E C O 12题D A B E C 13题D A B E C 14题D A B E C 15题D A B E C6题D A BE C 8题D A B E C 7题D A B E C 10题'9题《垂直平分线》练习题1.如图,△ABC 的边AB 的垂直平分线交AC 于点E,若AE=23,则BE= 。
2.如图,△ABC 中,AB=AC ,AB 的垂直平分线交AC 于点D, △ABC 和△DBC 的周长分别为60㎝和38㎝,则△ABC 的腰长为 ,底边长为 。
3.如图,△ABC 中,∠ACB=90°,CB 的垂直平分线DE 交AB 于点D,垂足为E ,①若∠B=20°,则∠ADC 的度数为 ;②若△ADC 的周长为14,AC=4,则AB= ;③若AB=8㎝,则CD= 。
4.如图,△ABC 中,∠A=52°,AB 、AC 的垂直平分线交于点O ,则∠BOC 的度数为 。
5.如图,∠ABC=50°,AD 垂直平分线段BC ,交BC 于点D ,∠ABC 的角平分线BE 交AD 于点E ,连接EC ,则∠AEC 的度数为 。
6.如图,△ABC 中,AC 的垂直平分线交BC 于点D ,垂足为E ,△ABD 的周长为12㎝,AC=5㎝,则△ABC 的周长为 。
7.如图,△ABC 中,AB=AC ,AB 的垂直平分线交AC 于点E ,垂足为D, ∠EBC ∶∠EBA=1∶2,则∠A 的度数为 。
8.如图,平行四边形ABCD 中,AB=3,BC=5,AC 的垂直平分线交AD 与点E,则△CDE 的周长为 。
9.如图,某广告公司为一厂家设计的商标图案,AD 垂直平分线段BC ,E 、F 都在线段AD 上,若AB=5,BC=6,则图中阴影部分面积为 。
10.如图,△ABC 中,AB=BC=2,∠ABC=90°,D 为BC 的中点,且它关于AC 的对称点D ’,则 BD ’= 。
八年级数学《线段垂直平分线角平分线》课后习题

八年级数学《线段垂直平分线角平分线》课后习题1. 选择题1. 以下哪个图形中的$\overline{AB}$既是线段$AC$的垂直平分线,也是∠$ACD$的角平分线?A. B. C. D. 2. 在直角三角形$ABC$中,$\overline{AC}$是∠$C$的角平分线,则∠$BAC$与∠$BCA$分别是$\underline{\qquad}$.A. 锐角,钝角B. 直角,锐角C. 钝角,直角D. 直角,钝角2. 填空题3. 设$\overline{PQ}$是线段$\overline{AB}$的垂直平分线,若∠$PAC=30^\circ$,则∠$PAB=\underline{\qquad}$.4. 在平行四边形$ABCD$中,$\overline{EF}$是线段$\overline{AD}$的垂直平分线,$\overline{GH}$是∠$GBF$的角平分线,则∠$EGH=\underline{\qquad}$.3. 解答题5. 在直角三角形$ABC$中,$\overline{AD}$是∠$A$的角平分线,如图所示.已知$\overline{AD}=2cm$,$\overline{AC}=10cm$,求∠$BAC$的度数.解:由于$\overline{AD}$是∠$A$的角平分线,根据角平分线定理可知$\dfrac{BD}{CD}=\dfrac{AB}{AC}$.设$\overline{BD}=x$,则$\overline{CD}=x$.根据勾股定理可得:$$(10+x)^2+x^2=4^2$$解得$x=\dfrac{48}{5}$.所以,$\overline{BD}=\dfrac{48}{5}$.根据正切函数的性质可得:$$\tan(\angleBAD)=\dfrac{BD}{AD}=\dfrac{\frac{48}{5}}{2}=\dfrac{24}{5}.$$因为∠$BAC=90^\circ$,所以∠$BAD=45^\circ$,所以∠$BAC=45^\circ$.答:∠$BAC$的度数是$45^\circ$.4. 应用题6. 请用尺规作图的方法,画一条线段的垂直平分线和角平分线,并标出垂足和角平分点.解:步骤:1. 以线段的一个端点为圆心,在纸上画一个与线段等长的圆.2. 以线段的另一个端点为圆心,画一个与上一个圆等大的圆.3. 连接两圆的交点和线段两个端点,所得的线段是原线段的垂直平分线.4. 以线段的一个端点为圆心,在纸上画一个与线段等长的圆.5. 以线段的另一个端点为圆心,画一个与上一个圆等大的圆.6. 连接两圆的交点和线段的一个端点,所得的线段是原线段的角平分线.按照上述步骤操作,即可作出线段的垂直平分线和角平分线,并标出垂足和角平分点.注意:尺规作图中只能使用直尺和圆规,无法精确度量线段长度和角度大小,所以标度不作要求.5. 拓展练7. 通过实际生活中的例子,描述线段的垂直平分线和角平分线的应用场景.解:线段的垂直平分线和角平分线在实际生活中有许多应用场景,以下是两个例子:例子1:钟面的分针和秒针当我们查看钟面上的时间时,钟面上的分针和秒针正好是指向钟面的圆心的单条线段的垂直平分线和角平分线。
垂直平分线和角平分线典型题

知识要点详解1、线段垂直平分线的性质(1)垂直平分线性质定理:线段垂直平分线上的点到这条线段两个端点的距离相等.定理的数学表示:如图1,已知直线m 与线段AB 垂直相交于点D ,且AD =BD ,若点C 在直线m 上,则AC =BC.定理的作用:证明两条线段相等 (2)线段关于它的垂直平分线对称.2、线段垂直平分线性质定理的逆定理(1)线段垂直平分线的逆定理:到一条线段两个端点距离相等的点在这条线段的垂直平分线上.定理的数学表示:如图2,已知直线m 与线段AB 垂直相交于点D ,且AD =BD ,若AC =BC ,则点C 在直线m 上.定理的作用:证明一个点在某线段的垂直平分线上.3、关于三角形三边垂直平分线的定理(1)关于三角形三边垂直平分线的定理:三角形三边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.定理的数学表示:如图3,若直线,,i j k 分别是△ABC 三边AB 、BC 、CA 的垂直平分线,则直线,,i j k 相交于一点O ,且OA =OB =OC.定理的作用:证明三角形内的线段相等.(2)三角形三边垂直平分线的交点位置与三角形形状的关系:若三角形是锐角三角形,则它三边垂直平分线的交点在三角形内部;若三角形是直角三角形,则它三边垂直平分线的交点是其斜边的中点;若三角形是钝角三角形,则它三边垂直平分线的交点在三角形外部.反之,三角形三边垂直平分线的交点在三角形内部,则该三角形是锐角三角形;三角形三边垂直平分线的交点在三角形的边上,则该三角形是直角三角形;三角形三边垂直平分线的交点在三角形外部,则该三角形是钝角三角形.图1图2经典例题:例1 如图1,在△ABC 中,BC =8cm ,AB 的垂直平分线交AB 于点D ,交边AC 于点E ,△BCE 的周长等于18cm ,则AC 的长等于( )A .6cmB .8cmC .10cmD .12cm课堂笔记:针对性练习::1)如图,AB=AC=14cm,AB 的垂直平分线交AB 于点D ,交AC 于点 E ,如果△EBC 的周长是24cm ,那么BC= 2) 如图,AB=AC=14cm,AB 的垂直平分线交AB 于点D ,交AC 于点E ,如果BC=8cm ,那么△EBC 的周长是3) 如图,AB=AC,AB 的垂直平分线交AB 于点D ,交AC 于点E ,如果∠A=28 度,那么∠EBC 是例2. 已知: AB=AC ,DB=DC ,E 是AD 上一点,求证:BE=CE 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级数学《线段的垂直平分线与角平分线》练习题
班级姓名
一、选择题
1.如图1,在△ABC中,BC=8cm,AB的垂直平分线交AB于点D,交
边AC于点E,△BCE的周长等于18cm,则AC的长等于()
A.6cm B.8cm C.10cm D.12cm
2.如图,AC=AD,BC=BD,则()
A.CD垂直平分AD
B.AB垂直平分CD
C.CD平分∠ACB
D.以上结论均不对
3.如果三角形三条边的中垂线的交点在三角形的外部,
那么,这个三角形是()
A.直角三角形
B.锐角三角形
C.钝角三角形
D.等边三角形
4.下列命题中正确的命题有()
①线段垂直平分线上任一点到线段两端距离相等;②线段上任一点到垂直平分线两端距离相等;③经过线段中点的直线只有一条;④点P在线段AB外且PA=PB,过P作直线MN,则MN是线段AB的垂直平分线;⑤过线段上任一点可以作这条线段的中垂线.
A.1个
B.2个
C.3个
D.4个
5.△ABC中,AB的垂直平分线交AC于D,如果AC=5 cm,BC=4cm,那么△DBC的周长是()
A.6 cm
B.7 cm
C.8 cm
D.9 cm
二.填空题
1、如图,(1)、AB=AC=14cm,AB的垂直平分线交AB于点D,交AC于点E,
如果△EBC的周长是24cm,那么BC=
(2)、AB=AC=14cm,AB的垂直平分线交AB于点D,交AC于点E,
如果BC=8cm,那么△EBC的周长是
(3)、AB=AC,AB的垂直平分线交AB于点D,交AC于点E,
如果∠A=28°,那么∠EBC是
2.在△ABC中,AB=AC,AB的垂直平分线与边AC所在的直线
.....相交所成锐角为50°,
△ABC的底角∠B的大小为_______________。
3. △ABC中,AB=AC,AC的中垂线交AB于E,△EBC的周长为21cm,AB=2BC,则腰长为________________。
三.解答题
1、已知:在△ABC中,ON是AB的垂直平分线,OA=OC,求证:点O在BC的垂直平分线上
2.已知如图,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC,求证:AO⊥BC.
3.如图,在△ABC中,AB=AC,∠A=120°,AB的垂直平分线MN分别交BC、AB于点M、N. 求证:CM=2BM.
4.已知:如图所示,∠ACB,∠ADB都是直角,且AC=AD,P是AB上任意一点,
求证:CP=DP。
5、已知:如图,点B、C在∠A的两边上,且AB=AC,P为∠A内一点,PB=PC,
PE⊥AC,PF⊥AB,垂足分别是E、F。
求证:PE=PF
6.如图,在△ABC中,∠C=90°,M为AB的中点,DM⊥AB,CD平分∠ACB,求证:MD=AM.
7.如图7,在△ABC 中,AC =23,AB 的垂直平分线交AB 于点D ,交BC 于点E ,△ACE 的周长为50,求BC 长.
8.如图8,已知AD 是△ABC 的BC 边上的高,且∠C =2∠B ,求证:BD =AC +CD.
9、如图,已知在四边形ABCD 中,对角线BD 平分∠ABC ,且∠BAD 与∠BCD 互补, 求证:AD =CD.
10、如图10,已知在直角梯形ABCD 中,AB ∥CD ,AB ⊥BC ,E 为BC 中点,连接AE 、DE ,DE
平分∠ADC ,求证:AE 平分∠BAD.
11. 如图,已知:线段CD 垂直平分AB ,AB 平分DAC . 求证:BC AD //.
图7E D A
C B B C
D A 图10F C D
A E
12.已知:如图,∠B=∠C=90°,DM 平分∠ADC ,AM 平分∠DAB 。
求证:MB=MC.
13.如图,︒=∠90C ,DE 是AB 的垂直平分线,E 为垂足,交BC 于D ,AC AB 2=. 求证:DE CD =.
14.如图,已知BE ⊥AC 于E ,CF ⊥AB 于F ,BE 、CF 相交于点D ,若BD=CD.
求证:AD 平分∠BAC.
15.如图,已知:AD 是ABC ∆的高,E 为AD 上一点,且CE BE =.
求证:ABC ∆是等腰三角形.
16. 如图,在ABC ∆中,BAC ∠的平分线交BC 于D ,且AB DE ⊥,AC DF ⊥,垂足分别是E 、F. 求证:AD 是EF 的垂直平分线.。
