2006年辽宁沈阳中考数学试题课改试验区
中考数学试卷2006-课标卷答案

2006年北京市高级中等学校招生统一考试(课标A 卷)数学试卷参考答案一、选择题1.A2.C3.A4.D5.B6.C7.D8.B二、填空题9.m ≤94 10.211.10 2612.30三、解答题13.解:12320061201+---+-||()() =+-+=+2331213314.解不等式组315260x x -<+>⎧⎨⎩,①②解:由不等式①解得x <2由不等式②解得 x >-3则不等式组的解集为 -<<32x15.解:()()()()x x x x x ++-=+-121211x x x x ++-=-1222222x =3经检验x =3是原方程的解。
所以原方程的解是x =316.证明:因为AB ∥ED ,则∠A =∠D又AF =DC则AC =DF在△ABC 与△DEF 中 AB DE A D AC DF ==⎧⎨⎪⎩⎪∠=∠所以△ABC ≌△DEF所以BC =EF17.解:x x x x x ()()2259-+-- =-+--=-x x x x x 322325949当230x -=时,原式=-=+-=49232302x x x ()()18.解:如图,过点D 作DF ∥AB 交BC 于点F因为AD ∥BC所以四边形ABFD 是平行四边形所以BF =AD =1由DF ∥AB得∠DFC =∠ABC =90°在Rt △DFC 中,∠C =45°,CD =22由 cos C CFCD =求得 CF =2所以 BC =BF +FC =3在△BEC 中,∠BEC =90°s i n C BEBC =求得 BE =322四、解答题19.解:(1)证明:如图,连结OA 。
因为sin B =12所以 ∠B =30°故∠O =60°又OA =OC ,所以△ACO 是等边三角形故∠OAC =60°因为∠CAD =30°所以∠OAD =90°所以 AD 是⊙O 的切线。
2006-2016沈阳数学中考试题证明题汇总
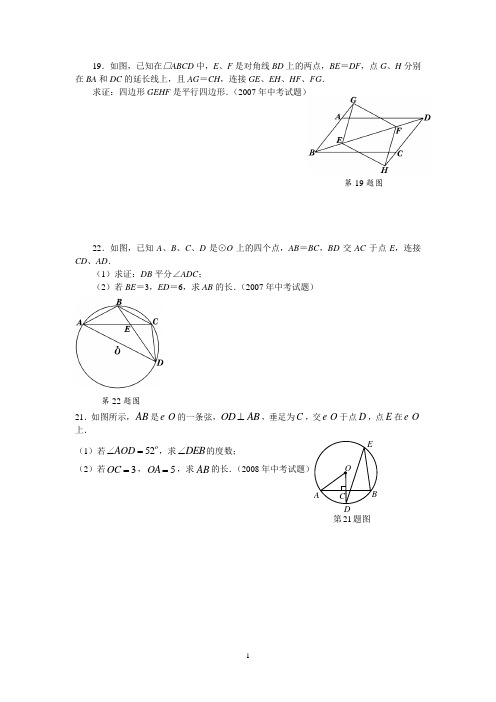
19.如图,已知在□ABCD 中,E 、F 是对角线BD 上的两点,BE =DF ,点G 、H 分别在BA 和DC 的延长线上,且AG =CH ,连接GE 、EH 、HF 、FG .求证:四边形GEHF 是平行四边形.(2007年中考试题)22.如图,已知A 、B 、C 、D 是⊙O 上的四个点,AB =BC ,BD 交AC 于点E ,连接CD 、AD .(1)求证:DB 平分∠ADC ;(2)若BE =3,ED =6,求AB 的长.(2007年中考试题)21.如图所示,AB 是O 的一条弦,OD AB ⊥,垂足为C ,交O 于点D ,点E 在O上.(1)若52AOD ∠=,求DEB ∠的度数;(2)若3OC =,5OA =,求AB 的长.(2008第22题图 第19题图 第21题图A B C DEFM N 19.如图,AB 是⊙O 的直径,点C 在AB 的延长线,CD 与⊙O 相切于点D ,∠C =20º.求∠ADC 的度数.(2009年中考试题)21.如图,在□ABCD 中,点E 在AD 上,连接BE ,DF ∥BE 交BC 于点F ,AF 与BE 交与点M ,CE 与DF 交于点N .求证:四边形MFNE 是平行四边形. (2009年中考试题)19. 如图,菱形ABCD 的对角线AC 与BD 相交于点O ,点E 、F 分别为边 AB 、AD 的中点,连接EF 、OE 、OF 。
求证:四边形AEOF 是菱形。
(2010年中考试题)21. 如图,AB 是 O 的直径,点C 在BA 的延长线上,直线CD 与 O 相切于点D ,弦DF ⊥AB 于点E ,线段CD =10,连接BD ; (1) 求证:∠CDE =2∠B ;(2) 若BD :AB =3:2,求 O 的半径及DF 的长。
(2010年中考试题)19.如图,在△ABC 中,AB =AC ,D 为BC 边上一点,∠B =30°,∠DAB =45°.⑴求∠DAC 的度数; ⑵求证:DC =AB(2011年中考试题)第19题图DA BCDE F O21.如图,点A 、B 在⊙O 上,直线AC 是⊙O 的切线,OD ⊥OB ,连接AB 交O C 于点D .⑴求证:AC =CD⑵若AC =2,AOOD 的长度.(2011年中考试题)19.已知,如图,在荀ABCD 中,延长DA 到点E ,延长BC 到点F ,使得AE =CF ,连接EF ,分别交AB ,CD 于点M ,N ,连接DM ,BN .(1)求证:△AEM ≌△CFN ;(2)求证:四边形BMDN 是平行四边形. (2012年中考试题)22.如图,⊙O 是△ABC 的外接圆,AB 是⊙O 的直径,D 为⊙O 上一点,OD ⊥AC ,垂足为E ,连接BD .(1)求证:BD 平分∠ABC ;(2) 当∠ODB =30°时,求证:BC =OD . (2012年中考试题)A第21题图19.如图,ABC ∆中,AB=BC ,BE ⊥AC 于点E ,AD ⊥BC 于点D ,45BAD ∠=︒,AD 与BE 交于点F ,连接CE , (1)求证:BF=2AE(2)若CD =AD 的长。
2006年辽宁省十一市中等学校招生考试

2006年辽宁省十一市中等学校招生考试物理试卷(供课改实验区考生使用)理化考试时间150分钟,物理试卷满分120分。
一、填空题(第4、6小题除外,每空1分,共24分)1.地球上的水在不停地循环着.阳光照暖了海洋,水经过_________变成了水蒸气升到空中,水蒸气在空中遇到冷空气后_______形成小水滴。
2.小红同学多才多艺,不仅钢琴弹得好,小提琴拉得也很棒。
当她用不同的力弹钢琴时,钢琴发出声音的______不同.她弹钢琴、拉小提琴时,你是依据_____.的不同来分辨琴声的。
有一次她用收音机听钢琴曲时,索性拆开了收音机做了如图所示的实验.她发现在放钢琴曲时收音机扬声器纸盆上的小纸团“翩翩起舞”,这说明__________,她又猜想如果把此实验拿到月球上面去做,在月球上________(填“能”或“不能”)听到钢琴声。
3.“超导”是20世纪初科学家的重大发现,超导现象是某些物质在很低的温度时电阻________,随着科学的发展,目前已经开发出一些“高温”超导材料,请你举出一个利用超导材料的例子:_____________________________4.(3分)有一只“220V l00W”的灯泡,使其工作2h,灯泡消耗的电能是_____J,如果把它单独接在如图所示的电能表上.电能表转盘转过_________转。
5.我们生活在电磁波的海洋中,移动电话(手机)__________(填“能"或“不能")发射电磁波,紫外线和可见光都_________(填“是”或“不是”)电磁波。
6.(3分)下列几个实例中属于减小摩擦的是__________(填序号)。
①用力捏自行车的车闸;②汽车轮胎上的花纹;③汽垫船向下喷出强气流,在船底和水之间形成一层空气垫。
请发挥你的想象,写出一个自然界中如果不存在摩擦的情景:_______。
7.如图,有一束光从某种介质斜射人空气时,在界面上发生了反射和折射,其中入射角是________度,折射角是________度。
中考数学试题沈阳市2006年中考数学试题(非课改实验区).doc

2006年中考数学试题*考试时间120分钟,试题满分150分一、选择题(每小题3分,共24分)1.下列各式中,与2是同类二次根式的是()A.3B.4C.12D.122.若点()23P-,与点()Q a b,关于x轴对称,则a,b的值分别是()A.2-,3B.2,3C.2-,3-D.2,3-3.已知Rt ABC△中,90C=∠,9BC=,15AB=,则sin A的值是()A.34B.35C.45D.434.如图1,已知点A,B,C,D,E是O的五等分点,则BAD∠的度数是()A.36B.48C.72D.965.抛物线()2361y x=-+-的对称轴是直线()A.6x=-B.1x=-C.1x=D.6x=6.已知两个圆的半径分别是5和3,圆心距是2,则这两个圆的位置关系是()A.内切B.相交C.外切D.外离7.已知圆锥的侧面积是212πcm,底面半径是3cm,则这个圆锥的母线长是()A.3cmB.4cmC.5cmD.8cm8.图2是某班40名学生一分钟跳绳测试成绩的频率分布直方图,从左起第一、二、三、四个小长方形的高的比是1:4:3:2,那么一分钟跳绳次数在100次以上的学生有()A.6人B.8个C.16人20图1频率组距次数图2二、填空题(每小题3分,共24分)9.一元二次方程()30x x +=的根是____________.10.已知点I 是ABC △的内心,130BIC =∠,则BAC ∠的度数是____________.11.函数y =x 的取值范围是____________.12.在ABC △中,2AB AC ==,BD 是AC 边上的高,且BD =ACB ∠的度数是____________.13.用换元法解分式方程224232x x x x-=--,若设22x x y -=,则原方程可化为关于y 的整式方程是____________. 14.在O 中,90的圆心角所对的弧长是2πcm ,则O 的半径是____________cm .15.若甲、乙两名同学五次数学模拟考试成绩的平均分都是135分,且甲同学成绩的方差2 1.05s =甲,乙同学成绩的方差20.41s =乙,则甲、乙两名同学成绩相对稳定的是___________.(填“甲”或“乙”)16.有一个边长是5cm 的正六边形,若要剪一张圆形纸片完全盖住这个正六边形,则这个圆形纸片的最小半径是____________cm . 三、(第17小题6分,第18、19小题各8分,第20小题10分,共32分)1718.解方程组:221870x y y x -=⎧⎨-+=⎩19.已知关于x 的一元二次方程2410x x m ++-=.(1)请你为m 选取一个合适的整数,使得到的方程有两个不相等的实数根; (2)设αβ,是(1)中你所得到的方程的两个实数根,求22αβαβ++的值.20.如图3,已知直线2y x =-与双曲线()0ky x x=>交于点()3Am ,. (1)求m ,k 的值;(2)连结OA ,在x 轴的正半轴上是否存在点Q ,使AOQ △是等腰三角形?若存在,请直接写出所有符合条件的点Q 的坐标;若不存在,请说明理由.四、(每小题10分,共20分)21.如图4,已知O 的直径8cm AB =,直线DM 与O 相切于点E ,连结BE ,过点B 作BC DM ⊥于点C ,BC 交O 于点F ,6cm BC =. 求:(1)线段BE 的长; (2)图中阴影部分的面积.22.随着我国经济的发展,对技术工人的需求量不断增加.某技工学校2005年秋季招收了600名新生,学校为了了解这600名新生中考成绩(成绩为整数)的情况,从中随机抽取部分学生的中考成绩进行分析,绘制了下面尚未完成的频率分布表:分组 频数累计 频数 频率 350.5~360.5 正 40.08 360.5~370.5 正正 6370.5~380.5 正正0.20 380.5~390.5 正正正 150.30 390.5~400.5 正正正 11400.5~410.5 正 40.08 合计1.00图3图4(1)补全上面的频率分布表;(2)你从表格信息中能否确定抽取的部分学生的中考成绩的众数落在哪一个小组内? 答:__________(填“能”或“不能”)(3)从表格信息可知抽取的部分学生的中考成绩的中位数在_________小组内; (4)在2005年秋季招收的新生中,中考成绩在390.5~410.5的新生约有多少人? 五、(12分)23.如图5,某市郊外景区内一条笔直的公路a 经过三个景点A B C ,,.景区管委会又开发了风景优美的景点D .经测量景点D 位于景点A 的北偏东30方向8千米处,位于景点B 的正北方向,还位于景点C 的北偏西75方向上.已知5AB =千米.(1)景区管委会准备由景点D 向公路a 修建一条距离最短的公路,不考虑其他因素,求出这条公路的长;(结果精确到0.1千米) (2)求景点C 与景点D 之间的距离.(结果精确到1千米)(参考数据:3 1.73=,5 2.24=,sin 53cos370.80==,sin 37cos530.60==, tan 53 1.33=,tan 370.75=,sin 38cos520.62==,sin 52cos380.79==, tan 380.78tan 52 1.28==,,sin750.97cos750.26tan 75 3.73===,,.)六、(12分)24.某小型企业获得授权生产甲、乙两种奥运吉祥物,生产每种吉祥物所需材料及所获利润如下表:A 种材料(2m )B 种材料(2m )所获利润(元)每个甲种吉祥物 0.3 0.5 10 每个乙种吉祥物0.60.2 20该企业现有A 种材料2900m ,B 种材料2850m ,用这两种材料生产甲、乙两种吉祥物共东 北 A B C D a2000个.设生产甲种吉祥物x 个,生产这两种吉祥物所获总利润为y 元.(1)求出y (元)与x (个)之间的函数关系式,并求出自变量x 的取值范围;(2)该企业如何安排甲、乙两种吉祥物的生产数量,才能获得最大利润?最大利润是多少? 七、(12分) 25.如图6,在O 中,BC BD =,点M 是CD 上任意一点,弦CD 与弦BM 交于点F ,连结MC ,MD ,BD .(1)请你在图6中过点B 作O 的切线AE ,并证明AE CD ∥;(不写作法,作图允许使用三角板)(2)求证:MC MD MF MB =;(3)如图7,若点M 是BC 上任意一点(不与点B ,点C 重合),弦BM ,DC 的延长线交于点F ,连结MC ,MD ,BD ,则结论MC MD MF MB =是否仍然成立?如果成立,请写出证明过程;如果不成立,请说明理由. 八、(14分) 26.如图8,在平面直角坐标系中,直线31y x =-+分别与x 轴,y 轴交于点A ,点B . (1)以AB 为一边在第一象限内作等边ABC △及ABC △的外接圆M (用尺规作图,不要求写作法,但要保留作图痕迹);(2)若M 与x 轴的另一个交点为点D ,求A ,B ,C ,D 四点的坐标;(3)求经过A ,B ,D 三点的抛物线的解析式,并判断在抛物线上是否存在点P ,使ADP △的面积等于ADC △的面积?若存在,请直接写出所有符合条件的点P 的坐标;若不存在,请说明理由.图6 图7图8。
《2006年沈阳市中等学校招生统一考试考试说明》解读

《2006年沈阳市中等学校招生统一考试考试说明》解读《2006年沈阳市中等学校招生统一考试考试说明》昨日下发,作为沈阳市中考命题的权威性文件,这既是中考命题的依据和蓝本,对中考命题做出了明确规定,减少了命题的随意性,也是考生的备考大纲,为广大考生指明了复习备考的方向。
昨日,本报在第一时间邀请到东北育才学校初中部的名师,就《说明》的具体内容为考生点评考纲变化,提出复习建议。
据东北育才初中部几位参加点评的名师分析,今年考纲的题型、难易比例与去年相比,总的来说变化不大,语文考纲中增加了课外文言文的考查,英语题型与去年相比略有变化,如完成对话今年将以选择题形式出现。
历史与社会学科增加了中国历史部分的考试内容,思想政治学科考查的知识点增加,同时增加了2分的法律常识。
据分析,预计今年各科题型要比去年灵活,更注重考查学生对知识的理解和实际运用能力。
因此点评教师提醒考生,在加强基础知识记忆的同时,更要注重对知识的理解和运用。
相关内容请继续关注明日本报。
命题原则:强调积累、突出读写,进一步创新。
着重考查学生的阅读能力和表达能力。
考试范围:以《语文课程标准》的要求和内容为依据,参照义务教育课程标准实验教科书《语文》进行命题。
其中诗文背诵默写的考查篇目为《标准》推荐背诵的50篇优秀诗文及教材九年级中的毛泽东《词两篇》;古诗词赏析的考查篇目为《标准》附录推荐背诵的相应篇目;文言文阅读的考查,包括课内、课外两部分,课内阅读考查的具体篇目见附录;现代文阅读的考查,阅读材料均源于课外。
考试形式及试卷结构:闭卷考试。
考试时间150分钟。
满分150分,共三部分。
第一部分为积累与运用,主要题型为选择题、填空题和简答题,满分25分;第二部分为阅读理解,包括现代文阅读和文言文阅读,主要题型为选择题、填空题和简答题,满分为65分;第三部分为写作,满分60分。
积累与运用约占17%,阅读理解约占43%,写作约占40%.试卷中选择题分数不超过15%.试题易、中、难的比例约为6:2:2.名师点评点评人:东北育才学校初中部一级教师田美荣考纲分析:文言文难度增加今年考纲与去年相比,变化较大的是文言文和诗文的考查,文言文的难度增加。
中考数学--2006中考数学试题课标卷

)
A.①②④ B.②③④ C.①③④ D.①②③ 6.在一个不透明的口袋中,装有若干个除颜色不同其余都相同的球,如果口袋中装有 4 个红
1 球且摸到红球的概率为 , 个 D.3 个 7.小刚学习了有理数运算法则后,编了一个计算程序.当他输入任意一个有理数时,显示屏 上出现的结果总等于所输入的有理数的平方与1的和.当他第一次输入 −2 ,然后又将所得的 结果再次输入后,显示屏上出现的结果应是( )
1 中,自变量 x 的取值范围是 x−2
11.右图中阴影部分是一个正方体的表面展开平面图形的一部分,请你 在方格纸中补全这个正方体的表面展开平面图. (只填一种情形即可) 12 .如图, A,B,C 是⊙ O 上三点,∠ ACB=30 °,则∠ BAO 的度数 . 是
x − 2 > −1 13.不等式组 的解集为 3 x + 1 < 8
3.一鞋店试销一种新款女鞋,一周内各种型号的鞋卖出的情况如下表所示: 型号 数量(双) ) 22 3 22.5 5 23 10 23.5 15 24 8 24.5 4 25 2
对这个鞋店的经理来说,他最关注的是数据的( ) A.平均数 B.众数 C.中位数 D.极差 4.一个三角形的两边长为 3 和 6,第三边的边长是方程 ( x − 2)( x − 4) = 0 的根,则这个三角形 的周长是( ) A.11 B.11 或 13 C.13 D.11 和 13 5.李明设计了下面四种正多边形的瓷砖图案,用同一种瓷砖可以平面密铺的是(
.
14.已知二次函数 y = ax 2 + bx + c(a ≠ 0) ,其中 a b c
第 2 页 共 9 页
ERROR: limitcheck OFFENDING COMMAND: string STACK: 66038 33018 32512 33019
2006年中考数学(新课标)备考分析
11 数、 . 式运 算及 不等 式 解 法仍 然必 考
学 改革 进程 .新 课 标 )实验 区 中考 数 学试 题 体 现 (
了课 程 改革 的方 向 , 观 近两 年 课 改 实 验 区 中考 纵 数 学试 题 , 题 内容 进 一 步 突 出 了数 学 与 社 会 背 试 景及 学 生实 际 生 活 的联 系 , 加 注重 考 查 学 生 的 更
维普资讯
.
刊一 0① qt半 - 矧 0年∽ H
匿
是( )
2 4 重视 数形 结合 , 用 网格 线搭 桥 解题 . 巧
题 4 ( 0 5 山西 )如 图 , 方形 网格 中, 20 年 正 每
个 小 正 方 形 的边 长 为 1 则 网 ,
活 的联 系 , 聚焦 社 会热 点 ,
要 求 函数 的解 析 式 , 键 是 要 抓 住 图象 上 关 关
键 点 的坐标 .
2 传统 知 识点转 换 角度 是 “ 课标 ”的 出题特 点 新
2 1 重视 对 图形 特征 的观 察 、 想 、 明 . 猜 证 从生 活 实际 中探 究 出比例 、 相似 等 知识 点 题 1 ( 0 5年 山 20
下面 将根 据 以上对 近 年 的中考 ( 新课标 )的趋
势分 析 , 分类 透 视 中考各 部 分考 查 热点 , 希望 对读
者的中考复习有所帮助. 毕 业 要求类 试 题 各实验 区的中考数学毕业要求类试题在形式 上有许多创新 , 尤以新增的概率和图形变换突出,
东 )如 图 , 正 方 形 的 小 边 长 均 为 1 则 下 列 图 , 中 的 三 角 形 ( 影 部 阴 分)与 /AB 相 似 的 k C 题i
2006年全国中考数学压轴题全析全解2
2006年全国中考数学压轴题全解全析31、(辽宁沈阳卷)如图,在平面直角坐标系中,直线13y x =-+分别与x 轴,y 轴交于点A ,点B .(1)以AB 为一边在第一象限内作等边ABC △及ABC △的外接圆M (用尺规作图,不要求写作法,但要保留作图痕迹);(2)若M 与x 轴的另一个交点为点D ,求A ,B ,C ,D 四点的坐标;(3)求经过A ,B ,D 三点的抛物线的解析式,并判断在抛物线上是否存在点P ,使AD P △的面积等于ADC △的面积?若存在,请直接写出所有符合条件的点P 的坐标;若不存在,请说明理由.[解] (1)如图,正确作出图形,保留作图痕迹(2)由直线13y x =-+,求得点A的坐标为),点B 的坐标为()01,∴在Rt AOB △中,OA =1OB =2AB ∴=,tan OAOBA OB==∠60OBA ∴=∠9030OAB OBA ∴=-=∠∠ ABC △是等边三角形 2CA AB ∴==,60CAB =∠90CAD CAB OAB ∴=+=∠∠∠∴点C的坐标为),连结BMABC △是等边三角形 1302MBA ABC ∴==∠∠90OBM OBA MBA ∴=+=∠∠∠ OB BM ∴⊥∴直线OB 是M 的切线2OB OD OA ∴=213OD ∴=OD ∴=∴点D 的坐标为0⎫⎪⎪⎝⎭(3)设经过A ,B ,D 三点的抛物线的解析式是(y a x x ⎛= ⎝⎭把()01B ,代入上式得1a =∴抛物线的解析式是21y x =+ 存在点P ,使ADP △的面积等于ADC △的面积点P 的坐标分别为123P ⎛⎫⎪ ⎪⎝⎭,,223P ⎛⎫⎪ ⎪⎝⎭,. [点评]本题是一道综合性很强的压轴题,主要考查二次函数、一次函数、圆、几何作图等大量知识,第3小题是比较常规的结论存在性问题,运用方程思想和数形结合思想可解决。
32、(山东滨州卷)已知:抛物线2:(1)(2)M y x m x m =+-+-与x 轴相交于12(0)(0)A x B x ,,,两点,且12x x <.(Ⅰ)若120x x <,且m 为正整数,求抛物线M 的解析式; (Ⅱ)若1211x x <>,,求m 的取值范围;(Ⅲ)试判断是否存在m ,使经过点A 和点B 的圆与y 轴相切于点(02)C ,,若存在,求出m 的值;若不存在,试说明理由;(Ⅳ)若直线:l y kx b =+过点(07)F ,,与(Ⅰ)中的抛物线M 相交于P Q ,两点,且使12PF FQ =,求直线l 的解析式. [解] (Ⅰ)解法一:由题意得, 1220x x m =-<. 解得,2m <.m 为正整数,1m ∴=.21y x ∴=-.解法二:由题意知,当0x =时,20(1)0(2)0y m m =+-⨯+-<.(以下同解法一) 解法三:22(1)4(2)(3)m m m ∆=---=-,12(1)(3)122m m x x x m --±-∴=∴=-=-,,.又122020x x x m <∴=->,.2m ∴<.(以下同解法一.)解法四:令0y =,即2(1)(2)0x m x m +-+-=,12(1)(2)012x x m x x m∴++-=∴=-=-,,.(以下同解法三.) (Ⅱ)解法一:1212111010x x x x <>∴-<->,,,.12(1)(1)0x x ∴--<,即1212()10x x x x -++<.1212(1)2x x m x x m +=--=-,, (2)(1)10m m ∴-+-+<.解得 1m <.m ∴的取值范围是1m <.解法二:由题意知,当1x =时,1(1)(2)0y m m =+-+-<.解得:1m <.m ∴的取值范围是1m <.解法三:由(Ⅰ)的解法三、四知,1212x x m =-=-,.121121x x m <>∴->,,,1m ∴<.m ∴的取值范围是1m <. (Ⅲ)存在.解法一:因为过A B ,两点的圆与y 轴相切于点(02)C ,,所以A B ,两点在y 轴的同侧,120x x ∴>.由切割线定理知,2OC OA OB =, 即2122x x =.124x x ∴=,12 4.x x ∴=2 4.6m m ∴-=∴=.解法二:连接O B O C '',.圆心所在直线11222b m m x a --=-=-=, 设直线12mx -=与x 轴交于点D ,圆心为O ', 则122mO D OC O C OD -''====,.2132ABAB x x m BD =-==-=,, 32m BD -∴=.在Rt O DB '△中, 222O D D B O B ''+=.即22231222m m --⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭.解得 6m =.(Ⅳ)设1122()()P x y Q x y ,,,,则22112211y x y x =-=-,.过P Q ,分别向x 轴引垂线,垂足分别为112(0)(0)P x Q x ,,,.则11PP FO QQ ∥∥.所以由平行线分线段成比例定理知,11PO PF OQ FQ=.因此,120102x x -=-,即212x x =-. 过P Q ,分别向y 轴引垂线,垂足分别为2122(0)(0)P y Q y ,,,, 则22PP QQ ∥.所以22FP P FQ Q △∽△.22P F FPFQ FQ∴=. 127172y y -∴=-.12212y y ∴-=.22122211212(1) 1.2324 1.x x x x ∴--=-∴-=-21142x x ∴=∴=,,或12x =-.当12x =时,点(23)P ,.直线l 过(23)(07)P F ,,,,7032.k b k b =⨯+⎧∴⎨=⨯+⎩, 解得72.b k =⎧⎨=-⎩,当12x =-时,点(23)P -,.直线l 过(23)(07)P F -,,,,703(2).k b k b =⨯+⎧∴⎨=⨯-+⎩, 解得72.b k =⎧⎨=⎩,故所求直线l 的解析式为:27y x =+,或27y x =-+.[点评]本题对学生有一定的能力要求,涉及了初中数学的大部分重点章节的重点知识,是一道选拔功能卓越的好题。
2006年辽宁省十一市中等学校招生考试(非课改)
2006年辽宁省十一市中等学校招生考试语文试卷※考试时间150分钟,试卷满分150分。
卷面文字书写要求工整、清楚,标点正确。
一、积累与运用(满分30分)1.给下面这段话中加点字注音,并改正其中的两个..错别字。
(4分)()()追求成功犹.如开花结果,成功就是果实,追.求就是开花到结果前最美丽的过程。
成功固然辉皇,但追求不是更美得令人淘醉吗?改为改为2.下面两个句子中各有一处....语病,请将改正后的句子写在下面的空白处。
(2分)(1)由于加强了管理,我市的社会安全和隐患都有了保障。
(2)自从他上学那天起,就认真刻苦学习。
3.仿写一个比喻句,使之与前后两句构成一组排比句。
{分)诚信好像那黑夜中的明灯,失去它你将寸步难行;,;诚信好像那夏日的微风,失去它你将难当酷暑。
4.把下列相关的作家、作品、人物、情节用线连起来。
(4分)吴承恩《童年》孙悟空结识“好事情”高尔基《西游记》阿廖沙三打白骨精施耐庵《钢铁是怎样炼成的》林冲因宣传革命而被捕奥斯特洛夫斯基《水浒传》朱赫来风雪山神庙5.请根据你平时的积累,在横线上写出相应的名言(任选三题....,多答者按所答题的前三题计分)。
(3分)(1)人不应该被流言所左右,鲁迅曾说“无论如何‘流言’总不能吓哑我的嘴。
”但丁在他的《神曲》中更坚持“走自己的路,!”(2)华罗庚说:“勤能补拙是良训,。
”(3)司马迁在《史记》中曾说:“智者千虑,必有一失;,。
”(4)在今天和平幸福的生活环境中,我们要居安思危,正如孔子所说:“人无远虑,。
”6.文言诗文填空。
(11分)⑴安得广厦千万间,!⑵无可奈何花落去,。
⑶,波撼岳阳城。
⑷,化作春泥更护花。
⑸受任于败军之际,,尔来二十有一年矣。
⑹李白的《行路难》中让我们感受到诗人执着地追求理想的强大精神力量的诗句是:,。
⑺辛弃疾在《破阵子·为陈同甫赋壮词以寄之》中表达自己爱国激情和建功立业的雄心壮志的词句是:,。
⑻范仲淹在《岳阳楼记》中抒发自己的政治理想的句子是:,。
2006年辽宁省大连市中考数学试卷(大纲卷)
第1页(共24页)2006年辽宁省大连市中考数学试卷(大纲卷)、选择题(共8小题,每小题3分,满分24 分)I[7. (3分)某鞋店试销一种新款女鞋,销售情况如下表所示:鞋店经理最关心的是,哪种型 号的鞋销量最大•对他来说,下列统计量中最重要的是( ) 型号 22 22.5 23 23.5 24 24.5 25 数量(双) 351015 83 2A .平均数B .众数C .中位数D .方差& (3分)如图,点A 、B 、C 、D 、E 、F 、G 、H 、K 都是7X 8方格纸中的格点,为使△ DEMABC ,则点M 应是F 、G 、H 、K 四点中的()1.( 3分)在平面直角坐标系中,点 P (- 2, A .第一象限B .第二象限2. ( 3分)-a 的相反数是()3. ( 3分)下列各式运算正确的是( 2 3 5 A . a +a = a 2小3 5B . a ?a = a 4. ( 3分)计算一一的结果是( )A . 6B .--3 )在()C .第三象限D .第四象限C . - aD . -2、3C . (ab ) = ab10 2 5D . a * a = aC . 2D .余下部分的展开图为 ( )在对称轴处剪下一块, 5. (3分)如图,将矩形沿对称轴折叠,、填空题(共7小题,每小题3分,满分21 分)9. ( 3分)今年4月某天的最高气温为 8C,最低气温为 2 C,则这天气温t C 的t 的取值范围是 _______10. (3 分)在 Rt △ ABC 中,/ C = 90°, AB = 5, AC = 4,贝U si nA 的值为 : _ I_I _____ I_I_I_I ________ I _I_I_l_^ -3 -2 -1 0 1 2 3 4 5 6 714. (3 分) 用计算器计算:,,…,请你猜测.的结果为个 个 个15. (3 分) 如图是二次函数2y i = ax +bx+c 和一次函数 y 2= mx+n 的图象,观察图象写出y 2> y i 时, x 的取值范围第2页(共24页)C . H,AC = 3,则厶ABC 的周长为216. (9分)已知关于x的方程x +kx- 2 = 0的一个解与方程解相同.(1 )求k的值;(2)求方程x +kx-2 = 0的另一个解.17. ( 9分)某校初二年级全体320名学生在电脑培训前后各参加了一次水平相同的考试,考分都以统一标准划分为“不合格”“合格” “优秀”三个等级.为了了解电脑培训的效果,用抽签方式得到其中32名学生的两次考试考分等级,所绘制的统计图如图所示.试根据统计图提供的信息回答下列问题:(1 )这32名学生培训前考分的中位数所在的等级是 ___________,培训后考分的中位数所在等级是_______ .(2)________________________________________________________ 这32名学生经过培训,考分等级“不合格”的百分比由_____________________________________ 下降到 ________ .(3)_____________________________________________________________________ 估计该校整个初二年级中,培训后考分等级为“合格”与“优秀”的学生共有 _________________ 名.(4)你认为上述估计合理吗?理由是什么?30 r18. (10分)已知:如图,四边形ABCD是菱形,E是BD延长线上一点,F是DB延长线上一点,且DE = BF .请你以F为一个端点,和图中已标明字母的某一点连成一条新的线段,猜想并证明它和图中已有的某一条线段相等(只须证明一组线段相等即可) .(1)___________ 连接(2)猜想:_________19. (10分)如图,是一个8X 10正方形格纸,△ ABC中A点坐标为(-2, 1).(1 )△ ABC和厶A' B' C '满足什么几何变换;(直接写答案)(2)作厶A' B ' C'关于x轴对称图形△ A” B〃C〃;(3)△ ABC和厶A〃B” C〃满足什么几何变换?求A”、B〃、C〃三点坐标(直接写答案).20. (10分)在围棋盒中有x颗黑色棋子和y颗白色棋子,从盒中随机地取出一个棋子,如果它是黑色棋子的概率是 -.(1)试写出y与x的函数关系式.(2)若往盒中再放进10颗黑色棋子,则取得黑色棋子的概率变为-,求x和y的值.21. (7分)如图,直线y= k和双曲线y -相交于点P,过P点作PA0垂直x轴,垂足为A0, x轴上的点A o、A1、A2、…A n的横坐标是连续的整数,过点A1、A2、…A n分别作x 轴的垂线,与双曲线y - (x> 0)及直线y= k分别交于点B1、B2、…B n, 6、C2、… ?n.(1 )求A o点坐标;(2 )求 ---- 及----- 的值;22.(8分)A 玉米试验田是边长为 a 米的正方形减去一个边长为1米的正方形蓄水池后余下部分,B 玉米试验田是边长为(a - 1)米的正方形,两块试验田的玉米都收获了 500千克.(1 )哪种玉米的单位面积产量高?(2 )高的单位面积产量是低的单位面积产量的多少倍?23. (8分)如图①、②、③中,点E 、D 分别是正厶ABC 、正四边形 ABCM 、正五边形 ABCMN 中以C 点为顶点的相邻两边上的点,且BE = CD , DB 交AE 于P 点.(1 )求图①中,/ APD 的度数 ________ ;(2) 图②中,/ APD 的度数为 ______ ,图③中,/ APD 的度数为 _________ ;(3) 根据前面探索,你能否将本题推广到一般的正 n 边形情况?若能,写出推广问题和 结论;若不能,请说明理由.24. (12分)如图,在大连到烟台 160千米的航线上,某轮船公司每天上午8点(x 轴上0小时)到下午16点每隔2小时有一只轮船从大连开往烟台,同时也有一只轮船从烟台开往大连,轮船在途中花费 8小时,求:今天上午 8点从大连开往烟台的轮船在航行途中(不包括大连和烟台)遇到几只从对面开来的本公司的轮船,在遇到第三只从对面开来 的本公司1 C l C2 …Q\Bn1…X(3)试猜想的值.(直接写答案)轮船时的时间及离大连的距离.乱小时》225. (12分)如图,抛物线 E : y = x+4x+3交x 轴于A 、B 两点,交y 轴于M 点,抛物线E 关于y 轴对称的抛物线 F 交x 轴于C 、D 两点.(1 )求F 的解析式;(2)在x 轴上方的抛物线 F 或E 上是否存在一点 N ,使以A 、C 、N 、M 为顶点的四边26. (10分)如图1 , Rt A ABC 中AB = AC ,点D 、E 是线段 AC 上两动点,且 AD = EC , AM 垂直BD ,垂足为M , AM 的延长线交BC 于点N ,直线BD 与直线NE 相交于点F .试判 断厶DEF 的形状,并加以证明. 说明:(1)如果你经历反复探索,没有找到解决问题的方法,请你把探索过程中的某种 思路写出来(要求至少写 3步);(2)在你经历说明(1)的过程之后,可以从下列 ①、 ②中选取一个补充或者更换已知条件,完成你的证明.1、 画出将△ BAD 沿BA 方向平移BA 长,然后顺时针旋转 90°后图形;2、点K 在线段BD 上,且四边形 AKNC 为等腰梯形(AC // KN ,如图2).附加题:如图3,若点D 、E 是直线AC 上两动点,其他条件不变,试判断△ DEF 的形状, 并说明理由.杠(千米}4610 I- H 10形是平行四边形?若存在,求点N 的坐标;若不存在,请说明理由;2006年辽宁省大连市中考数学试卷(大纲卷)参考答案与试题解析、选择题(共8小题,每小题3分,满分24 分)(3分)在平面直角坐标系中,点 P (- 2,- 3 )在( )A .第一象限 B. 第二象限 C. 第三象限 D. 第四象限•••点P ( - 2, - 3)在第三象限. 故选:C .故选:A .23【解答】解:A 、a 与a 不是同类项,不能直接合并,故本选项错误; B 、a 2?a 3= a 5,计算正确,故本选项正确;C 、 (ab 2) 3= a 3b 6,原式计算错误,故本选项错误;10D 、 a 故选:【解答】解:•••点P 的横坐标-2 V 0, 纵坐标为-3V 0, 1.2. (3分)-a 的相反数是(【解答】解:根据相反数的概念,得- 的相反数是a .3.(3分)下列各式运算正确的是( 235A . a +a = aB . a 2?a 3= a 5C . (ab 2) 3= ab 6D . a 10十 a 2= a 5十 a 2= a 8,原式计算错误,故本选项错误;4(3 分) 计算的结果是(.C. 2【解答】解:故选:D.5(3分)如图, 将矩形在对称轴处剪下一块,余下部分的展开图为().IC . _____ L_【解答】解:根据对称的性质,可得余下部分的展开图为D ,故选D .【解答】解:•••/ PQR 等于138 ° , QT 丄PQ ,•••/ PQS = 138° - 90°= 48°, 又••• SQ 丄 QR , •••/ PQT = 90 ° , •••/ SQT = 42°. 故选:A .7. (3分)某鞋店试销一种新款女鞋,销售情况如下表所示:鞋店经理最关心的是,哪种型 号的鞋销量最大•对他来说,下列统计量中最重要的是( ) 型号 22 22.5 23 23.5 24 24.5 25 数量(双) 351015 83 2A .平均数B .众数C .中位数D .方差【解答】解:鞋店经理最关心的是,哪种型号的鞋销量最大,而众数是数据中出现次数 最多的数,故鞋店经理关心的是这组数据的众数. 故选:B .& (3分)如图,点A 、B 、C 、D 、E 、F 、G 、H 、K 都是7X 8方格纸中的格点,为使△ DEMABC ,则点M 应是F 、G 、H 、K 四点中的()SQ 丄QR , QT 丄PQ .则/ SQT 等于(C . 48°D . 24°A .6.C. H【解答】解:根据题意,△ DEM s\ ABC, AB= 4, AC = 6 DE = 2••• DE : AB= DM : AC•DM = 3•M应是H故选:C.二、填空题(共7小题,每小题3分,满分21分)9. (3分)今年4月某天的最高气温为8C,最低气温为2 C,则这天气温t C的t的取值范围是 2 w t w 8【解答】解:因为最低气温是2C,所以2w t,最高气温是8C, t w 8,则今天气温t(C)的范围是2w t w 8.故答案为:2w t w &10. (3 分)在Rt △ ABC 中,/ C= 90°, AB = 5, AC= 4,贝U si nA 的值为一AB= 5, AC= 4,【解答】解:根据题意画出图形如图所示:• BC= 3.贝U sinA -.11. (3分)如图,在O O中,/ ACB =/ D = 60°, AC = 3,则厶ABC的周长为9【解答】解:•••/ ACB =Z D = 60°,/ D = Z A•••/ A=/ ACB= 60 °•••/ ABC= 60 °•△ ABC是等边三角形•△ ABC 的周长=3AC= 9.故答案为:912. (3分)如图,AB是O O的切线,OB = 2OA,则/ B的度数是30 度.【解答】解:I AB是O O的切线,•OA 丄AB,•/ OB= 2OA,•••/ B= 30°.13. (3分)在如图的数轴上,用点A大致表示—.请参考答图.-3 -2 -1 0 1 2 3 4 5 6 7【解答】解:•••—<—<—,•- 6 V V 7.•••点A在6和7之间均正确.h I I I I I I I I 寸了-3 -2 -1 0 1 2 3 4 5 6 714. (3分)用计算器计算:, ,,…,请你猜测. 的结果为10n.【解答】解:根据题意可知原式10n.215. (3分)如图是二次函数y i = ax+bx+c和一次函数y2= mx+n的图象,观察图象写出y2【解答】解:T y i与y的两交点横坐标为-2, 1,当y2》y1时,y2的图象应在的图象上面,即两图象交点之间的部分,二此时x的取值范围是-2w x W 1.三、解答题(共11小题,满分105分)216. (9分)已知关于x的方程x +kx- 2 = 0的一个解与方程解相同.(1 )求k的值;2(2)求方程x +kx-2 = 0的另一个解.【解答】解:(1)由——解得x = 2,经检验x= 2是方程的解.把x = 2代入方程x2+kx- 2 = 0,得:22+2k- 2= 0,解得:k=- 1;(2)由(1)知方程x2+kx- 2= 0 化为:x2- x - 2 = 0,方程的一个根为2,则设它的另一根为X2,则有:2x2 =- 2• I X2=- 1 .17. (9分)某校初二年级全体320名学生在电脑培训前后各参加了一次水平相同的考试,考分都以统一标准划分为“不合格”“合格” “优秀”三个等级.为了了解电脑培训的效第12页(共24页)第13页(共24页)果,用抽签方式得到其中32名学生的两次考试考分等级,所绘制的统计图如图所示•试根据统计图提供的信息回答下列问题:(1 )这32名学生培训前考分的中位数所在的等级是不合格,培训后考分的中位数所在等级是合格•(2)这32名学生经过培训,考分等级“不合格”的百分比由75% 下降到25% •(3)估计该校整个初二年级中,培训后考分等级为“合格”与“优秀”的学生共有240 名.(4)你认为上述估计合理吗?理由是什么?■ 培训前训后【解答】解:(1) 32个数据的中位数应是第16个和第17个数据的平均数,则这32名学生培训前考分的中位数所在的等级是不合格,培训后考分的中位数所在等级是合格;(2)培训前考分等级“不合格”的百分比为24十32= 75% ;培训后考分等级“不合格”的百分比为8-32= 25%;(3)培训后考分等级为“合格”与“优秀”的学生共有( 1 - 25% )X 320 = 240 (人);(4)合理,该样本是随机样本(或该样本具有代表性)18. (10分)已知:如图,四边形ABCD是菱形,E是BD延长线上一点,F是DB延长线上一点,且DE = BF .请你以F为一个端点,和图中已标明字母的某一点连成一条新的线段,猜想并证明它和图中已有的某一条线段相等(只须证明一组线段相等即可) •(1)连接AF ;(2)猜想:AF = AE ;(3)证明:(说明:写出证明过程的重要依据)A/V7V【解答】解:(1)如图,连接AF;(2)AF = AE;(3)证明:四边形ABCD是菱形.••• AB= AD ,•••/ ABD = Z ADB ,•••/ ABF = Z ADE ,在厶ABF和厶ADE中• △ ABF◎△ ADE ,19. (10分)如图,是一个8X 10正方形格纸,△ ABC中A点坐标为(-2, 1).(1 )△ ABC和厶A B' C '满足什么几何变换;(直接写答案)(2)作厶A' B ' C'关于x轴对称图形△ A” B〃C〃;(3)△ ABC和厶A〃B” C〃满足什么几何变换?求A〃、B〃、C〃三点坐标(直接写答案).(1)轴对称变换;(2 分)(2)图形正确(A ”、B ”、C 〃三点对一个点得1 分) ; ( 5 分)(3 )中心对称变换,(7分)20. (10分)在围棋盒中有 x 颗黑色棋子和y 颗白色棋子,从盒中随机地取出一个棋子,如 果它是黑色棋子的概率是 -(1)试写出y 与x 的函数关系式.(2)若往盒中再放进10颗黑色棋子,则取得黑色棋子的概率变为-,求x 和y 的值.坐标为 A "( 2,- 1)、B "( 1,-2)、C 〃( 3,【解解:【解答】解:(1)根据题意得:一 -,(3分)5x= 3y,;(5 分)整理,得8x= 3x+3y, (4 分)整理,得2x+20 = x+y+10,y= x+10, (8 分)5x= 3 (x+10),x= 15, y= 25.解法二:(2 )根据题意,可得,整理得,解得.(8分)21. (7分)如图,直线y= k和双曲线y -相交于点P,过P点作PA o垂直x轴,垂足为A0, x轴上的点A o、A i、A2、…A n的横坐标是连续的整数,过点A l、A2、…A n分别作x 轴的垂线,与双曲线y - (x> 0)及直线y= k分别交于点B i、B2、…B n, C i、C2、… ?n.(1 )求A o点坐标;(2 )求-- 及----- 的值;(3)试猜想----- 的值.(直接写答案)(2)解法一:根据题意,得(7 分)【解答】解:(1)依题意得点A o坐标满足x= 1,•••点A o坐标为(1, 0);第22页(共24页)•••高的单位面积产量是低的单位面积产量的倍.(2)由于A o、A i、A2点的横坐标为连续整数,••• A i、A2 点的坐标为(2, 0)、( 3, 0).(3)——.22. (8分)A玉米试验田是边长为a米的正方形减去一个边长为1米的正方形蓄水池后余下部分,B玉米试验田是边长为(a - 1)米的正方形,两块试验田的玉米都收获了500千克.(1 )哪种玉米的单位面积产量高?(2 )高的单位面积产量是低的单位面积产量的多少倍?【解答】解:(1) A玉米试验田面积是(a2- 1 )米2,单位面积产量是——千克/米2;B玉米试验田面积是(a- 1) 2米2,单位面积产量是------------- 千克/米2;2 2•/ a2- 1-( a- 1) 2= 2 (a- 1)2 2•/ a - 1>0,二0<( a - 1) < a2- 1•----- < --------•B玉米的单位面积产量高;(2) ---------- ----------23. (8分)如图①、②、③中,点E、D分别是正厶ABC、正四边形ABCM、正五边形ABCMN 中以C点为顶点的相邻两边上的点,且BE = CD , DB交AE于P点.(1 )求图①中,/ APD的度数60°;(2)图②中,/ APD的度数为90°,图③中,/ APD的度数为108°;(3)根据前面探索,你能否将本题推广到一般的正n边形情况?若能,写出推广问题和结论;若不能,请说明理由.【解答】解:(1)v^ ABC是等边三角形,• AB= BC ,Z ABE = Z BCD = 60°•/ BE= CD ,• △ ABE◎△ BCD .E匚•••/ BAE =Z CBD .•••/ APD = Z ABP+Z BAE = Z ABP+Z CBD = Z ABE = 60(2)同理可证:△ ABE也厶BCD ,•Z AEB+Z DBC = 180°- 90°= 90°,•Z APD = Z BPE = 180°- 90°= 90°;△ ABE◎△ BCD ,•Z AEB+Z DBC = 180°- 108°= 72 ° ,•Z APD = Z BPE = 180°-(Z AEB+ Z DBC)= 180°- 72°= 108° .第24页(共24页)•••高的单位面积产量是低的单位面积产量的倍.(3)能.如图,点E、D分别是正n边形ABCM中以C点为顶点的相邻两边上的点, 且BE = CD, BD与AE交于点P,则Z APD的度数为------------- .24. (12分)如图,在大连到烟台160千米的航线上,某轮船公司每天上午8点(x轴上0小时)到下午16点每隔2小时有一只轮船从大连开往烟台,同时也有一只轮船从烟台开往大连,轮船在途中花费8小时,求:今天上午8点从大连开往烟台的轮船在航行途中(不包括大连和烟台)遇到几只从对面开来的本公司的轮船,在遇到第三只从对面开来【解答】解:由图象可知,今天上午8点从大连开往烟台的轮船在航行中遇到4只从对面开来的本公司轮船;由图象可知,A点坐标为(8,160),B点坐标为(4, 160),C点坐标为(12,0)设直线OA的解析式为y= kx,•••160= 8k,••• k= 20,•直线OA的解析式为y= 20x设直线BC的解析式y = mx+ n,• y=- 20x+240•••今天上午8点从大连开往烟台的轮船在航行途中遇到第三只从对面开来的本公司轮船的时间和•••高的单位面积产量是低的单位面积产量的 倍.第26页(共24页)离大连的距离分别为 14点和120千米. 第19页(共24页)225. (12分)如图,抛物线E: y= x+4x+3交x轴于A、B两点,交y轴于M点,抛物线E 关于y轴对称的抛物线F交x轴于C、D两点.(1 )求F的解析式;(2)在x轴上方的抛物线F或E上是否存在一点N,使以A、C、N、M为顶点的四边形是平行四边形?若存在,求点N的坐标;若不存在,请说明理由;2(3)若将抛物线E的解析式改为y= ax +bx+c,试探索问题(2).【解答】解:(1)解法一:当y= 0时,x2+4x+3 = 0,解得X1=- 3, X2=- 1,••• A、B 点坐标分别为(-3, 0)、(- 1, 0);当x = 0 时,y= 3,•M点坐标为(0, 3) , A、B、M三点关于y轴得对称点分别是D、C、M ,•D、C 坐标为(3, 0)、(1, 0);2设F的解析式为y= ax +bx+3,则有:,•・ a = 1, b=—4•抛物线F的解析式为y= x - 4x+3.解法二:•••抛物线E与抛物线F关于y轴对称,且抛物线E: y= x2+4x+3,2 2•抛物线F 的方程是:y=( - x) +4 x( - x) +3 = x - 4x+3,即抛物线F的解析式为y= x2- 4x+3 ;(2)存在.假设MN // AC,•N点的纵坐标为3.2若在抛物线F上,当y= 3时,3= x - 4x+3,贝U X1= 0, x2= 4•N点坐标为(4, 3),••• MN = 4,由(1)可求AC = 4,•MN = AC,•四边形ACNM为平行四边形.根据抛物线F和E关于y轴对称,故N点坐标为(4, 3)或(-4, 3).(3)存在•假设MN // AC,•N点的纵坐标为c.设y = 0,. 2--ax + bx+ c= 0•A点坐标为(------------- ,0),B点坐标为(,0)•C点坐标为(------------ ,0),•AC -2在抛物线 E 上,当y = c 时,c= ax +bx+c , x i = 0 , X2 —•N点坐标为(-,c)NM = 0-( -)-,•NM = AC ,•四边形ACMN为平行四边形.根据抛物线F和E关于y轴对称,故N点坐标为(-,c)或(—,c).26. (10分)如图1 , Rt A ABC中AB = AC ,点D、E是线段AC上两动点,且AD = EC, AM 垂直BD,垂足为M , AM的延长线交BC于点N,直线BD与直线NE相交于点F.试判断厶DEF的形状,并加以证明.说明:(1)如果你经历反复探索,没有找到解决问题的方法,请你把探索过程中的某种思路写出来(要求至少写3步);(2)在你经历说明(1)的过程之后,可以从下列①、②中选取一个补充或者更换已知条件,完成你的证明.1、画出将△ BAD沿BA方向平移BA长,然后顺时针旋转90°后图形;2、点K在线段BD上,且四边形AKNC为等腰梯形(AC// KN,如图2).附加题:如图3,若点D、E是直线AC上两动点,其他条件不变,试判断△ DEF的形状,并说明理由.【解答】解:△ DEF是等腰三角形证明:如图,过点C作CP丄AC,交AN延长线于点P•/ Rt△ ABC 中AB= AC•••/ BAC= 90。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C.在7和8之间
D.在8和9之间
2006年辽宁省沈阳市中考数学试题(课改实验区)
考试时间120分钟,试题满分150分
6.下列事件:(1)阴天会下雨;(2 )随机掷一枚均匀的硬币,正面朝上; 有两人的出生月份相同;(4) 2008年奥运会在北京举行.其中不确定事件有( )
7.估算.24 3的值(
)
A.在5和6之间
B.在6和7之间1. 2.
、选择题(每小题
3分, F 列物体中, 主视图为图
A. B.
共 24 分) 1的是(
F 列计算中,
正确的是( a 34 =a 7
a 4 a 3 = a
4
C. (-a)
(-a)3 二 a 7
D. a 5 + a 3 二 a 2
D. 4个
D. 8
5. 把不等式组
“一4》0的解集表示在数轴上,
6 - x , 3
正确的是(
(3) 12名同学中,
A. 1个
B. 2个
C. 3个
D. 4个
)
7
A.
B
C. 6 A. 1 B. 5
&已知点I 为△ ABC 的内心,Z BIC =130:,则/ BAC 的度数是( A. 65 B . 75
C. 80
D. 100:
二、填空题(每小题 3分,共24分) 9. 2006年是我国公民义务植树运动开展 个数字可以用科学记数法表示为
10•分解因式: 2x 2 - 4x - 2工 ___________ . 11•如图3,已知△
ABC 的一边BC 与以AC 为直径的
O 相切于点C ,若BC = 4, AB = 5 ,则 c oBs= _____ .
k _3
12.如果反比例函数y
的图象位于第二、四象限内,
X
那么满足条件的正整数 k 的值是 __________ .
13•已知等腰三角形 ABC 中,AB 二AC , D 为BC 边上一点, 连接AD ,若△
ACD 和△ ABD 都是等腰三角形,则 Z C 的度
数是 _________ .
14.如图 4,已知△ ABC DBE , AB =6, DB =8,则 S A
ABC :
S A
DBE 二 -------- .
15.
观察下列等式:21 =2,22 =4,23 =8,24 =16 , 2^32,26 = 64 ,
27 =128 ,…….通 过观察,用你所发现的规律确定 _____________ 22006的个
位数字是
___________________________
16. 如图5,已知在O O 中,直径MN -10,正方形ABCD 的四个 顶点分别在半径 OM , OP 以及O O 上,并且Z POM -45,则AB
图5 的长为
_______________ .
三、(第17小题6分,第18、19小题各8分,第20小题10分,共32分) 仃. 计算:(―3),+曲 _1 _2巨—(J© _3)0 . 18.
先化简,再求值:(x * 1 -」5
)"匕彳,其中x =5、2 - 4 .
25周年,25年来我市累计植树 154000000株,这 株.
图3
X-1 X-1
19.如图6,在方格纸(每个小方格都是边长为1
个单位长度的正方形)中,我们称每个小正方形的顶点为格点,以格点为
△ ABC称为格点顶点的图形称为格点图形.如图6中的
厂目男读者 |女读者
(1)如果A D 两点的坐标分别是(1,)和(0, _ 1),请你在方格纸中建立平面直角坐标系,
并直接写出点B ,点C 的坐标;
(2)请根据你所学过的平移、旋转或轴对称等知识,说明图 6中“格点四边形图案”是如
何通过“格点 △ ABC 图案”变换得到的.
20•—个不透明的袋子中装有三个完全相同的小球,分别标有数字
3, 4, 5 •从袋子中随机
取出一个小球,用小球上的数字作为十位上的数字,然后放回,再取出一个小球,
用小球上
的数字作为个位上的数字, 这样组成一个两位数. 试问:按这种方法能组成哪些两位数?十 位上的数字与个位上的数字之和为 9的两位数的概率是多少?用列表法或画树状图法加以
说明.
四、(每小题10分,共20分)
21 •某工程队在我市实施棚户区改造过程中承包了一项拆迁工程, 原计划每天拆迁1250m 2,
因为准备工作不足,第一天少拆迁了
20%从第二天开始,该工程队加快了拆迁速度,第三
2
天拆迁了 1440m • 求:(1 )该工程队第一天拆迁的面积;
(2)若该工程队第二天、第三天每天的拆迁面积比前一天增长的百分数相同,求这个百分 数.
22 •学校鼓励学生参加社会实践,小萌所在班级的研究性学习小组在假期对她们所在城市的 一家晚报的读者进行了一次问卷调查,
以便了解读者对该种报纸四个版面的喜欢情况.
她们
调查了男女读者各 500名,要求每个读者选出自己最喜欢的一个版面, 并将得到的数据绘制
了下面尚未完成的统计图.
百分比(%)
(1) 请直接将图7所示的统计图补充完整;
(2) 请分别计算出喜欢各版面的总人数,并根据计算结果利用图 8画出折线统计图;
(3 )请你根据上述统计情况,对该报社提出一条合理化建议. 五、(12分)
23•如图9,某市郊外景区内一条笔直的公路
a 经过三个景点
A B , C •景区管委会又开发了风景优美的景点 D •经测量景 点D 位
于景点A 的北偏东30方向8km 处,位于景点B 的正北方 向,还位于景点 C 的北偏西75方向上•已知 AB = 5km •
(1 )景区管委会准备由景点 D 向公路a 修建一条距离最短的公路,不考虑其他因素,求出 这条公路的长.(结果精确到0.1km )
(2)求景点C 与景点D 之间的距离.(结果精确到1km )
(参考数据:3 =1.73 , 、. 5 =2.24 , sin 53;二 cos37:二 0.80, sin 37:二 cos53° 二
0.60,
tan53 =1.33, tan 37 =0.75 , sin 38; =cos52 =0.62 , sin 52; = cos38 = 0.79 , tan38 =0.78, tan 52, =1.28 , sin75; = 0.97, cos75‘; =0.26, tan75‘: =3.73 .)
六、(12分)
24 •某企业信息部进行市场调研发现: 信息一:如果单独投资 A 种产品,则所获利润
y A (万元)与投资金额 x (万元)之间存在
正比例函数关系: y A 二kx ,并且当投资5万元时,可获利润 2万元. 信息二:如果单独投资
B 种产品,则所获利润 y B (万元)与投资金额 x (万元)之间存在
2
二次函数关系:y B =ax bx ,并且当投资2万元时,可获利润 2.4万元;当投资4万元
人数
■t
版面
生活版
OOOOOOOOO 05050505 4 3 3 2 2 11
C
北
B
A
东D
时,可获利润 3.2万元.
(1 )请分别求出上述的正比例函数表达式与二次函数表达式;
(2)如果企业同时对 A, B 两种产品共投资10万元,请你设计一个能获得最大利润的投资 方案,并求出按此方案能获得的最大利润是多少? 七、(12分)
25.如图10,在正方形 ABCD 中,点E, F 分别为边BC, CD 的中点,AF ,DE 相交于 点G ,则可得结论:① AF =DE •,②AF _ DE .(不需要证明)
(1) 如图11,若点E , F 不是正方形 ABCD 的边BC , CD 的中点,但满足 CE =DF , 则上面的结论①,②是否仍然成立?(请直接回答“成立”或“不成立”
)
(2) 如图12,若点E , F 分别在正方形 ABCD 的边CB 的延长线和 DC 的延长线上,且
CE =DF ,此时上面的结论 1, 2是否仍然成立?若成立,请写出证明过程,若不成立, 请说明理
由. (3)
如图13 ,在(2 )的基础上,连接AE 和EF ,若点M , N, P Q 分别为
中的哪一种?并写出证明过程.
八、(14分) 26.如图14,在平面直角坐标系中,两个全等的直角三角形的直角顶点及一条直角边重合, 点A 在第二象限内,点 B ,点C 在x 轴的负半轴上,Z CAO =30[ 0A =4 . (1) 求点C 的坐标; (2) 如图15,将厶
ACB 绕点C 按顺时针方向旋转 30到厶A CB 的位置,其中 A C 交直 线0A
于点E , A B 分别交直线 OA CA 于点F , G ,则除△ A B C AOC 外,还有 哪几对全等的三角形,请直接写出答案; (不再另外添加辅助线)
AE, EF
FD A 的中点,请判断四边形 MNPQ 是“矩形、菱形、正方形、等腰梯形”
C
F
P
C F
4
x
(3)在(2)的基础上,将厶
ACB •绕点C 按顺时针方向继续旋转, 当△ COE 的面积为
时,求直线CE 的函数表达式.
图14。
