向量乘法小题,基础。高一数学

合集下载

人教版高中数学必修第二册6.2.3 向量的数乘运算同步精练(含解析)

人教版高中数学必修第二册6.2.3向量的数乘运算同步精练【考点梳理】考点一向量数乘的定义实数λ与向量a 的积是一个向量，这种运算叫做向量的数乘，记作λa ，其长度与方向规定如下：(1)|λa |＝|λ||a |.(2)λa (a ≠0)的方向当λ>0时，与a 的方向相同；当λ<0时，与a 的方向相反.特别地，当λ＝0时，λa ＝0.，当λ＝－1时，(－1)a ＝－a .考点二向量数乘的运算律1.(1)λ(μa )＝(λμ)a .(2)(λ＋μ)a ＝λa ＋μa .(3)λ(a ＋b )＝λa ＋λb .特别地，(－λ)a ＝－λa ＝λ(－a )，λ(a －b )＝λa －λb .2.向量的线性运算向量的加、减、数乘运算统称为向量的线性运算，对于任意向量a ，b ，以及任意实数λ，μ1，μ2，恒有λ(μ1a ±μ2b )＝λμ1a ±λμ2b .考点三向量共线定理向量a (a ≠0)与b 共线的充要条件是：存在唯一一个实数λ，使b ＝λa .【题型归纳】题型一：向量的线性运算1．（2021·山东邹城·高一期中）已知向量a ，b ，实数m ，n （0m ≠，0n ≠），则下列关于向量的运算错误的是（）A ．()m a b ma mb -=-B ．()m n a ma na -=-C ．若0ma =，则0a =D ．若ma na =，则m n=2．（2021·全国·高一课前预习）若a b c =+，化简()()()32232a b b c a b +-+-+的结果为（）A ．a-B ．4b-C ．cD ．a b-3．（2021·四川省蒲江县蒲江中学高一阶段练习）已知m ，n 是实数，a ，b 是向量，则下列命题中正确的为（）①()m a b ma mb -=-；②()m n a ma na -=-；③若ma mb =，则a b =；④若ma na =，则m n =．A ．①④B ．①②C ．①③D ．③④题型二：平面向量的混合运算4．（2021·全国·高一课时练习）若O 为ABC 所在平面内一点，且满足()(2)0OB OC OB OC OA -⋅+-=，则ABC 的形状为（）A ．等腰三角形B ．直角三角形C ．正三角形D ．等腰直角三角形5．（2021·福建福州·高一期中）在五边形ABCDE 中EB a =，AD b =，M ，N 分别为AE ，BD 的中点，则MN =（）A ．3122a b+B ．2133a b+C ．1122a b+D ．3144a b+6．（2020·全国·高一课时练习）在△ABC 中，P ，Q 分别是边AB ，BC 上的点，且11,.33AP AB BQ BC ==若AB a =，AC b =，则PQ ＝（）A ．1133a b+B ．1133a b-+C ．1133a b-D ．1133a b--题型三：向量的线性运算的几何应用7．（2021·四川·宁南中学高一阶段练习（文））如图，ABC 中，AD 、BE 、CF 分别是BC 、CA 、AB 上的中线，它们交于点G ，则下列各等式中不正确．．．的是（）A ．23BG BE =B ．12DG AG =；C ．121332DA FC BC +=uu u r uu u r uu u r D ．2CG FG=-8．（2021·四川资阳·高一期末）如图，在ABC 中，D 为线段BC 上一点，2CD DB =，E 为AD 的中点．若AE AB AC λμ=+，则λμ+=（）A ．14B ．13C ．12D ．239．（2021·内蒙古·林西县第一中学高一期中（文））已知点M 是ABC 的边BC 的中点，点E 在边AC 上，且2EC AE =，则向量EM =（）A ．1123AC AB +B ．1162AC AB +C ．1126AC AB +D ．1263AC AB +题型四：三角形的心的向量表示10．（2021·陕西渭滨·高一期末）已知O 为三角形ABC 所在平面内一点，0OA OB OC ++=，则:OBCABCS S=（）A ．12B ．13C ．14D ．1511．（2021·山东师范大学附中高一期中）如图，O 是ABC 的重心，AB a =，AC b =，D 是边BC 上一点，且4BD DC =，则（）A ．271515OD a b =-+B ．271515OD a b =-C ．271515OD a b =--D ．271515OD a b =+12．（2021·全国·高一课时练习）已知点O 、N 、P 在ABC 所在平面内，且||||||OA OB OC ==，0NA NB NC ++=，PA PB PB PC PC PA ⋅=⋅=⋅uu u r uu u r uu u r uuu r uuu r uu u r，则点O 、N 、P 依次是ABC 的（）A ．重心、外心、垂心B ．重心、外心、内心C ．外心、重心、垂心D ．外心、重心、内心【双基达标】一、单选题13．（2021·全国·高一课时练习）下列运算正确的个数是（）①()326a a -⋅=-；②()()223a b b a a +--=；③()()220a b b a +-+=．A ．0B ．1C ．2D ．314．（2021·全国·高一课时练习）已知O 是平面上的一定点，A ，B ，C 是平面上不共线的三个动点，若动点P 满足=+()OP OA AB AC λ→→→→+，()0,λ∈+∞，则点P 的轨迹一定通过ABC 的（）A ．内心B ．外心C ．重心D ．垂心15．（2021·全国·高一课时练习）若23AB BC =-，则下列各式中不正确的是（）．A ．32CB AB =B ．2BA AC=C ．13CA BC=-D ．12AC AB =16．（2021·上海·高一课时练习）已知平面上不共线的四点,,,O A B C ，若430OA OB OC -+=，则AB BC等于（）A ．13B ．12C ．3D ．217．（2021·全国·高一课时练习）设向量1OA e =，2OB e =，若1e 与2e 不共线，且点P 在线段AB 上，:2AP PB =，则OP =（）A ．121233e e -B ．122133e e +C ．121233e e +D ．122133e e -18．（2021·安徽·定远县育才学校高一阶段练习（文））下列叙述不正确的是（）A ．若,a b 共线，则存在唯一的实数λ，使λa b =．B ．3b a =(a 为非零向量)，则,a b 共线C ．若334,22m a b n a b =+=+，则//m nu r r D ．若0a b c ++=，则a b c+=-19．（2021·福建浦城·高一阶段练习）如图，在△ABC 中，AN ＝23NC ，P 是BN 上一点，若AP ＝t AB ＋13AC ，则实数t 的值为（）．A ．16B ．13C ．23D ．5620．（2021·云南隆阳·高一期中）已知在平行四边形ABCD 中，点E ，F 分别在边AB ，AD 上，连接EF 交AC 于点M ，且满足4BE EA =，3AF FD =，23AM AB AC λμ=-，则1952λμ-=（）A ．-3B ．1C ．32-D ．1221．（2021·河南郑州·高一期末）已知ABC 的边BC 上有一点D 满足2BD DC →→=-，则AD →可表示为（）A ．2AD AB AC →→→=-+B ．1233AD AB AC →→→=+C ．2AD AB AC→→→=-D ．2133AD AB AC →→→=+22．（2021·江西宜春·高一期末）如图，在ABC 中，13AN NC =，P 是BN 上的一点，若2299AP m AB BC ⎛⎫=++ ⎪⎝⎭，则实数m 的值为()A ．19B ．13C ．1D ．3【高分突破】一：单选题23．（2021·全国·高一专题练习）已知点,O N 在△ABC 所在平面内，且||||||,0OA OB OC NA NB NC ==++=，则点,O N 依次是△ABC 的（）A ．重心外心B ．重心内心C ．外心重心D ．外心内心24．（2021·湖南·常德市第二中学高一期末）在等边ABC 中，点E 在中线CD 上，且6CE ED =，则AE =（）A ．1377AC AB +B ．13377AC AB -C ．3177AC AB +D ．31377AC AB -25．（2021·全国·高一课时练习）下列算式中，正确的个数为（）①()7642a a -⨯=-；②()2223a b a b a -++=；③()0a b a b +-+=.A ．0B ．1C ．2D ．326．（2021·江苏省梅村高级中学高一阶段练习）在ABC 中，E 为AB 边的中点，D 为AC 边上的点，BD ，CE 交于点F ．若3177AF AB AC =+，则 ACAD的值为（）A ．2B ．3C ．4D ．527．（2021·全国·高一课时练习）设a ，b 都是非零向量.下列四个条件中，使||||a ba b =成立的条件是（）A ．a b =-B ．//a b r rC ．2a b=D ．//a b r r且=a b28．（2020·全国·高一）点M ，N ，P 在ABC 所在平面内，满足MA MB MC ++=0，|NA NB NC ==∣，且PA PB ⋅=PB PC PC PA ⋅=⋅，则M 、N 、P 依次是ABC 的（）A ．重心，外心，内心B ．重心，外心，垂心C ．外心，重心，内心D ．外心，重心，垂心二、多选题29．（2021·全国·高一课时练习）（多选）已知43AB AD AC -=，则下列结论正确的是（）A ．A ，B ，C ，D 四点共线B ．C ，B ，D 三点共线C ．||||AC DB =D ．||3||BC DB =30．（2021·浙江·嘉兴市第五高级中学高一阶段练习）下列说法错误的是（）A ．若//,//a b b c ，则//a cB ．若230OA OB OC ++=，AOCS，ABCS分别表示△AOC ，△ABC 的面积，则:1:6AOC ABC S S =△△C ．两个非零向量,a b ，若a b a b -=+，则a 与b 共线且反向D ．若向量a b ≠，则a 与b 一定不是共线向量31．（2021·河北承德第一中学高一阶段练习）对于非零向量a →，下列说法正确的是（）A ．2a →的长度是a →的长度的2倍，且2a →与a →方向相同B ．3a →-的长度是a →的长度的13，且3a →-与a →方向相反C ．若0λ=，则a λ→等于零D ．若1aλ→=，则a λ→是与a →同向的单位向量32．（2021·湖南·高一期末）已知ABC 的重心为G ，过G 点的直线与边AB ，AC 的交点分别为M ，N ，若AM MB λ=，且AMN 与ABC 的面积之比为920，则λ的可能取值为（）A ．43B ．32C ．53D ．333．（2021·福建三明·高一期中）八卦是中国文化中的基本哲学概念，如图①是八卦模型图，其平面图形记为图②中的正八边形ABCDEFGH ，其中1OA =，则下列结论中正确的是（）A ．//AD BCuuu r uu u r B ．22OA OD ⋅=-C ．0=OB OD D ．22AF =-三、填空题34．（2021·全国·高一课时练习）已知D ，E ，F 分别为ABC 的边BC ，CA ，AB 的中点，BC a =，CA b =．给出下列五个命题：①AB a b =+uu u r r r ；②12BE a b =+；③1122CF a b =-+；④1122AF a b =--；⑤0AD BE CF ++=．其中正确的命题是________．（填序号）35．（2021·全国·高一课时练习）在平行四边形ABCD 中，12DE EC BF FC ==，，若AC =λA E +μAF ，其中λ，μ∈R ，则λ+μ=_______.36．（2021·上海大学附属南翔高级中学高一阶段练习）已知△ABC 中，点D 在边AB 上，且2BD DC =，设AB a =，BC b =，那么AD 等于________（结果用a 、b 表示）37．（2021·全国·高一课时练习）设平面内四边形ABCD 及任一点O ，,OA a OB b ==uu r r uu u r r ．,OC c OD d ==．若a c b d+=+r r r u r且||||a b a d -=-．则四边形ABCD 的形状是_________．四、解答题38．（2021·全国·高一课时练习）在四边形ABCD 中，已知2AB a b =+，4BC a b =--，53CD a b =--，其中a ，b 是不共线的向量，试判断四边形ABCD 的形状．39．（2021·全国·高一课时练习）计算：（1）()()35326a b a b --+；（2）()()4352368a b c a b c -+---+．40．（2021·全国·高一课时练习）（1）已知32a i j →→→=+，2b i j →→→=-，求12(2)33a b a b b a →→→→→→⎛⎫⎛⎫---+- ⎪ ⎪⎝⎭⎝⎭.（2）已知向量,a b →→，且52x y a →→→+=，3x y b →→→-=，求x →，y →.41．（2021·全国·高一课时练习）如图，在ABC 中，D ，F 分别是BC ，AC 的中点，23AE AD =，AB a =，AC b =．（1）用a ，b 表示AD ，A E ，AF ，BE ，BF ；（2）求证：B ，E ，F 三点共线．42．（2021·全国·高一课时练习）如图，在ABC 中，D 是BC 边上一点，G 是线段AD 上一点，且2AG BDDG CD==，过点G 作直线与AB ，AC 分别交于点E ，F .（1）用向量AB ，AC 表示AD .（2）试问2AB AC AE AF+是否为定值？若是，求出该定值；若不是，请说明理由.【答案详解】1．D 【分析】根据向量数乘运算判断AB 选项的正确性，通过m 的特殊情况判断C 选项的正确性，根据向量运算判断D 选项的正确性.【详解】由题意，向量a ，b ，实数m ，n （0m ≠，0n ≠），由向量的运算律可得，()m a b ma mb -=-，故选项A 正确；由向量的运算律可得，()m n a ma na -=-，故选项B 正确；若0ma =，因为0m ≠，则0a =，故选项C 正确；当0a =时，ma na =，此时m 和n 不一定相等，故选项D 错误．故选：D ．2．A 【分析】根据已知条件结合a b c =+，利用向量的线性运算即可求解.【详解】()()()32232a b b c a b+-+-+366222a b b c a b=+----()2222a b c b c b c b c a =--=+--=-+=-，故选：A.3．B 【分析】①②结合平面向量的数乘运算即可判断，③④举出反例即可说明.【详解】对于①：根据数乘向量的法则可得：()m a b ma mb -=-，故①正确；对于②：根据数乘向量的法则可得：()m n a ma na -=-，故②正确；对于③：由ma mb =可得()0m a b -=，当m ＝0时也成立，所以不能推出a b =，故③错误；对于④：由ma na =可得()0m n a -=，当0a =，命题也成立，所以不能推出m ＝n .故④错误；故选：B4．A 【分析】利用向量运算化简已知条件，由此确定正确选项.【详解】依题意()(2)0OB OC OB OC OA -⋅+-=，()0CB OB OA OC OA ⋅-+-=,()()220AB AC AB AC AB AC -⋅+=-=，所以AB AC c b =⇒=，所以三角形ABC 是等腰三角形.故选：A 5．C 【分析】由向量的加法运算得到MN MA AB BN =++，进而利用中点的条件，转化为向量的关系，化简整理即得.【详解】12MN MA AB BN EA AB =++=++12BD()()1122EA AB AB BD =+++12EB =+111222AD a b =+,故选：C 6．A 【分析】由已知得到11,.33AP AB BQ BC ==利用PB AB AP =-，得到23PB AB =，利用PQ PB BQ =+及BC AC AB =-和平面向量的线性运算法则运算即得.【详解】由已知可得11,.33AP AB BQ BC ==1233PB AB AP AB AB AB =-=-=，()2121111133333333PQ PB BQ AB BC AB AC AB AB AC a b =+=+=+-=+=+.故选：A.【点睛】本题考查平面向量的线性运算，是基础题，只要熟练掌握平面向量的加减数乘运算法则,并注意将有关向量转化为基底向量表示，即可得解.7．B【分析】利用向量运算对选项进行分析，由此确定正确选项.【详解】依题意ABC 中，AD 、BE 、CF 分别是BC 、CA 、AB 上的中线，所以G 是三角形ABC 的重心.所以23BG BE =，A 选项正确.12DG AG =-，B 选项错误.121332DA FC DG GC DC BC +=+==，C 选项正确.2CG FG =-，D 选项正确.故选：B8．C【分析】根据平面图形的性质以及平面向量的基本定理和线性运算，对应系数相等即可求出λμ，的值，进而求出结果.【详解】因为D 为线段BC 上一点，2CD DB =，所以2133AD AB AC =+u u u r u u u r u u u r ，且E 为AD 的中点，所以112111223336AE AD AB AC AB AC ⎛⎫==+=+ ⎪⎝⎭，又因为AE AB AC λμ=+，因此1136λμ==，，所以12λμ+=，故选：C.9．B【分析】根据向量的加法运算可得EM EC CM =+和减法运算可得CB AB AC =-，结合条件,可得答案.【详解】由2EC AE =，则23EC AC =则()212113231622EM EC CM AC CB A AB AC AB A C C =+=+=+=-+故选：B10．B【分析】题目考察三角形四心的问题，易得：O 为三角形的重心，位于中线的三等分点处，从而求出三角形面积的比例关系【详解】如图所示，由0OA OB OC ++=得：O 为三角形ABC 的重心，是中线的交点，且23AO AD =，所以，1:3OBC ABC h h =，底边为BC ，所以，1::3OBC ABC OBC ABC h SS h ==故选：B11．A【分析】由O 是ABC 的重心，可知()13OB BA BC =-+，又OD OB BD =+,45BD BC =,BC AC AB =-，化简即可.【详解】由O 是ABC 的重心，可知()13OB BA BC =-+，又OD OB BD =+,45BD BC =,BC AC AB =-,故()141735315OD OB BD BA BC BC BA BC =+=-++=-+()17272731515151515AB AC AB AB AC a b =+-=-+=-+，故选：A.12．C【分析】由||||||OA OB OC ==知O 是ABC 的外心；利用共起点向量加法将0NA NB NC ++=变形为共线的两向量关系，得到N 点在中线上的位置，从而判断为重心；由PA PB PB PC ⋅=⋅移项利用向量减法变形为0PB CA ⋅=，得出PB 为CA 边上的高，同理得PC 为AB 边上的高，故为垂心.【详解】||||||OA OB OC ==，则点O 到ABC 的三个顶点距离相等，∴O 是ABC 的外心.0NA NB NC ++=，NA NB NC ∴+=-，设线段AB 的中点为M ，则2NM NC =-，由此可知N 为AB 边上中线的三等分点(靠近中点M )，所以N 是ABC 的重心.PA PB PB PC ⋅=⋅，()0PB PA PC PB CA ∴⋅-=⋅=.即PB CA ⊥，同理由PB PC PC PA ⋅=⋅，可得PC AB ⊥.所以P 是ABC 的垂心.故选：C.【点睛】关于ABC 四心的向量关系式：O 是ABC 的外心||||||OA OB OC ⇔==222OA OB OC ⇔==；O 是ABC 的重心0OA OB OC ⇔++=；O 是ABC 的垂心OA OB OB OC OC OA ⇔⋅=⋅=⋅；O 是ABC 的内心0aOA bOB cOC ⇔++=.(其中a b c 、、为ABC 的三边)13．C【分析】利用平面向量的加法，减法，数乘运算及其运算律判断.【详解】①()326a a -⋅=-，由数乘运算知正确；②()()223a b b a a +--=，由向量的运算律知正确；③()()220a b b a +-+=，向量的加法，减法和数乘运算结果是向量，故错误.故选：C14．C【分析】取BC 的中点D ，由已知条件可知动点P 满足=+()OP OA AB AC λ→→→→+，()0,λ∈+∞，易得2AP AD λ→→=，则点,,A D P 三点共线，进而得到点P 的轨迹一定通过ABC 的重心.【详解】解：设D 为BC 的中点，则=+()2OP OA AB AC OA AD λλ→→→→→→+=+，则2OP OA AD λ→→→-=，即2AP AD λ→→=，,,A D P ∴三点共线，又因为D 为BC 的中点，所以AD 是边BC 的中线，所以点P 的轨迹一定通过ABC 的重心.故选：C.15．D【分析】根据向量的数乘的定义判断．【详解】如图，由23AB BC =-知C 在BA 延长线上，且12AC AB =，因此由向量数乘定义知ABC 三个选项均正确，D 错误．故选：D ．16．C【分析】由已知可得()3OA OB OB OC --=，即3AB BC -=-，从而可得答案.【详解】解：由430OA OB OC -+=，得()3OA OB OB OC --=，即3AB BC -=-，所以3AB BC =，即3AB BC =，故选：C.17．C【分析】根据向量线性关系的几何意义得到,,OP OA OB 的线性关系，即可知正确选项.【详解】由2,,3OP OA AP AP AB AB OB OA =+==-，∴121122212()()3333OP OA OB OA e e e e e =+-=+-=+.故选：C18．A【分析】选项A ：要注意0b =时不成立；选项B ：由3b a =得到,a b 方向相同，从而得到,a b 共线；选项C ：由条件得到2m n =，从而//m n u r r ；选项D ：通过移项可知选项D 显然正确.【详解】选项A ：当0b =时，满足,a b 共线，但不满足存在唯一的实数λ，使λa b =成立，此时不存在实数λ，使λa b =成立，所以选项A 错误；选项B ：若3b a =，则,a b 方向相同，所以,a b 共线，所以选项B 正确；选项C ：因为3342222m a b a b n ⎛⎫=+=+= ⎪⎝⎭，所以//m n u r r ，所以选项C 正确；选项D ：若0a b c ++=，则a b c +=-，选项D 正确.故选：A ．19．A【分析】由向量的线性运算可得56AP t AB AN =+，再由平面向量共线定理的推论即可得解.【详解】因为AN 23NC =，所以25AN AC =，所以AP =t AB 11553326AC t AB AN t AB AN +=+⨯=+，又P 是BN 上一点，所以516t +=，解得16t =.故选：A.20．D【分析】因为E ，F ，M 三点共线，故可考虑将AM 用,AE AF 表示，再结合三点共线满足的性质计算即可【详解】因为AC AB AD =+，所以2323()(23)3AM AB AC AB AB AD AB AD λμλμλμμ=-=-+=--.因为4BE EA =，3AF FD =，故45,3AB AE AD AF ==,所以5(23)4AM AE AF λμμ=--.因为E ，F ，M 三点共线，所以4(2)531λμμ--=，10191λμ-=，所以191522λμ-=.故选：D21．A【分析】由已知得出向量BC 与向量BD 的关系，再利用平面向量基本定理即可求解．【详解】因为ABC 的边BC 上有一点D 满足2BD DC →→=-，所以2BD CD →→=，则12BC BD DC BD →→→→=+=，所以22()2AD AB BD AB BC AB AC AB AB AC →→→→→→→→→→=+=+=+-=-+，故选：A22．A【分析】利用向量的线性运算将条件2299AP m AB BC ⎛⎫=++ ⎪⎝⎭化为89AP mAB AN =+，再根据B 、P 、N 三点共线，得出819m +=，解得19m =.【详解】由题意可知，13AN NC =，所以4AC AN =，又29AP mAB AC =+，即89AP mAB AN =+.因为B 、P 、N 三点共线，所以819m +=，解得19m =.故选：A ．23．C【分析】由外心O 到三角形顶点距离相等、重心N 的性质：2NB NC ND +=且2AN ND =，结合题设即可判断,O N 是△ABC 的哪种心.【详解】∵||||||OA OB OC ==，∴O 到△ABC 的三个顶点的距离相等，故O 是△ABC 的外心，如下图，若N 是△ABC 三条中线的交点，AD 是BC 上的中线，∴2NB NC ND +=，又2AN ND =，∴0NA NB NC ++=，故题设中的N 是△ABC 的重心.故选：C24．A【分析】利用向量的加、减以及数乘运算即可求解.【详解】因为66()77AE AC CE AC CD AC AD AC =+=+=+-，12AD AB =，所以1377AE AC AB =+.故选：A25．C【分析】由平面向量的线性运算和数乘运算可判断①②③的正误.【详解】对于①，()7642a a -⨯=-，①正确；对于②，()2223a b a b a -++=，②正确；对于③，()0a b a b +-+=，③错误.故选：C.26．C【分析】设AC AD λ=，可得3177AF AB AD λ=+，由B ，F ，D 三点在同一条直线上，可求得λ的值，即可得解．【详解】设AC AD λ=，因为3177AF AB AC =+，所以3177AF AB AD λ=+，因为B ，F ，D 三点在同一条直线上，所以31177λ+=，所以4λ=，所以4AC AD=．故选：C27．C【分析】根据a a 、b b 的含义，逐一分析选项，即可得答案.【详解】aa 、b b 分别表示与a 、b 同方向的单位向量，对于A ：当a b =-r r 时，a b a b=-，故A 错误；对于B ：当//a b r r 时，若,a b 反向平行，则单位向量方向也相反，故B 错误；对于C ：当2a b =时，22a bba b b ==，故C 正确；对于D ：当//a b r r 且=a b 时，若a b =-r r 满足题意，此时a b a b=-，故D 错误.故选：C28．B【分析】由三角形五心的性质即可判断出答案．【详解】解：0MA MB MC ++=，∴MA MB MC +=-，设AB 的中点D ，则2MA MB MD +=，C ∴，M ，D 三点共线，即M 为ABC ∆的中线CD 上的点，且2MC MD =．M ∴为ABC 的重心．||||||NA NB NC ==，||||||NA NB NC ∴==，N ∴为ABC 的外心；PA PB PB PC =，∴()0PB PA PC -=，即0PB CA =，PB AC ∴⊥，同理可得：PA BC ⊥，PC AB ⊥，P ∴为ABC 的垂心；故选：B ．【点睛】本题考查了三角形五心的性质，平面向量的线性运算的几何意义，属于中档题．29．BD【分析】由43AB AD AC -=可得3DB BC =，从而可对ABD 进行判断，再对43AB AD AC -=变形化简可对C 进行判断【详解】因为43AB AD AC -=，所以33AB AD AC AB -=-，所以3DB BC =，因为,DB BC 有公共端点B ，所以C ，B ，D 三点共线，且||3||BC DB =，所以BD 正确，A 错误，由43AB AD AC -=，得333AC AB AD AB DB AB =-+=+，所以||||AC DB ≠，所以C 错误，故选：BD30．AD【分析】A 向量平行传递性的前提是都为非零向量；B 若,D E 分别是,AC BC 的中点，结合已知得2OE OD =-，再过,,E O B 作AC 上的高，由线段比例确定高的比例关系即可；C 由向量反向共线的性质即可判断；D 根据共线向量的定义即可判断.【详解】A ：如果,a c 都是非零向量，而0b =，显然满足已知条件，但是结论不一定成立，错误；B ：若,D E 分别是,AC BC 的中点，由题设有()()20OA OC OB OC +++=，即420OD OE +=，2OE OD =-，所以,,O D E 三点共线且2OE OD =，过,,E O B 作AC 上的高123,,h h h ，易知211311,32h h h h ==，则2316h h =，所以:1:6AOC ABC S S =△△，正确；C ：两个非零向量,a b ，若a b a b -=+，则a 与b 共线且反向，正确；D ：若向量a b ≠，则a 与b 可能是共线向量，如相反向量，错误.故选：AD31．ABD【分析】对于选项ABD 可以直接利用向量和数乘向量的定义判断，对于选项C ，a λ等于零向量，不是零，故C 错误.【详解】解：对于A ：2a →的长度是a →的长度的2倍，且2a →与a →方向相同，故A 正确；对于B ：3a →-的长度是a →的长度的13，且3a →-与a →方向相反，故B 正确；对于C ：若0λ=，则a λ→等于零向量，不是零，故C 错误；对于D ：若1a λ→=，则a λ→是与a →同向的单位向量，故D 正确.故选：ABD32．BD【分析】设AC t AN =，利用重心的性质，把AG 用AM 、AN 表示，再由M ，G ，N 三点共线得关于λ，t 的方程，再由三角形面积比得关于λ，t 的另一方程，联立即可求得实数λ的值．【详解】解：如图，()AM MB AB AM λλ==-，1AM AB λλ∴=+，即1AB AM λλ+=，设AC t AN =，则11()333t AG AB AC AM AN λλ+=+=+，M G N 、、三点共线，1=133t λλ+∴+，12t λ∴=-，所以12AC AN λ⎛⎫=- ⎪⎝⎭，AMN ∴与ABC 的面积之比为920，191sin sin 2202AM AN A AB AC A ∴=⨯⨯，即112029λλλ+⎛⎫⎛⎫-= ⎪⎪⎝⎭⎝⎭，化简得22990λλ-+=，解得32λ=或3.故选：BD33．ABC【分析】结合正八边形的特点，分为8个全等的三角形，将圆周角分为8份，每个圆心角为4π.结合向量的计算法则，即可得出结果.【详解】A.正八边形ABCDEFGH 中，//AD BC ，那么//AD BC uuu r uu u r ，故A 对； B.32cos 42OA OD OA OD π⋅=⋅=-，故B 对；C.OB 与OD uuu r 夹角为2π，故0=OB OD ，故C 对； D.222()222AF OF OA OF OA OF OA OF OA =-=-=+-⋅=+，故D 错；故选：ABC34．②③④⑤【分析】根据平面向量线性运算法则计算可得；【详解】解：因为BC a =，CA b =，所以()AB AC CB CA BC a b =+=-+-=--uu u r uuu r uu r uu r uu u r r r ，1122BE BC CE BC CA a b =+=+=+，()11112222CF CA AF CA AB b a b a b =+=+=+--=-+，()11112222AF AB a b a b ==--=--，()()()111222AD BE CF AB AC BA BC CA CB ++=+++++()()11022AB AC BA BC CA CB AB AC AB BC AC BC =+++++=+-+--=，即0AD BE CF ++=，即正确的有：②③④⑤故答案为：②③④⑤35．75【分析】利用向量的加减法及数乘化简可得AC =32AB AD λμμλ⎛⎫⎛⎫+++ ⎪ ⎪⎝⎭⎝⎭，又AC AB AD =+计算即可.【详解】由平面向量的加法运算，有AC AB AD =+.因为AC =λA E +μAF =λ(AD DE +)+μ(AB BF +)=λ13AD AB ⎛⎫+ ⎪⎝⎭+μ12AB AD ⎛⎫+ ⎪⎝⎭=32AB AD λμμλ⎛⎫⎛⎫+++ ⎪ ⎪⎝⎭⎝⎭.所以32AB AD AB AD λμμλ⎛⎫⎛⎫+=+++ ⎪ ⎪⎝⎭⎝⎭，即1312λμμλ⎧+=⎪⎪⎨⎪+=⎪⎩，，解得3545λμ⎧=⎪⎪⎨⎪=⎪⎩，，故答案为：75或1.236．23a b +【分析】根据AD AB BD =+以及23BD BC =进行线性运算，由此可求得AD 的表示.【详解】因为23AD AB A D BC B B ==++，所以23AD a b =+，故答案为：23a b +.37．菱形【分析】由a c b d +=+r r r u r 易得BA CD =，即ABCD 为平行四边形，再由||||a b a d -=-即可判断ABCD 的形状.【详解】由a c b d +=+r r r u r 得a b d c -=-r r u r r ，即OA OB OD OC -=-，∴BA CD =，于是AB 平行且等于CD ，∴四边形ABCD 为平行四边形，又||||a b a d -=-，从而||||OA OB OA OD -=-，∴||||BA DA =，即四边形ABCD 为菱形．故答案为：菱形38．四边形ABCD 是梯形【分析】根据共面向量基本定理可知，2(4)2AD AB BC CD a b BC =++=--=，即可判断四边形形状.【详解】如图所示，2453822(4)AD AB BC CD a b a b a b a b a b =++=+----=--=--，所以2AD BC =，即//AD BC ，且2AD BC =.所以四边形ABCD 是梯形.39．（1）311a b-（2）104a c+【分析】(1)利用向量运算律可化解合并(2)利用向量运算律可化解合并（1）原式=()()35326=159122=311a b a b a b a b a b --+----（2）原式=()()4352368=4122061216=104a b c a b c a b c a b c a c-+---+-+++-+40．（1）-53i →-5j →；（2）311a →-511b→.【分析】(1)利用向量的数乘及加减法计算即可；（2）解方程即可得出结果.【详解】解(1)原式12(2)33a b a b b a →→→→→→⎛⎫⎛⎫---+- ⎪ ⎪⎝⎭⎝⎭=1113⎛⎫-- ⎪⎝⎭a →+2123⎛⎫-++ ⎪⎝⎭b →=-53a →+53b →.∵32a i j →→→=+，2b i j →→→=-，∴原式=-53(3i →+2j →)+53(2i →-j →)=1053⎛⎫-+ ⎪⎝⎭i →+10533⎛⎫-- ⎪⎝⎭j →=-53i →-5j →.(2)将3x →-y →=b →两边同乘2，得6x →-2y →=2b →.与5x →+2y →=a →相加，得11x →=a →+2b →，∴x →=111a →+211b→.∴y →=3x →-b →=3121111a b →→⎛⎫+ ⎪⎝⎭-b →=311a →-511b →..41．（1）答案见解析；（2）证明见解析．【分析】（1）根据平面向量的线性运算即可求解；（2）利用平面向量共线定理可得求证.【详解】（1）如图，延长AD 到点G ，使2AG AD =，连接BG ，CG ，得到平行四边形ABGC ，则AB AC A a G b =+=+，因为D 是BC 的中点，所以()1122AD AG a b ==+，()2133AE AD a b ==+，因为F 是AC 的中点，所以1122==AF AC b ，()()11323a b a b B a E AE AB =-=+-=-，()11222BF AF AB b a b a =-=-=-；（2）由（1）知，()123BE b a =-，()122b a BF =-，所以23BE BF =，所以BE ，BF 共线，又BE ，BF 有公共点B ，所以B ，E ，F 三点共线．42．（1）1233AD AB AC =+；（2）是定值，定值为92.【分析】（1）结合图形利用向量的加法运算求解；（2）设AB AE λ=，AC AF μ=，则22AB AC AE AF λμ+=+，然后根据题意将AG 用,AB AC 表示出来，从而可用,AE AF 表示，再由,,E F G 三点共线可得结论【详解】解：（1）A AB BDD =+23AB BC =+()23AB BA AC =++1233AB AC =+.（2）设AB AE λ=，AC AF μ=，则22AB AC AE AF λμ+=+，因为2AG BD DG CD==所以23AG AD =uuu r uuu r 212333AB AC ⎛⎫=+ ⎪⎝⎭2499AB AC =+2499AE AF λμ=+，所以24199λμ+=，即922λμ+=，故292AB AC AE AF +=为定值.。

高中数学 3.1.2空间向量的数乘运算练习新人教A版选修

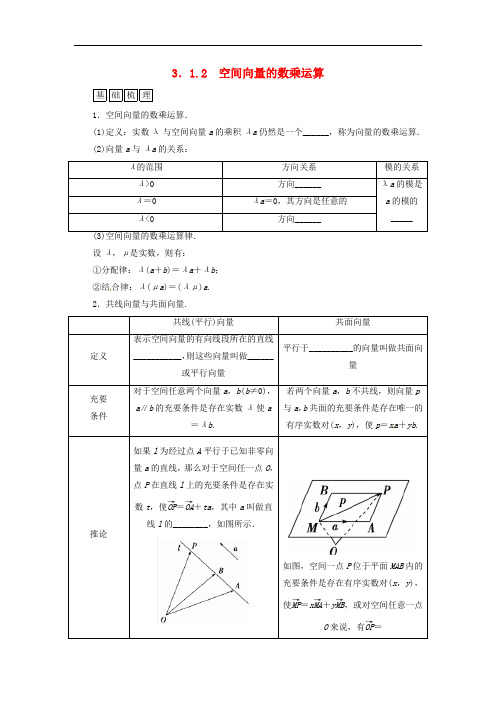
3． 1.2 空间向量的数乘运算基础梳理1．空间向量的数乘运算．(1)定义：实数λ与空间向量a 的乘积λa 仍然是一个______，称为向量的数乘运算． (2)向量a 与λa 的关系：λ的范围方向关系模的关系 λ>0 方向______λa 的模是a 的模的_____λ＝0 λa ＝0，其方向是任意的λ<0方向______(3)空间向量的数乘运算律．设λ，μ是实数，则有： ①分配律：λ(a ＋b )＝λa ＋λb ； ②结合律：λ(μa )＝(λμ)a . 2．共线向量与共面向量.共线(平行)向量共面向量定义表示空间向量的有向线段所在的直线___________，则这些向量叫做______或平行向量平行于__________的向量叫做共面向量充要条件对于空间任意两个向量a ，b (b ≠0)，a ∥b 的充要条件是存在实数λ使a＝λb .若两个向量a ，b 不共线，则向量p 与a ，b 共面的充要条件是存在唯一的有序实数对(x ，y )，使p ＝xa ＋yb .推论如果l 为经过点A 平行于已知非零向量a 的直线，那么对于空间任一点O ，点P 在直线l 上的充要条件是存在实数t ，使OP →＝OA →＋ta ，其中a 叫做直线l 的________，如图所示．如图，空间一点P 位于平面MAB 内的充要条件是存在有序实数对(x ，y )，使MP →＝xMA →＋yMB →，或对空间任意一点O 来说，有OP →＝若在l 上取AB →＝a ，则OP →＝__________.______________________.想一想：1.当我们说a ，b 共线时，表示a ，b 的两条有向线段所在直线一定是同一条直线吗？2．已知空间任意一点O 和不共线的三点A ，B ，C ，满足向量关系式OP →＝xOA →＋yOB →＋zOC →(其中x ＋y ＋z ＝1)的点P 与点A ，B ，C 是否共面？基础梳理1．(1)向量 (2)相同相反 |λ|倍2．互相平行或重合共线向量同一个平面方向向量 OA →＋tAB → OM →＋xMA →＋yMB →想一想：1.不一定，也可能是两条平行直线． 2．解析：四点共面．∵x＋y ＋z ＝1，∴x ＝1－y －z ，又∵OP →＝xOA →＋yOB →＋zOC →， ∴OP →＝(1－y －z)OA →＋yOB →＋zOC →， ∴OP →－OA →＝y(OB →－OA →)＋z(OC →－OA →)， ∴AP →＝yAB →＋zAC →， ∴点P 与点A ，B ，C 共面．自测自评1．直三棱柱ABCA 1B 1C 1中，若CA →＝a ，CB →＝b ，CC 1→＝c ，则A 1B →等于( ) A ．a ＋b －c B ．a －b ＋c C ．－a ＋b ＋c D ．－a ＋b －c2．已知O 、A 、B 是平面上的三个点，直线AB 上有一点C ，满足2AC →＋CB →＝0，则OC →等于( )A ．2OA →－OB → B ．－OA →＋2OB →C .23OA →－13OB → D ．－13OA →－23OB →3．在长方体ABCDA 1B 1C 1D 1中，若E 为矩形ABCD 对角线交点，则A 1E →＝A 1A →＋xA 1B 1→＋yA 1D 1→中的x ，y 值应为x ＝________，y ＝________．自测自评 1．D2．解析：∵2AC →＋CB →＝0， ∴2(OC →－OA →)＋(OB →－OC →)＝0， ∴OC →＝2OA →－OB →. 答案：A3．解析：A 1E →＝A 1A →＋AE →＝A 1A →＋12(AB →＋AD →)＝A 1A →＋12(A 1D 1→＋A 1B 1→)，∴x ＝y ＝12.答案：12 12基础巩固 1．在下列命题中：①若a 、b 共线，则a 、b 所在的直线平行；②若a 、b 所在的直线是异面直线，则a 、b 一定不共面； ③若a 、b 、c 三向量两两共面，则a 、b 、c 三向量一定也共面；④已知三向量a 、b 、c ，则空间任意一个向量p 总可以唯一表示为p ＝xa ＋yb ＋zc . 其中正确命题的个数为( ) A ．0个 B ．1个 C ．2个 D ．3个1．解析：根据空间向量的基本概念知四个命题都不对．答案：A2．已知点M 在平面ABC 内，并且对空间任意一点O ，有OM →＝xOA →＋13OB →＋13OC →，则x 的值为( )A ．1B ．0C ．3 D.132．解析：∵OM →＝xOA →＋13OB →＋13OC →，且M ，A ，B ，C 四点共面，∴x ＋13＋13＝1，x ＝13，故选D .答案：D3．如图所示，已知A ，B ，C 三点不共线，P 为平面ABC 内一定点，O 为平面ABC 外任一点，则下列能表示向量OP →的为( )A.OA →＋2AB →＋2AC →B.OA →－3AB →－2AC →C.OA →＋3AB →－2AC →D.OA →＋2AB →－3AC →3．解析：根据A ，B ，C ，P 四点共面的条件可知AP →＝xAB →＋yAC →.由图知x ＝3，y ＝－2，∴OP →＝OA →＋3AB →－2AC →，故选C .答案：C4．已知平行四边形ABCD 的对角线交于点O ，且OA →＝a ，OB →＝b ，则BC →＝________________． 4．解析：BC →＝BO →＋OC →＝BO →－OA →＝－b －a . 答案：－b －a 能力提升5．当|a |＝|b |≠0，且a 、b 不共线时，a ＋b 与a －b 的关系是( ) A ．共面 B ．不共面 C ．共线 D ．无法确定5．解析：由加法法则知，a ＋b 与a －b 可以是菱形的对角线．答案：A6．如图，空间四边形OABC 中，M 、N 分别是OA 、BC 的中点，点G 在线段MN 上，且MG ＝2GN ，则OG →＝xOA →＋yOB →＋zOC →，则( )A ．x ＝13，y ＝13，z ＝13B ．x ＝13，y ＝13，z ＝16C ．x ＝16，y ＝16，z ＝13D ．x ＝16，y ＝13，z ＝136．解析：∵OG →＝OM →＋MG →＝12OA →＋MG →，①OG →＝OC →＋CN →＋NG →，② OG →＝OB →＋BN →＋NG →，③又BN →＝－CN →，MG →＝－2NG →，∴①＋②＋③，得3OG →＝12OA →＋OB →＋OC →，即x ＝16，y ＝13，z ＝13.答案：D7．已知O 是空间任一点，A 、B 、C 、D 四点满足任三点均不共线，但四点共面，且OA →＝2xBO →＋3yCO →＋4zDO →，则2x ＋3y ＋4z ＝________．7．解析：∵A 、B 、C 、D 共面， ∴OA →＝OB →＋λBC →＋μBD →＝OB →＋λ(OC →－OB →)＋μ(OD →－OB →)＝(1－λ－μ)OB →＋λOC →＋μOD →＝(λ＋μ－1)BO →－λCO →－μDO →＝2xBO →＋3yCO →＋4zDO →.∴2x ＋3y ＋4z ＝(λ＋μ－1)＋(－λ)＋(－μ)＝－1. 答案：－18．在三棱锥ABCD 中，若△BCD 是正三角形，E 为其中心，则AB →＋12BC →－32DE →－AD →化简的结果为________．8．解析：延长DE 交边BC 于点F ，连接AF ，则有AB →＋12BC →＝AF →，32DE →＋AD →＝AD →＋DF →＝AF →，故AB →＋12BC →－32DE →－AD →＝0.答案：09．已知i 、j 、k 是不共面向量，a ＝i －2j ＋k ，b ＝－i ＋3j ＋2k ，c ＝－3i ＋7j ，证明a 、b 、c 三个向量共面．9．证明：设a ＝λb ＋μc ，则i －2j ＋k ＝(－λ－3μ)i ＋(3λ＋7μ)j ＋2λk ，因为i ，j ，k 不共面，所以⎩⎪⎨⎪⎧－λ－3μ＝1，3λ＋7μ＝－22λ＝1，，所以⎩⎪⎨⎪⎧λ＝12，μ＝－12.故存在实数λ＝12，μ＝－12，使a ＝λb ＋μc ，故a ，b ，c 共面．10．如右图所示，E 、F 分别为正方体ABCDA 1B 1C 1D 1的棱B 1C 1和AD 的中点．求证： (1)四边形D 1EBF 为平行四边形；(2)AB 1∥平面D 1EBF .10．分析：(1)要证明四边形D 1EBF 是平行四边形，只需证明D 1E →＝FB →即可； (2)证明AB 1∥平面D 1EBF ，只要证明AB 1→∥FE →即可．证明：(1)D 1E →＝D 1C 1→＋C 1E →＝AB →＋FA →＝FB →， ∴四边形D 1EBF 为平行四边形．(2)AB 1→＝AB →＋BB 1→＝AF →＋FB →＋BE →＋EB 1→＝AF →＋EB 1→＋FB →＋BE →＝0＋FE →＝FE →. ∴AB 1∥FE .又∵AB 1⊄平面D 1EBF ，FE ⊂平面D 1EBF ， ∴AB 1∥平面D 1EBF .。

人教B版高中数学必修第二册6.1.4数乘向量【含答案】

6．1.4数乘向量必备知识基础练进阶训练第一层1．若点C 在直线AB 上，且AC →＝3AB →，则BC →＝()A ．－2AB →B ．13AB →C ．－13AB →D ．2AB →2．如图，已知AB →＝a ，AC →＝b ，BD →＝3DC →，用a ，b 表示AD →，则AD →＝()A ．a ＋34bB ．34a ＋14bC ．14a ＋14bD ．14a ＋34b 3．设a 是非零向量，λ是非零实数，则以下结论正确的个数是()①a 与－λa 的方向相反；②|－λa |≥|a |；③a 与λ2a 方向相同；④|－2λa |＝2|λ|·|a |.A ．1个B ．2个C ．3个D ．4个4．已知|a |＝6，b 与a 的方向相反，且|b |＝3，a ＝m b ，则实数m ＝________．5．已知a ，b 是两个非零向量，则下列说法中正确的有________(填序号).①－2a 与a 是共线向量，且－2a 的模是a 的模的两倍；②3a 与5a 的方向相同，且3a 的模是5a 的模的35；③－2a 与2a 是一对相反向量；④a －b 与－(b －a )是一对相反向量．6．(1)已知非零向量e 1，e 2不共线．如果AB →＝e 1＋e 2，BC →＝2e 1＋8e 2，CD →＝3(e 1－e 2)，求证：A ，B ，D 三点共线．(2)已知e 1，e 2是共线向量，a ＝3e 1＋4e 2，b ＝6e 1－8e 2，求证a ∥b .关键能力综合练进阶训练第二层7．已知点O 为线段AB 的中点，则下列结论错误的是()A ．AB →＝2AO →B ．AO →＝OB →C ．OB →＝12AB →D ．OB →＝12BA →8．如图，D ，E ，F 分别是△ABC 的边AB ，BC ，CA 的中点，则()A ．AD →＋BE →＋CF →＝0B ．BD →－CF →＋DF →＝0C ．AD →＋CE →－CF →＝0D ．BD →－BE →－FC →＝09．(多选)设a ，b 都是非零向量．下列四个条件中，使a |a |＝b |b |成立的条件是()A ．2a ＝b B ．a ∥b C ．a ＝2b D ．a ∥b 且|a |＝|b |10．如图，△ABC 中，AB →＝a ，AC →＝b ，DC →＝3BD →，AE →＝2EC →，则DE →等于()A ．－13a ＋34bB ．512a －34b C ．34a ＋13b D ．－34a ＋512b 11．在平行四边形ABCD 中，对角线AC 与BD 交于点O ，AB →＋AD →＝λAO →，则λ＝________．12．如图所示，已知AD →＝23AB →，AE →＝23AC →，求证：DE →∥BC →.核心素养升级练进阶训练第三层13．(多选)下列命题中正确的是()A．对于实数m和向量a，b，恒有m(a－b)＝m a－m bB.对于实数m，n和向量a，恒有(m－n)a＝m a－n aC.若m a＝m b(m∈R)，则有a＝bD．若m a＝n a(m，n∈R，a≠0)，则m＝n14．已知△ABC的三个顶点A，B，C及平面内一点P，且PA→＋PB→＋PC→＝AB→，则()A．P在△ABC内部B．P在△ABC外部C．P在AB边上或其延长线上D．P在AC边上参考答案与解析1．答案：D解析：∵AC →＝3AB →，∴BC →＝2AB →.2．答案：D解析：∵BD →＝3DC →，∴BD →＝34BC →＝34(b －a )，∴AD →＝AB →＋BD →＝a ＋34(b －a )＝14a ＋34b .3．答案：B解析：①②不正确，③④正确．4．答案：－2解析：|a ||b |＝63＝2，所以|a |＝2|b |.又a 与b 的方向相反，所以a ＝－2b ，所以m ＝－2.5．答案：①②③解析：①∵－2<0，∴－2a 与a 方向相反，两向量共线．又|－2a |＝2|a |，∴①正确．②∵3>0，∴3a 与a 方向相同，且|3a |＝3|a |；∵5>0，∴5a 与a 方向相同，且|5a |＝5|a |.∴3a 与5a 方向相同，且3a 的模是5a 的模的35.∴②正确．③按照相反向量的定义可以判断正确．④∵－(b －a )＝－b ＋a ＝a －b ，∴a －b 与－(b －a )为相等向量．∴④不正确．6．证明：(1)∵AB →＝e 1＋e 2，BD →＝BC →＋CD →＝2e 1＋8e 2＋3e 1－3e 2＝5(e 1＋e 2)＝5AB →，∴AB →，BD →共线，又AB →，BD →有公共点B ，∴A ，B ，D 三点共线．(2)因为e 1，e 2共线，所以存在λ∈R ，使e 1＝λe 2，所以a ＝3e 1＋4e 2＝(3λ＋4)e 2，b ＝6e 1－8e 2＝(6λ－8)e 2.当λ≠43时，a ＝3λ＋46λ－8b ，所以a ，b 共线；当λ＝43时，b ＝0，a ，b 也共线．综上，a 与b 共线，即a ∥b .7．答案：D解析：A ，B ，C 正确；OB →＝－12BA →，故D 错误．8．答案：A解析：AD →＋BE →＋CF →＝12AB →＋12BC →＋12CA →＝12(AB →＋BC →＋CA →)＝0.9．答案：AC解析：a |a |，b |b |分别表示a ，b 的单位向量．对于A ，当2a ＝b 时，2a |2a |＝a |a |＝b |b |；对于B ，当a ∥b 时，可能有a ＝－b ，此时a |a |≠b |b |；对于C ，当a ＝2b 时，a |a |＝2b |2b |＝b |b |；对于D ，当a ∥b 且|a |＝|b |时，可能有a ＝－b ，此时a |a |≠b |b |.综上所述，使a |a |＝b |b |成立的条件是a ＝2b ，2a ＝b .10．答案：D解析：DE →＝DC →＋CE →＝34BC →＋(－13AC →)＝34(AC →－AB →)－13AC →＝－34AB →＋512AC →＝－34a ＋512b .故选D.11．答案：2解析：因为四边形ABCD 为平行四边形，对角线AC 与BD 交于点O ，所以AB →＋AD →＝AC →，又O 为AC 的中点，所以AC →＝2AO →，所以AB →＋AD →＝2AO →.因为AB →＋AD →＝λAO →，所以λ＝2.12．证明：由已知得DE →＝AE →－AD →＝23AC →－23AB →＝23(AC →－AB →)＝23BC →，∴DE →∥BC →.13．答案：ABD解析：根据向量的数乘满足分配律知，恒有m (a －b )＝m a －m b ，故A 正确．根据向量的数乘满足分配律知，恒有(m －n )a ＝m a －n a ，故B 正确．若m ＝0，满足m a ＝m b ，则不一定有a ＝b ，故C 错误．由m a ＝n a 得，(m －n )a ＝0，由于a ≠0，所以m －n ＝0，则m ＝n ，故D 正确．14．答案：D解析：由已知得PA →＋PB →＋PC →＝PB →－PA →，∴PC →＝－2PA →，∴P 在AC 边上．。

【推荐下载】湘教版高一下册数学《向量与实数相乘》练习题及答案

1.若 b=λa(λ∈R)，则 b 与 a 共线.由此可以判断向量共线问题.若 b 与 a(a≠0)共线，则必存在唯一实数λ，使 b=λa.据此可以求两个共线向量中的系数问题. 2.用向量证明三点共线时，关键是能否找到一个实数λ，使得 a=λb(a，b 为这三点构成的其中任意两个向量).证明步骤是先证明两个向量共线，然后再由两个向量有公共点，证得三点共线. 三、向量线性运算的应用 =a，=b 为边的平行四边形.又 BM=BC，CN=CD，试用 a，b 表示，，. 思路分析：利用向量加法的平行四边形法则、三角形法则以及减法的三角形法则对向量进行分解，同时结合向量的数乘运算将未知向量用 a，b 表示.===(-)=(a-b)， &there4;=+=b+a-b=a+b， ==. &there4;=+=+= =(+)=(a+b)=a+b. =-=(a+b)-a-b=a-b. 要想让自己在考试时取得好成绩，除了上课要认真听讲外还需要课后多做练习，接
1
[键入文字]
=a-b-a-b+a+b =a+b =0-a+0-b=0+0=0. 计算：(1)3(6a+b)-9; (2)-2; (3)2(5a-4b+c)-3(a-3b+c)-7a. 解：(1)原式=18a+3b-9a-3b=9a. (2)原式=-a-b =a+b-a-b=0. (3)原式=10a-8b+2c-3a+9b-3c-7a=b-c. 向量的数乘运算类似于实数运算，先算小括号里面的，再算中括号里面的，将相同的向量看作同类项进行合并. 二、向量共线条件的应用

向量的数乘运算题型练习-高一下学期数学人教A版(2019)必修第二册

第六章 6.2.3向量的数乘运算【基础篇】题型1 向量的数乘的定义与运算法则 1．已知λ∈R ，则下列结论正确的是( ) A ．|λa |＝λ|a | B ．|λa |＝|λ|a C ．|λa |＝|λ||a |D ．|λa |>02．若a ，b 为已知向量，且 23(4a －3c )＋3(5c －4b )＝0，则c ＝________.题型2 向量的数乘的应用3．如图，在△ABC 中，D 是边BC 的中点，AG →＝2GD →，则用向量AB →，AC →表示BG →为( )A .BG →＝－23AB →＋13AC →B .BG →＝－13AB →＋23AC →C .BG →＝23AB →－13AC →D .BG →＝23AB →＋13AC →4．如图，在平面四边形ABCD 中，E ，F 分别为AB ，DC 的中点，AD →＝m ，BC →＝n ，则EF →＝( ) A .12m ＋12n B .23m ＋13n C.34m ＋14nD .13m ＋23n题型3 向量共线的判定5．已知AB →＝a ＋5b ，BC →＝－2a ＋8b ，CD →＝3(a －b )，且a ，b 不共线，则( ) A ．A ，B ，C 三点共线 B ．A ，B ，D 三点共线 C ．A ，C ，D 三点共线D ．B ，C ，D 三点共线6．在四边形ABCD 中，对角线AC 与BD 交于点O.若2OA →＋3OC →＝2OD →＋3OB →，则四边形ABCD 一定是( ) A ．矩形B ．梯形C ．平行四边形D ．菱形7．已知向量a ＝2e 1－3e 2，b ＝2e 1＋3e 2，c ＝2e 1－9e 2，其中e 1，e 2不共线．问是否存在实数λ，μ，使向量d ＝λa ＋μb 与c 共线？题型4 向量共线定理的应用8．如图，在△ABC 中，AN →＝14NC →，P 是BN 上一点．若AP →＝mAB →＋211AC →，则实数m 的值为( )A .911B .211C .311D .1119．在△ABC 中，点D 在边BC 的延长线上，且BC →＝3CD →.若AO →＝xAB →＋(1－x)AC →，－13<x<0，则点O 在( ) A ．线段BC 上 B ．线段CD 上 C ．线段AC 上D ．线段AD 上10．在△ABC 中，点D 满足AD →＝16AB →＋12AC →，直线AD 与BC 交于点E ，则|CE →||CB →|的值为( ) A .12 B .13 C .14D .1511．设e 1，e 2是空间内两个不共线的向量，已知AB →＝e 1＋ke 2，BC →＝5e 1＋4e 2，DC →＝－e 1－2e 2，且A ，B ，D 三点共线，则实数k ＝________．【提升篇】1．在平行四边形ABCD 中，AC ，BD 交于点O ，则( ) A .AO →＝AB →＋AD → B .AO →＝12(AB →＋AD →)C .AO →＝AB →－AD → D .AO →＝12(AB →－AD →)2．已知向量a ，b 不共线．若向量a ＋λb 与b ＋λa 的方向相反，则λ的值为( ) A ．1 B ．0C ．－1D ．±13．庄严美丽的国旗和国徽上的五角星是革命和光明的象征，正五角星是一个非常优美的几何图形，且与黄金分割有着密切的联系，在如图所示的正五角星中，以A ，B ，C ，D ，E 为顶点的多边形为正五边形，已知PTAP ＝5－12，则( )A .CT →＝3－52CA →＋3－52CE →B .CT →＝5－12CA →＋5－12CE →C .CT →＝3－54CA →＋3－54CE →D .CT →＝3－54CA →＋5－12CE →4．已知O 是平面内一定点，A ，B ，C 是平面上不共线的三个点，动点P 满足OP →＝OA →＋λ⎝ ⎛⎭⎪⎫AB →|AB →|＋AC →|AC →|(λ∈[0，＋∞))，则点P 的轨迹一定通过△ABC 的( ) A ．外心 B ．内心C ．重心D ．垂心5．(多选)[重庆南开中学2022质量检测]已知点P 是△ABC 的中线BD 上一点(不包含端点)且AP →＝xAB →＋yAC →，则下列说法正确的是( ) A ．x ＋2y ＝1B ．2x ＋y ＝1C ．2x ＋4y ≥2 2D ．log 2x ＋log 2y≥－36．(多选)[山东师范大学附属中学2022高一月考]已知点P 为△ABC 所在平面内一点，且PA →＋2PB →＋3PC →＝0.若E 为AC 的中点，F 为BC 的中点，则下列结论正确的是( ) A ．向量PA →与PC →可能平行 B ．点P 在线段EF 的延长线上 C ．点P 在线段EF 上 D ．PE ∶PF ＝2∶17．已知M 是△ABC 所在平面内的一点．若满足6AM →－AB →－2AC →＝0，且S △ABC ＝λS △ABM ，则实数λ的值是________．8．[山东历城二中、章丘四中等校2022高一联考]在△ABC 中，点P 满足BP ＝2PC ，过点P 的直线与AB ，AC 所在的直线分别交于点M ，N ，若AB →＝λAM →，AC →＝μAN →(λ>0，μ>0)，求1λ＋1μ的最小值．9．已知e 1，e 2是平面上两个不共线的向量，且AB →＝k e 1－4e 2，CD →＝－e 1＋k e 2，BD →＝e 1＋2e 2.(1)若AB →，CD →方向相反，求k 的值； (2)若A ，C ，D 三点共线，求k 的值．答案及解析1.【答案】C【详解】当λ<0时，|λa |＝λ|a |不成立，A 错误；|λa |是一个非负实数，而|λ|a 是一个向量，B 错误；当λ＝0或a ＝0时，|λa |＝0，D 错误．故选C. 2.【答案】1213b －839a【详解】∵23(4a －3c )＋3(5c －4b )＝0，∴83a －2c ＋15c －12b ＝0，化简得13c ＝12b －83a ，∴c ＝1213b －839a . 3.【答案】A【详解】由题意可得BG →＝BA →＋AG →＝BA →＋23AD →＝BA →＋23×12(AB →＋AC →)＝BA →＋13AB →＋13AC →＝13AC→－23AB →.故选A. 4.【答案】A【详解】由已知可得CF →＋DF →＝0，EA →＋EB →＝0，由平面向量的加法可得⎩⎪⎨⎪⎧EF →＝EA →＋AD →＋DF →，EF →＝EB →＋BC →＋CF →，上述两个等式相加可得2EF →＝AD →＋BC →＝m ＋n ，则EF →＝12(m ＋n )．故选A. 5.【答案】B【详解】∵AB →＝a ＋5b ，BC →＝－2a ＋8b ，CD →＝3(a －b )，且a ，b 不共线，∴BD →＝BC →＋CD →＝－2a ＋8b ＋3(a －b )＝a ＋5b .∵AB →＝a ＋5b ，∴BD →＝AB →，即BD →与AB →共线，则A ，B ，D 三点共线，故选B. 6.【答案】B【详解】∵2OA →＋3OC →＝2OD →＋3OB →，∴2(OA →－OD →)＝3(OB →－OC →)，∴2DA →＝3CB →，∴四边形ABCD 一定是梯形．故选B.7.【答案】由题意得d ＝λa ＋μb ＝(2λ＋2μ)e 1＋(－3λ＋3μ)e 2，若d 与c 共线，则存在实数k ≠0，使d ＝kc ，即(2λ＋2μ)e 1＋(－3λ＋3μ)e 2＝2ke 1－9ke 2，即⎩⎪⎨⎪⎧2λ＋2μ＝2k ，－3λ＋3μ＝－9k ，解得λ＝－2μ. 故存在实数λ，μ，且λ＝－2μ，使d 与c 共线． 8.【答案】D【详解】由题意可得AC →＝5AN →，则AP →＝mAB →＋211×5AN →＝mAB →＋1011AN →.因为B ，P ，N 三点共线，所以m ＋1011＝1，即m ＝111.9.【答案】B【详解】由向量共线定理可知O ，B ，C 三点共线． ∵BC →＝3CD →，∴AC →－AB →＝3AD →－3AC →，∴AD →＝－13AB →＋43AC →.又∵－13<x <0，∴点O 在线段CD 上，且不与C ，D 两点重合．10.【答案】C【解析】设AE →＝λAD →＝λ6AB →＋λ2AC →，则CE →＝AE →－AC →＝λAD →－AC →＝λ6AB →＋λ2AC →－AC →＝λ6AB →＋⎝⎛⎭⎫λ2－1AC →， CB →＝AB →－AC →，且CE →，CB →共线，设CE →＝kCB →，则λ6AB →＋⎝⎛⎭⎫λ2－1AC →＝k (AB →－AC →)，所以⎩⎨⎧λ6＝k ，λ2－1＝－k ，所以λ6＝1－λ2，解得λ＝32，此时CE →＝14AB →－14AC →，所以CE →＝14CB →，故|CE →||CB →|＝14.故选C. 11.【答案】1【详解】依题意，CD →＝e 1＋2e 2，故AD →＝AB →＋BC →＋CD →＝7e 1＋(k ＋6)e 2. 已知A ，B ，D 三点共线，可设AD →＝λAB →，则7e 1＋(k ＋6)e 2＝λ(e 1＋ke 2)，所以⎩⎪⎨⎪⎧7＝λ，k ＋6＝kλ，解得k ＝1.1.【答案】B【详解】如图，在平行四边形ABCD 中，AC ，BD 交于点O ，由平行四边形法则得AB →＋AD→＝AC →＝2AO →，所以AO →＝12(AB →＋AD →)．故选B.2.【答案】C【详解】∵向量a ＋λb 与b ＋λa 的方向相反，∴(a ＋λb )∥(b ＋λa )．由向量共线的充要条件可知，存在一个实数m ，使得a ＋λb ＝m (b ＋λa )，即(1－mλ)a ＝(m －λ)b .∵a 与b 不共线，∴1－mλ＝m －λ＝0，可得m ＝λ.∴1－λ2＝0，λ＝±1.当λ＝1时，向量a ＋b 与b ＋a 是相等向量，其方向相同，不符合题意，故舍去．∴λ＝－1.3.【答案】A【详解】设AP ＝1，则PT ＝5－12＝TS ，CP ＝1＋5－12＝5＋12＝CS ， CT →＝CA →＋AT →＝CA →＋25－1TS →＝CA →＋25－1(CS →－CT →)＝CA →＋25－1(1＋5－122＋5－12CE →－CT →)＝CA→＋CE →－5＋12CT →，所以5＋32CT →＝CA →＋CE →，所以CT →＝3－52CA →＋3－52CE →. 故选A. 4.【答案】B【详解】AB →|AB →|为AB →上的单位向量，AC →|AC →|为AC →上的单位向量，设∠BAC 的平分线为AD ，则AB →|AB →|＋AC →|AC →|的方向为AD → 的方向．又∵λ∈[0，＋∞)，∴λ⎝ ⎛⎭⎪⎫AB →|AB →|＋AC →|AC →|的方向与AB →|AB →|＋AC →|AC →|的方向相同．∵OP →＝OA →＋λ⎝ ⎛⎭⎪⎫AB →|AB →|＋AC →|AC →|，∴点P 在射线AD 上移动． ∴点P 的轨迹一定通过△ABC 的内心． 5.【答案】AC【详解】因为AP →＝xAB →＋yAC →，所以AP →＝xAB →＋2yAD →.又B ，P ，D 三点共线，所以x ＋2y ＝1，所以选项A 正确，选项B 错误．x ＋2y ＝1，所以2x ＋4y ＝2x ＋22y ≥2 2x ·22y ＝2 2x＋2y＝2 2(当且仅当x ＝12，y ＝14时等号成立)，所以选项C 正确．因为x ＋2y ＝1≥2 2xy ，所以xy ≤18⎝⎛⎭⎫当且仅当x ＝12，y ＝14时等号成立，所以log 2x ＋log 2y ＝log 2(xy )≤log 218＝－3，所以选项D 错误．故选AC. 6.【答案】CD【详解】点P 为△ABC 所在平面内一点，E 为AC 的中点，F 为BC 的中点，则P A →＋PC →＝2PE →，PB →＋PC →＝2PF →，而P A →＋2PB →＋3PC →＝0，即(PA →＋PC →)＋2(PB →＋PC →)＝0，于是得2PE →＋4PF →＝0，即EP →＝2PF →，所以点P 在线段EF 上，且PE ∶PF ＝2∶1，即点P ，A ，C 不共线，则向量PA →与PC →不可能平行，A 不正确，B 不正确，C 正确，D 正确．故选CD .7.【答案】3【详解】如图，记2AM →＝AN →.∵AN →－AB →＋2AN →－2AC →＝0， ∴BN →＝2NC →，S △ABC ＝32S △ABN .又∵S △ABM ＝12S △ABN ，∴S △ABC ＝3S △ABM ，∴λ＝3.8.【答案】【详解】连接AP ，如图．∵△ABC 中，BP →＝BA →＋AP →，PC →＝PA →＋AC →，点P 满足BP →＝2PC →， ∴－AB →＋AP →＝2(AC →－AP →)， ∴AP →＝23AC →＋13AB →.又∵AB →＝λAM →，AC →＝μAN →(λ>0，μ>0)， ∴AP →＝2μ3AN →＋λ3AM →.又∵M ，P ，N 三点共线， ∴2μ3＋λ3＝1，λ>0，μ>0， ∴1λ＋1μ＝⎝⎛⎭⎫1λ＋1μ·⎝⎛⎭⎫2μ3＋λ3＝2μ3λ＋λ3μ＋1≥2 2μ3λ·λ3μ＋1＝2 23＋1, 当且仅当2μ3λ＝λ3μ，即⎩⎪⎨⎪⎧μ＝3（2－2）2，λ＝3（2－1）时取“＝”，则1λ＋1μ的最小值为2 23＋1. 9.【答案】(1)由题意知，AB →∥CD →，则存在λ∈R ，使得AB →＝λCD →，即k e 1－4e 2＝λ(－e 1＋k e 2)，整理得(k ＋λ)e 1＝(kλ＋4)e 2. 由e 1，e 2是不共线的向量，得⎩⎪⎨⎪⎧k ＋λ＝0，kλ＋4＝0，解得⎩⎪⎨⎪⎧λ＝2，k ＝－2或⎩⎪⎨⎪⎧λ＝－2，k ＝2. 又AB →，CD →方向相反，则λ＝－2，k ＝2，故k 的值为2.(2)由题意知，AD →＝AB →＋BD →＝(k ＋1)e 1－2e 2.由A ，C ，D 三点共线得，存在μ∈R ，使得AD →＝μCD →，即(k ＋1)e 1－2e 2＝μ(－e 1＋k e 2)，整理得(k ＋μ＋1)e 1＝(kμ＋2)e 2. 由e 1，e 2是不共线的向量，得⎩⎪⎨⎪⎧k ＋μ＋1＝0，kμ＋2＝0，解得⎩⎪⎨⎪⎧k ＝1，μ＝－2或⎩⎪⎨⎪⎧k ＝－2，μ＝1.综上，k ＝1或k ＝－2.。

高中数学平面向量数乘运算与数量积讲解及练习

高中数学平面向量数乘运算与数量积讲解及练习专题一平面向量的数乘运算探究一：已知非零向量→a ，作出→→→++a a a 和)()()(→→→-+-+-a a a ，它们的长度和方向分别是怎样的？1.向量的数乘运算的定义一般地，我们规定实数λ与向量→a 的积是一个向量，这种运算叫作向量的数乘，记作→a λ，它的长度与方向规定如下：（1）→→⋅=a a λλ；（2）当0>λ时，→a λ与→a 的方向相同；当0<λ时，→a λ与→a 的方向相反；当0=λ时，→→=0a λ.由向量的数乘的定义可知： ①→→=a a )()(λμμλ②→→→+=+a a a μλμλ）（ ③→→→→+=+b a b a λλλ)(2.向量的线性运算向量的加、减、数乘运算统称为向量的线性运算，向量的线性运算的结果仍是向量. 对于任意向量→a ，→b ，以及任意实数，，，21μμλ恒有→→→→±=±b a b a 2121)(λμλμμμλ.题型1 向量的数乘运算例1.设a 是非零向量，a λ，λ是非零实数，则下列结论中正确的是（） A ．a 与a λ的方向相同 B ．a 与a λ-的方向相反 C ．a 与2a λ的方向相同 D ．a a λλ=例2. 化简：（1）5(32)4(23)a b b a -+-；（2）111(2)(32)()342a b a b a b -----；例3.设平行四边形ABCD 的两条对角线AC 与BD 交于点O ，AB a =，AD b =，则向量OA =（）A ．1122a b + B ．1122a b -+ C ．1122a b - D ．1122a b --练习1.在ABC ∆中，D 是BC 上一点，且13BD BC =，则AD =（） A ．13AB AC + B ．13AB AC -C ．2133AB AC +D ．1233AB AC +探究：已知非零向量→a ，作出向量→a 2，→a 21，→-a 3，→-a 31，你能发现这些向量与原向量的位置关系吗？3.向量共线定理向量）（→→→≠0a a 与→b 共线的充要条件是：存在唯一一个实数λ，使→→=a b λ.题型2 向量共线定理的应用例4.判断下列各小题中的向量→a ，→b 是否共线（其中1e ，2e 是两个非零不共线向量）.()1110,51e b e a -==→→；()212123,31212e e b e e a -=-=→→；()212133,3e e b e e a -=+=→→.例5.已知21,e e 是两个不共线的向量，(1)如果2182e e AB -=→，213e e CB +=→,212e e CD -=→,求证：D B A ,,三点共线. (2)欲使ke 1＋e 2和e 1＋ke 2共线，试确定实数k 的值．专题二平面向量的数量积1.两向量的夹角(1)定义：已知两个非零向量a ，b ，O 是平面上的任意一点，作OA →＝a ，OB →＝b ，则∠AOB ＝θ(0≤θ≤π)叫做向量a 与b 的夹角． (2)特例：①当θ＝0时，向量a 与b 同向； ②当θ＝π2时，向量a 与b 垂直，记作a ⊥b ；③当θ＝π时，向量a 与b 反向．2．向量的数量积已知两个非零向量a 与b ，它们的夹角为θ，把数量θcos b a ⋅叫做向量a 与b 的数量积(或内积)，记作a ·b ，即θcos b a b a ⋅=⋅. 规定:零向量与任一向量的数量积为0．题型1 向量数量积的运算例6.已知向量a ，b 满足1a =，2b =，a 与b 夹角为30，那么a b ⋅等于（） A ．1-B ．2C ．3D ．2练习2.已知|a |＝10，|b |＝12，且()36)51(3-=⋅b a ，则a 与b 的夹角为( ) A ．60° B ．120° C ．135° D ．150°3．投影向量如图(1)，设a ，b 是两个非零向量，AB →＝a ，CD →＝b ，我们考虑如下变换：过AB →的起点A 和终点B ，分别作CD →所在直线的垂线，垂足分别为A 1，B 1，得到A 1B 1→，我们称上述变换为向量a 向向量b 投影(project)，A 1B 1→叫做向量a 在向量b 上的投影向量．如图(2)，在平面内任取一点O ，作OM →＝a ，ON →＝b ，过点M 作直线ON 的垂线，垂足为M 1，则OM 1→就是向量a 在向量b 上的投影向量．4．向量数量积的几何意义向量数量积a ·b 等于b 的长度b 与向量a 在向量b 上的投影θcos ⋅a 的乘积（其中θcos ⋅a 称为向量a 在向量b 上的投影，也可以表示为bba ⋅）题型2 投影向量的运用例7.已知|a |＝3，|b |＝5，a 与b 的夹角为45°，则向量a 在向量b 方向上的投影为________．练习3.已知|a|＝3，|b|＝5，a·b＝－12，则a在b上的投影向量为______．4．向量数量积的性质设a，b是非零向量，它们的夹角是θ，e是与b方向相同的单位向量，则(1)a·e＝e·a＝|a|cos .(2)a⊥b⇔a·b＝0．(3)当a与b同向时，a·b＝|a||b|；当a与b反向时，a·b＝－|a||b|．特别地，a·a＝|a|2或|a|＝a·a.(4)|a·b|≤|a||b|.5．向量数量积的运算律(1)a·b＝b·a(交换律)．(2)(λa)·b＝λ(a·b)＝a·(λb)(结合律)．(3)(a＋b)·c＝a·c＋b·c(分配律)．题型3 向量数量积性质的综合运用例8.已知|a|＝1，|b|＝ 2.(1)若a∥b，求a·b；(2)若a，b的夹角为60°，求|a＋b|；(3)若a－b与a垂直，求a与b的夹角．练习4.已知非零向量a ，b ，满足|a |＝1，(a －b )·(a ＋b )＝12，且a ·b ＝12.(1)求向量a ，b 的夹角； (2)求|a －b |.课后作业1．已知向量a ，b 满足|a |＝1，|b |＝4，且a·b ＝2，则a 与b 的夹角θ为( )A.π6 B.π4 C.π3D.π22．已知单位向量a ，b ，则(2a ＋b )·(2a －b )的值为( )A. 3B.5 C ．3D ．53．若向量a 与b 的夹角为60°，|b |＝4，(a ＋2b )·(a －3b )＝－72，则|a |＝( )A ．2B ．4C ．6D ．124．已知向量a 与b 的夹角是π3，且|a |＝1，|b |＝2，若(3a ＋λb )⊥a ，则实数λ＝________．。

向量数乘和线性运算精选题32道附参考答案与试题解析

向量数乘和线性运算精选题32道附参考答案与试题解析一．选择题（共12小题）1．如图，在平行四边形ABCD中，E是BC的中点，F是线段AE上靠近点A的三等分点，则＝（）A．B．C．D．2．如图，在△ABC中，，，若，则的值为（）A．﹣3B．3C．2D．﹣23．如图，若＝，＝，＝，B是线段AC靠近点C的一个四等分点，则下列等式成立的是（）A．＝﹣B．＝+C．＝﹣D．＝+4．O是平面上一定点，A、B、C是平面上不共线的三个点，动点P满足，λ∈[0，+∞），则P的轨迹一定通过△ABC的（）A．外心B．内心C．重心D．垂心5．如图所示，矩形ABCD的对角线相交于点O，E为AO的中点，若，则λ•μ等于（）A．B．C．D．6．已知点O是△ABC内部一点，满足+2＝m，＝，则实数m为（）A．2B．﹣2C．4D．﹣47．在平行四边形ABCD中，＝，＝，若E是DC的中点，则＝（）A．B．C．﹣+D．﹣+8．已知D为△ABC所在平面内一点，3＝，则＝（）A．﹣+B．+C．﹣D．+9．在△ABC中，，则＝（）A．B．C．D．10．如图，在△ABC中，，，BE和CD相交于点F，则向量等于（）A．B．C．D．11．△ABC中，AB＝6，BC＝8，AB⊥BC，M是△ABC外接圆上一动点，若＝λ+μ，则λ+μ的最大值是（）A．1B．C．D．212．设点M是线段BC的中点，点A在直线BC外，||2＝16，|+|＝|﹣|，则||＝（）A．8B．4C．2D．1二．多选题（共4小题）（多选）13．设点M是△ABC所在平面内一点，则下列说法正确的是（）A．若＝，则点M是边BC的中点B．若＝，则点M在边BC的延长线上C．若＝，则点M是△ABC的重心D．若＝，且x+y＝，则△MBC的面积是△ABC面积的（多选）14．若点O是线段BC外一点，点P是平面上任意一点，且（λ，μ∈R），则下列说法正确的有（）A．若λ+μ＝1且λ＞0，则点P在线段BC的延长线上B．若λ+μ＝1且λ＜0，则点P在线段BC的延长线上C．若λ+μ＞1，则点P在△OBC外D．若λ+μ＜1，则点P在△OBC内（多选）15．已知正方形ABCD的边长为2，向量，满足，，则（）A．B．C．D．（多选）16．下列四式可以化简为的是（）A．+（）B．（）+（）C．+D．三．填空题（共12小题）17．如图，在四边形ABCD中，∠B＝60°，AB＝3，BC＝6，且＝λ，•＝﹣，则实数λ的值为，若M，N是线段BC上的动点，且||＝1，则•的最小值为．18．已知O在△ABC内，且S△AOB：S△BOC：S△AOC＝4：3：2，，则λ+μ＝19．已知，，，，…，（k∈N*）是平面内两两互不相等的向量，满足||＝1，且|﹣|∈{1，2}（其中i＝1，2，j＝1，2，…，k），则k的最大值是．20．在△ABC中，点D，E分别在边AB，BC上，且AD＝DB，BE＝2EC，记，＝，若，则x+y的值为．21．在四边形ABCD中，AB＝6，若，则＝．22．已知△ABC的一内角，AB＝10，AC＝6，O为△ABC所在平面上一点，满足|OA|＝|OB|＝|OC|，设＝m+n，则m+3n的值为．23．在直角坐标系中，O为原点，，则x+y＝．24．已知，，，则＝．25．已知G为△ABC的重心，过点G的直线与边AB，AC分别相交于点P，Q．若＝，则当ABC与△APQ的面积之比为时，实数λ的值为．26．如图，给定单位向量和，它们的夹角为120°，点C在以O为圆心的上运动．若，其中x，y∈R，则x+2y的最大值是．27．已知点O是△ABC内部一点，并且满足，△BOC的面积为S1，△ABC 的面积为S2，则＝．28．设λ是正实数，三角形ABC所在平面上的另三点A1，B1，C1满足：＝λ（+），＝λ（+），＝λ（+），若三角形ABC与三角形A1B1C1的面积相等，则λ的值为．四．解答题（共4小题）29．如图，已知△ABC中，D为BC的中点，AE＝EC，AD，BE交于点F，设＝，＝．（1）用，分别表示向量，；（2）若＝t，求实数t的值．30．如图所示，在△ABO中，，，AD与BC相交于点M，设，．（1）试用向量，表示；（2）过点M作直线EF，分别交线段AC，BD于点E，F．记，，求证：为定值．31．如图，在平面直角坐标系中，点A（﹣，0），B（，0），锐角α的终边与单位圆O 交于点P．（Ⅰ）用α的三角函数表示点P的坐标；（Ⅱ）当•＝﹣时，求α的值；（Ⅲ）在x轴上是否存在定点M，使得||＝||恒成立？若存在，求出点M的横坐标；若不存在，请说明理由．32．已知O是△ABC所在平面内一点，D为BC边中点．（1）若点O满足，求证：；（2）已知E为AC边中点，O在线段DE上，且满足，△BOC的面积为2，求△ABC的面积．向量数乘和线性运算精选题32道参考答案与试题解析一．选择题（共12小题）1．如图，在平行四边形ABCD中，E是BC的中点，F是线段AE上靠近点A的三等分点，则＝（）A．B．C．D．【解答】解：由可知，＝﹣＝﹣＝﹣++＝，故选：C．2．如图，在△ABC中，，，若，则的值为（）A．﹣3B．3C．2D．﹣2【解答】解：∵＝+，＝＝（﹣）＝﹣＝×﹣＝﹣，∴＝+（﹣）＝+；又＝λ+μ，∴λ＝，μ＝；∴＝×＝3．故选：B．3．如图，若＝，＝，＝，B是线段AC靠近点C的一个四等分点，则下列等式成立的是（）A．＝﹣B．＝+C．＝﹣D．＝+【解答】解：＝，＝，＝，则＝+＝+＝+（﹣）＝﹣＝﹣．故选：C．4．O是平面上一定点，A、B、C是平面上不共线的三个点，动点P满足，λ∈[0，+∞），则P的轨迹一定通过△ABC的（）A．外心B．内心C．重心D．垂心【解答】解：∵、分别表示向量、方向上的单位向量∴+的方向与∠BAC的角平分线一致又∵，∴＝λ（+）∴向量的方向与∠BAC的角平分线一致∴一定通过△ABC的内心故选：B．5．如图所示，矩形ABCD的对角线相交于点O，E为AO的中点，若，则λ•μ等于（）A．B．C．D．【解答】解：由题意及图，可知：＝+＝+＝+（+）＝﹣，∴λ＝，μ＝﹣，∴λ•μ＝﹣．故选：A．6．已知点O是△ABC内部一点，满足+2＝m，＝，则实数m为（）A．2B．﹣2C．4D．﹣4【解答】解：如图所示，点O是△ABC内部一点，满足+2＝m，延长OB到D点，以OA，OD为邻边作平行四边形AODF，连接CF分别交AB，AD于E，G点．则点E是△OAD的重心．∵＝，不妨设CE＝7，则OC＝3，OE＝4，EG＝2，OF＝12．∴m＝＝﹣4，解得m＝﹣4．故选：D．7．在平行四边形ABCD中，＝，＝，若E是DC的中点，则＝（）A．B．C．﹣+D．﹣+【解答】解：如图所示，平行四边形ABCD中，＝，＝，则＝＝﹣＝﹣，又E是DC的中点，则＝+＝（﹣）+＝﹣＝﹣+．故选：C．8．已知D为△ABC所在平面内一点，3＝，则＝（）A．﹣+B．+C．﹣D．+【解答】解：因为D为△ABC所在平面内一点，3＝，所以．故选：A．9．在△ABC中，，则＝（）A．B．C．D．【解答】解：∵；∴；∴．故选：B．10．如图，在△ABC中，，，BE和CD相交于点F，则向量等于（）A．B．C．D．【解答】解：设＝k＝k（﹣）＝k（﹣），∵＝+＝k（﹣）+﹣＝（k﹣1）+（1﹣k），＝﹣＝﹣．∵∥，∴＝λ，则（k﹣1）+（1﹣k）＝λ（﹣）．∴，∴k＝，＝﹣，∴＝+＝+．故选：B．11．△ABC中，AB＝6，BC＝8，AB⊥BC，M是△ABC外接圆上一动点，若＝λ+μ，则λ+μ的最大值是（）A．1B．C．D．2【解答】解：以B为坐标原点，BC方向为X轴正方向建立直角坐标系，∴A（0，6）C（8，0），∴外接圆的方程为：（x﹣4）2+（y﹣3）2＝25，即，∴设M（4+5cosθ，3+5sinθ），∴，，∵，∴，∴，∴，故选：C．12．设点M是线段BC的中点，点A在直线BC外，||2＝16，|+|＝|﹣|，则||＝（）A．8B．4C．2D．1【解答】解：由＝16，得||＝4，∵＝||＝4，而∴＝2故选：C．二．多选题（共4小题）（多选）13．设点M是△ABC所在平面内一点，则下列说法正确的是（）A．若＝，则点M是边BC的中点B．若＝，则点M在边BC的延长线上C．若＝，则点M是△ABC的重心D．若＝，且x+y＝，则△MBC的面积是△ABC面积的【解答】解：若＝，则点M是边BC的中点，故A正确；若＝，即有﹣＝﹣，即＝，则点M在边CB的延长线上，故B错误；若＝，即++＝，则点M是△ABC的重心，故C正确；若＝，且x+y＝，可得2＝2x+2y，设＝2，由右图可得M为AN的中点，则△MBC的面积是△ABC面积的，故D正确．故选：ACD．（多选）14．若点O是线段BC外一点，点P是平面上任意一点，且（λ，μ∈R），则下列说法正确的有（）A．若λ+μ＝1且λ＞0，则点P在线段BC的延长线上B．若λ+μ＝1且λ＜0，则点P在线段BC的延长线上C．若λ+μ＞1，则点P在△OBC外D．若λ+μ＜1，则点P在△OBC内【解答】解：因为若λ+μ＝1且λ＞0，故即又λ＞0则点P在线段BC或其反向延长线上，A错误；若λ+μ＝1且λ＜0，同上可得而λ＜0则点P在线段BC的延长线上，B正确；若λ+μ＞1，，同上可得，当λ+μ＞1时，λ+μ﹣1＞0根据向量加法的平行四边形法则可以看出则点P在△OBC外，C正确；若λ+μ＜1，不防令λ＝0，μ＝﹣1则，很显然此时点P在线段CO的延长线上，不在△OBC内，D错误．故选：BC．（多选）15．已知正方形ABCD的边长为2，向量，满足，，则（）A．B．C．D．【解答】解：由条件可得：，所以，A正确；，与不垂直，B错误；，C错误；，根据正方形的性质有AC⊥BD，所以，D项正确．故选：AD．（多选）16．下列四式可以化简为的是（）A．+（）B．（）+（）C．+D．【解答】解：＝＝，A正确；+＝＝，B正确；＝，C正确；＝，D错误．故选：ABC．三．填空题（共12小题）17．如图，在四边形ABCD中，∠B＝60°，AB＝3，BC＝6，且＝λ，•＝﹣，则实数λ的值为，若M，N是线段BC上的动点，且||＝1，则•的最小值为．【解答】解：以B为原点，以BC为x轴建立如图所示的直角坐标系，∵∠B＝60°，AB＝3，∴A（，），∵BC＝6，∴C（6，0），∵＝λ，∴AD∥BC，设D（x0，），∴＝（x0﹣，0），＝（﹣，﹣），∴•＝﹣（x0﹣）+0＝﹣，解得x0＝，∴D（，），∴＝（1，0），＝（6，0），∴＝，∴λ＝，∵||＝1，设M（x，0），则N（x+1，0），其中0≤x≤5，∴＝（x﹣，﹣），＝（x﹣，﹣），∴•＝（x﹣）（x﹣）+＝x2﹣4x+＝（x﹣2）2+，当x＝2时取得最小值，最小值为，故答案为：，．18．已知O在△ABC内，且S△AOB：S△BOC：S△AOC＝4：3：2，，则λ+μ＝【解答】解：如图，根据题意不妨设△ABC的边，AB＝4，AC＝2，BC＝＝2，建立如图坐标系，则BC的方程为x+2y﹣4＝0，则3a﹣4＜0，设O点坐标为（a，a），点O在三角形内，则O到BC的距离d＝＝，则根据S△AOB：S△BOC：S△AOC＝4：3：2，得（•4a）：（2×）：（×2a），解得a＝，∴＝（，），＝（4，0），＝（0，2），由，得，解得，，所以：λ+μ＝，故填：19．已知，，，，…，（k∈N*）是平面内两两互不相等的向量，满足||＝1，且|﹣|∈{1，2}（其中i＝1，2，j＝1，2，…，k），则k的最大值是6．【解答】解：如图，设，，由||＝1，且|﹣|∈{1，2}，分别以A1，A2为圆心，以1和2为半径画圆，其中任意两圆的公共点共有6个．故满足条件的k的最大值为6．故答案为：6．20．在△ABC中，点D，E分别在边AB，BC上，且AD＝DB，BE＝2EC，记，＝，若，则x+y的值为．【解答】解：如图，∵AD＝DB，BE＝2EC；∴，＝，且；∴＝；又；∴根据平面向量基本定理得，；∴．故答案为：．21．在四边形ABCD中，AB＝6，若，则＝12．【解答】解：根据题意，如图，在AB上取一点E，使＝，则有＝+＝+＝+（﹣）＝+，又由，则有＝，四边形AECD为平行四边形，则有＝＝，又由AB＝6，则＝6×2＝12；故答案为：12．22．已知△ABC的一内角，AB＝10，AC＝6，O为△ABC所在平面上一点，满足|OA|＝|OB|＝|OC|，设＝m+n，则m+3n的值为．【解答】解：由得：||＝||＝||，则点O是△ABC的外心，则，由＝10×＝30所以，所以，所以m+3n＝，故答案为：23．在直角坐标系中，O为原点，，则x+y＝0．【解答】解：∵，∴x+y＝2（﹣），∴（x+2）+（y﹣2）＝，∴x＝﹣2，y＝2，x+y＝0，故答案为：0．24．已知，，，则＝2．【解答】解：因为，，，所以＝7，所以＝1，则2＝＝4﹣4×1+4＝4，则＝2．故答案为：2．25．已知G为△ABC的重心，过点G的直线与边AB，AC分别相交于点P，Q．若＝，则当ABC与△APQ的面积之比为时，实数λ的值为或．【解答】解：G为△ABC的重心，所以＝+，设＝μ，故＝+，因为P，G，Q三点共线，故+＝1①，所以+＝3，＝＝＝②，由①②得或，故答案为：或．26．如图，给定单位向量和，它们的夹角为120°，点C在以O为圆心的上运动．若，其中x，y∈R，则x+2y的最大值是．【解答】解：根据题意，建立如图所示的坐标系，则A（1，0），B（cos120°，sin120°），即B（﹣，）；设∠AOC＝α，则＝（cosα，sinα），∵，∴（cosα，sinα）＝（x，0）+（﹣y，y）；即cosα＝x﹣y，sinα＝y，解得：x＝sinα+cosα，y＝sinα；∴x+2y＝sinα+cosα＝sin（α+θ），其中tanθ＝；又sin（α+θ）≤1，∴x+2y≤．故答案为：．27．已知点O是△ABC内部一点，并且满足，△BOC的面积为S1，△ABC 的面积为S2，则＝．【解答】解：因为，所以，分别取AC，BC的中点D，E，则，，所以，即O，D，E三点共线且，则，因为D为AC中点，所以，所以．故答案为：．28．设λ是正实数，三角形ABC所在平面上的另三点A1，B1，C1满足：＝λ（+），＝λ（+），＝λ（+），若三角形ABC与三角形A1B1C1的面积相等，则λ的值为．【解答】解：△ABC的重心为点G，由题意可知△ABC与△A1B1C1关于中心点G对称，由，＝（+）＝λ（+），故，故答案为：．四．解答题（共4小题）29．如图，已知△ABC中，D为BC的中点，AE＝EC，AD，BE交于点F，设＝，＝．（1）用，分别表示向量，；（2）若＝t，求实数t的值．【解答】解：（1）由题意，D为BC的中点，且＝，∵+＝2，∴＝2﹣，∴＝﹣＝2﹣﹣＝﹣+2；（2）∵＝t＝t，∴＝﹣＝﹣+（2﹣t），∵＝﹣+2，，共线，∴，∴t＝．30．如图所示，在△ABO中，，，AD与BC相交于点M，设，．（1）试用向量，表示；（2）过点M作直线EF，分别交线段AC，BD于点E，F．记，，求证：为定值．【解答】解：（1）由A，M，D三点共线，可设＝，由B，M，C三点共线，可设＝，因为，不共线，所以，解得，，故．（2）因为E，M，F三点共线，设＝，由（1）知，，即，，所以，故为定值，即得证．31．如图，在平面直角坐标系中，点A（﹣，0），B（，0），锐角α的终边与单位圆O 交于点P．（Ⅰ）用α的三角函数表示点P的坐标；（Ⅱ）当•＝﹣时，求α的值；（Ⅲ）在x轴上是否存在定点M，使得||＝||恒成立？若存在，求出点M的横坐标；若不存在，请说明理由．【解答】解：锐角α的终边与单位圆O交于点P．（Ⅰ）用α的三角函数表示点P的坐标为（cosα，sinα）；（Ⅱ），，•＝﹣时，即（cos）（cos）+sin2α＝，整理得到cos，所以锐角α＝60°；（Ⅲ）在x轴上假设存在定点M，设M（x，0），，则由||＝||恒成立，得到＝，整理得2cosα（2+x）＝x2﹣4，所以存在x＝﹣2时等式恒成立，所以存在M（﹣2，0）．32．已知O是△ABC所在平面内一点，D为BC边中点．（1）若点O满足，求证：；（2）已知E为AC边中点，O在线段DE上，且满足，△BOC的面积为2，求△ABC的面积．【解答】解：（1）∵D为BC边中点；∴；∴由得，；∴；（2）如图，根据条件：＝＝；∴；∴DE＝3DO；又AB＝2DE；∴AB＝6DO；∴S△ABC＝6S△BOC＝12；即△ABC的面积为12．。

高中数学第六章平面向量及其应用-向量的数乘运算课件及答案

【对点练清】 1．若典例 3 中条件“―A→B ＝2e1－8e2”改为“―A→B ＝2e1＋ke2”且 A，B，D
三点共线，如何求 k 的值？
解：因为 A，B，D 三点共线，所以―A→B 与―B→D 共线．设―A→B ＝λ―B→D (λ∈R)， ∵―B→D ＝―C→D －―C→B ＝2e1－e2－(e1＋3e2)＝e1－4e2，
2e2＝3e1＋6e2， ―B→D ＝―B→C ＋―C→D ＝－5e1＋6e2＋7e1－2e2＝2e1＋4e2， ―A→C ＝―A→B ＋―B→C ＝e1＋2e2－5e1＋6e2＝－4e1＋8e2. (1)―A→D ＝3(e1＋2e2)＝3―A→B ，∴―A→B 与―A→D 共线． (2)―B→C 与―B→D 不共线．(3)―C→D 与―A→C 不共线．
【对点练清】
1．设向量
a
＝3i＋2j，b
＝2i－j，求13a
－b
－a
－23b
＋(2b
－a
)．
解：原式＝13a －b －a ＋23b ＋2b －a
＝13－1－1a ＋－1＋23＋2b ＝－53a ＋53b
＝－53(3i＋2j)＋53(2i－j)＝－53i－5j.
2．已知 a 与 b ，且 5x＋2y ＝a ,3x－y ＝b ，求 x，y .
知识点一向量的数乘运算 (一)教材梳理填空 1．向量的数乘运算：
定义
一般地，实数 λ 与向量 a 的积是一个_向__量___，这种运算叫做向量的数乘，记作 λa
长度
|λa |＝|λ||a |
λ＝0
方向
λ＞0
λ＝0
λa 的方向与 a 的方向_相__同___ λa ＝_0__
λa 的方向与 a 的方向_相__反___

6.2.3 向量的数乘运算(精练)(解析版)(练习))

2022春·云南楚雄·高三校考阶段练习）如图，2AE EF +=（3122AB AD + 3322AB AD +1322AB AD +．2AB AD +【答案】B【详解】在ADE 中由向量加法的三角形法则得：AE AD DE =+，又因为E 是DC 的中点，所以12DE DC =, 所以1122AE AD DC AD AB =+=+.ECF 中由向量加法的三角形法则得：EF EC CF =+ 又因为E ，F 分别是矩形ABCD 的边CD ，BC 的中点，所以1122EF EC CF AB AD =+=- 111332222222AE EF AD AB AB AD AD AB ⎛⎫⎛⎫+=++-=+ ⎪ ⎪⎝⎭⎝⎭.故选：B.2．（2022秋·新疆哈密·高一哈密市第一中学校考期中）已知5,28,3()AB a b BC a b CD a b =+=-+=-，则（）A ．ABC ，，三点共线 B ．A CD ，，三点共线C ．A B D ，，三点共线 D ．【答案】C【详解】对于A:不存在实数λ ，使得AB BC λ=，故,A 三点不共线；13,3(),AB BC a b CD a A b C +=-==+-不存在实数使得AC CD λ=，故,A 三点不共线；C:283()5a b a BD BC b CD b a =-++-=+=+ ,故 AB BD =，所以，使得BC CD λ=，故B C 在线段AB 上，且34AC CB =，若AB BC λ=，则λC 74D ．74-【详解】不妨设4CB a =，则334AC CB a ==， AB 上，则74AB BC =-，·河南商丘·高一商丘市第一高级中学校考阶段练习）已知点是ABC 所在平面内一点，若3255AP AB AC =+，则ABP 与△B ．2:3 C 【详解】由()()323232555555AP AB AC AP PB AP PC AP PB PC =+=+++=++ 可得32PC BP =，即点P 在线段BC 上，且32PC BP = 则ABP 与ACP △的面积之比等于:BP PC =2:3 故选：B．（2022春·北京大兴等的直角三角形和一个正方形构成现仿照赵爽弦图，用四个三角形和一个小平行四边形构成如下图形，若AG x AB y AD =+，2x y +等于（24由题意可得()1111=2224AG AB BG AB BH AB BC CH AB BC CE =+=+=++++，是平行四边形，所以AG CE =-，所以1124AG AB BC AG =+-，所以4255AG AB BC =+，因为AG xAB y AD =+，所以42,55x y ==，422255y +=⨯+=． :D（2022秋·山东聊城·高一山东聊城一中校考阶段练习）已知点内一点，满足0GA GB GC ++=，则B ．内心【详解】因为0GA GB GC ++=，所以 GA GB GC CG +=-=.为邻边作平行四边形GADB ，连接GD 交AB 于点O则CG GD =，所以13GO CO =，CO 是故选：D．（2022·高一课时练习）在ABC 中，若(0,AD AB AC λμλ=+>21λμ+的最小值为（）22D ．422+三点共线，所以λ+已知ABC ，I ．1()3AI AB AC =+．cAB bACAI a a=+．bAB c ACAI a b c a b c =+++++ ．c AB bACAI a b a c=+++ 【答案】C【详解】延长,,AI BI CI ，分别交,,E F .内心是三角形三个内角的角平分线的交点.在三角形ABD 和三角形ACD 中，由正弦定理得： b c+所以()c c AD AB BD AB BC AB AC AB b c b c=+=+=+-++ b cAB AC b c b c+++，则b c b c b c b c AI AD AB AC AB AC a b c a b c b c b c a b ca b c ++⎛⎫=⋅=⋅+=+ ⎪++++++++++⎝⎭.故选：C二、多选题高一课时练习）在ABC 中，12,33AE AB AD AC ==，记,BC a CA b ==，则下列．()13AE a b =-- B ．AD b =- C ．()13DE b a =- D ．AB a b =+【答案】AC【详解】解：因为12,33AE AB AD AC ==，,BC a CA b ==，所以22,33AB AC CB b a AD AC b =+=--==-，所以()1133AE AB a b ==--，()()211333DE DA AE b a b b a =+=-+=-. 故选：AC.10．（2022秋·广东清远·高一校考阶段练习）如图所示，在ABC 中，点D 在边BC 上，且上，且3AD AE =，则（．1233AD AC AB =+ ．13CE AD AC =-．2899CE AB AC =+ ．28–99CE AB AC =上，3AD AE =，()22123333AD AC CD AC CB AC AB AC AC AB =+=+=+-=+，1122839999CE AE AC AD AC AC AB AC AB AC =-=-=+-=-．故选：ABD ．三、填空题．（2022秋·上海宝山·高一上海交大附中校考期末）古代典籍《周易》中的我国的建筑有一定影响．图1是受“八卦”启示设计的正八边形的八角窗．在正八边形中，若(,AC x AB y AH x y =+∈【答案】## ABCH ，，即()21HC AB =+，()21AC AH HC AB AH =+=++，则21,1=+=x y ，22x y +=+. 故答案为：22+.12．（2022秋·江西景德镇·高一统考期末）已知点O 在直线AB 外，,,()OC OA OB R λμλμ=+∈在直线AB 外；③若λμ+=且01λ≤≤，则点C 在线段AB 上；④若1λμ+=，且0λ<，则点C 在射线AB 上，⑤若1λμ+=，且1λ>，则点C 在射线BA 上：其中真命题的是___________.（填序号）【答案】①②③④⑤ 【详解】①若1λμ+=，则(1)()OC OA OB OA OB OB OA OB OB BA λμλλλλ=+=+-=+-=+，有OC OB BC BA λ-==，所以B C A 、、三点共线，故①为真命题； ②假设点C 在直线AB 上，则()(1)OC OA AC OA k AB OA k OB OA k OA kOB =+=+=+-=-+，又OC OA OB λμ=+，所以1k k λμ=-=，，得1λμ+=，与条件中1λμ+≠矛盾，故假设不成立，即点C 不在直线AB 上，故②为真命题； ③若1λμ+=，则(1)()OC OA OB OA OB OB OA OB OB BA λμλλλλ=+=+-=+-=+，有OC OB BC BA λ-==，当01λ≤≤时，由BC BA λ=可知B C A 、、三点共线且C 在B A 、之间（或与B 、A 重合），所以点C 在线段AB 上，故③为真命题； ④若1λμ+=，则(1)()OC OA OB OA OB OB OA OB OB BA λμλλλλ=+=+-=+-=+，有OC OB BC BA λ-==，当0λ<时，由BC BA λ=可知B C A 、、三点共线且B 在A C 、之间，所以点C 在射线AB 上，故④为真命题； ⑤若1λμ+=，则(1)()OC OA OB OA OB OB OA OB OB BA λμλλλλ=+=+-=+-=+，有OC OB BC BA λ-==，当1λ>时，由BC BA λ=可知B C A 、、三点共线且A 在B C 、之间，所以点C 在射线BA 上，故⑤为真命题；故答案为：①②③④⑤ 四、解答题13．（2022·全国·高一专题练习）（1）已知1e ，2e 是两个不共线的向量，若1228AB e e =-，123CB e e =+，122CD e e =-，求证：A ，B ，D 三点共线．（2）已知A ，B ，P 三点共线，O 为直线外任意一点，若OP xOA yOB =+，求x y +的值．【答案】（1）证明见解析；（2）1）124BD CD CB e e =-=-，又12282AB e e BD =-=，所以AB ，BD 共线为直线外任意一点，所以设AB BD λ=，所以()AO OB BO OP λ+=+，所以111OP OA OB λλ⎛⎫=-++ ⎪⎝⎭，因为OP xOA yOB =+，所以x =，11y λ=+，所以1x y +=.14．（2022·全国·高一假期作业）如图所示，在△ABC 中，D ，F 分别是BC ，AC 2,,3AE AD AB a AC b ===.(1)用,a b 表示,,,,AD AE AF BE BF ；求证：B ，E ，F 三点共线．【答案】(1)1122AD a b =+，1133AE a b =+，12=AF b ，1233BE b a =-，12BF b a =-证明见解析【详解】（1）解：在△ABC 中，D ，F 分别是BC ，AC 的中点，则()111111222222AD AB BD AB BC AB AC AB AB AC a b =+=+=+-=+=+，故211333AE AD a b ==+， 1122==AF AC b ， 11123333BE AE AB a b a b a =-=+-=-，12BF AF AB b a =-=-；（2）证明：因为()1212333BE b a b a =-=-，()122b a BF =-，所以23BE BF =，所以BE BF ∕∕，又因,BE BF 有公共点B ，高一专题练习）用向量运算刻画三角形的重心．已知ABC ，求一点G 满足0GA GB GC ++=．求证：满足条件0GA GB GC ++=的点G 是ABC 的重心．（提示：说明点同时在ABC 的三条中线上．）【答案】(1)详解见解析；证明见解析. AB 、BC 的中点，连接、AF 交于点为ABC 的重心，DE=GD ，连接由向量加法的平行四边形法则，得2GA GB GE GD +==，因为G 为ABC 的重心，所以2CG GD =，故2CG GD =，所以20GA GB GC GD GC CG GC ++=+=+=，所以ABC 的重心G 满足题意； (2)因为0GA GB GC ++=，所以GA GB GC CG +=-=，以GA 、GB 为邻边作GAEB，连接GA GB GE +=，所以CG GE =，设AB 与GE 交于点D ，由平行四边形的性质可知点所以2GE GD CG ==，即G 在中线同理可证G 也在其它两边的中线上，即所以G 为ABC 的重心.16．（2022春·黑龙江哈尔滨·高二哈九中校考开学考试）如图，分别是边OA 、OB 上的动点，且(1)设PG PQ λ=，将OG 用λ，OP ，OQ 表示；设OP xOA =，OQ yOB =，证明：11x y+是定值．【答案】（1）见解析；（2）见解析【详解】(1)解＝＋＝＋λ＝＋λ(－)＝(1－λ)＋λ.(2)证明一方面，由(1)，得＝(1－λ)＋λ＝(1－λ)x ＋λy ；① 另一方面，∵G 是△OAB 的重心，∴＝＝× (＋)＝＋.②而，不共线，∴由①②，得解得∴＋＝3(定值)．C 综合素养高一专题练习）已知ABC 中，过重心G 的直线交边AB 于P APQ △的面积为1S ，ABC 的面积为2S ，AP pPB =，AQ qQC =. ）求GA GB GC ++；）求证：111p q+=. 12S S 的取值范围.）0；（2）证明见解析；（+2GB GC GD ∴=,G 是重心，2GA GD ∴=-，2+20GA GB GC GD GD ∴++=-=；（2）设,AB a AC b ==,AP pPB =，1+p AP a p =∴， AQ qQC =，1+q AQ b q∴=， ,,P G Q 三点共线，则存在λ，使得PQ PG λ=，即()AQ AP AG AP λ-=-，即11++1+1+331+31+3q p p p a a b a b q p b a p p λλλλ⎛⎫⎛⎫-=-=- ⎪ ⎪⎝⎭⎝⎭， 1+31+3p p p p q λλλ⎧-=-⎪⎪∴⎨=，整理得33211p q p q λ==-+， 11q -+=1121-=+111+=）1+p AP AB p =，1+q AQ AC q =， sin 1+1+sin AP AQ BAC AP AQ p p AB AC AB AC BAC ⋅⋅∠⋅==⋅⋅⋅⋅∠111p q +=，1p q p =-，可知1p >，1 p>，∴则当1 p =11p≠，则。

向量的数乘运算(练习)(含解析)高一下学期数学(人教A版2019 必修第二册)

6.2.3向量的数乘运算1.[2022·浙江台州高一期末]3(2a －b )－2(a ＋3b )的化简结果为( )A ．4a ＋3bB ．4a －9bC ．8a －9bD ．4a －3b2．[2022·广东惠州高一期末]在△ABC 中，D 为BC 上一点，且BD ＝2DC ，则AD → ＝( )A ．AB → ＋13 AC → B ．AB → －13AC → C ．23 AB → ＋13 AC → D ．13 AB → ＋23AC → 3．已知非零向量e 1，e 2不共线，如果AB → ＝e 1＋2e 2，BC → ＝－5e 1＋6e 2，CD → ＝7e 1－2e 2，则共线的三个点是________．4．化简：(1)2(a －b )＋3(a ＋b )；(2)12 (a ＋b )＋12(a －b )； (3)3(a ＋2b )－2(a ＋3b )－2(a ＋b ).5.若AP → ＝14PB → ，AB → ＝λBP → ，则实数λ的值是( ) A ．45 B ．－45C ．54D ．－546．[2022·福建泉州高一期中]如图，已知△ABC 中，D 为边BC 上靠近B 点的三等分点，连接AD ，E 为线段AD 的中点，若CE → ＝mAB → ＋nAC → ，则2m ＋n ＝( )A ．－16B ．－12C ．－14D ．127．[2022·广东广州高一期中]设e 1、e 2是两个不共线的向量，已知AB → ＝2e 1＋k e 2，BC → ＝e 1＋3e 2，CD → ＝2e 1－e 2，若A ，B ，D 三点共线，求k 的值为________．8．两个非零向量a ，b 不共线，若AB → ＝a ＋b ，BC → ＝2a ＋8b ，CD → ＝3(a －b )，求证：A ，B ，D 三点共线．9．已知D 为△ABC 的边BC 的中点，E 为AD 上一点，且AE → ＝3ED → ，若AD → ＝a ，试用a 表示EA → ＋EB → ＋EC → .10．设a ，b ，c 为非零向量，其中任意两向量不共线，已知a ＋b 与c 共线，且b ＋c 与a 共线，则b 与a ＋c 是否共线？请证明你的结论．11.[2022·山东潍坊高一期中]在△ABC 中，AP → ＝119 AB → －29AC → ，则P 点( ) A ．在线段BC 上，且BP BC ＝29B ．在线段CB 的延长线上，且BP BC ＝29C ．在线段BC 的延长线上，且BP BC ＝29D ．在线段BC 上，且CP BC ＝2912．如图所示，在△ABC 中，D ，F 分别是BC ，AC 的中点，AE → ＝23AD → ，AB → ＝a ，AC → ＝b .(1)用a ，b 表示AD → ，AE → ，AF → ，BE → ，BF → ；(2)求证：B ，E ，F 三点共线．答案：1．解析：由题意，3(2a －b )－2(a ＋3b )＝4a －9b .故选B.答案：B2．解析：因为在△ABC 中，D 为BC 上一点，且BD ＝2DC ，所以AD → ＝AB → ＋BD → ＝AB → ＋23 BC → ＝AB → ＋23 (AC → －AB → )＝13 AB → ＋23AC → ，故选D. 答案：D3．解析：∵AB → ＝e 1＋2e 2，BD → ＝BC → ＋CD → ＝－5e 1＋6e 2＋7e 1－2e 2＝2(e 1＋2e 2)＝2AB → . ∴AB → ，BD → 共线，且有公共点B ，∴A ，B ，D 三点共线．答案：A ，B ，D4．解析：(1)2(a －b )＋3(a ＋b )＝2a －2b ＋3a ＋3b＝5a ＋b .(2)12 (a ＋b )＋12(a －b ) ＝12 a ＋12 b ＋12 a －12b ＝a .(3)3(a ＋2b )－2(a ＋3b )－2(a ＋b )＝3a ＋6b －2a －6b －2a －2b＝－a －2b .5．解析：由AP → ＝14 PB → ，则A ，P ，B 三点共线，且AP → ＝15AB → ，所以PB → ＝45 AB → ，即AB → ＝－54BP → .故选D. 答案：D6．解析：依题意得，AD → ＝AB → ＋BD → ＝AB → ＋13 BC → ＝AB → ＋13 (AC → －AB → )＝23 AB → ＋13AC → ，故CE → ＝CA → ＋AE → ＝CA → ＋12 AD → ＝－AC → ＋12 (23 AB → ＋13 AC → )＝13 AB → －56AC → ，所以m ＝13 ，n ＝－56，故2m ＋n ＝2×13 －56 ＝－16.故选A. 答案：A7．解析：由A 、B 、D 三点共线，可得AB → ＝λBD → (λ≠0)，又AB → ＝2e 1＋k e 2，BD → ＝BC →＋CD → ＝3e 1＋2e 2，则2e 1＋k e 2＝3λe 1＋2λe 2，又e 1、e 2不共线，则⎩⎪⎨⎪⎧2＝3λk ＝2λ ，解得k ＝43 . 答案：438．证明：因为AB → ＝a ＋b ，BC → ＝2a ＋8b ，CD → ＝3(a －b )，所以BD → ＝BC → ＋CD → ＝2a ＋8b ＋3(a －b )＝5a ＋5b ，则BD → ＝5AB → ，所以BD → ，AB → 共线，两个向量有公共点B ，所以A ，B ，D 三点共线．9．解析：如图，∵AE → ＝3ED → ，且AD → ＝a ，∴ED → ＝14 AD → ＝14 a ，EA → ＝－34 AD → ＝－34a ，又D 为边BC 的中点，∴EB → ＋EC → ＝2ED → ＝12a ， ∴EA → ＋EB → ＋EC → ＝－34 a ＋12 a ＝－14a . 10．解析：b 与a ＋c 共线．证明如下：∵a ＋b 与c 共线，∴存在唯一实数λ，使得a ＋b ＝λc .①∵b ＋c 与a 共线，∴存在唯一实数μ，使得b ＋c ＝μ a .②由①－②得，a －c ＝λc －μa .∴(1＋μ) a ＝(1＋λ)c .又∵a 与c 不共线，∴1＋μ＝0，1＋λ＝0，∴μ＝－1，λ＝－1，∴a ＋b ＝－c ，即a ＋b ＋c ＝0.∴a ＋c ＝－b .故a ＋c 与b 共线． 11．解析：由题设，AP → －AB → ＝29 (AB → －AC → )，则BP → ＝29CB → ，所以C ，P ，B 共线且P 在CB 延长线上，BP CB ＝29.故选B. 答案：B12．解析：(1)在△ABC 中，D ，F 分别是BC ，AC 的中点，则AD → ＝AB → ＋BD → ＝AB → ＋12 BC → ＝AB → ＋12 (AC → －AB → )＝12 AB → ＋12 AC → ＝12 a ＋12b ，故AE → ＝23 AD → ＝13 a ＋13b ， AF → ＝12 AC → ＝12b ， BE → ＝AE → －AB → ＝13 a ＋13 b －a ＝13 b －23a ， BF → ＝AF → －AB → ＝12b －a ； (2)证明：因为BE → ＝13 b －23 a ＝13 (b －2a )，BF → ＝12(b －2a )，所以BE → ＝23BF → ，所以BE→∥BF→，又因为BE→，BF→有公共点B，所以B，E，F三点共线．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1、
2、
3、
4、5、6、7、8、9、
10、
11、
12、
13、
14、
15、
16、
17、
18、
19、
20、
21、设O 为△ABC 所在平面内一点，且满足OA →·OB →
＝OB →
·OC →
＝OA →
·OC →
，则O 是△ABC 的( )
A ．内心
B ．外心
C ．垂心
D ．重心
22、在△ABC 中，|AB →
|＝|AC →
|＝2，且AB →·AC →
＝2，则△ABC 的形状是________．
23、已知平面上三点A ，B ，C 满足|AB →
|＝2，|BC →
|＝1，|CA →
|＝3，则AB →·BC →
＋BC →·CA →
＋CA →·AB
→
＝___
24、在四边形ABCD 中，AB →
＝DC →
＝(1,1)，1|BA →
|
BA →
＋1|BC →|
BC →
＝
3|BD →
|
BD →
，则四边形ABCD
的面积为____ 25、已知A (
3，－2)与B (－
3，4)，若PA ＝PB ，求动点P 的轨迹方程．
26、平面向量a 与b 的夹角为60°，a ＝(2,0)，|b |＝1，则|a ＋2b |＝( ) 27、已知向量a ＝(－2，－1)，a ·b ＝10，|a －b |＝
5，则|b |＝( )
28、若向量AB →
＝(3，－1)，n ＝(2,1)，且n ·AC →
＝7，则n ·BC →
＝( ) 29、a ＝(0,1)，b ＝(1,1)，且(a ＋λb )⊥a ，则λ＝( )
30、若a ＝(2,3)，b ＝(－4,7)，则a 在b 方向上的射影为____
31、平面向量a ，b 中，已知a ＝(4,3)，|b |＝1，且a ·b ＝5，则b ＝______
32、已知a ＝(1,3)，b ＝(1,1)，c ＝a ＋λb ，a 和c 的夹角为锐角，则实数λ的取值范围是____ 33、已知a ＝(1，x )，b ＝(2x ＋3，－x )．
(1)若a ⊥b ，求x 的值；(2)若a 与b 共线，求|a －b |.
34、已知点A (1,2)，B (4，－1)，问能否在y 轴上找到一点C ，使∠ACB ＝90°，若能，请求出点C 的坐标；若不能，请说明理由．
35、已知平面xOy 内有向量OA →
＝(1,7)，OB →
＝(5,1)，OP →
＝(2,1)，点X 为直线OP 上的一个动点．
(1)当XA →·XB →
取最小值时，求OX →
的坐标；(2)当点X 满足(1)的条件时，求cos ∠AXB 的值． 36、若向量a ，b ，c 满足a ∥b 且a ⊥c ，则c ·(a ＋2b )＝( )
37、平面向量a 与b 的夹角为60°，|a |＝2，|b |＝1，则|a ＋2b |等于( ) 38、设非零向量a ，b ，c 满足|a |＝|b |＝|c |，a ＋b ＝c ，则a 与b 的夹角θ为( ) 39、已知|a |＝2|b |≠0，且关于x 的方程x 2＋|a |x ＋a ·b ＝0有实根，则a 与b 的夹角的取值范围是( )
40、在△OAB 中，OA →
＝a ，OB →
＝b ，OD →
是AB 边上的高，若AD →
＝λAB →
，则λ等于( ) 41、已知e 1，e 2是夹角为2
3π的两个单位向量，a ＝e 1－2e 2，b ＝k e 1＋e 2，若a ·b ＝0，则实
数k 的值为_____
42、若AB →·BC →
＋AB →
2＝0，则△ABC 为________三角形．
43、已知|a |＝3，|b |＝4，且a 与b 不共线，k 为何值时，向量a ＋k b 与a －k b 互相垂直． 44、已知|a |＝4，|b |＝3，(2a －3b )·(2a ＋b )＝61.
(1)求a 与b 的夹角θ；(2)求|a ＋b |与|a －b |.
45、已知AB →＝(6,1)，BC →＝(x ，y )，CD →＝(－2，－3)，且BC →∥DA →
，则x ＋2y 的值为( ) 46、已知向量a ＝(1，m )，b ＝(m,2)，若a ∥b ，则实数m 等于( ) 47、若a ＝(1＋2λ，2－3λ)与b ＝(4,1)共线，则λ＝__
48、已知向量a ＝(3,1)，b ＝(1,3)，c ＝(k,7)，若(a －c )∥b ，则k ＝___
49、在平面直角坐标系中，四边形ABCD 的边AB ∥DC ，AD ∥BC ，已知A (－2,0)，B (6,8)，
C (8,6)，则
D 点的坐标为__
50、若向量a ＝(2，－1)，b ＝(x,2)，c ＝(－3，y )，且a ∥b ∥c ，求x ，y 的值
51、已知OA →
＝(3，－4)，OB →
＝(6，－3)，OC →
＝(5－m ，－(3＋m ))，若A ，B ，C 不能构成三角形，求实数m 应满足的条件．。