规划计算题

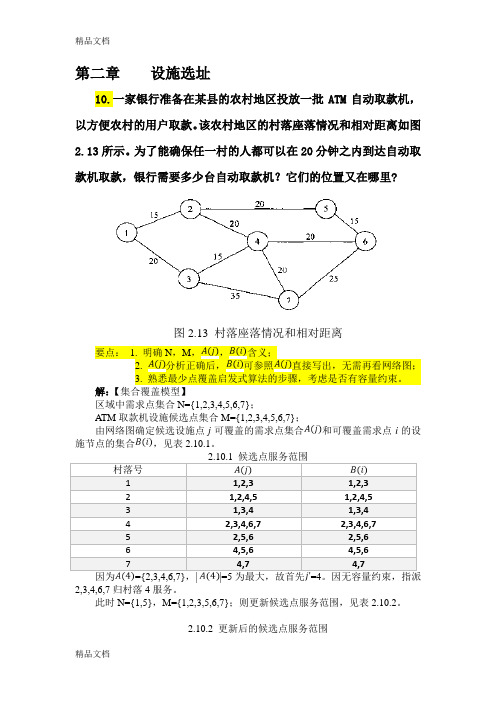
第二章设施选址10.一家银行准备在某县的农村地区投放一批ATM自动取款机，以方便农村的用户取款。

该农村地区的村落座落情况和相对距离如图所示。

为了能确保任一村的人都可以在20分钟之内到达自动取款机取款，银行需要多少台自动取款机它们的位置又在哪里图村落座落情况和相对距离要点： 1. 明确N，M，A(j)，B(i)含义；2. A(j)分析正确后，B(i)可参照A(j)直接写出，无需再看网络图；3. 熟悉最少点覆盖启发式算法的步骤，考虑是否有容量约束。

解：【集合覆盖模型】区域中需求点集合N={1,2,3,4,5,6,7}；ATM取款机设施候选点集合M={1,2,3,4,5,6,7}；由网络图确定候选设施点j可覆盖的需求点集合A(j)和可覆盖需求点i的设施节点的集合B(i)，见2,3,4,6,7归村落4服务。

此时N={1,5}，M={1,2,3,5,6,7}；则更新候选点服务范围，见表综上所述，银行需要2台自动取款机，分别至于村落号为2和4的位置，2号为1,5村落服务，4号为 2,3,4,6,7村落服务。

11. —个临时帮助服务中心计划在一个大城市的郊外开设一个新的办公室。

在经过一定的精简之后，该公司有5个大的合作伙伴。

在一个以km 为单位的笛卡尔坐标系中，它们的坐标分别为：(4，4)，(4，11)，(7 ，2)，(11，11)， (14，7)。

它们的服务需求量的权重分别为：wl=3，w2=2，w3=2，w4=4，w5=1。

对于该服务中心来说，主要的日常费用是他们员工完成任务过程中的运输费用。

因此，用城市距离进行考虑，要求新的办公室到各个合作伙伴之间运输的运输费用最小。

1）请确定一个新办公室的地址，用笛卡尔坐标来表达相应结果。

2）如果由于该地区的人口稀少，城市还没有达到一定的规模，可以用欧几米德距离进行计算，新办公室又得在哪里投建请比较两次结果，分析它们之间的关系。

要点：1. 补充交叉中值模型知识点关键句：将n 点需求的选址问题转化为∑w i n i=1点需求的选址问题。

2.笛卡尔距离即直角距离，欧基米德距离即直线距离；3.重心法：初始化+迭代公式+Excel/C 编程/matlab 编程迭代+迭代终止条件解：（1）设新办公室的地址的坐标为(x,y ),给题目已知的5个点编号1~5。

由于笛卡尔距离d i =|x -x i |+|y -y i |。

则目标函数为时总运输距离H 最短。

H =∑w i 5i=1d i =∑w i 5i=1|x −x i |+∑w i 5i=1|y −y i |i可得x =7，y ∈[7,11]。

H =81。

（2）设初始点为（x 0， y 0）有题意得，阿基米德距离为d i (0)=√(x 0−x i )2+(y 0−y i )2, 目标函数H(运输总费用)=∑w i 5i=1d i ,利用不动点算法，取一个初始的迭代点（x 0(0),y 0(0)）=(8,7),此时H 0= 令x 0(1)=∑w i x id i5i=1∑x i d i5i=1, y 0(1)=∑w i y id i5i=1∑y i d i5i=1,d i (1)=√(x 0(1)−x i )2+(y 0(1)−y i )2H 1=∑w i 5i=1d i (1)= 由EXCEL迭代得，结果如图费用结果保留四位小数得最优解为 x=,y=,此时费用最小为H=（3）比较两次结果可知欧基米德中的费用小于笛卡尔距离，因直线距离是＜直角距离，因此用欧基米德距离更为精确。

直角距离比较适合于城区范围内的选址，欧基米德距离比较适合于远距离的选址。

12.一台机器工具小制造商要迁址，并确定了两个地区以供选择。

A 地的年固定成本为800000元，可变成本为14000元/台；B 地的年固定成本为920000元，可变成本为13000元/台。

产品最后售价为17000元/台。

（1） 当产量为多少时，两地的总成本相等（2） 当产量处于什么范围时，A 地优于B 地当产量处于什么范围时，B 地优于A 地解：答：设x 为之制造商的年产量 A 地，总成本C(A)=800000+14000x B 地，总成本C(B)=920000+13000x 1)若两地成本相等，则C(A)=C(B) 解得：x=1202）若A 地优于B 地，则C(A)<C(B),因此得0<x<120 同理，当x>120时，B 地优于A 地。

13．利用表所示的因素评分，以最大综合得分为基础，建模分析应选择地点A 、B 、C 中的哪一个表 因素评分表解：权重矩阵设为W ，则W T =[0,15 0.20 0.18 0.27 0.10 0.10] 三个位置的因素评分作为3行构成因素矩阵S 。

S =[80 72 88 94 98 9670 76 90 86 90 8560 92 90 80 82 75]可得综合加权矩阵E=S*W=[87.0282.6280.90]。

可知E(A)> E(B)> E(C)。

即选择A 点。

14.一个玩具制造商在全国的五个地区生产玩具，原材料将从一个新的中心仓库运出，而此仓库的地点还有待确定。

运至各地的原材料数量相同，已建立一个坐标城，各地的坐标位置如表所示。

请确定中心仓库的坐标位置。

表 各地的坐标位置解：设仓库的坐标为（x 0，y 0)，五个生产地为(x i ,y i ),仓库到各生产地的距离为d i ,因运至各地的原材料数量相同，故可设w i =1(i =1,2,…5）; 初始解：n n ()()j j j j xx ,y y n n ====∑∑00001111，即x 0(0)=5，y 0(0)=4。

直线距离为d i (0)=√(x 0−x i )2+(y 0−y i )2目标函数运输总费用H=∑w i 5i=1d i ，其中 w i =1(i =1,2,…5）H (0)=∑d j 5j=1=13.6094根据下列进行迭代： x 0(1)=∑x i d i5i=1∑1di5i=1， y 0(1)=∑y i d i5i=1∑1di5i=1，d i (1)=√(x 0(1)−x i )2+(y 0(1)−y i )2直到运费无法减小。

用MATLAB 进行编码：运行结果得，迭代78次得到最优解。

其中选址坐标为（,），最小运费为H=。

或由EXCEL 迭代得，结果如图费用结果保留三位小数得最优解为X=，y=,H=15.某物流公司拟建一仓库负责向四个工厂进行物料供应配送，各工厂的具体位置与年物料配送量见表，设拟建物流公司仓库对各工厂的单位运输成本相等。

利用重心法计算确定物流公司的仓库坐标位置为多少。

表 各工厂的具体位置与年物料配送量解：设仓库的坐标为（x 0，y 0)，4个工厂的坐标为(x i ,y i ),仓库到各生产地的距离为d i =√(x 0−x i )2+(y 0−y i )2,目标函数运输总费用H=∑αi c i 5i=1d i =∑w i 5i=1d i ，αi 为工厂年配送量，c i 为单位运输成本，因单位运输成本相等，故令c i =1，于是有w 1 =2000,w 2=1200,w 3 =1000,w 4=2500初始解x 0=1n ∑x i =, y 0=1n ∑y i = d i (0)=√(x 0−x i )2+(y 0−y i )2, 此时H 0= 令x 0(1)=∑w i x id i5i=1∑x i d ii=1, y 0(1)=∑w iy id i5i=1∑y i d ii=1,d i (1)=√(x 0(1)−x i )2+(y 0(1)−y i )2H 1=∑w i 5i=1d i (1)=由EXCEL 迭代得，结果如图结果保留整数得最优解为（，）,H=188709 或用MATLAB 进行编码（文件见附件）：运行结果得，迭代59次得到最优解。

其中选址坐标为（, ），最小运费为H= 。

16. 筹建一农副产品流通加工厂，可供选择的候选厂址有D 、E 、F 三处，因地址不同各厂加工成本亦有区别，各厂址每年费用如表所示。

此外，为决定厂址还考虑了一些重要的非成本因素，如当地竞争能力、气候变化和周围环境是否适合农副产品流通加工等。

对于竞争能力而言，F地最强，D、E两地相平；就气候来说，D比E好，F地最好；至于环境，E地最优，其次为F 地、D地。

如果各主观因素的重要性指数a、b、c依次为、和，要求用因次分析法评定最佳厂址在何处。

表各候选厂址每年加工成本费用要点：P中值法分5个步骤进行。

解:（1）计算客观量度值OM i，[OM i=C i∑1C i]−1OM D=[523∗(1+1+1)]−1=0.3395同理可得：OM E=0.3382,OM F=0.3223。

（2）计算主观评比值S ik（有3个不同的主观因素）①竞争能力（F>D=E）注：D=E，比较记为两两相比②气候（F>D>E）两两相比③环境（E>F>D ）两两相比（3）计算主观量度值S Mi ， SM i =∑I k S ik 3k=1，其中I k 为各主观因素的重要性指数。

计算可得SM D =0.167∗0.6+0.33∗0.3+0∗0.1=0.1992 SM E =0.167∗0.6+0∗0.3+0.67∗0.1=0.1672 SM F =0.666∗0.6+0.67∗0.3+0.33∗0.1=0.6336（4）计算位置量度值LM i ，LM i =X ∗SM i +（1−X ）∗OM i由于题中没有给出主观因素与客观因素的相互比重，假设两者相等即同种重要，即主客观比重值X =0.5。

LM D =0.5∗0.3395+0.5∗0.1992=0.26935 LM E =0.5∗0.3382+0.5∗0.1672=0.2527 LM F =0.5∗0.3223+0.5∗0.6336=0.47795（5）决策根据各位置量度值LM i 的大小，F 厂址所得位置量度值在3个候选地址中最高，故选F 为建厂厂址。

17.在某区域需规划建设若干个农贸市场为将来该区9个主要居民点提供服务，除第6居民点外，其他各点均有建设市场的条件，如图2－6所示。

已知市场的最大服务直径为3km ，为保护该区域的环境，希望尽可能少地建造农贸市场。

问应如何规划3图2－6 小区居民点位置图解：N＝{1,2,3,4,5,6,7,8,9}，M＝{1,2,3,4,5,7,8,9}，由图2－6两点间的最短距离，根据最大服务半径为3km的约束及第6居民点不适合建市场的要求，可确定集合A(j)和B(i)。

如表2－3所示。

表2－3 候选点服务范围因为A(4)={1,3,4,5,6,7}，A(3)={1,2,3,4,5,6},|A(4)|= |A(3)|=6为最大,随机选取j’＝4。