著名几何定理
(完整版)初中几何几个著名定理及证明

① AC(BP+DP)=AD ・ BC+AB ・ DC ・ 即 AC ・ BD=AB ・ CD+AD ・ BC.2.托勒密定理的逆定理若一个凸四边形两对对边乘积的和等于两条对角线的乘积,则这 个凸四边形內接于一圆。
己知:在凸四边形ABCD 中,AB • CD+AD • BC 二 BD • AC 。
求证:A 、B 、C 、D 四点共圆。
证明:分别以E 、A 为顶点,在 四边形ABCD初屮见何甩个著名炙龌及证明 识玻堵泗阳展療口屮曇蒐疋屮 一.托勒密定理 1.托勒密定理 圆內接四边形中,两条对角线的乘积等于两组对边乘积之和。
己知:圆內接四边形AECD,求证:AC ・BD 二AB • CD+AD ・BC 。
证明:如图所示,过C 作CP 交BD 于P, 使Z1=Z2,又Z3=Z4, AACD^ABCP. 冴 BP BC EP • AC 二 AD • BC 又 ZACB=ZDCP, Z5= Z6,,即 •:A ACB S A DCP . 得需=舘,即DP ・AC =AB ・DC内,作ZABF= ZDBC> ZBAF=ZBDC,—=—=> AB CD^BD-AF则厶ABF^ADBC 〜Ar CDAH _Bn亦—斎又•,• ZABD = Z ABF +ZEBF= ZEBF + ZDBC = ZFBC•'•△ABD S A FB C =x> —=—=>JD-/R-=Hzrc/--HC CF•••AB ・ CD+AD ・ BC=BD* (AF+CF)又VAB・CD+AD ・BC=BD・AC (己知〉,•••AC=AF + CF;「.A、F、C三点共线;ZBAC=ZBAF = ZBDC;:4、B、C、D 四点共圆。
3.托勒密不等式在任意凸四边形中,两组对边乘积的和不小于其两条对角线的乘积。
〈托勒密定理可视作托勒密不等式的特殊情况。
)即在任意凸四边形ABCD中,必有AC ・BDWAB • CD+AD * BC,当且仅当A、B、C、D四点共圆(托勒密定理)或共线(欧扌立几何定理)时取等号。
一些有名的几何定理.

取材自维基百科-中文版. 没事的时候大家可以证着玩! 答案在这里.1. 阿基米德中点定理说明:圆上有两点A,B,M为弧AB的中点,随意选圆上的一点C,D 为AC上的点使得MD垂直AC。
若M、C在弦AB异侧,则AD=DC+BC;若M、C在弦AB 同侧,则AD=DC-CB。
2. 婆罗摩笈多定理指出:若圆内接四边形的对角线相互垂直,则垂直于一边且过对角线交点的直线将平分对边。
婆罗摩笈多是印度数学家。
3. 凡·奥贝尔定理(van Aubel's theorem)说明:给定一个四边形,在其边外侧构造一个正方形。
将相对的正方形的中心连起,得出两条线段。
线段的长度相等且垂直。
4. 芬斯勒–哈德维格尔定理(Finsler-Hadwiger Theorem)说明:若两个正方形ABCD和AB'C'D'拥有同一个顶点A。
B'D的中点、BD'的中点、ABCD的中心和AB'C'D'的中心将组成一个正方形。
5. 莫雷角三分线定理(Morley's theorem)说明对所有的三角形,其三个内角作角三分线,靠近公共边三分线的三个交点,是一个等边三角形。
此定理由法兰克·莫雷在1899年发现。
对外角作外角三分线,也会有类似的性质,可以再作出4个等边三角形。
此定理有趣的地方是我们没办法用尺规作图作出其等边三角形,因为已经证明出尺规做图无法做出三等分角。
6. 拿破仑定理,是拿破仑发现的平面几何学定理:“以三角形各边为边分别向外侧作等边三角形,则他们的中心构成一个等边三角形。
”该等边三角形称为拿破仑三角形。
如果向内作三角形,结论同样成立。
同时拿破仑留下这样的名言:''一个国家只有数学蓬勃发展,才能表现他的国力强大。
——拿破仑7. 泰博定理是法国几何学家维克多·泰博(Victor Thébault,1882年-1960年))提出的平面几何问题。
平面几何的著名定理
平面几何的著名定理一、毕达格拉斯定理(即勾股定理)在任何一个直角三角形中,两条直角边的长的平方和等于斜边长的平方,这就叫做勾股定理。
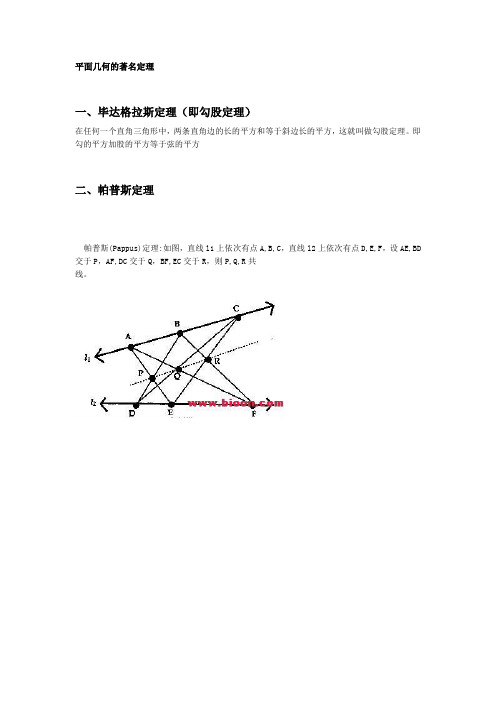
即勾的平方加股的平方等于弦的平方二、帕普斯定理帕普斯(Pappus)定理:如图,直线l1上依次有点A,B,C,直线l2上依次有点D,E,F,设AE,BD 交于P,AF,DC交于Q,BF,EC交于R,则P,Q,R共线。
三、影射定理(与相似三角形和比例有关)直角三角形射影定理(又叫欧几里德(Euclid)定理):直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项。
每一条直角边是这条直角边在斜边上的射影和斜边的比例中项。
公式Rt△ABC中,∠BAC=90°,AD是斜边BC上的高,则有射影定理如下:(1)(AD)^2;=BD·DC,(2)(AB)^2;=BD·BC ,(3)(AC)^2;=CD·BC 。
等积式 (4)ABXAC=BCXAD(可用面积来证明)四、梅涅劳斯定理梅涅劳斯(Menelaus)定理(简称梅氏定理)是由古希腊数学家梅涅劳斯首先证明的。
它指出:如果一条直线与△ABC的三边AB、BC、CA或其延长线交于F、D、E点,那么(AF/FB)×(BD/DC)×(CE/EA)=1。
或:设X、Y、Z分别在△ABC的BC、CA、AB所在直线上,则X、Y、Z共线的充要条件是(AZ/ZB)*(BX/XC)*(CY/YA)=1 。
证明一过点A作AG∥BC交DF的延长线于G,则AF/FB=AG/BD , CE/EA=DC/AG。
三式相乘得:(AF/FB)×(BD/DC)×(CE/EA)=(AG/BD)×(BD/DC)×(DC/AG)=1证明二过点C作CP∥DF交AB于P,则BD/DC=FB/PF,CE/EA=PF/AF所以有AF/FB×BD/DC×CE/EA=AF/FB×FB/PF×PF/AF=1它的逆定理也成立:若有三点F、D、E分别在△ABC的边AB、BC、CA或其延长线上,且满足(AF/FB)×(BD/DC)×(CE/EA)=1,则F、D、E三点共线。
2.3几个著名的几何定理

例10 在⊿ABC中, AB>AC, 点O是外心,两条高BE, CF交于H点,点M, N分别在线段BH, HF上, 且满足 BM=CN. MH NH 求证: 3 的充分必要条件是∠A=60°.
OH
[证明]
连OB、OC,则
F O
A
∠BOC=2∠A, ∠BHC=180°-∠HBC- ∠HCB=∠B+∠C=180 - ∠A
A
F
B
K
· · · · · · · · ··
I J E H L D
G
C
9. 蝴蝶定理 设AB是⊙O的弦, M 是AB 的中点, 过M作任意二弦CD, EF, 记P, Q依次为与CF, ED 的交点. 则 PM=PQ.
证法一:利用对称造全等形.
· 1` 1 · O
Q
B
3 4 2` D
bdmdbembedmeacmaafmfcfmc???mcfbdeacfmdemcfbcabdebeamdebeabcaacfssmpbqapmqssssssssss???????????????????由mfedcbaqpmfmcbdedbeaeabbcmemdabaebcacafcfmfmcbdbeedmemdacafcfmfmcmdmbmememdmamfmcmb????????????????????????mbma?mpmqmambapbqmpmqambmmpmq???????从而合比分比mfedcbaqp证法三
DE AO1 AG . DF AO2 AH
P P
·
AH AG . 故 FD ED
G ·
O1
又CE=CG, 则
·
·
·
A
· ·
O ·
立体几何的八个判定定理

立体几何的八个判定定理立体几何的八个判定定理是指由英国数学家约翰·威尔逊(John Wallis)在17th century所提出的一套定理。
其中包括:(1)贝瑟尔定理:任意一个平面三角形的内角之和等于180度。
(2)杨氏定理:任意一个对角相交的多边形,其内部角之和等于其外部角之和。
(3)特斯克定理:在同样边上的三个面有关的角相加等于180度。
(4)柯尔定理:在同样边上的四个面有关的角相加等于360度。
(5)高斯定理:任意一个多面体的角之和等于360度乘以面的数量。
(6)伯尔定理:任意一个多边形的角之和大于360度。
(7)双旋定理:任意一个多面体的内角之和等于多边形的角之和减去多边形的边的数量。
(8)欧几里得定理:任意一个多面体的角之和等于多边形的角之和加上多边形的边的数量乘以180度。
贝瑟尔定理是最重要的立体几何判定定理,表明任意一个平面三角形的三个内角之和都等于180度。
这个定理是用来表示平面三角形的构成的,而这个定理也被用来表示一个多边形的构成。
杨氏定理是贝瑟尔定理的推广,即任意一个对角相交的多边形,其内部角之和等于其外部角之和。
特斯克定理是杨氏定理的一个特殊情况,表示在同样边上的三个面有关的角相加等于180度。
柯尔定理也是杨氏定理的一个特殊情况,表示在同样边上的四个面有关的角相加等于360度。
高斯定理是一个重要的立体几何判定定理,即任意一个多面体的角之和等于360度乘以面的数量。
这个定理与贝瑟尔定理的相似之处在于,它们都可以用来表明多面体的构成,它们都表示了一个多面体的性质。
伯尔定理是高斯定理的一个推广,表明任意一个多边形的角之和大于360度。
双旋定理是一个重要的立体几何判定定理,表明任意一个多面体的内角之和等于多边形的角之和减去多边形的边的数量。
欧几里得定理也是一个重要的立体几何判定定理,表明任意一个多面体的角之和等于多边形的角之和加上多边形的边的数量乘以180度。
总的来说,立体几何的八个判定定理是一个重要的数学工具,它们不仅可以帮助人们更好地理解多面体和多边形的构造,还可以帮助人们解决一些复杂的问题,比如求解三角形的面积,求解多面体的体积等等。
著名的几何定理

著名的几何定理1、勾股定理(毕达哥拉斯定理)2、射影定理(欧几里得定理)3、三角形的三条中线交于一点,并且,各中线被这个点分成2:1的两部分4、四边形两边中心的连线的两条对角线中心的连线交于一点5、间隔的连接六边形的边的中心所作出的两个三角形的重心是重合的。
6、三角形各边的垂直一平分线交于一点。
7、从三角形的各顶点向其对边所作的三条垂线交于一点8、设三角形ABC的外心为O,垂心为H,从O向BC边引垂线,设垂足不L,则AH=2OL9、三角形的外心,垂心,重心在同一条直线上。
10、(九点圆或欧拉圆或费尔巴赫圆)三角形中,三边中心、从各顶点向其对边所引垂线的垂足,以及垂心和各顶点连线的中点,这九个点在同一个圆上,11、欧拉定理:三角形的外心、重心、九点圆圆心、垂心依次位于同一直线(欧拉线)上12、库立奇*大上定理:(圆内接四边形的九点圆)圆周上有四点,过其中任三点作三角形,这四个三角形的九点圆圆心都在同一圆周上,我们把过这四个九点圆圆心的圆叫做圆内接四边形的九点圆。
13、(内心)三角形的三条内角平分线交于一点,内切圆的半径公式:r=(s-a)(s-b)(s-c)ss 为三角形周长的一半14、(旁心)三角形的一个内角平分线和另外两个顶点处的外角平分线交于一点15、中线定理:(巴布斯定理)设三角形ABC的边BC的中点为P,则有AB2+AC2=2(AP2+BP2)16、斯图尔特定理:P将三角形ABC的边BC内分成m:n,则有n×AB2+m×AC2=(m+n)AP2+mnm+nBC217、波罗摩及多定理:圆内接四边形ABCD的对角线互相垂直时,连接AB中点M和对角线交点E的直线垂直于CD18、阿波罗尼斯定理:到两定点A、B的距离之比为定比m:n(值不为1)的点P,位于将线段AB分成m:n的内分点C和外分点D为直径两端点的定圆周上19、托勒密定理:设四边形ABCD内接于圆,则有AB×CD+AD×BC=AC20、以任意三角形ABC的边BC、CA、AB为底边,分别向外作底角都是30度的等腰△BDC、△CEA、△AFB,则△DEF是正三角形,21、爱尔可斯定理1:若△ABC和三角形△都是正三角形,则由线段AD、BE、CF的重心构成的三角形也是正三角形。
几何八大定理

几何八大定理
几何学中的“八大定理”并不是一个标准的术语,但可能指的是古典几何中的几个基本定理,这些定理在欧几里得的《几何原本》中有所描述。
如果我们要提到几何学中一些非常基础和重要的定理,可以考虑以下几个:
1. 欧几里得平行公理:通过直线外一点有且仅有一条直线与已知直线平行。
2. 欧几里得菱形定理:在菱形中,对角线互相垂直平分。
3. 欧几里得矩形定理:在矩形中,对角线相等。
4. 欧几里得正方形定理:在正方形中,对角线互相垂直平分且相等。
5. 相似定理:如果两个多边形的对应角相等,并且对应边的比例相等,则这两个多边形相似。
6. 三角形的内角和定理:三角形的三个内角之和等于180度。
7. 圆的相等定理:圆中,相等的圆心角对应相等的弧。
8. 圆周率定理:圆的周长与其直径的比值是一个常数,这个常数被称为圆周率π。
请注意,这些定理只是几何学中的一小部分,而且几何学中有许多其他的定理和理论。
如果你指的是特定的“八大定理”,请提供更多的上下文信息。
立体几何经典定理概述(八大定理)

立体几何经典定理概述(八大定理)立体几何经典定理概述(八大定理)本文将概述立体几何中的八大经典定理。
立体几何是研究三维空间中的图形和形体的数学学科,定理是在研究过程中得出的具有重要意义的数学命题。
1. 欧拉定理欧拉定理是立体几何中最著名的定理之一。
它规定了三维物体的面、顶点和边的关系。
具体来说,如果一个多面体满足面+顶点-边=2的关系,那么它就是一个封闭的多面体。
欧拉定理形象地描述了三维世界中多面体的特性。
2. 柯西定理柯西定理是关于立体几何中平行四边形的定理。
它指出,对于一个平行四边形,其对角线互相平分彼此。
这个定理在解决平行四边形的性质和关系时非常有用,能够帮助我们更好地理解平面几何的性质。
3. 形心定理形心定理是关于多边形形心的定理。
形心是多边形中所有顶点的连线的交点,该定理指出,任意多边形的形心一定在多边形的重心和质心连线的上面。
形心定理可以帮助我们确定多边形的形心位置,从而研究多边形的性质和变形。
4. 二等分线定理二等分线定理是关于立体几何中等分线的定理。
它规定了等分线在多面体中的特性,即等分线和相应的两个面以及它们的交点构成的平面垂直。
这个定理在解决多面体的等分线问题时非常有用,能够帮助我们进一步理解多面体的性质。
5. 范恩艾克线定理范恩艾克线定理是关于球面上切线和交角的定理。
它指出,在球面上,任意切线与相应交角的正弦值等于球心到交点的距离和切线长的比值。
这个定理在解决球面上的切线和交角问题时非常有用,能够帮助我们研究球面的性质和切线关系。
6. 斯坦纳定理斯坦纳定理是关于三维空间中图的生成树的定理。
生成树是一个无圈连通图的子图,其中包含了所有顶点并且边的数量最少。
斯坦纳定理指出,在三维空间中的图中,生成树的条数等于顶点数减去连通分量的数量。
这个定理在解决三维空间图的生成树问题时非常有用。
7. 勾股定理勾股定理是立体几何中最基础的定理之一。
它规定了直角三角形边长之间的关系,即直角三角形的两个直角边的平方和等于斜边的平方。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
29、相交弦定理:若圆内任意弦AB、弦CD交于点P,则PA· PB=PC· PD
性质4:直角三角形斜边上的旁切圆的半径等于三角形周长的一半。
性质5:∠BI1C=90°-∠A/2. 性质6:AP1=r1· cot(A/2)=(a+b+c)/2. 性质7:∠AI1B=∠C/2. 性质8:S△ABC=r1(b+c-a)/2.
性质9:r1=rp/(p-a).
性质10:r1=(p-b)(p-c)/r. 性质11:1/r1+1/r2+1/r3=1/r. 性质12:r1=r/(tanB/2)(tanC/2).
10、斯图尔特定理:P将三角形ABC的边BC内分成m:n,则有
n×AB^2+m×AC^2=(m+n)AP^2+m×PB^2+n×PC^2 设θ是m和d的夹角,θ'是n和d的夹角。θ+θ'=π, cos θ′ = −cos θ。那么,根据余弦定理: a θ' d θ m c
20、塞瓦定理是指在△ABC内任取一点O,延长AO、BO、CO分别交对边于D、E、F,则 是D、E、R,则D、E、R共线(这条直线叫西摩松线)。
22、卡诺定理:在外接圆半径为R,内接圆半径为r的三角形ABC中,r和R有如下关系 r = 4 R sin 两条线段。线段的长度相等且互相垂直(凡· 奥贝尔定理适用于凸凹四边形)。
著名几何定理
目录(带“*”的表示作为了解或“证明:略”):
*25、莫利定理(Morley's theorem):将三角形的三个内角三等分,靠近某边的两条三分角线相交得到一 个交点,则这样的三个交点可以构成一个正三角形。这个三角形常被称作莫利正三角形。
26、笛沙格定理1:平面上有两个三角形△ABC、△DEF,设它们的对应顶点(A和D、B和E、C和F)的连
证明: 作ABC的外接圆,直径CN,连接AN、BN ∵CN是直径 ∴NB⊥BC,NA⊥AC ∵AB⊥BC,BE⊥AC ∴NB//AB,NA//BE ∴四边形ANBH是平行四边形 ∴AH=NB ∵OM⊥BC ∴M是BC的中点 而O是CN的中点 ∴OM是△BCN的中位线 ∴OM=NB/2 ∴AH=2OM
23、凡· 奥贝尔定理:任意一个四边形,在其边外侧构造一个正方形。将相对的正方形的中心连起,得出
A B C sin sin 2 2 2
*24、清宫定理:设P、Q为△ABC的外接圆的异于A、B、C的两点,P点的关于三边BC、CA、AB的对称 点分别是U、V、W,这时,QU、QV、QW和边BC、CA、AB或其延长线的交点分别是D、E、F,则D、 E、F三点共线 。
9、中线定理:(巴布斯定理)设三角形ABC的边BC的中点为P,则有AB^2+AC^2=2(AP^2+BP^2)
方法一:
方法二:
如图,AI是△ABC的中线,AH是高线。利用勾股定理来证明。 在Rt△ABH中,有AB² =AH² +BH² 同理,有AI² =AH² +HI² ,AC² =AH² +CH² 并且BI=CI 那么,AB² +AC² =2AH² +BH² +CH² =2(AI² -HI² )+(BI-IH)² +(CI+IH)² =2AI² -2HI² +BI² +IH² -2BI×IH+CI² +IH² +2CI×IH =2AI² +2BI²
著名几何定理
目录(带“*”的表示作为了解或“证明:略”):
1、勾股定理(毕达哥拉斯定理) 2、射影定理(欧几里得定理)
3、三角形的三条中线交于一点,并且,各中线被这个点分成2:1的两部分(重心定理)
4、设三角形ABC的外心为O,垂心为H,从O向BC边引垂线,设垂足为L,则AH=2OL 5、欧拉定理:三角形的外心、重心、垂心依次位于同一直线(欧拉线),而且重心到外心的距离是重心 到垂心距离的一半 6、三角形三边的中点,三高的垂足和三个欧拉点(连结三角形各顶点与垂心所得三线段的中点)九点共
OL平行等于PH
OLPH为平行四边形,V是PL中点,就是OH中点
7、库立奇*大上定理:(圆内接四边形的九点圆)
如图,四边形ABCD是圆内接四边形,O1,O2,O3,O4分
别是△ABC,△BCD,△CDA,△DAB的 九点圆圆心,H1,H2,H3,H4分别是 显然AE过H4点,容易证明△DH4E和△ABE相似,所以
OF//CM.所以有∠OFC=∠MCF
联结FD,有FD平行AC,且有DF:AC=1:2。FD平行 AC,所以∠DFC=∠FCA,∠FDA=∠CAD,又 ∠OFC=∠MCF,∠ODA=∠EAD,相减可得 ∠OFD=∠HCA,∠ODF=∠EAC,所以有 △OFD∽△HCA,所以OD:HA=DF:AC=1:2;又 GA:GD=2:1所以HA:OD=GA:GD=2:1 又∠ODA=∠EAD,所以△OGD∽△HGA。所以 ∠OGD=∠AGH,又联结AG并延长,所以 ∠AGH+∠DGH=180°,所以∠OGD+∠DGH=180°。 即O、G、H三点共线。
②∵CD^2=AD· BD(已证)
∴CD^2+AD^2=AD· BD+AD^2 ∴AC^2=AD· (BD+AD) ∴AC^2=AD· AB ③BC^2=CD^2+BD^2 BC^2=AD×BD+BD^2 BC^2=(AD+BD)· BD BC^2=AB· BD ∴BC^2=AB· BD ④∵S△ACB=1/2AC×BC=1/2AB×CD ∴1/2AC×BC=1/2AB×CD ∴AC×BC=AB×CD
AF BD CE
18、梅涅劳斯定理的应用定理1:设△ABC的∠A的外角平分线交边CA于Q、∠C的平分线交边AB于R,、
*19、梅涅劳斯定理的应用定理2:过任意△ABC的三个顶点A、B、C作它的外接圆的切线,分别和BC、
CA、AB的延长线交于点P、Q、R,则P、Q、R三点共线 。
BD CE AF × × =1 DC EA FB 21、西摩松定理:从△ABC的外接圆上任意一点P向三边BC、CA、AB或其延长线作垂线,设其垂足分别
∴PMRDL五点共圆。
C等于∠LCE所以∠PEL等于180减去∠ADC ∴∠LEP等于90°
∴PEMRDL六点点共圆,PL为直径,同理PFNQL五点共圆,PL为直
径 ∴PEMRDLQNF九点共圆,PL为直径,PL中点(设为V)就是圆心 下证 九点圆的圆心在垂心与外心连线的中点 O为外心,OL平行等于AH一半(这个小定理我就不证明了)所以
到三角形三边的距离相等。一个三角形有三个旁心(每条边对应一个)。
若设O为△ABC的旁心,用向量表示则有 aOA bOB cOC 1、三角形一内角平分线和另外两顶点处的外角平分线交于一点,该点即为三角形的旁心。 2、每个三角形都有三个旁心。 性质1 :三角形的一条内角平分线与其他两个角的外角平分线交于 一点,该点即为三角形的旁心。 性质2:旁心到三角形三边的距离相等。 性质3:三角形有三个旁切圆,三个旁心。旁心一定在三角形外。
6、三角形三边的中点,三高的垂足和三个欧拉点(连结三角形各顶点与垂心所得三线段的中点)九点
共圆。通常称这个圆为九点圆(nine-point circle),或欧拉圆、费尔巴哈圆。 作图如下:△ABC的BC边垂足为D,BC边中点为L, AC边垂足为E,AC边中点为M,AB边垂足为F,AB边中点为N, 垂心为H,AH,BH,CH中点分别为P,Q,R (思路:以PL为直径,其它任意某点,去证P某L为90°) 证明:(由中位线)PM∥CH,LM∥AB,又CH⊥AB∴PM⊥LM, 又PD⊥LD ∴PMDL共圆。 (由中位线)PR∥AC,LR∥BH,BH⊥AC,所以PR⊥LR
5、欧拉定理:三角形的外心、重心、垂心依次位于同一直线(欧拉线),而且重心到外心的距离是重
心到垂心距离的一半 设H,G,O,分别为△ABC的垂心、重心、外心 。联结AG并延长交BC于D, 则可知D为BC中点。
联结OD ,又因为O为外心,所以OD⊥BC。联结
AH并延长交BC于E,因H为垂心,所以 AE⊥BC。所 以OD//AE,有∠ODA=∠EAD。由于G为重心,则 GA:GD=2:1。 联结CG并延长交BA于F,则可知F为AB中点。同理,
著名几何定理
目录(带“*”的表示作为了解或“证明:略”):
15、爱尔可斯定理1:若△ABC和△DEF都是正三角形,则由线段AD、BE、CF的中心构成的三角形也是正 三角形。
*16、爱尔可斯定理2:若△ABC、△DEF、△GHI都是正三角形,则由三角形△ADG、△BEH、△CFI的重心
构成的三角形是正三角形。 17、梅涅劳斯定理:当直线交△ABC三边所在直线 BC,AC,AB 于点 D,E,F时 FB × DC × EA = 1 ∠B的平分线交边CA于Q,则P、Q、R三点共线。
所以四边形ABCD与四边形好H1H2H3H4对应边相等,
对应角相等,即两个图形全等,所以H1,H2,H3,H4四点 共圆.
8、旁心定理及其性质
如左图,点M就是△ABC的一个旁心。这个交点到三角形三边距离相等。旁心是三角形的 一个内角平分线(如图中AZ)与其不相邻的两个外角平分线(如图中BX与CY)的交点,它
△ABC,△BCD,△CDA,△DAB的垂心,E为DB边上A的投影,
有
DH4AB=DEAE=cos∠ADB 同理有 CH1AB=cos∠ACB=cos∠ADB 所以CH1和DH4平行(垂直于同一条边)且相等,所以
四边形CH1H4D是平行四边形,所以H1H4和CD平行且
