实验三K均值聚类算法实验报告
聚类分析实验报告

聚类分析实验报告一、实验目的:通过聚类分析方法,对给定的数据进行聚类,并分析聚类结果,探索数据之间的关系和规律。
二、实验原理:聚类分析是一种无监督学习方法,将具有相似特征的数据样本归为同一类别。
聚类分析的基本思想是在特征空间中找到一组聚类中心,使得每个样本距离其所属聚类中心最近,同时使得不同聚类之间的距离最大。
聚类分析的主要步骤有:数据预处理、选择聚类算法、确定聚类数目、聚类过程和聚类结果评价等。
三、实验步骤:1.数据预处理:将原始数据进行去噪、异常值处理、缺失值处理等,确保数据的准确性和一致性。
2.选择聚类算法:根据实际情况选择合适的聚类算法,常用的聚类算法有K均值算法、层次聚类算法、DBSCAN算法等。
3.确定聚类数目:根据数据的特征和实际需求,确定合适的聚类数目。
4.聚类过程:根据选定的聚类算法和聚类数目进行聚类过程,得到最终的聚类结果。
5. 聚类结果评价:通过评价指标(如轮廓系数、Davies-Bouldin指数等),对聚类结果进行评价,判断聚类效果的好坏。
四、实验结果:根据给定的数据集,我们选用K均值算法进行聚类分析。
首先,根据数据特点和需求,我们确定聚类数目为3、然后,进行数据预处理,包括去噪、异常值处理和缺失值处理。
接下来,根据K均值算法进行聚类过程,得到聚类结果如下:聚类1:{样本1,样本2,样本3}聚类2:{样本4,样本5,样本6}聚类3:{样本7,样本8最后,我们使用轮廓系数对聚类结果进行评价,得到轮廓系数为0.8,说明聚类效果较好。
五、实验分析和总结:通过本次实验,我们利用聚类分析方法对给定的数据进行了聚类,并进行了聚类结果的评价。
实验结果显示,选用K均值算法进行聚类分析,得到了较好的聚类效果。
实验中还发现,数据预处理对聚类分析结果具有重要影响,必要的数据清洗和处理工作是确保聚类结果准确性的关键。
此外,聚类数目的选择也是影响聚类结果的重要因素,过多或过少的聚类数目都会造成聚类效果的下降。
k-means算法实验报告

.哈尔滨工业大学数据挖掘理论与算法实验报告(2014年度秋季学期).课程编码S1300019C授课教师高宏学生姓名赵天意学号14S101018学院电气工程及自动化学院一、实验内容设计实现 k 均值聚类算法。
二、实验设计随机生成 2 维坐标点,对点进行聚类,进行k=2 聚类, k=3 聚类,多次 k=4 聚类,分析比较实验结果。
三、实验环境及测试数据实验环境: Windows7操作系统,Python2.7 IDLE测试数据:随机生成 3 个点集,点到中心点距离服从高斯分布:集合大小中心坐标半径11005,52 210010,62 31008,102四、实验过程编写程序随机生成测试点集,分别聚成2, 3, 4 类,观察实验结果多次 4 聚类,观察实验结果五、实验结果初始随机点:2聚类迭代 -平方误差1234561337677639634633633聚类中心与类中点数9.06 ,8.291915.05 ,5.011093聚类123456789101112 810692690688686681565385369.4369.8373700 4.99 ,5.05108,7.92 ,10.489310.15 ,6.16994聚类迭代 27次,平方误差 344.897291273 7.95,,10.56904.89,5.001038.41,6.313810.75 ,6.1,469多次4聚类迭代27次平方误差 352.19 4.95 ,5.031069.79 ,6.03937.85 ,10.509012.71 ,8.1611迭代 8 次平方误差356.1910.15 ,6.16997.92 ,10.48935.54 ,5.01674.09 ,5.1041迭代 7 次平方误差352.3510.39 ,6.04874.91 ,4.981038.00 ,10.79797.71 ,7.6931六、遇到的困难及解决方法、心得体会K-Means初值对最终的聚类结果有影响,不同初值,可能会有不同的聚类结果,也就是说, K-Means收敛于局部最优点K-Means趋向于收敛到球形,每类样本数相近K-Means随着k的增加,平方误差会降低,但聚类效果未必变好该例子, 2 聚类误差 633 , 3 聚类 370 ,4 聚类 350 ,可以发现 2 聚类到 3 聚类误差下降较快, 3 到 4 聚类误差下降较慢,所以 3 是最佳聚类个数。
如何使用K均值算法进行聚类分析(Ⅲ)

K均值算法是一种常用的聚类分析方法,它可以根据数据的特征将数据集分成若干个簇。
在实际应用中,K均值算法被广泛用于数据挖掘、模式识别、图像分割等领域。
本文将详细介绍如何使用K均值算法进行聚类分析,并且探讨一些常见的应用场景。
1. 算法原理K均值算法的原理比较简单,首先需要确定簇的数量K,然后随机选择K个数据点作为初始的聚类中心。
接着,将数据集中的每个数据点分配到与其最近的聚类中心所在的簇中。
然后重新计算每个簇的中心点,直到簇中心不再发生变化或者达到预设的迭代次数为止。
最终得到K个簇,每个簇包含一组相似的数据点。
2. 数据预处理在使用K均值算法进行聚类分析之前,需要对数据进行预处理。
首先需要对数据进行标准化处理,使得各个特征的取值范围相对一致。
其次,需要对数据进行降维处理,以减少计算复杂度和提高聚类效果。
最后,需要对数据进行缺失值处理和异常值处理,以确保数据的完整性和准确性。
3. 选择簇的数量K选择簇的数量K是K均值算法中的一个关键步骤。
通常情况下,可以通过肘部法则来确定最优的簇的数量。
肘部法则是通过绘制簇内平方和与簇的数量K的关系图,找到拐点所对应的K值作为最佳的簇的数量。
另外,可以通过轮廓系数等指标来评估不同K值下的聚类效果,选择使得聚类效果最优的簇的数量。
4. 聚类结果评估在得到聚类结果之后,需要对聚类结果进行评估。
通常可以使用簇内平方和、轮廓系数、Davies-Bouldin指数等指标来评估聚类的效果。
除此之外,还可以通过可视化的方式来展示聚类的结果,比如绘制簇的中心点、簇的分布图等。
通过对聚类结果的评估,可以调整算法参数,优化聚类效果。
5. 应用场景K均值算法在各个领域都有着广泛的应用。
在市场营销领域,可以使用K均值算法对客户进行分群,以便针对不同的客户群体制定个性化的营销策略。
在医疗领域,可以使用K均值算法对患者进行分组,以便进行疾病风险评估和治疗方案制定。
在金融领域,可以使用K均值算法对金融产品进行分群,以便推荐个性化的金融产品。
实验三-K-均值聚类算法实验报告

实验三K-Means聚类算法一、实验目的1) 加深对非监督学习的理解和认识2) 掌握动态聚类方法K-Means 算法的设计方法二、实验环境1) 具有相关编程软件的PC机三、实验原理1) 非监督学习的理论基础2) 动态聚类分析的思想和理论依据3) 聚类算法的评价指标四、算法思想K-均值算法的主要思想是先在需要分类的数据中寻找K组数据作为初始聚类中心,然后计算其他数据距离这三个聚类中心的距离,将数据归入与其距离最近的聚类中心,之后再对这K个聚类的数据计算均值,作为新的聚类中心,继续以上步骤,直到新的聚类中心与上一次的聚类中心值相等时结束算法。
实验代码function km(k,A)%函数名里不要出现“-”warning off[n,p]=size(A);%输入数据有n个样本,p个属性cid=ones(k,p+1);%聚类中心组成k行p列的矩阵,k表示第几类,p是属性%A(:,p+1)=100;A(:,p+1)=0;for i=1:k%cid(i,:)=A(i,:); %直接取前三个元祖作为聚类中心m=i*floor(n/k)-floor(rand(1,1)*(n/k))cid(i,:)=A(m,:);cid;endAsum=0;Csum2=NaN;flags=1;times=1;while flagsflags=0;times=times+1;%计算每个向量到聚类中心的欧氏距离for i=1:nfor j=1:kdist(i,j)=sqrt(sum((A(i,:)-cid(j,:)).^2));%欧氏距离end%A(i,p+1)=min(dist(i,:));%与中心的最小距离[x,y]=find(dist(i,:)==min(dist(i,:)));[c,d]=size(find(y==A(i,p+1)));if c==0 %说明聚类中心变了flags=flags+1;A(i,p+1)=y(1,1);elsecontinue;endendiflagsfor j=1:kAsum=0;[r,c]=find(A(:,p+1)==j);cid(j,:)=mean(A(r,:),1);for m=1:length(r)Asum=Asum+sqrt(sum((A(r(m),:)-cid(j,:)).^2));endCsum(1,j)=Asum;endsum(Csum(1,:))%if sum(Csum(1,:))>Csum2% break;%endCsum2=sum(Csum(1,:));Csum;cid; %得到新的聚类中心endtimesdisplay('A矩阵,最后一列是所属类别'); Afor j=1:k[a,b]=size(find(A(:,p+1)==j));numK(j)=a;endnumKtimesxlswrite('data.xls',A);五、算法流程图六、实验结果>>Kmeans6 iterations, total sum of distances = 204.82110 iterations, total sum of distances = 205.88616 iterations, total sum of distances = 204.8219 iterations, total sum of distances = 205.886........9 iterations, total sum of distances = 205.8868 iterations, total sum of distances = 204.8218 iterations, total sum of distances = 204.82114 iterations, total sum of distances = 205.88614 iterations, total sum of distances = 205.8866 iterations, total sum of distances = 204.821Ctrs =1.0754 -1.06321.0482 1.3902-1.1442 -1.1121SumD =64.294463.593976.9329七、实验心得初始的聚类中心的不同,对聚类结果没有很大的影响,而对迭代次数有显著的影响。
聚类分析算法实验报告(3篇)

第1篇一、实验背景聚类分析是数据挖掘中的一种重要技术,它将数据集划分成若干个类或簇,使得同一簇内的数据点具有较高的相似度,而不同簇之间的数据点则具有较低相似度。
本实验旨在通过实际操作,了解并掌握聚类分析的基本原理,并对比分析不同聚类算法的性能。
二、实验环境1. 操作系统:Windows 102. 软件环境:Python3.8、NumPy 1.19、Matplotlib 3.3.4、Scikit-learn0.24.03. 数据集:Iris数据集三、实验内容本实验主要对比分析以下聚类算法:1. K-means算法2. 聚类层次算法(Agglomerative Clustering)3. DBSCAN算法四、实验步骤1. K-means算法(1)导入Iris数据集,提取特征数据。
(2)使用Scikit-learn库中的KMeans类进行聚类,设置聚类数为3。
(3)计算聚类中心,并计算每个样本到聚类中心的距离。
(4)绘制聚类结果图。
2. 聚类层次算法(1)导入Iris数据集,提取特征数据。
(2)使用Scikit-learn库中的AgglomerativeClustering类进行聚类,设置链接方法为'ward'。
(3)计算聚类结果,并绘制树状图。
3. DBSCAN算法(1)导入Iris数据集,提取特征数据。
(2)使用Scikit-learn库中的DBSCAN类进行聚类,设置邻域半径为0.5,最小样本数为5。
(3)计算聚类结果,并绘制聚类结果图。
五、实验结果与分析1. K-means算法实验结果显示,K-means算法将Iris数据集划分为3个簇,每个簇包含3个样本。
从聚类结果图可以看出,K-means算法能够较好地将Iris数据集划分为3个簇,但存在一些噪声点。
2. 聚类层次算法聚类层次算法将Iris数据集划分为3个簇,与K-means算法的结果相同。
从树状图可以看出,聚类层次算法在聚类过程中形成了多个分支,说明该算法能够较好地处理不同簇之间的相似度。
K均值聚类
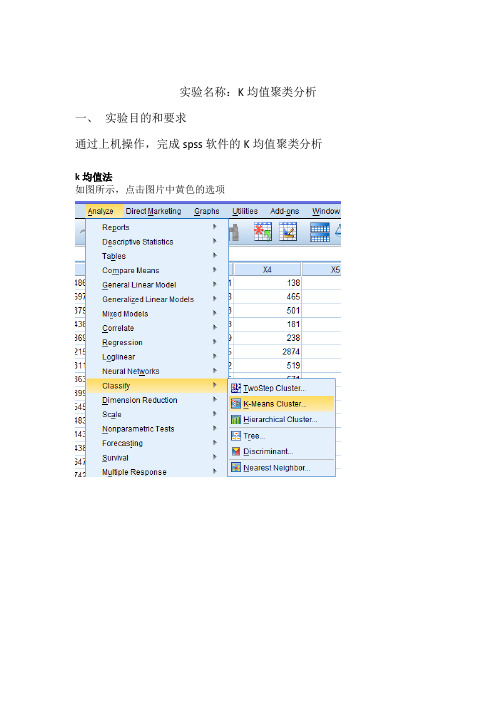
实验名称:K均值聚类分析一、实验目的和要求通过上机操作,完成spss软件的K均值聚类分析k均值法如图所示,点击图片中黄色的选项如图所示进行操作点击interate,按下图进行操作点击options,按下图进行操作点击Save 按下图进行操作结果与分析上表为初始类中心,通过该表可得到9个变量的初始类中心,该表为迭代历史表,该表给出了迭代过程中类中心的变动量,可以看出本次聚类过程进行了2次迭代,就收敛了。
Cluster MembershipCase Number 地区Cluster Distance1 北京 1 44568.4152 天津 4 42381.8363 石家庄4 26915.6304 太原 4 19555.5815 沈阳 4 16337.7836 大连 4 31007.6277 长春 4 20010.7888 哈尔滨 4 26575.1529 上海 4 93352.22910 南京 4 32733.44811 杭州 4 32602.47012 宁波 4 36201.89113 合肥 4 5489.31414 福州 4 13379.26515 厦门 4 56926.08916 南昌 4 22419.76817 济南 4 6901.07318 青岛 4 16839.72719 郑州 4 21258.50020 武汉 4 20666.40321 长沙 4 18185.01222 广州 1 44568.41523 深圳 2 .00024 南宁 4 35043.52425 海口 4 29088.11726 重庆 3 25822.76627 成都 3 25822.76628 贵阳 4 31336.32529 昆明 4 25999.05930 西安 4 24853.28631 兰州 4 32964.15932 西宁 4 39390.80633 银川 4 21601.67134 乌鲁木齐 4 17507.292该表为聚类成员,从表中可以看出,将34个地方分为4类北京,广州为第一类,深圳的为第二类,重庆,成都为第三类,剩下的为第四类。
聚类分析实验报告

聚类分析实验报告
《聚类分析实验报告》
在数据挖掘和机器学习领域,聚类分析是一种常用的技术,用于将数据集中的对象分成具有相似特征的组。
通过聚类分析,我们可以发现数据集中隐藏的模式和结构,从而更好地理解数据并做出相应的决策。
在本次实验中,我们使用了一种名为K均值聚类的方法,对一个包含多个特征的数据集进行了聚类分析。
我们首先对数据进行了预处理,包括缺失值处理、标准化和特征选择等步骤,以确保数据的质量和可靠性。
接着,我们选择了合适的K值(聚类的数量),并利用K均值算法对数据进行了聚类。
在实验过程中,我们发现K均值聚类方法能够有效地将数据集中的对象分成具有相似特征的组,从而形成了清晰的聚类结构。
通过对聚类结果的分析,我们发现不同的聚类中心代表了不同的数据模式,这有助于我们更好地理解数据集中的内在规律和特点。
此外,我们还对聚类结果进行了评估和验证,包括使用轮廓系数和肘部法则等方法来评价聚类的质量和效果。
通过这些评估方法,我们得出了实验结果的可靠性和有效性,证明了K均值聚类在本次实验中的良好表现。
总的来说,本次实验通过聚类分析方法对数据集进行了深入的挖掘和分析,得到了有意义的聚类结果,并验证了聚类的有效性和可靠性。
通过这一实验,我们对聚类分析方法有了更深入的理解,也为今后在实际应用中更好地利用聚类分析提供了有力支持。
K均值实验

K均值聚类一、实验意义及目的掌握K均值聚类算法原理,能够利用Matlab编制程序实现K均值聚类,熟悉基于Matlab 的算法处理函数,并能够利用算法解决简单问题。
二、实验内容(1)使用Matlab中的kmeans函数,对其进行聚类。
(2)针对实例数据~:按照K均值聚类原理,采用欧氏距离作为衡量,基于Matlab编制程序,将数据聚集为两类。
三、Matlab相关函数介绍(可采用help kmeans命令查看kmeans函数的使用方法)(1)kmeans函数1)[IDX, C] = kmeans(X, K):将输入的N个点分为K类。
参数:X:N×n的矩阵,每一行对应一个点,每个点为n维;K:要聚成的类别数;IDX:N×1的向量,其元素为每个点所属类的类序号;C:K个类的类重心坐标矩阵,一个K×n的的矩阵,每一行是每一类的类重心坐标。
2)[IDX, C, SUMD, D] =kmeans(..., 'PARAM1',val1, 'PARAM2',val2, ...):允许用户设置更多的参数及参数值,用来控制函数所用的迭代算法。
参数:sumd:1×K的向量,类内距离和向量(即类内各点与类重心距离之和);D:N×K的矩阵,每个点与每个类重心之间的距离矩阵。
其余参数:(2)silhouette函数根据聚类结果绘制轮廓图,从轮廓图上看每个点的分类是否合理。
轮廓图上第i个点的轮廓值定义为:其中是第i个点与同类的其他点之间的平均距离,b为一个向量,其元素是第i个点与不同类的类内各点之间的平均距离。
轮廓值的取值范围为[-1,1],值越大,说明第i个点的分类越合理;当时,说明第i个点的分类不合理,还有比目前分类更合理的方案。
调用格式:[S,H] = silhouette(X, CLUST,DISTANCE))参数:X:N×n的矩阵,每一行对应一个点,每个点为n维;CLUST:聚类结果,是由每个观测所属类的类序号构成的数值向量,或是由类名称构成的字符矩阵或字符串元胞数组;S:轮廓值向量,N×1的向量,其元素为相应点的轮廓值;h:图形句柄,指定h时绘制轮廓图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验三 K-Means聚类算法
一、实验目的
1) 加深对非监督学习的理解和认识
2) 掌握动态聚类方法K-Means 算法的设计方法
二、实验环境
1) 具有相关编程软件的PC机
三、实验原理
1) 非监督学习的理论基础
2) 动态聚类分析的思想和理论依据
3) 聚类算法的评价指标
四、算法思想
K-均值算法的主要思想是先在需要分类的数据中寻找K组数据作为初始聚类中心,然后计算其他数据距离这三个聚类中心的距离,将数据归入与其距离最近的聚类中心,之后再对这K个聚类的数据计算均值,作为新的聚类中心,继续以上步骤,直到新的聚类中心与上一次的聚类中心值相等时结束算法。
实验代码
function km(k,A)%函数名里不要出现“-”
warning off
[n,p]=size(A);%输入数据有n个样本,p个属性
cid=ones(k,p+1);%聚类中心组成k行p列的矩阵,k表示第几类,p是属性
%A(:,p+1)=100;
A(:,p+1)=0;
for i=1:k
%cid(i,:)=A(i,:); %直接取前三个元祖作为聚类中心
m=i*floor(n/k)-floor(rand(1,1)*(n/k))
cid(i,:)=A(m,:);
cid;
end
Asum=0;
Csum2=NaN;
flags=1;
times=1;
while flags
flags=0;
times=times+1;
%计算每个向量到聚类中心的欧氏距离
for i=1:n
for j=1:k
dist(i,j)=sqrt(sum((A(i,:)-cid(j,:)).^2));%欧氏距离 end
%A(i,p+1)=min(dist(i,:));%与中心的最小距离
[x,y]=find(dist(i,:)==min(dist(i,:)));
[c,d]=size(find(y==A(i,p+1)));
if c==0 %说明聚类中心变了
flags=flags+1;
A(i,p+1)=y(1,1);
else
continue;
end
end
i
flags
for j=1:k
Asum=0;
[r,c]=find(A(:,p+1)==j);
cid(j,:)=mean(A(r,:),1);
for m=1:length(r)
Asum=Asum+sqrt(sum((A(r(m),:)-cid(j,:)).^2)); end
Csum(1,j)=Asum;
end
sum(Csum(1,:))
%if sum(Csum(1,:))>Csum2
% break;
%end
Csum2=sum(Csum(1,:));
Csum;
cid; %得到新的聚类中心
end
times
display('A矩阵,最后一列是所属类别');
A
for j=1:k
[a,b]=size(find(A(:,p+1)==j));
numK(j)=a;
end
numK
times
xlswrite('data.xls',A);
五、算法流程图
六、实验结果
>>Kmeans
6 iterations, total sum of distances = 204.821
10 iterations, total sum of distances = 205.886
16 iterations, total sum of distances = 204.821
9 iterations, total sum of distances = 205.886
........
9 iterations, total sum of distances = 205.886
8 iterations, total sum of distances = 204.821
8 iterations, total sum of distances = 204.821
14 iterations, total sum of distances = 205.886
14 iterations, total sum of distances = 205.886
6 iterations, total sum of distances = 204.821
Ctrs =1.0754 -1.06321.0482 1.3902-1.1442 -1.1121
SumD =64.294463.593976.9329
七、实验心得
初始的聚类中心的不同,对聚类结果没有很大的影响,而对迭代次数有显著的影响。
数据的输入顺序不同,同样影响迭代次数,而对聚类结果没有太大的影响。
