2016美国大学生数学建模比赛H奖
美国大学生数学建模竞赛数据及评阅分析_吴孟达
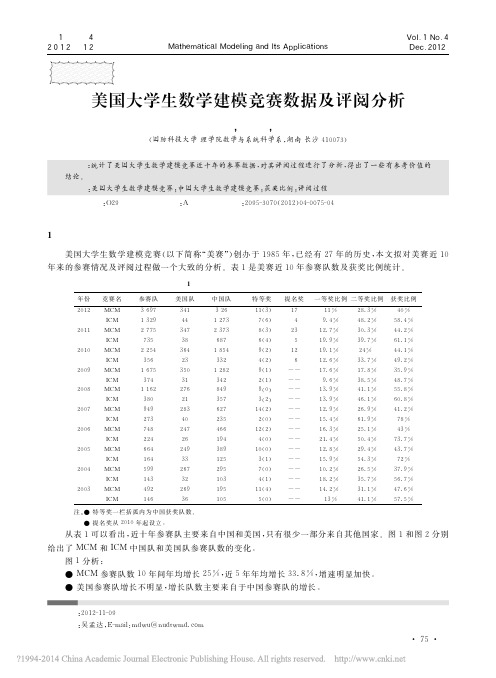
给出了 ＭＣＭ 和ＩＣＭ 中国队和美国队参赛队数的变化。
图１分析：
● ＭＣＭ 参赛队数１０年间年均增长２５％，近５年年均增长３３．８％，增速明显加快。
● 美国参赛队增长不明显，增长队数主要来自于中国参赛队的增长。
收 稿 日 期 ：２０１２－１１－０９ 通 讯 作 者 ：吴 孟 达 ，Ｅ－ｍａｉｌ：ｍｄｗｕ＠ｎｕｄｔｗｍｄ．ｃｏｍ
摘 要：统计了美国大学生数学建模竞赛近十年的参赛数据，对其评阅过程进行 了 分 析，得 出 了 一 些 有 参 考 价 值 的 结论。 关 键 词 ：美 国 大 学 生 数 学 建 模 竞 赛 ；中 国 大 学 生 数 学 建 模 竞 赛 ；获 奖 比 例 ；评 阅 过 程
中 图 分 类 号 ：Ｏ２９ 文 献 标 志 码 ：Ａ 文 章 编 号 ：２０９５－３０７０（２０１２）０４－００７５－０４
３ ２６ １ ２７３ ２ ３７３ ６８７ １ ８５４ ３３２ １ ２８２ ３４２ ８４９ ３５７ ６２７ ２３５ ４６６ １９４ ３８９ １２５ ２９５ １０３ １９５ １０５
１１（３） ７（６） ８（３） ６（４） ９（２） ４（２） ９（１） ２（１） ９（０） ３（２）
图２ ＩＣＭ 参赛队数变化图 图３ ＭＣＭ 获奖比例 图４ ＩＣＭ 获奖比例
２ 评 阅 过 程 分 析
据 美 赛 “评 委 评 论 ”介 绍 ，美 赛 评 阅 过 程 大 致 分 为 三 轮 。 第一轮可以称为“淘汰轮（ｔｈｅ Ｔｒｉａｇｅ Ｒｏｕｎｄ）”。此轮评阅主要以摘要信息以及论文整体结构为 评 判 依 据 ，时 间 大 约 是 ５～１０ 分 钟 。 每 个 评 委 以 “通 过 ”、“不 通 过 ”计 分 ，事 先 应 当 设 置 有 大 致 的 “通 过 ”比 例 （此 轮 与 国内研赛的网评阶段相类似）。当两位 评 委 意 见 不 一 致 时 可 以 协 商 达 成 一 致 意 见，如 果 仍 不 能 达 成 一 致 意 见 ，则 请 第 三 位 评 委 评 阅 。 有 “评 论 ”介 绍 说 ，这 一 轮 的 淘 汰 率 大 约 为 ４５％ ，通 过 这 一 轮 评 审 的 参 赛 队 大 约 有 ８０％ 的 获 奖 概 率 。 关 于 如 何 通 过 这 一 轮 评 审 ，评 委 给 出 的 建 议 是 ： １）摘 要 至 关 重 要 ，必 须 清 晰 且 信 息 量 充 分 。 评 委 关 心 的 是 你 对 问 题 的 理 解 是 否 准 确 ，你 建 立 的 模 型 及 使 用的方法是否恰当，以及根据你所建模型得到的主要结果和主要结论是否合理 。 过 于 冗 长 的 技 术 性 描 述 将 · ７６ ·
历年美国大学生数学建模竞赛试题MCM.翻译版doc
1985 年美国大学生数学建模竞赛MCM 试题1985年MCM:动物种群选择适宜的鱼类和哺乳动物数据准确模型。
模型动物的自然表达人口水平与环境相互作用的不同群体的环境的重要参数,然后调整账户获取表单模型符合实际的动物提取的方法。
包括任何食物或限制以外的空间限制,得到数据的支持。
考虑所涉及的各种数量的价值,收获数量和人口规模本身,为了设计一个数字量代表的整体价值收获。
找到一个收集政策的人口规模和时间优化的价值收获在很长一段时间。
检查政策优化价值在现实的环境条件。
1985年MCM B:战略储藏管理钴、不产生在美国,许多行业至关重要。
(国防占17%的钴生产。
1979年)钴大局部来自非洲中部,一个政治上不稳定的地区。
1946年的战略和关键材料储藏法案需要钴储藏,将美国政府通过一项为期三年的战争。
建立了库存在1950年代,出售大局部在1970年代初,然后决定在1970年代末建立起来,与8540万磅。
大约一半的库存目标的储藏已经在1982年收购了。
建立一个数学模型来管理储藏的战略金属钴。
你需要考虑这样的问题:库存应该有多大?以什么速度应该被收购?一个合理的代价是什么金属?你也要考虑这样的问题:什么时候库存应该画下来吗?以什么速度应该是画下来吗?在金属价格是合理出售什么?它应该如何分配?有用的信息在钴政府方案在2500万年需要2500万磅的钴。
美国大约有1亿磅的钴矿床。
生产变得经济可行当价格到达22美元/磅(如发生在1981年)。
要花四年滚动操作,和thsn六百万英镑每年可以生产。
1980年,120万磅的钴回收,总消费的7%。
1986 年美国大学生数学建模竞赛MCM 试题1986年MCM A:水文数据下表给出了Z的水深度尺外表点的直角坐标X,Y在码(14数据点表省略)。
深度测量在退潮。
你的船有一个五英尺的草案。
你应该防止什么地区的矩形(75200)X(-50、150)?1986年MCM B:Emergency-Facilities位置迄今为止,力拓的乡牧场没有自己的应急设施。
2016全国大学生数学建模竞赛获奖名单
2016高教社杯全国大学生数学建模竞赛获奖名单（初稿）（异议期：2016年11月7日-2016年11月20日）
本科组高教社杯获得者：张滕翔、夏智康、郑安琪（东南大学）
专科组高教社杯获得者：吴伟龙、杨婷、段玲（湖南化工职业技术学院）
本科组MATLAB创新奖获得者：王毅然、纪昀红、张伟（中国人民大学）
专科组MATLAB创新奖获得者：刘苏生、祝王缘、王柏熙（海军蚌埠士官学校）
[注]以下每一获奖等级内，按赛区顺序排列（同一赛区内，按学校笔画顺序排列）。
本科组一等奖（共294名）
本科组二等奖（共1621名）
曹小
专科组一等奖（共60名）。
2016年美国大学生数学建模竞赛C题H奖论文
Contents1.Introduction (1)1.1 Background (1)1.2 Foundation & ROI (1)2 Task (1)3 Fundamental assumptions (2)4 Definitions and Notations (2)5 Models (3)5.1 Filter data (3)5.2 Object Selection Model (Grey Relational Analysis) (4)5.2.1 Model analysis (4)5.2.2 Model solution (4)5.3 ROI Model (Principal Component Analysis) (5)5.3.1 Model analysis (5)5.3.2 Model solution (6)5.4 Verify the possibility (9)5.4.1 Comparison (9)5.4.2 External factor (10)5.5 Investment Forecast Model (11)5.5.1 Linear Regression Forecasting Model (11)5.5.2 School potential Prediction (TOPSIS) (12)5.5.3 Final investment (TOPSIS) (13)6 Conclusions (16)7 Strengths and Weaknesses (18)7.1 Strengths (19)7.2 Weaknesses (20)8 Letter to Mr. Alpha Chiang (21)9 References (22)Team # 44952 Page 1 of 221 Introduction1.1 BackgroundThe Goodgrant Foundation is a charitable organization that wants to help improve educational performance of undergraduates attending colleges and universities in the United States. To do this, the foundation intends to donate a total of $100,000,000 (US100 million) to an appropriate group of schools per year, for five years, starting July 2016. In doing so, they do not want to duplicate the investments and focus of other large grant organizations such as the Gates Foundation and Lumina Foundation.Our team has been asked by the Goodgrant Foundation to develop a model to determine an optimal investment strategy that identifies the schools, the investment amount per school, the return on that investment, and the time duration that the organi zation’s money should be provided to have the highest likelihood of producing a strong positive effect on student performance. This strategy should contain a 1 to N optimized and prioritized candidate list of schools you are recommending for investment bas ed on each candidate school’s demonstrated potential for effective use of private funding, and an estimated return on investment (ROI) defined in a manner appropriate for a charitable organization such as the Goodgrant Foundation.1.2 Foundation & ROIFoundation (charitable foundation) refers to the nonprofit legal person who uses the property of the natural persons, legal persons or other organizations to engage in public welfare undertakings. In terms of its nature, foundation is a kind of folk non-profit organizations.ROI is a performance measure used to evaluate the efficiency of an investment or to compare the efficiency of a number of different investments. ROI measures the amount of return on an investment relative to the investment’s cost. To calculate ROI, the benefit (or return) of an investment is divided by the cost of the investment, and the result is expressed as a percentage or a ratio.2 Task●One-page summary for our MCM submission●Using our models to achieve the candidate list of schools●Calculate the time durati on that the organization’s money should be provided to have thehighest likelihood of producing a strong positive effect on student performance●Calculate the investment amount Goodgrant Foundation would pay for each school●Calculate the ROI of the Goodgrant Foundation●Forecast the development of this kind of investment mode●Write a letter to the CFO of the Goodgrant Foundation, Mr. Alpha Chiang, that describesthe optimal investment strategy。
2016全国大学生数学建模竞赛获奖名单
2016高教社杯全国大学生数学建模竞赛获奖名单（初稿）（异议期：2016年11月7日-2016年11月20日）
本科组高教社杯获得者：张滕翔、夏智康、郑安琪（东南大学）
专科组高教社杯获得者：吴伟龙、杨婷、段玲（湖南化工职业技术学院）
本科组MATLAB创新奖获得者：王毅然、纪昀红、张伟（中国人民大学）
专科组MATLAB创新奖获得者：刘苏生、祝王缘、王柏熙（海军蚌埠士官学校）
[注]以下每一获奖等级内，按赛区顺序排列（同一赛区内，按学校笔画顺序排列）。
本科组一等奖（共294名）
本科组二等奖（共1621名）
曹小
专科组一等奖（共60名）。
2017年国际(美国)大学生数学建模竞赛获奖情况
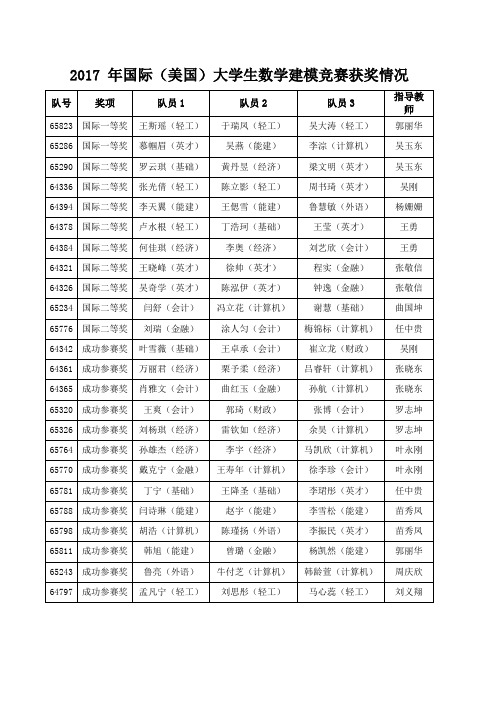
杨凯然（能建）
郭丽华
65243
成功参赛奖
鲁亮（外语）
牛付芝（计算机）
韩龄萱（计算机）
周庆欣
64797
成功参赛奖
孟凡宁（轻工）
刘思彤（轻工）
马心蕊（轻工）
刘义翔
张敬信
64326
国际二等奖
吴奇学（英才）
陈泓伊（英才）
钟逸（金融）
张敬信
65234
国际二等奖
闫舒（会计）
冯立花（计算机）
谢慧（基础）
曲国坤
65776
国际二等奖
刘瑞（金融）
涂人匀（会计）
梅锦标（计算机）
任中贵
64342
成功参赛奖
叶雪薇（基础）
王卓承（会计）
崔立龙（财政）
吴刚
64361
成功参赛奖
万丽君（经济）
张光倩（轻工）
陈立影（轻工）
周书琦（英才）
吴刚
64394
国际二等奖
李天翼（能建）
王偲雪（能建）
鲁慧敏（外语）
杨姗姗
64378
国际二等奖
卢水根（轻工）
丁浩珂（基础）
王莹（英才）
王勇
64384
国际二等奖
何佳琪（经济）
李奥（经济）
刘艺欣（会计）
王勇
64321
国际二等奖
王晓峰（英才）
徐帅（英才）
程实（金融）
65770
成功参赛奖
戴克宁（金融）
王寿年（计算机）
徐李珍（会计）
叶永刚
65781
成功参赛奖
丁宁（基础）
王降圣（基础）
李珺彤（英才）
任中贵
参加美国大学生数学建模竞赛 - 知乎
1.组队
我们队 一个应用数学的学渣（就是我） 一个化学院的女森 加上一个 计算机院物联网的男生 一般组队都是 数院 电气 电信 经管 这样 我们一次模拟都没有做过，但是分析过大概10多篇08年一等奖的文章，当时觉得 他们的模型都看不懂= =
2.场地
因为学校机房有限，都给了参加过过赛的同学的队，比赛的时候 出去开了两间房，白天就在一起做题。酒店没有 桌子，就坐在地上然后把电脑放床上= =
比赛：最理想是国赛前定下美国赛队伍，拿国赛练级攒经验比较恰当。其他如教工杯之类的比赛，鉴于真实比 赛环境和练习的机会不多，建议当成美赛认真练。只要认真练，几次真赛历练之后，建模和配合方面问题就不 应该太大了。 学术论文写作：难点不是专业词汇或格式排版的问题，这些问题阅卷人可能会对外国参赛者宽容些，真正困难 是表达如何逻辑清晰严密、符合学术规范了。有条件的最好找英语国家教授或学术期刊编辑帮忙不断改，找不 到就只能是找海归教授、理工专业外国留学生将就了，再没条件的只能研读outstanding和英文经典论文了。
赛前准备程度基本决定了比赛的时间充裕度 ，赛前准备不足往往要靠比赛时不眠不休、争分夺秒拼命抢时间来 弥补，这种情况下能做出多少创造性工作就难说了。
三、练级篇：
练习：练习的时候要根据队伍的特点有针对性的训练提高——模型方面，多积累实际问题产生背景，注意培养 思考的深度，善用发散和逆向思维；实现方面，注意提升各种算法求解效率的方法，多积累算法调试、测试、 参数调整、有效性检验等方面的经验；
大家要有信心 一等奖不难 加油噢~ 编辑于 2013-07-23 9 条评论
参加美国大学生数学建模竞赛 - 知乎
改名中，我的头像更适合做知乎吉祥物 李曈、Steve Balaba、张镇麟 等人赞同 首先说一下自己的参赛经历：2013年S奖，2014年M奖，两次参赛是不同的队伍。
中国大学生数学建模竞赛发展史
2000网易杯全国大学生数学建模竞赛举行，27省（市、自治区）517所院校的3210队参加，其中608队参加大专组竞赛，香港城市大学有1个队首次参赛
2000.12.6～8
2000年各赛区负责人工作会议暨颁奖仪式在中山大学珠海校区举行，119队获一等奖（其中大专组23队），245队获二等奖（其中大专组55队）。
1998年全国大学生数学建模竞赛举行，26省（市、自治区）400所院校的2103队参加。
1998.12.10～13
1998年各赛区负责人工作会议暨颁奖仪式在上海华东理工大学举行，79队获一等奖，153队获二等奖。
1999.2.6～8
1999年美国大学生数学建模竞赛举行，我国参赛院校43个，占总数的19%，参赛队155个，占总数的32%，浙江大学获一项特等奖。从1999年起增加交叉学科建模竞赛（作为C题）。
2003.2
2003年美国大学生数学建模竞赛（MCM）和交叉学科竞赛（ICM）举行，我国共参加300队，占总数的47%，浙江大学、北京大学、东南大学、东华大学各一队获特等奖。
2003.9.22~25
2003高教社杯全国大学生数学建模竞赛举行，30省（市、自治区）637所院校的5406队参加。
2003.12.6~7
2003年各赛区工作会议暨颁奖仪式在厦门举行，厦门大学承办，608队获全国奖，其中本科组一等奖151队，二等奖306队，大专组一等奖48队，二等奖103队。
2004.2
2004年美国大学生数学建模竞赛（MCM）和交叉学科竞赛（ICM）举行，我国共参加398队，占总数的54%，成都电子科技大学一队获特等奖。
数学建模发展史
1992.11.27～29
1992年部分城市大学生数学模型联赛举行，这是全国性的首届竞赛，10省（市）79所院校的314队参加。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
For task five, we analyze from the perspective of the source of the available water, and project the water availability of Qingdao on the basis of intervention plans.
For task three, we use the grey prediction model to predict agricultural production water, industrial water, domestic water, ecological water, exports of virtual water, imports of virtual water, and available water resources quantity of Qingdao in 15 years. By using the evaluation model we get the conclusions: In 2030, Qingdao city is still in a condition of water scarcity, and need to obtain water from the surrounding area. But the economic benefits of per unit water are large, and the utilization ratio is large, as well.
For task four, we design intervention plans from the perspectives of the virtual water trade, the economic performance of water footprint, the physical water footprint, and the source of water. Then we analyze the effects of these plans on the ecosystem and the surrounding areas of Qingdao.
2 Problem analysis
In order to build a model to measure the clean water supply capacity in a region, We introduce the concept of virtual water [1] and water footprint [2] to build the model. The water footprint can be used to measure the direct and indirect water consumption in the process of production. It also can be used to measure the real demand and occupation status of the water resources in a region from the point of view of consumption. We calculate the agricultural production water, industrial production water, residents living water, and ecological environment water by using the virtual water theory. We set up three overall evaluation indexes to evaluate the condition of water resources in a region. These indexes can analyze problems from the points of physical and economic scarcity. According to the UN water scarcity map, the water in Qingdao in China is heavily overloaded, so we select the Qingdao in China to study. We put the relevant data into the model and get the evaluation conclusion of water resources condition in Qingdao.
For task two, we take Qingdao as an example. Qingdao is a serious water scarcity city, located in the eastern part of Shandong Province, China. We put the relevant data of Qingdao city in 2014 into the evaluation model we built in task one, and then get the conclusions: Qingdao is in a condition of water scarcity, the water resources are not enough to meet the needs of its population. In addition, the economic benefit of unit water consumption is not large, the waste rate of water resource is high, and the utilization rate of water resource is low.
For office use only T1 ________________ T2 ________________ T3 ________________ T4 ________________
Team Control Number
53674
Pnly F1 ________________ F2 ________________ F3 ________________ F4 ________________
For task one, a dynamic evaluation model is established by using the theory of virtual water and the water footprint to evaluate the water supply ability of a region. We consider agricultural water consumption, industrial water consumption, ecological and environmental water, domestic water consumption, and the import and export of virtual water in our dynamic evaluation module. We establish five main evaluation indexes to analyze the situation of water supply ability and the water resources in a region.
2016 MCM/ICM Summary Sheet
Analyzing the Water Scarcity Bsaed on the Water Footprint Theory
Abstract