龙贝格积分法C语言(西安交大)
龙贝格公式及实现

龙贝格公式就是逐次对分积分区间的方法,可以把前面计算的结果作为一个整体带入对分后的计算公式中,只需要增加新的分点的函数值。
以)(0k T表示],[b a 二分k 次后的梯形值,)(k mT 表示)(0k T 的m 次加速值,则有),2,1(,141144)(14)1(1)( =---=-+-k TTTk m k m mmk m龙贝格算法:步1 初始化:计算)]()([2)0(0b f a f ab T+-=,置1:=k (k记录区间],[b a 的二分次数),a b h -=;步2(二分) 计算积分值: ∑-=+---+=122/11)1(0)(01)(221k j j k k k x f h TT;步3(加速) 求加速值:计算)(1)1(1)(141144j k j jj k j jjj k jTTT--+------=,),,2,1(k j =;步4 精度检验:对指定的精度ε,若ε<--)0(1)0(k kTT,则终止计算,并取)0(kT作为所求的结果;否则置1:+=k k ,hh 21:=,转步2。
计算次序:(0)0T第1次循环 二分:(1)0T加速:(0)1T 第2次循环二分:(2)1T加速:(1)(0)12,T T第3次循环 二分:(3)2T加速:(2)(1)(0)123,,T T T第4次循环 二分:(4)3T加速:(3)(2)(1)(0)1234,,,T T TT……在命令窗口输入: a = 0; b = 1;epsilon = 5e-6;f = @(x)sin(x);%@(X)申请变量空间,计算sin 积分y = romberg(f,a,b,epsilon) %函数调用安回车,出结果。
西安交通大学计算方法C讲义

计算方法(C)目录第1章绪论1。
1 数值计算1。
2 数值方法的分析1.2.1计算机上数的运算1.2.2算法分析第2章线性代数方程组2。
1 Gauss消去法2.1.1消去法2.1.2主元消去法2.2 矩阵分解2.2.1Gauss消去法的矩阵意义2.2.2矩阵的LU分解及其应用2.2.3其他类型矩阵的分解2.2.4解三对角矩阵的追赶法2.3线性方程组解的可靠性2.3.1向量和矩阵范数2.3.2残向量与误差的代数表征2.4解线性方程组解的迭代法2.4.1基本迭代法2.4.2迭代法的矩阵表示2.4.3收敛性第3章数据近似3。
1 多项式插值3.1.1插值多项式3.1.2Lagrange插值多项式3.1.3Newton插值多项式3.1.4带导数条件的插值多项式3.1.5插值公式的余项3. 2 最小二乘近似3.2.1 最小二乘问题的法方程3.2.2 正交化算法第4章数值微积分4.1 内插求积,Newton-Cotes公式4.1.1Newton—Cotes公式4.1.2复化求积公式4.1.3步长的选取4.1.4Romberg方法4.1.5待定系数法4.2数值微分4.2.1插值公式方法4.2.2Taylor公式方法 (待定系数法)4.2.3外推法第5章非线性方程求解5。
1 解一元方程的迭代法5.1.1简单迭代法5.1.2Newton法5.1.3割线法5.1.4区间方法5。
2 收敛性问题5.2.1简单迭代—-不动点5.2.2收敛性的改善5.2.3Newton法的收敛性5.2.4收敛速度第1章绪论1。
1数值计算现代科学的发展,已导致科学与技术的研究从定性前进到定量,尤其是现代数字计算机的出现及迅速发展,为复杂数学问题的定量研究与解决,提供了强有力的基础.通常我们面对的理论与技术问题,绝大多数都可以从其物理模型中抽象出数学模型,因此,求解这些数学模型已成为我们面临的重要任务.一、本课程的任务:寻求解决各种数学问题的数值方法—-如何将高等数学的问题回归到初等数学(算术)的方法求解—-了解计算的基础方法,基本结构(否则只须知道数值软件)——并研究其性质.立足点:面向数学——解决数学问题面向计算机—-利用计算机作为工具充分发挥计算机的功能,设计算法,解决数学问题例如:迭代法、并行算法二、问题的类型1、离散问题:例如,求解线性方程组bAx= -—从离散数据:矩阵A和向量b,求解离散数据x;2、连续问题的离散化处理:例如,数值积分、数值微分、微分方程数值解;3、离散问题的连续化处理:例如,数据近似,统计分析计算;1.2数值方法的分析在本章中我们不具体讨论算法,首先讨论算法分析的基础--误差.一般来讲,误差主要有两类、三种(对科学计算):1)公式误差-—“截断误差”,数学↔计算,算法形成——主观(人为):数学问题-数值方法的转换,用离散公式近似连续的数学函数进行计算时,一般都会发生误差,通常称之为“截断误差”;——以后讨论2)舍入误差及输出入误差——计算机,算法执行—-客观(机器):由于计算机的存储器、运算器的字长有限,在运算和存储中必然会发生最末若干位数字的舍入,形成舍入误差;在人机数据交换过程中,十进制数和二进制数的转换也会导致误差发生,这就是输入误差.这两种误差主要是由于计算机的字长有限,采用浮点数系所致。
龙贝格算法

第1章 龙贝格算法研究问题阐述计算二重积分⎰⎰=b adcdxdy y x f I ),(------------------------------------(1-1)对工科生要求计算如下3个二重积分:算例1:1110()1I x y dxdy =+=⎰⎰算例2:/2200()I x y dxdy πππ=+=⎰⎰-----------------------(1-2)算例3: 1130sin()x y I dxdy x y+=+⎰⎰通常将积分区间等分数依次取2k ,并得到相应的递推式子如(2-5)所示,相应对到过程不再累述详情可以参考教材。
1112221[()()],21[(21)]222k k k k k i b a T f a f b b a b a T T f a i --=-⎧=+⎪⎪⎨--⎪=++-⎪⎩∑----------------------------(2-5) 最终得到计算机计算步骤如下:(1)计算初值T1; (2)K 1;(3)计算新的T2,一直迭代计算2kT ;(4)精度控制:如果122||kk T T ε--<,则停止计算,并将2k T 作为积分的近似数值,否则循环将不停止。
对第四点,通常可以加入一个循环最高次数,防止程序陷入死循环。
function f=fxy(x,y,w) if w==1f=x+y; %函数1elseif w==2f=sin(abs(x-y)); %函数2elseif w==3f=sin(x+y)/(x+y); %函数3if x+y==0f=1;end;end;function gy=gy(y,a,b,w,error)k=1;lock=0;count=0;T1=(b-a)*(fxy(a,y,w)+fxy(b,y,w))/2;while lock==0&&count<100 %限定最多迭代20次T2=T2kx(y,T1,a,b,k,w);if abs(T2-T1)<errorgy=T2;lock=1;elseT1=T2;count=count+1;k=k+1;end;end% count%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%% 龙贝格算法%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%% 作者:XXXX %%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%% 时间:2012/4/16 %%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%clear all; clc;%% 详情见报告Romberg公式介绍部分clear all;clc;which=1; %表示计算的函数f1,f2,f3%积分区间a=0;if which==1||which==3b1=1;b2=1; %函数1和2的区间elseb1=pi;b2=pi/2; %函数2的区间end%% 计算主程序k=1;lock=0;count=0; %辅助量error=0.0001; %计算精度% gy=gy(y,a,b,w,error)T1=(b2-a)*(gy(a,a,b1,which,error)+gy(b2,a,b1,which,error))/2; while lock==0&&count<100 %限定最多迭代20次T2=T2ky(T1,a,b1,b2,k,which,error);if abs(T2-T1)<errorI=T2;lock=1;elseT1=T2;function T2kx=T2kx(y,T2kx_1,a,b,k,w)temp1=0;for i=1:2^(k-1)temp1=temp1+fxy(a+(2*i-1)*(b-a)/2^k,y,w);endT2kx=0.5*T2kx_1+temp1*(b-a)/2^k;function T2ky=T2ky(T2ky_1,a,b1,b2,k,w,error)temp1=0;for i=1:2^(k-1)temp1=temp1+gy(a+(2*i-1)*(b2-a)/2^k,a,b1,w,error);endT2ky=0.5*T2ky_1+temp1*(b2-a)/2^k;。
龙贝格算法

龙贝格积分1. 算法原理采用复化求积公式计算时,为使截断误差不超过ε,需要估计被积函数高阶导数的最大值,从而确定把积分区间[]b a ,分成等长子区间的个数n 。
首先在整个区间[]b a ,上应用梯形公式,算出积分近似值T1;然后将[]b a ,分半,对 应用复化梯形公式算出T2;再将每个小区间分半,一般地,每次总是在前一次的基础上再将小区间分半,然后利用递推公式进行计算,直至相邻两个值之差小于允许误差为止。
实际计算中,常用ε≤-n n T T 2作为判别计算终止的条件。
若满足,则取n T f I 2][≈;否则将区间再分半进行计算,知道满足精度要求为止。
又经过推导可知,∑=-++=ni i i n n x x f h T T 112)2(221,在实际计算中,取kn 2=,则k a b h 2-=,112)1*2(2++--+=+k i i ab i a x x 。
所以,上式可以写为∑=++--+-+=+kk i k k ab i a f a b T T 211122)2)12((2211k开始计算时,取())()(21b f a f ab T +-=龙贝格算法是由递推算法得来的。
由梯形公式得出辛普森公式得出柯特斯公式最后得到龙贝格公式。
根据梯形法的误差公式,积分值n T 的截断误差大致与2h 成正比,因此步长减半后误差将减至四分之一,即有21114n n T T -≈-将上式移项整理,知2211()3n n n T T T -≈-由此可见,只要二分前后两个积分值n T 和2n T 相当接近,就可以保证计算保证结果计算结果2n T 的误差很小,这种直接用计算结果来估计误差的方法称作误差的事后估计法。
按上式,积分值2n T 的误差大致等于21()3n n T T -,如果用这个误差值作为2n T 的一种补偿,可以期望,所得的()222141333n n n n n T T T T T T =+-=-应当是更好的结果。
龙贝格求 积分

龙贝格(Romberg )求积法1.算法理论Romberg 求积方法是以复化梯形公式为基础,应用Richardson 外推法导出的数值求积方法。
由复化梯形公式 )]()(2)([2222b f h a f a f h T +++=可以化为)]()]()([2[212112h a f h b f a f hT +++==)]([21211h a f h T ++一般地,把区间[a,b]逐次分半k -1次,(k =1,2,……,n )区间长度(步长)为kk m a b h -=,其中mk =2k -1。
记k T =)1(k T由)1(k T =]))12(([21211)1(1∑=---++km j k k k h j a f h T 从而⎰badxx f )(=)1(kT-)(''122k f h a b ξ- (1)按Richardson 外推思想,可将(1)看成关于k h ,误差为)(2k h O 的一个近似公式,因而,复化梯形公式的误差公式为⎰badxx f )(-)1(k T =......4221++kkh K h K =∑∞=12i i k i h K (2)取1+k h =k h 21有⎰badxx f )(-)1(1+k T=∑∞=+121221i i k iihK (3)误差为)(2jh O 的误差公式 )(j kT=)1(-j kT+141)1(1)1(------j j k j k T T 2.误差及收敛性分析(1)误差,对复化梯形公式误差估计时,是估计出每个子区间上的误差,然后将n 个子区间上的误差相加作为整个积分区间上的误差。
(2)收敛性,记h x i =∆,由于∑=++=ni i i n x f x f h f T 01))]()([2)(=))()((21101∑∑-==∆+∆n i ni i i i i x x f x x f上面两个累加式都是积分和,由于)(x f 在区间],[b a 上可积可知,只要],[b a 的分划的最大子区间的长度0→λ时,也即∞→n 时,它们的极限都等于积分值)(f I 。
龙贝格算法求数值积分程序说明及流程图
In(k,2)=4*In(k+1,1)/3-In(k,1)/3;
end
flag(2)=i+3;
for k=flag(3)+1:i+2
In(k,3)=16*In(k+1,2)/15-In(k,2)/15;
end
flag(3)=i+2;
for k=flag(4)+1:i+1
end
In(i+5,1)=In(i+5,1)/2^(i+5)+In(i+4,1)/2;
In(i+4,2)=4*In(i+5,1)/3-In(i+4,1)/3;
In(i+3,3)=16*In(i+4,2)/15-In(i+3,2)/15;
In(i+2,4)=64*In(i+3,3)/63-In(i+2,3)/63;
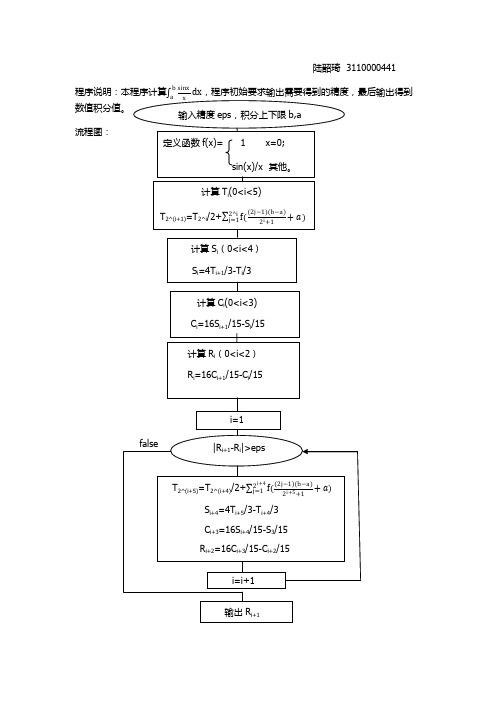
陆韶琦 3110000441
程序说明:本程序计算
数值积分值。
b sinx
a x
dx,程序初始要求输出需要得到的精度,最后输出得到
输入精度 eps,积分上下限 b,a
流程图:
定义函数 f(x)=
1
x=0;
sin(x)/x 其他。
计算 Ti(0<i<5)
T2^(i+1)=T2^i/2+
2j−1 b−a
2^i
j=1 f(
2 i +1
+ )
计算 Si(0<i<4)
Si=4Ti+1/3-Ti/3
计算 Ci(0<i<3)
用C语言编程:龙贝格-数值积分

#include"math.h"
#define e 0.001
double f(double x)
{
double y;
ielse y=sin(x)/x;
return y;
}
void romberg(double a,double b)
以此类推,在判断|Tn(0)-Tn-1(0)|<e即可利用加速递推公式算出结果
3.2.2 龙贝格算法计算步骤
步骤1:输入区间端点 ,精度控制值 ,循环次数 ,定义函数 ,取 ,
步骤2:for to
步骤3:数据积分近似值 。
利用Romberg方法计算函数
3.3
用龙贝格算法计算:
3.4
3.4.1 代码
romberg(a,b);
}
3.4.2 实验结果
3.5
*************************************************************************************************************************************
班级:信科
学号:******
姓名:
成绩:________
数值分析实验报告
实验3
3.1
通过本实验理解数值积分与微分的基本原理。掌握数值积分中常见的复合求积公式的编程实现。
掌握龙贝格算法的基本思路和迭代步骤;
培养编程与上机调试能力。
3.2
3.2.1 龙贝格算法基本思路
先算出他T0(0),从而计算T0(1)
{
double a,b;
龙贝格(Romberg)求积法

龙贝格(Romberg)求积法
复化求积方法对于提高计算精度是行之有效的 方法,但复化公式的一个主要缺点在于要先估计出 步长。若步长太大,则难以保证计算精度,若步长 太小,则计算量太大,并且积累误差也会增大。在 实际计算中通常采用变步长的方法,即把步长逐次 分半,直至达到某种精度为止。
1.1变步长的梯形公式 变步长复化求积法的基本思想是在求积过程中,
)
0.9397933
进一步二分求积区间,并计算新分点上的函数值
f
(
1 4
)
0.9896158
,
f
(
3 4
)
0.9088516
有
T4
1 2 T2
1 4
f
(
1 4
)
f
(
3 4
)
0.9445135
这样不断二分下去,计算结果如P139列表所 示。积分的准确值为0.9460831,从表中可
看出用变步长二分10次可得此结果。
的考积察分T值与nS等n 。份辛卜生公式 S n之间的关系。将
复化梯形公式
Tn
h 2
f
(a)
2
n1 k 1
f
(xk ) f (b)
梯形变步长公式
T2 n
Tn 2
h n1
2 k 0
f (xk1 ) 2
代入(6.9) T 表达式得
h
n1
n1
T
6 f (a) 4k0
f
(
x k
1
)
2
(
2
输入 a,b,ε
)
变
b-ah,
h 2
f(a)+f(b)T1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
{
double fx;
fx=1/(1+x);
return(fx);
}
double fx2(double i,double a,double b) /*编写T的高次迭代函数*/
{
//double fx1(double z);
scanf("%f",&a);
printf("请输入积分下界b=\n"); /*输入X的上界*/
scanf("%f",&b);
printf("请输入计算精度e=\n");
scanf("%lf",&e);
fa=fx1(a); /*计算fx函数上下界的值*/
fb=fx1(b);
printf("a=%3.7f\nb=%3.7f\nfa=%3.7f\nfb=%3.7f\ne=%3.10f",a,b,fa,fb,e); /*输出上、下界值,上下界fx函数值,计算精度e*/
printf("\n");
/*程序开始*/
T1=(b-a)*(fa+fb)/2;
for(i=0;;i++)
{
double fx2(double i,double a,double b);
double Tkk;
Tkk=fx2(i,a,b); /*调用fx函数*/
T=T1/2+Tkk;
T1=T;
S=T+(T-T1)/(pow(4,1)-1);
#include<stdio.h>
#include<math.h>
void main()
{
int i;
float a,b,fa,fb;
double T,T1,S,S1,C,C1,R,R1,e;
double fx1(double x);
printf("请输入积分下界a=\n"); /*输入X的下界*/
S1=S;
if(i>=1)
{
C=S+(S-S1)/(pow(4,2)-1);
C1=C;
}
if(i>=2)
R=C+(C-C1)/(pow(4,3)-1);
if(abs(R-R1)<0.0000001) /*判断是否满足计算精度,满足则退出迭代,不满足则继续*/
break;
R1=R;
}
printf("积分计算数值为\n"); /*输出计算结果*/
double m,l;
double Tk,Tkk,z;
m=pow(2,i);
Tk=0;
for(l=1;l<=m;l++)
{
z=a+(2*l-1)*(b-a)/(2*m);
Tk+=fx1(z);
}
Tkk=(b-a)*Tk/(m*2);
return(Tkk);
}
