龙贝格求解积分
龙贝格公式及实现

龙贝格公式就是逐次对分积分区间的方法,可以把前面计算的结果作为一个整体带入对分后的计算公式中,只需要增加新的分点的函数值。
以)(0k T表示],[b a 二分k 次后的梯形值,)(k mT 表示)(0k T 的m 次加速值,则有),2,1(,141144)(14)1(1)( =---=-+-k TTTk m k m mmk m龙贝格算法:步1 初始化:计算)]()([2)0(0b f a f ab T+-=,置1:=k (k记录区间],[b a 的二分次数),a b h -=;步2(二分) 计算积分值: ∑-=+---+=122/11)1(0)(01)(221k j j k k k x f h TT;步3(加速) 求加速值:计算)(1)1(1)(141144j k j jj k j jjj k jTTT--+------=,),,2,1(k j =;步4 精度检验:对指定的精度ε,若ε<--)0(1)0(k kTT,则终止计算,并取)0(kT作为所求的结果;否则置1:+=k k ,hh 21:=,转步2。
计算次序:(0)0T第1次循环 二分:(1)0T加速:(0)1T 第2次循环二分:(2)1T加速:(1)(0)12,T T第3次循环 二分:(3)2T加速:(2)(1)(0)123,,T T T第4次循环 二分:(4)3T加速:(3)(2)(1)(0)1234,,,T T TT……在命令窗口输入: a = 0; b = 1;epsilon = 5e-6;f = @(x)sin(x);%@(X)申请变量空间,计算sin 积分y = romberg(f,a,b,epsilon) %函数调用安回车,出结果。
复化辛普森公式及龙贝格方法求解积分

一、实验目的及题目1. 实验目的:(1) 学习用复化辛普森公式及龙贝格方法求解积分并掌握这种方法。
(2)了解这些辛普森公式及龙贝格方法的概念,参考课本写出用复化辛普森算法以及龙贝格方法计算目标题目的程序,在matlab 中实现,并用matlab 内置的函数计算出结果,并提出存在的问题。
2. 题目:利用复化辛普森公式和龙贝格方法计算下列积分:(1)dx e x ⎰-5.002(2)dx x x ⎰202sin )2sin(cos π二、实验用仪器设备、器材或软件环境计算机、matlab 软件。
三、实验原理、程序框图、程序代码1.实验原理:根据微积分学基本定理,若被积函数f(x)在区间[a,b]上连续,只要能找到f(x)的一个原函数F(x),便可利用牛顿-莱布尼茨公式求得积分值。
但会经常遇到如下问题:找不到用初等函数,找到了原函数,但因表达式过于复杂而不便计算等等。
此时则不能用牛顿-莱布尼茨公式,因此有必要研究如下公式。
1)复化求积公式及原理由于高阶插值的不稳定性,为了提高计算积分的精度,可把积分区间分为若干个小区间,将()I f 写成这些小区间上的积分之和,然后对每一个小区间上的积分应用到辛普森公式,或柯特斯公式,并把每个小区间上的结果累加,所得到的求积公式就称为复化求积公式。
辛普森公式的数值积分公式为:⎰+++-≈ba b f b a f a f a b dx x f )]()2(4)([6)(它的集合意义为用通过三点))(,()),2(,2()),(,(b f b b a f b a a f a =+的抛物线围城的曲边形面积来代替给定函数的积分。
同梯形公式一样,也有复化辛普森公式:)()(),()()]()(4)([6)(010121b f x f a f x f x f x x f h dx x f n n k k k k ba ==++≈∑⎰-=++ 其中 n ab h x x xk k k -=+=++,2121。
龙贝格积分算法实验[1]
![龙贝格积分算法实验[1]](https://img.taocdn.com/s3/m/1c3c3ec18bd63186bcebbcf8.png)
且 ( 为等份次数)
2.按梯形公式的递推关系,计算
3.按龙贝格公式计算加速值
4.精度控制。对给定的精度 ,若
则终止计算,并取 作为所求结果;否则 ,重复2~4步,直到满足精度为止。
问题
(1)程序运行如下:
I = Romberginterg(inline('x.^2.*exp(x)'),0,1,25,1e-6)
function I = GaussInterg(fun, type, a, b, tol)
% GaussInterg用Gauss型求积公式求积分,具体形式由使用者选取
%
% Synopsis: I = GaussInterg(fun, type, a, b)
% I = GaussInterg(fun, type, a, b, tol)
if nargin < 4
npanel = 25;
end
if nargin < 5
tol = 5e-9;
end
if nargin < 6
flag = 0;
end
T(1,1) = TrapezoidInteg(fun, a, b, npanel); %T0(h) = T(h)
err = 1; %初始化误差值
if nargin < 4
npanel = 25;
end
nnode = npanel + 1; %节点数=段数+ 1
h = (b-a)/(nnode-1); %步长
x = a:h:b; %将积分区间分段
f = feval(fun,x);%求节点处被积函数的值
I = h * ( 0.5*f(1) + sum(f(2:nnode-1)) + 0.5*f(nnode) );
龙贝格求 积分

龙贝格(Romberg )求积法1.算法理论Romberg 求积方法是以复化梯形公式为基础,应用Richardson 外推法导出的数值求积方法。
由复化梯形公式 )]()(2)([2222b f h a f a f h T +++=可以化为)]()]()([2[212112h a f h b f a f hT +++==)]([21211h a f h T ++一般地,把区间[a,b ]逐次分半k -1次,(k =1,2,……,n)区间长度(步长)为kk m a b h -=,其中mk =2k -1。
记k T =)1(k T由)1(k T =]))12(([21211)1(1∑=---++km j k k k h j a f h T 从而⎰badxx f )(=)1(kT-)(''122k f h a b ξ- (1)按Richardson 外推思想,可将(1)看成关于k h ,误差为)(2k h O 的一个近似公式,因而,复化梯形公式的误差公式为⎰badxx f )(-)1(k T =......4221++kkh K h K =∑∞=12i i k i h K (2)取1+k h =k h 21有 ⎰ba dx x f )(-)1(1+k T =∑∞=+121221i ik ii hK (3)误差为)(2jh O 的误差公式 )(j kT=)1(-j kT+141)1(1)1(------j j k j k T T2。
误差及收敛性分析(1)误差,对复化梯形公式误差估计时,是估计出每个子区间上的误差,然后将n 个子区间上的误差相加作为整个积分区间上的误差。
(2)收敛性,记h x i =∆,由于∑=++=ni i i n x f x f h f T 01))]()([2)(=))()((21101∑∑-==∆+∆n i ni i i i i x x f x x f上面两个累加式都是积分和,由于)(x f 在区间],[b a 上可积可知,只要],[b a 的分划的最大子区间的长度0→λ时,也即∞→n 时,它们的极限都等于积分值)(f I 。
龙贝格求积公式

2
f( ) 2
T3 , 1 T3 , 2
T3 , 3
T4 , 1 T5 , 1
M
T4 , 2 T5 , 2
M
T4, 3 T5 , 3
M
T4 , 4 T5 , 4
M
用龙贝格方法计算积分的步骤为:
(1):准备初值,先用梯形公式计算积分近
似 (值 2)::T1按 变b 2步a[长f (a梯) 形f (公b)]式计算积分近似值:
4 0.918741799 0.916327874 0.916297224 0.916294351
5 0.916905342 0.916293190 0.916290077 0.916290776
T5 , 4 0.916290776
例3:取=0.00001,用龙贝格方法计算积分
1
I
4
dx
01 x2
解:由题意
f(x)=4/(1+x2) a=0 b=1 f(0)=4 f(1)=2 由梯形公式得
T1=1/2[f(0)+f(1)]=3 计算f(1/2)=16/5 用变步长梯形公式得
T2=1/2[T1+f(1/2)]=3.1 由加速公式得
S1=1/3(4T2-T1)=3.133333333
求出f(1/4) f(3/4) 进而求得 T4=1/2{T2+1/2[f(1/4)+f(3/4)]}
Simpson加速公式: Cn
42 S2n Sn 42 1
I
C2n
1 43 1(C2n
Cn )
43C2n Cn 43 1
Cotes加速公式:Rn
43C2n Cn 43 1
Romberg 值序列
龙贝格算法

龙贝格积分1. 算法原理采用复化求积公式计算时,为使截断误差不超过ε,需要估计被积函数高阶导数的最大值,从而确定把积分区间[]b a ,分成等长子区间的个数n 。
首先在整个区间[]b a ,上应用梯形公式,算出积分近似值T1;然后将[]b a ,分半,对 应用复化梯形公式算出T2;再将每个小区间分半,一般地,每次总是在前一次的基础上再将小区间分半,然后利用递推公式进行计算,直至相邻两个值之差小于允许误差为止。
实际计算中,常用ε≤-n n T T 2作为判别计算终止的条件。
若满足,则取n T f I 2][≈;否则将区间再分半进行计算,知道满足精度要求为止。
又经过推导可知,∑=-++=ni i i n n x x f h T T 112)2(221,在实际计算中,取kn 2=,则k a b h 2-=,112)1*2(2++--+=+k i i ab i a x x 。
所以,上式可以写为∑=++--+-+=+kk i k k ab i a f a b T T 211122)2)12((2211k开始计算时,取())()(21b f a f ab T +-=龙贝格算法是由递推算法得来的。
由梯形公式得出辛普森公式得出柯特斯公式最后得到龙贝格公式。
根据梯形法的误差公式,积分值n T 的截断误差大致与2h 成正比,因此步长减半后误差将减至四分之一,即有21114n n T T -≈-将上式移项整理,知2211()3n n n T T T -≈-由此可见,只要二分前后两个积分值n T 和2n T 相当接近,就可以保证计算保证结果计算结果2n T 的误差很小,这种直接用计算结果来估计误差的方法称作误差的事后估计法。
按上式,积分值2n T 的误差大致等于21()3n n T T -,如果用这个误差值作为2n T 的一种补偿,可以期望,所得的()222141333n n n n n T T T T T T =+-=-应当是更好的结果。
4.4龙贝格求积公式

4 1 T1 ( k 1) T0 ( k ) T0 ( k 1) 3 3 16 1 T2 ( k 1) T1 ( k ) T1 ( k 1) 15 15 64 1 T3 ( k 1) T2 ( k ) T2 ( k 1) 63 63
k 1, 2 ,
1 h n1 Tn f ( x 1 ) j 2 2 j 0 2 1 b a n 1 1 Tn f (a ( j )h) 2 2n j 0 2 1 b a n 1 ba Tn f ( a ( 2 j 1) ) 2 2 n j 0 2n
Romberg算法的代 数精度为m的两倍 Romberg算法的收敛 阶高达m+1的两倍
T0 (0 ) T0 (1) T0 ( 2 ) T0 ( 3) T1 (0 ) T1 (1) T1 ( 2 ) T2 (0 ) T2 (1)
T3 (0 )
龙贝格积分
例:计算
I T2n 1 I Tn 4
令
--------(7)
即 当然
Cn C2 k 1 T2 (k 1) C 2 n T2 (k )
--------(8)
同样由复合Cotes公式的余项
I C2 n 1 (C2 n Cn ) 63
64 1 64 1 得 I C2 n Cn T2 ( k ) T2 ( k 1) 63 63 63 63
43 C 2n C n Rn 3 4 1
Romberg
T1 = T0( 0 )
T2 = T0( 1 )
<?
算法: T4 = T0( 2 )
T8 = T0
(3)
S1 = T1( 0 ) S2 = T1
龙贝格算法求数值积分程序说明及流程图
In(k,2)=4*In(k+1,1)/3-In(k,1)/3;
end
flag(2)=i+3;
for k=flag(3)+1:i+2
In(k,3)=16*In(k+1,2)/15-In(k,2)/15;
end
flag(3)=i+2;
for k=flag(4)+1:i+1
end
In(i+5,1)=In(i+5,1)/2^(i+5)+In(i+4,1)/2;
In(i+4,2)=4*In(i+5,1)/3-In(i+4,1)/3;
In(i+3,3)=16*In(i+4,2)/15-In(i+3,2)/15;
In(i+2,4)=64*In(i+3,3)/63-In(i+2,3)/63;
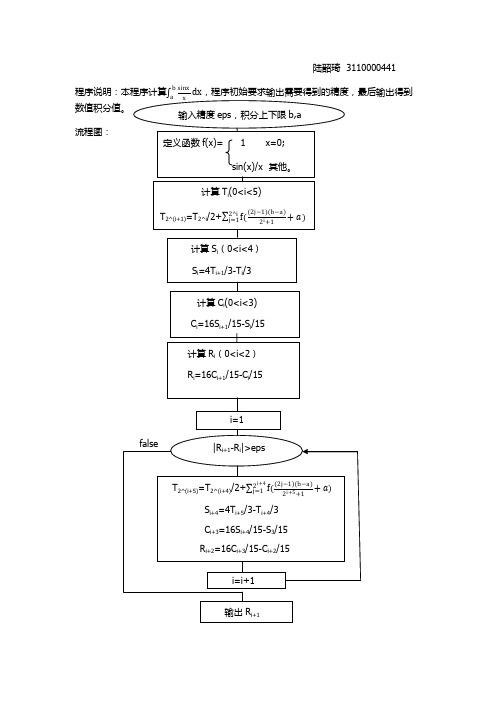
陆韶琦 3110000441
程序说明:本程序计算
数值积分值。
b sinx
a x
dx,程序初始要求输出需要得到的精度,最后输出得到
输入精度 eps,积分上下限 b,a
流程图:
定义函数 f(x)=
1
x=0;
sin(x)/x 其他。
计算 Ti(0<i<5)
T2^(i+1)=T2^i/2+
2j−1 b−a
2^i
j=1 f(
2 i +1
+ )
计算 Si(0<i<4)
Si=4Ti+1/3-Ti/3
计算 Ci(0<i<3)
