龙贝格积分的程序实现
龙贝格积分的程序实现

龙贝格积分的程序实现(总5页)本页仅作为文档封面,使用时可以删除This document is for reference only-rar21year.March计算方法实验报告3【课题名称】龙贝格积分的程序实现【目的和意义】函数变化有急有缓,为了照顾变化剧烈部分的误差,我们需要加密格点。
对于变化缓慢的部分,加密格点会造成计算的浪费。
以此我们介绍一种算法,可以自动在变化剧烈的地方加密格点计算,而变化缓慢的地方,则取稀疏的格点。
实际计算中,由于要事先给出一个合适的步长往往很困难,所以我们往往采用变步长的计算方案,即在步长逐步分半的过程中,反复利用复化求积公式进行计算,直到所求得的积分值满足精度要求为止。
在步长逐步分半过程中将粗糙的积分值逐步加工为精度较高的积分值,或者说将收敛缓慢的梯形值序列加工成收敛迅速的积分值序列。
这种加速方法称为龙贝格算法。
【计算公式】设表示复化梯形求得的积分值,其下标是等分数,由此则有递推公式其中 ,其中由复化梯形公式的截断误差公式可得, 。
由此可知, 。
这样导出的加速公式是辛普森公式: 同理可得n n n S S C 15115162-= n n n C C R 631_63642=。
由此便可得加速的算法:龙贝格算法。
【龙贝格求积算法流程图】∑-=++=10212)(221n k k n n x f h T T h k a x n a b h k )21(,21++=-=+)(''12)()()(2ξf h a b f T f I n --=-)(''212)()()(22ηf h a b f T f I n ⎪⎪⎭⎫ ⎝⎛--=-n n T T I 31342-≈n n n T T S 31342-=【龙贝格求积算法Matlab主程序】function[t]=rbg(f,a,b,c) %定义龙贝格积分函数,f为待积函数,a与b为积分上下限,c为精度控制;t=zeros(15,4); %生成一零矩阵,用于存放t值;t(1,1)=(b-a)/2*(f(a)+f(b)); %由于矩阵行列值均从1开始,所以将原本的t(0,0)记为t(1,1),行列均加1;for k=2:4 %先算出第一列的4个(包括t(1,1))值,以便程后面可以直接循环计算;sum=0;for i=1:2^(k-2)sum=sum+f(a+(2*i-1)*(b-a)/2^(k-1));endt(k,1)=*t(k-1,1)+(b-a)/2^(k-1)*sum;for i=2:kt(k,i)=(4^(i-1)*t(k,i-1)-t(k-1,i-1))/(4^(i-1)-1);endendfor k=5:15 %循环按照公式计算出t值;sum=0;for i=1:2^(k-2)sum=sum+f(a+(2*i-1)*(b-a)/2^(k-1));endt(k,1)=*t(k-1,1)+(b-a)/2^(k-1)*sum;for i=2:4t(k,i)=(4^(i-1)*t(k,i-1)-t(k-1,i-1))/(4^(i-1)-1);endif k>6 %可知最小二分次数,防止假收敛;if abs(t(k,4)-t(k-1,4))<c %若此时t值满足精度,则输出积分值;disp(['答案 ',num2str(t(k,4))]);break;endendendif k>=15disp(['不收敛']); %二分次数达15次仍不收敛;end【调用函数解题】由于被积函数sin(x)/x在积分下限0时函数值难定,故取积分下限为10^(-60)。
龙贝格求积公式

2
f( ) 2
T3 , 1 T3 , 2
T3 , 3
T4 , 1 T5 , 1
M
T4 , 2 T5 , 2
M
T4, 3 T5 , 3
M
T4 , 4 T5 , 4
M
用龙贝格方法计算积分的步骤为:
(1):准备初值,先用梯形公式计算积分近
似 (值 2)::T1按 变b 2步a[长f (a梯) 形f (公b)]式计算积分近似值:
4 0.918741799 0.916327874 0.916297224 0.916294351
5 0.916905342 0.916293190 0.916290077 0.916290776
T5 , 4 0.916290776
例3:取=0.00001,用龙贝格方法计算积分
1
I
4
dx
01 x2
解:由题意
f(x)=4/(1+x2) a=0 b=1 f(0)=4 f(1)=2 由梯形公式得
T1=1/2[f(0)+f(1)]=3 计算f(1/2)=16/5 用变步长梯形公式得
T2=1/2[T1+f(1/2)]=3.1 由加速公式得
S1=1/3(4T2-T1)=3.133333333
求出f(1/4) f(3/4) 进而求得 T4=1/2{T2+1/2[f(1/4)+f(3/4)]}
Simpson加速公式: Cn
42 S2n Sn 42 1
I
C2n
1 43 1(C2n
Cn )
43C2n Cn 43 1
Cotes加速公式:Rn
43C2n Cn 43 1
Romberg 值序列
龙贝格积分法C语言(西安交大)

{
double fx;
fx=1/(1+x);
return(fx);
}
double fx2(double i,double a,double b) /*编写T的高次迭代函数*/
{
//double fx1(double z);
scanf("%f",&a);
printf("请输入积分下界b=\n"); /*输入X的上界*/
scanf("%f",&b);
printf("请输入计算精度e=\n");
scanf("%lf",&e);
fa=fx1(a); /*计算fx函数上下界的值*/
fb=fx1(b);
printf("a=%3.7f\nb=%3.7f\nfa=%3.7f\nfb=%3.7f\ne=%3.10f",a,b,fa,fb,e); /*输出上、下界值,上下界fx函数值,计算精度e*/
printf("\n");
/*程序开始*/
T1=(b-a)*(fa+fb)/2;
for(i=0;;i++)
{
double fx2(double i,double a,double b);
double Tkk;
Tkk=fx2(i,a,b); /*调用fx函数*/
T=T1/2+Tkk;
T1=T;
S=T+(T-T1)/(pow(4,1)-1);
#include<stdio.h>
计算方法用龙贝格程序计算数值积分的值(附程序代码)

2第二题 求数值积分11sin 3sin x dx x x -+⎰精确到610-。
龙贝格的算法思想:Romberg 方法也称为逐次分半加速法。
它是在复化梯形公式的基础上,利用Richardson 外推法,构造出一种高精度的数值积分方法。
在等距基点的情况下,用计算机计算积分值通常都采用把区间逐次分半的方法进行。
这样,前一次分割得到的函数值在分半以后仍可被利用,且易于编程 。
2.2.1程序设计关键步骤(1)准备初值aa[0][0]=(b-a)*(F(a)+F(b))/2.0来实现就算初值。
(2)用 for ( n=i,j=1; n>0;n--,j++)aa[j][n]=(pf(2*j+1)*aa[j-1][n+1]-aa[j-1][n])/(pf(j*2+1)-1) 来实现(2)(k )00T T 到的计算。
(3)用fabs(aa[i][1]-aa[i][0])判断数值的精度,如果fabs(aa[i][1]-aa[i][0]<e,则返回gcc(a,b,aa,i+1)进行计算下一个要用到得值; 如果fabs(aa[i][1]-aa[i][0]> e ,则根据aa[i+1][0]=(pf(2*i+3)*aa[i][1]-aa[i][0])/(pf(2*i+3)-1)而得到结果。
2.2.2程序运行结果如下图所示#include "stdafx.h"#include <iostream>#include <math.h>#define F(x) (sin(x)/(3*x+sin(x))) //函数举例。
using namespace std;//------------步长及4,16,64.......的实现----------double pf (int i){int s=1;for (int j=0;j<i;j++)s*=2;return s/2;}//---------定义一个求t1,t2......的函数-------------double gcc (double a, double b,double aa[][20],int i){double s,h,x;h=(b-a)/pf(i);s=0;x=a+h/3;do{s+=F(x);x+=h;}while (x<b);aa[0][i]=aa[0][i-1]/2+h/2*s;return 0;}//----------------------主函数---------------------------int main(){double aa[20][20]={0},e,a,b,h;int j,i,n;cout <<"请输入积分区间:\na= ";cin >>a;cout <<"b= ";cin >>b;cout <<"请输入精度:e=";cin >>e;aa[0][0]=(b-a)*(F(a)+F(b))/2.0;gcc(a,b,aa,1);aa[1][0]=(4*aa[0][1]-aa[0][0])/3;for (i=1;i<20;i++){gcc(a,b,aa,i+1);//求下一个要用的t。
龙贝格算法求数值积分程序说明及流程图
In(k,2)=4*In(k+1,1)/3-In(k,1)/3;
end
flag(2)=i+3;
for k=flag(3)+1:i+2
In(k,3)=16*In(k+1,2)/15-In(k,2)/15;
end
flag(3)=i+2;
for k=flag(4)+1:i+1
end
In(i+5,1)=In(i+5,1)/2^(i+5)+In(i+4,1)/2;
In(i+4,2)=4*In(i+5,1)/3-In(i+4,1)/3;
In(i+3,3)=16*In(i+4,2)/15-In(i+3,2)/15;
In(i+2,4)=64*In(i+3,3)/63-In(i+2,3)/63;
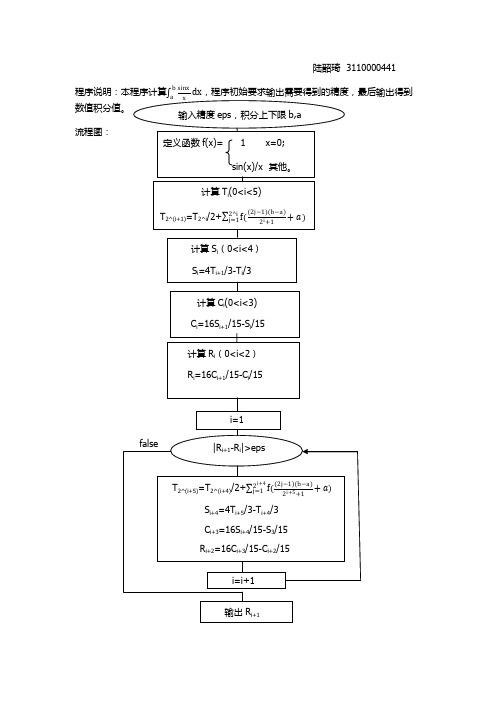
陆韶琦 3110000441
程序说明:本程序计算
数值积分值。
b sinx
a x
dx,程序初始要求输出需要得到的精度,最后输出得到
输入精度 eps,积分上下限 b,a
流程图:
定义函数 f(x)=
1
x=0;
sin(x)/x 其他。
计算 Ti(0<i<5)
T2^(i+1)=T2^i/2+
2j−1 b−a
2^i
j=1 f(
2 i +1
+ )
计算 Si(0<i<4)
Si=4Ti+1/3-Ti/3
计算 Ci(0<i<3)
龙贝格算法

龙贝格算法11医软2班刘名奎简介:龙贝格求积公式也称为逐次分半加速法。
它是在梯形公式、辛卜生公式和柯特斯公式之间的关系的基础上,构造出一种加速计算积分的方法。
作为一种外推算法, 它在不增加计算量的前提下提高了误差的精度.在等距基点的情况下,用计算机计算积分值通常都采用把区间逐次分半的方法进行。
这样,前一次分割得到的函数值在分半以后仍可被利用,且易于编程。
解题思路:步骤一:先确定积分上下限a、b,精度值e,再定义函数f(x),取n=1,h=(b-a)/2,=h*(f(a)+f(b))/2。
步骤二:根据求出……,再根据公式Simpson公式=-,Cotes公式=-,Romberg公式R n=-分别求出,,。
步骤三:数值积分近似值,根据Romberg公式求出函数I=。
代码:#include"iostream.h"#include"math.h"#define e 0.0000000001double f(double x){double y;if(x==0)return y=1.0;else y=sin(x)/x;return y;}void romberg(double a,double b){int i,n=1;double h,T2,S2=0,C2=0,R2=0,T1,C1,S1,R1;h=(b-a)/2;T2=h*(f(a)+f(b));while(fabs(R2-R1)>e){R1=R2;T1=T2;S1=S2;C1=C2;double sum=0;for(i=1;i<=n;i++)sum=sum+f(a+(2*i-1)*h);T2=T1/2+sum*h;S2=(4*T2-T1)/3;C2=(16*S2-S1)/15;R2=(64*C2-C1)/63;n=n*2;h=h/2;}cout<<"最后结果为:"<<"I="<<R2<<endl;}void main(){double a,b;cout<<"请输入积分上下限a,b的值并用空格隔开:"<<endl;cin>>a>>b;cout<<"积分下限a="<<a<<endl; cout<<"积分上限b="<<b<<endl;cout<<"被积函数为:y=sin(x)/x"<<endl; cout<<"结果如下"<<endl;romberg(a,b);}当I=10sin()x dx x⎰,调试结果为:当I=221x dx ⎰时,调试结果为:当I=212xdx ⎰时,调试结果为:。
龙贝格算法实验报告

实验二:龙贝格算法一、实验目的1、通过本实验理解数值积分与微分的基本原理2、掌握数值积分中常见的复合求积公式的编程实现3、掌握龙贝格算法的基本思路和迭代步骤二、实验原理三、运行结果三、代码using System;using System.Collections.Generic;using System.Linq;using System.Text;namespace ConsoleApplication4{public delegate double F(double x);class Program{const double Precision = 0.00000000001;const int MAXRepeat = 10;static double f1(double x){double s=4/(1+x*x );return s;}static double Romberg(double a,double b, F f){int m,n,k;double[] y = new double[MAXRepeat];double h,ep,p,xk,s,q=0;h=b-a;y[0]=h*(f(a)+f(b))/2.0;//计算T`1`(h)=1/2(b-a)(f(a)+f(b));m=1;n=1;ep=Precision+1;while((ep>=Precision)&&(m<MAXRepeat)){p=0.0;for(k=0;k<n;k++){xk = a + (k + 0.5) * h; // n-1p = p + f(xk); //计算∑f(xk+h/2),T} // k=0p = (y[0] + h * p) / 2.0; //T`m`(h/2),变步长梯形求积公式s = 1.0;for (k = 1; k <= m; k++){s = 4.0 * s;// pow(4,m)q = (s * p - y[k - 1]) / (s - 1.0);//[pow(4,m)T`m`(h/2)-T`m`(h)]/[pow(4,m)-1],2m阶牛顿柯斯特公式,即龙贝格公式y[k - 1] = p;p = q;}ep = Math.Abs(q - y[m - 1]);//前后两步计算结果比较求精度m = m + 1;y[m - 1] = q;n = n + n; // 2 4 8 16h = h / 2.0;//二倍分割区间}return q;}static void Main(string[] args){double a, b, result;Console.WriteLine("请输入积分下限:");a = Convert.ToDouble(Console.ReadLine());Console.WriteLine("请输入积分上限:");b = Convert.ToDouble(Console.ReadLine());result = Romberg(a, b, new F(f1));Console.Write("定积分计算结果为:{0}:", result);Console.ReadLine();}}}四、分析本次试验使我认识到了计算机计算能力的强大,通过本次实验对数值积分与微分的基本原理有了深刻理解。
龙贝格积分 python

龙贝格积分 python龙贝格积分 python一、什么是龙贝格积分?龙贝格积分(Romberg integration)是一种数值积分方法,它是对梯形法的递推加速处理。
梯形法是一种比较简单的数值积分方法,但它的精度不高,而且需要很多次计算。
龙贝格积分通过递推计算,可以大大提高计算精度,并且减少计算次数。
二、如何实现龙贝格积分?在 Python 中实现龙贝格积分可以使用以下代码:```pythondef romberg(f, a, b, n):"""Calculate the Romberg Integration of f(x) from a to b with n iterations"""R = [[0] * (n+1) for _ in range(n+1)]h = b - aR[0][0] = 0.5 * h * (f(a) + f(b))for i in range(1, n+1):h = 0.5 * hsum = 0for k in range(1, 2**i, 2):sum += f(a + k*h)R[i][0] = 0.5 * R[i-1][0] + sum*hfor j in range(1, i+1):R[i][j] = (4**j*R[i][j-1] - R[i-1][j-1]) / (4**j - 1)return R[n][n]```三、代码解析1. 定义函数 romberg(f, a, b, n),其中 f 为被积函数,a 和 b 分别为积分上下限,n 为迭代次数。
2. 创建一个n+1 行n+1 列的二维数组R,用于存储递推计算的结果。
3. 计算初始值 R[0][0],即使用梯形法计算第一次迭代的结果。
4. 进行 n 次迭代,每次将步长 h 减半,并且计算新的递推值。
具体过程如下:a. 计算当前步长 h。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(b a ) h I(f ) T2n(f ) f ''( ) 12 2
ቤተ መጻሕፍቲ ባይዱ
由此可知, 。这样导出的加速公式是辛普森公式: I T2 n Tn 同理可得 C n 贝格算法。
4 1 4 1 S n T2 n Tn 3 3 3 3 16 1 64 1 S 2n Sn Rn C 2n _ C n 。由此便可得加速的算法:龙 15 15 63 63
计算方法实验报告 3
【课题名称】
龙贝格积分的程序实现
【目的和意义】
函数变化有急有缓,为了照顾变化剧烈部分的误差,我们需要加密格点。对于变化缓慢 的部分,加密格点会造成计算的浪费。以此我们介绍一种算法,可以自动在变化剧烈的地方 加密格点计算,而变化缓慢的地方,则取稀疏的格点。 实际计算中, 由于要事先给出一个合适的步长往往很困难, 所以我们往往采用变步长的 计算方案,即在步长逐步分半的过程中,反复利用复化求积公式进行计算,直到所求得的积 分值满足精度要求为止。 在步长逐步分半过程中将粗糙的积分值逐步加工为精度较高的积分值, 或者说将收敛缓 慢的梯形值序列加工成收敛迅速的积分值序列。这种加速方法称为龙贝格算法。
【龙贝格求积算法流程图】
定义被积函数 f,积分上下 限 a,b 和精度 c
定义一个 15×4 的零矩 阵,用于存放 t 值
k>=15
【龙贝格求积算法 Matlab 主程序】
function[t]=rbg(f,a,b,c) t=zeros(15,4); t(1,1)=(b-a)/2*(f(a)+f(b)); for k=2:4 %定义龙贝格积分函数,f 为待积函数,a 与 b 为积 分上下限,c 为精度控制; %生成一零矩阵,用于存放 t 值; %由于矩阵行列值均从 1 开始,所以将原本的 t(0,0)记 为 t(1,1),行列均加 1; %先算出第一列的 4 个(包括 t(1,1))值,以便程后 面可以直接循环计算;
sum=0; for i=1:2^(k-2) sum=sum+f(a+(2*i-1)*(b-a)/2^(k-1)); end t(k,1)=0.5*t(k-1,1)+(b-a)/2^(k-1)*sum; for i=2:k t(k,i)=(4^(i-1)*t(k,i-1)-t(k-1,i-1))/(4^(i-1)-1); end end for k=5:15 sum=0; for i=1:2^(k-2) %循环按照公式计算出 t 值;
sum=sum+f(a+(2*i-1)*(b-a)/2^(k-1)); end t(k,1)=0.5*t(k-1,1)+(b-a)/2^(k-1)*sum; for i=2:4 t(k,i)=(4^(i-1)*t(k,i-1)-t(k-1,i-1))/(4^(i-1)-1); end if k>6 if abs(t(k,4)-t(k-1,4))<c disp(['答案 ',num2str(t(k,4))]); break; end end end if k>=15 disp(['不收敛']); end %可知最小二分次数,防止假收敛; %若此时 t 值满足精度,则输出积分值;
【计算公式】
设表示复化梯形求得的积分值,其下标是等分数,由此则有递推公式其中
T2n ,其中 Tn
1 2
h
2
f(x k k
0
n 1
1 2
)
h
b a 1 ,x 1 a (k ) h k n 2 2
2
由复化梯形公式的截断误差公式可得
(b a ) 2 I(f, ) Tn(f ) h f ''( ) 。 12
%二分次数达 15 次仍不收敛;
【调用函数解题】
1 0
������������������������ ������������ ������
由于被积函数 sin(x)/x 在积分下限 0 时函数值难定,故取积分下限为 10^(-60)。调用函数 解题如下:
