[2]龙贝格积分[数据]
龙贝格求 积分

龙贝格(Romberg )求积法1.算法理论Romberg 求积方法是以复化梯形公式为基础,应用Richardson 外推法导出的数值求积方法。
由复化梯形公式 )]()(2)([2222b f h a f a f h T +++=可以化为)]()]()([2[212112h a f h b f a f hT +++==)]([21211h a f h T ++一般地,把区间[a,b ]逐次分半k -1次,(k =1,2,……,n)区间长度(步长)为kk m a b h -=,其中mk =2k -1。
记k T =)1(k T由)1(k T =]))12(([21211)1(1∑=---++km j k k k h j a f h T 从而⎰badxx f )(=)1(kT-)(''122k f h a b ξ- (1)按Richardson 外推思想,可将(1)看成关于k h ,误差为)(2k h O 的一个近似公式,因而,复化梯形公式的误差公式为⎰badxx f )(-)1(k T =......4221++kkh K h K =∑∞=12i i k i h K (2)取1+k h =k h 21有 ⎰ba dx x f )(-)1(1+k T =∑∞=+121221i ik ii hK (3)误差为)(2jh O 的误差公式 )(j kT=)1(-j kT+141)1(1)1(------j j k j k T T2。
误差及收敛性分析(1)误差,对复化梯形公式误差估计时,是估计出每个子区间上的误差,然后将n 个子区间上的误差相加作为整个积分区间上的误差。
(2)收敛性,记h x i =∆,由于∑=++=ni i i n x f x f h f T 01))]()([2)(=))()((21101∑∑-==∆+∆n i ni i i i i x x f x x f上面两个累加式都是积分和,由于)(x f 在区间],[b a 上可积可知,只要],[b a 的分划的最大子区间的长度0→λ时,也即∞→n 时,它们的极限都等于积分值)(f I 。
梯形法的递推化和龙贝格算法

梯形法的递推化和龙贝格算法
梯形法(Trapezoid Rule)是一种数值积分的方法,用于计算函数在给定区间上的定积分。
梯形法的递推化可以通过将区间等分为若干个小梯形来实现。
具体步骤如下:
1. 将给定区间[a, b]分成n个等距的子区间,每个子区间的宽度为h = (b - a) / n。
2. 计算每个子区间的矩形面积(等于底边长度乘以高度),然后将所有子区间的矩形面积相加,得到梯形法的近似积分值。
梯形法的递推公式可以表示为:
I = h/2 * [f(a) + 2*f(a+h) + 2*f(a+2h) + ... + 2*f(a+(n-1)h) + f(b)] 其中,f(x)为要积分的函数。
龙贝格算法(Romberg Integration)是一种数值积分的方法,可以通过多次应用梯形法来逐步提高积分结果的精度。
龙贝格算法的具体步骤如下:
1. 利用梯形法计算区间[a, b]上的第一次近似积分值T(1,1)。
2. 利用递推公式T(m, 1) = 1/2 * [ T(m-1, 1) + h(m-1) *
Sigma(2^(m-2) * f(a + (2k-1) * h(m-1))), k=1 to 2^(m-2)],计算T(m, 1),其中h(m-1)为区间[a, b]的步长。
3. 计算T(m, n) = T(m, n-1) + 1 / (4^(n-1) - 1) * ( T(m, n-1) - T(m-1, n-1) ),其中n > 1,m > n。
4. 重复步骤3,直到达到所需的精度要求。
龙贝格算法通过递归和递推来不断提高积分结果的精度,可以较快地得到比较准确的近似积分值。
龙贝格算法

龙贝格积分1. 算法原理采用复化求积公式计算时,为使截断误差不超过ε,需要估计被积函数高阶导数的最大值,从而确定把积分区间[]b a ,分成等长子区间的个数n 。
首先在整个区间[]b a ,上应用梯形公式,算出积分近似值T1;然后将[]b a ,分半,对 应用复化梯形公式算出T2;再将每个小区间分半,一般地,每次总是在前一次的基础上再将小区间分半,然后利用递推公式进行计算,直至相邻两个值之差小于允许误差为止。
实际计算中,常用ε≤-n n T T 2作为判别计算终止的条件。
若满足,则取n T f I 2][≈;否则将区间再分半进行计算,知道满足精度要求为止。
又经过推导可知,∑=-++=ni i i n n x x f h T T 112)2(221,在实际计算中,取kn 2=,则k a b h 2-=,112)1*2(2++--+=+k i i ab i a x x 。
所以,上式可以写为∑=++--+-+=+kk i k k ab i a f a b T T 211122)2)12((2211k开始计算时,取())()(21b f a f ab T +-=龙贝格算法是由递推算法得来的。
由梯形公式得出辛普森公式得出柯特斯公式最后得到龙贝格公式。
根据梯形法的误差公式,积分值n T 的截断误差大致与2h 成正比,因此步长减半后误差将减至四分之一,即有21114n n T T -≈-将上式移项整理,知2211()3n n n T T T -≈-由此可见,只要二分前后两个积分值n T 和2n T 相当接近,就可以保证计算保证结果计算结果2n T 的误差很小,这种直接用计算结果来估计误差的方法称作误差的事后估计法。
按上式,积分值2n T 的误差大致等于21()3n n T T -,如果用这个误差值作为2n T 的一种补偿,可以期望,所得的()222141333n n n n n T T T T T T =+-=-应当是更好的结果。
龙贝格算法

2)理查森外推加速 从梯形公式出发, 将区间[a,b]逐次二分可以提高求积公式精度, 当[a,b] 分为 n 等份时,若记T������ = T ℎ ,当区间[a,b]分为 2n 等份时,则有 T2������ = T
ℎ 2
。再有泰勒公式展开为: T ℎ = ������ + ������1 ℎ2 + ������2 ℎ+ ⋯ +
建立一个命名为Romberg.m的function文件:
function[T]=Romberg(f,a,b,e) T=zeros(10,10); T(1,1)=(b-a)/2*(f(a)+f(b)); for k=2:10, sum=0; for i=1:2^(k-2), x=a+(2*i-1)*(b-a)/2^(k-1); sum=sum+f(x); end T(k,1)=T(k-1,1)/2+[(b-a)/2^(k-1)]*sum; for j=2:k, end %第一列用递推梯形公式 %定义龙贝格函数 %定义10阶的零元矩阵
1 3/2 ������ 0
������������。
算,并取������ ������, ������ ≈ ������ ;否则令 k=k+1,转(3)继续计算。 6)下图为我按照自己的算法所设计的示意表: 算法设计表:
k 1 2 3 4 …
h b-a (b-a)/2 (b-a)/4 (b-a)/8 …
������ ������, 1 T(1,1) T(2,1) T(3,1) T(4,1)
������ ������, 2
������ ������, 3
������ ������, 4
������ ������, 5
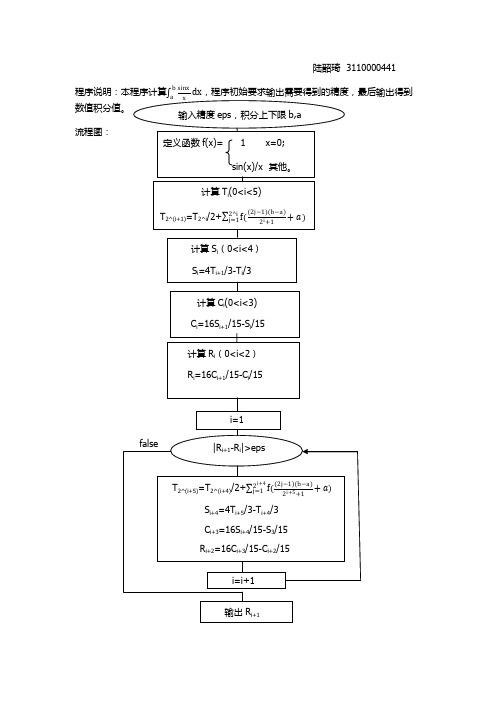
龙贝格算法求数值积分程序说明及流程图
In(k,2)=4*In(k+1,1)/3-In(k,1)/3;
end
flag(2)=i+3;
for k=flag(3)+1:i+2
In(k,3)=16*In(k+1,2)/15-In(k,2)/15;
end
flag(3)=i+2;
for k=flag(4)+1:i+1
end
In(i+5,1)=In(i+5,1)/2^(i+5)+In(i+4,1)/2;
In(i+4,2)=4*In(i+5,1)/3-In(i+4,1)/3;
In(i+3,3)=16*In(i+4,2)/15-In(i+3,2)/15;
In(i+2,4)=64*In(i+3,3)/63-In(i+2,3)/63;
陆韶琦 3110000441
程序说明:本程序计算
数值积分值。
b sinx
a x
dx,程序初始要求输出需要得到的精度,最后输出得到
输入精度 eps,积分上下限 b,a
流程图:
定义函数 f(x)=
1
x=0;
sin(x)/x 其他。
计算 Ti(0<i<5)
T2^(i+1)=T2^i/2+
2j−1 b−a
2^i
j=1 f(
2 i +1
+ )
计算 Si(0<i<4)
Si=4Ti+1/3-Ti/3
计算 Ci(0<i<3)
龙贝格求积公式

Romberg积分公式正是由此思想产生 积分公式正是由此思想产生
类似于梯形加速公式的处理方法,得到: 类似于梯形加速公式的处理方法,得到: 加速公式的处理方法
2 1 4 S2 n − Sn I ≈ S2 n + 2 ( S2 n − Sn ) = 2 4 −1 4 −1 2 4 S2 n − Sn Simpson加速公式: C n = 加速公式 加速公式: 2 4 −1 3 1 4 C2n − Cn I ≈ C 2 n + 3 (C 2 n − C n ) = 3 4 −1 4 −1
求出f(1/4)
f(3/4) 进而求得
T4=1/2{T2+1/2[f(1/4)+f(3/4)]} =3.131176471 S2=1/3(4T4-T2)=3.141568628 C1=1/15(16S2-S1)=3.142117648 计算f(1/8) f(3/8) f(5/8) f(7/8)进而求得 T8=1/2{T4+1/4[f(1/8)+f(3/8)+f(5/8)+f(7/8)]} =3.138988495 S4=1/3(4T3-T4)=3.141592503 C2=1/15(16S4-S2)=3.141594095 R1=1/63(64C2-C1)=3.141585784
梯形值序列
4个积分值序列: 个积分值序列: 个积分值序列
T2k
S 2k =
C 2k =
4T2k +1 − T2k 4 −1 2 4 S2k +1 − S2k
4 −1
2
2k
2k 2k
R2k =
4 C 2k +1 − C 2k
3
4 −1
3
5.3龙贝格(Romberg)算法

一、复合梯形公式的递推化
将定积分I = ∫ f ( x )dx的积分区间[ a , b ]分割为n等份 a b−a xk = a + jh , j = 0 ,1,L , n 各节点为 h= n 复合梯形(Trapz)公式为
n−1 b−a Tn = [ f ( a ) + 2 ∑ f ( x j ) + f (b )] 2n j =1
k −3
if(fabs(t3[k-3]-t2[k-2])<0.000000001) // 若 | R2 { printf("k=%3d,I=%12.9f\n",k,t3[k-3]); break; } } } double f(double x) { double y; y=sqrt(1.0+x*x); return y; }
13
其中外推加速公式可简化为
1 Tm ( k − 1) = m [ 4 m Tm − 1 ( k ) − Tm − 1 ( k − 1)] 4 −1
--------(11)
并且m可以推广到 m = 1,2 ,L
Romberg算法求解步骤
k = 1 , 2 ,L
Romberg算法的代 数精度为m的两倍 Romberg算法的收敛 阶高达m+1的两倍
第6章 数值积分与数值微分
龙贝格(Romberg)算法 算法 龙贝格
1
龙贝格(Romberg)算法 算法 龙贝格
综合前几节的内容,我们知道 梯形公式,Simpson公式,Cotes公式的代数精度分别为 1次,3次和5次 复合梯形、复合Simpson、复合Cotes公式的收敛阶分别为 2阶、4阶和6阶 无论从代数精度还是收敛速度,复合梯形公式都是较差的 有没有办法改善梯形公式呢?
龙贝格积分 python

龙贝格积分 python龙贝格积分 python一、什么是龙贝格积分?龙贝格积分(Romberg integration)是一种数值积分方法,它是对梯形法的递推加速处理。
梯形法是一种比较简单的数值积分方法,但它的精度不高,而且需要很多次计算。
龙贝格积分通过递推计算,可以大大提高计算精度,并且减少计算次数。
二、如何实现龙贝格积分?在 Python 中实现龙贝格积分可以使用以下代码:```pythondef romberg(f, a, b, n):"""Calculate the Romberg Integration of f(x) from a to b with n iterations"""R = [[0] * (n+1) for _ in range(n+1)]h = b - aR[0][0] = 0.5 * h * (f(a) + f(b))for i in range(1, n+1):h = 0.5 * hsum = 0for k in range(1, 2**i, 2):sum += f(a + k*h)R[i][0] = 0.5 * R[i-1][0] + sum*hfor j in range(1, i+1):R[i][j] = (4**j*R[i][j-1] - R[i-1][j-1]) / (4**j - 1)return R[n][n]```三、代码解析1. 定义函数 romberg(f, a, b, n),其中 f 为被积函数,a 和 b 分别为积分上下限,n 为迭代次数。
2. 创建一个n+1 行n+1 列的二维数组R,用于存储递推计算的结果。
3. 计算初始值 R[0][0],即使用梯形法计算第一次迭代的结果。
4. 进行 n 次迭代,每次将步长 h 减半,并且计算新的递推值。
具体过程如下:a. 计算当前步长 h。
