2015山西中考数学试题及答案
2015年山西省中考数学试题及解析

年山西省中考数学试卷2015分。
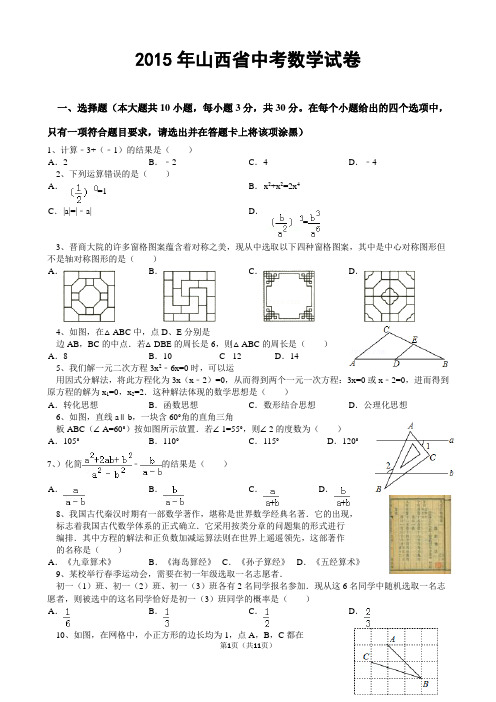
在每个小题给出的四个选项中,只有一项符合题30小题,每小题3分,共一、选择题(本大题共10目要求,请选出并在答题卡上将该项涂黑)))的结果是(?山西)计算﹣3+(﹣11.(3分)(2015 4 2 4 ﹣.2 C .D﹣A.B.2.(3分)(2015?山西)下列运算错误的是()224A.B.x+x=2x =1|a|=|﹣a| C.D.=3.(3分)(2015?山西)晋商大院的许多窗格图案蕴含着对称之美,现从中选取以下四种窗格图案,其中是中心对称图形但不是轴对称图形的是()A.B.C.D.,的周长是6AB,BC的中点.若△DBEE.(3分)(2015?山西)如图,在△ABC中,点D、分别是边4 )则△ABC的周长是(8 10 12 14 A.B.C.D.25.(3分)(2015?山西)我们解一元二次方程3x﹣6x=0时,可以运用因式分解法,将此方程化为3x(x﹣2)=0,从而得到两个一元一次方程:3x=0或x﹣2=0,进而得到原方程的解为x=0,x=2.这种解法体2现的数学思想是A.转化思想B.函数思想C.数形结合思想D.公理化思想6.(3分)(2015?山西)如图,直线a∥b,一块含60°角的直角三角板ABC(∠A=60°)按如图所示放置.若∠1=55°,则∠2的度数为()110°115°120°105°DB..C .A.7.﹣(3分)(2015?山西)化简的结果是()1.D A.B.C.山西)我国古代秦汉时期有一部数学著作,堪称是世界数学经典名著.它的出现,标志?(20158.(3分)着我国古代数学体系的正式确立.它采用按类分章的问题集的形式进行编排.其中方程的解法和正负数加)减运算法则在世界上遥遥领先,这部著作的名称是(五经算术》《《孙子算经》D.A.《九章算术》B.《海岛算经》C.)2分)(2015?山西)某校举行春季运动会,需要在初一年级选取一名志愿者.初一(1)班、初一(9.(3名同学中随机选取一名志愿者,则被选中的这名同学6班、初一(3)班各有2名同学报名参加.现从这)班同学的概率是(恰好是初一(3)C.D.A.B.ABC都在格点上,则∠B,C3(分)(2015?山西)如图,在网格中,小正方形的边长均为1,点A,10.)的正切值是(2D.A.CB..分)6二、填空题(本大题共小题,每小题3分,共18.山西)不等式组.11(3分)(2015?的解集是山西)如图是一组有规律的图案,它们是由边长相同的正方形和正三角形镶嵌而成,第3?分)(201512.(依此规律,个三角形,…1041)个图案有个三角形,第(2)个图案有7个三角形,第(3)个图案有(的代数式表示)个三角形(用含n第n个图案有,C点为的中点.若∠°A=40的直径,为⊙,内接于⊙四边形山西)2015分)(13.3(?如图,ABCDOABO 则∠B=度. 2的两张卡片,另一个装2?山西)现有两个不透明的盒子,其中一个装有标号分别为1,14.(3分)(2015的三张卡片,卡片除标号外其他均相同.若从两个盒子中各随机抽取一张卡片,则3,2,有标号分别为1 .两张卡片标号恰好相同的概率是山西)太原市公共自行车的建设速度、单日租骑量等四项指标稳居全国首位.公共自行?分)(201515.(3,HG,AB=80cmEF∥HG,EH⊥AD,AD⊥DC,点B,C在EF上,车车桩的截面示意图如图所示,AB⊥cm.到地面的距离是AD=24cm,BC=25cm,EH=4cm,则点A,D′D落在边AB上,对应点为分)(2015?山西)如图,将正方形纸片ABCD沿MN折叠,使点(16.3 .′=2,则折痕MN的长为AB=6点C落在C′处.若,AD个小题,共872分。
2015年山西省中考数学试题及参考答案(word解析版)

2015年山西省中考数学试题及参考答案一、选择题(本大题共10小题,每小题3分,共30分)1.计算﹣3+(﹣1)的结果是()A.2 B.﹣2 C.4 D.﹣42.下列运算错误的是()A.112⎛⎫=⎪⎝⎭B.x2+x2=2x4C.|a|=|﹣a| D.3326b ba a⎛⎫=⎪⎝⎭3.晋商大院的许多窗格图案蕴含着对称之美,现从中选取以下四种窗格图案,其中是中心对称图形但不是轴对称图形的是()A.B.C.D.4.如图,在△ABC中,点D、E分别是边AB,BC的中点.若△DBE的周长是6,则△ABC的周长是()A.8 B.10 C.12 D.145.我们解一元二次方程3x2﹣6x=0时,可以运用因式分解法,将此方程化为3x(x﹣2)=0,从而得到两个一元一次方程:3x=0或x﹣2=0,进而得到原方程的解为x1=0,x2=2.这种解法体现的数学思想是()A.转化思想B.函数思想C.数形结合思想D.公理化思想6.如图,直线a∥b,一块含60°角的直角三角板ABC(∠A=60°)按如图所示放置.若∠1=55°,则∠2的度数为()A.105°B.110°C.115°D.120°7.化简22222a ab b ba b a b++---的结果是()A.aa b-B.ba b-C.aa b+D.ba b+8.我国古代秦汉时期有一部数学著作,堪称是世界数学经典名著.它的出现,标志着我国古代数学体系的正式确立.它采用按类分章的问题集的形式进行编排.其中方程的解法和正负数加减运算法则在世界上遥遥领先,这部著作的名称是()A.《九章算术》B.《海岛算经》C.《孙子算经》D.《五经算术》9.某校举行春季运动会,需要在初一年级选取一名志愿者.初一(1)班、初一(2)班、初一(3)班各有2名同学报名参加.现从这6名同学中随机选取一名志愿者,则被选中的这名同学恰好是初一(3)班同学的概率是()A.16B.13C.12D.2310.如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是()A.2 B C D.1 2二、填空题(本大题共6小题,每小题3分,共18分)11.不等式组21736xx-⎧⎨⎩>>的解集是.12.如图是一组有规律的图案,它们是由边长相同的正方形和正三角形镶嵌而成,第(1)个图案有4个三角形,第(2)个图案有7个三角形,第(3)个图案有10个三角形,…依此规律,第n个图案有个三角形(用含n的代数式表示)13.如图,四边形ABCD内接于⊙O,AB为⊙O的直径,点C为BD的中点.若∠A=40°,则∠B=度.14.现有两个不透明的盒子,其中一个装有标号分别为1,2的两张卡片,另一个装有标号分别为1,2,3的三张卡片,卡片除标号外其他均相同.若从两个盒子中各随机抽取一张卡片,则两张卡片标号恰好相同的概率是.15.太原市公共自行车的建设速度、单日租骑量等四项指标稳居全国首位.公共自行车车桩的截面示意图如图所示,AB ⊥AD ,AD ⊥DC ,点B ,C 在EF 上,EF ∥HG ,EH ⊥HG ,AB=80cm ,AD=24cm ,BC=25cm ,EH=4cm ,则点A 到地面的距离是 cm .16.如图,将正方形纸片ABCD 沿MN 折叠,使点D 落在边AB 上,对应点为D′,点C 落在C′处.若AB=6,AD′=2,则折痕MN 的长为 .三、解答题(本大题共8个小题,共72分)17.(10分)(1)计算:()2313131222-⎛⎫⎛⎫--⨯--÷- ⎪ ⎪⎝⎭⎝⎭. (2)解方程:11321242x x =---. 18.(6分)阅读与计算:请阅读以下材料,并完成相应的任务.斐波那契(约1170﹣1250)是意大利数学家,他研究了一列数,这列数非常奇妙,被称为斐波那契数列(按照一定顺序排列着的一列数称为数列).后来人们在研究它的过程中,发现了许多意想不到的结果,在实际生活中,很多花朵(如梅花、飞燕草、万寿菊等)的瓣数恰是斐波那契数列中的数.斐波那契数列还有很多有趣的性质,在实际生活中也有广泛的应用.斐波那契数列中的第n1122n n ⎡⎤⎛⎛⎥- ⎥⎝⎭⎝⎭⎦表示(其中,n≥1).这是用无理数表示有理数的一个范例.任务:请根据以上材料,通过计算求出斐波那契数列中的第1个数和第2个数.19.(6分)如图,在平面直角坐标系xOy 中,一次函数y=3x+2的图象与y 轴交于点A ,与反比例函数k y x=(k≠0)在第一象限内的图象交于点B ,且点B 的横坐标为1.过点A 作AC ⊥y轴交反比例函数kyx(k≠0)的图象于点C,连接BC.(1)求反比例函数的表达式.(2)求△ABC的面积.20.(8分)随着互联网、移动终端的迅速发展,数字化阅读越来越普及,公交、地铁上的“低头族”越来越多.某研究机构针对“您如何看待数字化阅读”问题进行了随机问卷调查(问卷调查表如图1所示)并将调查结果绘制成图2和图3所示的统计图(均不完整).请根据统计图中提供的信息,解答下列问题:(1)本次接受调查的总人数是人.(2)请将条形统计图补充完整.(3)在扇形统计图中,观点E的百分比是,表示观点B的扇形的圆心角度数为度.(4)假如你是该研究机构的一名成员,请根据以上调查结果,就人们如何对待数字化阅读提出你的建议.21.(10分)如图,△ABC是直角三角形,∠ACB=90°.(1)尺规作图:作⊙C,使它与AB相切于点D,与AC相交于点E,保留作图痕迹,不写作法,请标明字母.(2)在你按(1)中要求所作的图中,若BC=3,∠A=30°,求DE的长.22.(7分)某蔬菜经营户从蔬菜批发市场批发蔬菜进行零售,部分蔬菜批发价格与零售价格如表:蔬菜品种西红柿青椒西兰花豆角批发价(元/kg) 3.6 5.4 8 4.8零售价(元/kg) 5.4 8.4 14 7.6请解答下列问题:(1)第一天,该经营户批发西红柿和西兰花两种蔬菜共300kg ,用去了1520元钱,这两种蔬菜当天全部售完一共能赚多少元钱?(2)第二天,该经营户用1520元钱仍然批发西红柿和西兰花,要想当天全部售完后所赚钱数不少于1050元,则该经营户最多能批发西红柿多少kg ?23.(12分)综合与实践:制作无盖盒子任务一:如图1,有一块矩形纸板,长是宽的2倍,要将其四角各剪去一个正方形,折成高为4cm ,容积为616cm 3的无盖长方体盒子(纸板厚度忽略不计).(1)请在图1的矩形纸板中画出示意图,用实线表示剪切线,虚线表示折痕.(2)请求出这块矩形纸板的长和宽.任务二:图2是一个高为4cm 的无盖的五棱柱盒子(直棱柱),图3是其底面,在五边形ABCDE 中,BC=12cm ,AB=DC=6cm ,∠ABC=∠BCD=120°,∠EAB=∠EDC=90°.(1)试判断图3中AE 与DE 的数量关系,并加以证明.(2)图2中的五棱柱盒子可按图4所示的示意图,将矩形纸板剪切折合而成,那么这个矩形纸板的长和宽至少各为多少cm ?请直接写出结果(图中实线表示剪切线,虚线表示折痕.纸板厚度及剪切接缝处损耗忽略不计).24.(13分)综合与探究如图1,在平面直角坐标系xOy 中,抛物线W 的函数表达式为241642121y x x =-++.抛物线W 与x 轴交于A ,B 两点(点B 在点A 的右侧,与y 轴交于点C ,它的对称轴与x 轴交于点D ,直线l 经过C 、D 两点.(1)求A 、B 两点的坐标及直线l 的函数表达式.(2)将抛物线W 沿x 轴向右平移得到抛物线W′,设抛物线W′的对称轴与直线l 交于点F ,当△ACF 为直角三角形时,求点F 的坐标,并直接写出此时抛物线W′的函数表达式.(3)如图2,连接AC ,CB ,将△ACD 沿x 轴向右平移m 个单位(0<m≤5),得到△A′C′D′.设A′C′交直线l 于点M ,C′D′交CB 于点N ,连接CC′,MN .求四边形CMNC′的面积(用含m 的代数式表示).参考答案与解析一、选择题(本大题共10小题,每小题3分,共30分)1.计算﹣3+(﹣1)的结果是()A.2 B.﹣2 C.4 D.﹣4【知识考点】有理数的加法.【思路分析】根据同号两数相加的法则进行计算即可.【解题过程】解:﹣3+(﹣1)=﹣(3+1)=﹣4,故选:D.【总结归纳】本题主要考查了有理数的加法法则,解决本题的关键是熟记同号两数相加,取相同的符号,并把绝对值相加.2.下列运算错误的是()A.112⎛⎫=⎪⎝⎭B.x2+x2=2x4C.|a|=|﹣a| D.3326b ba a⎛⎫=⎪⎝⎭【知识考点】分式的乘除法;绝对值;合并同类项;零指数幂.【思路分析】A、原式利用零指数幂法则计算得到结果,即可做出判断;B、原式合并同类项得到结果,即可做出判断;C、原式利用绝对值的代数意义判断即可;D、原式利用乘方的意义计算得到结果,即可做出判断.【解题过程】解:A、原式=1,正确;B、原式=2x2,错误;C、|a|=|﹣a|,正确;D、原式36ba=,正确,故选B【总结归纳】此题考查了分式的乘除法,绝对值,合并同类项,以及零指数幂,熟练掌握运算法则是解本题的关键.3.晋商大院的许多窗格图案蕴含着对称之美,现从中选取以下四种窗格图案,其中是中心对称图形但不是轴对称图形的是()A.B.C.D.【知识考点】中心对称图形;轴对称图形.【思路分析】根据轴对称图形与中心对称图形的概念求解.【解题过程】解:A、是轴对称图形,也是中心对称图形.故错误;B、不是轴对称图形,是中心对称图形.故正确;C、是轴对称图形,也是中心对称图形.故错误;D、是轴对称图形,也是中心对称图形.故错误.故选B.【总结归纳】本题考查了中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.。
2015山西中考数学真题试卷.docx

2015年山西省高中阶段教育学校招生统一考试数学试题(含答案全解全析)第Ⅰ卷(选择题,共30分)一、选择题(本大题共10个小题,每小题3分,共30分.在每个小题给出的四个选项中,只有一项符合题目要求)1.计算-3+(-1)的结果是( )A.2B.-2C.4D.-4 2.下列运算错误的是( ) A.(12)0=1B.x 2+x 2=2x 4C.|a|=|-a|D.(ba 2)3=b 3a 63.晋商大院的许多窗格图案蕴含着对称之美,现从中选取以下四种窗格图案,其中是中心对称图形但不是轴对称图形的是( )4.如图,在△ABC 中,点D,E 分别是边AB,BC 的中点.若△DBE 的周长是6,则△ABC 的周长是( )A.8B.10C.12D.145.我们解一元二次方程3x 2-6x=0时,可以运用因式分解法,将此方程化为3x(x-2)=0,从而得到两个一元一次方程:3x=0,x-2=0,进而得到原方程的解为x 1=0,x 2=2.这种解法体现的数学思想是( ) A.转化思想B.函数思想C.数形结合思想D.公理化思想6.如图,直线a ∥b,一块含60°角的直角三角板ABC(∠A=60°)按如图所示放置.若∠1=55°,则∠2的度数为( )A.105°B.110°C.115°D.120°7.化简a2+2ab+b2a2-b2-ba-b的结果是()A.aa-b B.ba-bC.aa+bD.ba+b8.我国古代秦汉时期有一部数学著作,堪称是世界数学经典名著.它的出现,标志着我国古代数学体系的正式确立.它采用按类分章的问题集的形式进行编排.其中方程的解法和正负数加减运算法则在世界上遥遥领先,这部著作的名称是()A.《九章算术》B.《海岛算经》C.《孙子算经》D.《五经算术》9.某校举行春季运动会,需要在初一年级选取一名志愿者.初一(1)班、初一(2)班、初一(3)班各有2名同学报名参加.现从这6名同学中随机选取一名志愿者,则被选中的这名同学恰好是初一(3)班同学的概率是()A.16B.13C.12D.2310.如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是()A.2B.2√55C.√55D.12第Ⅱ卷(非选择题,共90分)二、填空题(本大题共6个小题,每小题3分,共18分)11.不等式组{2x-1>7,的解集是.3x>612.如图是一组有规律的图案,它们是由边长相同的正方形和正三角形镶嵌而成.第(1)个图案有4个三角形,第(2)个图案有7个三角形,第(3)个图案有10个三角形,……依此规律,第n个图案有个三角形(用含n的代数式表示).⏜的中点.若∠A=40°,则∠B= 13.如图,四边形ABCD内接于☉O,AB为☉O的直径,点C为BD度.14.现有两个不透明的盒子,其中一个装有标号分别为1,2的两张卡片,另一个装有标号分别为1,2,3的三张卡片,卡片除标号外其他均相同.若从两个盒子中各随机抽取一张卡片,则两张卡片标号恰好相同的概率是.15.太原市公共自行车的建设速度、单日租骑量等四项指标稳居全国首位.公共自行车车桩的截面示意图如图所示,AB⊥AD,AD⊥DC,点B,C在EF上,EF∥HG,EH⊥HG,AB=80cm,AD=24 cm,BC=25cm,EH=4cm,则点A到地面的距离是cm.16.如图,将正方形纸片ABCD沿MN折叠,使点D落在边AB上,对应点为D',点C落在C'处.若AB=6,AD'=2,则折痕MN的长为.三、解答题(本大题共8个小题,共72分.解答应写出文字说明、证明过程或演算步骤) 17.(本题共2个小题,每小题5分,共10分) (1)计算:(-3-1)×(-32)2-2-1÷(-12)3.(2)解方程:12x -1=12-34x -2.18.(本题6分)阅读与计算:请阅读以下材料,并完成相应的任务.任务:请根据以上材料,通过计算求出斐波那契数列中的第1个数和第2个数.19.(本题6分)如图,在平面直角坐标系xOy 中,一次函数y=3x+2的图象与y 轴交于点A,与反比例函数y=k(k≠0)在第一象限内的图象交于点B,且点B的横坐标为1.过点A作AC⊥y轴交x(k≠0)的图象于点C,连结BC.反比例函数y=kx(1)求反比例函数的表达式.(2)求△ABC的面积.20.(本题8分)随着互联网、移动终端的迅速发展,数字化阅读越来越普及,公交、地铁上的“低头族”越来越多.某研究机构针对“您如何看待数字化阅读”问题进行了随机问卷调查(问卷调查表如图所示),并将调查结果绘制成图1和图2所示的统计图(均不完整).请根据统计图中提供的信息,解答下列问题:(1)本次接受调查的总人数是人.(2)请将条形统计图补充完整.图1图2(3)在扇形统计图中,观点E的百分比是,表示观点B的扇形的圆心角度数为度.(4)假设你是该研究机构的一名成员,请根据以上调查结果,就人们如何对待数字化阅读提出你的建议.21.(本题10分)实践与操作如图,△ABC是直角三角形,∠ACB=90°.(1)尺规作图:作☉C,使它与AB相切于点D,与AC相交于点E.保留作图痕迹,不写作法.请标明字母.(2)在你按(1)中要求所作的图中,若BC=3,∠A=30°,求DE⏜的长.22.(本题7分)某蔬菜经营户从蔬菜批发市场批发蔬菜进行零售,部分蔬菜批发价格与零售价格如下表:蔬菜品种西红柿青椒西兰花豆角批发价(元/kg) 3.6 5.48 4.8零售价(元/kg) 5.48.4147.6请解答下列问题:(1)第一天,该经营户批发西红柿和西兰花两种蔬菜共300kg,用去了1520元钱,这两种蔬菜当天全部售完后一共能赚多少元钱?(2)第二天,该经营户用1520元钱仍然批发西红柿和西兰花,要想当天全部售完后所赚钱数不少于1050元,则该经营户最多能批发西红柿多少kg?23.(本题12分)综合与实践:制作无盖盒子任务一:如图1,有一块矩形纸板,长是宽的2倍,要将其四角各剪去一个正方形,折成高为4cm,容积为616cm3的无盖长方体盒子(纸板厚度忽略不计).(1)请在图1的矩形纸板中画出示意图,用实线表示剪切线,虚线表示折痕.(2)请求出这块矩形纸板的长和宽.图1任务二:图2是一个高为4cm的无盖的五棱柱盒子(直棱柱),图3是其底面,在五边形ABCDE中,BC=12cm,AB=DC=6cm,∠ABC=∠BCD=120°,∠EAB=∠EDC=90°.(1)试判断图3中AE与DE的数量关系,并加以证明.(2)图2中的五棱柱盒子可按图4所示的示意图,将矩形纸板剪切折合而成,那么这个矩形纸板的长和宽至少各为多少cm?请直接写出结果(图中实线表示剪切线,虚线表示折痕.纸板厚度及剪切接缝处损耗均忽略不计).24.(本题13分)综合与探究如图1,在平面直角坐标系xOy中,抛物线W的函数表达式为y=-421x2+1621x+4.抛物线W与x轴交于A,B两点(点B在点A的右侧),与y轴交于点C,它的对称轴与x轴交于点D,直线l经过C,D两点.(1)求A,B两点的坐标及直线l的函数表达式.(2)将抛物线W沿x轴向右平移得到抛物线W',设抛物线W'的对称轴与直线l交于点F.当△ACF为直角三角形时,求点F的坐标,并直接写出此时抛物线W'的函数表达式.(3)如图2,连结AC,CB.将△ACD沿x轴向右平移m个单位(0<m≤5),得到△A'C'D'.设A'C'交直。
2015山西中考数学试卷及答案
2015年山西省中考数学试卷一、选择题(本大题共10小题,每小题3分,共30分。
在每个小题给出的四个选项中,只有一项符合题目要求,请选出并在答题卡上将该项涂黑). =1= .用因式分解法,将此方程化为3x (x ﹣2)=0,从而得到两个一元一次方程:3x=0或x ﹣2=0,进而得到7、)化简﹣的结果是( ) .标志着我国古代数学体系的正式确立.它采用按类分章的问题集的形式进行编排.其中方程的解法和正负数加减运算法则在世界上遥遥领先,这部著作初一(1)班、初一(2)班、初一(3)班各有2名同学报名参加.现从这6名同学中随机选取一名志.D二、填空题(本大题共6小题,每小题3分,共18分)11、不等式组的解集是.12、如图是一组有规律的图案,它们是由边长相同的正方形和正三角形镶嵌而成,第(1)个图案有4个三角形,第(2)个图案有7个三角形,第(3)个图案有10个三角形,…依此规律,第n个图案有个三角形(用含n的代数式表示)13、如图,四边形ABCD内接于⊙O,AB为⊙O的直径,点C为的中点.若∠A=40°,则∠B=度.14、现有两个不透明的盒子,其中一个装有标号分别为1,2的两张卡片,另一个装有标号分别为1,2,3的三张卡片,卡片除标号外其他均相同.若从两个盒子中各随机抽取一张卡片,则两张卡片标号恰好相同的概率是.15、太原市公共自行车的建设速度、单日租骑量等四项指标稳居全国首位.公共自行车车桩的截面示意图如图所示,AB⊥AD,AD⊥DC,点B,C在EF上,EF∥HG,EH⊥HG,AB=80cm,AD=24cm,BC=25cm,EH=4cm,则点A到地面的距离是cm.16、如图,将正方形纸片ABCD沿MN折叠,使点D落在边AB上,对应点为D′,点C落在C′处.若AB=6,AD′=2,则折痕MN的长为.三、解答题(本大题共8个小题,共72分。
解答应写出文字说明、证明过程或演算步骤)17、(1)计算:(﹣3﹣1)×﹣2﹣1÷.(2)解方程:=﹣.18、阅读与计算:请阅读以下材料,并完成相应的任务.斐波那契(约1170﹣1250)是意大利数学家,他研究了一列数,这列数非常奇妙,被称为斐波那契数列(按照一定顺序排列着的一列数称为数列).后来人们在研究它的过程中,发现了许多意想不到的结果,在实际生活中,很多花朵(如梅花、飞燕草、万寿菊等)的瓣数恰是斐波那契数列中的数.斐波那契数列还有很多有趣的性质,在实际生活中也有广泛的应用.斐波那契数列中的第n个数可以用[﹣]表示(其中,n≥1).这是用无理数表示有理数的一个范例.任务:请根据以上材料,通过计算求出斐波那契数列中的第1个数和第2个数.19、如图,在平面直角坐标系xOy中,一次函数y=3x+2的图象与y轴交于点A,与反比例函数y=(k≠0)在第一象限内的图象交于点B,且点B的横坐标为1.过点A作AC⊥y轴交反比例函数y=(k≠0)的图象于点C,连接BC.(1)求反比例函数的表达式.(2)求△ABC的面积.20、随着互联网、移动终端的迅速发展,数字化阅读越来越普及,公交、地铁上的“低头族”越来越多.某研究机构针对“您如何看待数字化阅读”问题进行了随机问卷调查(问卷调查表如图1所示)并将调查结果绘制成图2和图3所示的统计图(均不完整).请根据统计图中提供的信息,解答下列问题:(1)本次接受调查的总人数是人.(2)请将条形统计图补充完整.(3)在扇形统计图中,观点E的百分比是,表示观点B的扇形的圆心角度数为度.(4)假如你是该研究机构的一名成员,请根据以上调查结果,就人们如何对待数字化阅读提出你的建议.21、如图,△ABC是直角三角形,∠ACB=90°.(1)尺规作图:作⊙C,使它与AB相切于点D,与AC相交于点E,保留作图痕迹,不写作法,请标明字母.(2)在你按(1)中要求所作的图中,若BC=3,∠A=30°,求的长.(1)第一天,该经营户批发西红柿和西兰花两种蔬菜共300kg,用去了1520元钱,这两种蔬菜当天全部售完一共能赚多少元钱?(2)第二天,该经营户用1520元钱仍然批发西红柿和西兰花,要想当天全部售完后所赚钱数不少于1050元,则该经营户最多能批发西红柿多少kg?23、综合与实践:制作无盖盒子任务一:如图1,有一块矩形纸板,长是宽的2倍,要将其四角各剪去一个正方形,折成高为4cm,容积为616cm3的无盖长方体盒子(纸板厚度忽略不计).(1)请在图1的矩形纸板中画出示意图,用实线表示剪切线,虚线表示折痕.(2)请求出这块矩形纸板的长和宽.任务二:图2是一个高为4cm的无盖的五棱柱盒子(直棱柱),图3是其底面,在五边形ABCDE中,BC=12cm,AB=DC=6cm,∠ABC=∠BCD=120°,∠EAB=∠EDC=90°.(1)试判断图3中AE与DE的数量关系,并加以证明.(2)图2中的五棱柱盒子可按图4所示的示意图,将矩形纸板剪切折合而成,那么这个矩形纸板的长和宽至少各为多少cm?请直接写出结果(图中实线表示剪切线,虚线表示折痕.纸板厚度及剪切接缝处损耗忽略不计).24、综合与探究如图1,在平面直角坐标系xOy中,抛物线W的函数表达式为y=﹣x2+x+4.抛物线W与x轴交于A,B两点(点B在点A的右侧,与y轴交于点C,它的对称轴与x轴交于点D,直线l经过C、D两点.(1)求A、B两点的坐标及直线l的函数表达式.(2)将抛物线W沿x轴向右平移得到抛物线W′,设抛物线W′的对称轴与直线l交于点F,当△ACF为直角三角形时,求点F的坐标,并直接写出此时抛物线W′的函数表达式.(3)如图2,连接AC,CB,将△ACD沿x轴向右平移m个单位(0<m≤5),得到△A′C′D′.设A′C交直线l于点M,C′D′交CB于点N,连接CC′,MN.求四边形CMNC′的面积(用含m的代数式表示).2015年山西省中考数学试卷参考答案一、选择题(本大题共10小题,每小题3分,共30分。
山西省2015年中考数学真题试题(含答案)

中考衣食住用行衣:中考前这段时间,提醒同学们出门一定要看天气,否则淋雨感冒,就会影响考场发挥。
穿着自己习惯的衣服,可以让人在紧张时产生亲切感和安全感,并能有效防止不良情绪产生。
食:清淡的饮食最适合考试,切忌吃太油腻或者刺激性强的食物。
如果可能的话,每天吃一两个水果,补充维生素。
另外,进考场前一定要少喝水!住:考前休息很重要。
好好休息并不意味着很早就要上床睡觉,根据以往考生的经验,太早上床反而容易失眠。
考前按照你平时习惯的时间上床休息就可以了,但最迟不要超过十点半。
用:出门考试之前,一定要检查文具包。
看看答题的工具是否准备齐全,应该带的证件是否都在,不要到了考场才想起来有什么工具没带,或者什么工具用着不顺手。
行:看考场的时候同学们要多留心,要仔细了解自己住的地方到考场可以坐哪些路线的公交车?有几种方式可以到达?大概要花多长时间?去考场的路上有没有修路堵车的情况?考试当天,应该保证至少提前20分钟到达考场。
山西省2015年中考数学真题试题第I卷选择题(共30分)一、选择题(本大题共10个小题,每小题3分,共30分。
在每个小题给出的四个选项中,只有一项符合题目要求,请选出并在答题卡上将该选项涂黑)1.将 -3+(-1)的结果是()。
A. 2B. -2C. 4D. -42.下列运算错误的是( )241642121y x x =-++ A. 0112⎛⎫= ⎪⎝⎭B.2242x x x +=C.a a =-D.3326b b a a⎛⎫= ⎪⎝⎭ 3.晋商大院的许多窗格图案蕴含着对称之美,现从中选取以下四种窗格图案,其中是中心称图形但是不是轴对称图形的是( )4.如图,在△ABC 中,点D,E 分别是边AB,BC 的中点,若 △DBE 的周长是6,则△的周长是( )。
A.8B.10C.12D.145.我们解一元二次方程2360x x -=时,可以运用因式分解法,将 此方程化为3(2)0x x -=,从而得到两个一元一次方程:30x = 或20x -=,进而得道原方程的解为120,2x x ==。
2015年山西省中考数学真题及部分答案

2015年山西省中考数学试卷(含答案)一、选择题(每小题3分,共30分). =1= .4.(3分)如图,在△ABC 中,点D 、E 分别是边AB,BC 的中点.若△DBE 的周长是6,则△ABC 的周长是( )5.(3分)我们解一元二次方程3x 2﹣6x=0时,可以运用因式分解法,将此方程化为3x (x ﹣2)=0,从而得到两个一元一次方程:3x=0或x ﹣2=0,进而得到原方程的解为x 1=0,x 2=2.这种解法体现的数学思想是6.(3分)如图,直线a ∥b ,一块含60°角的直角三角板ABC (∠A=60°)按如图所示放置.若∠1=55°,则∠2的度数为( )7.(3分)化简﹣的结果是().8.(3分)我国古代秦汉时期有一部数学著作,堪称是世界数学经典名著.它的出现,标志着我国古代数学体系的正式确立.它采用按类分章的问题集的形式进行编排.其中方程的解法和正负数加减运算法则在世界上遥遥领先,这部著作的名称是()9.(3分)某校举行春季运动会,需要在初一年级选取一名志愿者.初一(1)班、初一(2)班、初一(3)班各有2名同学报名参加.现从这6名同学中随机选取一名志愿者,则被选中的这名同学恰好是初一(3).()二、填空题(每小题3分,共18分)11.(3分)不等式组的解集是.12.(3分)如图是一组有规律的图案,它们是由边长相同的正方形和正三角形镶嵌而成,第(1)个图案有4个三角形,第(2)个图案有7个三角形,第(3)个图案有10个三角形,…依此规律,第n个图案有个三角形(用含n的代数式表示)13.(3分)如图,四边形ABCD内接于⊙O,AB为⊙O的直径,点C为的中点.若∠A=40°,则∠B=度.14.(3分)现有两个不透明的盒子,其中一个装有标号分别为1,2的两张卡片,另一个装有标号分别为1,2,3的三张卡片,卡片除标号外其他均相同.若从两个盒子中各随机抽取一张卡片,则两张卡片标号恰好相同的概率是.15.(3分)太原市公共自行车的建设速度、单日租骑量等四项指标稳居全国首位.公共自行车车桩的截面示意图如图所示,AB⊥AD,AD⊥DC,点B,C在EF上,EF∥HG,EH⊥HG,AB=80cm,AD=24cm,BC=25cm,EH=4cm,则点A到地面的距离是cm.16.(3分)如图,将正方形纸片ABCD沿MN折叠,使点D落在边AB上,对应点为D′,点C落在C′处.若AB=6,AD′=2,则折痕MN的长为.三、解答题(本大题共8个小题,共72分)17.(10分)(1)计算:(﹣3﹣1)×﹣2﹣1÷.(2)解方程:=﹣.18.(6分)阅读与计算:请阅读以下材料,并完成相应的任务.斐波那契(约1170﹣1250)是意大利数学家,他研究了一列数,这列数非常奇妙,被称为斐波那契数列(按照一定顺序排列着的一列数称为数列).后来人们在研究它的过程中,发现了许多意想不到的结果,在实际生活中,很多花朵(如梅花、飞燕草、万寿菊等)的瓣数恰是斐波那契数列中的数.斐波那契数列还有很多有趣的性质,在实际生活中也有广泛的应用.斐波那契数列中的第n个数可以用[﹣]表示(其中,n≥1).这是用无理数表示有理数的一个范例.任务:请根据以上材料,通过计算求出斐波那契数列中的第1个数和第2个数.19.(6分)如图,在平面直角坐标系xOy中,一次函数y=3x+2的图象与y轴交于点A,与反比例函数y=(k≠0)在第一象限内的图象交于点B,且点B的横坐标为1.过点A作AC⊥y轴交反比例函数y=(k≠0)的图象于点C,连接BC.(1)求反比例函数的表达式.(2)求△ABC的面积.20.(8分)随着互联网、移动终端的迅速发展,数字化阅读越来越普及,公交、地铁上的“低头族”越来越多.某研究机构针对“您如何看待数字化阅读”问题进行了随机问卷调查(问卷调查表如图1所示)并将调查结果绘制成图2和图3所示的统计图(均不完整).请根据统计图中提供的信息,解答下列问题:(1)本次接受调查的总人数是人.(2)请将条形统计图补充完整.(3)在扇形统计图中,观点E的百分比是,表示观点B的扇形的圆心角度数为度.(4)假如你是该研究机构的一名成员,请根据以上调查结果,就人们如何对待数字化阅读提出你的建议.21.(10分)如图,△ABC是直角三角形,∠ACB=90°.(1)尺规作图:作⊙C,使它与AB相切于点D,与AC相交于点E,保留作图痕迹,不写作法,请标明字母.(2)在你按(1)中要求所作的图中,若BC=3,∠A=30°,求的长.(1)第一天,该经营户批发西红柿和西兰花两种蔬菜共300kg,用去了1520元钱,这两种蔬菜当天全部售完一共能赚多少元钱?(2)第二天,该经营户用1520元钱仍然批发西红柿和西兰花,要想当天全部售完后所赚钱数不少于1050元,则该经营户最多能批发西红柿多少kg?23.(12分)综合与实践:制作无盖盒子任务一:如图1,有一块矩形纸板,长是宽的2倍,要将其四角各剪去一个正方形,折成高为4cm,容积为616cm3的无盖长方体盒子(纸板厚度忽略不计).(1)请在图1的矩形纸板中画出示意图,用实线表示剪切线,虚线表示折痕.(2)请求出这块矩形纸板的长和宽.任务二:图2是一个高为4cm的无盖的五棱柱盒子(直棱柱),图3是其底面,在五边形ABCDE中,BC=12cm,AB=DC=6cm,∠ABC=∠BCD=120°,∠EAB=∠EDC=90°.(1)试判断图3中AE与DE的数量关系,并加以证明.(2)图2中的五棱柱盒子可按图4所示的示意图,将矩形纸板剪切折合而成,那么这个矩形纸板的长和宽至少各为多少cm?请直接写出结果(图中实线表示剪切线,虚线表示折痕.纸板厚度及剪切接缝处损耗忽略不计).24.(13分)综合与探究如图1,在平面直角坐标系xOy中,抛物线W的函数表达式为y=﹣x2+x+4.抛物线W与x轴交于A,B两点(点B在点A的右侧,与y轴交于点C,它的对称轴与x轴交于点D,直线l经过C、D两点.(1)求A、B两点的坐标及直线l的函数表达式.(2)将抛物线W沿x轴向右平移得到抛物线W′,设抛物线W′的对称轴与直线l交于点F,当△ACF为直角三角形时,求点F的坐标,并直接写出此时抛物线W′的函数表达式.(3)如图2,连接AC,CB,将△ACD沿x轴向右平移m个单位(0<m≤5),得到△A′C′D′.设A′C交直线l于点M,C′D′交CB于点N,连接CC′,MN.求四边形CMNC′的面积(用含m的代数式表示).2015年山西省中考数学试卷参考答案一、选择题1.D 2.B 3.B 4.C 5.A 6.C 7.A 8.A 9.B 10.D二、填空题(本大题共6小题,每小题3分,共18分)11.x>4 12.3n+1 13.70 14.15. 16.2三、解答题(本大题共8个小题,共72分。
山西2015中考数学试题(含答案)

2015年XX省中考数学试卷一、选择题〔本大题共10小题,每小题3分,共30分。
在每个小题给出的四个选项中,只有一项符合题目要求,请选出并在答题卡上将该项涂黑〕1.〔3分〕〔2015•XX〕计算﹣3+〔﹣1〕的结果是〔〕A.2B.﹣2 C.4D.﹣42.〔3分〕〔2015•XX〕下列运算错误的是〔〕A.B.x2+x2=2x4=1C.|a|=|﹣a| D.=3.〔3分〕〔2015•XX〕晋商大院的许多窗格图案蕴含着对称之美,现从中选取以下四种窗格图案,其中是中心对称图形但不是轴对称图形的是〔〕A.B.C.D.4.〔3分〕〔2015•XX〕如图,在△ABC中,点D、E分别是边AB,BC的中点.若△DBE 的周长是6,则△ABC的周长是〔〕A.8B.10 C.12 D.145.〔3分〕〔2015•XX〕我们解一元二次方程3x2﹣6x=0时,可以运用因式分解法,将此方程化为3x〔x﹣2〕=0,从而得到两个一元一次方程:3x=0或x﹣2=0,进而得到原方程的解为x1=0,x2=2.这种解法体现的数学思想是〔〕A.转化思想B.函数思想C.数形结合思想D.公理化思想6.〔3分〕〔2015•XX〕如图,直线a∥b,一块含60°角的直角三角板ABC〔∠A=60°〕按如图所示放置.若∠1=55°,则∠2的度数为〔〕A.105°B.110°C.115°D.120°7.〔3分〕〔2015•XX〕化简﹣的结果是〔〕A.B.C.D.8.〔3分〕〔2015•XX〕我国古代秦汉时期有一部数学著作,堪称是世界数学经典名著.它的出现,标志着我国古代数学体系的正式确立.它采用按类分章的问题集的形式进行编排.其中方程的解法和正负数加减运算法则在世界上遥遥领先,这部著作的名称是〔〕A.《九章算术》B.《海岛算经》C.《孙子算经》D.《五经算术》9.〔3分〕〔2015•XX〕某校举行春季运动会,需要在初一年级选取一名志愿者.初一〔1〕班、初一〔2〕班、初一〔3〕班各有2名同学报名参加.现从这6名同学中随机选取一名志愿者,则被选中的这名同学恰好是初一〔3〕班同学的概率是〔〕A.B.C.D.10.〔3分〕〔2015•XX〕如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是〔〕A.2B.C.D.二、填空题〔本大题共6小题,每小题3分,共18分〕11.〔3分〕〔2015•XX〕不等式组的解集是.12.〔3分〕〔2015•XX〕如图是一组有规律的图案,它们是由边长相同的正方形和正三角形镶嵌而成,第〔1〕个图案有4个三角形,第〔2〕个图案有7个三角形,第〔3〕个图案有10个三角形,…依此规律,第n个图案有个三角形〔用含n的代数式表示〕13.〔3分〕〔2015•XX〕如图,四边形ABCD内接于⊙O,AB为⊙O的直径,点C为的中点.若∠A=40°,则∠B=度.14.〔3分〕〔2015•XX〕现有两个不透明的盒子,其中一个装有标号分别为1,2的两X卡片,另一个装有标号分别为1,2,3的三X卡片,卡片除标号外其他均相同.若从两个盒子中各随机抽取一X卡片,则两X卡片标号恰好相同的概率是.15.〔3分〕〔2015•XX〕XX市公共自行车的建设速度、单日租骑量等四项指标稳居全国首位.公共自行车车桩的截面示意图如图所示,AB⊥AD,AD⊥DC,点B,C在EF上,EF∥HG,EH⊥HG,AB=80cm,AD=24cm,BC=25cm,EH=4cm,则点A到地面的距离是cm.16.〔3分〕〔2015•XX〕如图,将正方形纸片ABCD沿MN折叠,使点D落在边AB上,对应点为D′,点C落在C′处.若AB=6,AD′=2,则折痕MN的长为.三、解答题〔本大题共8个小题,共72分。
2015年山西中考数学真题+答案

2015年山西中考数学真题+答案(真题部分)第I 卷 选择题(共30分)一、选择题(本大题共10小题,每小题3分,共30分.在每个小题给出的四个选项中,只有一项符合题目要求)1.计算﹣3+(﹣1)的结果是( ) A .2B .﹣2C .4D .﹣42.下列运算错误的是( ) A .(12)0=1B .x 2+x 2=2x 4C .|a |=|﹣a |D .(b a 2)3=b 3a63.晋商大院的许多窗格图案蕴含着对称之美,现从中选取以下四种窗格图案,其中是中心对称图形但不是轴对称图形的是( )A .B .C .D .4.如图,在△ABC 中,点D ,E 分别是边AB ,BC 的中点.若△DBE 的周长是6,则△ABC 的周长是( )A .8B .10C .12D .145.我们解一元二次方程3x 2﹣6x =0时,可以运用因式分解法,将此方程化为3x (x ﹣2)=0,从而得到两个一元一次方程:3x =0或x ﹣2=0,进而得到原方程的解为x 1=0,x 2=2.这种解法体现的数学思想是( ) A .转化思想B .函数思想C.数形结合思想D.公理化思想6.如图,直线a∥b,一块含60°角的直角三角板ABC(∠A=60°)按如图所示放置.若∠1=55°,则∠2的度数为()A.105°B.110°C.115°D.120°7.化简a2+2ab+b2a2−b2−ba−b的结果是()A.aa−b B.ba−bC.aa+bD.ba+b8.我国古代秦汉时期有一部数学著作,堪称是世界数学经典名著.它的出现,标志着我国古代数学体系的正式确立.它采用按类分章的问题集的形式进行编排.其中方程的解法和正负数加减运算法则在世界上遥遥领先,这部著作的名称是()A.《九章算术》B.《海岛算经》C.《孙子算经》D.《五经算术》9.某校举行春季运动会,需要在初一年级选取一名志愿者.初一(1)班、初一(2)班、初一(3)班各有2名同学报名参加.现从这6名同学中随机选取一名志愿者,则被选中的这名同学恰好是初一(3)班同学的概率是()A.16B.13C.12D.2310.如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是()A .2B .2√55C .√55D .12第Ⅱ卷 非选择题(共90分)二、填空题(本大题共6小题,每小题3分,共18分) 11.不等式组{2x −1>7,3x >6的解集是 .12.如图是一组有规律的图案,它们是由边长相同的正方形和正三角形镶嵌而成,第(1)个图案有4个三角形,第(2)个图案有7个三角形,第(3)个图案有10个三角形,…依此规律,第n 个图案有 个三角形(用含n 的代数式表示)13.如图,四边形ABCD 内接于⊙O ,AB 为⊙O 的直径,点C 为BD ̂的中点.若∠A =40°,则∠B = °.14.现有两个不透明的盒子,其中一个装有标号分别为1,2的两张卡片,另一个装有标号分别为1,2,3的三张卡片,卡片除标号外其他均相同.若从两个盒子中各随机抽取一张卡片,则两张卡片标号恰好相同的概率是 .15.太原市公共自行车的建设速度、单日租骑量等四项指标稳居全国首位.公共自行车车桩的截面示意图如图所示,AB ⊥AD ,AD ⊥DC ,点B ,C 在EF 上,EF ∥HG ,EH ⊥HG ,AB =80 cm ,AD =24 cm ,BC =25 cm ,EH =4 cm ,则点A 到地面的距离是 cm .16.如图,将正方形纸片ABCD 沿MN 折叠,使点D 落在边AB 上,对应点为D ′,点C 落在C ′处.若AB =6,AD ′=2,则折痕MN 的长为 .三、解答题(本大题共8个小题,共72分.解答应写出文字说明、证明过程或演算步骤) 17.(本题共2个小题,每小题5分,共10分) (1)计算:(﹣3﹣1)×(−32)2−2﹣1÷(−12)3; (2)解方程:12x−1=12−34x−2. 18.(本题6分)阅读与计算:请阅读以下材料,并完成相应的任务.)是意大利数学家,他研究了一列数,这列数非任务:请根据以上材料,通过计算求出斐波那契数列中的第1个数和第2个数. 19.(本题6分)如图,在平面直角坐标系xOy 中,一次函数y =3x +2的图象与y 轴交于点A ,与反比例函数y =kx (k ≠0)在第一象限内的图象交于点B ,且点B 的横坐标为1.过点A 作AC ⊥y 轴交反比例函数y =kx (k ≠0)的图象于点C ,连接BC . (1)求反比例函数的表达式. (2)求△ABC 的面积.20.(本题8分)随着互联网、移动终端的迅速发展,数字化阅读越来越普及,公交、地铁上的“低头族”越来越多.某研究机构针对“您如何看待数字化阅读”问题进行了随机问卷调查(问卷调查表如图1所示)并将调查结果绘制成图2和图3所示的统计图(均不完整).请根据统计图中提供的信息,解答下列问题:(1)本次接受调查的总人数是人.(2)请将条形统计图补充完整.(3)在扇形统计图中,观点E的百分比是,表示观点B的扇形的圆心角度数为°.(4)假如你是该研究机构的一名成员,请根据以上调查结果,就人们如何对待数字化阅读提出你的建议.21.(本题10分)实践与操作如图,△ABC是直角三角形,∠ACB=90°.(1)尺规作图:作⊙C,使它与AB相切于点D,与AC相交于点E,保留作图痕迹,不写作法,请标明字母.̂的长.(2)在你按(1)中要求所作的图中,若BC=3,∠A=30°,求DE22.(本题7分)某蔬菜经营户从蔬菜批发市场批发蔬菜进行零售,部分蔬菜批发价格与零售价格如表:请解答下列问题:(1)第一天,该经营户批发西红柿和西兰花两种蔬菜共300 kg,用去了1520元钱,这两种蔬菜当天全部售完一共能赚多少元钱?(2)第二天,该经营户用1520元钱仍然批发西红柿和西兰花,要想当天全部售完后所赚钱数不少于1050元,则该经营户最多能批发西红柿多少kg?23.(本题12分)综合与实践:制作无盖盒子任务一:如图1,有一块矩形纸板,长是宽的2倍,要将其四角各剪去一个正方形,折成高为4 cm,容积为616 cm3的无盖长方体盒子(纸板厚度忽略不计).(1)请在图1的矩形纸板中画出示意图,用实线表示剪切线,虚线表示折痕.(2)请求出这块矩形纸板的长和宽.任务二:图2是一个高为4 cm的无盖的五棱柱盒子(直棱柱),图3是其底面,在五边形ABCDE中,BC=12 cm,AB=DC=6 cm,∠ABC=∠BCD=120°,∠EAB=∠EDC =90°.(1)试判断图3中AE与DE的数量关系,并加以证明.(2)图2中的五棱柱盒子可按图4所示的示意图,将矩形纸板剪切折合而成,那么这个矩形纸板的长和宽至少各为多少cm?请直接写出结果(图中实线表示剪切线,虚线表示折痕.纸板厚度及剪切接缝处损耗忽略不计).24.(本题13分)综合与探究如图1,在平面直角坐标系xOy中,抛物线W的函数表达式为y=−421x2+1621x+4.抛物线W与x轴交于A,B两点(点A在点B左侧,与y轴交于点C,它的对称轴与x轴交于点D,直线l经过C,D两点.(1)求A,B两点的坐标及直线l的函数表达式.(2)将抛物线W沿x轴向右平移得到抛物线W′,设抛物线W′的对称轴与直线l交于点F,当△ACF为直角三角形时,求点F的坐标,并直接写出此时抛物线W′的函数表达式.(3)如图2,连接AC,CB,将△ACD沿x轴向右平移m个单位(0<m≤5),得到△A′C′D′.设A′C′交直线l于点M,C′D′交CB于点N,连接CC′,MN.求四边形CMNC′的面积(用含m的代数式表示).2015年山西中考数学真题+答案(答案部分)1.D 2.B 3.B 4.C 5.A 6.C 7.A 8.A 9.B 10.D 11.x >4 12.(3n +1) 13.70 14.13 15.404516.2√10【解析】解:如解图作NF ⊥AD ,垂足为F ,连接DD ′.由折叠知DD ′⊥MN . 因为∠A =∠DEM =90°,∠ADD ′=∠EDM ,所以△DAD ′∽△DEM .所以∠DD ′A =∠DME .在△NFM 和△DAD ′中{∠DD ′A =∠NMF ,∠A =∠NFM ,NF =DA ,所以△NFM ≌△DAD ′(AAS ).所以FM =AD ′=2.又因为在Rt △MNF 中,FN =6,所以根据勾股定理得MN =√FN 2+FM 2=√62+22=2√10.17.(1)解:原式=﹣4×94−12÷(−18)(3分)=﹣9+4 (4分)=﹣5. (5分)(2)解:去分母,得2=2x﹣1﹣3,(3分)解得x=3. (4分)经检验x=3是分式方程的解.(5分)18.解:第1个数,当n=1时,1√5[(1+√52)n−(1−√52)n]=√5(1+√52−1−√52)(1分)=√5√5=1.(2分)第2个数,当n=2时,1√5[(1+√52)n−(1−√52)n]=√5[(1+√52)2−(1−√52)2](3分)=√5(1+√52+1−√52)(1+√52−1−√52)(4分)=√5×(1+√52+1−√52)(1+√52−1−√52)=√5×1×√5(5分)=1.(6分)19.解:(1)∵一次函数y=3x+2的图象过点B,且点B的横坐标为1,∴y=3×1+2=5.∴点B 的坐标为(1,5). (1分) ∵点B 在反比例函数y =kx 的图象上,∴k =1×5=5.∴反比例函数的表达式为y =5x . (2分)(2)∵一次函数y =3x +2的图象与y 轴交于点A , ∴当x =0时,y =2. ∴点A 的坐标为(0,2). ∵AC ⊥y 轴,∴点C 的纵坐标是2. (3分) ∵点C 在反比例函数y =5x 的图象上, ∴当y =2时,2=5x,解得x =52.∴AC =52. (4分)过B 作BD ⊥AC 于D ,则BD =y B ﹣y C =5﹣2=3. (5分) ∴S △ABC =12AC •BD =12×52×3=154. (6分)20.解:(1)5000 (2分) (2)条形统计图补充如下:(4分)(3)4% 18 (6分)(4)应充分利用数字化阅读获取信息方便等优势,但不要成为“低头族”而影响人际交往.(答案不唯一,合理即可) (8分) 21.解:(1)如解图,⊙C 即为所求. (2分)(2)∵⊙C 切AB 于D ,∴CD ⊥AB .∴∠ADC =90°. (4分)∵∠A=30°,∴∠DCE =90°﹣∠A =90°﹣30°=60°.∴∠BCD =90°﹣∠ACD =30°. (5分)在Rt △BCD 中,cos ∠BCD =CD BC ,BC=3, ∴CD =3cos 30°=3√32. (8分) ∴DE ̂的长为60⋅π⋅3√32180=√32π. (10分) 22.解:(1)设批发西红柿x kg ,西兰花y kg . (1分)由题意,得{x +y =300,3.6x +8y =1520.解得{x =200,y =100. (3分) 200×(5.4-3.6)+100×(14-8)=960(元).答:这两种蔬菜当天全部售完一共能赚960元. (4分)(2)设批发西红柿a kg .由题意,得(5.4﹣3.6)a +(14﹣8)×1520−3.6a 8≥1050,解得a ≤100.(6分)答:该经营户最多能批发西红柿100 kg . (7分)23.解:任务一:(1)解图1即为所求.(1分)(2)设矩形纸板的宽为x cm ,则长为2x cm .由题意,得4(x ﹣2×4)(2x ﹣2×4)=616,解得:x 1=15,x 2=﹣3(舍去). (4分) ∴2x =2×15=30.答:矩形纸板的长为30 cm ,宽为15 cm . (5分)任务二:(1)AE =DE . (6分)证明:如解图2,延长EA ,ED 分别交直线BC于点M ,N . (7分)∵∠ABC =∠BCD =120°,∴∠ABM =∠DCN =60°.∵∠EAB =∠EDC =90°,∴∠M =∠N =30°.∴EM =EN . (8分)在△MAB 与△NDC 中,{∠M =∠N ,∠ABM =∠DCN ,AB =DC ,∴△MAB ≌△NDC .∴AM =DN . (9分)∴EM ﹣AM =EN ﹣DN .∴AE =DE . (10分)(2)矩形纸板的长至少为(18+4√3)cm ,矩形纸板的宽至少为(4+8√3)cm .(12分)【提示】如解图3,过点B ,C ,E 分别作BP ⊥AD 于P ,CQ ⊥AD 于Q ,GI ⊥KH 于点F , 则KH 即为矩形纸板的长,GI 即为矩形纸板的宽.∴PQ =BC =12.∵∠ABC =∠BCD =120°,∴∠BAP =∠CDQ =60°.∵AB =CD =6,∴AP =DQ =3,BP =CQ =FJ =3√3.∴AF =12AD =12(3+3+12)=9.∴AE =6√3,FE =3√3.∵∠AED =120°,∴∠MEN =60°.∵ME =NE =4,∴GE =2√3.∴GI =GE +EJ +JI =2√3+6√3+4=8√3+4.∵∠KAS =90°﹣∠P AB =30°=∠HDT ,∴AK =DH =2√3.∴KH =KA+AP+PQ+QD+DH =2√3+3+12+3+2√3=18+4√3.∴矩形纸板的长至少为(18+4√3)cm ,矩形纸板的宽至少为(4+8√3)cm .24.解:(1)当y =0时,−421x 2+1621x +4=0,解得x 1=﹣3,x 2=7.∴点A 坐标为(﹣3,0),点B 的坐标为(7,0). (2分)∵−b 2a =−16212×(−421),∴抛物线w 的对称轴为直线x =2.∴点D 坐标为(2,0).当x =0时,y =4,∴点C 的坐标为(0,4). (3分)设直线l 的表达式为y =kx +b ,把C ,D 两点的坐标分别代入,得{b =4,2k +b =0.解得{k =−2,b =4.∴直线l 的解析式为y =﹣2x +4. (4分)(2)如解图,∵抛物线w 向右平移,只有一种情况符合要求,即∠F AC =90°.此时抛物线w ′的对称轴与x 轴的交点为G .∵∠1+∠2=90°,∠2+∠3=90°,∴∠1=∠3.∴tan ∠1=tan ∠3.∴FG AG =AO CO .设点F 的坐标为(n ,﹣2n +4),∴−(−2n+4)n−(−3)=34,解得n =5.∴﹣2n +4=﹣6.∴点F 的坐标为(5,﹣6). (7分)此时抛物线w ′的函数表达式为y =−421x 2+4021x . (8分)(3)由平移,得C ′(m ,4),A ′(﹣3+m ,0),D ′(2+m ,0),CC ′∥x 轴,C ′D ′∥CD .由待定系数法,得直线BC 的表达式为y =−47x +4.由平移,得直线A ′C ′的表达式为y =43x +4−43m .直线C ′D ′的表达式为y =﹣2x +4+2m . (9分)当43x +4−43m=−2x +4时,x =25m ,此时y =−45m +4.∴点M 的坐标为(25m ,−45m +4). 当−2x +2m +4=−47x +4时,x =75m ,此时y =−45m +4.∴点N 的坐标为(75m ,−45m +4). (10分)∴MN ∥x 轴.∵CC ′∥x 轴,∴CC ′∥MN .∵C ′D ′∥CD ,∴四边形CMNC ′是平行四边形. (11分)∴S =m [4−(−45m +4)]=45m 2. (13分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015山西中考数学试题及答案A 、 ⎪ = 1B 、 x 2 + x 2 = 2 x 4C 、 a = - aD 、2015 年山西省中考数学试题及答案数学第1卷选择题(共 30 分)一、选择题(本大题共 10 个小题,每小题 3 分,共 30 分,在每个小题给出的 四个选项中,只有一项符合题目要求,请选出并在答题卡上将该项涂黑) 1.计算-3+(-1)的结果是( ) A 、2 B 、-2 C 、4 D 、B-4 答案:D2.下列运算错误的是( )⎛ 1 ⎫0⎛ b ⎫3b 3 ⎪ =⎝ 2 ⎭⎝ a 2 ⎭ a 6答案:B3.晋商大院的许多窗格图案蕴含着对称之美,现从中选取以下四种窗格图案, 其中是中心对称图案但不是轴对称图形的是( )答案:B4.如图,在△ ABC 中,点 D,E 分别是边 AB,BC的中点,若△ DBE 的周长是 6,则△ ABC 的周长是( )A.8B.10C.12D.14答案:C=0,xb5.我们解一元二次方程3x2-6x=0时,可以运用因式分解法,将此方程化为3x(x-2)=0,从而得到两个一元一次方程:3x=0或x-2=0,从而得到原方程的解为x2=2这种解法体现的数学思想是()A.转化思想 B.函数思想C.数形结合思想D.公理化思想答案:A6.如图,直线a∥b,一块含60°角的直角三角板ABC(∠A=60°)按如图所示放置。
若∠1=55°,则∠2的度数为()A.105°B.110°C.115°D.120°答案:C7.化简a2+2ab+b2b-a2-b2a-b的结果是()A.aB.C.aD.a-b a-b a+bba+b答案:A8.我国古代秦汉时期有一部数学著作,堪称是世杰数学经典名著。
它的出现,标志着我国古代数学体系的正式确立。
它采用按类分章的问题集的形式进行编排。
其中方程的解法和正负数加减运算法则在世界上遥遥领先,这部著作的名称是()A.《九章算术》B.《海岛算经》C.《孙子算经》D.《五经算术》答案:A9.某校举行春季运动会,需要在初一年级选取一名志愿者。
初一(1)班、初一(2)班、初一(3)班各有2名同学报名参加。
现从这6名同学中随机选取一名志愿者,则被选中的这名同学恰好是初一(3)班同学的概率是()A.1B.1C.1D.26323答案:B⎨10.如图在网格中,小正方形的边长均为 1,点A,B,C 都在格点上,则∠ABC 的正切值是( )A.2B. 25 C. 5D.1 552答案:D第 II 卷 非选择题(共 90 分)二、填空题(本大题共 6 个小题,每小题 3 分,共 18 分)11.不等式组 ⎧2 x - 1 > 7 的解集是_______⎩3x > 6答案:x>412.如图是一组有规律的图案,它们是由边长相同的正方形和正三角形镶嵌而成。
第( 1)个图案有 4 个正三角形,第(2)个图案有 7 个三角形,第(3)个图形有 10 个三角形,.....依此规律,第n个图案有______个三角形(用含n的代数式表示)答案:3n+113.如图,四边形ABCD内接于⊙o,AB为⊙o 的直径,点C为弧BD的中点。
若∠A=40°,则∠B=___度答案:70度14.现有两个不透明的盒子,其中一个装有标号为别为1,2的两张卡片,另一个装有标号分别为1,2,3的三张卡片,卡片除标号外其他均相同。
若从两个盒子中随机抽取一张卡片,则两张卡片标号恰好相同的概率是__答案:1315.太原市公共自行车的建设速度、单日租骑量等四项指标稳居全国首位,公共自行车车桩的截面示意图如图所示,AB⊥AD,AD⊥DC,点⎪(1)计算:(-3-1)⨯⎛ -3⎫⎪⎛1⎫3(2)解方程:-2÷-⎪⎪B,C在EF上,EF∥HG,EH⊥HG,AB=80cm,AD=24cm,BC=25cm,EH=4cm,则点A到地面的距离是_______答案:80.8⎛或404⎫cm⎝5⎭16.如图,将正方形纸片ABCD沿MN折叠,使点D落在边AB上,对应点为D’,点C落在C’处。
若AB=6,AD’=2,则折痕MN的长为_______答案:210三、解答题(本大题共8个小题,共72分)17.(本题共2个小题,每小题5分,共10分)2-1⎝2⎭⎝2⎭113=-2x-124x-2答案(1)解:原式=-4⨯9-1÷⎛-1⎫42⎝8⎭=-9-(-4)=-52,1 ⎡⎛ 1 + 5 ⎫n ⎛ 1 - 5 ⎫n ⎤5 ⎢⎝ 2 ⎭⎝ 2 ⎪ ⎥答案(2)解:方程左右两边同时乘以 (2x-1)得 2=2x-1-3化简,得 2x=6,解得 x=3检验:当 x=3 时,2(2x-1)≠ 0所以,x=3 是原方程的解18.(本题 6 分)阅读与计算:阅读以下材料,并完成相应的任务斐波那契(约 1170-1250)是意大利数学家,他研究了一列数,这列数非常奇妙,被称为斐波那契数列(按照一定顺序排列着的一列数称为数列)后来人们在研究它的过程中,发现了许多意向不到的结果,在实际生活中,很多花朵(如梅花,飞燕草,万寿菊等)的瓣数恰是斐波那契数列中的数,斐波那契额数列还有很多有趣的性质,在实际生活中也有广泛的应用斐波那契额数列中的第 n 个数列可以用⎢⎪ - ⎪ ⎥ ⎪⎣ ⎭ ⎦ 表示任务:情根据以上材料,通过计算求出斐波那契额数列中的第1个数和第2个数.解:第1个数:当n=1时1 15151 15 15115 1 5n522n=1 1 5 1 5 5 22=1 55 1第 2 个数:当 n=2 时nn=225225 2 2=1 1 5 1 5 1 5 1 5 5 22 2 2=151 5 119 (本题 6 分)如图,在平面直角坐标系 x0y中,一次函数 y3x 2的图象与 y 轴交于点 A ,与反比例函数y=k(k≠0)在第一象限内的图象交于点xB,且点B的横坐标为1,过点A作AC⊥y轴交反比例函数y=k(k≠0)的图象于点C,连接BC x(1)求反比例函数的表达式。
(2△)求ABC的面积。
解:(1)∵点B在一次函数y=3x+2的图像上,且点B的横坐标为1∴y=3⨯1+2=5∴点B的坐标为(1,5)∵点B在反比例函数y=kx的图像上,∴5=k,∴k=51∴反比例函数的表达式为y=5 x(2)∵一次函数y=3x+2的图像与y轴交于点A ∴当x=0时,y=2,∴点A的坐标为(0,2)∵AC⊥y轴∴点C的纵坐标为2∵点C在反比例函数y=5x的图像上∴当y=2时,2=5,x=5 x2∴AC=52过点B作BD⊥AC于点D,∴BD=yB -yc=5-2=3∴S△ABC=11⨯5152224AC.BD=⨯3=20.(本题8分)随着互联网、移动终端的迅速发展,数字化阅读越来越普及,公交、地铁上的“低头族”越来越多。
某研究机构针对“您如何看待数字化阅读”问题进行了随机问卷调查(问卷调查表如右图所示),并将调查结果绘制成图1和图2所示的统计图(均不完整)。
请根据统计图中提供的信息,解答下列问题:您如何看待数字化阅读问卷调查表您好!这是一份关于您如何看待数字化阅读问卷调查表,请在表格中选择一项您最认同的观点,在其后空格内打√,非常感谢您的合作代码ABCD观点获取信息方便,可以随时随地观看价格便宜易得使得人们成为“低头族”,不利于人际交往内容丰富,比纸质书涉猎更广E其他(1)本次接受调查的总人数是______人。
(2)请将条形统计图补充完整(3)在扇形统计图中,观点E的百分比是____,表示观点B的扇形的圆心角度为____度。
(4)假如你是该研究机构的成员,请根据以上调查结果,就人们如何对待数字化阅读提出你的建议答案:50004%18°21.(本题10分)实践与操作如图,△ABC是直角三角形∠ABC=90°。
(1)尺规作图:作⊙C,使它与AB相切于点D,与AC交于点E。
保留作图痕迹,不写作法,请标明字母。
2 π.(2)在你按(1)中要求所作的图中,若BC=3,∠ A=30°,求 DE 的长。
解:(1)作图,如图所示(2)∵ ⊙C 切 AB 于点 D∴CD ⊥AB∴∠ADC=90°∵∠ACB=90°,∠A=30°∴∠B=∠ACD=60°在 △RTBCD 中,BC=3,∴CD=BC.sinB=3.sin60°= 332∴DE 的弧长=60π 3 3 2 180=3⎨22.(7 分)某蔬菜经营户从蔬菜批发蔬菜进行零售,不分蔬菜批发价于零售价格如下表:蔬菜品种西红柿 青椒 西兰花 豆角 批发价(元/kg ) 3.6 5.4 84.8零售价(元/kg )5.48.414 7.6请解答下列问题(1)第一天,该经营户批发西红柿和西兰花两种蔬菜共 300kg ,用去了 1520 元钱,这两种蔬菜当天全木售完一共能赚多少钱?(2)第二天,该经营户用 1520 元钱仍然批发西红柿和西兰花,要想当天全部售完后所赚的钱不少于 1050 元,则该经营户最多能批发西红柿多少 kg ?解:(1)设批发西红柿 xkg ,西兰花 ykg由题意得 ⎧x + y = 300⎩3.6 x + 8 y = 1520解得: ⎧⎨x = 200⎩ y = 100200 ⨯ (5.4-3.6)+100 ⨯ (14-8)=960(元)答:这两种蔬菜当天全部售完一共能赚 960 元钱(2)设批发西红柿xkg,由题意得:(5.4-3.6)x+(14-8)1520 3.6x10508解得:x100答:该经营户最多批发西红柿100kg23.(本题12分)综合与实践:制作无盖盒子任务一:如图1,有一块矩形纸板,长是宽的2倍,要将其四个角各减去一个正方形,折成高伟4cm,溶剂为616m的无盖长方体盒子(纸板厚度忽略不计)。
(1)请在图1的矩形纸板中画出示意图,用实线表示剪切线,虚线表示折痕。
(2)请求出这块矩形纸板的长和宽。
任务二:图2是一个高为4cm的无盖的五棱柱盒子(直棱柱),图3是其底面,在五边形ABCDE 中,BC=12cm,AB=AD=6cm,∠ABC=∠BCD=120°,∠EAB=∠EDC=90°。
(1)试判断图3中AE与DE的数量关系,并加以证明。
(2)图2中的五棱柱盒子可按图4所示的示意图,将矩形纸板剪切折合而成,那么这个矩形纸板的长和宽至少为多少cm?请直接写出结果(途中实线表示剪切线,虚线表示折痕,纸板厚度及剪切接缝处损耗忽略不计)任务一:(1)按要求画出示意图(如右图)(2)解:设矩形纸板的宽为xcm,则长为2xcm,由题意得:⎨∠ABM = ∠DCN ⎪ A B = DC4(x-2 ⨯ 4)(2x-2 ⨯ 4)=616解得: x = 15 , x = -3 (不合题意,舍去) 1 22x=2 ⨯ 15=30答:矩形纸板的长为 30cm ,宽为 15cm任务二:(1)AE=DE证明如下延长 EA ,ED 分别交直线 BC 于点 M,N∵ ∠ ABC= ∠ BCD=120 °∴∠ABM=∠DCN=60°又∵∠ EAB= ∠ E DC=120 °∴∠ M=∠N=90°-60°=30°∴EM=EN在△MAB 与△NDC 中⎧∠M = ∠N⎪⎩∴△MAB ≌△NDC (AAS )∴AM=ND∴EM-AM=EN-DN∴AE=DE(2)长至少为(18+ 4 3 )cm ,宽至少为(4+ 8 3 )cm24.(本题13分)综合与探究如图1,在平面直角坐标系x0y中,抛物线W的函数表达式为y=-4x2+16x+4,抛物线W与x轴交于A,B两2121点(点B在点A的右侧),与y轴交于点C,它的对称轴与x轴交于点D,直线L经过C,D 两点。
