弹性力学 第七章3PPT课件
合集下载
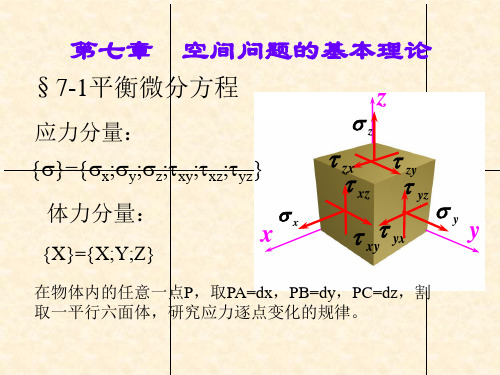
弹性力学-第7章 空间问题
zx
z
dz
zy
zy
z
dz
z 0
y
y
yx yz
xy
x
yz
yz
y
dy
fz
fy fx
xz
yx
y yx dy
y
y y
dy
zx zy
x
x
x x
dx
z
根椐平衡条件: Fx 0
xz
xzx
x
dx
x
x
x
dx dydz
xdydz
(
yx
yx
x
dy)dxdz
yxdxdz
( zx
zx
z
dz)dxdy
zxdxdy
Xdxdydz
0
§7-1平衡微分方程
x x
yx y
zx
z
fx
0
xy
y
x
y
zy
z
f y
0
xz yz
x
y
z z fz 0
(7-1)
平面应力问题:
1、平面应力问题z方向应力为零:
0
xz
yz
0
z
2、所有的应力、应变和位移分量均与z无关,仅是x,y的函数。 以上方程可以直接转化为平面应力的平衡方程。
在计算任一平面上的应力时,方向余弦l,m,n可变化,但 均为有限值,故必存在某个平面,其上正应力取得极值。
主平面:正应力取得极值的平面。 主应力:主平面上的正应力。 主方向:主应力的方向,也称应力主向。 在主平面上,正应力取极值、剪应力为零。
二、主应力的确定:
设主平面存在,其外法线为n,
《弹性力学》第七章 平面问题的差分解

4 f 1 2 2 4 [4 f 0 2( f1 f 2 f 3 f 4 ) ( f 5 f 6 f 7 f8 )] x y h 0 4 f 4 y 1 4 [6 f 0 4( f 2 f 4 ) ( f10 f12 )] h 0
弹性力学的经典解法存在一定的局限性,当弹性体的边 界条件和受载情况复杂一点,往往无法求得偏微分方程的边 值问题的解析解。因此,各种数值解法便具有重要的实际意 义。差分法就是数值解法的一种。 所谓差分法,是把基本方程和边界条件(一般均为微分 方程)近似地改用差分方程(代数方程)来表示,把求解 微分方程的问题改换成为求解代数方程的问题。
T (T0 Te ) x 0
其中 Te 为边界以外的介质的已知温度。应用差分公式,可得:
T1 T3 (T0 Te ) 2h
解出 T1 ,代入(1)式,即得修正的差分方程:
2h 2h 4 T0 T2 2T3 T4 Te
第七章 平面问题的差分解
§7-1 差分公式的推导 §7-2 稳定温度场的差分解 §7-3 不稳定温度场的差分解 §7-4 应力函数的差分解 §7-5 应力函数差分解的实例 §7-6 温度应力问题的应力函数差分解 §7-7 位移的差分解 §7-8 位移差分解的实例 §7-9 多连体问题的位移差分 解 习题课
2 2 2 T h T 2 T0 TA h 2 x A x A 2 1 T 2 2 T T3 TA (1 )h (1 ) h 2 x x A 2 A
§7-2
稳定温度场的差分解
本节以无热源的、平面的、稳定的温度场为例,说明差分 法的应用。 在无热源的平面稳定场中,t 0, z 微分方程简化为调和方程 2T 0 ,即:
人教版八年级物理下册 课件第七章力第二节弹力共46张PPT

哪些类似 橡皮筋(或橡皮泥)?
例如:尺子、橡皮擦、白纸、钢锯条、泥巴、面粉团、皮肤……
想一 想
发现它们的共同特点了吗?试 概括一下。
类似橡皮筋:尺子、橡皮擦、钢锯条、 皮肤
类似橡皮泥:白纸、面粉团、泥巴
1/21/2021
弹性:
类似于弹簧,物体受力时会发生形变,不受力又恢复到原来的形状,这种特性叫弹性.
❖ 7.某同学用一只弹簧秤做研究弹簧的伸长与拉力关系的实验,具体记录数据如下表:
拉力/N 1
2
3
4
5
6
7
8
9
❖
10
11
1
2
弹❖簧长(1)根据6实.0验数据7.0,能做8一.0个测9量.0范围是10多.0大的弹11簧.0秤?理1由2.是0 什么13?.10 14.30 度❖/cm (2)当悬挂某物体时,弹簧长度为8.5 cm,问该物体对弹簧的拉力是多少?
的拉力时,弹簧伸长_____,此时弹簧长度为_______.
分度值
零刻线
量程
2cm
18cm
6cm
❖ 6.一弹簧秤竖直悬挂时,给秤钩施力,示数为8 N,若把弹簧秤拿下来,用两手拉弹簧测力计的秤钩 和吊环时,每只手用力8 N.那么,弹簧测力计的示数是______.(不计弹簧秤重) 8N
想一
想 生 活 中 在 哪 儿 应 用 到 了 弹 力 ?
②绳的弹力----拉力 挂在绳下的物体,在重力的作用下拉紧绳子,使物体和绳子同时发生微小的形变。
物体对绳 子的拉力
绳子对物 体的拉力
可见,拉力也是弹力。
拉力的方向:绳子对物体的拉力总是沿着绳而指 向绳子收缩的方向。
例题1.
关于弹力,下列叙述正确的是( )
弹性力学课件07-杆件的扭转

15
x 0
三、位移分量:
u x x v y y
x 0
不计刚体位移
y 0
z 0
xy 0
zy
zx
1 G x
u yz v zx
为单位长度的相对扭转角
z
w z
v u x y w v y z u w z x
2
弹性解:
x y z t xy 0
Mx t zy Ip
t zx
My Ip
(1 ) t zx
2
2 0 zx
2 2 2 2 2 2 2 x y z
4
2. 应变分量: x y z t xy 0
A
3
用应力表示的相容方程:
2 (1 ) x 0 2 x 2 2 (1 ) y 0 2 y 2 2 (1 ) z 0 2 z 2 2 (1 ) t xy 0 xy 2 (1 ) 2t yz 0 yz
12
2 2 2 2 2 2 2 x y z
边界条件:
侧面:
l dy dx ,m ,n 0 ds ds
o
dx dy ds
x
l x mt yx nt zx 0 lt xy m y nt zy 0 lt xz mt yz n z 0
l x m t yx nt zx Fx lt xy m y nt zy F y lt xz m t yz n z Fz
A A
侧面: 端面:
x y l ,m ,n 0 R R
l 0, m 0, n 1
x 0
三、位移分量:
u x x v y y
x 0
不计刚体位移
y 0
z 0
xy 0
zy
zx
1 G x
u yz v zx
为单位长度的相对扭转角
z
w z
v u x y w v y z u w z x
2
弹性解:
x y z t xy 0
Mx t zy Ip
t zx
My Ip
(1 ) t zx
2
2 0 zx
2 2 2 2 2 2 2 x y z
4
2. 应变分量: x y z t xy 0
A
3
用应力表示的相容方程:
2 (1 ) x 0 2 x 2 2 (1 ) y 0 2 y 2 2 (1 ) z 0 2 z 2 2 (1 ) t xy 0 xy 2 (1 ) 2t yz 0 yz
12
2 2 2 2 2 2 2 x y z
边界条件:
侧面:
l dy dx ,m ,n 0 ds ds
o
dx dy ds
x
l x mt yx nt zx 0 lt xy m y nt zy 0 lt xz mt yz n z 0
l x m t yx nt zx Fx lt xy m y nt zy F y lt xz m t yz n z Fz
A A
侧面: 端面:
x y l ,m ,n 0 R R
l 0, m 0, n 1
弹力 高中物理必修课件PPT 人教版

.
2、点面接触:垂直于面。
3、点点接触:垂直于公切面。
4、轻绳(不计质量):沿绳子收缩的方向。
5、轻杆(不计质量):不一定沿杆的方向, 可由平衡条件分析力的方向。
练习1、关于弹力产生的原因,下列
说法正确的是: D
A、木块放在桌面上受到向上的支持力, 这是木块发生微小弹性形变而产生的。
B、用一根细竹竿拨动水中的木头, 木头受到竹竿的推力,这是由于木头 发生弹性形变而产生的。
有的形变明显、有的形变微小
二、弹力
施力物体
1、定义:发生弹性形变的物体由于要恢复原来的形 状,对与它接触的物体发生力的作用,这种力叫做
弹力
受力物体
2、产生条件
①物体间相互接触 ②物体发生弹性形变
3、弹力的种类
F支
F拉
F推
F压
支持力、压力、拉力等
三、弹力的方向:与恢复形变方向相同
1、两平面接触:垂直于接触面。
第七章 第2节 弹力
恢复到原来形状
没有恢复到原来形状
一、弹性形变、塑性形变
弹性形变:物体受力发生形变,撤掉外力,能自动 恢复到原状 塑性形变:物体受力发生形变,撤掉外力,不能自 动恢复生形变 形变消失
原状 施加外力 停止用力 产生形变 形变保留
弹性形变 弹性限度 塑性形变
C、绳对物体的拉力方向总是竖直向上。 D、挂在电线下面的电灯受到向上的拉力,
是由于电线发生微小弹性形变而产生的 。
弹性力学第七章 主应力

2mn yz 2nl zx 2lm xy
(7-3)
p2
2 n
2 n
px2
p
2 y
pz2
2 n
px2
p
2 y
pz2
2 n
(7-4)
弹性力学简明教程
NORTHEASTERN UNIVERSITY
§7-2 物体内一点的应力状态
如果ABC是边界面,px, py , pz 成为面力分量
fx, fy, fz
弹性力学简明教程
NORTHEASTERN UNIVERSITY
§7-5 轴对称问题的基本方程
弹性力学简明教程
NORTHEASTERN UNIVERSITY
§7-5 轴对称问题的基本方程
轴对称问题: 在空间问题中,如果弹性体的几何形状、约束情况,以及所受的外
力作用,都是对称于某一轴(通过这个轴的任一平面都是对称面),则 所有的应力、变形和位移也就对称于这一轴。轴对称问题的弹性体的形 状一般为是圆柱或半空间。
( x
1)
m1 l1
yx
n1 l1
zx
0
xy
m1 l1
( y
1)
n1 l1
zy
0
可以求得 m1 , n1 的比值,再利用 l 2 m2 n2 1 求出:
l1 l1
l1
1
2
2
1
m1 l1
n1 l1
同样也可以求出其他主应力的方向余弦。
弹性力学简明教程
NORTHEASTERN UNIVERSITY
E
(7-13)
弹性力学简明教程
NORTHEASTERN UNIVERSITY
§7-4 几何方程及物理方程
(7-3)
p2
2 n
2 n
px2
p
2 y
pz2
2 n
px2
p
2 y
pz2
2 n
(7-4)
弹性力学简明教程
NORTHEASTERN UNIVERSITY
§7-2 物体内一点的应力状态
如果ABC是边界面,px, py , pz 成为面力分量
fx, fy, fz
弹性力学简明教程
NORTHEASTERN UNIVERSITY
§7-5 轴对称问题的基本方程
弹性力学简明教程
NORTHEASTERN UNIVERSITY
§7-5 轴对称问题的基本方程
轴对称问题: 在空间问题中,如果弹性体的几何形状、约束情况,以及所受的外
力作用,都是对称于某一轴(通过这个轴的任一平面都是对称面),则 所有的应力、变形和位移也就对称于这一轴。轴对称问题的弹性体的形 状一般为是圆柱或半空间。
( x
1)
m1 l1
yx
n1 l1
zx
0
xy
m1 l1
( y
1)
n1 l1
zy
0
可以求得 m1 , n1 的比值,再利用 l 2 m2 n2 1 求出:
l1 l1
l1
1
2
2
1
m1 l1
n1 l1
同样也可以求出其他主应力的方向余弦。
弹性力学简明教程
NORTHEASTERN UNIVERSITY
E
(7-13)
弹性力学简明教程
NORTHEASTERN UNIVERSITY
§7-4 几何方程及物理方程
弹性力学讲义(徐芝纶版)-PPT

换,
E
1
E
2
,
。 1
边界条件
边界条件--应用极坐标时,弹性体的 边界面通常均为坐标面,即:
常数,或 常数,
故边界条件形式简单。
平面应力问题在极坐标下的基本方程
1
f
0
1
2
f
0
4 1
u
,
1
u
u
,
u
1
u
u
。
1 E
(
),
1 E
(
),
x ρ x φ x
Φ y
Φ ρ
ρ y
Φ φ
φy .
一阶导数
而
cos,
x
sin , x
sin;
y
y
cos 。
代入,即得一阶导数的变换公式,
Φ cosφ Φ sin Φ (cosφ sinφ )Φ
x
ρ ρ φ
ρ ρ φ
,
(e)
Φ sinφ Φ cos Φ (sinφ cosφ )Φ。
σ x σ ρ cos2 φσφsin2 φ2τ ρφ cosφsinφ,
而
σ
x
2Φ y 2
2Φ ρ2
sin
2
φ(
1 ρ
Φ ρ
1 ρ2
2Φ ρ2
)cos2
φ
2[ ( 1 Φ )]cosφsinφ, ρ ρ
比较两式的 cos2 φ,sin2 φ,cosφsinφ 的系数,便 得出 σ ρ,σφ,τ ρφ 的公式。
2(1 E
)
。
4 2
物理方程
物理方程
对于平面应变问题,只须将物理方程作如下 的变换即可。
弹性力学及有限元法chapter7精品PPT课件

e
i
j
m
v
j
w j
u
m
i
m
p
vm
wm
j y
u
p
x
vp
w p
第七章 空间问题和空间轴对称问题
7-2-1 位移函数
单元内任一点的位移 {f}假定为座标的线性函数
u
f
v
N
e
w
u 1 2x3y 4z v 5 6x7 y 8z w9 10x 11y 12z
节点i, j, m及 p的坐标分别为(xi,yi,zi),(xj,yj,zj),(xm,ym,zm) 及 (xp,yp,zp),把它们代入上式的第一式,得出各节点在x方 向的位移
第七章 空间问题和空间轴对称问题
ui 1 2 xi 3 yi 4 zi u j 1 2x j 3 y j 4z j um 1 2 xm 3 ym 4 zm up 1 2xp 3 yp 4zp
解方程组,求得 1,2,3,4,代入第一式,整理后得到
u N iu i N ju j N m u m N p u p
其中
Ni 61 Vaibixciydiz
N j 6 1 Vajbjxcjydjz
Nm61 Vambmxcmydmz
Np61 Vapbpxcpydpz
称为形函数,其系数是
第七章 空间问题和空间轴对称问题
xj yj zj ai xm ym zm
xp yp zp
1 xj zj ci 1 xm zm
同样,可以得到
vNivi Njvj NmvmNpvp wNiwi Njwj NmwmNpwp
单元内任一点的位移可以写成如下形式:
f N 0 i N 0 i 0 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解:首先检验 Φ,已满足 4Φ0。由 Φ
求应力,代入应力公式得
r 2 B s2 ijn 2 C j ,
j 2 B s2 ijn 2 C j,
rj 2B co 2 j sC 。
再考察边界条件。有:
( j)j20, 得C0;
(rj )j2q, 得Bq2。
代入公式,得应力解答,
rqsi2nj, jqsi2n j,
由于圆柱坐标,是和直角坐标一样的正交坐标,所以可直 接根据虎克定律得物理方程:
r
1 E
r
j
z
j
1 E
j
z r
z
1 E
z
r j
zrG 1zr21E zr
应力分量 用形变分量 表示的物理 方程:
r
E 1
1
2
r
j
E 1
1
2
j
z
E 1
1
2
z
zr 21Ezr
z
o j
x
zr
zr
z
dz
z
z
z
j
r
fz
rz
fr
j zr
dz
rz
rz r
dr
r
r r
dr
Fz 0
rz
rz r
r
dr
djdz
rz rdjdz
z
z
z
dz rdjdr
z rdjdr
fz rdjdrdz 0
z
j
dj
r
r dj/2 dr
y
r
r r
dr
z
z
rz r
rz r
fz
0
rr zzrrrjfr0
3j
再求出边界上的面力:
r a q rc3 o j , j s a q rc3 o j ,r s ja q rs3 ijn
j300:j 0,r jqar; ra:r qco3js,r jqs i3nj.
面力分布如图
习题4-9
半平面体表面受有均布水平力q,试用应力 函数 Φρ2(Bsi2nφCφ)求解应力分量。
rjqco2j s。
习题4-18
设半平面体在直 边界上受有集中 力偶,单位宽度 上的力矩为M,试 求应力分量。
解:应用半逆解法求解。
(1)按量纲分析方法,单位宽度 上的力偶矩与力的量纲相同。应力应
与 M,r,j有关,由于应力的量纲是单
位面积上的力,即 L1ML2,应力只能
以 M r2 形式组合。
z h h 1 ,z r z j 0
习题4—8 试考察下列应力函数能解决如图所示弹性体的何 种受力问题?
q r3cos3j
6a
解:本题应用逆解法求解:
首先校核相容方程是满足的;
然后.代入教科书中应力公式(4—5),
求出应力分量
r
q r cos a
3j
j
q a
r
cos
3j
rj
q r sin a
(2)Φ应比应力的长度量纲高二次幂,
可假设 ΦΦ。(φ)
rz r
dr
取图示微元体。
根据连续性假设,微 元体的正面相对负面
rz
Байду номын сангаас
fr
j zr
r
r r
dr
其应力分量都有微小 增量。注意:此时环 向正应力的增量为零。
z
j
dj
由径向和轴向平衡, y 并利用:
r
r dj/2 dr
r
r r
dr
sin d j d j , 22
j
cos dj 1 2
z
o j
例5:一圆柱形厚壁容器内盛液体,
设液体容重为,试用柱坐标写出
应力边界条件。
解:1. 在内壁 ra
1 hh 1zh
rrjrz 0
2 0zh h 1
r h h 1 z ,r jr z 0
2. 在外壁 r b
rrjrz 0
3. 上部圆环端面 zh,arb z zrzj0
4. 下部水底面 z0,0ra
j
空间轴对称问题的平衡微分方程。
二、几何方程
通过与平面问题及极坐标中同样的分析,由径向位移引 起的形变分量为:
r
ur
r
,
j
ur
r
,
zr
ur z
由轴向位移引起的形变分量为:
z
w z
,
zr
w r
由叠加原理,即得空间轴对称问题的几何方程:
r
u r r
j
ur r
z
w z
zr
ur z
w
r
三、物理方程
其中: rjz
轴对称问题基本方程
平衡微 分方程 物理方程
几何方程
z
z
rz r
rz r
fz
0
rr zzrrrjfr0
r
1 E
r
j
z
j
1 E
j
z r
z
1 E
z
r
j
zrG 1zr21E zr
r
u r r
j
ur r
z
w z
zr
ur z
w
r
未知函数 10个,结 合边界条 件求解。
zj 0
zr
j jr
rz
rj r
rj 0
r j z rz 存在
jz
体力和位移:
o
dj
x
jr
j
jr
j
y
rj r fr
fj 0 uj 0
f z u z ur 存在
同时,存在的量应
该环向坐标无关。
z
o j
x
一、平衡微分方程
zr
zr
z
r
dz
z
fz
z
z
j
dz rz
12)。加上边界条件可解空间问题。
x
x
yyxzzxfx
0
xyy
x y
zzyfy
0 (7-1)
xz
x
yz
y
z
z
fz
0
εx
u x
,
γ xy
v x
u y
εy
v y
,
γ yz
w y
v z
(7-8)
εz
w z
,
γ zx
u z
w x
x
1 E
[
x
(
y
z )]
y
1 E
[
y
(
z
x )]
z
1 E
[
z
x
zr
zr
z
dz
z
z
z
j
r
fz
rz
fr
dz
rz
rz r
dr
r
r r
dr
Fr 0
r
r r
2 j drdz
r
dj
2
dr djdz r rdjdz
zr
zr
z
dz rdjdr
j zr
zr rdjdr fr rdjdrdz 0
z
j
dj
r
r dj/2 dr
j
y
r
r r
dr
rr zzrrrjfr0
空间问题的求解:
1. 基本未知函数15个:
(6个):
x, y, z, y zz,yz xz,xx yyx
位移分量(3个): u,v,w
(6个):
x , y ,z , y zz,yz xz,xx yyx
2. 基本方程15个:
平衡微分方程3个(7-1);几何方程6个(7-8);物理方程6个(7-
(
x
y )]
yz
2 (1 E
) yz
zx
2 (1 E
) zx
xy
2 (1 E
) xy
(7-12)
§7-5 空间轴对称问题
在空间问题中,若弹性体的几何形状、约束情况 以及所受的外力,都对称于某一轴(通过这个轴的任 一平面都是对称面),则所有的应力、形变和位移也 对称于这一轴。这种问题称为空间轴对称问题。
根据轴对称的特点,应采用圆柱坐标(r,j,z)表
示。若取对称轴为 z 轴,则轴对称问题的应力分量、
形变分量和位移分量都将只是r和z的函数,而与 j 坐
标无关。 轴对称问题的弹性体的形状一般为绕此轴的旋转
体,如圆柱体(包括圆筒),或(半)空间体。
任意对称面上单元体的 应力
z
对称面 z zj
应力:
