单元滚动检测卷(七)
青岛版四年级数学上册第六、七单元跟踪检测卷

第六、七单元跟踪检测卷一、用心思考,正确填写。
(每空1分,共22分)1.小玲从家到学校每分钟走70米,需要12分钟,小玲家到学校的距离是( )米,利用公式( )×( )=( )来计算。
2.一辆汽车5小时行驶420千米,平均每小时行驶多少千米?这是已知( )和( )求( ),结果是( )。
3.一瓶饮料的价格是8元,买10瓶这样的饮料需要( )元,120元能买这种饮料( )瓶。
4.计算9×240-40÷5时,( )和( )可以同时计算,计算结果是( )。
如果把运算顺序改为先求差,再求积,最后求商,则式子变为( )。
5.80÷(8+12)×2的计算结果是( ),如果去掉小括号,计算结果是( )。
6.在里填上“>”“<”或“=”。
23+17×8(23+17)×8 256-(56-34)256-56-34 42×7÷642÷6×7 180÷15×3180÷(15×3) 7.小刚2分钟能做18道口算题,照这样的速度,5分钟能做( )道,做完90道需要( )分钟。
二、仔细推敲,判断对错。
(对的打“√”,错的打“×”。
每题1分,共4分)1.58+37-58+37=0 ( )2.小明平均每分钟折12架纸飞机,可以写作12架/分。
( ) 3.在混合运算中,必须按照先算乘除法后算加减法的顺序计算。
( ) 4.花同样的钱买两种货物,A种货物买的数量多,B种货物买的数量少,说明A种货物的单价便宜些。
( ) 三、反复比较,择优录取。
(选择正确答案的序号填入括号,每空1分,共7分)1.在计算350÷[7×(45-40)]时,第一步求的是( )。
A.积B.商C.差2.汽车每小时行驶75千米,4小时行驶300千米,下列算式各表示什么意义?(1)4×75=300(千米)表示求( )。
单元滚动检测卷(五)

单元滚动检测卷(五)[测试范围:第八单元时间:120分钟分值:150分]第Ⅰ卷(选择题共40分)一、选择题(本大题有10小题,每小题4分,共40分.请选出各小题中唯一的正确选项,不选、多选、错选,均不得分)1.若一个多边形的每一个外角都等于40°,则这个多边形的边数是(C) A.7B.8C.9 D.10【解析】∵360°÷40°=9,∴这个多边形的边数是9.2.如图5-1,▱ABCD中,AE平分∠DAB,∠B=100°,则∠AED=(D)图5-1A.100°B.80°C.60°D.40°【解析】在▱ABCD中,∵AD∥BC,∴∠DAB=180°-∠B=180°-100°=80°.∵AE平分∠DAB,∴∠DAE=∠EAB=12∠DAB=40°.又∵AB∥DC,∴∠AED=∠EAB=40°.3.如图5-2,下列四组条件中,不能判定四边形ABCD是平行四边形的是(C)图5-2A.AB=DC,AD=BCB.AB∥DC,AD∥BCC.AB∥DC,AD=BCD.AB∥DC,AB=DC【解析】根据平行四边形的判定定理,A、B、D均符合判定平行四边形的条件,C则不能判定是平行四边形.4.如图5-3,在矩形ABCD中,对角线AC,BD交于点O.已知∠AOB=60°,AC=16,则图中长度为8的线段有(D)图5-3A.2条B.4条C.5条D.6条【解析】∵在矩形ABCD中,AC=16,∴AO=BO=CO=DO=12×16=8.∵AO=BO,∠AOB=60°,∴△AOB是等边三角形,∴AB=AO=8,∴CD=AB=8,∴共有6条线段长度为8.5.下列命题是假命题的是(C) A.平行四边形的对边相等B.四条边都相等的四边形是菱形C.矩形的两条对角线互相垂直D.等腰梯形的两条对角线相等6.已知菱形的边长和一条对角线的长均为2 cm,则菱形的面积为(D) A.3 cm2B.4 cm2C. 3 cm2D.2 3 cm2【解析】菱形的边长和一条对角线的长相等,则这条对角线把菱形分成两个全等的等边三角形,所以S菱形=12×32×2×2×2=23(cm2).选D.7.如图5-4,菱形ABCD的两条对角线相交于O,若AC=6,BD=4,则菱形ABCD的周长是(C)图5-4A.24 B.16C.413 D.2 38.顺次连结矩形四边中点所得的四边形一定是(C) A.正方形B.矩形C.菱形D.等腰梯形【解析】如图,连结AC,BD,在△ABD中,∵AH=HD,AE=EB,∴EH=12BD,同理FG=12BD,HG=12AC,EF=12AC.第8题答图又∵在矩形ABCD中,AC=BD,∴EH=HG=GF=FE,∴四边形EFGH为菱形.9.如图5-5所示,矩形纸片ABCD 中,AB =6 cm ,BC =8 cm ,现将其沿EF 对折,使得点C 与点A 重合,则AF 的长为( B )图5-5A.258 cm B.254cm C.252 cmD .8 cm【解析】 设AF =x cm ,则DF =(8-x )cm ,∵矩形纸片ABCD 中,AB =6 cm ,BC =8 cm ,现将其沿EF 对折,使得点C 与点A 重合, ∴DF =D ′F . 在Rt △AD ′F 中, ∵AF 2=AD ′2+D ′F 2,∴x 2=62+(8-x )2,解得x =254(cm).10.如图5-6,正方形ABCD 的边长为4,点E 在对角线BD 上,且∠BAE =22.5°,EF ⊥AB ,垂足为F ,则EF 的长为( C )图5-6A .1B. 2 C .4-2 2D .32-4【解析】 在正方形ABCD 中, ∠ABD =∠ADB =45°. ∵∠BAE =22.5°,∴∠DAE=90°-∠BAE=90°-22.5°=67.5°.在△ADE中,∠AED=180°-45°-67.5°=67.5°,∴∠DAE=∠AED,∴AD=DE=4.∵正方形的边长为4,∴BD=42,∴BE=BD-DE=42-4.∵EF⊥AB,∠ABD=45°,∴△BEF是等腰直角三角形,∴EF=22BE=22×(42-4)=4-2 2.故选C.第Ⅱ卷(非选择题共110分)二、填空题(本大题有6小题,每小题5分,共30分)11.如图5-7,梯形ABCD中,AD∥BC,AD=4,AB=5,BC=10,CD的垂直平分线交BC于E,连结DE,则四边形ABED的周长等于__19__.图5-7【解析】∵CD的垂直平分线交BC于E,∴DE=CE,∴四边形ABED的周长=AD+AB+BE+DE=AD+AB+BE+CE=AD+AB +BC.∵AD=4,AB=5,BC=10,∴四边形ABED的周长=4+5+10=19.12.菱形ABCD中,若对角线长AC=8 cm,BD=6 cm,则边长AB=__5__cm.【解析】设菱形ABCD的对角线AC与BD相交于点O,∵菱形ABCD中,对角线长AC=8 cm,BD=6 cm,∴AO=12AC=4 cm,BO=12BD=3 cm.∵菱形的对角线互相垂直,∴在Rt△AOB中,AB=AO2+BO2=42+32=5(cm).13.如图5-8,在四边形ABCD中,已知AB=CD,再添加一个条件__答案不唯一,如AB∥CD或AD=BC或∠A+∠D=180°或∠B+∠C=180°__(写出一个即可),使四边形ABCD是平行四边形(图形中不再添加辅助线).图5-8【解析】添加的条件可以是另一组对边AD与BC相等,也可以是AB与CD 这一组对边平行.14.在四边形ABCD中,AB=DC,AD=BC,请再添加一个条件,使四边形ABCD 是矩形.你添加的条件是__∠A=90°或∠B=90°或∠C=90°或∠D=90°或AC=BD(答案不唯一,写出一种即可)__(写出一种即可).【解析】填其中任一内角为90°或对角线相等即可.15.如图5-9,P是菱形ABCD对角线BD上一点,PE⊥AB于点E,PE=4 cm,则点P到BC的距离是__4__ cm.图5-9【解析】∵BD平分∠ABC,又∵PE⊥AB,PE=4 cm,∴点P到BC的距离为4 cm.16.如图5-10,在梯形ABCD中,DC∥AB,∠A+∠B=90°.若AB=10,AD =4,DC=5,则梯形ABCD的面积为__18__.图5-10【解析】 作CE ∥AD 交AB 于E ,CF ⊥AB 于F ,则易证CE ⊥CB ,BC =52-42=3, ∴CF =CE ·BC BE =125,∴S 梯形ABCD =5+102×125=18.三、解答题(本大题有8小题,第17~20题每题8分,第21题10分,第22、23题每题12分,第24题14分,共80分)17.在四边形ABCD 中,∠D =60°,∠B 比∠A 大20°,∠C 是∠A 的2倍,求∠A ,∠B ,∠C 的大小.解:设∠A =x ,则∠B =x +20°,∠C =2x .由四边形内角和定理得x +(x +20°)+2x +60°=360°,解得x =70°, ∴∠A =70°,∠B =90°,∠C =140°.18.如图5-11,四边形ABCD 是平行四边形,E ,F 分别是BC ,AD 上的点,∠1=∠2.求证:△ABE ≌△CDF .图5-11证明:∵四边形ABCD 是平行四边形, ∴∠B =∠D ,AB =CD ,∴在△ABE 与△CDF 中,⎩⎨⎧∠1=∠2,AB =CD ,∠B =∠D ,∴△ABE ≌△CDF (ASA ).19.如图5-12,四边形ABCD是菱形,对角线AC与BD相交于点O,∠ACD =30°,BD=6.(1)求证:△ABD是正三角形;(2)求AC的长(结果可保留根号).图5-12解:(1)证明:∵AC是菱形ABCD的对角线,∴AC平分∠BCD.∵∠ACD=30°,∴∠BCD=60°.∵∠BAD与∠BCD是菱形的一组对角,∴∠BAD=∠BCD=60°.∵AB,AD是菱形的两条边,∴AB=AD.∴△ABD是正三角形.(2)∵O为菱形对角线的交点,∴AC=2OC,OD=12BD=3,∠COD=90°.在Rt△COD中,ODOC=tan∠OCD=tan30°,∴OC=ODtan30°=333=3 3.∴AC=2OC=6 3.答:AC的长为6 3.20.如图5-13,四边形ABCD是矩形,E是AB上一点,且DE=AB,过C作CF⊥DE,垂足为F.(1)猜想AD与CF的大小关系;(2)请证明上面的结论.图5-13解:(1)AD=CF.(2)证明:∵四边形ABCD是矩形,∴CD∥AE,AB=CD.∴∠AED=∠FDC.∵DE=AB,∴DE=AB=CD.又∵CF⊥DE,∴∠CFD=∠A=90°.∴△ADE≌△FCD(AAS).∴AD=CF.21.已知:如图5-14,在▱ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连结EF,分别交AB,CD于点M,N,连结DM,BN.(1)求证:△AEM≌△CFN;(2)求证:四边形BMDN是平行四边形.图5-14证明:(1)∵四边形ABCD是平行四边形,∴∠DAB=∠BCD,∴∠EAM=∠FCN.又∵AD∥BC,∴∠E=∠F.∵AE=CF,∴△AEM≌△CFN.(2)由(1)得AM=CN,又∵四边形ABCD是平行四边形,∴AB綊CD,∴BM綊DN,∴四边形BMDN是平行四边形.22.如图5-15,△ABC中,∠B=90°,AB=6 cm,BC=8 cm.将△ABC沿射线BC方向平移10 cm,得到△DEF,A,B,C的对应点分别是D,E,F,连结AD,求证:四边形ACFD是菱形.图5-15证法一:∵∠B=90°,AB=6 cm,BC=8 cm,∴AC=AB2+BC2=10 cm.由平移变换的性质得CF=AD=10 cm,DF=AC=10 cm,∴AD=CF=AC=DF,∴四边形ACFD是菱形.证法二:由平移变换的性质得AD∥CF,AD=CF=10 cm,∴四边形ACFD是平行四边形.∵∠B=90°,AB=6 cm,BC=8 cm,∴AC=AB2+BC210 cm,∴AC=CF,∴平行四边形ACFD是菱形.23.已知:如图5-16,四边形ABCD的对角线AC,BD交于点O,BE⊥AC于点E,DF⊥AC于点F,点O既是AC的中点,又是EF的中点.(1)求证:△BOE≌△DOF;(2)若OA=12BD,则四边形ABCD是什么特殊四边形?请说明理由.图5-16解:(1)证明:∵BE⊥AC,DF⊥AC,∴∠BEO=∠DFO=90°.∵点O是EF的中点,∴OE=OF.又∵∠DOF=∠BOE,∴△BOE≌△DOF(ASA).(2)四边形ABCD是矩形.理由如下:∵△BOE≌△DOF,∴OB=OD.又∵OA=OC,∴四边形ABCD是平行四边形.∵OA=12BD,OA=12AC,∴BD=AC,∴▱ABCD是矩形.24.已知△ABC为等边三角形,点D为直线BC上一动点(点D不与B,C重合),以AD为边作菱形ADEF(A,D,E,F按逆时针排列),使∠DAF=60°,连结CF.(1)如图5-17(1),当点D在边BC上时,求证:①BD=CF;②AC=CF+CD;(2)如图5-17(2),当点D在边BC的延长线上且其他条件不变时,结论AC=CF+CD是否成立?若不成立,请写出AC,CF,CD之间存在的数量关系,并说明理由;(3)如图5-17(3),当点D在边CB的延长线上且其他条件不变时,补全图形,并直接写出AC,CF,CD之间存在的数量关系.(1)(2)(3)图5-17解:(1)①∵△ABC是等边三角形,∴AB=AC,∠BAC=60°.∵四边形ADEF为菱形,∴AD=AF.∵∠BAC=∠DAF=60°,∴∠BAC-∠DAC=∠DAF-∠DAC,即∠BAD=∠CAF,∴△ABD≌△ACF,∴BD=CF.②∵AC=BC=BD+CD,且由①知BD=CF,∴AC=CF+CD.(2)不成立.存在的数量关系为:CF=AC+CD.理由:由(1)同理可得△ABD≌△ACF,∴BD=CF.∵BD=BC+CD=AC+CD,∴CF=AC+CD.(3)CD=AC+CF.补全图形如图所示.第24题答图。
单元滚动检测卷(三)

单元滚动检测卷(三)[测试范围:第五单元时间:120分钟分值:150分]第Ⅰ卷(选择题共40分)一、选择题(本大题有10小题,每小题4分,共40分.请选出各小题中唯一的正确选项,不选、多选、错选,均不得分)1.如图3-1,在平面直角坐标系中,将点A(-2,3)向右平移3个单位长度后,那么平移后对应的点A′的坐标是(C)图3-1A.(-2,-3)B.(-2,6)C.(1,3) D.(-2,1)2.当x>0时,函数y=-5x的图象在(A)A.第四象限B.第三象限C.第二象限D.第一象限3.在平面直角坐标系中,下列函数的图象经过原点的是(C)A.y=-x+3 B.y=5 xC.y=2x D.y=-2x2+x-74.二次函数y=ax2+bx+c(a≠0)的图象如图3-2所示,则函数值y<0时x的取值范围是(C)图3-2A.x<-1B.x>3C.-1<x<3D.x<-1或x>3【解析】由图象可知,当-1<x<3时,函数图象在x轴的下方,此时y<0.5.如图3-3,正比例函数y1与反比例函数y2相交于点E(-1,2),若y1>y2>0,则x的取值范围在数轴上表示正确的是(A)图3-3图3-46.把抛物线y=12x2-1先向右平移1个单位,再向下平移2个单位,得到的抛物线的解析式为(B)A.y=12(x+1)2-3B.y=12(x-1)2-3C.y=12(x+1)2+1D.y=12(x-1)2+17.关于二次函数y=2(x-3)2+1有下列说法:①其图象的开口向下;②其图象的对称轴为直线x=-3;③其图象顶点坐标为(3,-1);④当x<3时,y随x的增大而减小.则其中正确的有(A) A.1个B.2个C.3个D.4个【解析】①∵a=2>0,∴图象的开口向上,故本说法错误;②图象的对称轴为直线x=3,故本说法错误;③图象顶点坐标为(3,1),故本说法错误;④当x<3时,y随x的增大而减小,故本说法正确.综上所述,说法正确的只有1个.故选A.8.某人驾车从A地上高速公路前往B地,中途在服务区休息了一段时间.出发时油箱中存油40升,到B地后发现油箱中还剩油4升,则出发后到B地油箱中所剩油y(升)与时间t(小时)之间函数的大致图象是(C)图3-5【解析】根据某人驾车从A地上高速公路前往B地,中途在服务区休息了一段时间,休息时油量不发生变化,再次出发后油量继续减小,即可得出符合要求的图象.9.如图3-6,二次函数y =ax 2+bx +c 的图象与y 轴正半轴相交,其顶点坐标为⎝ ⎛⎭⎪⎫12,1,下列结论:①ac <0;②a +b =0;③4ac -b 2=4a ;④a +b +c <0.其中正确结论的个数是( C )图3-6A .1B .2C .3D .4【解析】 根据图象可知: ①a <0,c >0,∴ac <0正确; ②∵顶点横坐标等于12,∴-b 2a =12, ∴a +b =0正确;③∵顶点纵坐标为1,∴4ac -b 24a =1, ∴4ac -b 2=4a ,正确;④当x =1时,y =a +b +c >0,错误. 正确的有3个,故选C.10.某公园草坪的防护栏是由100段形状相同的抛物线组成的.为了牢固起见,每段护栏需要间距0.4 m 加设一根不锈钢的支柱,防护栏的最高点距底部0.5 m(如图3-7),则这条防护栏需要不锈钢支柱的总长度至少为 ( C )A .50 mB .100 mC .160 mD .200 m图3-7【解析】 建立如图所示的直角坐标系.设抛物线解析式为y =a (x +1)(x -1), 将点(0,0.5)的坐标代入得a =-0.5, ∴y =-0.5x 2+0.5. 当x =0.2时,y =0.48; 当x =0.6时,y =0.32,第10题答图∴每一段护栏需用支柱的长度为2×(0.48+0.32)=1.6(m),1.6×100=160(m),选C.第Ⅱ卷(非选择题 共110分)二、填空题(本大题有6小题,每小题5分,共30分)11.在平行四边形ABCD 中,已知点A (-1,0),B (2,0),D (0,1),则点C 的坐标为__(3,1)__.【解析】 如图,∵平行四边形ABCD 中,已知点A (-1,0),B (2,0),D (0,1),∴AB =CD =2-(-1)=3,DC ∥AB ,第11题答图∴点C 的横坐标是3,纵坐标和点D 的纵坐标相等,是1, ∴点C 的坐标是(3,1).12.如图3-8,一次函数y 1=ax +b (a ≠0)与反比例函数y 2=kx (k ≠0)的图象交于A (1,4),B (4,1)两点,若y 1>y 2,则x 的取值范围是__1<x <4或x <0__.图3-8【解析】 根据图象,当x <0或1<x <4时,一次函数的图象在反比例函数的图象上方,即y 1>y 2.13.已知一次函数y =kx +b (k ≠0)经过(2,-1),(-3,4)两点,则它的图象不经过第__三__象限.14.如图3-9,已知二次函数y =x 2+bx +c 的图象经过点(-1,0),(1,-2),当y 随x 的增大而增大时,x 的取值范围是__x ≥12__.图3-9【解析】 依题意有⎩⎨⎧0=(-1)2-b +c ,-2=1+b +c ,解得⎩⎨⎧b =-1,c =-2,∴y =x 2-x -2,对称轴为x =12,∴当x ≥12时,y 随x 的增大而增大.15.二次函数y =ax 2+bx +c (a ,b ,c 是常数,a ≠0)图象的对称轴是直线x =1,其图象的一部分如图3-10所示.对于下列说法:①abc <0;②当-1<x <3时,y >0;③3a +c <0;④a -b +c <0,其中正确的是__①③④__(把正确的序号都填上).图3-10【解析】 根据图象可得:a <0,b >0,c >0, 则abc <0,故①正确;当-1<x <3时图象上有的点在x 轴的上方,有的点在x 轴的下方,故②错误; 根据图示知,该抛物线的对称轴是直线x =1,即-b2a =1,则b =-2a ,那么当x =-1时,y =a -b +c =a +2a +c =3a +c <0,故③正确;当x =-1时,对应的二次函数图象上的点一定在x 轴的下方,因而其纵坐标a -b +c <0,故④正确.16.抛物线y =ax 2+bx +c 上部分点的横坐标x ,纵坐标y 的对应值如下表:__①③④__(①抛物线与x 轴的一个交点为(3,0);②抛物线y =ax 2+bx +c 的最大值为6; ③抛物线的对称轴是x =12;④在对称轴左侧,y 随x 的增大而增大. 【解析】 观察可知抛物线对称轴为x =12,设抛物线解析式为y =a ⎝ ⎛⎭⎪⎫x -122+h ,把(-2,0)和(0,6)的坐标代入,得 ⎩⎪⎨⎪⎧0=a ⎝ ⎛⎭⎪⎫-522+h ,6=a ⎝ ⎛⎭⎪⎫-122+h , 解得⎩⎪⎨⎪⎧a =-1,h =254,∴y =-⎝ ⎛⎭⎪⎫x -122+254,∴正确的有①③④.三、解答题(本大题有8小题,第17~20题每题8分,第21题10分,第22、23 题每题12分,第24题14分,共80分)17.常用的确定物体位置的方法有两种.如图3-11,在4×4个边长为1的正方形组成的方格中,标有A,B两点.请你用两种不同方法表述点B相对点A 的位置.图3-11解:方法1:用有序实数对(a,b)表示.比如:以点A为原点,水平向右方向为x轴正方向,竖直向上方向为y轴正方向,建立直角坐标系,则B(3,3).方法2:用方向和距离表示.比如:B点位于A点的东北方向(北偏东45°等均可),距离A点32处.18.在直角坐标系xOy中,直线l过(1,3)和(3,1)两点,且与x轴,y轴分别交于A,B两点.(1)求直线l的函数关系式;(2)求△AOB的面积.图3-12解:(1)设直线l的函数关系式为y=kx+b(k≠0),把坐标(3,1),(1,3)代入,得⎩⎨⎧3k +b =1,k +b =3,解方程组得⎩⎨⎧k =-1,b =4,∴直线l 的函数关系式为y =-x +4; (2)当x =0时,y =4, ∴B (0,4);当y =0时,-x +4=0, 解得x =4, ∴A (4,0),∴S △AOB =12AO ·BO =12×4×4=8.19.已知点P (2,2)在反比例函数y =kx (k ≠0)的图象上. (1)当x =-3时,求y 的值; (2)当1<x <3时,求y 的取值范围.解:(1)∵点P (2,2)在反比例函数y =kx (k ≠0)的图象上, ∴2=k2,即k =4,∴反比例函数的解析式为y =4x , ∴当x =-3时,y =-43.(2)∵当x =1时,y =4;当x =3时,y =43,又反比例函数y =4x 在x >0时y 值随x 值的增大而减小,∴当1<x <3时,y 的取值范围为43<y <4.20.一名男生推铅球,铅球行进高度y (单位:m)与水平距离x (单位:m)之间的关系是y =-112x 2+23x +53,铅球运行路线如图3-13所示. (1)求铅球推出的水平距离;(2)通过计算说明铅球行进高度能否达到4 m?图3-13解:(1)当y =0时,-112x 2+23x +53=0, 解得x 1=10,x 2=-2(不合题意,舍去), 所以铅球推出的水平距离是10米.(2)y =-112x 2+23x +53=-112(x 2-8x +16-16)+53 =-112(x 2-8x +16)+53+43=-112(x -4)2+3, 当x =4时,y 取最大值3,所以铅球行进高度不能达到4 m ,最高只能达到3 m.21.如图3-14,二次函数y =ax 2+bx 的图象经过A (1,-1),B (4,0)两点. (1)求这个二次函数解析式;(2)点M 为坐标平面内一点,若以点O ,A ,B ,M 为顶点的四边形是平行四边形,请直接写出点M 的坐标.图3-14解:(1)∵二次函数y =ax 2+bx 的图象经过A (1,-1),B (4,0)两点, ∴⎩⎨⎧a +b =-1,16a +4b =0,解得⎩⎪⎨⎪⎧a =13,b =-43,∴二次函数的解析式为y =13x 2-43x .(2)根据题意,得M 1(3,1),M 2(-3,-1),M 3(5,-1).22.如图3-15,在平面直角坐标系xOy 中,一次函数y =kx +b (k ≠0)的图象与反比例函数y =m x的图象交于一、三象限内的A ,B 两点,直线AB 与x 轴交于点C ,点B 的坐标为(-6,n ),线段OA =5,E 为x 轴正半轴上一点,且tan ∠AOE =43.(1)求反比例函数的解析式;(2)求△AOB 的面积.图3-15解:(1)如图,过点A 作AD ⊥x 轴于点D ,第22题答图在Rt △AOD 中,tan ∠AOE =AD OD =43,设AD =4x ,OD =3x ,又OA =5,∴在Rt △AOD 中,根据勾股定理可得AD =4,OD =3,∴A (3,4).把A (3,4)的坐标代入反比例函数y =m x 的解析式中,解得m =12,则反比例函数的解析式为y =12x ;(2)把点B 的坐标(-6,n )代入y =12x 中,解得n =-2,则点B 的坐标为(-6,-2).把A (3,4)和B (-6,-2)的坐标分别代入一次函数y =kx +b (k ≠0)的解析式中,得⎩⎨⎧3k +b =4,-6k +b =-2,解得⎩⎪⎨⎪⎧k =23,b =2,则一次函数的解析式为y =23x +2.∵点C 在x 轴上,令y =0,得x =-3,即OC =3,∴S △AOB =S △AOC +S △BOC =12×3×4+12×3×2=9.23.在“母亲节”期间,某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y (个)与销售单价x (元/个)之间的对应关系如图3-16所示.(1)试判断y 与x 之间的函数关系,并求出函数关系式;(2)若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润w (元)与销售单价x (元/个)之间的函数关系式;(3)若许愿瓶的进货成本不超过900元,要想获得最大利润,试确定这种许愿瓶的销售单价,并求出此时的最大利润.图3-16解:(1)y 是x 的一次函数,设y =kx +b ,∵一次函数的图象过点(10,300),(12,240),∴⎩⎨⎧10k +b =300,12k +b =240,解得⎩⎨⎧k =-30,b =600,∴y =-30x +600.当x =14时,y =180;当x =16时,y =120,即点(14,180),(16,120)均在函数y =-30x +600的图象上,∴y 与x 之间的函数关系式为y =-30x +600.(2)w =(x -6)(-30x +600)=-30x 2+780x -3 600,即w 与x 之间的函数关系式为w =-30x 2+780x -3 600.(3)由题意,得6(-30x +600)≤900,解得x ≥15.w =-30x 2+780x -3 600图象的对称轴为x =-7802×(-30)=13, ∵a =-30<0,∴抛物线开口向下,当x ≥15时,w 随x 的增大而减小,∴当x =15时,w 最大=1 350,即以15元/个的价格销售这批许愿瓶可获得最大利润1 350元.24.在平面直角坐标系xOy 中,抛物线y =mx 2-2mx -2(m ≠0)与y 轴交于点A ,其对称轴与x 轴交于点B .(1)求点A ,B 的坐标;(2)设直线l与直线AB关于该抛物线的对称轴对称,求直线l的解析式;(3)若该抛物线在-2<x<-1这一段位于直线l的上方,并且在2<x<3这一段位于直线AB的下方,求该抛物线的解析式.图3-17解:(1)对于y=mx2-2mx-2,当x=0时,y=-2,∴A(0,-2).抛物线的对称轴为x=--2m2m=1,∴B(1,0).(2)易得A点关于对称轴x=1的对称点为A′(2,-2),第24题答图则直线l经过点A′,B.设直线l的解析式为y=kx+b,则⎩⎨⎧2k +b =-2,k +b =0,解得⎩⎨⎧k =-2,b =2, ∴直线l 的解析式为y =-2x +2.(3)∵抛物线的对称轴为x =1,抛物线在2<x <3这一段与抛物线在-1<x <0这一段关于对称轴x =1对称,结合图象可以观察到抛物线在-2<x <-1这一段位于直线l 的上方,在-1<x <0这一段位于直线l 的下方,∴抛物线与直线l 的其中一个交点横坐标为-1,由直线l 的解析式为y =-2x +2,当x =-1时,y =-2×(-1)+2=4,则抛物线过点(-1,4),故当x =-1时,m +2m -2=4,解得m =2,∴抛物线的解析为y =2x 2-4x -2.。
《高考总复习单元滚动卷》简介

学习过程中,不可避免地伴随着遗忘。
“艾宾浩斯遗忘曲线”告诉我们,知识的遗忘是有规律的,遵循“先快后慢”的原则。
在一轮复习过程中,“滚动复习”模式能加深对知识前后、左右的联系,对于夯实基础、防止遗忘,效果是十分明显的。
针对以上思路,我们经过探索,编写了这套深具“滚动复习”特点的备考试卷。
本试卷立足教材基础知识,科学划分单元、合理编排试题,并有侧重地进行滚动复习。
特点如下:一、全面系统,立足一轮复习。
一轮复习,主要是对教材基础知识的梳理,强调复习的全面性、系统性。
本书以单元(章)为单位命制试卷,注重知识点的合理搭配,关注大纲和考试说明的要求,关注学习中的薄弱环节,关注重点、难点以及高考热点。
二、精心命题,拓展前沿视野。
题目来源:百强名校、重点中学2010届高三最新模拟、联考、质检、月考等试题;教育专家、一线名师的原创题和改编题;近年高考卷中典型性强的试题等。
充分保证了试题的前瞻性、新颖性,使学生练有所得,备考事半功倍。
三、滚动测试,减少知识遗忘。
所谓“滚动测试”,就是后面的习题中,兼顾考查前面的知识点。
这种考查不是简单的重复,而是对与本单元知识结合最为紧密、高考中常综合命题的知识的滚动考查。
每一部分结束,还适当安排综合检测卷,进行“小综合”训练。
四、温馨栏目,有助轻松备考。
本书设有“动感地带”栏目,包括学习方法、趣味知识、答疑解惑等内容,关注考生的学习、生活和心理。
这个栏目只是个桥梁,通过在线答疑、书信往来、电话沟通等,编辑老师与考生进行互动,扫除诸多备考路上的障碍。
这套试卷共10科,包括语文、文科数学、理科数学、英语、物理、化学、生物、政治、历史、地理。
单册定价:15.00元。
一轮备考最佳方法——滚动复习,知识积累就像“滚雪球”!。
单元滚动检测卷(六)

单元滚动检测卷(六)[测试范围:第九单元时间:120分钟分值:150分]第Ⅰ卷(选择题共40分)一、选择题(本大题有10小题,每小题4分,共40分.请选出各小题中唯一的正确选项,不选、多选、错选,均不得分)1.下列结论正确的是(B) A.长度相等的两条弧是等弧B.半圆是弧C.相等的圆心角所对的弧相等D.弧是半圆【解析】A、根据圆的某些概念的相关定义,能够完全重合的弧是等弧,故本选项错误,B、弧分为优弧、劣弧、半圆,故本选项正确;C、根据在同圆或等圆内,相等的圆心角所对的弧相等,故本选项错误;D、弧分为优弧、劣弧、半圆,故本选项错误.2.如图6-1,已知⊙O的半径OA=10 cm,弦AB=16 cm,P为弦AB上的一个动点,则OP的最短距离为(B)图6-1A.5 cm B.6 cmC.8 cm D.10 cm【解析】当OP为垂线段,即OP⊥AB时,OP为最短,∴AP=BP=12AB=12×16=8(cm),而OA=10 cm,在Rt△OAP中,OP=OA2-AP2=102-82=6(cm).故选B.3.如图6-2是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB 宽为8 cm,水的最大深度为2 cm,则该输水管的半径为(C)图6-2A.3 cm B.4 cmC.5 cm D.6 cm【解析】如图所示,过点O作OD⊥AB于点D,连结OA.∵OD⊥AB,∴AD=12AB=12×8=4 (cm).设OA=r,则OD=r-2,第3题答图在Rt△AOD中,OA2=OD2+AD2,即r2=(r-2)2+42,解得r=5 cm.故选C.4.如图6-3,AB是⊙O的直径,∠AOC=110°,则∠D=(B)图6-3A.25°B.35°C .55°D .70°5.已知⊙O 1与⊙O 2外切,⊙O 1的半径R =5 cm ,⊙O 2的半径r =1 cm ,则⊙O 1与⊙O 2的圆心距是( D )A .1 cmB .4 cmC .5 cmD .6 cm【解析】 外切两圆的圆心距等于两圆半径的和,所以O 1O 2=R +r =5 cm + 1 cm =6 cm.6.用半径为3 cm ,圆心角是120°的扇形围成一个圆锥的侧面,则这个圆锥的底面半径为( D )A .2π cmB .1.5 cmC .π cmD .1 cm7.如图6-4,半圆O 的直径AB =10,弦AC =6 cm ,AD 平分∠BAC ,则AD 的长为( A )图6-4A .4 5 cmB .3 5 cmC .5 5 cmD .4 cm【解析】 如图,连结OD ,OC ,作DE ⊥AB 于E ,OF ⊥AC 于F .第7题答图∵∠CAD =∠BAD (角平分线的定义), ∴CD ︵=BD ︵,∴∠DOB =∠OAC =2∠BAD . 又∵OA =OD ,∠AFO =∠DEO =90°, ∴△AOF ≌△ODE ,∴OE =AF =12AC =3 cm.在Rt △DOE 中,DE =OD 2-OE 2=4 cm , 在Rt △ADE 中,AD =DE 2+AE 2=4 5 cm.故选A.8.如图6-5,P A ,PB 是⊙O 的切线,AC 是⊙O 的直径,∠P =40°,则∠BAC 的度数是( B )图6-5A .10°B .20°C .30°D .40°【解析】 ∵P A ,PB 是⊙O 的切线,∴P A =PB ,∠OAP =90°,∴∠P AB =∠ABP ,又∠P =40°,∴∠P AB =70°,∴∠BAC =90°-70°=20°. 9.如图6-6,AB 与⊙O 相切于点B ,AO 的延长线交⊙O 于点C ,连结BC ,若∠ABC =120°,OC =3,则BC ︵的长为( B )图6-6A .πB .2πC .3πD .5π【解析】 连结OB ,第9题答图∵AB 与⊙O 相切于点B ,∴∠ABO =90°. ∵∠ABC =120°, ∴∠OBC =30°.∵OB =OC ,∴∠OCB =30°, ∴∠BOC =120°,∴BC ︵的长为120π×3180=2π,故选B.10.如图6-7,MN 是半径为1的⊙O 的直径,点A 在⊙O 上,∠AMN =30°,B 为AN ︵的中点,点P 是直径MN 上一个动点,则P A +PB 的最小值为( B )图6-7A .2 2 B. 2 C .1D .2第Ⅱ卷(非选择题 共110分)二、填空题(本大题有6小题,每小题5分,共30分)11.图6-8中圆心角∠AOB =30°,弦CA ∥OB ,延长CO 与圆交于点D ,则∠BOD =__30°__.图6-812.平面上有⊙O 及一点P ,P 到⊙O 上的点的距离最长为6 cm ,最短为2 cm ,则⊙O 的半径为__4或2__cm.【解析】 当点P 在圆内时,则直径=6+2=8(cm),因而半径是4 cm ;当点P在圆外时,直径=6-2=4(cm),因而半径是2 cm.所以⊙O的半径为4 cm或2 cm.13.当宽为3 cm的刻度尺的一边与圆相切时,另一边与圆的两个交点处的读数如图6-9所示(单位:cm),那么该圆的半径为__256__cm.图6-9【解析】连结OA,过点O作OD⊥AB于点D,∵OD⊥AB,∴AD=12AB=12×(9-1)=4,设OA=r,则OD=r-3,在Rt△OAD中,OA2-OD2=AD2,即r2-(r-3)2=42,解得r=256cm.第13题答图14.如图6-10,“凸轮”的外围由以正三角形的顶点为圆心,以正三角形的边长为半径的三段等弧组成.已知正三角形的边长为1,则“凸轮”的周长等于__π__.图6-10【解析】 ∵△ABC 为正三角形,∴∠A =∠B =∠C =60°,AB =AC =BC =1, ∴AB ︵=BC ︵=AC ︵=60π×1180=π3,根据题意可知凸轮的周长为三个弧长的和, 即凸轮的周长=AB ︵+BC ︵+AC ︵=3×π3=π.15.底面半径为1,高为3的圆锥的侧面积等于__2π__. 【解析】 ∵高线长为3,底面半径是1, ∴由勾股定理知:母线长=(3)2+1=2, ∴圆锥侧面积=π×1×2=2π.16.如图6-11所示,AB 是⊙O 的直径,点D 在⊙O 上,∠AOD =130°,BC ∥OD 交⊙O 于点C ,则∠A =__40°__.图6-11【解析】 ∵∠AOD =130°, ∴∠BOD =50°, 又∵OD ∥BC ,∴∠ABC =∠BOD =50°, 又∵AB 为直径, ∴∠C =90°, ∴∠A =40°.三、解答题(本大题有8小题,第17~20题每题8分,第21题10分,第22、23 题每题12分,第24题14分,共80分)17.中华民族的科学文化历史悠久、灿烂辉煌,我们的祖先几千年前就能在生产实践中运用数学.1 300多年前,我国隋代建筑的赵州石拱桥的桥拱是圆弧形(如图6-12).经测量,桥拱下的水面距拱顶6 m时,水面宽34.64 m,已知桥拱跨度是37.04 m,运用你所学的知识计算出赵州桥的大致拱高.(运算时取37.04≈147,34.64≈203)图6-12解:如图,设圆弧所在圆的圆心为O,第17题答图AB=37.04≈147 m,CD=34.64≈20 3 m,GE=6 m.在Rt△OCE中,OE=OG-6,CE=103,∵OC2=CE2+OE2,∴OC2=(103)2+(OC-6)2,∴OC=28(m),∴OA=28.在Rt△OAF中,AF=77,∴OF=OA2-AF2=282-(77)2=21(m).∴拱高GF=28-21=7(m).18.如图6-13,⊙O的半径为4 cm,点P是⊙O外一点,OP=6 cm,求:图6-13(1)以P为圆心作⊙P与⊙O外切,小圆⊙P的半径是多少?(2)以P为圆心作⊙P与⊙O内切,大圆⊙P的半径是多少?(分别作出图形,并解答)解:(1)若两圆外切,则小圆⊙P的半径为6-4=2 (cm).第18题答图(2)若两圆内切,则大圆⊙P的半径为6+4=10 (cm).19.如图6-14,实线部分是半径为15 m的两条等弧组成的游泳池,若每条弧所在的圆都经过另一个圆的圆心,求游泳池的周长.图6-14解:设两个圆的交点分别为C,D,连结O1C.O1D2,O2C,O2D,则易证四边形O,CO2D是菱形,所以∠CO1D=∠CO2D=120°,所以两条等弧所对的圆心角均为360°-120°=240°.则游泳池的周长为2×nπr180=2×240π×15180=40π(m).20.如图6-15,⊙O经过菱形ABCD的三个顶点A,D,C,且与AB相切于点A.(1)求证:BC为⊙O的切线;(2)求∠B的度数.图6-15解:(1)证明:如图,连结AO,CO.∵AB是⊙O的切线,∴OA⊥AB.∴∠BAO=90°.∵四边形ABCD是菱形,∴AB=BC.∵AO=CO,BO=BO,∴△BAO≌△BCO(SSS).∴∠BCO=∠BAO=90°,即OC⊥BC.∴BC为⊙O的切线.第20题答图(2)如图,连结OD,则∠AOC=2∠ADC.由(1)知∠BAO=∠BCO=90°,且四边形ABCO的内角和为360°,∴∠B+∠AOC=360°-∠BAO-∠BCO=180°,即∠B+2∠ADC=180°.∵四边形ABCD是菱形,∴∠B=∠ADC.∴∠B+2∠B=180°.∴∠B=60°.21.如图6-16,已知AB是⊙O的直径,P为⊙O外一点,且OP∥BC,∠P=∠BAC.(1)求证:P A为⊙O的切线;(2)若OB=5,OP=253,求AC的长.图6-16解:(1)设AC与OP相交于点H,∵AB是⊙O的直径,∴∠ACB=90°.∵OP∥BC,∴∠AHO=∠ACB=90°,∴∠AOH+∠OAH=90°.∵∠P=∠OAH,∴∠AOH+∠P=90°,∴∠OAP=90°,即OA⊥AP,∴P A为⊙O的切线.(2)在Rt△OAP中,OA=OB=5,OP=25 3,∴AP=OP2-OA2=20 3.∵S△OAP =12OA·AP=12OP·AH.∴AH =OA ·AP OP =5×203253=4.∵OH ⊥AC ,∴AC =2AH =8.22.如图6-17,将一块三角板和半圆形量角器按图中方式叠放,三角板一边与量角器的零刻度线所在直线重合,重叠部分的量角器弧(AB ︵)对应的圆心角(∠AOB )为120°,OC 的长为2 cm ,求三角板和量角器重叠部分的面积.图6-17解:∵∠AOB =120°,∴∠BOC =60°.在Rt △OBC 中,OC =2 cm ,∠BOC =60°,∴∠OBC =30°,∴OB =4 cm ,BC =2 3 cm ,则S 扇形OAB =120π×42360=16π3,S △OBC =12OC ·BC =23,故S 重叠=S 扇形OAB +S △OBC =16π3+2 3.23.已知:如图6-18,在梯形ABCD 中,AD ∥BC ,DA =DC ,以点D 为圆心,DA 长为半径的⊙D 与AB 相切于点A ,与BC 交于点F ,过点D 作DE ⊥BC ,垂足为E .(1)求证:四边形ABED 为矩形;(2)若AB =4,AD BC =34,求CF 的长.图6-18解:(1)∵⊙D 与AB 相切于点A ,∴AB ⊥AD .∵AD ∥BC ,DE ⊥BC ,∴DE ⊥AD ,∴∠DAB =∠ADE =∠DEB =90°,∴四边形ABED 为矩形.(2)∵四边形ABED 为矩形,∴DE =AB =4.∵DA =DC ,∴点C 在⊙D 上.∵点D 为圆心,DE ⊥BC ,∴CF =2EC .∵AD BC =34,设AD =3k (k >0),则BC =4k ,∴BE =3k ,EC =BC -BE =4k -3k =k ,DC =AD =3k .在Rt △DEC 中,由勾股定理得DE 2+EC 2=DC 2,∴42+k 2=(3k )2,∴k 2=2.∵k >0,∴k =2,∴CF =2EC =2 2.24.如图6-19,AB 是⊙O 的直径,C 是半圆O 上的一点,AC 平分∠DAB ,AD ⊥CD ,垂足为D ,AD 交⊙O 于E ,连结CE .(1)判断CD 与⊙O 的位置关系,并证明你的结论;(2)若E 是AC ︵的中点,⊙O 的半径为1,求图中阴影部分的面积.图6-19解:(1)CD 与⊙O 相切,理由如下:∵AC 为∠DAB 的平分线,∴∠DAC =∠BAC .∵OA =OC ,∴∠OAC =∠OCA ,∴∠DAC =∠OCA ,∴OC ∥AD .∵AD ⊥CD ,∴OC ⊥CD ,∴CD 与⊙O 相切;(2)连结OE ,∵E 是AC ︵的中点,∴AE ︵=EC ︵,∴S 弧形AE ︵=S 弧形EC ︵,∴S 阴影=S △DEC .∵∠DAC =∠BAC ,∴EC ︵=BC ︵,即AE ︵=EC ︵=BC ︵.∴∠AOE =∠EOC =∠BOC =60°.又∵OE =OC ,∴△EOC 是等边三角形, ∴EC =OC =1,∠ECO =∠EOC =60°, ∴∠ECD =90°-∠ECO =30°.在Rt △EDC 中,∠ECD =30°,EC =1,∴ED =12EC =12,CD =EC 2-ED 2=32, ∴S 阴影=S △DEC =12ED ·CD =12×12×32 =38.。
部编版语文小学四年级上册单元试卷含答案(全册)

部编版语文小学四年级上册单元试卷含答案(全册)统编版四年级语文上册第一单元检测卷一、基础知识(42分)1.认真拼一拼,把字写漂亮。
(10分)zhújiàn。
pàn wàng。
kuān kuòzhuāng jia。
fēng súpútao。
shàshíchéng shúgǔn dòng。
zhāo dài2.分清这些字,分别组词。
(10分)堤()犹()震()剧()坑()提()优()振()据(。
)炕()3.补充词语,并选词填空。
(8分)风()浪()山()地()()天()地水天()()人()人()若()若()1)今天是个航海的好天气,海面上______________。
2)XXX还没有来,海塘大堤上早已______________。
4.按要求写句子。
(7分)1)月光是那样柔和,照亮了高高的点苍山,照亮了村头的大青树,也照亮了,照亮了村间的大道和小路……(仿写排比句)(3分)漫步在公园里,只见灿烂的阳光洒在_____________,洒在_____________,还洒在______________……2)霎时,潮头奔腾西去。
(用加点词造句)(2分)__________________________________________________ _______________(3)自古以来,人们把钱塘江大潮称为世界奇迹。
(改写成“被”字句)______________________________________________________ ___________5.我会查字典。
(4分)鼎”字用部首查字法,先查____部,再查____画,第六笔笔画的名称是:________。
“鼎”字在字典中的解释有:①古代煮工具的器物;②锅;③合理,正在。
在“人声鼎沸”一词当选第______种解释。
人教版数学高一单元测试卷第一、二章_滚动性检测含解析

C.-x3+x2D.x3-x2
答案:B
解析:令x<0,则-x>0,∴f(-x)=x2(1+x),又f(-x)=f(x),∴f(x)=x2(1+x)=x3+x2.
7.已知函数f(x)= 那么f(ln2)的值是()
A.0 B.1
C.ln(ln2) D.2
答案:B
解析:∵ln2<1,∴f(ln2)=eln2-1=2-1=1.
∴log2(a+9)<3=log28,
∴0<a+9<8,∴-9<a<-1.
(2)当a=1时,f(x)=log2(x2+4x+5),
令t=x2+4x+5,则t=(x+2)2+1≥1,
解:∵B⊆A,当B=∅时,得2m-1>m+1,m>2,
当B≠∅时,得 解得-1≤m≤2.
综上所述,m的取值范+5).
(1)若f(1)<3,求a的取值范围;
(2)若a=1,求函数f(x)的值域.
解:(1)∵f(1)=log2(a+9),
答案:C
解析:∵f(x)在R上是偶函数,
∴f(-π)=f(π),f(-4)=f(4),而3<π<4且f(x)在(0,+∞)上是增函数.
∴f(3)<f(π)<f(4),即f(3)<f(-π)<f(-4).
6.已知函数f(x)是定义在R上的偶函数,当x>0时,f(x)=x2(1-x),则当x<0时,f(x)=()
A.(-1,0)∪(0,1)
B.(-∞,-1)∪(1,+∞)
C.(-1,0)∪(1,+∞)
D.(-∞,-1)∪(0,1)
答案:C
解析:由题意可得 或 解得 或 ⇒a>1或-1<a<0.
二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横线上.
单元滚动检测卷(七)
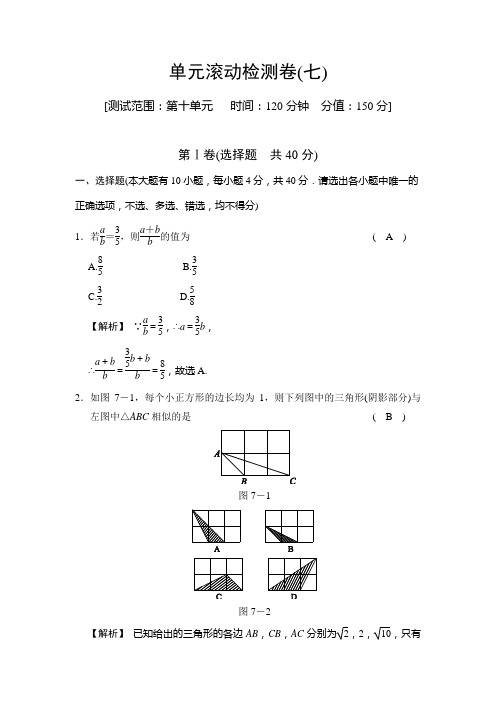
单元滚动检测卷(七)[测试范围:第十单元 时间:120分钟 分值:150分]第Ⅰ卷(选择题 共40分)一、选择题(本大题有10小题,每小题4分,共40分.请选出各小题中唯一的 正确选项,不选、多选、错选,均不得分) 1.若a b =35,则a +b b 的值为( A )A.85B.35C.32D.58【解析】 ∵a b =35,∴a =35b , ∴a +b b =35b +bb =85,故选A.2.如图7-1,每个小正方形的边长均为1,则下列图中的三角形(阴影部分)与左图中△ABC 相似的是( B)图7-1图7-2【解析】 已知给出的三角形的各边AB ,CB ,AC 分别为2,2,10,只有选项B 的各边分别为1,2,5与它的各边对应成比例.故选B.3.如图7-3所示,给出下列条件:①∠B=∠ACD;②∠ADC=∠ACB;③AC CD=ABBC;④AC2=AD·AB.其中单独能够判定△ABC∽△ACD的个数为(C)A.1 B.2C.3 D.4【解析】有3个.①∠B=∠ACD,再加上∠A为公共角,可以根据有两组角对应相等的两个三角形相似来判定.②∠ADC=∠ACB,再加上∠A为公共角,可以根据有两组角对应相等的两个三角形相似来判定.③中两组对应边的比相等,∠A不是对应边的夹角,故不正确.④可以根据两组对应边的比相等且相应的夹角相等的两个三角形相似来判定,故选C.图7-3图7-44.如图7-4是小明设计用手电来测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C 处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是(B) A.6米B.8米C.18米D.24米【解析】∵△ABP∽△CDP,∴ABCD=BPPD,∴CD=1.2×121.8=8(米).故选B.5.手工制作课上,小红利用一些花布的边角料,剪裁后装饰手工画,下面四个图案是她剪裁出的空心不等边三角形、等边三角形、正方形、矩形花边,其中每个图案花边的宽度都相等,那么,每个图案中花边的内外边缘所围成的几何图形不相似的是(D)图7-5【解析】虽然矩形的四个角相等,但每条边长减去同一个常数后,对应边不一定成比例,故选D.6.若△ABC∽△DEF,△ABC与△DEF的相似比为1∶2,则△ABC与△DEF 的周长比为(B) A.1∶4 B.1∶2C.2∶1 D.1∶ 2【解析】相似三角形的周长比等于相似比,故选B.7.如图7-6,在△ABC中,点D,E分别在AB,AC边上,DE∥BC,若AD∶AB =3∶4,AE=6,则AC等于(D)图7-6A.3 B.4C.6 D.8【解析】∵DE∥BC,∴ADAB=AEAC,∴34=6AC,解得AC=8.8.如图7-7,P AB,PCD为⊙O的两条割线,AD,BC相交于点E,则图中相似三角形共有(C)图7-7A .0对B .1对C .2对D .3对【解析】 ∵∠BEA =∠DEC ,∠B =∠D , ∴△ABE ∽△CDE .∵∠B =∠D ,∠P =∠P ,∴△PBC ∽△PDA , ∴共有两对相似三角形.9.如图7-8,直角梯形ABCD 中,AB ∥CD ,∠C =90°,∠BDA =90°,AB =a ,BD =b ,CD =c ,BC =d ,AD =e ,则下列等式成立的是( A )图7-8A .b 2=acB .b 2=ceC .be =acD .bd =ae【解析】 ∵CD ∥AB ,∴∠CDB =∠DBA ,又∵∠C =∠BDA =90°, ∴△CDB ∽△DBA ,∴CD DB =BC AD =BDAB , 即c b =d e =b a , ∴b 2=ac ,故选A.10.如图7-9,在平行四边形ABCD 中,AC 与BD 交于点O ,E 为OD 的中点,连结AE 并延长交DC 于点F ,则DF ∶FC =( D )图7-9A.1∶4 B.1∶3C.2∶3 D.1∶2第Ⅱ卷(非选择题共110分)二、填空题(本大题有6小题,每小题5分,共30分)11.如图7-10,小明在打网球时,使球恰好能打过网,而且落在离网4米的位置上,则球拍击球的高度h为__1.5__m.图7-1012.如图7-11所示,DE是△ABC的中位线,则△ADE与△ABC的面积比为__1∶4__.图7-1113.如图7-12,在▱ABCD中,∠ABC的平分线BE交AD边于点E,交对角线AC于点F,若ABBC=35,则AFAC=__38__.图7-12【解析】∵四边形ABCD是平行四边形,∴AD∥BC,∴∠EBC=∠AEB.∵BE 是∠ABC 的角平分线, ∴∠EBC =∠AEB =∠ABE , ∴AB =AE .∵AB BC =35,∴AE BC =35.∵AD ∥BC ,∴△AFE ∽△CFB ,∴AE BC =AF FC =35,∴AFAC =AF AF +FC =33+5=38.14.如图7-13所示,⊙O 的两弦AB ,CD 交于点P ,连结AC ,BD ,得S △ACP ∶S △DBP =16∶9,则AC ∶BD =__4∶3__.图7-13【解析】 相似三角形对应边的比等于面积比的算术平方根.由同弧所对的圆周角相等,易知∠B =∠C ,∠D =∠A , ∴△ACP ∽△DBP , ∴⎝ ⎛⎭⎪⎫AC BD 2=S △ACP S △DBP =169, ∴AC BD =169=43.15.如图7-14,△ABC 中,点D 在边AB 上,满足∠ACD =∠ABC ,若AC =2,AD =1,则DB =__3__.【解析】 由于∠ACD =∠ABC ,∠BAC =∠CAD ,所以△ADC ∽△ACB ,所以AC AB =AD AC ,即AB ·AD =AC 2,则AB =AC 2AD=4,所以BD =AB -AD =3.图7-14图7-1516.如图7-15,已知△ABC,AB=AC=1,∠A=36°,∠ABC的平分线BD交AC于点D,则AD的长是2,cos A的值是4结果保留根号).【解析】∵△ABC中,AB=AC=1,∠A=36°,∴∠ABC=∠ACB=180°-∠A2=72°.∵BD是∠ABC的平分线,∴∠ABD=∠DBC=12∠ABC=36°,∴∠A=∠ABD=∠DBC=36°,∠BDC=∠C=72°.又∵∠C=∠C,∴△ABC∽△BDC,∴ACBC=BCCD.设AD=x,则BD=BC=AD=x,则1x=x1-x,解得x=-5-12(舍去)或x=5-12,故x=5-1 2.过点D作DE⊥AB于点E,∵AD=BD,∴E为AB的中点,即AE=12AB=12.在Rt△AED中,cos A=AEAD=125-12=5+14.三、解答题(本大题有8小题,第17~20题每题8分,第21题10分,第22、23题每题12分,第24题14分,共80分)17.已知x2=y3=z4,(1)求x-2yz的值;(2)若x+3=z-y,求x的值.解:由x2=y3=z4,设x=2k,y=3k,z=4k,则(1)x-2yz=2k-6k4k=-1.(2)x+3=z-y可化为2k+3=k,∴2k+3=k2,即k2-2k-3=0,∴k=3或k=-1,经检验,k=-1不符合题意,∴k=3,从而x=2k=6,即x=6.18.如图7-16,△ABC∽△DAB,AB=8,BC=12,求AD的长.图7-16解:∵△ABC∽△DAB,∴BCAB=ABAD.∵AB=8,BC=12,∴128=8AD,∴AD=16 3.19.如图7-17,四边形ABCD是平行四边形,点F在BA的延长线上,连结CF交AD于点E.(1)求证:△CDE∽△F AE;(2)当E是AD的中点,且BC=2CD时,求证:∠F=∠BCF.图7-17证明:(1)∵四边形ABCD是平行四边形,∴CD∥AB,即CD∥F A,∴△CDE∽△F AE;(2)∵△CDE∽△F AE,DE=EA,∴△CDE≌△F AE,∴CD=AF,∴BF=2CD.∵BC=2CD,∴BF=BC,∴∠F=∠BCF.20.已知:如图7-18,在△ABC中,∠C=90°,点D,E分别在边AB,AC 上,DE∥BC,DE=3,BC=9.(1)求ADAB的值;(2)若BD=10,求sin A的值.图7-18 解:(1)∵DE∥BC,∴△ADE∽△ABC,∴ADAB=DEBC.又∵DE=3,BC=9,∴ADAB=39=13.(2)根据(1)中ADAB=DEBC得ADAD+BD=DEBC.∵BD=10,DE=3,BC=9,∴ADAD+10=3 9,∴AD=5,∴AB=3AD=15,∴sin A=BCAB=915=35.21.如图7-19,把矩形ABCD对折,折痕为MN,矩形DMNC与矩形ABCD 相似,已知AB=4.(1)求AD的长;(2)求矩形DMNC与矩形ABCD的相似比.图7-19解:(1)由已知得MN=AB,MD=12AD=12BC,∵矩形DMNC与矩形ABCD相似,∴DMAB=MNBC.∵MN=AB,DM=12AD,BC=AD,∴12AD2=AB2,∴由AB=4,得AD=42;(2)矩形DMNC与矩形ABCD的相似比为DMAB=224=22.22.已知如图7-20,在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32.连结BD,AE⊥BD,垂足为E.(1)求证:△ABE∽△DBC;(2)求线段AE的长.图7-20解:(1)证明:∵AB=AD=25,∴∠ABD=∠ADB.∵AD∥BC,∴∠ADB=∠DBC,∴∠ABD=∠DBC.∵AE⊥BD,∴∠AEB=∠C=90°,∴△ABE∽△DBC.(2)∵AB=AD,又AE⊥BD,∴BE=DE,∴BD=2BE.由△ABE∽△DBC,得ABBD=BEBC.∵AB=AD=25,BC=32,∴252BE=BE32,∴BE=20,∴AE=AB2-BE2=252-202=15.23.如图7-21,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,AB =12,BC=5,BE⊥DC交DC的延长线于点E.(1)求证:∠BCA=∠BAD;(2)求DE的长;图7-21 解:(1)∵AB=DB,∴∠BDA=∠BAD.又∵∠BDA和∠BCA是弧AB所对的圆周角,∴∠BDA=∠BCA.∴∠BCA=∠BAD.(2)∵在Rt△ABC中,AB=12,BC=5,∴AC=AB2+BC2=13.又∵∠BAC和∠BDC是弧BC所对的圆周角,∴∠BAC=∠BDC.∵∠ABC=∠DEB=90°,∠BAC=∠BDC,∴△ACB∽△DBE.∴ABDE=ACBD.∴DE=AB·BDAC=12×1213=14413.24.如图7-22,矩形ABCD中,∠ACB=30°,将一块直角三角板的直角顶点P放在两对角线AC,BD的交点处,以点P为旋转中心转动三角板,并保证三角板的两直角边分别与边AB,BC所在的直线相交,交点分别为E,F.图7-22(1)当PE⊥AB,PF⊥BC时,如图(1),则PEPF的值为________;(2)现将三角板绕点P逆时针旋转α(0°<α<60°)角,如图(2),求PEPF的值;(3)在(2)的基础上继续旋转,当60°<α<90°,且使AP∶PC=1∶2时,如图(3),PEPF的值是否有变化?证明你的结论.解:(1)3(2)如图(1),过点P作PH⊥AB,PG⊥BC,垂足分别为H,G,则∠PHE=∠PGB =∠PGF=90°.由(1)得PHPG= 3.第24题答图(1)又∵∠ABC=90°,∴四边形PHBG为矩形,∴∠HPG=90°,∴∠HPE+∠EPG=90°,又∵∠EPF=∠EPG+∠GPF=90°,∴∠HPE=∠GPE=α,又∵∠EHP=∠PGF=90°,∴Rt△PHE∽Rt△PGF,∴PEPF=PHPG,∴PEPF= 3.(3)PEPF的值有变化.证明:如图(2),过点P作PH⊥AB,PG⊥BC,垂足分别为H,G,第24题答图(2)(3)则∠AHP=∠ABC=∠PGC=90°,∴HP∥BC,∴∠APH=∠PCG,∴△APH∽△PCG,∴PHCG=APPC=12.在Rt△PCG中,∠PCG=30°,tan∠PCG=PGCG,∴PGCG=3 3,∴CG=3PG,∴PH3PG=12,∴PHPG=3 2.同(2)中可证得PEPF=PHPG=32.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
单元滚动检测卷(七)第Ⅰ卷选择题(共50分)1.(温州市2019届高三9月选考适应性测试)下列过程会释放出热量的是()A.浓硫酸稀释B.水的分解C.硝酸铵溶于水D.冰的融化答案A解析浓硫酸稀释放热,故A正确;水的分解吸热,故B错误;硝酸铵溶于水吸热,故C 错误;冰的融化吸热,故D错误。
2.氢能是一种理想的“绿色能源”,以下有关氢能开发的方式中最理想的是()A.大量建设水电站,用电力分解水制取氢气B.利用化石燃料燃烧放热,使水高温分解产生氢气C.在催化剂作用下,利用太阳能分解水制取氢气D.利用铁等金属与酸反应产生氢气答案C解析A项,消耗大量的电能,错误;B项,产生大量污染物,且造成能量的浪费,错误;C项,太阳能无污染,且取之不尽用之不竭,正确;D项,消耗大量的金属,错误。
3.(浙江省“七彩阳光”联盟2019届高三上学期期初联考)下列化学反应属于放热反应的是A.浓硫酸溶于水B. 镁溶于盐酸C.石灰石煅烧D.Ba(OH)2·8H2O晶体与NH4Cl晶体混合答案B解析浓硫酸溶于水是物理变化,而非化学变化,故不属于放热反应,选项A错误;镁溶于盐酸发生反应生成氯化镁和氢气且放出大量的热,属于放热反应,选项B正确;石灰石在高温条件下煅烧发生分解反应,属于吸热反应,选项C错误;Ba(OH)2·8H2O晶体与NH4Cl晶体混合属于吸热反应,选项D错误。
4.下列反应中生成物总能量高于反应物总能量的是()A.碳酸钙受热分解B.乙醇燃烧C.铝粉和氧化铁反应D.氧化钙溶于水答案A解析碳酸钙受热分解是吸热反应,生成物的总能量高于反应物总能量,A正确;乙醇燃烧是放热反应,B错误;铝粉和氧化铁反应是放热反应,C错误;氧化钙溶于水放热,D错误。
5.下列关于燃料充分燃烧的说法中,错误的是()A.氧气量充足,燃烧充分B.固体燃料块越大燃烧越充分C.液体燃料燃烧时可以雾状喷出D.温度必须达到着火点答案B解析固体燃料块越大,接触面积小,燃烧越不充分,B错误;液体燃料燃烧时可以雾状喷出增大反应物接触面积,加快反应速率,C正确。
6.(浙江省名校协作体2019届高三上学期考试)下列说法不正确的是()A.煤属于生物质能B.氢气是理想的绿色能源C.地沟油可加工成航空煤油D.沼气属于可再生能源答案A解析煤属于化石能源,故A错误;氢气燃烧后生成水,且氢气是可再生能源,故是理想的燃料,故B正确;沼气可以通过发酵而制得,属于可再生能源,故D正确。
7.(宁波市十校2019届高三9月联考)下列说法不正确的是()A.人类在远古时代就通过燃烧植物的方式开始利用生物质能B.氢能是理想的绿色能源,但人们只能将氢气的化学能转化为热能C.煤中含有硫元素,大量的直接燃烧煤会引起酸雨等环境问题D.太阳能以光和热的形式传送到地面,人们可以直接利用这些光和热答案B解析人类燃烧植物的方式获得热能,是开始利用生物质能的最早方式,故A正确;还可以让氢气构成燃料电池,使化学能转化成电能,故B错误;煤中含有硫元素,燃烧时产生SO2,引起酸雨等环境问题,故C正确;人们可以直接利用光和热,如太阳能热水器,故D正确。
8.(2019·金华市东阳中学高三月考)为消除目前燃料燃烧时产生的环境污染,同时缓解能源危机,有关专家提出了利用太阳能制取氢能的构想。
下列说法正确的是()A.H2O的分解反应是放热反应B.氢能源已被普遍使用C.2 mol H2O具有的总能量低于2 mol H2和1 mol O2的能量D.氢气不易贮存和运输,无开发利用价值答案C解析氢气燃烧生成水是放热反应,则水的分解反应是吸热反应,A项错误;由于氢气的获得目前还没有更好的技术,所以氢能源还没有被普通使用,B项错误;因为水的分解反应是吸热反应,所以2 mol液态H2O具有的总能量低于2 mol H2和1 mol O2的能量,C项正确;氢气属于新能源,具有很好的开发价值,D项错误。
9.(2019·浙江省嘉兴市高三模拟)下列对于太阳能、生物质能和氢能利用的说法不正确的是A.芒硝晶体(Na2SO4·10H2O)白天在阳光下曝晒后失水、分解吸热,夜里重新结晶放热,实现了太阳能转化为化学能继而转化为热能B.将植物的秸秆、枝叶、杂草和人畜粪便加入沼气发酵池中,在富氧条件下,经过缓慢、复杂、充分的氧化反应最终生成沼气,从而有效利用生物质能C.生活、生产中大量应用氢能源,首先要解决由水制备氢气的能耗、氢气的储存和运输等问题D.垃圾焚烧处理厂把大量生活垃圾中的生物质能转化为热能、电能,减轻了垃圾占地给城市造成的压力,改善了城市的环境答案B解析芒硝在白天光照下失水,是太阳能转化为化学能,晚上重新结晶放热,是化学能转化成热能,故A正确;将植物的秸秆、枝叶、杂草和人畜粪便加入沼气发酵池中,应在厌氧条件下进行,故B错误;氢能源开发利用过程中需要解决的问题是探索廉价制氢气的方法和怎样解决氢气的储存、运输问题,故C正确;利用垃圾发电可将生活垃圾中的生物质能转化为热能、电能等,故D正确。
10.沼气是一种新能源,它的主要成分是甲烷。
0.5 mol CH4完全燃烧生成CO2和H2O(l)时,放出445 kJ热量,则下列热化学方程式中正确的是()A.2CH4(g)+4O2(g)===2CO2(g)+4H2O(l)ΔH=890 kJ·mol-1B.CH4(g)+2O2(g)===CO2(g)+2H2O(l)ΔH=890 kJ·mol-1C.CH4(g)+2O2(g)===CO2(g)+2H2O(l)ΔH =-890 kJ·mol -1 D.12CH 4(g)+O 2(g)===12CO 2(g)+H 2O(l) ΔH =-890 kJ·mol -1答案 C解析 0.5 mol CH 4完全燃烧生成CO 2和液态水时放出445 kJ 的热量,则1 mol CH 4完全燃烧生成CO 2和液态水时放出890 kJ 的热量,因此热化学方程式是CH 4(g) + 2O 2(g)===CO 2(g) + 2H 2O(l) ΔH =-890 kJ·mol -1,故选项是C 。
11.(2019·嘉兴市高三检测)下列有关热化学方程式的叙述正确的是( )A .己知2H 2(g)+O 2(g)===2H 2O(g) ΔH =-483.6 kJ·mol -1,则H 2的标准燃烧热为-241.8 kJ·mol -1B .已知C(石墨,s)===C(金刚石,s) ΔH >0,则金刚石比石墨稳定C .含20.0 g NaOH 的稀溶液与稀盐酸完全中和,放出28.7 kJ 的热量,则该反应的热化学方程式为NaOH(aq)+HCl(aq)===NaCl(aq)+H 2O(l) ΔH =-57.4 kJ·mol -1D .已知 2SO 2(g)+O 2(g)2SO 3(g) ΔH =-Q kJ·mol -1(Q >0),则将2 mol SO 2(g)和10 mol O 2(g)置于一密闭容器中充分反应后放出Q kJ 的热量答案 C解析 燃烧热是1 mol 可燃物完全燃烧生成稳定的氧化物所释放的热量,水应为液态,故A 错误;ΔH >0说明此反应是吸热反应,即金刚石的能量大于石墨,物质能量越低,越稳定,即石墨比金刚石稳定,故B 错误;1 mol 氢氧化钠完全反应放出热量为28.70.5kJ =57.4 kJ ,故C 正确;此反应是可逆反应,不能完全进行到底,放出的热量小于Q ,故D 错误。
12.(2019·金华市东阳中学高三月考)已知:2CO(g)+O 2(g)===2CO 2(g) ΔH =-565.2 kJ·mol -1,下列说法不正确的是( )A .CO(g)+12O 2(g)===CO 2(g) ΔH =-282.6 kJ·mol -1 B .2 mol CO(g)与1 mol O 2(g)反应生成2 mol CO 2(s)放出热量小于565.2 kJC .相同条件下,2 mol CO(g)和1 mol O 2(g)的总能量大于2 mol CO 2(g)的总能量D .拆开2 mol CO 和1 mol O 2的化学键所需总能量低于形成2 mol CO 2化学键所放出总能量 答案 B解析 1 mol 一氧化碳燃烧放出的热量为282.6 kJ ,则反应热的化学方程式为CO(g)+12O 2(g)===CO 2(g) ΔH =-282.6 kJ·mol -1,故A 正确;气体变成固体要放出热量,所以2 molCO(g)与1 mol O2(g)反应生成2 mol CO2(s)放出的热量大于565.2 kJ,故B错误;正反应是放热反应,所以反应物的总能量高于生成物的总能量,所以2 mol CO(g)和1 mol O2(g)的总能量大于2 mol CO2(g)的总能量,故C正确;根据化学反应的实质,因为该反应为放热反应,则拆开反应物化学键所吸收的总能量小于形成生成物化学键所放出的总能量,故D正确。
13.(金华市2019届高三9月十校联考)用Cl2生产某些含氯有机物时会产生副产物HCl。
利用反应A,可实现氯的循环利用:4HCl(g)+O2(g)2Cl2(g)+2H2O(g)ΔH=-115.6 kJ·mol-1已知:Ⅰ.反应A中,4 mol HCl被氧化,放出115.6 kJ的热量。
下列说法正确的是()A.升高温度能提高HCl的转化率B.加入催化剂,能使该反应的焓变减小C.1 mol Cl2转化为2 mol Cl原子放出243 kJ热量D.断裂H2O(g)中1 mol H—O键比断裂HCl(g)中1 mol H—Cl键所需能量高答案D解析升高温度,平衡逆向移动,HCl的转化率减小,故A错误;加入催化剂,反应的焓变不变,故B错误;根据提示,1 mol Cl2转化为2 mol Cl原子吸收243 kJ热量,故C错误;E(H—O)、E(H—Cl)分别表示H—O的键能、H—Cl的键能,反应中,4 mol HCl被氧化,放出115.6 kJ的热量,反应热ΔH=反应物的总键能-生成物的总键能,故:4×E(H—Cl)+498 kJ·mol-1-[2×243 kJ·mol-1+4×E(H—O)]=-115.6 kJ·mol-1,整理得,4E(H—Cl)-4E(H—O)=-127.6 kJ·mol-1,即E(H—O)-E(H—Cl)=31.9 kJ·mol-1,故断开1 mol H—O键比断开1 mol H—Cl键所需能量高,故D正确。
